Communication in Neuronal Networks

Abstract

Brains perform with remarkable efficiency, are capable of prodigious computation, and are marvels of communication. We are beginning to understand some of the geometric, biophysical, and energy constraints that have governed the evolution of cortical networks. To operate efficiently within these constraints, nature has optimized the structure and function of cortical networks with design principles similar to those used in electronic networks. The brain also exploits the adaptability of biological systems to reconfigure in response to changing needs.

Neuronal networks have been extensively studied as computational systems, but they also serve as communications networks in transferring large amounts of information between brain areas. Recent work suggests that their structure and function are governed by basic principles of resource allocation and constraint minimization, and that some of these principles are shared with human-made electronic devices and communications networks. The discovery that neuronal networks follow simple design rules resembling those found in other networks is striking because nervous systems have many unique properties.

To generate complicated patterns of behavior, nervous systems have evolved prodigious abilities to process information. Evolution has made use of the rich molecular repertoire, versatility, and adaptability of cells. Neurons can receive and deliver signals at up to 10⁵ synapses and can combine and process synaptic inputs, both linearly and nonlinearly, to implement a rich repertoire of operations that process information (1). Neurons can also establish and change their connections and vary their signaling properties according to a variety of rules. Because many of these changes are driven by spatial and temporal patterns of neural signals, neuronal networks can adapt to circumstances, self-assemble, autocalibrate, and store information by changing their properties according to experience.

The simple design rules improve efficiency by reducing (and in some cases minimizing) the resources required to implement a given task. It should come as no surprise that brains have evolved to operate efficiently. Economy and efficiency are guiding principles in physiology that explain, for example, the way in which the lungs, the circulation, and the mitochondria are matched and co-regulated to supply energy to muscles (2). To identify and explain efficient design, it is necessary to derive and apply the structural and physicochemical relationships that connect resource use to performance. We consider first a number of studies of the geometrical constraints on packing and wiring that show that the brain is organized to reduce wiring costs. We then examine a constraint that impinges on all aspects of neural function but has only recently become apparent—energy consumption. Next we look at energy-efficient neural codes that reduce signal traffic by exploiting the relationships that govern the representational capacity of neurons. We end with a brief discussion on how synaptic plasticity may reconfigure the cortical network on a wide range of time scales.

Geometrical and Biophysical Constraints on Wiring

Reducing the size of an organ, such as the brain, while maintaining adequate function is usually beneficial. A smaller brain requires fewer materials and less energy for construction and maintenance, lighter skeletal elements and muscles for support, and less energy for carriage. The size of a nervous system can be reduced by reducing the number of neurons required for adequate function, by reducing the average size of neurons, or by laying out neurons so as to reduce the lengths of their connections. The design principles governing economical layout have received the most attention.

Just like the wires connecting components in electronic chips, the connections between neurons occupy a substantial fraction of the total volume, and the wires (axons and dendrites) are expensive to operate because they dissipate energy during signaling. Nature has an important advantage over electronic circuits because components are connected by wires in three-dimensional (3D) space, whereas even the most advanced VLSI (very large scale integration) microprocessor chips use a small number of layers of planar wiring. [A recently produced chip with 174 million transistors has seven layers (3).] Does 3D wiring explain why the volume fraction of wiring in the brain (40 to 60%; see below) is lower than in chips (up to 90%)? In chips, the components are arranged to reduce the total length of wiring. This same design principle has been established in the nematode worm Caenorhabditis elegans, which has 302 neurons arranged in 11 clusters called ganglia. An exhaustive search of alternative ganglion placements shows that the layout of ganglia minimizes wire length (4).

Cortical projections in the early sensory processing areas are topographically organized. This is a hallmark of the six-layer neocortex, in contrast to the more diffuse projections in older three-layer structures such as the olfactory cortex and the hippocampus. In the primary visual cortex, for example, neighboring regions of the visual field are represented by neighboring neurons in the cortex. Connectivity is much higher between neurons separated by less than 1 mm than between neurons farther apart (see below), reflecting the need for rapid, local processing within a cortical column—an arrangement that minimizes wire length. Because cortical neurons have elaborately branched dendritic trees (which serve as input regions) and axonal trees (which project the output to other neurons), it is also possible to predict the optimal geometric patterns of connectivity (5–7), including the optimal ratios of axonal to dendritic arbor volumes (8). These conclusions were anticipated nearly 100 years ago by the great neuroanatomist Ramon y Cajal: “After the many shapes assumed by neurons, we are now in a position to ask whether this diversity … has been left to chance and is insignificant, or whether it is tightly regulated and provides an advantage to the organism…. We realized that all of the various conformations of the neuron and its various components are simply morphological adaptations governed by laws of conservation for time, space, and material” [(9), p. 116].

The conservation of time is nicely illustrated in the gray matter of the cerebral cortex. Gray matter contains the synapses, dendrites, cell bodies, and local axons of neurons, and these structures form the neural circuits that process information. About 60% of the gray matter is composed of axons and dendrites, reflecting a high degree of local connectivity analogous to a local area network. An ingenious analysis of resource allocation suggests that this wiring fraction of 60% minimizes local delays (10). This fraction strikes the optimum balance between two opposing tendencies: transmission speed and component density. Unlike the wires in chips, reducing the diameter of neural wires reduces the speed at which signals travel, prolonging delays. But it also reduces axon volume, and this allows neurons to be packed closer together, thus shortening delays.

Global Organization of the Communication Network

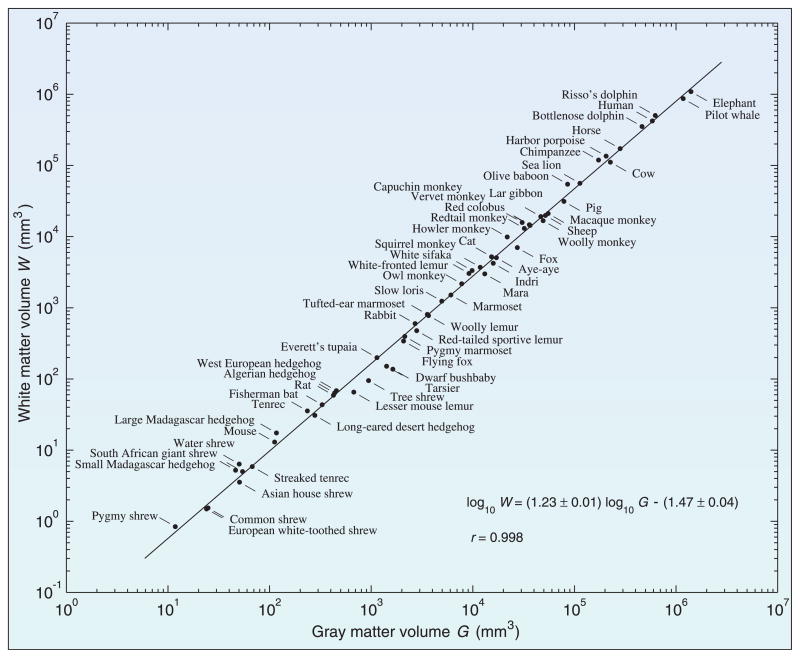
Long-range connections between cortical areas constitute the white matter and occupy 44% of the cortical volume in humans. The thickness of gray matter, just a few millimeters, is nearly constant in species that range in brain volume over five orders of magnitude. The volume of the white matter scales approximately as the 4/3 power of the volume of the gray matter, which can be explained by the need to maintain a fixed bandwidth of long-distance communication capacity per unit area of the cortex (11) (Fig. 1). The layout of cortical areas minimizes the total lengths of the axons needed to join them (12). The prominent folds of the human cortex allow the large cortical area to be packed in the skull but also allow cortical areas around the convolutions to minimize wire length; the location of the folds may even arise from elastic forces in the white matter during development (13).

Fig. 1.

Cortical white and gray matter volumes of 59 mammalian species are related by a power law that spans five to six orders of magnitude. The line is the least squares fit, with a slope around 1.23 ± 0.01 (mean ± SD) and correlation of 0.998. The number of white matter fibers is proportional to the gray matter volume; their average length is the cubic root of that volume. If the fiber cross section is constant, then the white matter volume should scale approximately as the 4/3 power of the gray matter volume. An additional factor arises from the cortical thickness, which scales as the 0.10 power of the gray matter volume. [Adapted from (11)]

The global connectivity in the cortex is very sparse, and this too reduces the volume occupied by long-range connections: The probability of any two cortical neurons having a direct connection is around one in a hundred for neurons in a vertical column 1 mm in diameter, but only one in a million for distant neurons. The distribution of wire lengths on chips follows an inverse power law, so that shorter wires also dominate (14). If we created a matrix with 10¹⁰ rows and columns to represent the connections between every pair of cortical neurons, it would have a relatively dense set of entries around the diagonal but would have only sparse entries outside the diagonal, connecting blocks of neurons corresponding to cortical areas.

The sparse long-range connectivity of the cortex may offer some of the advantages of small-world connectivity (15). Thus, only a small fraction of the computation that occurs locally can be reported to other areas, through a small fraction of the cells that connect distant cortical areas; but this may be enough to achieve activity that is coordinated in distant parts the brain, as reflected in the synchronous firing of action potentials in these areas, supported by massive feedback projections between cortical areas and reciprocal interactions with the thalamus (16, 17).

Despite the sparseness of the cortical connection matrix, the potential bandwidth of all of the neurons in the human cortex is around a terabit per second (assuming a maximum rate of 100 bits/s over each axon in the white matter), comparable to the total world backbone capacity of the Internet in 2002 (18). However, this capacity is never achieved in practice because only a fraction of cortical neurons have a high rate of firing at any given time (see below). Recent work suggests that another physical constraint—the provision of energy—limits the brain’s ability to harness its potential bandwidth.

Energy Usage Constrains Neural Communication

As the processor speeds of computers increase, the energy dissipation increases, so that cooling technology becomes critically important. Energy consumption also constrains neural processing. Nervous systems consume metabolic energy continuously at relatively high rates per gram, comparable to those of heart muscle (19). Consequently, powering a brain is a major drain on an animal’s energy budget, typically 2 to 10% of resting energy consumption. In humans this proportion is 20% for adults and 60% for infants (20), which suggests that the brain’s energy demands limit its size (21).

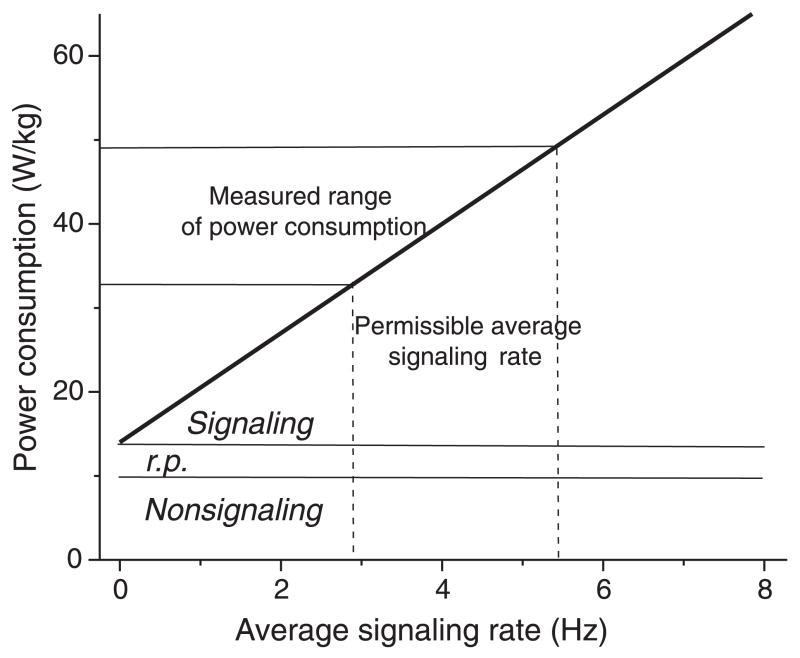
Energy supply limits signal traffic in the brain (Fig. 2). Deep anesthesia blocks neural signaling and halves the brain’s energy consumption, which suggests that about 50% of the brain’s energy is used to drive signals along axons and across synapses. The remainder supports the maintenance of resting potentials and the vegetative function of neurons and glia. Cortical gray matter uses a higher proportion of total energy consumption for signaling, more than 75% (Fig. 2), because it is so richly interconnected with axons and synapses (21). From the amounts of energy used when neurons signal, one can calculate the volume of signal traffic that can be supported by the brain’s metabolic rate. For cerebral cortex, the permissible traffic is ~5 action potentials per neuron per second in rat (Fig. 2) (22) and <1 per second in human (23). Given that the brain responds quickly, the permissible level of traffic is remarkably low, and this metabolic limit must influence the way in which information is processed. Recent work suggests that brains have countered this severe metabolic constraint by adopting energy-efficient designs. These designs involve the miniaturization of components, the elimination of superfluous signals, and the representation of information with energy-efficient codes.

Fig. 2.

Power consumption limits neural signaling rate in the gray matter of rat cerebral cortex. Baseline consumption is set by the energy required to maintain the resting potentials of neurons and associated supportive tissue (r.p.) and to satisfy their vegetative needs (nonsignaling). Signaling consumption rises linearly with the average signaling rate (the rate at which neurons transmit action potentials). The measured rates of power consumption in rat gray matter vary across cortical areas and limit average signaling rates to 3 to 5.5 Hz. Values are from (19), converted from rates of hydrolysis of adenosine triphosphate (ATP) to W/kg using a free energy of hydrolysis for a molecule of ATP under cellular conditions of 10⁻¹⁹ J.

Miniaturization, Energy, and Noise

The observation that 1 mm³ of mouse cortex contains 10⁵ neurons, 10⁸ synapses, and 4 km of axon (24) suggests that, as in chip design, the brain reduces energy consumption by reducing the size and active area of components. Even though axon diameter is only 0.3 μm (on average), sending action potentials along these “wires” consumes more than one-third of the energy supplied to cortical gray matter (22). Thus, as with computer chips, an efficient layout (discussed above) and a high component density are essential for energy efficiency—but, as is also true for chips, miniaturization raises problems about noise.

When a neuron’s membrane area is reduced, the number of molecular pores (ion channels) carrying electrical current falls, leading to a decline in the signal-to-noise ratio (SNR) (25–27). The noise produced by ion channels, and by other molecular signaling mechanisms such as synaptic vesicles, is potentially damaging to performance. However, the effects of noise are often difficult to determine because they depend on interactions between signaling molecules in signaling systems. These interactions can be highly nonlinear (e.g., the voltage-dependent interactions between sodium and potassium ion channels that produce action potentials) and can involve complicated spatial effects (e.g., the diffusion of chemical messengers between neurons and the transmission of electrical signals within neurons). A new generation of stochastic simulators is being developed to handle these complexities and determine the role played by molecular noise and diffusion in neural signaling (26, 28, 29). With respect to miniaturization, stochastic simulations (25) show that channel noise places a realistic ceiling on the wiring density of the brain by setting a lower limit of about 0.1 μm on axon diameter.

The buildup of noise from stage to stage may be a fundamental limitation on the logical depth to which brains can compute (30). The analysis of the relationships among signal, noise, and bandwidth and their dependence on energy consumption will play a central role in understanding the design of neural circuits. The cortex has many of the hallmarks of an energy-efficient hybrid device (28). In hybrid electronic devices, compact analog modules operate on signals to process information, and the results are converted to digital data for transmission through the network and then reconverted to analog data for further processing. These hybrids offer the ability of analog devices to perform basic arithmetic functions such as division directly and economically, combined with the ability of digital devices to resist noise. In the energy-efficient silicon cochlea, for example, the optimal mix of analog and digital data (that is, the size and number of operations performed in analog modules) is determined by a resource analysis that quantifies trade-offs among energy consumption, bandwidth for information transmission, and precision in analog and digital components. The obvious similarities between hybrid devices and neurons strongly suggest that hybrid processing makes a substantial contribution to the energy efficiency of the brain (31). However, the extent to which the brain is configured as an energy-efficient hybrid device must be established by a detailed resource analysis that is based on biophysical relationships among energy consumption, precision, and bandwidth in neurons.

Some research strongly suggests that noise makes it uneconomical to transfer information down single neurons at high rates (29, 31). Given that a neuron is a noise-limited device of restricted bandwidth, the information rate is improved with the SNR, which increases as the square root of the number of ion channels, making improvements expensive (25). Thus, doubling the SNR means quadrupling the number of channels, the current flow, and hence the energy cost. Given this relationship between noise and energy cost, an energy-efficient nervous system will divide information among a larger number of relatively noisy neurons of lower information capacity, as observed in the splitting of retinal signals into ON and OFF pathways (32). Perhaps the unreliability of individual neurons is telling us that the brain has evolved to be energy efficient (31).

Saving on Traffic

Energy efficiency is improved when one reduces the number of signals in the network without losing information. In the nervous system, this amounts to an economy of impulses (33) that has the additional advantage of increasing salience by laying out information concisely. Economy is achieved by eliminating redundancy. This important design principle is well established in sensory processing (34). Redundancy reduction is a goal of algorithms that compress files to reduce network traffic.

In the brain, efficiency is improved by distributing signals appropriately in time and space. Individual neurons adopt distributions of firing rate (35, 36) that maximize the ratio between information coded and energy expended. Networks of neurons achieve efficiency by distributing signals sparsely in space and time. Although it was already recognized that sparse coding improves energy efficiency (37), it was Levy and Baxter’s detailed analysis of this problem (38) that initiated theoretical studies of energy-efficient coding in nervous systems. They compared the representational capacity of signals distributed across a population of neurons with the costs involved. Sparse coding schemes, in which a small proportion of cells signal at any one time, use little energy for signaling but have a high representational capacity, because there are many different ways in which a small number of signals can be distributed among a large number of neurons. However, a large population of neurons could be expensive to maintain, and if these neurons rarely signal, they are redundant. The optimum proportion of active cells depends on the ratio between the cost of maintaining a neuron at rest and the extra cost of sending a signal. When signals are relatively expensive, it is best to distribute a few of them among a large number of cells. When cells are expensive, it is more efficient to use few of them and to get all of them signaling. Estimates of the ratio between the energy demands of signaling and maintenance suggest that, for maximum efficiency, between 1% and 16% of neurons should be active at any one time (22, 23, 38). However, it is difficult to compare these predictions with experimental data; a major problem confronting systems neuroscience is the development of techniques for deciphering sparse codes.

There is an intriguing possibility that the energy efficiency of the brain is improved by regulating signal traffic at the level of the individual synaptic connections between neurons. A typical cortical neuron receives on the order of 10,000 synapses, but the probability that a synapse fails to release neurotransmitter in response to an incoming signal is remarkably high, between 0.5 and 0.9. Synaptic failures halve the energy consumption of gray matter (22), but because there are so many synapses, the failures do not necessarily lose information (39, 40). The minimum number of synapses required for adequate function is not known. Does the energy-efficient cortical neuron, like the wise Internet user, select signals from sites that are most informative? This question draws energy efficiency into one of the most active and important areas of neuroscience: synaptic plasticity.

Reconfiguring the Network

Long-distance communication in the brain occurs through all-or-none action potentials, which are transmitted down axons and converted to analog chemical and electrical signals at synapses. The initiation of action potentials in the cortex can occur with millisecond precision (41) but, as we have just discussed, the communication at cortical synapses is probabilistic. On a short time scale of milliseconds to seconds, presynaptic mechanisms briefly increase or decrease the probability of transmission at cortical synapses over a wide range, depending on the previous patterns of activity (42). On longer time scales, persistent correlated firing between the presynaptic and postsynaptic neurons can produce long-term depression or potentiation of the synaptic efficacy, depending on the relative timing of the spikes in the two neurons (43).

A new view of the cortical network is emerging from these discoveries. Rather than being a vast, fixed network whose connection strengths change slowly, the effective cortical connectivity is highly dynamic, changing on fast as well as slow time scales. This allows the cortex to be rapidly reconfigured to meet changing computational and communications needs (44). Unfortunately, we do not yet have techniques for eavesdropping on a large enough number of neurons to determine how global reconfiguration is achieved. Local field potentials (LFPs), extracellular electric fields that reflect the summed activity from local synaptic currents and other ion channels on neurons and glial cells, may provide hints of how the flow of information in cortical circuits is regulated (16). Oscillations in the 20- to 80-Hz range occur in the LFPs, and the coherence between spikes and these oscillations has been found to be influenced by attention and working memory (45, 46).

Conclusions

The more we learn about the structure and function of brains, the more we come to appreciate the great precision of their construction and the high efficiency of their operations. Neurons, circuits, and neural codes are designed to conserve space, materials, time, and energy. These designs are exhibited in the geometry of the branches of dendritic trees, in the precise determination of wiring fractions, in the laying out of maps in the brain, in the processing of signals, and in neural codes. It is less obvious, but highly likely, that the unreliability of single neurons is also a mark of efficiency, because noise in molecular signaling mechanisms places a high price on precision. To an extent yet to be determined, the noise and variability observed among neurons is compensated by plasticity—the ability of neurons to modify their signaling properties. Neural plasticity also has the potential to direct the brain’s scarce resources to where they will be of greatest benefit.