Error-Driven Learning in Visual Categorization and Object Recognition: A Common Elements Model

Abstract

A wealth of empirical evidence has now accumulated concerning animals’ categorizing photographs of real-world objects. Although these complex stimuli have the advantage of fostering rapid category learning, they are difficult to manipulate experimentally and to represent in formal models of behavior. We present a solution to the representation problem in modeling natural categorization by adopting a common-elements approach. A common-elements stimulus representation, in conjunction with an error-driven learning rule, can explain a wide range of experimental outcomes in animals’ categorization of naturalistic images. The model also generates novel predictions that can be empirically tested. We report two experiments which show how entirely hypothetical representational elements can nevertheless be subject to experimental manipulation. The results represent the first evidence of error-driven learning in natural image categorization and they support the idea that basic associative processes underlie this important form of animal cognition.

In order to survive and to reproduce, all organisms must adapt to a complex and ever-changing environment. Even the same object never provides the same information to the sensory organs on two successive occasions, a problem which becomes particularly acute when the behavioral task involves recognizing several different objects from the same class.

Despite this variability in stimulation, humans and animals alike learn to respond similarly to nonidentical objects from the same category (categorization) as well as to respond differently to individual objects from the same category (identification). Underlying such categorization and identification behavior must be a psychological mechanism which detects and extracts those aspects of individual objects and classes of objects that are invariant, in order to support categorization, as well as those aspects that are specific to each stimulus, in order to support identification (Ashby & Lee, 1993; Fetterman, 1996; Serre et al., 2005; Serre, Oliva, & Poggio, 2007).

It seems parsimonious to assume that similar mechanisms lie at the root of both human and animal visual categorization. Even if a uniquely human ability to categorize stimuli using rules and other “higher-level” cognitive processes is assumed (see Lea & Wills, 2008; Mackintosh, 1995), most researchers would agree that any “lower-level” mechanisms of categorization which are present in animals are likely to be found in humans as well. If that is indeed the case, then animal research affords researchers a unique opportunity to study the psychological and neural mechanisms of categorization in a setting where the influence of past experience, genetic variability, language, and other higher-level forms of cognition can be controlled and manipulated. On the other hand, if the principles guiding categorization in humans and nonhuman animals prove to differ from one another, then it would still be particularly informative to know how the same behavioral problem is solved in different ways by different organisms as well as how evolution has shaped the strategies deployed by each.

Primates possess the most sophisticated visual system among mammals. The only other animals that have evolved such highly advanced vision are birds (Husband & Shimizu, 2001; Shimizu & Bowers, 1999). This fact helps to explain why the pigeon has been extensively used as a model animal to study the behavioral mechanisms of natural image categorization and object recognition (Wasserman, 1993). The visual capabilities of pigeons are indeed impressive; they include the ability to detect and to classify many different classes of objects as well as the ability to transfer this learning to novel exemplars from each class (Bhatt, Wasserman, Reynolds, & Knauss, 1988; Herrnstein & Loveland, 1964; for reviews, see Cook, 2001; Kirkpatrick, 2001; Lazareva & Wasserman, 2008; Wasserman, 1993, 1995; Wasserman & Bhatt, 1992; Zentall et al., 2008).

These forms of discrimination learning and stimulus generalization have now been studied for several decades and an extensive body of empirical data has accumulated during that time. Together with the many practical advantages of research using avian species instead of nonhuman primates, this accumulated knowledge affords a unique opportunity for studying the general mechanisms of visual categorization. Furthermore, this line of research in animal cognition could soon become especially important and relevant, given the increasing attention that is being paid to the study of vision using natural images (Felsen & Dan, 2005; Geisler, 2008; Simoncelli & Olshausen, 2001); such natural images more closely resemble the stimuli that are encountered by biological systems in the real world than the more commonly used artificial stimuli of the laboratory.

Surprisingly, empirical research in natural object categorization by pigeons and other animals has not been accompanied by a concomitant effort to provide a coherent theoretical explanation of this behavior, a fact which makes it difficult to draw connections between this realm of research and explorations of human vision and other forms of animal learning. Questions about the conditions that produce categorization learning, the contents of such learning, and the rules that map learning onto performance (Rescorla, 1988) remain unanswered. Some work has tried to identify the nature of the representation that pigeons store during categorization learning (Huber, 2001) and the conditions that foster categorization learning over simple discrimination learning (e.g., Wasserman & Bhatt, 1992; Wasserman, Kiedinger, & Bhatt, 1988). Yet, a full theoretical account including the formalization of a quantitative model has proven to be elusive.

This state of affairs is particularly perplexing given the popularity of the view that simple associative learning processes may be responsible for open-ended categorization in pigeons and other animals (e.g., Huber, 2001; Mackintosh, 2000) and given the fact that contemporary associative learning models offer a wide range of theoretical tools with which to model animal cognition, all of them developed to a high degree of formalization (for a review, see Vogel, Castro, & Saavedra, 2004). Indeed, the ability of quantitative models of Pavlovian conditioning to predict and to explain a wide range of experimental observations has led to their successful application to human cognition. The same principles that explain simple associative learning may be the foundation for verbal learning, contingency judgment, transitive inference, and important social and perceptual phenomena (for a review, see Siegel & Allan, 1996). What is even more ironic is the fact that researchers of human categorization have been applying animal learning theories to their data for nearly 20 years (Gluck & Bower, 1988; Kruschke, 2001; Shanks, 1991). We thus see that current theories of animal learning have been widely applied to human categorization phenomena, but not so prominently to visual categorization in animals.

Perhaps one factor contributing to this odd state of affairs is the nature of the stimuli that have commonly been used in studies of animal categorization. As noted earlier, many of these studies trained pigeons to discriminate photographs of real-world objects, whereas artificial categories are more commonly used in human categorization research. Research in Pavlovian conditioning and artificial categorization share the advantage of using elemental stimuli that can easily be controlled by the experimenter and that can straightforwardly be represented in computational models. Natural categories have the advantages of being more readily learned by pigeons (Lea, Wills, & Ryan, 2006) and better reflecting the complexity of the task faced by animals in their natural environment, but natural categories have the disadvantage of involving a large number of features which may act independently or in concert to control behavior. Despite several efforts to isolate the relevant features for classification (e.g., Aust & Huber, 2002; Lazareva, Freiburger, & Wasserman, 2006; Lubow, 1974), this task has proven to be very difficult. Even for the cases in which such features have been isolated, the same properties found to control behavior in one study may not control behavior in other studies using different subjects and deploying different training methods.

Therefore, anyone wishing to apply quantitative models of associative learning to the categorization of natural images is faced with a major problem: How to formalize a representation of these complex stimuli and the similarities and differences among them. The work that we present here represents a simple solution to the stimulus representation problem which arises from the use of complex stimuli in natural categorization tasks. This solution is implemented in a model which represents stimuli as overlapping collections of elements and which modifies their association with an outcome according to an error-driven learning rule.

In the next section, we review the history of the common-elements approach and its use in the explanation of discrimination and generalization phenomena in animal learning. Then, we show how this framework can be used to explain natural image categorization in animals, providing a much-needed link between research in this area and traditional animal learning theory. We conclude by presenting empirical evidence which confirms two new predictions from our model concerning the role of error-driven learning in visual categorization.

The Common Elements Approach

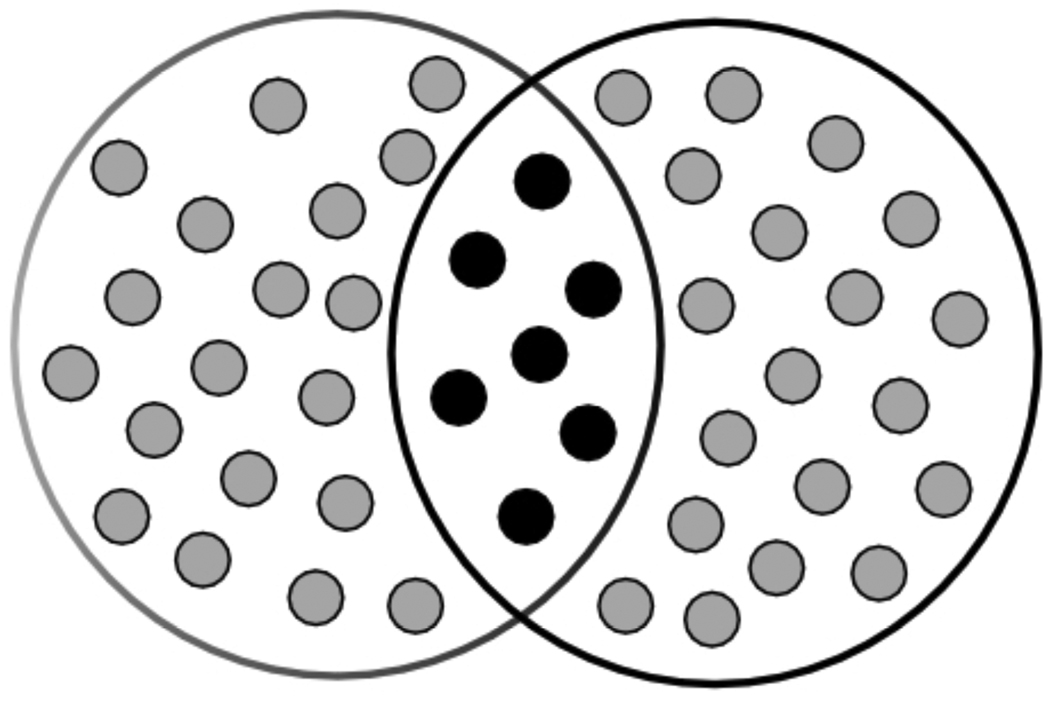
One of the best-known ways to represent stimuli and the similarity among them is through the notion of common elements. According this idea, diagrammed in Figure 1, every stimulus is processed as a set of representational elements. Two different stimuli can share representational elements; the perceptual similarity between them is a direct function of the proportion of elements that they share (black elements in Figure 1). Elements that are active only in the presence of one stimulus, but not the other (grey elements in Figure 1) represent the dissimilarity between them, thereby providing a basis for their discrimination.

Figure 1.

A common-elements representation of the similarity between stimuli.

Perhaps the first application of the common elements idea in animal learning theory was Konorski’s (1948) explanation of the generalization of conditioned reflexes in terms of overlapping “cortical centres,” which he proposed as an alternative to Pavlov’s interpretation of generalization in terms of the irradiation of excitation from the center representing the original conditioned stimulus. In Konorski’s words, “…the intimate nature of the phenomenon of similarity between various stimuli consists in the partial overlapping of the corresponding cortical centres. The more extensive the overlapping, the closer is the similarity […], and when this overlapping is virtually complete the similarity passes into ‘identity’” (p. 129).

Later, Estes and colleagues (Atkinson & Estes, 1963; Neimark & Estes, 1967) developed the common elements hypothesis within the framework of Stimulus Sampling Theory (SST), replacing Konorski’s neurophysiological language with a more abstract nomenclature. In SST, a stimulus is represented as a population of independently variable elements. On any given learning trial, each element may become active with a fixed probability and may be fully connected to the response that is reinforced on that trial. Generalization depends on both the proportion of elements connected to a response from the originally conditioned population and on the proportion of elements shared between that population and the one representing the novel test stimulus.

One problem with SST explanations of stimulus control is that the same common elements that account for generalization prevent the model from learning to discriminate perfectly between similar stimuli. Several contemporary theories of associative learning have implemented a stimulus representation in terms of collections of elements (Blough, 1975; Harris, 2006; McLaren & Mackintosh, 2000, 2002; Wagner, 1981), but they have solved the discrimination problem by including an error-driven learning rule, like the one proposed in the Rescorla-Wagner model (Rescorla & Wagner, 1972). The Rescorla-Wagner learning rule states that the change in the associative strength between a stimulus (or element) i, and an outcome j, on a particular trial, or ΔV_ij, is determined by the following equation:

$$\mathrm{\Delta }{V}_{\mathit{\text{ij}}}={\alpha }_i{\beta }_j({\lambda }_j-{\displaystyle \sum V_{\mathit{\text{ij}}})}$$ (1)

, where α_i and β_j are learning rate parameters influenced by the salience of i and j, respectively, λ_j is the maximum amount of associative strength supported by j, and ΣV_ij is the algebraic sum of the associative strengths of all of the stimuli presented on that particular trial. The most important feature of this and other error-driven learning rules (Pearce, 1987; Pearce & Hall, 1980; Wagner, 1981) is that the change in associative strength on each trial reduces a prediction error, represented by the disparity between the associative strength that is supported by the outcome, λ_j, and the associative strength of all of the stimuli that are presented on that trial, ΣV_ij. If several different stimuli are simultaneously paired with the outcome during training, then the Rescorla-Wagner learning rule will distribute associative strength among them according to their relative informational value in predicting the outcome.

The interplay between a common elements representation and an error-driven learning rule has proven to be extremely powerful in explaining stimulus control. Common representational elements allow one to explain the generalization of responding among different stimuli, whereas the error-driven learning rule allows one to explain why nearly perfect discrimination can be achieved even with highly similar stimuli (Gluck, 1992). Furthermore, the interaction between these factors leads to new predictions which are not explained by either factor alone.

For example, Blough (1975) proposed a model in which representational elements are sequentially ordered along a continuum representing a particular stimulus dimension. If a stimulus possesses the property represented by that dimension, then its presence will provoke the differential activation of several representational elements along the continuum. Coupled with an error-driven learning rule, this stimulus representation can account for contrast effects which have consistently been observed in the study of stimulus generalization gradients and which cannot be explained by traditional approaches (e.g., Spence, 1937).

Mackintosh and colleagues (Mackintosh, 1995; McLaren et al., 1995) have used a simpler version of Blough’s model to account for prototype effects in artificial categorization by pigeons and people. These authors proposed that the tendency to classify prototypes more accurately as members of a category than other exemplars might arise because prototypes typically have fewer elements in common with members of the other category. This common-elements account can explain several experimental results obtained by these authors and it is closely related to the model that we will present here. We will see how useful it is to represent complex naturalistic stimuli in terms of hypothetical elements, in the same way as Mackintosh and colleagues have represented stimulus dimensions.

A study by Rescorla (1976) provides yet another example of the utility of coupling a common elements representation with an error-driven learning rule; this example provides the inspiration for the model presented here. Rescorla assumed that simple stimuli, such as tones or lights, could be represented as compounds of both unique and shared elements (e.g., AX and BX). This idea leads to the prediction that a target stimulus might be more strongly associated with an outcome by training involving a different, similar stimulus than by training with the target itself. The notion is that, if target stimulus AX is paired with an unconditioned stimulus (US), both A and X should acquire associative strength until the two together perfectly predict the US. Later training with AX will not increase its potential to evoke a response because learning cannot occur if there is no error in predicting the US. But later training with a similar stimulus, BX, should result in an increase in the associative strengths of both B and X—the unique and common elements, respectively—because, in the absence of A, the US is no longer perfectly predicted. The result should be a conditioned response to AX that is enhanced through training with BX, but not through training with AX itself. Rescorla (1976) found evidence for this prediction, which not only stands as impressive confirmation of a common elements theory of stimulus generalization, but which also suggests that it may be possible to devise ingenious ways to manipulate entirely hypothetical components of a stimulus representation, a point to which we will later return.

The Model

Stimulus Representation

One of the goals of the present work is to show that the simple principles of the common elements approach can also be used to represent even the complex multidimensional stimuli that are used in natural image categorization research. The idea is the same: Two photographs of natural objects can be represented as collections of elements: some unique to each particular photograph and some shared by both.

The complexity in the representation of a whole category, instead of just two stimuli, arises when we appreciate that perceptual categories have limitless members. With a larger number of exemplars in a category, some elements could be common to all N members, whereas others could be common to N–1, N–2, N–3… and to just one member. In this case, different elements will be more or less representative and diagnostic of the category, depending on how many exemplars possess any given element. The diagnosticity of a particular element for the category will be a direct function of the number of exemplars that activate that element, given that members of other categories do not produce the same level of activation.

In this way, the notion of common elements offers a straightforward means to represent stimulus properties with different levels of specificity, ranging from stimulus-specific properties, in the form of elements that are unique to only one member of the category, to category-specific properties, in the form of elements that are common to most members of the category. Elements near the category-specific side of the range can be used as the basis for categorization. Elements that are peculiar to specific exemplars of a category can be used as the basis for more fine-grained discriminations among the individual category members.

It might seem that this idea takes us back to the starting point: if we have no knowledge about the similarity relations among the stimuli in a categorization experiment, then there is no way to specify representations of them in terms of shared and specific elements. What we will show here is that, even if we assign relatively arbitrary representations to stimuli which do not capture the specific similarity relations among them or among different categories, then it is still possible to explain a great deal of what is known about animal categorization by having representations that adhere to a simple principle: stimuli belonging to the same category should have a higher likelihood of sharing elements than stimuli belonging to different categories.

To capture this basic idea, our model represents all stimuli in a categorization task through a large pool of elements that can either be active or inactive when a stimulus is presented. Each of the categories that are used in the task determines a different probability distribution over the elements, so that the elements have a variable probability of being active when a particular exemplar of the category is presented. Because we know nothing about the similarity relations among the different categories involved in a simulation, these distributions are generated through a completely random process. The only requirement is to assign different probability distributions to different categories, capturing the principle of category representation described in the prior paragraph.

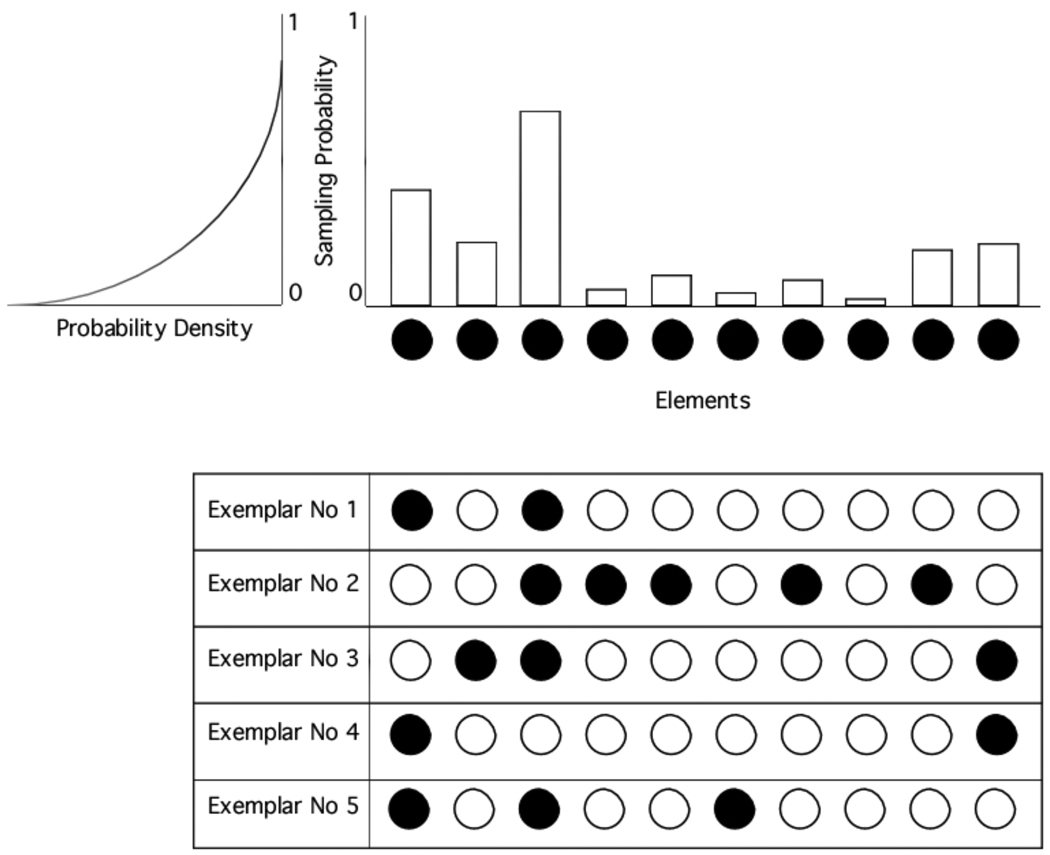
Figure 2 presents a summary of the stimulus representation in our model, whose properties can be described at three different levels. At the first level, we have the specific representations that are assigned to each stimulus in a categorization experiment. As noted before, the presentation of a stimulus is assumed to activate a small proportion of all of the elements in the pool. The bottom part of Figure 2 shows five examples of stimulus representations created from a pool of 10 elements. Common elements between representations at this level determine the similarity between the stimuli that they represent.

Figure 2.

A schematic representation of the common-elements model of natural image classification that is described in this article.

Categories comprise a large number of individual representations, one for each exemplar. If we had access to all of these representations for one specific category, then it would be possible to calculate the relative frequency with which each element is sampled in that category, resulting in an empirical probability distribution over the elements. This empirical distribution would approach the actual distribution determined by the category, from which the observed individual exemplars were sampled. Thus, we can think of different categories as represented by different probability distributions over elements, with the overlap among distributions representing the similarity relations among categories. This is the second level of description in our stimulus representation, exemplified in the top portion of Figure 2 as the probability distribution from which the stimulus representations at the bottom were generated.

For each category, an element in the pool can either be specific to a particular exemplar or to the entire category. Whether an element is specific to a particular stimulus or to an entire category depends on how many exemplars in the category share this element, which in turn depends on the sampling probability that this element has in the category representation. Elements which have a low, nonzero probability tend to be part of the representation of one or only a few stimuli, carrying predominately stimulus-specific information; as the sampling probability increases, the stimulus-specificity of the element decreases and its category-specificity correspondingly increases.

Just as all of the stimuli are represented through the same pool of elements, any category is also represented as a probability distribution over the elements. If we had access to all of these probability distributions, then it would be possible to calculate the relative frequency with which each sampling probability is used across categories. The final result would be the third level of description in our stimulus representation: the distribution over the sampling probabilities themselves, as exemplified in the top-left portion of Figure 2 (note that the distribution shown here is rotated counterclockwise, with probability density placed along the x-axis). Because each sampling probability determines the level of specificity-invariance for a particular element, we can think of this higher-order distribution as a specificity distribution, which gives information not about specific stimuli or categories, but about the general coding strategy used by the animal to represent the stimuli involved in the categorization task. In the example shown in Figure 2, across categories, low sampling probabilities are more frequent than high sampling probabilities, meaning that the system uses representations with many stimulus-specific elements, but few category-specific elements.

As suggested earlier, our model focuses on the highest level description of the stimulus representation, simply ignoring the similarity relations among categories and stimuli. Describing how elements with varied levels of specificity gain control over behavior will later be shown to be adequate to explain an impressive number of experimental results.

The only aspect of the stimulus representation that can be manipulated in our model is the specificity distribution, which determines the proportion of elements in the representations that are stimulus-specific, category-specific, or anywhere between these extremes. However, specificity can only be determined in relation to a particular category and the number of categories in which each individual stimulus can participate is enormous. A photograph of a person might lead to the identification of a single individual or to its classification in the basic category “people,” in the superordinate category “mammal,” or in the subordinate category “female.” We wanted to give our model enough flexibility to permit the possibility that different visual tasks might involve different distributions of specificity for the representational elements. What we needed was a way to represent the specificity distribution via a function which could assume many different shapes; here, the beta distribution represents a very good choice (Grinstead & Snell, 1997). The beta density function is defined by the following equation:

$$B(a,b,x)=\left\{\begin{array}{cc}\frac{1}{B(a,b)}{x}^{a-1}{(1-x)}^{b-1},\hfill & \mathit{\text{if \hspace{1em}}}0\le x\le 1,\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{otherwise}}.\hfill \end{array}\right\}$$ (2)

In the context of our model, the variable x in Equation 2 represents the sampling probability or the specificity level. Equation 2 determines the likelihood with which this specificity level is used in the category representations. The parameters a and b are positive numbers and B(a,b) is the beta function given by:

$$B(a,b)={\displaystyle {\int }_0^1{x}^{a-1}{(1-x)}^{b-1}\mathit{\text{dx}}}$$ (3)

The beta density function was useful for our purposes because it determines a family of functions which can assume one of several possible shapes depending on the values of a and b. When a = b = 1, the function takes the form of a uniform density, with the consequence that all of the specificity levels are equally likely in the final representational scheme. This outcome is shown in Panel A of Figure 3. When the values of the parameters differ from 1, the representations start being “biased:” exhibiting more stimulus-specific than category-specific elements, more category-specific than stimulus-specific elements, or anything between these extremes.

Figure 3.

Some examples of the shape that the beta density function acquires with different values of parameters a and b.

For example, if a =1 and b > 1, as shown in Panel B of Figure 3, the distribution is monotonically decreasing from 0 to 1; the consequence is that stimulus-specific elements (which are related to a low sampling probability) are more frequent than category-specific elements (which are related to a high sampling probability). The opposite trend is true when a > 1 and b = 1, as shown in Panel C of Figure 3. The function has sufficient flexibility to exhibit almost any other distribution in which we might be interested, including nonmonotonic distributions with a peak at a particular sampling probability (like the one shown in Panel D of Figure 3) or U-shaped distributions (like the one shown in Panel E of Figure 3). Moreover, interpreting the shape taken by the function in terms of category-specific and stimulus-specific elements is straightforward.

The stimulus representations are generated from the model in three steps. In the first step, a specificity function is chosen by assigning values to the parameters in the beta distribution as explained earlier. In our simulations with the model, we have been successful in reproducing the qualitative aspects of empirical data with many different shapes of the beta distribution, but the particular form that has produced the most satisfactory results is similar to the one presented in Panel B of Figure 3. Critically, this distribution produces a high number of exemplar-specific elements and a low number of category-specific elements. Also important is that the stimulus representations tend to be highly sparse; that is, each stimulus activates only a small proportion of the elements in the pool. Similar results might be obtained with the model if any other monotonically decreasing function were used (such as exponential or Gaussian functions).

It is interesting to note that the kind of sparse coding that we have found to be more useful in our simulations has been found in several visual areas of the primate brain in response to natural images (e.g., Baddeley et al., 1997; Foldiak & Young, 2002; Olshausen & Field, 2004; Vine & Gallant, 2000). Furthermore, hierarchical models of human object recognition which incorporate properties of the primate visual cortex also represent stimuli through processing units which vary in their level of specificity and invariance (Serre et al., 2005; Serre et al., 2007).

In the second step, the representation of each category in the simulated experiment is generated by independently assigning a random value between 0 and 1 to each element in the pool. The process is “biased” by generating random numbers according to the specificity distribution that is chosen in the first step; random numbers following the beta distribution can easily be obtained from numerical computing software packages such as MATLAB. The specificity distribution that we chose in our simulations generated category representations with many low sampling probabilities and almost no high sampling probabilities. Beyond the constraints that are imposed by the specificity distribution, the category representations are generated in a completely random way and always using the same parameter values, reflecting the fact that we make no assumptions about the similarity relations among categories.

In the third and final step, representations of all of the stimuli in the experiment are generated from the distributions that were obtained in the previous step. Representations of all of the stimuli belonging to the same perceptual category are generated using the same probability distribution, but it is not important which particular probability distribution is assigned to which particular category. A random process determines if each element is or is not activated by the presentation of a stimulus. The random process is again “biased” by the sampling probability of the element for a specific category by generating a random number from a Bernoulli distribution with the probability of success equal to the sampling probability of the element. The sampling process is independent for each individual element in the representation, with the consequence that the number of active elements is not fixed across different stimuli.

The framework presented here is essentially an extension of the ideas of SST to the representation of categories instead of individual stimuli. We have a pool of elements with an assigned sampling probability, which in SST represented all possible instances of a particular stimulus and in our model represents all possible exemplars from a category. The representation of a particular experience with a stimulus was obtained in SST by randomly sampling elements from the pool; here, the same sampling process yields the representations of particular exemplars of a category.

From our theoretical perspective, these similarities are not trivial; rather, they suggest that basically the same principles of stimulus representation can be at work in learning situations which are of apparently very different complexity. As recognized by SST, two instances of a stimulus are probably never experienced in the same way by an organism. Whether the relevant stimulus is a simple light or a whole category of objects, the task of the organism is to recognize which properties are invariant across the different instances of a stimulus and which properties are specific to each particular stimulus instance. The invariant properties help to generalize knowledge across different environmental situations, whereas the specific properties help to make important distinctions among similar situations that are linked to different consequences.

One important disparity between SST and our framework is that in the former the probability of sampling an element given a stimulus was always set to either 0 or a fixed value, whereas our model adds more flexibility by allowing this value to vary between 0 and 1. Another disparity lies in the learning rule that is used to modify the association between each element and an outcome, which is explained next.

Learning Rule

Following previous models in the common-elements tradition, we propose that the associations between each element and an outcome are updated according to an error-driven learning rule. Specifically, we apply the Rescorla-Wagner learning rule described in Equation 1, where V_ij represents the strength of the association between element i and response j.

Although the conceptualization of stimuli as collections of unique and shared elements is the main contribution of our model—as it offers a solution to the representation problem in modeling natural categorization—adopting an error-driven learning rule is not trivial, because it radically changes the predictions of the model for most experimental tasks. This learning algorithm permits us to explain how category-specific and stimulus-specific elements acquire control over behavior in a discrimination task. Categorization learning happens when category-specific elements acquire control over behavior, whereas identification learning happens when stimulus-specific elements acquire control over behavior. More importantly, the rule is useful in explaining the dynamics of categorization learning: that is, how the interplay between learning and generalization determines which elements in the representation gain or lose associative strength across training. In our upcoming simulations, this interactive aspect of the learning rule helps to explain how performance in some categorization tasks is dominated by categorization learning early in training, whereas identification learning dominates later in training.

Adopting an error-driven learning rule is also important because this kind of rule captures, at least partially, many of the principles guiding associative learning in Pavlovian conditioning and other conditioning situations. If the algorithm proves to be useful in explaining natural image categorization as well, then we would have important evidence concerning the generality of associative learning principles.

Finally, we fully appreciate that there are several arguments against the adequacy of both an elemental stimulus representation and an error-driven learning rule for explaning simple associative learning. We address some of these arguments in the General Discussion section of this article. We have nevertheless chosen to present a model with strong similarities to the widely-known Rescorla-Wagner model because this theory has a long tradition of application to areas of research outside of Pavlovian conditioning (Siegel & Allan, 1996) and because this theory’s formal properties and relationship to models from other research areas and disciplines is widely known (Gluck & Bower, 1988; Sutton & Barto, 1981; Widrow & Hoff, 1960). One of our goals is to show how a quantitative model—built using ideas from traditional animal learning theory—can explain several phenomena in natural categorization with pigeons. We think of this as an initial proving ground for the use of formal models in this area of research; we thereby hope to highlight the key experimental questions that need to be answered in order to gain a fuller understanding of the mechanisms underlying animal and human categorization.

Choice Rule

Most categorization tasks involve an animal’s sorting several different stimuli into two or more separate categories, each represented by a distinctively different response. In such forced-choice procedures, subjects are often asked to give a single discrete response to finalize the trial. To predict categorization behavior in such situations, one needs to formalize a rule for the selection of a response when a stimulus is presented, given the strength of the association between that stimulus and all of the possible responses on a trial. Here, we assume that the total associative strength between a stimulus S and a response j equals the sum of the associative strengths between all of the elements activated by the stimulus and response j. That is:

$$V_{\mathit{\text{Sj}}}={\displaystyle \sum _i{V}_{\mathit{\text{ij}}}}$$ (4)

V_Sj can also be interpreted as the expectation of reinforcement or incentive value of response j given the presentation of stimulus S. After computing these incentive values for each response, choice probabilities are obtained from them using a modification of Luce’s ratio rule (Luce, 1959), known as exponential ratio (Wills et al., 2000) or softmax rule (Bridle, 1990). The main difference between Luce’s choice rule and softmax is that, in the latter, the associative strengths are transformed according to an exponential function before computing the choice probability:

$$p(R_j/S)=\frac{e^{\theta V_{\mathit{\text{Sj}}}}}{{\displaystyle \sum _j{e}^{\theta V_{\mathit{\text{Sj}}}}}}$$ (5)

The probability of choosing response R_j given the presentation of stimulus S is computed by taking a transformation of its incentive value and dividing it by the sum of the transformed incentive values of each of the available responses. In this way, the rule reflects the relative incentive value of response j given the presentation of stimulus S. The exponential transformation constrains the result to positive values which can be interpreted as probabilities; the parameter θ determines the decisiveness of the choice rule, with higher values leading to stronger preferences for the choice with the larger incentive value.

Several empirical and theoretical reasons motivated the use of the softmax choice rule in our model. First, a relation like the one proposed in Equation 5 holds between relative frequency of choice and relative reinforcement value of each alternative in empirical studies of operant behavior in the form of the matching law (Herrnstein, 1961). Second, the ratio rule is often used in models of human categorization (see Kruschke, 2008), making future comparisons between such models and the present one easier to perform, if they are adapted in the future to the stimuli and procedures of natural image categorization experiments. Finally, softmax is equivalent to the Boltzmann exploration strategy used in reinforcement learning models (Kaelbling, Littman, & Moore, 1996), whose formal properties have been and continue to be explored in Artificial Intelligence research.

We do acknowledge that other choice rules might prove to be more useful to explain some data patterns in the future. For example, some human data do suggest that the ratio rule may not provide a good description of choice in categorization tasks involving more than two alternatives (Wills et al., 2000). However, the version of the ratio rule that Wills et al. (2000) tested was not the same choice rule that we present here (see Equation 8 below); direct comparison between them has not yet been conducted.

Not all categorization experiments involve a selection among several available responses as implied by Equation 5. In Go/No-go procedures, a single response is reinforced in the presence of some stimuli (“Go” trials) and nonreinforced in their absence (“No-go” trials). Furthermore, Go/No-go tasks are usually free-operant procedures, meaning that subjects are free to perform a response at any time and reinforcement can be programmed to occur as a function of several experimental variables, such as the number of responses or the time elapsed since a prior event. This task contrasts with the discrete-trial procedures discussed before, in which a single response determines the end of a trial and the delivery of reinforcement.

The choice rule described by Equation 5 can be extended to free-operant tasks following a line of reasoning first advanced by Herrnstein (1970) to explain operant behavior as a function of rate of reinforcement. In situations in which only one response is being measured, an animal still faces a choice between performing this response or any of the other available responses in the experimental environment, including simply doing nothing. If we express the unknown incentive value of all such other responses as V₀, then choice probability in Go/No-go tasks is described by the following equation:

$$p(R/S)=\frac{e^{\theta V_S}}{e^{\theta V_S}+e^{\theta V_0}}$$ (6)

In this way, response probabilities in both choice and Go/No-go tasks can be seen to arise from the same choice process in which the likelihood of a response equals its relative incentive value. Because the value of V₀ is unknown, it should be considered to be another free parameter used by the model to simulate Go/No-go experiments. Nonetheless, the results of our simulations of Go/No-go experiments are a direct consequence of the associative values that are predicted by the Rescorla-Wagner learning algorithm; the new free parameter that is presented in Equation 6 is not introduced here to provide a better fit of the model to the data, but simply to follow the theoretical motivation of using the same choice mechanism for all of the categorization tasks.

The performance measure that is commonly used in free-operant procedures is not response probability, but response rate (number of responses per time unit). We assume that response rates are directly proportional to the probabilities that are computed via Equation 6; thus, all of the simulation results are presented in terms of response probabilities. However, if better fits to actual data need to be obtained, then the following transformation can be used to compute response rates:

$$\mathit{\text{Rate}}(R/S)=p(R/S)k$$ (7)

where k representes the asymptotic rate of responding or the total number of responses that the animal can produce per time unit.

In more general terms, Equations 5 and 6 can be seen as instantiations of the following response rule:

$$p(R_j/S)=\frac{e^{\theta V_{\mathit{\text{Sj}}}}}{{\displaystyle \sum _j{e}^{\theta V_{\mathit{\text{Sj}}}}+e^{\theta V_0}}}$$ (8)

Note that V₀ has no impact in a discrete-trial forced-choice procedure, because one of the responses being measured must be produced in order to advance the trial. Under those circumstances, Equation 8 is equal to Equation 5. However, V₀ might play a role in free-operant choice procedures, which to date have not been used in the study of categorization behavior.

Application to Previous Research in Natural Categorization by Pigeons

We now present the simulated results of several experiments, which represent a large sample of the most important findings concerning the conditions that foster effective learning and transfer of open-ended categories in pigeons. In these simulations, we did not attempt to fit the free parameters of the model to the data or to perform a systematic search of the parameter space to find those parameter values that would yield the most accurate predictions. Rather, we performed an unsystematic search for the parameters that would give good results for one particular experiment (Wasserman et al., 1988, Experiment 1) and we then used those parameters in all of the other simulations. Our primary aim was to document the ability of the model to reproduce the behavioral patterns that were observed in the experimental data, even with the constraint of using the same parameters in every simulation.

The parameters a and b in the beta distribution were fixed to the values of 1.0 and 4.5, respectively, which produced a function like that depicted in Panel B of Figure 3. The value of learning rate parameter β was set to 0.02 for reinforced trials and to 0.01 for nonreinforced trials. This disparity follows the original Rescorla-Wagner formulation and it is based on the idea that the presentation of an outcome is more salient than is its absence. The value of learning rate parameter α was set to 0.1; this value should not be deemed to be another free parameter in the model, as it simply scales the result of Equation 1, something that could be obtained by changing the β parameters. Finally, the value of parameter θ in Equation 8 was set to 3.0 and the value of V₀ was set to 0.0 in simulations of the choice experiments and to 0.5 in simulations of the Go/No-go experiments.

All of the simulations were performed in an attempt to reproduce the training conditions in the original studies as accurately as possible in terms of trial, block, and session structure as well as trial randomization and other experimental procedures. A complication in simulating the results of animal studies is that, in most, there is no direct feedback about the correct response for a trial, as in the human counterpart. The only feedback given to pigeons is the presence or absence of food reinforcement; this feedback provides complete information in case of a correct trial, but it provides ambiguous information in the case of an incorrect trial if more than two choices are available. Most experiments give unambiguous feedback to the pigeon by using one or more correction trials after every incorrect response, which are repeated until the bird makes the correct response and receives food reinforcement. We did not attempt to simulate all of these procedural details; every trial simply included the presentation of a stimulus, the prediction of the model, and feedback to the model regarding the correct response on that trial.

Because the stimulus representations in the model were generated randomly, for each simulation, we present the average of 10 runs of the model, each using different probability distributions over elements and different sampled representations for individual stimuli. Note that this averaging process generates learning curves that are much smoother than the actual data, but the results of each individual simulation show a pattern of random variation which is similar to that observed in the data from individual subjects.

Category Learning and Transfer to Novel Exemplars

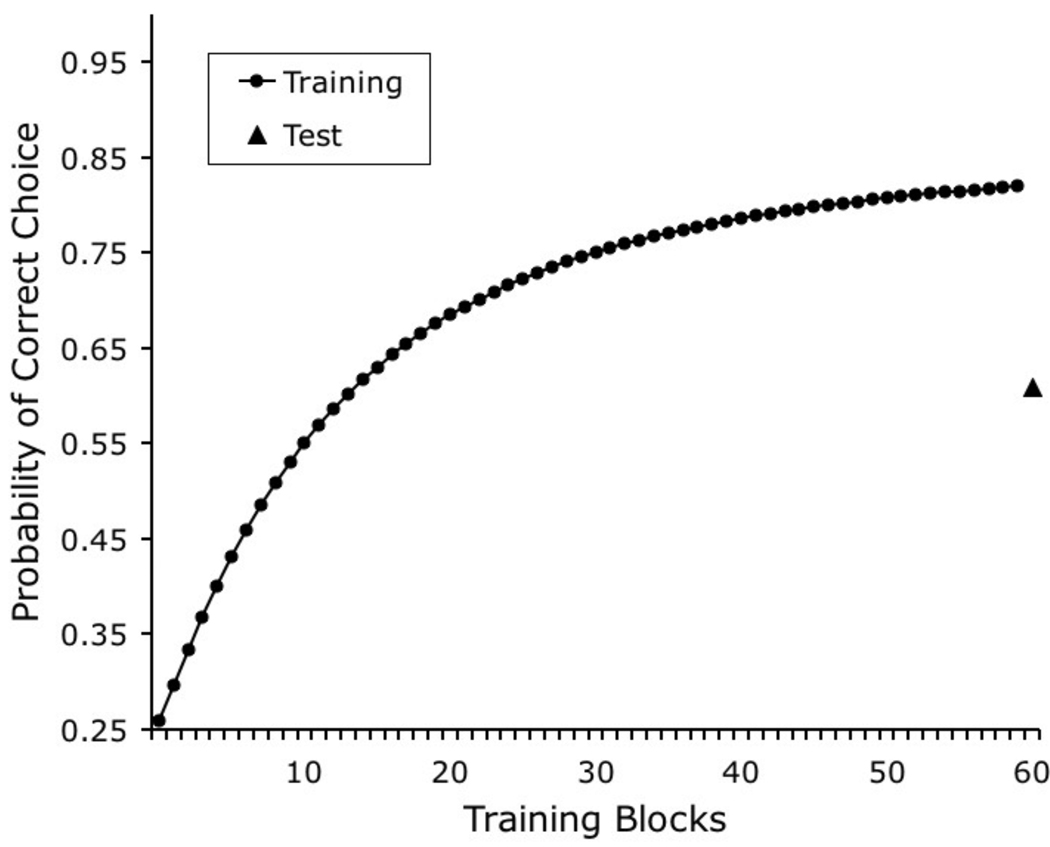
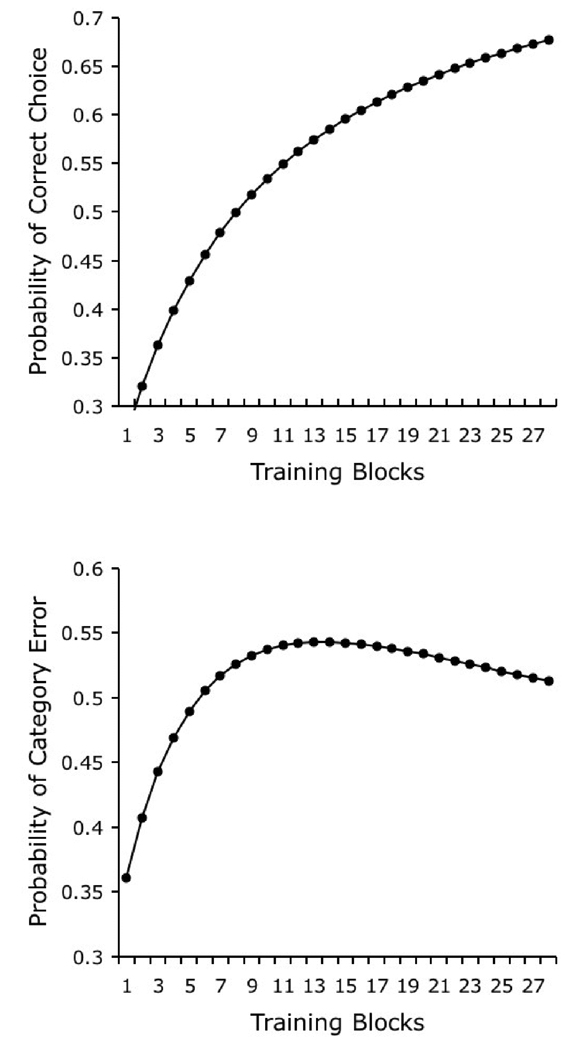
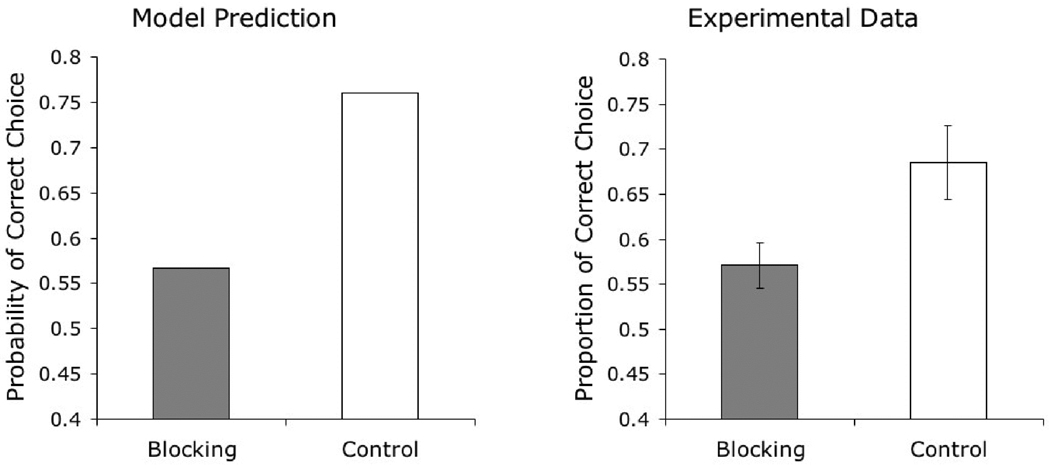
The first phenomenon that must be explained by any model of categorization is the acquisition of such behavior. In one experiment, Bhatt and colleagues (1988, Experiment 1) presented pigeons with 10 photographs from each of four real-world categories: cats, flowers, cars, and chairs. After an image was presented to the pigeon, a response to one of the four available response keys was permitted. Each key was the correct response for one of the four categories. Pigeons were reinforced with food when they chose the correct response key; they had to repeat the trial if they chose an incorrect key. Figure 4 depicts the results of a simulation of this experiment. Discrimination performance with the training exemplars increased monotonically as a function of the number of training trials, showing the negatively accelerated form that is typically produced by error-correcting models of associative learning and also found in studies of categorization by pigeons (Bhatt et al., 1988).

Figure 4.

Simulated results of Bhatt and colleagues’ (1988) experiment in categorization learning and transfer to novel exemplars of the trained categories.

A more interesting aspect of pigeon categorization performance is the transfer of discriminative behavior to novel exemplars. This transfer is interesting because it is typically interpreted as evidence of open-ended categorization (Herrnstein, 1990); thus, transfer represents a test for the presence of a behavioral phenomenon that goes beyond mere identification. The typical pattern of results in such generalization tests is reliable discrimination performance with novel images, but at a lower level of accuracy than to the original training stimuli (Bhatt et al., 1988). The same pattern can be observed in Figure 4, which shows simulated discrimination performance with novel test stimuli.

The above-chance level of transfer to new exemplars is the result of the associative value that is acquired by the category-specific elements. Recall that these elements are common to the representation of several of the stimuli in a category; therefore, their association with the correct response will frequently be strengthened during training. This frequent strengthening counteracts the lower number of category-specific elements than stimulus-specific elements in each of the hypothesized stimulus representations, thereby producing a higher rate of acquisition of category-specific associative strength than stimulus-specific associative strength. Nevertheless, stimulus-specific elements also acquire associative strength during training, which have a lower likelihood of contributing to performance to the novel test exemplars; in this way, the model produces the generalization decrement that is typically observed in tests with novel exemplars.

Effects of Category Size

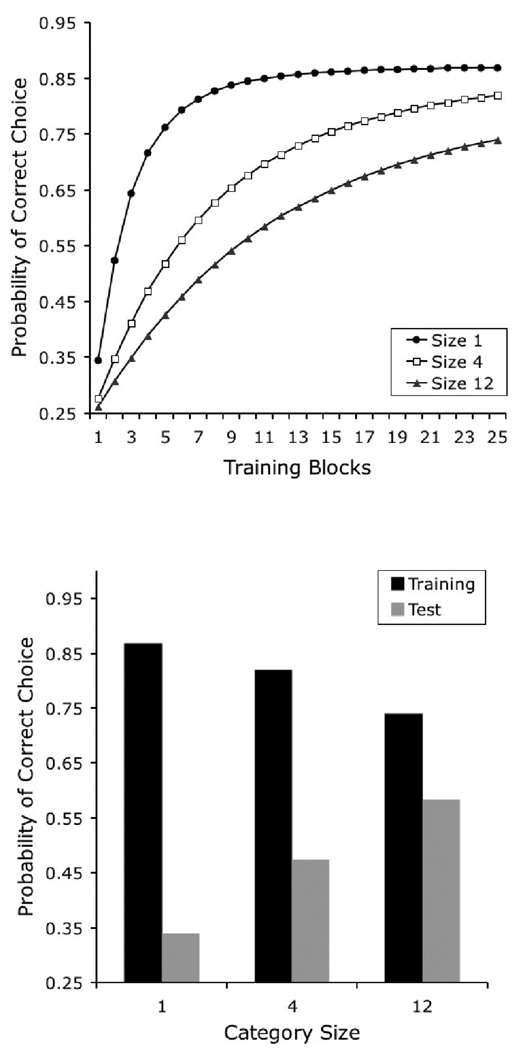
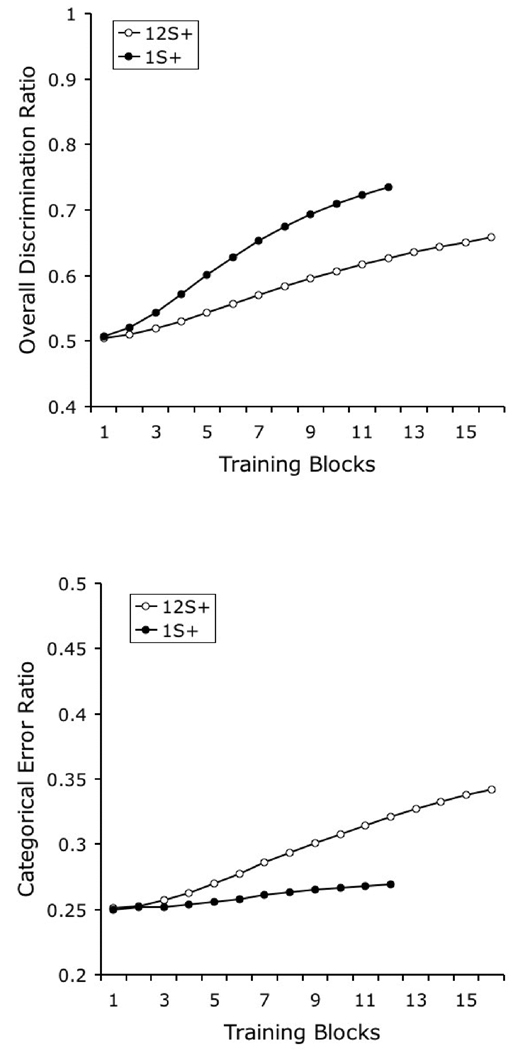
One of the most straightforward experimental manipulations that affects category learning and generalization involves changes in the number of exemplars in each trained category. In one experiment (Wasserman & Bhatt, 1992; also described in Wasserman, 1993), three groups of pigeons were given 48 daily training trials on the 4-choice task. In Group 1, each of the four categories was composed of only 1 exemplar, seen 12 times in each daily session. Group 4 was given 4 different photographs from each category, each repeated 3 times in each daily session. Group 12 was given 12 different photographs from each category, each shown only 1 time in each daily session. There were two important results of this study.

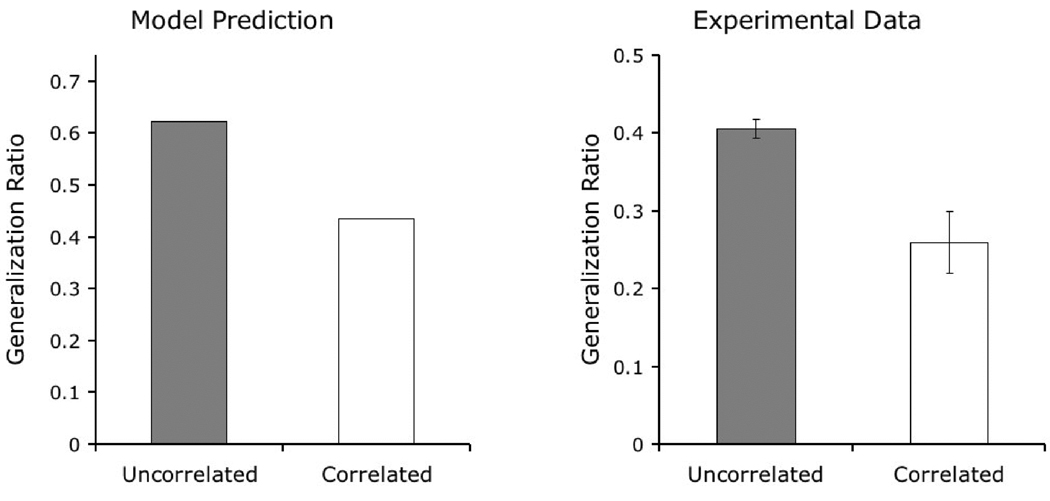
First, the speed of learning was inversely related to category size. It took about 5 daily sessions to reach a criterion of 70% correct for those pigeons trained with 1 exemplar, about 10 sessions for those trained with 4 exemplars, and more than 20 sessions for those trained with 12 exemplars. The top panel of Figure 5 shows the predictions of the model for the three training conditions in the Wasserman and Bhatt study, plotted as the probability of making a correct choice across trials. The original finding was correctly reproduced: learning speed decreased with increases in category size.

Figure 5.

Simulated results of Wasserman and Bhatt’s (1992) experiment assessing the effect of category size on category learning. The top panel shows the probability of correct choice across training and allows the comparison of learning rates for different category sizes. The bottom panel compares final performance to the training stimuli (black columns) and to the novel test stimuli (grey columns).

The correct prediction of the model is the consequence of the benefit in learning from the repetition of the same stimuli in tasks with lower category sizes. On the first trial of learning with category Size 1, all of the elements in the representation acquire some associative strength. On the second trial, when the same stimulus is presented, the response will be determined by all of the associative strength previously acquired by these elements. When category size is increased well beyond 1 item, a new exemplar is likely to be presented on the second trial with a particular category; the response on this trial will be determined by the associative strength acquired by the category-specific elements only, not by the stimulus-specific elements, which are likely to be presented for the first time. The associative strength acquired by the stimulus-specific elements will start to contribute to choice responding only when the individual exemplars are repeated; at that point, a subject trained with a lower category size will show the cumulative benefits of several previous training trials with the same exemplar.

The second relevant result observed by Wasserman and Bhatt was that the amount of generalization to novel exemplars was a direct function of category size, an effect reported by other authors using different procedures (Kendrick, Wright, & Cook, 1990). Pigeons trained with only 1 exemplar exhibited generalization performance in the test only slightly above 25% correct, those trained with 4 exemplars about 45% correct, and those trained with 12 exemplars over 55% correct. The results of our simulation of testing performance are illustrated in the bottom panel of Figure 5. Final discrimination performance with training exemplars proved to be an inverse function of the number of exemplars in each category, a consequence of the disparity in learning rate discussed above. More importantly, there was a direct relationship between the number of exemplars in each category and the extent of generalization to new test stimuli.

Remember that generalization is determined by the amount of associative strength that is acquired by the category-specific elements, because the testing items are novel and the stimulus-specific elements cannot contribute to performance. A larger category size increases the likelihood of including the same category-specific element as part of the representation of several training exemplars. If more training exemplars activate the same category-specific element, then that element acquires associative strength at a higher rate, quickly blocking the acquisition of associative strength by the stimulus-specific elements. Because generalization of performance to novel exemplars depends on the category-specific elements, if they acquire more of the available associative strength, then generalization will be higher. Moreover, a larger category size also increases the likelihood of novel testing items activating the elements that are associated with the correct response during training—that is, it increases the likelihood that a test stimulus will have a representation that is similar to one or more of the training stimuli—also contributing to higher generalization performance.

Effect of Stimulus Repetition

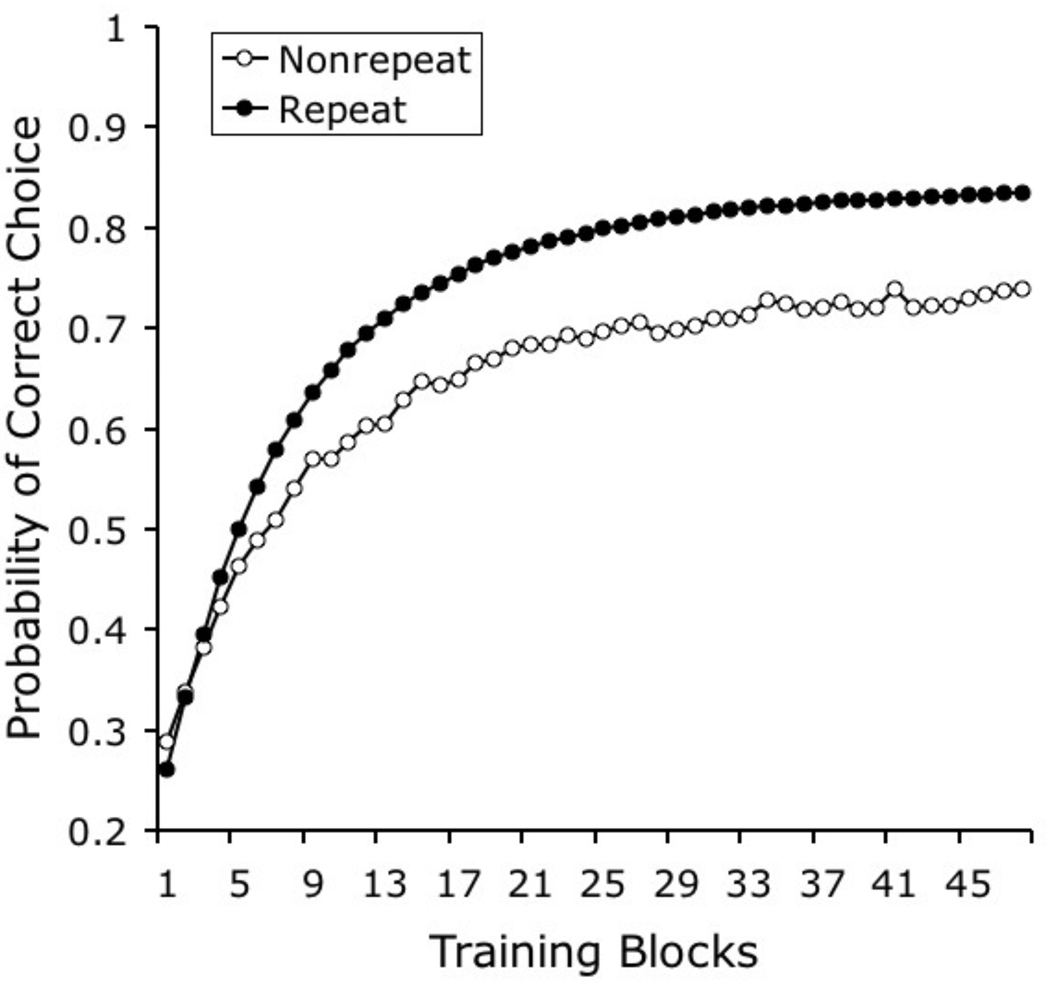
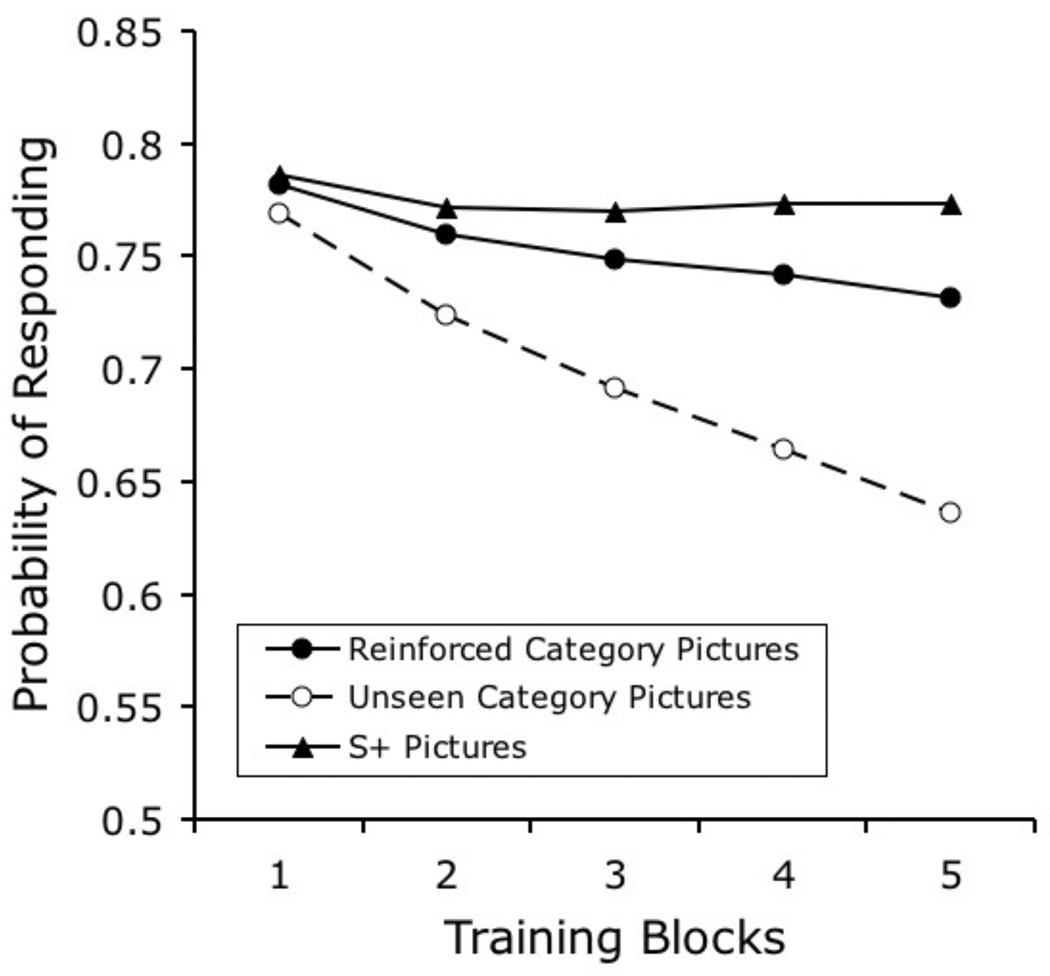
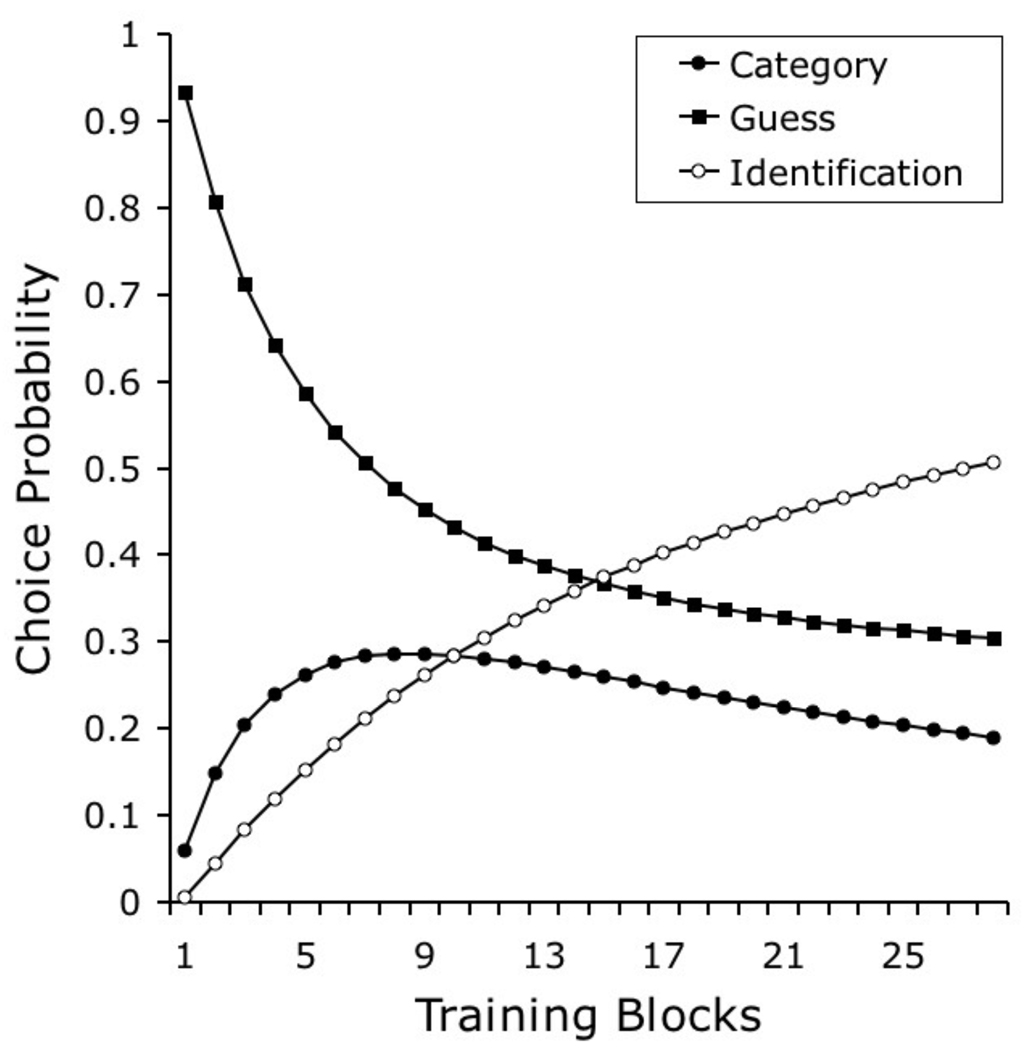
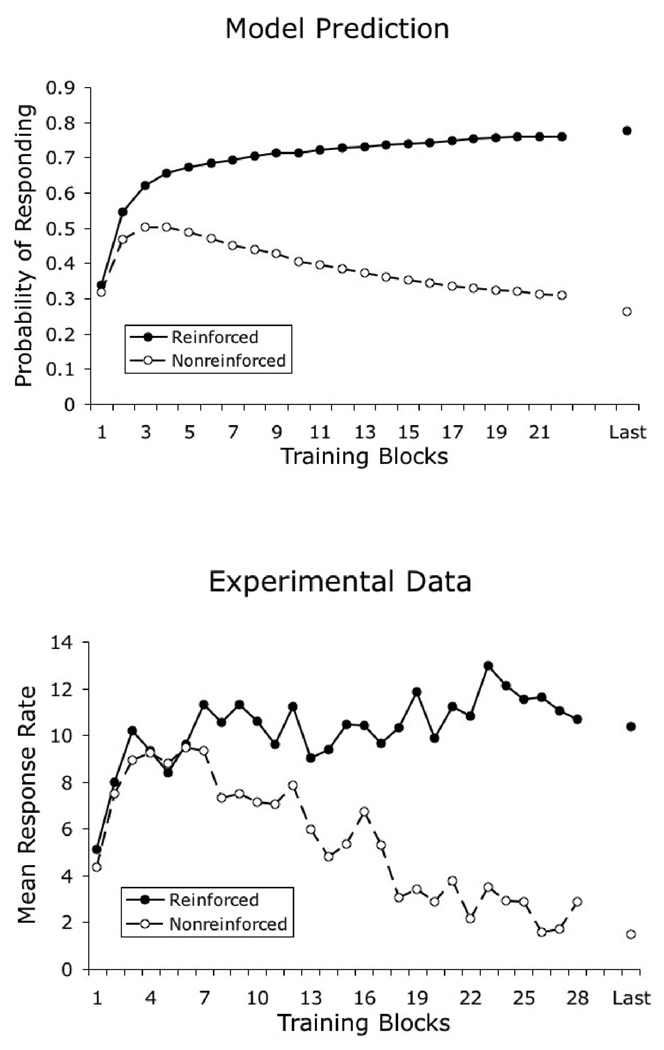
Bhatt et al. (1988, Experiment 3) found that pigeons can learn to categorize photographs of natural stimuli even when the individual photographs are never repeated. According to the model presented here, this learning is supported by the category-specific elements that are repeated on every trial, even when the specific pictorial stimuli that are shown are different on every trial.

Bhatt and colleagues (1988, Experiment 4) conducted a second experiment in the same study, in which a single group of pigeons was trained to discriminate the same 10 photographs of each category on odd-numbered days and to discriminate 10 novel exemplars of those categories on even-numbered days. The result was higher accuracy in the classification of repeating stimuli across training. Performance with repeated stimuli rose from 29% correct in the first 4 training sessions to 85% correct in the last 4 sessions; performance with non-repeated stimuli rose from 26% correct in the first training sessions to 66% correct in the last sessions.

The results of our simulation are shown in Figure 6. The predictions of the model fit the experimental results, properly reproducing the observed disparity in learning rate that develops in training with repeating and with non-repeating sets of stimuli. This disparity reflects the fact that only category-specific elements can support learning with non-repeating stimuli, whereas both stimulus-specific elements and category-specific elements can jointly support learning with repeating stimuli.

Figure 6.

Simulated results of Bhatt and colleagues’ (1988) experiment on the effect of stimulus repetition on categorization learning.

Pseudocategorization

A very important question regarding perceptual categorization concerns the possibility that pigeons recognize the perceptual coherence among members of the same category even when they are not required to do so by the training procedure. A second possibility is that pigeons independently represent information about each exemplar and associate such information with the correct response.

Evidence for the former notion comes from studies in which true category learning is compared with pseudocategory learning, pseudocategories being arbitrary sets of stimuli with no perceptual resemblance to each other. Most studies (Herrnstein & De Villiers, 1980; Wasserman et al., 1988) have found that pigeons learn to sort photographs into pseudocategories much more slowly than into true categories involving the same pictures (but see Kendrick et al., 1990). Evidence for the latter notion comes from the fact that pseudocategories are learned at all; such learning can only be achieved if pigeons are able to perceive visual properties that are idiosyncratic to each stimulus and base their discriminative responses on these properties.

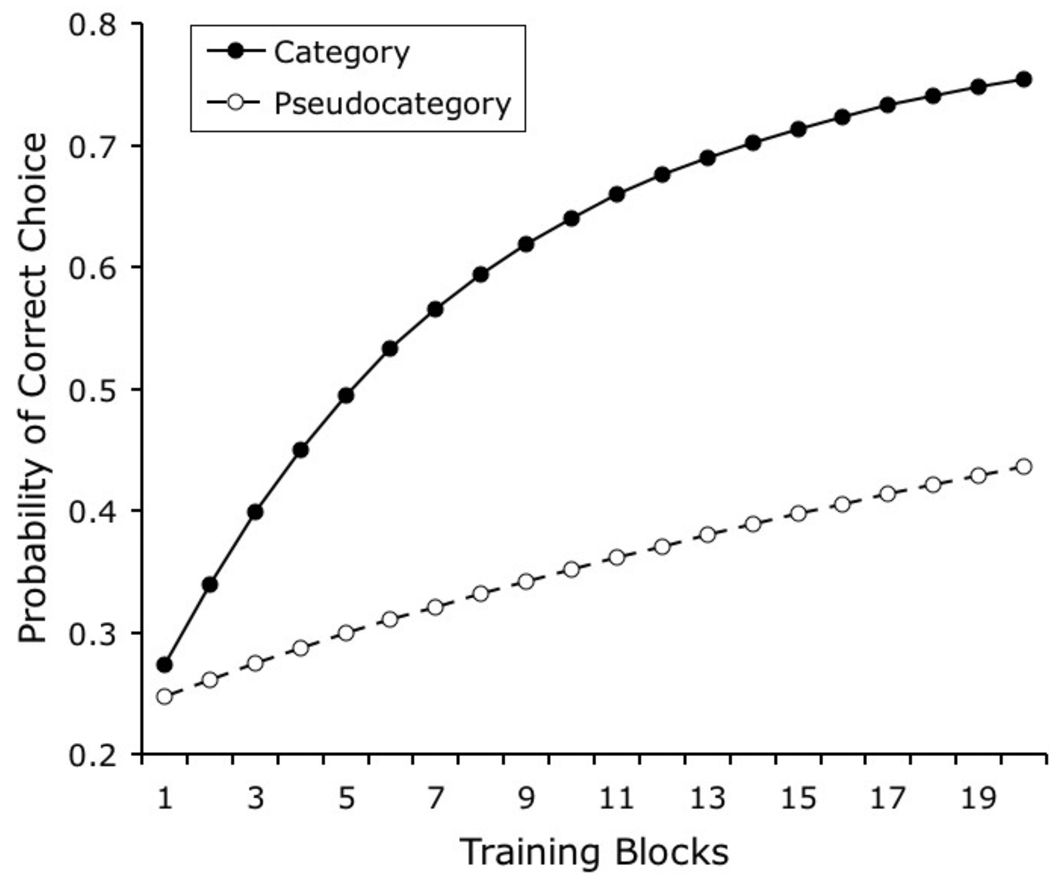
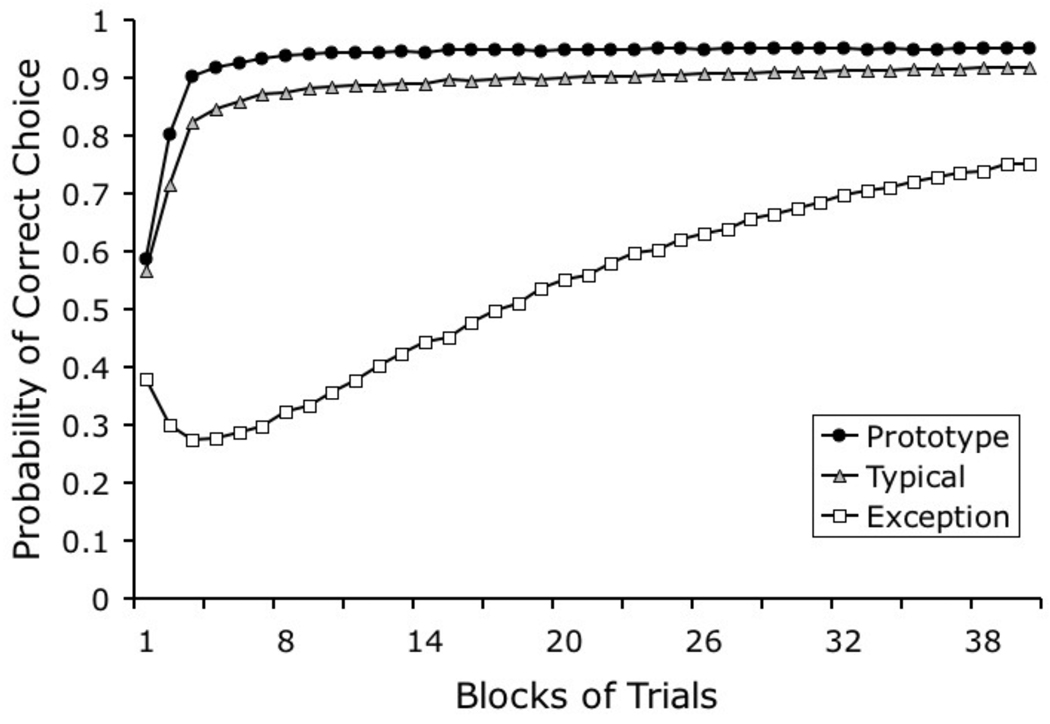
Figure 7 depicts the results that are predicted by the model when it is trained under the conditions arranged by Wasserman et al. (1988, Experiment 2). Both curves show categorization learning with the same set of 20 stimuli in each of 4 categories; the only procedural disparity is that in the pseudocategory group the stimuli were randomly assigned to arbitrary groups sharing the same outcome (5 stimuli in each category were assigned to each of the 4 pseudocategorization sets), whereas in the true category group the training categories coincided with the 4 human language groupings.

Figure 7.

Simulated results of Wasserman and colleagues’ (1988) experiment comparing learning rates for categorization and pseudocategorization tasks.

In the original study, learning of the true categorization task was quick and reached an asymptote of almost 80% correct, whereas learning of the pseudocategorization task was much slower and reached only about 40% correct at the end of the experiment. The model correctly predicts faster learning of the true categorization task; in this condition, the category-specific elements are consistently associated with the same outcome. In the pseudocategorization task, the category-specific elements have much lower informational value in predicting the outcome of a trial, as they are equally likely to be associated with each of the 4 categories. Under these conditions, performance does slowly improve with training, but this improvement is presumably ascribable to the associative strength acquired by the stimulus-specific elements.

Feature-Positive and Feature-Negative Effects

Following the methods of the pioneering experiment by Herrnstein and Loveland (1964), several studies in pigeon natural categorization have used a Go/No-go procedure, in which responses to photographs containing an exemplar from the category are reinforced and responses to photographs not containing an exemplar from the category are not reinforced. A variation of this procedure involves presenting the same background information in both category/present and category/absent slides, in order to make it difficult for the pigeons to solve the task by relying on background information alone. In this matched background task, exemplars of the category become a “feature” in the images; this feature can signal the availability of reinforcement after a response is performed, in a “feature-positive” discrimination, or it can signal the absence of reinforcement after a response is performed, in a “feature-negative” discrimination (Jenkins & Sainsbury, 1970; Sainsbury, 1971).

Some research has suggested that pigeons learn decidedly different things in the feature-positive and feature-negative tasks (Aust & Huber, 2001; Edwards & Honig, 1987). Perhaps the most basic disparity is that feature-positive discriminations are learned faster than feature-negative discriminations (Edwards & Honig, 1987).

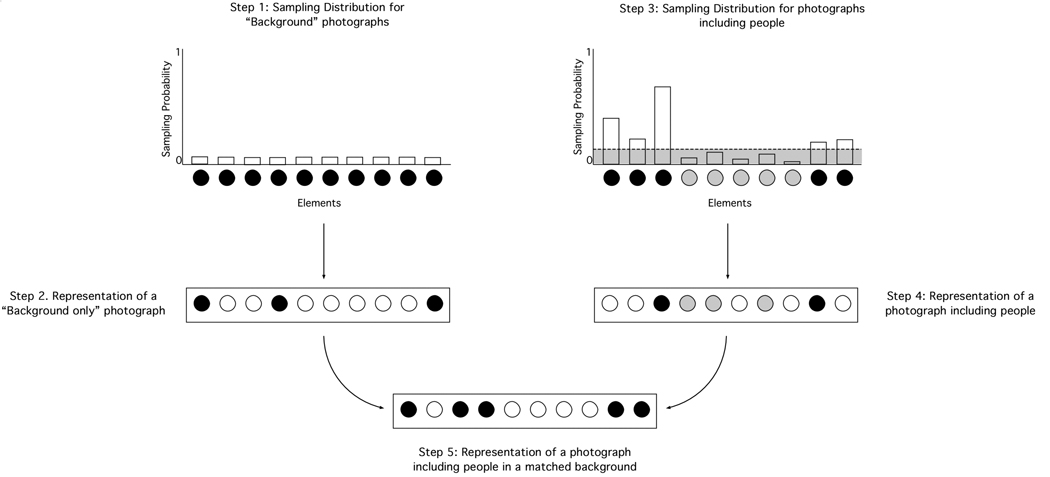
Consider the Edwards and Honig experiment. It included photographs of people on background scenes as well as photographs of the same background scenes without people; as noted above, this is a “matched” discrimination. One problem with simulating this kind of experiment involves separating the portion of the stimulus representation that represents the “background” from the portion of the stimulus representation that represents the “people.” This chore is particularly difficult in our model, in which each fragment of a photograph cannot be directly linked to a particular portion of the stimulus representation. So, it was necessary to take further steps to simulate experiments involving photographs with matched backgrounds.

In order to do so, we assumed that information about the background of an image is coded through the stimulus-specific elements in the stimulus representation, especially those with very low sampling probabilities. The reason behind this assumption is that the background of an image provides the most idiosyncratic information in any categorization task; thus, these background features should be represented through the most stimulus-specific elements. On the other hand, the objects that are presented over that background—the category exemplars and their features—are more similar to each other across different images; thus, they should be represented by more category-specific elements.

Figure 8 shows a diagram of the procedure that we used to create representations of the photographs with a matched background. The left side of the diagram shows how we created the representation for photographs of backgrounds without people. The first step was to create a sampling distribution for “background” photographs by assigning a uniformly low sampling probability to each of the elements in the pool. A uniform distribution was chosen under the assumption that backgrounds do not convey any category information which is useful in the tasks to be simulated in this section. Thus, all of the elements in the pool should have a similar likelihood of being sampled to form the representation of a background photograph. The sampling probability that was assigned to each element was set to the mean probability in the “people” distribution over elements, which allowed us to obtain representations in which the numbers of active elements were similar to those in the “people” category, but in which the active elements were more randomly distributed across the pool. These representations (Step 2 in Figure 8) were used to directly simulate the presentation of the background alone during training.

Figure 8.

Diagrammatic description of the procedure that was used to create representations of the stimuli that involved matching backgrounds. The main disparity between the matched representations is in the presence or absence of information about a category exemplar (see text for details).

The rest of the diagram in Figure 8 shows how we created representations of the photographs that included people over a given background. To solve this problem, we generated representations for images including “people” in the same way as in all of our other simulations. Thus, the third step in the process was to create a sampling distribution for the category of photographs including people. However, the representation of the category “people” was split into two parts, depending on whether an element had a sampling probability below or above a threshold value of 0.1. In Figure 8, this arbitrarily chosen threshold is represented by a dashed line in the distribution for the category “people.” Elements with a sampling probability above the threshold are assumed to convey information about the presence of “people” in the images. These elements are shown in black in the diagram. Elements with a sampling probability below the threshold are assumed to be uninformative about the presence of “people” in the images; that is, they include the “background” information in the representation. These elements are shown in grey in the diagram; taking them out of the representation (assigning them a value of zero) would be more or less equivalent to removing the background in an image including people, thus generating a “people only” representation (Step 4 in the diagram of Figure 8).

The fifth and final step that is shown in Figure 8 involved adding up the “background only” representation generated in Step 2 with the “people only” representation generated in Step 4. This process would be analogous to superimposing the fragment of an image showing people over a different background image. This representation, together with the “background only” representation that was generated in Step 2, were used to represent photographs with matched backgrounds.

Of course, the representations that were generated this way can only be thought as approximations to the representations that would be used in a matched discrimination, but they do have a theoretical foundation within our framework. The only arbitrary aspect in this process is the threshold that is chosen to classify elements as informative or uninformative about the presence of a category member. We found that the results of our simulations are robust across variations of this threshold value.

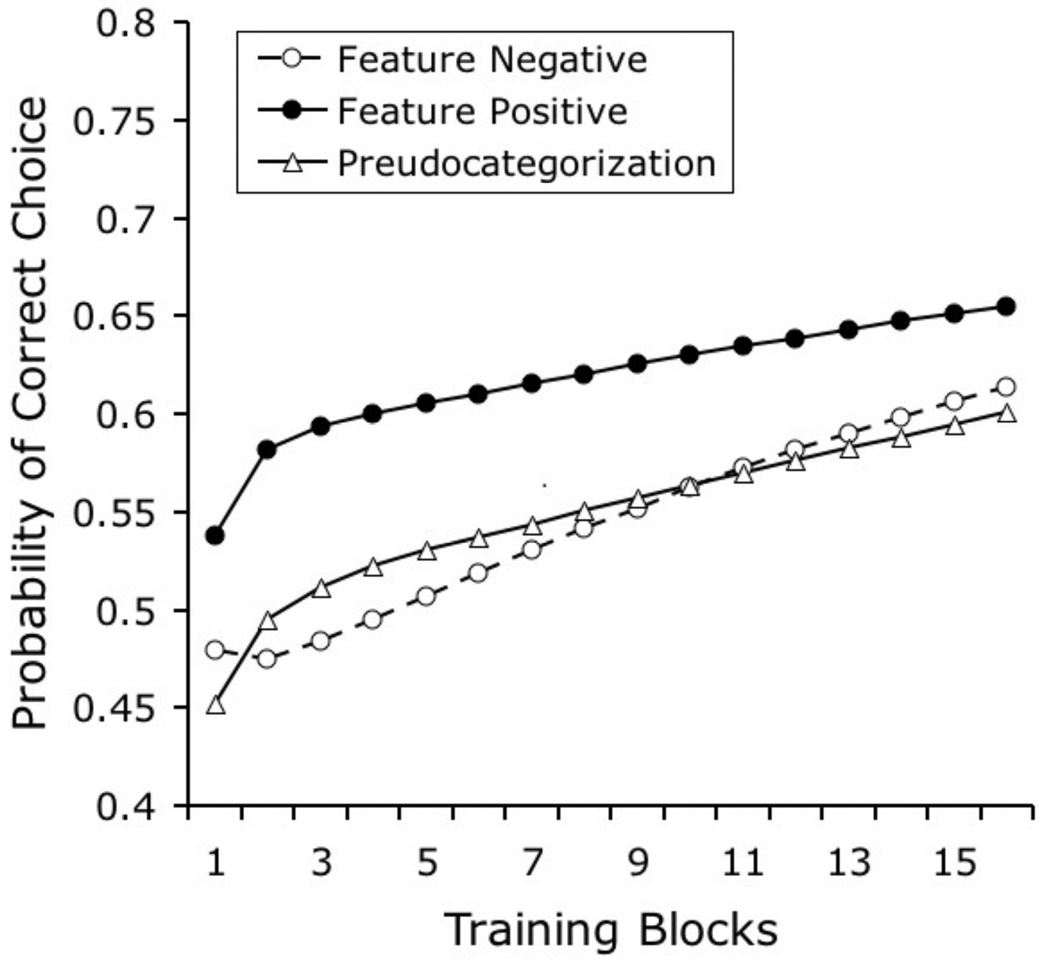
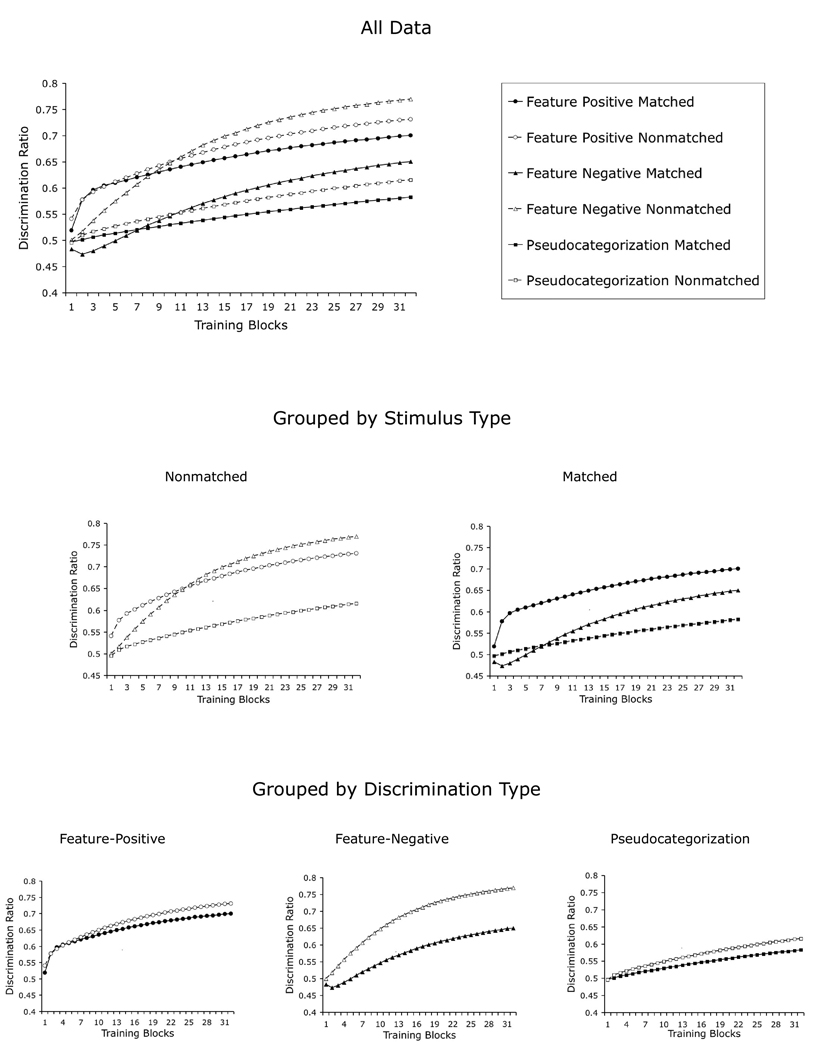
Figure 9 plots the learning curves that were obtained from our model when it was exposed to training conditions similar to those that were described by Edwards and Honig in their experiment involving matched feature-positive and feature-negative discriminations (1987, Experiment 1). The original experiment also included a pseudocategorization condition, which provided a benchmark for how fast the pigeons could learn the task if they were simply memorizing each slide and its relation with reinforcement. The feature-positive discrimination was learned faster than the other two tasks, but the feature-negative discrimination was not learned faster than the pseudocategorization task. Depending on the stimuli used, performance on the feature-positive discrimination reached a discrimination ratio of from .65 to .77; performance on the feature-negative and pseudocategorization tasks were barely above .50 across training. Figure 9 shows that the model correctly predicts the qualitative pattern of results, although it performs a bit better than the pigeons on the feature-negative and pseudocategorization tasks.

Figure 9.

Simulated results of Edwards and Honig’s (1987) Experiment 1, which compared learning rates of feature-positive and feature-negative categorization tasks with images using matched backgrounds (see text for details).

In the feature-positive condition, the category-specific elements are presented often and they very quickly acquire associative strength (on reinforced “people plus background” trials). The discrimination is complete when the associative strength that is acquired by the stimulus-specific background elements is extinguished (on nonreinforced “background alone” trials); this latter process proceeds more slowly, because these stimulus-specific background elements are occasionally reinforced.

In the feature-negative discrimination, the reinforced background stimuli are slower to acquire excitatory associative strength. Recall that the background stimuli do not share any category-specific elements; they involve only stimulus-specific elements. Therefore, the acquisition of excitatory associative strength here occurs more slowly than when such category-specific elements are presented and reinforced frequently, as in the feature-positive discrimination. Moreover, the elements representing backgrounds are also nonreinforced on some trials, further slowing learning.

In Experiment 4, Edwards and Honig (1987) studied the effect of using the same or different backgrounds for slides that did or did not include category information. The procedure involved a between-groups comparison of a feature-positive discrimination, a feature-negative discrimination, and a pseudocategorization control for memorization. More importantly, Edwards and Honig exposed each pigeon to slides that were both matched and nonmatched in their background information, alternating both sets in consecutive sessions.

The top section of Figure 10 shows the complete pattern of results for our simulation of this experiment. In order to more easily explain the successes and shortcomings of our simulation, the same results are also grouped according to the types of stimuli that were used during training (matched vs. nonmatched, see middle panel of Figure 10) and the discrimination to which each group was exposed (feature-positive, feature-negative and pseudocategorization; see bottom panel of Figure 10).

Figure 10.

Simulation of Edwards and Honig’s (1987) Experiment 4, which involved a factorial design with feature-positive and feature-negative discriminations using both matched and nonmatched backgrounds (see text for details).

As to the comparison between matched and nonmatched stimuli, in the original experiment, the nonmatched procedure led to an attenuation of the feature-positive effect that was previously observed with the matched procedure. This result is observed in the simulated results that are presented in the middle panel of Figure 10, where the disparity between the feature-positive and the feature-negative learning curves is larger in the matched than in the nonmatched procedure. This disparity arises because partial reinforcement of the common backgrounds in the matched tasks slows learning in the feature-negative discrimination more than in the feature-positive discrimination.

To understand this result, note that mastery of any of these discriminations requires the acquisition of excitatory associative strength by the elements that get consistently reinforced and the acquisition of inhibitory associative strength by the elements that get consistently nonreinforced. More importantly, excitatory learning has to occur earlier than inhibitory learning because, according to the Rescorla-Wagner learning rule, inhibitory learning only happens in an excitatory context (only when there is “something to inhibit”). With all of this in mind, note that in a feature-positive discrimination, whether matched or nonmatched, excitatory learning occurs quickly from the beginning of training because of the consistent and repetitive reinforcement of category-specific elements. The main effect of partial reinforcement of the backgrounds in the matched condition is to slow inhibitory learning late in training. In a feature-negative discrimination, the acquisition of excitatory strength depends on the background elements, which are the only ones that are present on reinforced trials. Partial reinforcement of the backgrounds in the matched condition has the effect of slowing excitatory learning at the outset of training and, as a consequence, inhibitory learning later in training.

The empirical data also showed that, for the nonmatched stimuli, performance on both feature-positive and feature-negative discriminations was similar and higher than performance on the pseudocategorization task, with an advantage of the feature-positive discrimination over the feature-negative discrimination early in training, a relation that was later reversed. All of these results are also observed in the simulated results (see the middle panel of Figure 10). On the contrary, for the matched stimuli, performance on the feature-negative discrimination and the pseudocategorization task was lower than on the feature-positive discrimination, a pattern that was also observed in the early stages of our simulation. Note that our simulation shows an advantage of the feature-negative discrimination over the pseudocategorization in later stages of training, which was not observed in the experiment. This result is difficult to interpret in light of the available data, in which all of the matched tasks supported rather low levels of performance like those observed only early in training in our simulation.

As to the comparison between matched and nonmatched tasks within each type of discrimination, Edwards and Honig observed that all of the discriminations were acquired more rapidly with nonmatched stimuli than with matched stimuli. These authors also highlight the fact that the feature-negative discrimination group showed the greatest disparity in performance between problems. The graphs in the bottom section of Figure 10 illustrates that our model correctly predicts faster acquisition of all of the nonmatched discriminations than the matched discriminations. This disparity arises because in matched discriminations the same background is presented in both “people present” and “people absent” photographs, leading to partial reinforcement of the elements representing the background; this process slows learning in the matched condition, but it is absent in the nonmatched condition.

The main aspect of the experimental data that is not reproduced by our simulation is that performance in all of the nonmatched conditions exceeded that in all of the matched conditions throughout training. It can easily be observed in the top panel of Figure 10 that our simulation does not capture this aspect of the data: not all of the nonmatched conditions, represented by open shapes, are above the matched conditions, represented by solid shapes. Only the feature-positive and feature-negative discriminations differ in this way late in training.

We suspect that this failure to account for this aspect of the data is due in part to our inability to more reliably reproduce the disparities between the matched and nonmatched stimuli. The method used here to represent stimuli sharing a background (see Figure 8) takes stimulus-specific elements out of one representation with the goal of extracting its “background” information. Such a procedure does not make a distinction between the stimulus-specific elements actually representing the background of a photograph and those representing specific properties of a category exemplar; thus, our simulation should be considered only a rough approximation to the way animals actually represent matched stimuli. Despite this limitation, our model is still able to reproduce several of the most salient disparities between conditions found in the original experiment by Edwards and Honig.

As well, nonsystematic explorations of the parameter space of our model suggest that it is possible to reproduce the ordinal arrangement of conditions found by Edwards and Honig in the later stages of training, which is are data used by these authors in their statistical analyses. Specifically, higher values for α (0.60) and the cutoff parameter used to build matched representations (0.35) yield such results. An even more systematic exploration of the parameter space is necessary to determine whether it is possible to offer a better fit of the model to the data.

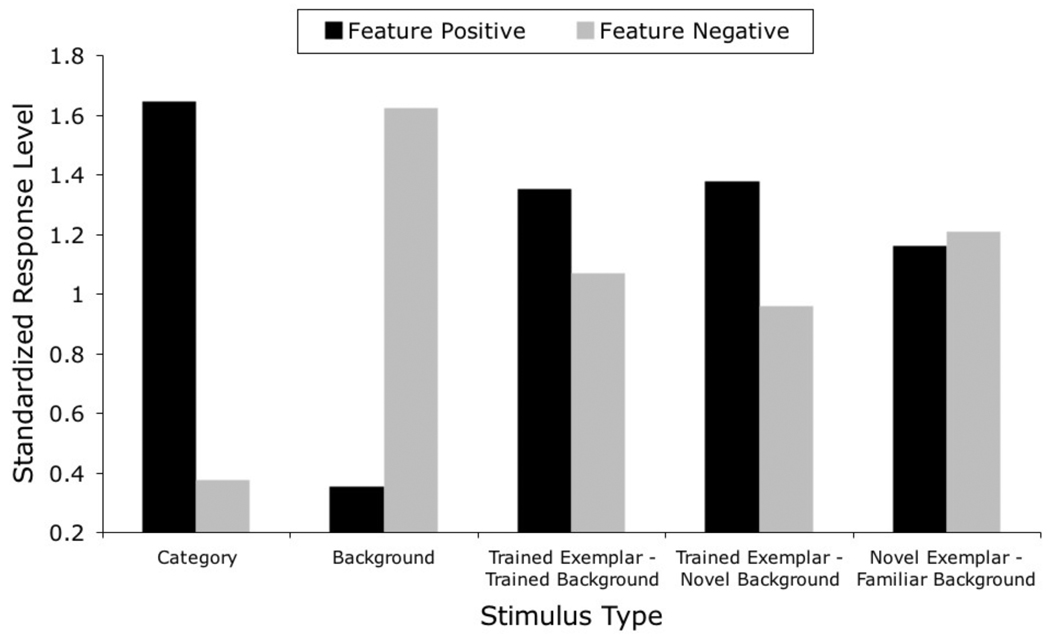
In a more recent study, Aust and Huber (2001, Experiment 3) reported evidence that feature-positive and feature-negative discriminations also differ in the degree to which discriminative behavior generalizes to untrained stimuli. In this experiment, after nonmatched feature-positive and feature-negative training, pigeons were given several combinations of trained and novel category exemplars placed on trained and novel backgrounds, with the goal of pitting category information against background information. The more interesting testing stimuli involved combinations of category exemplars and backgrounds that involved conflicting information. These combinations included familiar exemplars on a familiar background (which involved contradictory information acquired through training) and novel exemplars on a familiar background (which put into conflict information acquired in training about the backgrounds and any general learning about the category). Familiar exemplars on a novel background were included as a control, because they did not present conflicting information.

The key result was that, for pigeons trained on the feature-positive procedure, responding to all of the testing stimuli was generally similar to responding to the training exemplars of the relevant category. Because the testing stimuli included information about both the trained category and various backgrounds, this result suggests that discriminative performance was controlled mainly by categorical information in the images, with lesser behavioral control exerted by background information. On the other hand, pigeons trained on the feature-negative procedure did not show such robust generalization; rather, their responding was intermediate to that between the positive and negative training stimuli.

Figure 11 shows the simulated results for both the trained stimuli and the untrained (testing) stimuli. The y-axis represents the standardized response level, computed as the mean response probability acquired by stimuli in that testing condition over the mean response probability for the trained stimuli. A standardized response level equal to 1.00 indicates no preference to classify a stimulus either as a member or a non-member of the category. The standardization process was used to make the simulated results more readily comparable to the data published by Aust and Huber (2001). In the feature-positive condition, a value higher than 1.00 indicates a tendency to classify the stimulus as a member of the category, whereas a value lower than 1.00 indicates a tendency to classify the stimulus as a non-member of the category. The reverse is true for the feature-negative condition.

Figure 11.

Simulated results of Aust and Huber’s (2001) categorization study of feature-positive effects on generalization performance to novel exemplars of the trained category.

The general pattern of results is very similar to the empirical data. For the simulated feature-positive condition, the standardized response level of the testing stimuli is always higher than 1.00, indicating that these testing stimuli are classified as category members. In the original data, this measure of performance was between 1.5 and 2.0 for all stimulus types. The same level of categorical control was not found in the feature-negative condition, in which the testing stimuli showed a more intermediate level of standardized response level. In the original data, the standardized response rate was between 0.75 and 1.25 for all stimulus types in the feature-negative condition.

In the feature-positive discrimination, a high level of excitatory associative strength is acquired by the category-specific elements, which are presented and reinforced very often (on feature plus background trials). The background representations presented on nonreinforced trials have their active elements more uniformly distributed in the pool, so the likelihood of sampling a category-specific element is not very high (on background only trials). When one of the category-specific elements is activated on these trials, all of the other elements in the representation acquire inhibitory associative strength in equal amounts. The final result is that excitatory associative strength converges mostly on a small group of category-specific elements, whereas some small amount of inhibitory associative strength is spread among all of the other stimulus-specific elements. This distribution of excitation and inhibition is transferred to the test stimuli, so that when an exemplar of a person is presented on a novel or a familiar background, the presence of highly excitatory category-specific elements produces standardized associative strength scores that are higher than 1.0.

The learning process in the feature-negative discrimination is different, because here the more distributed stimulus-specific background representations are reinforced, which allocates excitatory associative strength more or less equally among all of the elements in the pool. When the more localized representations of category exemplars are presented, only a subgroup of these excitatory elements in the pool is sampled and a small amount of inhibition is allocated, mostly to the category-specific elements. This inhibition does generalize to the test stimuli, but so too does the excitation that is widely spread across the pool of elements as a consequence of the reinforcement of stimulus-specific background representations. The net result is a level of performance that is generally intermediate between those shown to the reinforced and the nonreinforced training stimuli.

One aspect of the data that were reported by Aust and Huber (2001) that is not captured by the simulation is that pigeons’ performance with test stimuli in the feature-positive condition did not differ significantly from performance with stimuli reinforced during training. Our simulation predicts a generalization decrement for all test stimuli. This prediction reflects the stimulus representation of our model and is consistent with the results of numerous reports of this effect in the literature (e.g., Bhatt et al., 1988; Kendrick & Wright, 1990; Wasserman, 1993). We suggest that it would be hasty to conclude that Aust and Huber’s results constitute an exception to this empirical finding, especially because that conclusion would be based on a null result obtained with only two pigeons.

As to specific disparities in performance among the test stimuli, our simulation reproduces the ordinal relations found in the feature-positive condition, but the magnitude of one difference is exaggerated. Specifically, the model predicts a substantially lower level of responding for Novel Exemplar–Familiar Background stimuli that was not observed in the empirical data. In the feature-negative condition, the ordinal relations among the test stimuli are not reproduced by our simulation, mainly because performance with Trained Exemplar–Novel Background stimuli is predicted to be slightly below 1.0, whereas in the empirical data it is slightly above 1.0.

Aust and Huber report no consistent disparities in performance to these various test stimuli; thus, the disparities that are predicted by our model are again compared to a null result obtained with a very small number of pigeons. Furthermore, Aust and Huber did not test whether performance with their stimuli was significantly above or below 1.0.

In conclusion, our model is able to reproduce the most important results in Aust and Huber’s experiment: generalization of categorization learning in a feature-positive discrimination and the absence of such generalization in a feature-negative discrimination. The model predicts some disparities among test stimuli that were not found in the data, but it is difficult to draw a conclusion based on null results from a test entailing low statistical power.

Within-Category Stimulus Generalization

Some researchers have proposed that animals’ categorization behavior is the direct result of perceptual mechanisms (Astley & Wasserman, 1992; Herrnstein & De Villiers, 1980). Members of the same class of objects are directly perceived to be more similar to each other than to members of other classes of objects, which in turn is the basis for the stronger generalization of responding within the category than across categories.

To test this hypothesis, Astley and Wasserman (1992, Experiments 1 and 2) conducted a study in which pigeons were first trained to receive food reinforcement for pecking several different photographs from each of four categories. In their first experiment (Condition 1S+), pigeons during discrimination training kept receiving food for pecking one of the photographs, but not for pecking any of the other photographs. These nonreinforced photographs were composed of a set of 12 images from the same category as the reinforced stimulus plus 12 images from each of 3 other categories. Extinction of responding should have been slower for negative stimuli from the same category as the positive stimulus if these stimuli were directly perceived to be more similar to each other than to members of the other 3 categories. In a second experiment (Condition 12S+), 12 different exemplars of the target category were reinforced during discrimination training instead of only 1 exemplar.

The results were presented in terms of two behavioral measures: the Overall Discrimination Ratio (ODR) and the Categorical Error Ratio (CER). The ODR is a measure of the level to which response rate to the reinforced stimuli was higher than response rate to all of the negative stimuli; it showed that discrimination learning was faster for pigeons trained with only 1 photograph as the positive stimulus than for pigeons trained with 12 photographs as the positive stimuli, with both groups reaching comparably high levels of performance at the end of training (ODR higher than 0.9). The CER is a measure of the level to which the response rate to the negative stimuli from the same category as the reinforced pictures exceeds the response rate to the negative stimuli from the 3 different categories. The CER approaches 1.00 if all of the responses to the negative stimuli are allocated to the reinforced category and it approaches .25 if responses are evenly distributed across the 4 categories. This CER measure rose slightly and irregularly over .25 for pigeons trained with only 1 reinforced exemplar, whereas there was a more marked increase for pigeons trained with 12 different reinforced exemplars. The measure seemed to reach an asymptotic level in both groups between 6 and 10 sessions of training, reaching a value higher than 0.5 for pigeons trained with 12 exemplars and about 0.4 for pigeons trained with 1 exemplar. With further training, the CER fell slightly in both cases.

Astley and Wasserman (1992) interpreted this pattern of results as evidence of greater generalization of responding to members of the same category, consistent with the proposal that perceptual mechanisms underlie the categorization of photographs by pigeons. The low level of within-category generalization observed in the 1S+ condition was explained as the result of perceptual disparities among members of the same category. With only 1 reinforced stimulus, the chance of that 1 stimulus resembling the 12 negative stimuli from the same category would be much lower than the chance that 1 or more of 12 reinforced stimuli would resemble the 12 negative stimuli from the same category.

Perceptual coherence among members of the same category is the most important principle underlying our model’s stimulus representation; therefore, it has no problem reproducing the data reported by Astley and Wasserman (1992). We ran a simulation of the two previously described experiments and computed the two behavioral measures reported in the original study directly from the associative strength acquired by each stimulus. The results are portrayed in Figure 12, with ODR plotted in the top panel and CER plotted in the lower panel. The model reproduced the key experimental results: (a) there was faster discrimination learning in the 1S+ condition than in the 12S+ condition according to the ODR and (b) the CER rose more markedly in the 12S+ condition than in the 1S+ condition. Although not shown in Figure 12, the model also predicts that with enough training the ODR for both groups should reach similar asymptotic levels and that the CER in both groups should quickly reach its highest point (higher for the 12S+ condition) and fall slowly with further training. Thus, the model captures the full pattern of data observed by Astley and Wasserman at a learning rate comparable to that shown by the pigeons.

Figure 12.

Simulated results of Astley and Wasserman’s (1992) experiment comparing generalization of responding to members of a reinforced category and to exemplars from different categories. ODR and CER measures (see text for details) are reported in the top and bottom panels, respectively.

The mechanisms underlying the effect of category size on the rate of discrimination learning have already been explained; therefore, we focus on the CER effect. During baseline training, all of the stimuli are reinforced and associative strength is allocated to each of the presented elements. In discrimination training, the elements representing the S+ retained most of their associative strength due to continuing reinforcement, whereas the associative strengths of all of the other elements was extinguished. Thus, disparities in response rate among the nonreinforced stimuli were due to differences in the proportion of elements that they shared with the reinforced stimuli. Because stimuli belonging to the same category have a higher likelihood of sharing elements than do stimuli belonging to different categories, response rate was higher to the negative stimuli belonging to the same category as the positive stimuli. This effect is clearly evident in the 12S+ condition, where larger category size provides a greater opportunity to sample and reinforce category-specific elements supporting generalization to other exemplars of the same category. The same is not true in the 1S+ condition, where the same small group of elements is repeatedly presented and reinforced. Just as proposed by Astley and Wasserman (1992), the results of their experiments should be the direct consequence of the principle of perceptual coherence in natural categories that we formalized in the model.

Sutton and Roberts (2002) proposed a different interpretation for the results of Astley and Wasserman. Sutton and Roberts suggested that pigeons do not immediately perceive objects in the same category to be more similar to one another than to members of other categories; rather, the process of differential reinforcement leads them to direct their attention to disparities among the pictures.

To test this hypothesis, Sutton and Roberts (2002, Experiment 2) trained pigeons to peck 20 exemplars in one category to obtain reinforcement, but without any other training trials involving nonreinforcement of another category. Without the requirement of discrimination performance, the pigeons did generalize their pecking behavior to novel exemplars from the same category that was previously reinforced; however, the pigeons also generalized their pecking behavior to novel exemplars from a different category that was never previously reinforced. Specifically, novel stimuli from both the trained and unseen category supported similarly high levels of responding in the first 2 sessions of training; afterward, responding to stimuli in the unseen category dropped, whereas responding to novel stimuli in the reinforced category stayed at a high level, slightly below responding to the training stimuli. The authors contended that these results “appear to challenge the conclusions … that perceptual constraints lead pigeons to detect within-category similarity immediately upon the perception of pictures in the same category” (Sutton & Roberts, 2002, p. 342).

Although the model that we have formalized includes perceptual coherence as an important principle underlying categorization, generalization among stimuli is not simply the result of perceptual similarity, because the elements that support generalization can acquire different amounts of associative strength depending on their associative histories with the relevant categories. This way, a category-specific element that has been repeatedly paired with the same outcome, if it is not presented together with any other elements that are also good competitors to acquire associative strength, will support high levels of generalization to new members of the category. However, if the category-specific element is presented together with good competitors which can prevent it from acquiring associative strength, then the amount of categorical generalization that it can support will be substantially lower.

Our model can explain the results reported by Sutton and Roberts if a seemingly small detail of their experimental procedure is taken into account: as is customary in categorization experiments, pigeons were given a pretraining phase in which they learned to peck a white screen to obtain food. Learning in the pretraining phase has to proceed effectively in order for pigeons to sustain high and stable rates of responding to the white screen; more importantly, whatever properties of the white screen control behavior, they must also be present in any new training stimuli in order to foster high generalized pecking to them. In most cases, later training with discrimination tasks renders these properties uninformative as to the occurrence or nonoccurrence reinforcement; so, their control over responding is gradually decreased, passing to the more relevant properties in the training stimuli. Sutton and Robert’s study did not involve a phase of discrimination training; thus, the influence of properties that are common to all of the stimuli could have prevailed during testing.

Our model can explain the results of the Sutton and Roberts experiment by representing the properties that acquire control over behavior during pretraining through a small set of elements, which acquire associative strength due to repeated pairing with reinforcement. This associative strength is then generalized to the training stimuli, which share these elements with the stimulus presented during pretraining. The fast and high transfer of responding that is usually observed between pretraining and discrimination training in pigeon experiments like those reviewed above lends support for this assumption.

The high generalization that is controlled by the white screen elements effectively limits the amount of associative strength that is available during the training phase, thereby blocking acquisition of the association between all of the other elements and the reinforcer. At the beginning of the subsequent testing phase, there is high generalization of responding to new exemplars from both the same category and from a different category, because of the associative strength that is acquired by these pretrained elements.

We performed a simulation involving a pretraining phase, in which a set of only five elements was presented and reinforced. This set of elements represented the aspects of the training situation and the white pretraining screen that are shared with all of the other stimuli in this experiment. Therefore, the same five elements were included in the representation of all of the other stimuli throughout the simulation. The results are shown in Figure 13. The pattern of results is similar to that found by Sutton and Roberts. At the beginning of testing, associative strength generalizes to exemplars of both the reinforced and novel categories; however, in later sessions, associative strength drops precipitously only for the novel category exemplars. Other simulations have confirmed that the model can still nicely reproduce the results of Astley and Wasserman (1992) if the pretraining phase is included in the simulation as well. The disparity between the 1S+ and 12S+ conditions is reduced in comparison to the previously reported simulations, but the general pattern is the same as that illustrated in Figure 12.

Figure 13.

Simulated results of Sutton and Roberts’ (2002) experiment comparing generalization of responding to members of a reinforced category (the only one that was presented during training) and exemplars from a different category.

To summarize the results and analysis so far, our account of the discrimination and generalization of natural categories importantly depends on the notion of perceptual resemblance among members of the same category. Nonetheless, our account is not purely a result of stimulus generalization based on perceptual similarity. Instead, this account places special emphasis on the interaction between perceptual similarity and error-driven learning. Together, these two processes allow us to explain the results of Sutton and Roberts (2002) without abandoning the principle of perceptual coherence that is basic to the stimulus representation in the model.

A final study examining the issue of within-category similarity was conducted by Wasserman, Kiedinger, and Bhatt (1988, Experiment 1). This study is particularly important because it sought evidence of both the ability of pigeons to discriminate the exemplars within a natural category and their ability to perceive these exemplars as more similar to each other than to exemplars from other natural categories.

In this experiment, Wasserman and colleagues used 20 exemplars from each of 4 natural categories (cats, flowers, cars, and chairs) and assigned them to 2 subcategories composed of 10 exemplars each. In any given session, the pigeons were presented with photographs from 2 of the 4 categories, which had to be sorted into 4 subcategories, each associated with an individual response key. This design allowed the experimenters to evaluate the ability of pigeons to discriminate among members of the categories, because only by identifying the individual members of each subcategory could the birds raise their choice accuracy above 50%.

The study also allowed the experimenters to examine the types of errors that pigeons make when they are learning the subcategorization problem. If the pigeons did not perceive the members of one category to be more similar to each other than to members of the other categories, then the pigeons’ errors should have been evenly distributed across the choice responses. But, if the pigeons did perceive the visual coherence of the 4 natural categories, then they should have made a disproportionate number of errors to the response key that was associated with the same category as the correct choice.

The pigeons were indeed able to learn this subcategorization task and to discriminate among members of the same natural class at high levels of accuracy (about 70% on average in the last 8 daily sessions). As well, the percentage of categorical errors that were committed by the pigeons rose monotonically as a function of the amount of training, from the chance level of 33% to a final level near 55%. The latter result can be construed as support for a perceptual mechanism underlying natural categorization in pigeons.

The results of a simulation of this experiment are shown in the top and bottom panels of Figure 14. The model faithfully reproduces both pigeons’ ability to discriminate among stimuli within the same category (top) and the initial increment in their commission of categorical errors (bottom). Discriminative performance (top) is possible because of the presence of exemplar-specific elements to support it. Categorical errors (bottom) are the outcome of a rapid increase in the association between category-specific elements and reinforced responses. Although category-specific elements are not good predictors of the correct response, they are active any time an exemplar of a particular category is presented. The fact that category-specific elements occur much more often than stimulus-specific elements puts the latter elements at a decided disadvantage to compete for the acquisition of behavioral control. Thus, category-specific elements rapidly get associated with the two choice keys that are assigned to exemplars of a particular category, thereby supporting high error rates to those choice keys whenever members of that category are presented.

Figure 14.

Simulated results of Wasserman and colleagues’ (1988) experiment assessing pigeons’ performance in a subcategorization task. The top panel shows the probability of correct choice as a function of training. The bottom panel shows the proportion of categorical errors across training.

One point of divergence between our simulation and the experimental data is that the latter does not show a decline in the percentage of categorical errors late in training. In our simulation, the probability of categorical error rises to a ceiling of 0.54 and then slowly decreases to reach 0.51 at the end of the experiment. It is possible that an effect of only 4 percentage points was simply obscured by random variability in the original experiment. However, the model predicts that categorical errors should steadily decline with further training. Therefore, a replication of the original experiment by Wasserman and colleagues with a larger number of training sessions should lead to a detectable decrement in the proportion of categorical errors. This prediction remains to be tested.

Precedence of Categorization Learning over Identification Learning

The two most influential approaches to explaining human categorization are prototype theories (Posner & Keele, 1968; Reed, 1972) and exemplar theories (Kruschke, 1992; Nosofsky, 1986; Medin & Schaffer, 1978). These theories differ in the role that each proposes for the abstraction of category information from experience with exemplars of the category.

Prototype theories propose that, in categorization tasks, humans store a unique representation summarizing their experience with all of the exemplars of the category. This prototype represents an abstraction of the central tendency in the experienced distribution of exemplars insofar as their perceptual properties are concerned. Classification of a new stimulus as a member of a category will depend on its similarity to the stored category prototype.

Exemplar theories propose that humans store representations of the individual instances of a category that are experienced; therefore, no process of abstraction intervenes between the perceived exemplars and their representation and storage. Classification of a new stimulus as a member of a category depends on its similarity to all of the exemplars that have been stored as members of that category.

The category-specific elements in the stimulus representation of our model play the role of a summary representation of the experiences that organisms have had with several category members, in a process akin to prototype abstraction. But, our model also includes stimulus-specific elements, which convey more particular information about previous experience with the exemplar(s) that activate(s) them. What is more important, the part that is played by either kind of information in stimulus classification is completely constrained by learning from exposure to the experienced environmental conditions. This aspect of the model allows it to faithfully reproduce several interesting aspects of the interplay between categorization and identification.

The subcategorization experiment of Wasserman et al. (1988), discussed in the prior section, allowed these authors to indirectly evaluate the relative roles of these processes in the discrimination behavior of their pigeons. Wasserman et al. re-analyzed their data according to the following logic: when a pigeon makes a choice, it might be (a) correctly identifying the stimulus and making the correct response, (b) correctly categorizing the stimulus and evenly distributing its pecks to the 2 responses that are associated with the correct category, or (c) guessing, leading to evenly distributed choices of all 4 responses. Their re-analyzed results revealed that, as training advanced, guessing progressively fell, identification progressively rose, and categorization initially increased, but later decreased. Even more interestingly, pigeons were initially inclined to process the stimuli at the categorical level, but this inclination shifted in favor of processing the stimuli at the identification level in later stages of training.

The results of our simulation of this experiment were analyzed according to the same logic that was originally applied by Wasserman et al. to their pigeon data. The results are shown in Figure 15. The model was able to reproduce each of the aforementioned aspects of the original data. The results of this simulation are mainly due to the different rates of presentation of the category-specific and stimulus-specific elements. As explained in the previous section, at the beginning of training, category-specific elements strengthen their associations with the two responses with which the category is paired, producing above chance accuracy; but these category-specific elements also engender a large proportion of categorical errors due to within-category generalization. These category-specific elements acquire most of the associative strength because they are presented more often than the exemplar-specific elements on trials involving the category in question. To reduce such categorical errors, inhibitory associations grow between the stimulus-specific elements and the incorrect categorical response. Inhibitory learning is rather slow due to the relatively low rate of presentation of stimulus-specific elements; but such inhibitory learning eventually leads to better discrimination performance at the end of training by canceling generalized excitation from one subcategory to the other.

Figure 15.

Results of a simulation of Wasserman and colleagues’ (1988) experiment, after a reanalysis of the data aimed at elucidating the relative contributions of categorization performance, identification performance, and guessing to the pigeon’s choices in a subcategorization task.

The previous simulation nicely illustrates the way in which some patterns of behavior in animal categorization tasks can arise as a consequence of the interaction between stimulus generalization and error-driven learning. An interactive learning model can account for the dynamics of learning in this kind of situation better than a purely similarity-based model. A more recent experiment by Cook and Smith (2006) also addressed the interplay between identification and categorization, but in a more direct way.

Cook and Smith constructed two artificial categories comprising stimuli which varied in 6 binary dimensions. Each category contained 1 prototype, 5 typical exemplars that shared 5 features in common with the prototype, and 1 exception that shared 5 features in common with the prototype of the other category. Because of the category structure that was arranged by Cook and Smith, their subjects were required to rely at least in part on the particular configuration of features of the exception items in order to reach perfect discrimination performance.

The results of this “rule-exception” task were analogous to those observed for the subcategorization task: both pigeons and humans learned to classify the prototypes and the typical exemplars faster than the exceptions. More importantly for the present discussion, when prototype and exemplar models of categorization were fitted to the data, the former performed better during the early stages of training, whereas the latter performed better during the final stages of training. Thus, neither of the two accounts alone could explain the entire pattern of data across training. This observation led Cook and Smith to conclude that their results, “show the value of a mixed theoretical perspective that permits behavior to be determined by different categorization systems operating at different times” (p. 1065). The problem with such a “mixed model” approach is that it does not give a principled explanation of how experience with the categorization task would lead pigeons to shift from one strategy to the other.

Our explanation in terms of stimulus elements and error-driven learning does specify why learning occurs the way it does and it is far more parsimonious than proposing a shift between altogether different categorization systems. In fact, we have found that a simulation of the Cook and Smith experiment using the “unique cue” model—first proposed by Wagner and Rescorla (1972) as an extension of the Rescorla-Wagner model and more recently deployed by Gluck (1991) to explain human categorization—can reproduce all of the important aspects of its results. The unique cue model proposes that each stimulus feature is processed independently and forges its own association with the outcome, but that every particular configuration of features also activates a configural unit which represents that unique combination.

The results of our simulation are shown in Figure 16. The parameter values for learning rate and the choice process in this simulation were the same as in our own model. Although the unique cue model learns the task faster than the pigeons with the parameter values used in this simulation, it can reproduce the faster learning of the prototypes and the typical exemplars, as well as the slower learning of exception stimuli, shown in the experimental data. Just as our model of natural image categorization can explain the results of Wasserman et al. (1988), the unique-cue model, also based on the error-driven learning rule of Rescorla and Wagner, can account for the results reported by Cook and Smith (2006) in artificial categorization by pigeons.

Figure 16.

Simulated results of Cook and Smith’s (2006) experiment using the configural cue model of associative learning.

Retroactive Interference Between Categorization and Identification

Another interesting interplay between categorization and identification is the possible retrospective interference that one strategy might exert over the other. The idea here is that discriminative behavior in categorization tasks can either be controlled by stimulus-specific properties or by category-specific properties which are shared by most of the exemplars in the category. Control by one of these two kinds of properties may depend on the demands of the task and, what may be even more important, on prior control by the other (Restle, 1957).

Loidolt, Aust, Meran, and Huber (2003, Experiment 1) tested this idea in a study which took advantage of the different demands that are posed by categorization and subcategorization tasks. In a subcategorization task, exemplars of the same category must be sorted into two or more different groups, so that categorical information should interfere with the required discrimination; here, subjects must rely on exemplar-specific information to increase their discrimination accuracy. In a categorization task, on the other hand, accurate performance can be achieved by using either of these sources of information; nevertheless, learning should proceed faster if it is based on categorical information because what is learned about one stimulus can be easily transferred to several other exemplars of the category.

Loidolt and colleagues investigated retrospective interference of category learning over identification learning with a 3-phase experimental design. In Phase 1, pigeons received training on a Go/No-go subcategorization task involving 20 human faces of the same sex: 10 reinforced and 10 nonreinforced. Separate groups received training with male and female faces. Phase 2 involved training on a categorization task with 100 stimuli: half of them male human faces and the other half female human faces. In Phase 3 testing, the pigeons were presented with completely novel stimuli from the categories that were used in Phase 2 as well as with the same 20 stimuli that were used during the subcategorization task in Phase 1.

The most important result was that pigeons in Phase 3 classified all of the items included in the subcategorization task—both reinforced and nonreinforced—in accord with the category rule that was learned in Phase 2 categorization and regardless of the subcategorization experience that each bird had gained with each exemplar in Phase 1. For example, those pigeons that received subcategorization training with male faces (both reinforced and nonreinforced) in Phase 1, followed in Phase 2 by categorization training with male faces reinforced, showed high rates of responding in Phase 3 to all of the stimuli from the subcategorization phase, including those that were nonreinforced and that had produced low rates of response in Phase 1. Furthermore, this retrospective interference effect was virtually complete; the response rate was almost identical to all of the subcategorization stimuli and comparable to that shown to novel stimuli from the same category.

The predictions of the model for this experiment, plotted as mean response probability of the relevant training and testing stimuli, are presented in Figure 17. The top panel presents the results of a simulation in which the category that was used during subcategorization training was reinforced during categorization training; the bottom panel represents the condition in which this category was nonreinforced during categorization training. The model accurately reproduces the observed pattern of data, particularly the radical change in response rate to those stimuli from the subcategorization task that were exposed to the conflicting contingencies of reinforcement. In both the original data and in the simulations presented here, these stimuli show a change in their associative value toward the value that was acquired by the category during the immediately prior training.

Figure 17.

Simulated results of Loidolt and colleagues’ (2003) experiment which reported retroactive interference of identification learning by categorization learning.

During categorization training in this simulation, 50 exemplars from the relevant category were consistently reinforced or nonreinforced. Each of these exemplars was represented by some of the same elements that were used to represent the stimuli that were involved in the previous subcategorization task, with the consequence that their change in associative strength was transferred to those stimuli as well. Because of the large number of exemplars involved in categorization training, most of the elements representing the stimuli in the subcategorization task (both category-specific and stimulus-specific elements) were presented, resulting in a very strong retrospective interference effect.

New Predictions: Manipulating the Representational Elements

The simulation work that was presented in the previous sections documents how a substantial number of experimental outcomes can be explained by simply assuming that animals represent natural images as collections of common and unique elements. The representation that is chosen for the stimuli might be deemed to be nothing more than an arbitrary or expedient selection in order to make quantitative modeling easier, but we believe that thinking about natural image classification in terms of category-specific and stimulus-specific elements also provides fresh insights and suggests new ways of studying this interesting form of animal learning. Although these elements are completely hypothetical, unobservable entities, the role that they might play in learning different discriminations gives hints about how to manipulate their association with an outcome. In the words of Rescorla (1976, p. 96): “Our inability to separately present the shared and unique elements of a set of stimuli does not prevent them from being manipulated to make differential predictions.”

For example, we know that, in order to master a pseudocategorization task, animals must rely on the information that is provided by stimulus-specific elements, whereas category-specific elements are completely uninformative as to the correct responses. We also know that increasing category size enhances the control over behavior that is acquired by category-specific elements. Thus, these and other experimental manipulations can be used to partially isolate the control over behavior by a particular kind of element as well as to test our predictions about their role in category learning.

We next present two new predictions of our model and we report experimental evidence supporting both of them. We hope, in the process, to demonstrate the heuristic value of our theory as well as to test the novel notion that error-driven learning plays an important part in natural image categorization. We focus on the predictions of the model concerning competition between stimulus-specific and category-specific elements for the control of behavior in situations which produce blocking (Kamin, 1969) and relative validity (Wagner, Logan, Haberlandt, & Price, 1968) effects in Pavlovian conditioning: two key effects in the development of modern associative learning theory.

Experiment 1: Blocking of categorical control by prior individual exemplar learning

As we have already seen, our model predicts that, for a pseudocategorization task to be learned, pigeons must rely on stimulus-specific elements. Because of the error-driven nature of the Rescorla-Wagner learning rule, further training with some of the stimulus-response pairs from the original discrimination, which together create a true categorization task, should not foster any category learning. Because the pigeons have already learned the first discrimination through “rote memorization,” they should not be able to learn the systematic mapping between categories and responses in the second discrimination or to generalize this learning when novel exemplars of the categories are presented. Thus, the model predicts a “blocking” effect (Kamin, 1969), in which learning a discrimination by allocating associative strength to stimulus-specific elements interferes with further allocating associative strength to category-specific elements, under conditions that normally would produce such categorical learning.

The design of our experiment which tested this prediction is depicted in Table 1. The experiment is divided into two training phases and a testing phase. In Phase 1, for the Blocking condition, pigeons learned a pseudocategorization task in which 10 stimuli from each of two categories were paired with one choice key and 10 different stimuli from each of the same two categories were paired with a second choice key. In Phase 2, half of the trials in the pseudocategorization task were dropped, transforming it into a true categorization task, in which all 10 stimuli from one category were assigned to one choice key and all 10 stimuli from the other category were assigned to a second choice key. Simultaneously, the subjects began training on an additional categorization task involving two completely novel categories, which served as a Control condition. This control condition provided a benchmark for the proper amount of training that is needed to achieve robust category learning for each pigeon and it also provided a control for the amount of generalization to novel stimuli that is fostered by this training. Note that, because this was a within-subjects design, each pigeon received the same amount of training in both of the categorization tasks during Phase 2; so, any disparity in the amount of generalization to novel exemplars would have to be due to the prior pseudocategorization training in the Blocking condition. Such stimulus generalization was assessed in a final Testing phase, in which novel stimuli from each of the trained categories were presented to the pigeons.

Table 1.

Design of Experiment 1

	Phase 1: Pseudocategorization	Phase 2: Categorization	Generalization Test
Blocking Condition	10 images from Category 1 / Response 1	10 images from Category 1 / Response 1	Phase 2 training trials +
			10 new images from Category 1
	10 images from Category 2 / Response 2	10 images from Category 2 / Response 2	10 new images from Category 2
	10 images from Category 1 / Response 2
	10 images from Category 2 / Response 1
Control Condition	---	10 images from Category 3 / Response 3	Phase 2 training trials +
			10 new images from Category 3
	---	10 images from Category 4 / Response 4	10 new images from Category 4

The left panel of Figure 18 shows the predictions of the model for this experimental design. As we suspected, the model predicts lower generalization of categorization performance in the Blocking condition than in the Control condition. In the Blocking condition, the pigeons should not learn about the consistent assignment of responses to categories in Phase 2, because they should already have learned the assignment of each individual stimulus in the task to its correct response in Phase 1. In other words, the category-specific elements should not acquire associative strength in Phase 2 because they are redundant; all of the information about the correct response is already given by the stimulus-specific elements that were trained in Phase 1.

Figure 18.

Model predictions (left panel) and experimental results (right panel) of an experiment into blocking of categorization learning by previous identification learning of individual exemplars.

Method

Subjects and apparatus

The subjects were eight feral pigeons (Columba livia) kept at 85% of their free-feeding weights. The apparatus entailed eight operant conditioning chambers (Gibson, Wasserman, Frei, & Miller, 2004) that were located in a dark room with continuous white noise.

Procedure

The stimuli were 30 color photographs showing exemplars from each of four categories (cars, chairs, flowers, and people) in varied backgrounds. Each pigeon was concurrently trained on both conditions shown in Table 1, with each condition trained using a different pair of response keys in a two-alternative forced-choice task. The assignment of specific categories and response keys to the conditions shown in Table 1 was counterbalanced.

The stimuli were shown on a 107.0 × 70.5 cm rectangular screen positioned in the middle of a computer monitor; the four response keys were illuminated by square black-and white icons, positioned near the four corners of the display screen. A trial began with the pigeon being shown a black cross in the center of a white screen. Following one peck anywhere on the display, a training photograph appeared and the bird had to complete an observing response requirement to the stimulus (from 5 to 45 pecks for different birds as was necessary to promote learning); then a pair of response keys was shown (either left-top and bottom-right or right-top and bottom left) and the pigeon had to peck one in order to advance the trial. If the pigeon’s choice was correct, then food was delivered and an intertrial interval ensued. If the pigeon’s choice was incorrect, then the house light and the monitor screen darkened and a correction trial was given after a timeout of from 5 to 30 s. Correction trials continued to be given until the correct response was made. All of the report responses were recorded, but only the first report response of each trial was scored in data analysis. Reinforcement consisted of 1 to 3 food pellets.

In Phase 1, a session consisted of four blocks of 40 trials, arranging the Pseudocategorization discrimination that is detailed in Table 1. Training continued until the pigeon met a criterion of 85% accuracy on each of the four response keys; then, Phase 2 started. Phase 2 sessions consisted of four blocks of 40 trials, as shown in Table 1. When the pigeons met the criterion of 85% accuracy for each response key, stimulus generalization testing began.

Test sessions involved one block of 16 warm-up training trials that were randomly selected from the Phase 2 contingencies plus one testing block. The testing block included 10 novel stimuli from each category and three repetitions of every Phase 2 trial, totaling 176 trials. All of the trials involving novel test stimuli were nondifferentially reinforced. A test session was followed immediately by at least one session of Phase 2 training; pigeons were subsequently tested only if they met criterion. Data for three test sessions were collected and analyzed for each pigeon. Across the entire experiment, trials within each session were randomized in blocks.

Results and discussion

The right panel of Figure 18 shows the mean proportion of correct choices during generalization test trials for each of the two conditions. As expected, generalization performance was lower in the Blocking condition (M = .57, SD = .07) than in the Control condition (M = .69, SD = .12). This disparity was statistically significant by a one-tailed paired-samples t test, t(7) = 1.91, p < 0.05. [A one-tail test was appropriate given the directionality of our experimental hypothesis; we predicted the outcome of this experiment to be lower generalization in the Blocking condition.] Furthermore, the outcome of this experiment cannot be explained by better performance of the categorization itself in the Control condition, because both discrimination tasks were trained to the same high criterion of 85% accuracy and performance during the Test phase was actually slightly higher for the Blocking condition (M = .94, SD = .03) than for the Control condition (M = .92, SD = .03).

These results closely accord with the predictions that are shown in the left panel of Figure 18; to the best of our knowledge, this is the first reported evidence documenting competition for behavioral control between stimulus-specific and category-specific elements in natural image categorization. Perhaps even more interestingly, we obtained this blocking effect without any direct manipulation of these stimulus elements, only through the use of tasks which, according to our model, should affect learning with completely hypothetical stimulus elements.

In our second experiment, we wanted to confirm the role that is played by error-driven learning in natural image classification by exploring an analog of the relative validity experiment conducted by Wagner et al. (1968). If the predictions of the model were again confirmed, then we could make an even stronger case for its utility in explaining natural image categorization and object recognition in animals.

Experiment 2: Predictive validity of exemplar-specific properties affects categorical control

The relative validity design (Wagner et al., 1968; Wasserman, 1974) involves two conditions. In the Uncorrelated condition, subjects are presented with two compound stimuli, AX and BX, each paired with reinforcement 50% of the time. In the Correlated condition, the same two compound stimuli are presented, but now AX is reinforced 100% of the time, whereas BX is never reinforced. Even though, in both conditions, X is reinforced 50% of the time—and hence its absolute predictive value is always the same—animals in the Uncorrelated condition show more responding to this stimulus than do animals in the Correlated condition. Thus, instead of depending on its own informative value alone, conditioning to X depends on the informative value of the other stimuli that are presented in compound with it. When A and B are good predictors of the outcome, X does not acquire much associative strength despite its being paired with reinforcement 50% of the time.

The main goal of the present experiment was to investigate an analog of the relative validity design in natural image categorization, in which the roles of Stimuli A, B, and X were replaced by hypothetical stimulus-specific and category-specific elements. The design of the experiment is shown in Table 2. The Uncorrelated condition involved training with 20 exemplars from one category; pecks to any of them yielded reinforcement 50% of the time. The Correlated condition involved training with 20 exemplars from a second category; pecks to half of them were continuously reinforced, whereas pecks to the other half were never reinforced. In both cases, the category itself was reinforced and nonreinforced the same number of times. In the Correlated condition, reinforcement was assigned to particular stimuli, which should encourage stimulus-specific elements gaining control over behavior. However, in the Uncorrelated condition, stimulus-specific learning should not be encouraged, because none of these elements in the representation is informative as to whether or not reinforcement will occur. The result should be that category-specific elements acquire robust associative strength in the Uncorrelated condition, fostering generalization to new exemplars of the category, whereas in the Correlated condition, categorical generalization should be weakened because of the greater control gained by the more predictive stimulus-specific elements. The Test phase, in which 10 new exemplars from each category were presented, was included to evaluate this prediction.

Table 2.

Design of Experiment 2

	Training	Generalization Test
Uncorrelated	20 images from Category 1 / 50% reinforcement	Training trials +
		10 novel images from Category 1 / No reinforcement
Correlated	10 images from Category 2 / 100% reinforcement	Training trials +
		10 novel images from Category 2
	10 images from Category 2 / 0% reinforcement	/ No reinforcement

The predictions of the model are depicted in the left panel of Figure 19, which shows the percentage of generalized associative strength to the novel stimuli during the test, computed by taking the ratio of the associative strength of the test stimuli over the associative strength of the reinforced stimuli (consistently reinforced in the Correlated condition and partially reinforced in the Uncorrelated condition). The model does indeed predict a disparity between the conditions, with higher category generalization in the Uncorrelated than in the Correlated condition.

Figure 19.

Model predictions (left panel) and experimental results (right panel) of an experiment investigating the effect of the predictive validity of stimulus-specific elements on categorization learning.

This experiment also allowed us to explore a second prediction of our model, related to the phenomenon of discriminative conditioning in Pavlovian learning (Pavlov, 1927). In discriminative conditioning, two similar stimuli are presented separately and one of them is reinforced (CS+), whereas the second is not (CS−). In initial training, a CR arises to both the reinforced and nonreinforced stimuli; but, with further training, the response to the CS− gradually falls. Rescorla and Wagner (1972; Wagner & Rescorla, 1972) explained this pattern of results by assuming that CS+ and CS− were composed of common and unique elements. Common elements acquire associative strength on CS+ trials, which then generalizes to the CS−. This generalized associative strength produces a CR to the CS− at the beginning of training; but later, the unique elements of the CS− become inhibitory, leading to a reduction in responding to this stimulus.

In the present experiment, the task that was presented to the pigeons in the Correlated condition is analogous to Pavlovian discriminative conditioning. In this pseudocategorization task, responses to one group of category exemplars are reinforced and responses to a second group of exemplars from the same category are nonreinforced. In the context of a Go/No-go procedure like the one used here, the Rescorla-Wagner model again predicts strong acquisition of associative strength by the elements that are common to both groups of stimuli—the category-specific elements. This acquisition translates into an initial increment in response rate to all of the stimuli in the discrimination followed by a gradual decrement in responding to the nonreinforced stimuli due to inhibitory learning involving the pictures’ stimulus-specific elements. The predictions of the model for the learning curves of the reinforced and nonreinforced stimuli in the Correlated condition are shown in the top panel of Figure 20. It can be seen that the curve for the reinforced stimuli increases monotonically with training sessions, whereas the curve for the nonreinforced stimuli follows a nonmonotonic function with increments in associative strength early in training and decrements later.

Figure 20.

Learning curves for reinforced and nonreinforced stimuli in the Correlated condition of Experiment 2. The top panel shows the functions that were predicted by the model and the bottom panel shows the experimental results.

To summarize, the key predictions of our model for the present experiment are: (a) greater generalization to novel category exemplars in the Uncorrelated condition than in the Correlated condition (left panel of Figure 19) and (b) a nonmonotonic learning curve for the nonreinforced stimuli in the Correlated condition (top panel of Figure 20).

Method

Subjects and apparatus

The subjects were four pigeons kept at 85% of their free-feeding weights. The apparatus involved the same four operant chambers as Experiment 1.

Procedure

The stimuli were some of those that were described in Experiment 1 (categories: people and flowers). Each pigeon was concurrently trained on the two conditions shown in Table 2, using a Go/No-go procedure. The assignment of categories to each condition was counterbalanced.

All of the trials began with the presentation of a white rectangle in the center display area of the screen. A single peck anywhere within the rectangle led to the presentation of the stimulus. On a reinforced trial, the stimulus was presented and remained on for 15 s; the first response after this interval turned the display area black and led to the delivery of food. On a nonreinforced trial, the stimulus was presented and remained on for 15 s, after which the display area automatically darkened and the intertrial interval began. On both reinforced and nonreinforced trials, scored responses were recorded only during the first 15 s of stimulus presentation. The intertrial interval randomly ranged from 6 to 10 s. Reinforcement consisted of 1 to 3 food pellets.

In training, each session consisted of four blocks with the 40 trials described in Table 2. In the Correlated condition 10 stimuli from one category were reinforced and 10 other stimuli from the same category were nonreinforced, whereas in the Uncorrelated condition all of the stimuli in the category were equally often reinforced and nonreinforced. To evaluate performance, a Discrimination Ratio (DR) was computed for the stimuli in the Correlated condition by taking the mean response rate to the reinforced stimuli and dividing it by the sum of the mean response rate to the reinforced stimuli plus the mean response rate to the nonreinforced stimuli. Training continued until the bird achieved a DR higher than 0.85 for 2 consecutive sessions; then, testing followed.

In each testing session, one training block was followed by two testing blocks. Each testing block included one nonreinforced presentation of each of 10 novel stimuli from the two categories, randomly interspersed in a block of training trials. The total number of trials in each test session was 160. Testing continued until the DR for the training stimuli in the Correlated condition and the DR for the test stimuli in both conditions were above 0.85 for two consecutive sessions. This criterion guaranteed that testing data were collected up to the point where responding to the test stimuli was almost completely extinguished. Across the entire experiment, trials within each session were randomized in blocks.

Results and discussion

We computed a generalization ratio for the novel stimuli during testing by taking the mean rate of response to these stimuli and dividing it by the mean rate of response to the reinforced stimuli in each condition. We computed this measure because the level of responding to the reinforced training stimuli differed in both conditions, as expected from the different frequencies of reinforcement in each case (continuous reinforcement in the Correlated condition; partial reinforcement in the Uncorrelated condition). We wanted to compare between the conditions the proportion of responding to the reinforced stimuli that generalized to the new exemplars of the category, which is exactly what this measure of generalization represents.

The mean generalization ratio for each of the two conditions is shown in the right panel of Figure 19. As predicted by the model (left panel of Figure 19), stimulus generalization was higher in the Uncorrelated condition (M = .41, SD = .02) than in the Correlated condition (M = .26, SD = .08); the disparity was statistically significant according to a paired-samples t test, t(3) = 4.92, p < 0.01. These data thus show that the learning of open-ended visual categories does not depend simply on the informative value of the category to predict reinforcement, but also on the predictive value of each individual stimulus in the categorization task. Information carried by stimuli at these two levels—represented by stimulus-specific and category-specific elements—competes for control of behavior in natural image categorization. This result is analogous to the relative validity effect observed in Pavlovian conditioning preparations, but at the level of whole categories instead of individual stimuli.

The bottom panel of Figure 20 shows mean response rates across blocks of training for both reinforced (solid circles) and nonreinforced (open circles) stimuli in the Correlated condition. Because the speed of mastering the discrimination varied among pigeons, the data are presented up to the block in which the fastest pigeon met criterion (Block 28). The mean response rate in the last training block across all of the pigeons is also included as a point of reference. As predicted by the model, response rate to the nonreinforced stimuli rises at the beginning of training along with response rate to the reinforced stimuli; after about seven training blocks, response rate to the nonreinforced stimuli starts falling. This initial rise and later fall in mean response rate was exhibited by all four pigeons.

The data shown in Figure 20 were entered in a 2 (Reinforcement) × 28 (Training Block) ANOVA, which revealed a significant interaction of Reinforcement and Training Block, F(27, 81) = 5.26, p < .001), but no main effect of either Reinforcement, F(1, 3) = 5.31, p > .10), or Training Block, F(27, 81) = 1.17, p > .10). These results suggest that the changes in mean response rate across training differed significantly for the reinforced and nonreinforced stimuli.

The present results, together with those of Experiment 1, clearly illustrate three important contributions of our model. First, they show how our model can generate new predictions about the conditions that foster categorization learning, which can be empirically tested. Second, they serve as concrete examples of how the theoretical elements that we have proposed as the basis for categorization can be effectively manipulated in categorization experiments. Third, they serve as evidence that the same stimulus competition principles that account for simple associative learning are also involved in pigeons’ categorization of natural images, yielding strong empirical support for the incorporation of an error-driven learning rule into our model.

General Discussion

The present paper represents a focused effort to apply the principles of associative learning theory to explain perceptual categorization phenomena in animals. The resulting model proved to effectively explain a wide array of empirical data on natural categorization behavior in pigeons, despite the simplicity of its assumptions about stimulus representation and associative learning, and despite the fact that all of the simulations used the same set of parameter values. Furthermore, the model was able to generate testable predictions about the conditions that foster categorization learning with naturalistic stimuli and these predictions were clearly confirmed in two new experiments. Because these experiments involved the manipulation of completely hypothetical elements and their association with behavior, it would have been difficult even to envision them without a theoretical framework like the one that we proposed here.

The success of our model suggests that the formalization and application of associative theories in the tradition of animal learning research is possible even to explain the results of experiments using complex and uncontrolled stimuli, like the photographs that have often been used to study natural categorization behavior. The model permits us to build a bridge between very different traditions in animal learning research. As such, we hope that it represents a step forward in the development of a general theory of animal learning, one that explains both simple associative learning and more complex learning situations according to the same basic principles.

Despite the evident popularity of this “general principles” idea among many animal learning researchers (Huber, 2001; Mackintosh, 1995, 2000) and the fact that this idea has been used to explain studies of artificial stimulus categorization (Gluck & Bower, 1988; Mackintosh, 1995; Shanks, 1991), to the best of our knowledge, ours is the first attempt to formalize a model of natural categorization in the tradition of error-driven learning theories and to assiduously assess the predictions of the model against empirical data that have been collected in a long line of programmatic experiments. The notion that associative learning principles may underlie natural image categorization in animals had remained untested until now; we have presented here the first computational and empirical evidence favoring this possibility.

Do note that the distinction between category learning investigations involving natural images and artificial images is far from trivial, given that they differ both in the physical attributes of the stimuli (Simoncelli & Olshausen, 2001) and in the difficulty that different categorization problems pose for nonhuman animals (Lea et al., 2006). Our conceptualization of complex stimuli in natural categorization studies in terms of shared and unique representational elements suggests that, despite the disparities between artificial and natural categorization tasks, both can be explained using the same general principles of elemental stimulus representation and error-driven learning.

In the remainder of this article, we discuss the relation between our model and alternative schemes for categorization learning. First, we consider the possibility of developing models using alternative learning algorithms from those available in the animal learning literature. Second, we comment on the relation between our model and some of the most popular models in the human categorization literature. Finally, we propose how our model might be extended to accommodate some remaining challenges in the explanation of animal visual categorization.

Alternatives to the Rescorla-Wagner model

Attempting to explain perceptual categorization by elaboration of the Rescorla-Wagner model entails all of the strengths and weaknesses of this particular theory. Despite its many celebrated successes, there is a long list of empirical data that the Rescorla-Wagner model cannot explain (Miller, Barnet, & Grahame, 1995); it can be expected that our model will similarly fail to explain analogous results in categorization studies (Aitken, Bennett, McLaren, & Mackintosh, 1996; Aydin & Pearce, 1994). It is also clear to us that our model is still in its infancy; with time, it will be necessary to modify it or to replace it in order to give an even more complete account of natural categorization in animals. Other aspects of categorization, based on nonassociative processes like perceptual learning and attention (Goldstone, 1998; Kruschke, 2003), might force such changes.

It should be noted here that evidence suggesting the participation of such processes does exist in the avian categorization literature, coming from experiments that have used artificial stimuli (Aitken et al., 1996). Thus, we do not deny that there is a good chance that these processes, which are not captured by our model, might play an important role in the categorization of objects in natural scenes. However, until now there has not been a systematic research agenda directed to determine the impact of perceptual and attentional learning in the study of animals’ categorization of natural images. One reason for the absence of this agenda might be that clear evidence of such processes is difficult to gather without the use of stimuli that can be easily manipulated; we hope that the framework presented here will provide hints about how to tackle such difficult empirical questions. If, as we suspect, perceptual and attentional learning do have an important impact on avian natural image categorization, then our model should be modified or replaced by a theory incorporating these mechanisms.

Another interesting possibility is to implement our model using a common-elements representation together with Pearce’s highly successful theory of associative learning (Pearce, 1987, 1994, 2002). This theory involves an error-driven learning rule like the one that we used here; but, instead of proposing that the associative strength of a stimulus configuration is the simple sum of the associative strengths of each of its elements (as in Equation 4 and the summation term in Equation 1), Pearce’s theory proposes a more complex combination principle based on a configural representation of stimuli. Simulations with this configural version of our model (based on Pearce, 1994) have shown that, in order to reproduce the results of most of the experiments discussed here, all that is needed is to adjust the learning rate parameters. Thus, the data that we have considered here do not allow us to distinguish these two of associative learning models. We believe that many other models which treat associative learning as an error correction process may also effectively reproduce the results that we have reviewed above.

However, we do not believe that comparing these two models, or any other models of associative learning, ought to be the primary research objective in the study of natural image categorization. These models were developed to explain simple associative learning; experiments using Pavlovian preparations and easily manipulable stimulus compounds are more likely to be informative about their relative utility. We believe that a much more interesting line of research should focus on those aspects of natural image categorization that are not shared with associative learning processes, as we discuss below.

Also, not all theories of Pavlovian conditioning are straightforwardly applicable to the stimulus representation in our model. Some “classic” theories of compound generalization (e.g., Pearce, 1987; Rescorla & Wagner, 1972) explain how much associative strength is generalized from one stimulus compound to another as a function of the components that are shared between them. That is, each discrete stimulus that is given to an animal in a Pavlovian preparation is represented through a single, discrete unit in these models. Because of this feature, the generalization and learning rules in those theories can be straightforwardly applied within the framework of our model—if it is assumed that the elements in our representations take the place of stimulus components, which is exactly what was done here with the Rescorla-Wagner model.

More recent elemental theories of associative learning use componential representations, meaning that they represent each individual stimulus through a number of representational elements. Our model is itself a componential model, in which a single image is represented by a number of elements varying in their level of category specificity. Contemporary componential models of Pavlovian conditioning include Wagner’s (2003) replaced elements model, Harris’ (2006) “attentional buffer” model, and McLaren and Mackintosh’s (2000) elemental model. Whereas classic models take discrete stimuli to be their elements, componential models add a new representational layer by treating each stimulus as composed of sub-elements. Furthermore, these elements interact in a nonlinear fashion, with each of them increasing or decreasing the activation of the others depending on factors such as the similarity relations between the stimuli that they represent. This feature allows these models to represent the same stimulus in different ways depending on the context in which it is presented or to solve discriminations which are not linearly separable without proposing a configural stimulus coding. However, the generalization rules that are included in these models are built on the sub-elements in their representation; they do not offer any straightforward way to compute generalization across compounds as a function of their components, as in classic models.

If a researcher wanted to apply these componential models to our stimulus representation, then one of two strategies could be taken, each leading to an underspecified model. First, it is possible to imagine that the elements in our representations are analogous to the elements in componential models of conditioning. In this case, in order to specify stimulus generalization principles it would be necessary to group the elements into components representing “discrete stimuli” and then to determine how these grouped representations should interact with each other (for example, by determining how similar one group of elements is to another). It is obvious that this solution leaves us facing the same problem that we have tried to solve in this paper: we do not know how to parse natural photographs into components and we know even less about the similarity relations between such components in each photograph.

A second possibility would be to imagine that our elements are analogous to the discrete stimuli in these models, as in classic models of associative learning. In this case, each of the elements in our representation would itself be represented through a pool of sub-elements and again the interactions among the elements themselves must be determined. In sum, we cannot apply componential models to our stimulus representation, which is itself componential, without making assumptions about how natural images are parsed into components and how these components interact with each other. Even if this task were possible, then we believe that pursuing it would be ill-advised; the final result would be a considerably more complex model than what we currently have and it would entail a step that is not called for by the available data in the area of research that is our focus in this paper.

Our conclusion is that it is unclear whether componential models of associative learning can explain natural image categorization phenomena at all. Although those models are similar to the present theory in that they use elements to represent different stimuli, that similarity is only superficial because none of these models includes a way to represent the variability in category specificity across elements that is essential to explain stimulus categorization. As we noted earlier, in this respect, our model is more closely related to the original ideas of stimulus sampling theory than to contemporary elemental theories of associative learning.

Relation to models of human categorization

One of the main goals of our work is to build a bridge between traditional animal learning theory and natural image categorization research. With this aim, we focused on learning rules which were taken from the animal learning literature, although we are well aware that the literature in human categorization contains an even larger number of models that we have not taken into account. Without actually testing modifications of these models against the data, it is impossible for us to assess their value in describing the principles of animal visual categorization. Nevertheless, we suspect that at least some of those models of human categorization are not well suited to explain the learning dynamics seen in many animal studies.

Our model can explain these results because it uses an interactive learning rule (Nosofsky, Kruschke, & McKinley, 1992), in which generalization and learning interact with each other during training, explaining the dynamics of category learning as a function of the competition among elements to become associated with a response. Some of the most popular models of human categorization (Ashby, 1992; Estes, 1986; Medin & Schaffer, 1978; Nosofsky, 1984; Reed, 1972) simplify the category learning process by just counting co-occurrences of exemplars (or their features) and responses. Classification is then treated as a decision process based on similarity and frequency information. We believe that this kind of model would have considerable difficulty explaining, for example, the precedence of categorization learning over identification learning that was found by Wasserman et al. (1988), just as they have difficulty explaining analogous training effects in artificial categorization with humans (Smith & Minda, 1998) and animals (Cook & Smith, 2006). The learning data that were presented in Experiment 2 (see Figure 20) would also be difficult to explain using traditional categorization models or any other model which does not include an interactive learning rule.

Connectionist models of human categorization, which do include interactive, error-correction learning rules, are more likely to provide a good account of the results discussed here. Some of these models (Gluck & Bower, 1988) have been found to be equivalent to the Rescorla-Wagner model under special circumstances. Others, like ALCOVE (Kruschke, 1992), are more similar to Pearce’s model, in that they involve a configural stimulus representation combined with an error-driven learning rule.

Although we grant that models like ALCOVE capture some of the learning principles that are involved in our model, we also consider that this and other theories of human category learning are unnecessarily complex and flexible in comparison with models of animal learning that can account for the data reviewed here. Also, ALCOVE and other models of human categorization learning do not use a common-elements approach to explain generalization among category exemplars; instead, they use a “distinctive-elements” rule in which generalization is an inverse function of the mismatch between stimuli (Sattath & Tversky, 1987). Because both rules compute similarity in fundamentally different ways (Young & Wasserman, 2002), we are uncertain whether a model involving a distinctive-elements generalization rule can explain the results that are accounted for by our common-elements model.

Remaining questions and extensions of the model

As we noted earlier, there are important aspects of natural image classification that our model leaves unexplained. One of them is the tendency for animals to group together stimuli that are not perceptually similar (e.g., chairs and people) after training involving associations with a common response (Wasserman, DeVolder, & Coppage, 1992) or reinforcer (Astley & Wasserman, 1999), a phenomenon that is called learned stimulus equivalence. A simple modification of our model which could account for this kind of behavior involves adding a layer of hidden units between stimulus and response representations and modifying the connection weights in the final network according to the backpropagation learning algorithm (Rumelhart, Hinton, & Williams, 1986). This error-correcting learning rule has the convenient property of assigning similar representations in the hidden layer to stimuli that have been paired with similar outcomes, which accounts for several aspects of learned stimulus equivalence according to our own modeling work.

Another challenge for the future is finding a way to build common-elements representations that better reflect the similarity relations between stimuli in a categorization task. Currently, the model shows considerable explanatory power by simply assuming that stimuli in the same category share common representational elements. If we were able to build representations that more precisely captured the similarity between stimuli, then the explanatory power of the model would be even greater. One approach that could be taken in this direction involves the use of additive clustering techniques (Navarro & Griffiths, 2008; Shepard & Arabie, 1979) to infer, from measures of stimulus generalization, the common-elements representations that animals use to compute the similarity between natural images. These representations could be deployed to predict performance in categorization tasks, an approach that has been very useful in human categorization research (Nosofsky, 1986).

One of the most important aspects of natural image classification that is left unexplained by our model is how a representation which is composed of stimulus-specific and category-specific elements can be abstracted from natural images by the visual system. It seems clear to us that, in order for animals to exhibit categorization performance which is invariant across different members of a category, some more or less invariant aspect(s) of the stimulus should be extracted from the images to control behavior; but, the question as to exactly how this process occurs is still open. Theories of human object recognition could be very useful to guide research along this line. These theories focus mainly on describing the format of the representations that are stored to achieve invariant recognition and how they are extracted from the visual input (Palmeri & Gauthier, 2004), precisely the kind of processing that is not addressed by our model.

For example, according to the theory of Recognition-by-Components (RBC; Biederman, 1987), we might expect members of a category to share a high percentage of perceptual units, or “geons,” and for those geons to be spatially arranged in similar ways, despite possible disparities in other stimulus-specific geons or surface properties. Support for RBC has been reported for pigeons (for a review, see Kirkpatrick, 2001), which makes this and similar structural-description theories particularly promising for future research and theoretical development. As mentioned before, there are also important links between the representation that is implemented in our model and the one that is proposed by hierarchical models of object recognition based on properties of the primate visual cortex (Serre et al., 2005, 2007); such hierarchical models directly extract from natural images a representation that is composed of units with varying levels of specificity and invariance.

It is an open question whether the process of extracting invariant information from natural images is the same in different species, although there is growing evidence that humans and pigeons use similar features in at least some object recognition tasks (Gibson, Lazareva, Gosselin, Schyns, & Wasserman, 2007; Gibson, Wasserman, Gosselin, & Schyns, 2005; Lazareva, Wasserman, & Biederman, 2008). On the other hand, theories of object recognition and natural image classification are relatively silent as to the mechanisms by which different properties of a stimulus gain control over performance in an identification task as a function of the demands that such task impose (Palmeri & Gauthier, 2004).

Error-driven learning is a natural candidate for such a mechanism and we have shown how our model suggests ways to empirically test for the presence of this form of learning in natural image categorization. The experimental designs that we used in the two experiments reported here could be easily adapted to the study of natural image categorization in humans.

In fact, we have done some preliminary work with humans using a blocking design like the one that was described here for our first experiment. To our surprise, the results have been very similar to those found with pigeons. Thus, we have encouraging evidence which suggests that the same associative learning principles may underlie natural image categorization in animals and people. More generally, our model provides a fresh way of thinking about visual categorization that may prove useful in designing experimental tests for the applicability of different learning rules to this behavioral phenomenon in any species.

In sum, although it is not altogether clear whether the mechanisms that are involved in natural image classification are the same across different species, growing evidence suggests that common principles underlie the visual categorization behaviors of birds and primates, both in the extraction of invariant and specific information from natural images and in the associative processes that determine which of these two types of information is more useful in solving a specific behavioral task. Our model represents a step forward toward better understanding the latter process by proposing that associative learning principles can explain the way in which different stimulus properties acquire control over behavior in natural image categorization.

We have presented a theoretical framework which: (a) offers a much-needed organization and interpretation of established empirical findings in the animal literature on natural image categorization, (b) makes strong links to other important areas of animal learning theory, (c) paves the way for future theoretical development, and (d) has true heuristic value by stimulating new behavioral tests like those reported in this paper. There is still much work to be done in order to gain a full understanding of natural image categorization in different species; but, it is clear that theoretical efforts like the one we have offered here are necessary to attain this goal.