Adaptive multiscale model for simulating cardiac conduction

Abstract

We present a multiscale model and an adaptive numerical scheme for simulating cardiac action potential propagation along a linear strand of heart muscle cells. This model couples macroscale partial differential equations posed over the tissue to microscale equations posed over discrete cellular geometry. The microscopic equations are used only near action potential wave fronts, and the macroscopic equations are used everywhere else. We study the effects of gap-junctional and ephaptic coupling on conduction in the multiscale model and its fully macroscale and fully microscale analogues. Our simulations reveal that the adaptive multiscale model accurately reproduces the action potential wave forms and wave speeds of the fully microscale model. They also demonstrate that, at low gap-junctional conductivities, the accuracy of fully macroscale simulations is sensitive to numerical grid spacing. Moreover, adaptive multiscale simulations capture the effect of ephaptic coupling, whereas fully macroscale simulations do not. We propose two ways of generalizing our multiscale model to higher dimensions, and we argue that such generalizations may be necessary to obtain accurate three-dimensional simulations of cardiac conduction in certain pathophysiological parameter regimes.

Mathematical models and computer simulations of physiological systems promise to enhance understanding of biological processes and to aid development of medical treatments. One difficulty in making such simulations realistic is that biological systems are often multiscale. In cardiac electrophysiology, for example, ionic flow at the subcellular level ultimately causes excitation and contraction of muscle at the tissue level. To gauge the computational challenge posed by simulating this system with a fully microscopic model, consider a 10 cm × 10 cm × 1 cm rectangular slab of tissue. If a typical cardiac myocyte has dimensions of roughly 10^-2 cm × 10^-3 cm × 10^-3 cm, then this slab contains approximately 10¹⁰ myocytes. If each of these cells must be described using tens of spatial nodes, and if tens of state variables per node are required to account for the dynamics of the transmembrane ion channels, such a model would involve approximately 10¹² degrees of freedom and would require enormous computational resources.

To avoid such prohibitively expensive simulations, many investigators use macroscopic descriptions of cardiac conduction, such as the bidomain equations, which can be derived from macroscopic first principles (1) or through the mathematical process of homogenization (1, 2). These approaches average out descriptions of the structure and behavior of individual cells. Simulations using such homogenized descriptions are generally less expensive because the macroscopic equations permit the use of coarser grids. For example, because wave fronts in normal tissue are many hundreds of microns wide, an accurate macroscopic grid spacing might be around 200 μm. Using a uniform discretization with this grid spacing, the same 10 cm × 10 cm × 1 cm rectangular slab model would involve about 10⁸ degrees of freedom. Such simulations are tractable yet still expensive. Bordas et al. (3) argue that at this spatial resolution, a three-dimensional bidomain simulation of a human heart beating for 1 s would require weeks to months of computation time on modern supercomputers.

To reduce the cost of macroscopic models, adaptive methods for simulating cardiac conduction have been developed. For example, Cherry et al. (4, 5) and Colli Franzone et al. (6) present adaptive methods for the monodomain and bidomain equations that allow high spatial resolution to be used only locally near features of interest such as action potential wave fronts. They observed a speedup of approximately 2 orders of magnitude over nonadaptive, uniformly fine simulations. We remark that in these adaptive simulations, the coarsely and finely resolved regions all satisfy discretizations of the same macroscale equation. In the present article, we argue that there are cases in which such mesh adaptivity must be combined with model adaptivity.

One such case of physiological interest is tissue with abnormally low levels of gap-junction expression. For example, a gene-knockout study has shown that conduction is slowed but not eliminated in connexin43 deficient mice (7). One proposed mechanism that might explain this finding is known as ephaptic coupling or as the electric-field mechanism (8–12). In it, adjacent cells are coupled through a narrow cleft space at intercalated discs, which are located at the ends of cardiomyocytes. When one cell’s Na⁺ channels activate and draw inward current, the potential within the cleft drops, depolarizing the membrane of the neighboring cell. Under certain conditions, this depolarization may be sufficient to induce an action potential, thereby resulting in excitation propagation without gap junctions.

Kucera et al. (13) studied a mathematical model of ephaptic conduction along a single strand of cells. In their model, cells are described as one-dimensional cables and are coupled through resistors representing gap junctions. Neighboring cells share a cleft that is resistively connected to grounded extracellular space. Motivated by histological observations that Na⁺ channels are preferentially localized to intercalated discs, they performed numerical simulations exploring the dependence of conduction velocity on this localization and on the level of gap-junctional coupling. Their results show that ephaptic coupling can increase wave speed relative to models without the mechanism. The effect requires that most Na⁺ channels be localized to the intercalated discs and that gap-junctional coupling be at levels significantly below normal.

Large-scale simulations of ephaptic conduction are difficult for at least two reasons. First, to date, most models in the literature have been posed at the microscopic, cellular level. As described above, this level of detail is too expensive for large-scale, three-dimensional simulations. Second, the validity of the macroscopic equations relies upon the assumption that the potential and gating variables do not change significantly between cells. Especially in the low gap-junctional regime, wave fronts are quite narrow; sometimes, they can be only one cell wide. Hence, macroscopic models of ephaptic conduction may not capture the dynamics of the underlying microscopic system. Indeed, Hand and Peskin (14) derived macroscopic equations describing ephaptic cardiac conduction via the mathematical process of homogenization. Unfortunately, the equations they derived were empirically accurate only at normal levels of gap-junctional coupling. The multiscale approach we introduce herein proposes to circumvent this limitation by employing a homogenized model away from action potential wave fronts. Near these wave fronts, we use a detailed cellular model. We compare the predictions of this multiscale model to fully microscopic and fully macroscopic models, and we argue that using adaptive methods may be crucial for large-scale simulations involving low gap-junctional coupling or ephaptic conduction.

Models

Microscale Model.

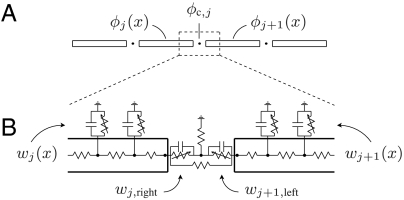
Similar to the models of refs. 13 and 14, we consider a single strand of idealized myocytes, each described as a one-dimensional cable of radius r and length ℓ. In this monodomain-type model, extracellular space is taken to be grounded. Neighboring cells are coupled in two ways: through gap junctions, modeled as direct resistive connections between the interiors of cells; and through a shared equipotential cleft connecting the active membranes at the ends of cells. The clefts are resistively connected to grounded extracellular space. Fig. 1 provides the equivalent circuit for this model. In a typical nonephaptic model, the clefts are grounded, and neighboring cells are coupled only by gap junctions.

Fig. 1.

The geometry and equivalent circuit diagram for the microscale model of cardiac conduction in the presence of gap-junctional and ephaptic coupling. We describe cells as active cables connected by resistors and shared cleft potentials. A and B show the potential and gating variables in Eqs. 1–7, respectively. A depicts a continuum of interior points, and B presents its numerical discretization. In the model, clefts are idealized as having zero width. A model without ephaptic conduction is the special case in which the cleft-to-ground resistance is zero.

Let ϕ_j(x) for 0 ≤ x ≤ ℓ be the intracellular potential in the jth cell. Let ϕ_c,j be the potential of the cleft to the right of the jth cell. Similarly, let w_j(x) represent the gating variables along the sides of the jth cell. Denote the gating variables at the left and right ends of the jth cell by w_j,left and w_j,right, respectively. The ephaptic and nonephaptic microscale equations governing these potentials and membrane gating variables are

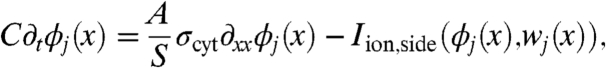[1]

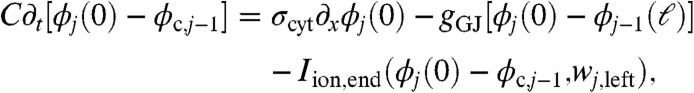[2]

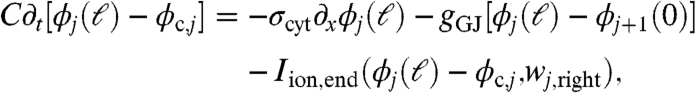[3]

[4]

[5]

[6]

[7]

where A = πr² is the area of a cell’s cross-section (cm²), S = 2πr is the perimeter of a cross-section (cm), σ_cyt is the cytosolic conductivity (mS/cm), g_GJ is the gap-junctional conductance per unit area (mS/cm²) at the ends of cells, C is the membrane capacitance per unit area (μF/cm²), R_c is the cleft-to-ground resistance (kΩ), I_ion,side and I_ion,end are the ionic current densities (μA/cm²) flowing out of the side and end membranes of cells, respectively, and g represents the gating variable dynamics (1/ms). In a nonephaptic case, R_c = 0, and, hence, ϕ_c,j = 0 for all j. We discriminate between I_ion,side and I_ion,end to explore the effects of Na⁺ channel localization to the intercalated discs. Observe that Eqs. 2 and 3 can be substituted into Eq. 4 to relate a cleft’s potential to the ionic and capacitive current flowing directly into that cleft.

Macroscale Model.

A macroscopic analogue of the microscopic model (Eqs. 1–7) can be derived using the mathematical tool of homogenization (14). Here, we present only the nonephaptic case that is used directly in the multiscale model. We refer the reader to SI Text for the macroscale ephaptic model introduced by Hand and Peskin (14). In the nonephaptic limit R_c → 0, the macroscale equations governing potential and membrane gating variables are

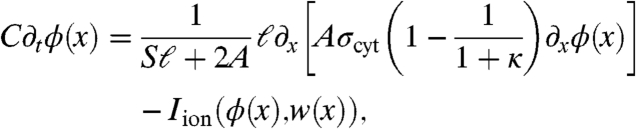[8]

[9]

where ϕ(x) is the intracellular potential in cells near x, w(x) represents the gating variables on the sides and ends of cells near x, and κ = ℓg_GJ/σ_cyt is a nondimensional parameter comparing gap-junctional and cytosolic conductances.

Multiscale Model.

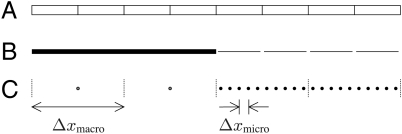
The main weakness of the ephaptic and nonephaptic macroscopic models is their assumption that potentials and gating variables vary slowly over the length scale of cells. To address this weakness, we propose a multiscale approach in which the macroscale model is applied only in regions where potential does vary slowly—that is, far from action potential wave fronts. Near such wave fronts, the microscale model is employed. Fig. 2 provides a schematic depiction of the microscale domain, a particular multiscale representation of that domain, and the discretization of that multiscale representation. We remark that, even in ephaptic models, sizable cleft potentials arise only near wave fronts, where there is appreciable Na⁺ current. Hence, away from an action potential upstroke, it suffices to use a nonephaptic model.

Fig. 2.

An illustration of a strand of idealized cells (A), a possible multiscale representation (B), and the corresponding numerical discretization (C). In the multiscale model, the thick line represents the unresolved subdomain over which the macroscale model applies. Notice that this subdomain ignores the cellular microstructure. The disjoint thin lines represent the individually resolved cells over which the microscale model applies. Space for clefts is drawn for clarity, even though the model idealizes them as having no width. The boundary between the resolved and unresolved regions is called the coarse-fine interface. The computational grid in C is broken into blocks of m = 2 myocytes. When unresolved, a block is described by a single node. When resolved, each myocyte within the block is represented by n = 5 interior nodes and two boundary nodes located at the ends of the myocytes that, for clarity, are not depicted.

In the region of resolved cells, we model potential and gating variables by the microscale equations (Eqs. 1–7). Elsewhere, we model potential and gating variables by the nonephaptic, macroscale equations (Eqs. 8 and 9). Note that the ephaptic macroscale model is not used by our ephaptic multiscale model. Borrowing terminology from adaptive numerical methods for partial different equations, we refer to the boundary between these regions as the coarse-fine interface.

The microscale and macroscale descriptions are coupled exclusively through gap-junctional current. For concreteness, let x^∗ be a point at the coarse-fine interface. We present the case depicted in Fig. 2 in which the unresolved region is on the left of x^∗ and the resolved region is on the right. Let j^∗ be the index of the myocyte immediately to the right of x^∗. Eqs. 1–9 are supplemented with the following boundary conditions:

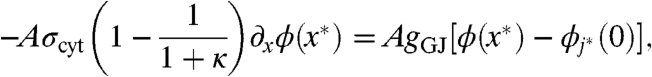[10]

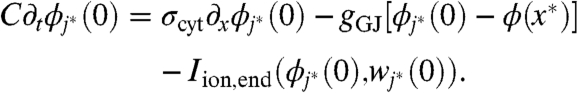[11]

Similar boundary conditions apply at any interface between resolved and unresolved regions.

Numerical Methods.

Our approach to discretizing the multiscale model employs a dynamic, nonuniform grid to solve Eqs. 1–7 in the resolved regions of the tissue and Eqs. 8 and 9 in the unresolved regions. Coupling between the regions is mediated by boundary conditions similar to Eqs. 10 and 11. Criteria for determining which regions are resolved are based on the size of spatial variations in potential and are intended to ensure that sharp wave fronts are preferentially resolved. See SI Text for details on the discretization, the adaptivity criteria, the operators for transferring the state variables from one dynamically constructed grid to another, and the time-stepping scheme. Our numerical method for the fully microscale model is obtained in the extreme case in which all myocytes are resolved. Our numerical methods for the fully macroscale models are similar to the extreme case in which none of the myocytes are resolved. Minor modifications are required to track the values of the homogenized cleft potentials of the ephaptic macroscale model; see ref. 15.

Numerical Simulations.

We performed simulations using the microscale, macroscale, and multiscale models for both nonephaptic and ephaptic cases. Our domain consisted of a single-file line of 40 myocytes. As in ref. 13, we considered cells of radius r = 11 μm, of length ℓ = 100 μm, and with cytosolic conductivity of σ_cyt = 6.67 mS/cm. We took the normal value of gap-junctional conductance per area to be g_GJ,normal = 666 mS/cm². We used the simplified Beeler–Reuter model of ref. 9 to provide the gating dynamics. This simplified model involves only the fast Na⁺ current and the inwardly rectifying K⁺ current of the original Beeler–Reuter model (16). In our simulations, initial conditions were set so that intracellular potential is 0 mV for the first eight myocytes. Where defined, all cleft potentials were initially set to be 0 mV. All other potentials and all gating variables were set to be at resting values for the modified Beeler–Reuter model. To compute conduction velocities, we determined the position of a traveling wave to be the point at which the potential surpasses -40 mV with ∂_tϕ > 0. We computed the conduction speed by linear regression on the wave position as a function of time.

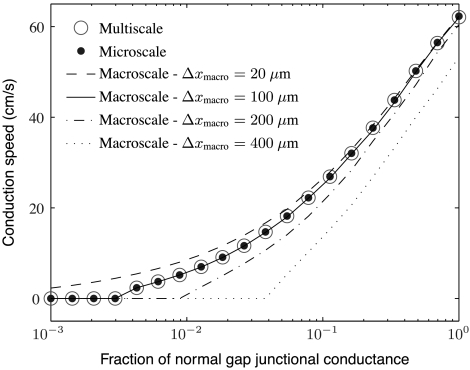
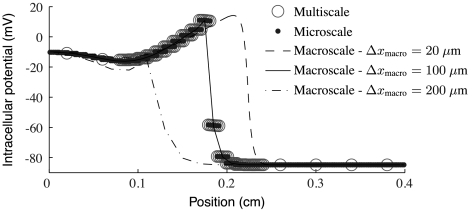
The first set of simulations was meant to investigate the effects of gap-junctional coupling on conduction speed in nonephaptic models. To that end, we simulated the microscale model with R_c = 0 and Δx_micro = 20 μm, where Δx_micro is the microscopic grid spacing; the nonephaptic macroscale model at resolutions Δx_macro = 400, 200, 100, and 20 μm, where Δx_macro is macroscopic grid spacing; and the adaptive multiscale model with R_c = 0, Δx_macro = 400 μm, and Δx_micro = 20 μm. Gap-junctional coupling was varied from 0.1% to 100% of its normal value. Results from these simulations are presented in Figs. 3 and 4.

Fig. 3.

A plot of conduction speed versus fraction of normal gap-junctional conductance for several nonephaptic models and levels of resolution. The coarse macroscale simulations incorrectly predict the value of gap-junctional conductance at which propagation block occurs. The fine macroscale simulations fail to predict propagation block at all. The macroscale simulations with one node per myocyte exhibit remarkable agreement with the microscale and adaptive multiscale simulations over a wide range of gap-junctional coupling levels.

Fig. 4.

A plot of intracellular potential at a fixed time for several different nonephaptic models with gap-junctional coupling at approximately 1% of normal. Observe that the multiscale model has unresolved regions on both the left and right of the wave front. Note that the multiscale and microscale models agree quite well and that the macroscale model agrees with them only if the grid spacing is 100 μm.

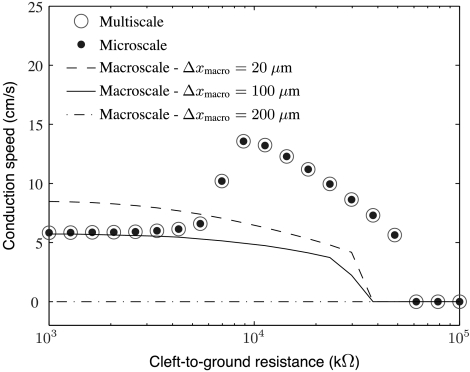
The second set of simulations was meant to investigate the effects of cleft-to-ground resistance on conduction speed in ephaptic models. To that end, we simulated the microscale model with Δx_micro = 20 μm; the ephaptic macroscale model (see SI Text) at resolutions Δx_macro = 200, 100, and 20 μm; and the adaptive multiscale model with Δx_macro = 400 μm and Δx_micro = 20 μm. Gap-junctional coupling was set to be at 1% of its normal value. Motivated by the histological analysis and modeling in ref. 13, we considered myocytes for which 90% of the Na⁺ channels are localized along the ends of the cells. As observed in prior mathematical studies (8, 13, 14), preferential excitability of myocyte ends is necessary for ephaptic conduction. In our simulations, cleft-to-ground resistance was varied over the range 10³–10⁵ kΩ. As remarked by Kucera et al. (13), cleft-to-ground resistance can be related to cleft width through the formula R_c = 1/8πσ_extw, where σ_ext is the conductivity (mS/cm) of the extracellular medium and w (cm) is the cleft width. Using this relation, the values of R_c we survey range from about w = 0.5 to 60 nm. Results from these ephaptic simulations are presented in Figs. 5 and 6.

Fig. 5.

A plot of conduction speed versus cleft-to-ground resistance for several ephaptic models and levels of resolution. The microscale and multiscale models show a nonmonotonic profile of conduction speed versus cleft-to-ground resistance, known as the ephaptic effect. In contrast, the macroscale simulations do not capture this effect at resolutions of 20 μm, 100 μm, or 200 μm. In these simulations, gap-junction levels are at 1% of their normal value of 666 mS/cm², and 90% of Na⁺ channels are localized to the ends of cells.

Fig. 6.

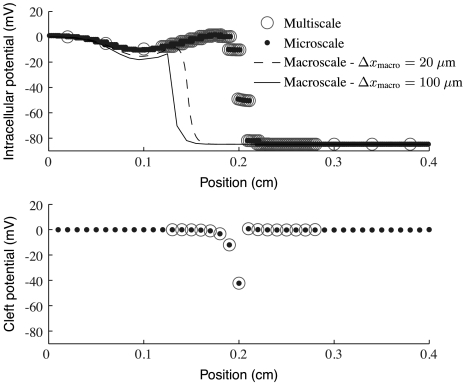
A plot of intracellular and cleft potentials at a fixed time for several different ephaptic models with gap-junctional coupling at 1% of normal and R_c = 8.85·10³ kΩ. (Top) Intracellular potential for each model; (Bottom) cleft potential only for the multiscale and microscale models. The macroscale cleft potentials are omitted for clarity. Note that the cleft potentials for the multiscale model are shown only in the resolved region, as the model assumes them to be identically zero everywhere else. Observe that the multiscale and microscale models agree quite well. The macroscale model does not agree with them for either grid spacing. Note that 20 μm is the spacing used by the microscale simulations and the microscale part of the multiscale simulations.

Results for Nonephaptic Simulations.

Fig. 3 shows computed conduction speed versus fraction of normal gap-junctional conductance for several nonephaptic simulations. Fig. 4 shows computed wave forms at one such level of gap-junctional conductance. Two features of importance in comparing models are the quantitative difference in conduction speeds and the threshold of gap-junctional coupling below which there is conduction block. The dotted line in Fig. 3 shows that the macroscopic model discretized with grid spacing Δx_macro = 400 μm systematically underestimates conduction speed by at least 10 cm/s over a wide range of coupling levels. Further, the value of coupling at which conduction block occurs is too large by about an order of magnitude. Macroscale simulations with Δx_macro = 200 μm are much more accurate. They are off by no more than about 5 cm/s over a wide range of coupling levels. Nonetheless, the threshold for conduction block is too large by about half an order of magnitude. Consequently, there are large fractional discrepancies with microscale simulations for low gap-junctional levels. Macroscale simulations with one biological cell per node and adaptive multiscale simulations are strikingly accurate in predicting conduction speeds and the level of coupling for conduction block. Macroscale simulations with subcellular spatial resolution are quantitatively accurate only for high levels of gap-junctional coupling. In particular, there are levels of gap-junctional coupling where the fully microscale model exhibits conduction block, yet the highly resolved, fully macroscale model does not.

Results for Ephaptic Simulations.

Fig. 5 shows computed conduction speed versus cleft-to-ground resistance for several ephaptic simulations. Fig. 6 shows computed wave forms at one such level of cleft-to-ground resistance. Note that the microscale and adaptive multiscale models give rise to the nonmonotonic relationship between cleft-to-ground resistance and conduction speed that is characteristic of the so-called “ephaptic effect.” In particular, there is a certain value of this resistance that maximizes conduction speed. This qualitative behavior is consistent with Kucera et al. (13), even though the two studies use different ionic models. The value of R_c that maximizes conduction velocity is determined by two competing biophysical effects of the cleft-to-ground resistance. First, Na⁺ channels at intercalated discs are subject to extra resistance and are hence marginalized. As a result, increased cleft-to-ground resistance can slow conduction. Second, larger values of R_c ensure that a given current through the cleft produces larger cleft potentials. As such variation can depolarize the cleft-facing membrane of a neighboring cell, larger values of R_c could speed conduction. The fully macroscale ephaptic simulations with Δx_micro = 200, 100, or 20 μm do not capture the nonmonotonic relation between R_c and conduction speed. Note that 20 μm is the grid spacing used both by the microscale simulations and by the microscale part of the multiscale simulations. Fig. 5 shows that the fully macroscale simulations are accurate only at low values of R_c, and then only for Δx_macro = 100 μm. By contrast, the multiscale model correctly predicts the conduction velocities and wave forms over a wide range of values of R_c.

Discussion

In this article, we introduce a multiscale model of cardiac conduction in a linear strand of cardiomyocytes, and we compare the results predicted by this model to fully microscopic and fully macroscopic models of cardiac conduction. We investigate the effects of gap-junctional and ephaptic coupling on conduction. We emphasize that our scheme is not simply an adaptive-grid method for a fixed partial differential equation; it is genuinely multiscale, involving two distinct partial differential equations posed over different geometric structures and spatial scales. The multiscale approach is useful because fully macroscale models can be inaccurate in the low gap-junctional regime and fully microscale models are too expensive to generalize to whole-heart simulations.

One source of inaccuracy in fully macroscale models is the sensitivity of conduction speed to grid spacing. In particular, our simulations demonstrate qualitative and quantitative discrepancies if Δx_macro is either too large or too small. Hence, it is difficult to know a priori how finely to discretize a macroscale model. For example, Fig. 3 shows that underresolving the macroscale equations results in a large error in determining the range of gap-junctional conductances that exhibit propagation block. Further, overresolving the macroscale equations introduces the qualitative error that propagation failure never occurs. This consequence of overly fine grid spacing is reasonable because of a pair of theoretical results: The bistable diffusion equation over a continuous domain allows propagation for arbitrarily small diffusion coefficients, and the discretization of that equation over a fixed grid exhibits propagation block for sufficiently small diffusion coefficients (1).

A further source of difficulty in fully macroscale simulations is that their best accuracy is sensitive to apparently small changes in the underlying biophysics. For example, Figs. 3 and 4 demonstrate the exceptional agreement between our nonephaptic, fully macroscale, low gap-junctional simulations with grid spacing of 1 node per cell and their underlying fully microscale model. The corresponding ephaptic macroscale simulations shown in Figs. 5 and 6, however, have marked disagreements with their underlying microscale model. Without a clear understanding of why this small change in posited biophysics causes such a variation of accuracy, it is hard to know whether low gap-junctional nonephaptic macroscale simulations are always accurate at that resolution.

We note that multiscale simulations are much less expensive than their fully microscale counterparts. In the simulations shown in Fig. 4, the multiscale model required around 120 nodes, whereas the microscale model used 280. For comparison, the macroscale model with grid spacing of 200 μm had 20 nodes. The multiscale model’s savings of about half the total number of nodes appears modest because our test problem is small. One can expect orders of magnitude in savings in a three-dimensional domain involving many cells. Further savings could be attained by varying the adaptivity rule and the grid spacing away from wave fronts, but we have not studied the effects of these parameters in detail.

The present study has several limitations. First, this is essentially a monodomain model, as it neglects bulk extracellular currents. There should be no significant barrier to extending these results to the bidomain case because extracellular space has a simpler mathematical structure than intracellular space. Second, the simplified ionic current model we used does not have an explicit Ca²⁺ current. In the low gap-junction regime, such currents play a more prominent role than they do in the high gap-junction regime (17). We expect that inclusion of a more comprehensive ionic model would cause minor quantitative, but not qualitative, changes in the conduction speeds and levels of gap junction that cause conduction block. Third, our model is one dimensional. Capturing the effects of fiber rotation on propagation requires three-dimensional simulations. We now present two extensions of our model to that case.

Possible Extensions to Three Dimensions

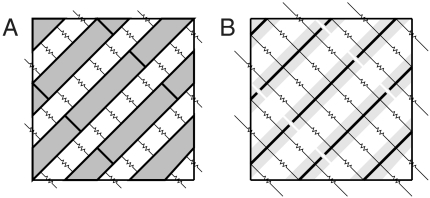
One generalization of our multiscale model to three dimensions is depicted in Fig. 7A. We refer to this extension as the detailed three-dimensional model. It describes resolved myocytes as three-dimensional domains, over which the potential satisfies the electrostatic Laplace equation. Cell membranes have flux boundary conditions corresponding to capacitive and ionic current. Cells are connected to each other through continuously distributed gap junctions, modeled through flux boundary conditions, as in Hand et al. (18). In the unresolved regions of this model, potential is governed by macroscale monodomain or bidomain equations. The two regions can be coupled at their interface through the constraints that potential is continuous and that current flux is conserved.

Fig. 7.

Resolved regions of two different three-dimensional generalizations of our multiscale model. Resistors that cross the boundary of the resolved regions couple the microscale model to the macroscale model at a coarse-fine interface. A presents a detailed model. Shaded regions represent myocytes connected to their neighbors through gap junctions on their sides (depicted as resistors) and ends (not depicted). Cells may also interact at their ends through an ephaptic mechanism similar to that in Fig. 1. Electric potential satisfies the Laplace equation, and resolved cells are coupled to unresolved cells by assuming the potential of intracellular space is continuous and current flux is conserved. B presents a reduced model. The thick lines represent one-dimensional cables that model the shaded cells. In this reduced model, electric potential satisfies equations similar to Eqs. 1–7. Resolved cells are coupled to unresolved cells through discretized cytosolic and gap-junctional resistances that intersect the coarse-fine interface.

A simpler generalization, which we call the reduced model, is depicted in Fig. 7B. It describes resolved myocytes as one-dimensional cables like those in the present paper. Cells are resistively coupled to each other in a prescribed three-dimensional arrangement. In the unresolved region of this model, potential satisfies the macroscale bidomain or monodomain equations. To detail the coupling between the macroscale and microscale models, we consider a discretization of the resolved cells. Each microscale node is connected to neighbors through resistive connections that represent cytosolic or gap-junctional currents. Some of these connections cross the coarse-fine interface and directly determine the coupling between scales. Flux through these interface resistors could be computed by treating the potentials within all cells of an unresolved block as constant, as done in the present one-dimensional case. We note that this approximation of macroscale potential introduces a first-order discretization error and could be replaced by a higher-order extrapolation procedure.

Both proposed models have strengths and weaknesses. The detailed model can account for transverse intracellular potential variation within cells, whereas the reduced model cannot. As a consequence, the detailed model is more expensive because it requires more nodes. Discretization is considerably more involved for the detailed model because the skewed arrangement of myocytes creates complicated shapes of cell fragments and their boundaries. In comparison, for the reduced model, the discretization structure is fixed in advance, and it is straightforward to determine which resistive connections cross the coarse-fine interface. Hence, the reduced model appears significantly easier to implement. Weighing these strengths and weaknesses requires further research.

Another challenge in extending our work to three dimensions is to understand the ephaptic effect better, even in a fully microscale model. For example, it is unclear whether cleft-like behavior is relevant in transverse directions. Nonetheless, our overall message should carry over: that large-scale, low gap-junctional, cardiac simulations may need to be adaptive and multiscale.