Rice yields in tropical/subtropical Asia exhibit large but opposing sensitivities to minimum and maximum temperatures

Abstract

Data from farmer-managed fields have not been used previously to disentangle the impacts of daily minimum and maximum temperatures and solar radiation on rice yields in tropical/subtropical Asia. We used a multiple regression model to analyze data from 227 intensively managed irrigated rice farms in six important rice-producing countries. The farm-level detail, observed over multiple growing seasons, enabled us to construct farm-specific weather variables, control for unobserved factors that either were unique to each farm but did not vary over time or were common to all farms at a given site but varied by season and year, and obtain more precise estimates by including farm- and site-specific economic variables. Temperature and radiation had statistically significant impacts during both the vegetative and ripening phases of the rice plant. Higher minimum temperature reduced yield, whereas higher maximum temperature raised it; radiation impact varied by growth phase. Combined, these effects imply that yield at most sites would have grown more rapidly during the high-yielding season but less rapidly during the low-yielding season if observed temperature and radiation trends at the end of the 20th century had not occurred, with temperature trends being more influential. Looking ahead, they imply a net negative impact on yield from moderate warming in coming decades. Beyond that, the impact would likely become more negative, because prior research indicates that the impact of maximum temperature becomes negative at higher levels. Diurnal temperature variation must be considered when investigating the impacts of climate change on irrigated rice in Asia.

The impacts of temperature and solar radiation on rice yield remain imperfectly understood, despite decades of agronomic research. Current knowledge is based primarily on field trials and greenhouse experiments. These experimental studies indicate that increased temperature (1–4) and decreased radiation (1, 3, 5) can reduce yield, with the impacts varying across the plant's three growth phases (vegetative, establishment to panicle initiation; reproductive, panicle initiation to flowering; ripening, flowering to mature grain). Unresolved issues remain with respect to the relative impacts of temperature during daytime (T_max) vs. nighttime (T_min), potentially confounding impacts of temperature and radiation, and the magnitude of impacts in nonexperimental settings. Here, we investigate these issues by analyzing data from the largest farm-level rice study conducted in Asia since the mid-1980s. We use disaggregated data from farmer-managed fields to disentangle the impacts of T_min, T_max, and solar radiation on rice yield.

With few exceptions (6, 7), most statistical studies on temperature and rice yield have focused on the impact of daily mean temperature (T_ave), despite evidence that that the effects of T_min and T_max on crop phenological development and physiological processes differ (4). It is well-established that extremely high levels of T_max during flowering can drastically reduce rice yield because of spikelet sterility, but recent studies have provided evidence that yield might be more sensitive to T_min than to T_max in locations where spikelet sterility is rarely observed (8). Rice simulation models began to include T_min and T_max as separate variables only recently (4). Better understanding of the impacts of temperature at different points in the diurnal cycle is needed, because T_min has been rising faster than T_max in some important Asian rice-growing countries, including the two largest, China (9) and India (10), and is projected to continue doing so in the future (p 882 in ref. 11).

Potentially confounding impacts of T_min and radiation on rice yield in field experiments have attracted recent attention (8, 12), although this was recognized as a challenge for yield studies decades ago (5). The difficulty stems from the complex meteorological effects of clouds, which reduce not only insolation but also back radiation, thus possibly increasing T_min by enhancing long-wave surface warming at night (12, 13). Understanding the relative impacts of T_min and radiation is important in view of evidence of a declining trend in surface radiation (global dimming) (14), which probably results from increased cloudiness caused by a combination of global warming and regional brown clouds of aerosol pollution (13–16). A study based on a small number of annual observations (twelve) from a research station in the Philippines reported that the yield of irrigated rice decreased by 10% for each 1 °C increase in T_min averaged over the growing season (8). A reanalysis of the data from that study concluded that the actual impact of T_min was much smaller, because T_min was negatively correlated with radiation, thus confounding the observed impact of T_min with the omitted impact of radiation (12). A recent review of the impacts of climate change on rice concluded that “the effect of high night temperature is not understood well” (p 75 in ref. 4).

Although experimental studies are essential for understanding physiological relationships and constructing crop simulation models, they do not necessarily replicate real agricultural settings. Researchers typically apply agronomically optimal levels of inputs that are not being investigated, which can accentuate the impact of weather by making it the factor that limits yield. Data from farmer-managed fields allow one to study how weather affects yield in a setting in which farmers make decisions based on the weather they observe every day and the prices they pay for inputs and receive for harvested crops. Although other studies have used nonexperimental data to study the relationship between weather (or climate) and agriculture (17–21), including for rice (6, 7, 22), with one exception, they have analyzed aggregate data (e.g., national, state, or county), which precludes careful matching of weather variables with farm-specific planting and harvesting dates and crop-growth phases. The exception was a farm-level study on rice yield in a single country (Thailand), which presented no detail on statistical results and evidently did not examine diurnal temperature variation or solar radiation (23).

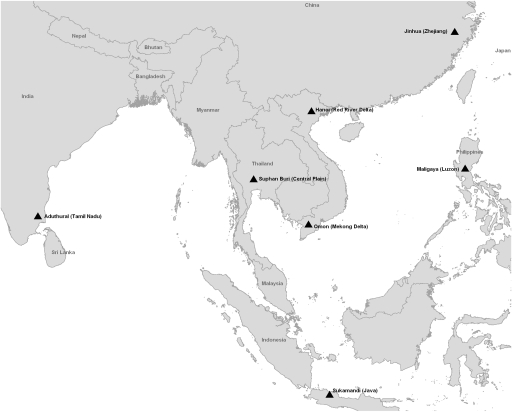
The data analyzed here are from a multiyear (1994–1999) study on productivity of intensively managed irrigated rice farms in Asia by the International Rice Research Institute (IRRI) and its partners in six countries (24). The farms were located in seven important rice-growing regions (sites) (Fig. 1) in six of the most important countries in terms of contributions to global rice supply. Each site represented an irrigated rice-growing area of more than 200,000 ha, ranging up to several million ha. All were located in inland plains or large river deltas with humid tropical or subtropical climate, with at least two rice crops grown each year. Such double- and triple-crop rice systems in similar climatic conditions occupy a land area of about 24 million ha in Asia, feed about 1.8 billion Asians, and account for 40% of global rice supply (25). Most of the sites are in areas where monthly average T_max is considered to be high (>33 °C) during the reproductive or ripening phase of one of the annual crops (p 97 in ref. 26).

Fig. 1.

Locations of study sites.

Farms at each site were selected to represent a range of the most common soil types, cropping systems, farm-management practices, and farm sizes. They were early adopters of Green Revolution technologies (modern high-yielding varieties adapted to local conditions, irrigation, fertilizers, pesticides, and mechanization) and had been under intensive management for decades. They were generally representative of intensively managed irrigated rice farms in their countries in terms of demographics, access to capital, and capital intensity of production (27). We analyzed all of the farms with complete data (227 farms) (Table S1).

Our objective was to determine the relative sensitivity of rice yield to changes in T_min, T_max, and radiation in a real-world setting, net of any responses (e.g., input adjustments) by farmers to these changes. Our general approach was to regress yield on weather variables and in some specifications, exogenously determined economic variables, whose inclusion improved the precision of the estimated weather impacts. IRRI and its partners collected data on crop establishment and harvest dates, production inputs, and yields for each farm in each season of each year. They also collected daily weather data from a single monitoring station at each site, which was within 15–20 km of nearly all farms at a site. This detail enabled us to construct farm-specific measures of weather variables defined according to the rice plant's three growth phases (for each phase, means for T_min, T_max, and radiation and sums for rainfall). The fact that the dataset included observations over multiple growing seasons enabled us to use fixed effects to control for unobserved factors that varied across space (i.e., were unique to each farm, such as soil) or time (were common to all farms at a given site in a given season and year, such as ambient CO₂ concentration). The inclusion of these fixed effects increased the likelihood that the impacts that we identified were indeed caused by temperature and radiation and not variables omitted from the regression models.

Results

Data Variability and Correlations.

Yield varied substantially in the sample (5,182 ± 1,468 kg·ha⁻¹; range = 288–10,838 kg·ha⁻¹), as did weather (Table S2). An understanding of correlations among the weather variables is important for interpreting the regression results. Three features of the correlation matrix are most notable (Table S3): T_min and radiation were not highly correlated, unlike in the Philippines study (8, 12), both variables were moderately (and positively) correlated with T_max, and their correlations with rainfall were smaller in absolute value than their correlations with T_max. These features suggest that the dataset affords the possibility to disentangle the impacts of T_min and radiation and that a failure to control for T_max could bias estimates of the impacts more than a failure to control for rainfall.

Regression Results.

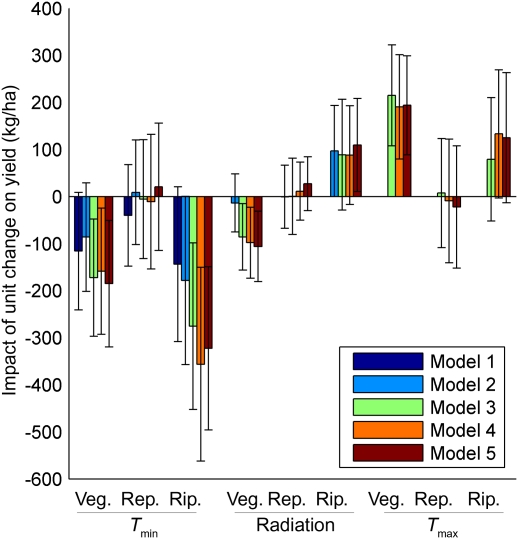
Multiple regression results support these contentions (Table S4). Fig. 2 shows, for different specifications of the regression model, parameter estimates for the temperature and radiation variables. Given the linear specification of the model, the estimates are interpretable as marginal effects: the impact of a one-unit change in a weather variable on yield, holding other variables constant. For example, in the model that included economic variables (Model 5), a 1 °C increase in T_min during the ripening phase reduced yield by 322.4 kg·ha⁻¹.

Fig. 2.

Impacts of temperature and radiation on rice yield, expressed per °C for temperature and per MJ·m⁻²·d⁻¹ for radiation. Each cluster shows estimates for a given variable from different regression-model specifications, distinguished by rice-growth phase (vegetative, reproductive, and ripening). Model 1 included only T_min. Model 2 added radiation. Model 3 added T_max. Model 4 added rainfall. Model 5 added economic variables. Bars show 95% confidence intervals.

Impacts varied by growth phase, with the most significant impacts occurring during the ripening and vegetative phases. T_min, T_max, and radiation had significant impacts (P < 0.05) during both of these phases in the more complete model specifications, with the exception of T_max during the ripening phase (P = 0.087 in Model 5). The lower significance of the latter variable resulted from its correlation with radiation during the same phase. The two variables were jointly significant (P < 0.001 in Model 5), however, and excluding either one sharply improved the significance of the other without affecting the signs or general magnitudes of the parameter estimates on the other weather variables (Table S5). These additional results imply that yield was significantly affected by both T_max and radiation during the ripening phase.

T_min and T_max had opposite impacts (negative and positive, respectively), whereas the impact of radiation differed between phases (positive for ripening and negative for vegetative). Differences in parameter estimates between the vegetative and ripening phases were more significant for radiation and T_min than for T_max (Table S6).

Parameter estimates on T_min changed only moderately when radiation was added (Fig. 2), which is expected given the small correlation between the two variables. The addition of T_max had a larger influence, causing the T_min parameter estimates to increase 1.5–2 times during both the vegetative and ripening phases. This resulted from the combination of the positive correlation of the two temperature variables and their opposing impacts on yield. Including T_max was, thus, necessary to accurately identify the impact of T_min. Otherwise, the T_min parameter estimate reflected the net impact of both temperature measures and was biased toward 0. In models that included both temperature measures, the absolute value of the (negative) impact of T_min differed significantly from the positive impact of T_max during the ripening phase (Table S6), which indicates that including both measures is more appropriate than including their mean, T_ave. This can also be shown by estimating the same models with T_ave included instead of T_min and T_max. Consistent with previous studies (28), T_ave tended to have negative impacts on yield during the reproductive and ripening phases, but the impacts were highly insignificant in nearly all specifications (Table S7).

Rainfall had a significant impact only during the ripening phase. The addition of rainfall affected the parameter estimates less than the addition of T_max, which is not surprising in view of the lower correlations of T_min and radiation with rainfall than with T_max. Correlations of the economic variables with the weather variables were very small, and therefore, their addition had a negligible impact on the parameter estimates. It mainly increased the precision of the estimates (lower SEs and P values).

The different units of the weather variables in Fig. 2 impede comparison of the variables’ impacts on yield. This can be overcome by expressing the marginal effects per SD of the weather variables (Table S8). The SDs were calculated after removing any variation explained by the fixed effects for farms and site/season-years, because only this residual variation was used to identify the variables’ impacts in the regression models. The largest marginal effect per SD was for T_min during ripening (−174.4 kg·ha⁻¹), followed by T_max and radiation during the vegetative phase (122.9 kg·ha⁻¹ and −124.1 kg·ha⁻¹). The smallest was for rainfall (68.4 kg·ha⁻¹), which is expected given that the farms were irrigated.

The marginal effects in Fig. 2 came from regression models that did not allow nonlinear responses of yield to weather. To examine the implications of this restriction, we also estimated a quadratic specification. The estimated parameters on the quadratic terms were mostly insignificant, and the marginal effects evaluated at mean values had the same signs as and were similar in magnitude to those in Fig. 2 (Table S9).

Joint Impacts.

The opposing effects of T_min and T_max indicate that warming has an ambiguous impact on rice yield. The effect that dominates depends on the magnitudes of not only the effects but also the trends in the two variables. Even if the absolute values of the variables’ opposing effects are not significantly different, as they are not during the vegetative phase (Table S6), differences in the variables’ trends could still result in a nonzero net impact of warming.

For each site and season, we investigated the joint impact of recent warming trends by summing the products of the marginal effects and corresponding trends in the two temperature variables during the vegetative and ripening phases. Analyzing observed trends instead of hypothetical future ones that might occur under accelerated warming is appropriate, because recent trends have been relatively small; combining marginal effects to calculate the joint impact of multiple temperature changes is valid only if the changes themselves are small (i.e., marginal). We also included radiation during the vegetative and ripening phases in the analysis, in view of concerns about its potentially confounding effect with T_min.

The analysis answered the question of how yield growth would have differed if observed weather trends had not occurred. Although our analysis is not the first to examine the impact of recent climate changes on agricultural yields, including for rice (6, 22), it differs in being based on farm-level data from multiple countries. Data series from the weather stations at the sites were too short to determine trends. Instead, trends in T_min and T_max were based on a global analysis of ground-station data for 1979–2004, whereas trends in surface radiation were based on satellite data for 1983–2004. Combining temperature data from ground stations with satellite data for radiation provides reliable estimates of weather impacts on crop yields (29). Trends were determined separately for each quarter of the year (December to February, etc.) and were assigned to seasons and growth phases using site-specific crop calendars (p 13 in ref. 24).

As expected, evidence of warming was stronger at night (Table S10); 16 of 28 site quarters had significant trends (P < 0.05) in the case of T_min, with 13 being positive, whereas only eight site quarters had significant trends in the case of T_max, with all being positive. Significant trends occurred for radiation in nine cases, with eight being negative. Significant warming and dimming thus occurred at some but not all sites.

Table 1 shows the joint impacts of these trends. The most obvious result is that the impacts varied substantially between seasons and sites. At most sites, yield would have grown more rapidly during the high-yielding season but less rapidly during the low-yielding season. The absolute values of the joint impacts were relatively large for one or both seasons at most sites, being equivalent to a fifth or more of the actual annual yield trends for the countries where the sites were located. The direction of the joint impact was influenced more by temperature than by radiation; the absolute value of the joint impact of T_min and T_max exceeded the absolute value of the impact of radiation for 11 of 14 season-sites and matched it for one.

Table 1.

Predicted changes in annual growth rate of rice yield if observed weather trends at the end of the 20th century had not occurred at each site

	Predicted change in yield growth (kg·ha−1·y−1) resulting from elimination of trend				Net impact relative to mean observed yield for site/season (%·y−1)	Observed national yield growth rate (annual, not seasonal; %·y−1)
Season and site	Tmin	Tmax	Radiation	Net impact
High yielding
China (Jinhua)	0.0	0.0	0.0	0.0	0.00	1.48
India (Aduthurai)	6.3	−12.6	4.1	−2.2	−0.04	2.05
Indonesia (Sukamandi)	12.0	0.0	0.3	12.3	0.22	1.13
Philippines (Maligaya)	21.8	0.0	−2.3	19.5	0.31	1.51
Thailand (Suphan Buri)	11.7	0.0	0.0	11.7	0.23	1.55
Vietnam (Hanoi)	16.6	0.0	6.2	22.8	0.38	3.18
Vietnam (Omon)	−9.0	0.0	−10.7	−19.8	−0.33	3.18
Low yielding
China (Jinhua)	9.8	−14.0	0.0	−4.1	−0.07	1.48
India (Aduthurai)	7.2	−10.7	0.0	−3.5	−0.07	2.05
Indonesia (Sukamandi)	7.1	0.0	0.0	7.1	0.17	1.13
Philippines (Maligaya)	12.5	0.0	0.0	12.5	0.32	1.51
Thailand (Suphan Buri)	0.0	−10.9	−6.8	−17.7	−0.35	1.55
Vietnam (Hanoi)	0.0	0.0	−11.8	−11.8	−0.22	3.18
Vietnam (Omon)	−16.9	−13.7	0.0	−30.6	−0.76	3.18

Second through fourth columns show annual changes in yield growth because of elimination of trends in individual weather variables summed across rice-growth phases. Fifth column (net impact) shows sum of these changes. Sixth column shows net impact expressed as change in annual growth rate. Seventh column shows observed growth rate in rice yield at national level (not site level) for both seasons combined (seasonal data were not available). Time periods for estimating trends: temperature and observed yield growth rate, 1979–2004; radiation, 1983–2004.

Discussion

The estimated impacts of weather variables reported here are unique in being based on repeated observations from a large number of farmer-managed fields in multiple countries. This data structure enabled us to investigate the simultaneous impacts of multiple weather variables, broken out by growth phase of the rice plant, and to control for unobserved factors that varied across farms and at the site level over time. Despite these methodological differences compared with previous studies, our findings corroborate recent ones that T_min has a large, negative impact on yield (8, 30). Although the mechanisms responsible for the negative impact have yet to be conclusively identified (4), our results could be explained by increased respiration losses during the vegetative phase (8) and reduced grain-filling duration and endosperm cell size during the ripening phase (31).

Our finding of a positive impact of T_max during the vegetative and ripening phases is perhaps more surprising. The literature emphasizes a negative impact of elevated T_max during all growth phases because of reduced photosynthesis caused by chloroplast damage (vegetative phase), spikelet sterility caused by reduced pollen production (reproductive), and increased energy consumption caused by higher respiration demand (ripening) (4). This difference can be explained by the fact that T_max within our sample seldom reached the extremes that cause these negative impacts. For example, fewer than 4% of the observations of T_max during the reproductive phase in our sample exceeded the frequently cited threshold of 35 °C, above which spikelet sterility becomes common under humid conditions (2, 4). Field trials for rice grown under ambient temperatures have reported a positive impact of T_max (5), and most controlled-environment studies use 29–30 °C as the optimal daytime growing temperature (32). Mean T_max was within or not much above the latter range at most of our sites (Table S2).

Although our finding of a negative correlation between yield and radiation during the vegetative phase contrasts with the literature's emphasis on a positive correlation during the ripening phase (which we found also), there is experimental evidence that yields of some crops can rise if small reductions in total radiation, which is what we measured, coincide with increases in diffuse radiation (14). Other possible explanations include photoinhibition and excessive production of tillers, which could cause mutual shading and reduced panicle size.

Our most important methodological finding is that it is necessary to analyze the impacts of T_min and T_max jointly. Because these two variables were moderately correlated in our data and had opposing impacts on yield, excluding T_max biased parameter estimates for T_min in a positive direction. Moreover, the absolute values of the impacts of the two variables were significantly different during the ripening phase. Although the absolute values were not significantly different during the vegetative phase, their opposing effects would cancel only if trends in the two variables were identical, but this has not been the case in recent decades. Recent efforts to develop rice simulation models that include both T_min and T_max are clearly justified. Our results for these two variables differ from those in two recent studies of national rice-yield data (6, 7), which reported that T_min and T_max (6), or T_ave and diurnal temperature range (T_max − T_min) (7), had insignificant impacts in most countries during 1961–2002. Our finding of significant impacts is likely because of a combination of reasons, including the larger number of observations in our sample, our ability to define weather variables specific to farms and rice-growth phases, and our inclusion of controls for solar radiation and economic variables, which increased the precision of the estimates.

We emphasize that the impact estimates in Fig. 2 refer to marginal effects of climate changes. They should not be extrapolated to the nonmarginal warming that is projected to occur in Asia by the end of the century (Table S11), which lies well outside the residual variation in the weather data that was used to identify warming impacts in our regression models (Table S8). For moderate warming in coming decades, however, our results imply a net negative impact on yield, because T_min is projected to rise more rapidly than T_max, and the combined negative marginal effects of T_min during the vegetative and ripening phases exceed the combined positive effects of T_max (Fig. 2 and Table S6). Beyond that, the impact would likely become even more negative, because increases in T_max would push it out of the optimal growth range and closer to, or beyond, the extremely high levels where it can damage chloroplasts and cause spikelet sterility.

Another caveat is that our estimates refer just to irrigated rice, not all rice, in tropical and subtropical regions of Asia, not all rice-growing areas of the world. The lack of a substantial rainfall impact in our study does not mean that irrigated rice is ultimately unaffected by rainfall. Rainfall is the primary source of irrigation water at all seven sites, but it had a negligible impact in our sample simply because we analyzed a period when it did not limit irrigation. This could change in the future, because climate models predict that the area of Asia affected by drought will likely increase (11).

Data and Methods

Data.

The farms were not selected randomly (24), which is one reason we preferred fixed-effects estimates to random-effects estimates. A consequence of the use of fixed effects is that our results do not necessarily generalize to farms outside the sample, but the regression results changed little if we used random effects instead (see below). Each farm had a parcel dedicated to a nutrient-management study, but the parcel was small compared with total farm size. We used only data from the remaining area of each farm, which was controlled by the farmer.

Although IRRI collected weather data from just a single station at each site, the staggering of crop establishment and harvest dates across farms created variation in the weather variables within each site, even for a given season-year. We included only farms with no more than 2 d of weather data missing in a particular season. We used standard definitions of the three growth phases of rice in constructing the weather variables: vegetative, crop establishment through 66 d before harvest; reproductive, 31–65 d before harvest; and ripening, last 30 d of the growing season, excluding the harvest date. We constructed the temperature and radiation variables as farm-specific means and the rainfall variables as farm-specific sums of the daily observations for each phase.

Some recent studies on future agricultural impacts of climate change have defined temperature variables in other ways, including growing-degree days (GDD) and number of days in 1° temperature bins, with the latter fitted either linearly or with flexible polynomials (19–21). We did not use GDD, because low temperature rarely constrains rice growth at tropical and subtropical sites. Temperature bins are useful for identifying significant nonlinearities in the relationship between yield and temperature, which is especially important when simulating the impacts of projected large future increases in temperature. We were unable to implement this approach for two reasons: we had too few observations to estimate precisely the large number of parameters involved, and the tails of our temperature distributions were too thin to detect the nonlinearities.

Rice price was farm-specific. Rice price reflected variation in the varieties grown, which changed little over time on a given farm, and the quality of the harvested crop. Some farms sold parts of their harvest at different prices; in those cases, the rice-price variable was the average of the reported prices. Wage rate was calculated at the site level by dividing aggregate expenditure on hired labor across farms by the aggregate number of person-days hired. This was done separately for each season in a given year. The price of nitrogen fertilizer was also calculated at the site/season-year level. Nutrient-specific fertilizer prices were generally not available because of the prevalence of compound fertilizers. The price of nitrogen fertilizer was approximated by the corresponding parameter estimate from a regression of total fertilizer expenditure on the total quantities of nutrients applied. The use of uniform wages and fertilizer prices across farms at a given site in a given season is reasonable, because the farms at each site were located in villages adjacent to each other and were well-served by transportation infrastructure.

Regression Analysis.

We used multiple regression to estimate the following statistical model (Eq. 1),

where y_it is the yield of farm i in season-year t, c_i is a farm-level fixed effect, which equals 1 for observations from farm i and 0 otherwise, θ_jt is a site-specific season-year fixed effect, which equals 1 for observations from site j in season-year t and 0 otherwise, w_it is an N × K matrix of weather variables, where N is the number of observations across farms and season-years and K is the number of variables, β is a K × 1 vector of parameters that gives the impact of weather, and u_it is a random error term that represents the impacts of factors other than weather on yield. (We discuss the inclusion of economic variables below.) Because the model included farm-level fixed effects, the impacts of climate change were identified from the random variation in weather over time as opposed to the mean differences between farms. This identification strategy has been used in other recent studies (19–23).

We used a Box-Cox transform to guide model specification (33). The estimate of the Box-Cox theta parameter for a model with the same variables as Model 5 in Table S4 was 0.886, which implied that a linear specification was more appropriate than log-log, semilog, or inverse specifications.

We intentionally excluded any variable over which farmers had control from the right-hand side of Eq. 1, which could have caused endogeneity bias. As a result, the parameters in β are more inclusive than the marginal effects of weather that would be obtained from a regression model that controlled for farm inputs such as labor and fertilizer. To see this, suppose that instead of Eq. 1, the model was (Eq. 2)

The key change is the addition of z_it, which is a farmer-controlled input (an N × 1 vector) whose impact on yield is given by the parameter γ. The farm-level fixed effects are now given by a_i, the parameters on w_it by α, and the error term by ε_it. Suppose further that farmers’ decisions about how much of the input to use are affected by weather in the following way (Eq. 3):

δ_0i and δ₁ are parameters, and 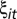is a random-error term. Inserting Eq. 3 into Eq. 2 yields an equation identical to Eq. 1, with c_i ≡ a_i + γ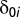, β ≡ α + γ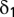, and u_it ≡ ε_it + γ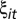. Hence, the expected value of estimates of β obtained by estimating Eq. 1 is the total marginal effect of weather on yield: the sum of the direct impact (α) and the indirect impact through weather's influence on input use (γ).

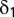The addition of exogenous economic variables does not fundamentally change this explanation. According to standard producer theory (34), input demand by farmers is determined by not only weather but also crop price (rice in our model), prices of inputs (labor and nitrogen), and stocks of fixed inputs (area planted with rice). The exclusion of these variables from Eq. 3 and thus, from Eq. 1 can bias estimates of β when the variables are significantly correlated with the weather variables. When the correlations are small, however, as they are in our dataset, then the bias is small, and exclusion of these variables mainly makes estimates of β less precise. Consistent estimates also require that the economic variables are not simultaneously determined with yield. This condition was met in our data: farmers were price takers in rice, labor, and fertilizer markets, and the area planted was determined months before each season's crop was harvested.

The panel structure of our data (i.e., both cross-sectional and time-series variation) allowed the estimation of models that included either fixed effects or random effects to control for unobserved farm characteristics. We used the generalized form of the Hausman test to test the validity of the random-effects model (pp 290–291 in ref. 35). We rejected the null that the regressors were uncorrelated with the farm-level random effects (P < 0.0001 in all cases). However, the random-effects estimates did not differ greatly from the fixed-effects estimates (Table S12). The results remained similar if we did not include either fixed or random effects to control for unobserved farm characteristics, but they changed substantially if we excluded fixed effects for site/season-years (Table S12). Evidently, the most influential unobserved effects in our sample were ones that varied over time at the sites. This suggests that parameter estimates from future studies that use cross-sectional farm-level data instead of panel data might not be very biased if the data are from multiple sites and regression models include site-level fixed effects.

Residuals in the models could be spatially correlated across farms within a site and serially correlated over time, despite the inclusion of the site-specific season-year fixed effects. We addressed this issue by clustering the SEs at the village/district level. The number of clusters was relatively small (just 32), which could cause the SEs to be inconsistent. To check this, we implemented a bootstrapping method for estimating consistent t statistics with a small number of clusters (36). Parameter estimates for T_min, radiation, and T_max during the vegetative phase and T_min during the ripening phase remained significant (P < 0.05) according to the bootstrapped t statistics, but estimates for T_max and radiation during the ripening phase did not (P = 0.118 and P = 0.148, respectively). Each of the latter two variables became significant (P = 0.002 and P = 0.02, respectively), however, if the other was excluded.

Analysis of Joint Impacts.

Estimated quarterly trends in T_min and T_max (°C y⁻¹) during 1979–2004 were provided by the US National Climatic Data Center and were generated using the methods described in ref. 37. They referred to 5 × 5° grid cells containing the sites. Trends in surface radiation were based on analysis of the series Insolation on Horizontal Surface (megajoules·m⁻²·d⁻¹) from the National Aeronautics and Space Administration Climatology Resource for Agroclimatology website (http://earth-www.larc.nasa.gov/cgi-bin/cgiwrap/solar/agro.cgi?email=agroclim@larc.nasa.gov). Daily data for this series were downloaded by entering the latitude, longitude, and elevation of each site. Data were averaged within each quarter of the year during 1983–2004 (1983 was the first year in the dataset), and then, the natural logarithm of each quarterly series for each site was regressed on an annual time trend. Hence, the radiation trends were expressed in percent change per year. Significance was tested using Newey–West SEs, which were robust to heteroskedasticity and first-order serial correlation.

Impacts in Table 1 were calculated by multiplying (i) temperature trends (Table S10) by the corresponding regression coefficients (Model 5 in Fig. 2) and (ii) radiation trends by the corresponding regression coefficients and means of the radiation variables. National yield trends were estimated by regressing the natural logarithm of national yield data (FAOStat; http://faostat.fao.org/default.aspx) on an annual time trend. Impacts changed little if they were based on weather trends that were significant at P < 0.1 instead of P < 0.05.