Reversing the size-dependence of surface plasmon resonances

Abstract

The size-dependence of surface plasmon resonances (SPRs) is poorly understood in the small particle limit due to complex physical/chemical effects and uncertainties in experimental samples. In this article, we report an approach for synthesizing an ideal class of colloidal Ag nanoparticles with highly uniform morphologies and narrow size distributions. Optical measurements and theoretical analyses for particle diameters in the d ≈ 2–20 nm range are presented. The SPR absorption band exhibits an exceptional behavior: As size decreases from d ≈ 20 nm it blue-shifts but then turns over near d ≈ 12 nm and strongly red-shifts. A multilayer Mie theory model agrees well with the observations, indicating that lowered electron conductivity in the outermost atomic layer, due to chemical interactions, is the cause of the red-shift. We corroborate this picture by experimentally demonstrating precise chemical control of the SPR peak positions via ligand exchange.

The ability to control surface plasmon resonances (SPRs) in metal nanostructures is critical for achieving advances in many areas, including chemical and biological sensing, imaging, optoelectronics, energy harvesting and conversion, and medicine (1–12). Metal nanoparticles (NPs), particularly those of the noble metals (e.g., Au and Ag) that exhibit strong SPRs, have been the focus of much work (13–17). SPRs have intense and broad optical absorption bands that arise from coherent oscillations of conduction electrons near the NP surfaces. In general, SPRs are influenced by their size, morphology, composition, surface chemistry, and surrounding environment (18, 19). However, the size-dependence of SPRs that is important for the aforementioned applications (1–12) is poorly understood in the small particle limit due to complex physical and chemical effects as well as uncertainties in experimental samples. Here, we report an approach for synthesizing an ideal class of colloidal Ag NPs with highly uniform morphologies and narrow size distributions. The SPR absorption band for particles with diameters, d, in the range of 2–20 nm is found to exhibit an exceptional behavior: As size decreases from d ≈ 20 nm it blue-shifts but then turns over near d ≈ 12 nm and strongly red-shifts. We have developed a multilayer Mie theory model and the corresponding calculation results agree well with the observations, indicating that the lowered electron conductivity in the outermost atomic layer, due to chemical interactions, is the cause of the red-shift. We corroborate this picture by experimentally demonstrating precise chemical control of the SPR peak positions via ligand exchange. Such chemical control of the NP surface layer may provide a promising strategy for sensitively probing species strongly adsorbed (or bonded) to the NPs.

For metal NPs with d or structural features larger than 20 nm, often a purely continuum-level, classical electrodynamics picture suffices for interpretation or prediction of their optical properties. In this approach the bulk dielectric constants for the various materials in the system are employed to define the problem, and Maxwell’s equations are solved subject to appropriate boundary conditions to yield optical spectra and field patterns. Analytical solutions are possible for simple geometries such as spheres (20), while approximate or numerical approaches are adopted for more complicated cases (18, 21). There can be size-dependent features in this “large particle” limit—for example, in general as d decreases the SPR band blue-shifts (18, 19, 22).

Being between the limits of clusters and larger nanoparticles, colloidal metal NPs with diameters in the 2–20 nm range are still poorly understood in terms of optical properties. For these metal NPs with d values much less than typical SPR wavelengths, a single dipolar-like SPR dominates. Nonetheless, the size-dependence of the SPR band in this limit can be complex (19, 22). As d decreases, size- and surface-related effects become increasingly more important: (i) The approximation of a single, local dielectric constant in metallic regions that is the same as the bulk value becomes questionable for a number of reasons (23), and (ii) chemical interactions with the surrounding medium or surfactant molecules that are often ignored in larger systems become pronounced. Observed SPR band positions have been reported to blue-shift or red-shift depending on a variety of features (18, 21, 24–26). Unfortunately, reliable theoretical predictions based on quantum mechanics are very difficult (or even impossible) to obtain at present, and approximate approaches also lead to conflicting predictions (18, 21, 27, 28). Experimentally deducing the correct SPR size-dependence of metal NPs in the 2–20 nm regime requires synthesis of NPs with: (i) very narrow size distributions (< 10%) to attenuate heterogeneous broadening, (ii) high uniformity in morphology and surface environment, and (iii) excellent dispersibility to eliminate the influence of aggregation. Here we show how to meet these needs with the synthesis of high-quality colloidal Ag NPs with precisely controlled sizes of 2–20 nm, uniform morphology and identical surface chemistry.

Results and Discussion

The synthesis of Ag NPs is based on reduction of silver nitrate (AgNO₃) in oleylamine (OAm), which serves as both solvent and reducing agent, at elevated temperatures. In a typical synthesis of d = 10.0( ± 0.5) nm Ag NPs, 170 mg AgNO₃ dissolved in 20 mL OAm was heated at 180 °C for 1 hr under nitrogen atmosphere, resulting in a dark-brown organosol. Washing the organosol with acetone followed by size-selection via centrifugation produced 10.0 nm Ag NPs with a very narrow size distribution of 5% (SI Text). The synthesized Ag NPs can be well dispersed in varying organic solvents (e.g., hexane, toluene, and chloroform) with the addition of excess OAm (0.05 ml) for long-term storage. The amine group of each OAm molecule coordinately bonds to the surface Ag atoms of the NPs, resulting in a hydrophobic capping layer to enable excellent dispersibility in organic media. Fourier transform infrared (FTIR) spectroscopy confirms the surfaces of the Ag NPs are coated with OAm (Fig. S1). The detailed synthetic conditions of the Ag NPs of various sizes are summarized in SI Text.

The Ag NPs synthesized in the above manner exhibit high uniformity in size, shape, and crystallinity. Panels A–I of Fig. 1 are transmission electron microscopy (TEM) images of the Ag NPs of various sizes from ∼2 nm to ∼18 nm, clearly showing their monodispersity and narrow size variation (with standard deviation < 10%). The inhomogeneous contrast that is reflected by the randomness of dark spots in individual NPs indicates the existence of twinning defects. The dark spots are indeed the real reflection of crystalline orientations of the NPs randomly sitting on the TEM grids. Focusing the electron beam on the Ag NPs even for half an hour did not induce variation in their morphology and contrast, confirming that the nanoparticles are stable under the electron beam. High resolution TEM (HRTEM) images of the spherical-like NPs reveal that each NP adopts an icosahedral morphology with multiple-twinned (MT) structure, having 20 {111} facets and containing 20 tetrahedral subunits joining along the (111) twin boundaries (29). One of the most distinguishing morphological characteristics of the icosahedral MT NPs is the coexistence of three types of rotational axes: twofold, threefold, and fivefold ones, which can be used to differentiate from other frequently observed MT NPs, such as decahedrons. Careful HRTEM studies on Ag NPs with different sizes confirm that they are all crystallized in icosahedral shapes (Fig. 1 J–L and Fig. S2) (SI Text). Time-dependent studies reveal that each icosahedral MT NP grows from an icosahedral MT seed followed by enlargement into different sizes determined by reaction conditions (see Fig. S3 and SI Text for detailed discussion). The consistent icosahedral morphology of the differently sized Ag NPs eliminates the complication of shape variation in the SPR properties when size-dependency is studied.

Fig. 1.

TEM images of Ag NPs of various diameters. (A) 2.2 ± 0.5 nm, (B) 3.3 ± 0.4 nm, (C) 3.9 ± 0.4 nm, (D) 5.3 ± 0.4 nm, (E) 7.3 ± 0.5 nm, (F) 10.0 ± 0.5 nm, (G) 12.5 ± 0.6 nm, (H) 15.6 ± 0.9 nm, and (I) 17.8 ± 1.6 nm (note the numbers following the ± sign are standard deviations). Representative HRTEM images of three 10-nm Ag NPs with their rotation axes oriented along or close to the electron beam show: (J) twofold, (K) threefold, and (L) fivefold symmetries. Scale bar in I represents 50 nm and applies for A–I and scale bar in L represents 5 nm and applies for J–L. The interplanar distance measured from adjacent lattice fringes in J–L is 0.236 nm, matching well with the (111) planes of face centered cubic (fcc) Ag.

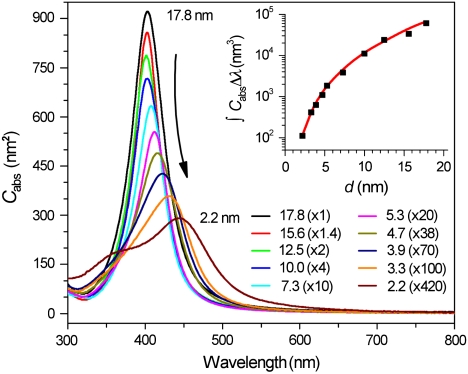
Due to their narrow size distribution, uniform morphology, and identical surface coatings, these Ag NPs represent an ideal class of material for studying the precise dependence of SPR on size. Quantitative absorption spectra of the Ag NPs with different sizes in hexane (Fig. 2) are measured by dissolving 20 μg of NPs (dried by evaporation) in 2.0 ml of hexane containing 10 μl of OAm (for stabilization). The concentration of each NP solution is determined using inductively coupled plasma optical emission spectroscopy (ICP-OES) (SI Materials and Methods). As a result, absolute absorption cross sections (C_abs,nm²) of fixed-size NPs as a function of wavelength can be inferred (Table S1, SI Text) (30). As particle size decreases the SPR peak heights are seen to dramatically decrease, and the spectral widths gradually become broader (Fig. 2 and Fig. S4). Integrated absorption cross sections (∫C_absΔλ, nm³, Fig. 2 Inset) also decrease with particle size in a manner very consistent with absolute values calculated according to the theoretical model discussed below. Such absolute comparison represents a very stringent test of the model.

Fig. 2.

Size-dependent absorption cross section (C_abs,nm²) per Ag NP of various diameters (d, nm) dispersed in hexane at room temperature. For clarity, each spectrum has been multiplied by an arbitrary factor listed in the parentheses. The numbers out of the parentheses represent the diameters of the Ag NPs. The inset plots the experimental (black squares) and theoretically calculated (red line) absorption areas integrated from 320 to 600 nm (∫C_absΔλ,nm³).

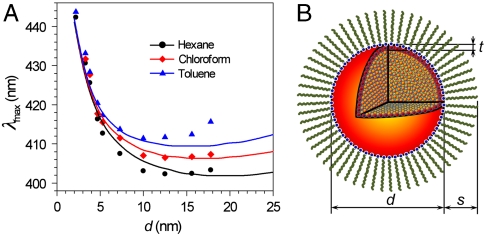
It is worth noting that the dependence of the absorption peak position (λ_max) on the particle size is quite interesting. The absorption peak blue-shifts as particle size decreases from d ∼ 20 nm to ∼12 nm (Fig. 2 and Fig. 3A). Such a blue-shift is well known in the larger particle limit and arises from radiative depolarization effects that occur when the particle size is not negligible compared to the size of the wavelength (19). However, as particle size is further decreased, a strong red-shift takes over. The Ag NPs also exhibit such exceptional behavior when dispersed in toluene and chloroform (Fig. 3A and Fig. S5 A and B), while TEM studies show that the NPs remain the same size, shape, and monodispersity (Fig. S5 C–J and K–R). Interestingly, the turnover point becomes smaller when the refractive index (n) of dispersant is higher. For example, the size-dependent peak positions turn over at ∼10 nm, 12.5 nm, and 15 nm for toluene (n = 1.497), chloroform (n = 1.446), and hexane (n = 1.379), respectively (Fig. 3A).

Fig. 3.

Comparison of experimental and theoretically calculated absorption spectra. (A) Experimental (symbols) and theoretically predicted (lines) SPR peak positions for Ag NPs of various sizes dispersed in hexane (black), chloroform (red), and toluene (blue). (B) Schematic illustration of the theoretical model: d represents the diameter of a Ag NP, t is the thickness of the outermost atomic Ag layer with lowered conductivity, and s is denoted as the thickness of the surfactant layer. Blue dots represent N atoms bonded to the surface of the NP.

There are several earlier experimental studies on Ag NPs that point out a turnover to a red-shifting SPR band as particle size decreases (31–33). However, all these studies involved relatively wide distributions of particle sizes and morphologies dispersed in glass or various matrices, making it difficult to unambiguously infer the true size-dependence. Although it was realized that some undetermined matrix-NP interaction beyond interfacial damping would be required to explain the results (34), neither experimental verification of the interactions nor a specific model was suggested. Here, we construct a simple model that is consistent with our current results. In this model we take the icosahedral Ag colloidal NPs to be spheres composed of a core that is treated with the bulk dielectric constant, and a thin shell in which the Ag dielectric response is modified compared to the bulk. In particular the electron conductivity in the outer layer of Ag atoms (of thickness, t) is assumed to be lowered compared to that of the inner Ag atoms because of the partial participation of these electrons in chemical bond interactions between surface and the surfactant molecules. The optical properties are calculated using analytical, multilayer Mie theory (35).

The overall model, shown in Fig. 3B, consists of (i) a central spherical metal core of radius r_c = d/2 - t, (ii) a surrounding shell from radius r_c to r_c + t = d/2 corresponding to the layer of reduced conductivity, (iii) a shell corresponding to the surfactant layer from radii d/2 to d/2 + s, and finally (iv) the relevant solvent surrounding the particle-surfactant complex for radii greater than d/2 + s. For region i we employ the bulk Ag dielectric constant (36). For region ii we break down the dielectric constant into interband and intraband terms and describe the latter with a Drude model, in which the conductivity is lowered from the bulk value by a factor g². Finally, standard values for the dielectric constants of the surfactant layer and solvent are employed. This model has three parameters, s, t, and g, but within our picture we fix t to be roughly the thickness of an atomic Ag layer, 0.25 nm, and s is fixed to 2.0 nm for OAm surfactant. We have also included a size-dependent interfacial damping correction (21, 37) that is known to be important at these smaller length scales. The complete details of the model and many of our other theoretical results may be found in the SI Text.

Comparison between theoretical and experimental size-dependent λ_max values for the Ag NPs dispersed in three different solvents (Fig. 3A) indicates that the level of agreement, given the simplicity of the model, is remarkable (g = 0.795 was employed). We have already noted the remarkable agreement (Fig. 2) in the integrated absolute intensities. Regarding the interfacial damping, calculations without the conductivity correction (i.e., g = 1) but retaining the size-dependent damping do show a turnover, but the maximum red-shift in the range considered is just 4 nm compared to shifts of 40 nm or more when including the conductivity lowering effect (Fig. S6). A very similar integrated intensity is also found whether or not damping is included (SI Text). However, the actual peak heights are significantly affected by the size-dependent damping, and Fig. S4A shows how these are lowered and in better agreement with experiment when damping is included.

Of course, even with the correction for damping, the calculated absolute absorption spectra can show some deviations from the experimental ones (Fig. S4 B–F). For example, in the case of the larger NPs, the theoretical results can be somewhat sharper and narrower (e.g., Fig. S4F). This may be due to the simplicity of the damping correction or possible size variation of Ag NPs of each sample. Nonetheless, the degree of both qualitative and quantitative agreement achieved with the model strongly suggests that the conductivity of the outer atomic layers of the NPs is a key, heretofore unappreciated feature to consider in the small particle limit of SPRs. We should note that the lowered conductivity is also consistent with the general notion of electron “spill-out” (19, 38) because both effects lead to a lowering of the density of free electrons near the surface of the metal NPs. The idea of electron spill-out across the metal interface is likely more appropriate when electrons can diffuse into free space, a situation significantly different from the real colloidal NPs of our samples. Nonetheless, the spill-out model of ref. 38 in fact does also predict a turnover. However, we were unsuccessful in using this model to achieve the same quantitative level of agreement across all the different surfactants and solvents studied here as seen with our model.

It is worth noting that surface oxidation of the Ag NPs may also lower the conductivity of the surface layer and lead to red-shift of the SPR (see SI Text). It turns out that calculations do show that a thin oxide layer, instead of a reduced conductivity metallic layer, could also lead to a similar reversal in the size-dependence of SPR peaks. However, our experimental results exclude the existence of oxide layers on the surfaces of the Ag nanoparticles. First, the syntheses were performed with a Schlenk line setup purged under inert N₂ atmosphere. Second, the absorption spectra of the Ag NPs measured right after synthesis and those measured after the NPs have been stored for nine months under ambient environment did not show variation in terms of both peak position and intensity, indicating the stability of the synthesized Ag NPs. Third, heating the Ag NPs at elevated temperatures when the dispersion was bubbled with air did not shift the position of their absorption peaks. For example, absorption spectra of a toluene dispersion of 5.3-nm Ag nanoparticles before and after heating at 70 °C for different times indicate no shift of the peak position (Fig. S7), further confirming the resistance of these Ag nanoparticles dispersed in organic solvents toward oxidation.

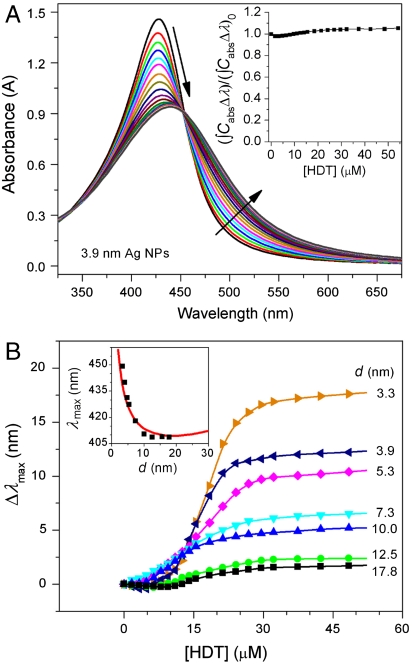
To further confirm the validation of the model (Fig. 3B), we carried out ligand exchange experiments to replace the native OAm on the Ag NPs with hexadecanethiol (HDT). The thiol (-SH) surfactant layer is more strongly chemically bound than the amine (-NH₂) surfactant layer to the Ag surface (39, 40), and thus there should be a larger conductivity reduction in the thiol case compared to the amine one. Consequently we expect a stronger turnover effect (greater red-shifting in the small size limit). For example, the absorption peak of the 3.9-nm Ag NPs dispersed in chloroform exhibits very noticeably shift to the red as HDT was added stepwise in small quantities (Fig. 4A) (SI Text). The ligand exchange process also leads to simultaneous broadening and damping of the peak. However, the integrated peak area remains essentially constant regardless of the concentration of HDT (Fig. 4A Inset), indicating that the SPR damping is not due to surface chemical reactions and the gradual deposition of Ag₂S over the surface (41). Titration of other sized NPs with HDT also shifts their absorption peaks to the red with different levels depending on their sizes (Fig. 4B and Fig. S8). TEM characterization of the Ag nanoparticles before and after they have undergone ligand exchange shows no observable structural and dimensional change (Fig. S9). When [HDT] is high enough (i.e., 30 μM), the shift of the absorption peaks stops due to a thorough replacement of the OAm with HDT molecules. It clearly shows that for small NPs the shift of the peak position is larger compared with that of the larger NPs. The difference in peak shift arises because the surface atomic layers account for a larger volume fraction in the smaller NPs and consequently the lowering of the surface conductivity plays a more pronounced role. The measured peak positions of the HDT-coated Ag NPs (Fig. 4B Inset) are in excellent accord with the result of our model calculations (g = 0.74, and s = 1.8 nm for HDT). The value of g used, considering that conductivity is proportional to g² (SI Text), corresponds to a 13% lower conductivity than for the OAm case and is consistent with somewhat stronger chemical interactions occurring in the HDT system.

Fig. 4.

Ligand exchange and SPR red-shift. (A) Variation of the absorption spectra of the 3.9-nm Ag NPs dispersed in chloroform upon titration with hexadecanethiol (HDT). The arrows indicate how the spectra change with increasing the concentration of HDT. The inset plots integrated absorption peak area (∫C_absΔλ) as a function of the concentrations of HDT. For easy comparison, the (∫C_absΔλ) is normalized against the initial integrated peak area, (∫C_absΔλ)₀, before the titration with HDT. The flat dependence indicates that dissolution of Ag NPs and formation of Ag₂S did not occur during the titration process. (B) Peak shift (Δλ_max, nm) of Ag NPs of various diameters (d) as a function of the concentration of HDT ([HDT], μM). The appearance of plateaus in the titration curves indicates that the OAm molecules of the Ag NPs are completely replaced with HDT molecules. The inset compares the dependence of absorption peak positions of the Ag NPs coated with HDT shells in chloroform on their diameters. The measurements (black squares) agree well with the calculated results (red line).

Conclusions

In summary, colloidal Ag NPs with highly uniform icosahedral shapes have been synthesized with sizes finely tuned in the range of 2–20 nm and with very narrow size distribution. We were able to unambiguously infer that the SPR band position of the NPs exhibits an exceptional size-dependence: a gradual blue-shift followed by a strong red-shift with decreasing size. A theoretical model based on a lowered conductivity in the outer metallic layer due to chemical interactions was found to describe the observations very well. The importance of this chemical effect has been further tested through gradual replacement of the original amine surfactant on the synthesized Ag NPs with a thiol surfactant. Chemically tuning the conductivity of the outer metallic layer in metal NPs, as demonstrated here, is a way of controlling SPR properties that might lead to useful applications. As one example, the high sensitivity of the absorption peak shift caused by addition of the thiol molecules (Fig. 4B), is comparable to what can be achieved with colorimetric organic dyes (42). The general concept of introducing a thin layer of differing conductivity from the core could also be useful in other areas such as surface-enhanced Raman spectroscopy (SERS), fluorescence, energy harvesting, and even catalysis. Furthermore, it is not necessary for the thin layer to always have lower conductivity than the core in order to achieve the strong tunability discussed here. For example, the optical conductivity of Pt in the ultraviolet range is actually higher than that of Ag, so multilayer Mie theory calculations show that small Ag NPs with a thin Pt layer will not show the strong red-shift with decreasing size discussed above; instead a strong blue-shift is found that contrasts with the weaker peak variation found for naked Ag NPs. This suggests that we can use such particles in studies of UV photocatalysis and fluorescence.

Materials and Methods

Synthesis of Ag NPs.

In a typical synthesis of ∼10.0 nm Ag NPs, 1 mmol AgNO₃ (Aldrich) was mixed with 20 ml OAm (Aldrich) at room temperature followed by heating up to 60 °C, which was maintained until the granular AgNO₃ crystals were completely dissolved. The solution was then quickly heated up (≥10 °C/ min) to 180 °C and the temperature was maintained for 1 hr before the reaction system was cooled down to room temperature. Nitrogen atmosphere and magnetic stirring (∼700 rpm) were maintained throughout the entire synthesis. The resulting dark-brown organosol was washed with acetone (Aldrich) and redispersed in hexane (VWR). Size-selective processes were used to narrow their size distribution. NPs with different sizes were synthesized by controlling the reaction conditions, (see SI Materials and Methods for further details).

Quantitative Measurements of Optical Absorption Spectra.

Ag NPs in hexane were dried under N₂, weighed, and redispersed in hexane with a concentration of 2.0 mg/ml. 10 μl of the NP dispersion was added to 2.0 ml of appropriate solvent [e.g. hexane, chloroform (Aldrich), and toluene (Aldrich)] together with 10 μl of excess OAm as stabilizer. Absorption spectra were immediately measured to avoid concentration variation caused by solvent evaporation.

Surface Ligand Exchange.

Diluted HDT solutions with varying concentrations (0.1 μl/ml, 1.0 μl/ml, and 10.0 μl/ml in CHCl₃) were prepared right before experiment. Absorption spectra of a dispersion of 40 μg NPs in 2.0 ml CHCl₃ and 10 μl OAm were measured before and after the HDT solutions were added stepwise to the dispersion.

Theoretical Calculations.

Optical properties of Ag nanoparticles were calculated using analytical, multilayer Mie theory (21, 35) and the model structure depicted in Fig. 3B. We fix t to be roughly the thickness of an atomic Ag layer, t = 0.25 nm. The surfactant thickness layer was taken to be s = 2 nm for OAm and s = 1.8 nm for HDT. Optimal values of g, based on comparison with the experimental results, were 0.795 and 0.74 for the OAm and HDT surfactants, respectively. Further details can be found in SI Materials and Methods.