Behavioral dynamics and influence in networked coloring and consensus

Abstract

We report on human-subject experiments on the problems of coloring (a social differentiation task) and consensus (a social agreement task) in a networked setting. Both tasks can be viewed as coordination games, and despite their cognitive similarity, we find that within a parameterized family of social networks, network structure elicits opposing behavioral effects in the two problems, with increased long-distance connectivity making consensus easier for subjects and coloring harder. We investigate the influence that subjects have on their network neighbors and the collective outcome, and find that it varies considerably, beyond what can be explained by network position alone. We also find strong correlations between influence and other features of individual subject behavior. In contrast to much of the recent research in network science, which often emphasizes network topology out of the context of any specific problem and places primacy on network position, our findings highlight the potential importance of the details of tasks and individuals in social networks.

Social organizations often need to perform coordination tasks in a networked and decentralized fashion. Decentralization introduces performance constraints, especially in situations where communication channels are much sparser than in a fully connected network, and it is of interest to researchers in sociology and the emerging field of network science to understand how the underlying networks affect collective performance.

We describe human-subject experiments in which decentralized coordination is modeled as the problems of coloring and consensus on a parametrized family of networks. The coloring problem may be viewed as a task of social differentiation or minimizing overlap between members of a decentralized group, while the consensus problem is a complementary task in which agreement or overlap is deliberately sought. Thus the two tasks entail local differentiation and global conformity respectively.

The (behavioral) coloring problem (1) requires each player in a network to choose a color from a fixed set that differs from the choice of all of their network neighbors, while consensus requires selecting a color that agrees with all network neighbors. In our experiments, each subject was assigned to a vertex in an exogenously chosen network, and given a financial incentive to strive for a global solution to the problem, even while being restricted to only their local neighborhood view of the network. It is worth noting that with respect to centralized computation, the coloring task is known to be NP-Complete, and thus likely computationally intractable, while consensus is clearly trivial.

One of our main findings is that even though coloring and consensus can both be viewed as forms of decentralized coordination, and the solution times of these problems varies with network structure, the way in which it varies is quite different in the two problems. Specifically, we find that as the networks become less clustered and more random, decentralized coloring becomes more difficult for humans to solve, while decentralized consensus becomes easier. Thus network properties alone are not sufficient to account for the observed patterns in collective behavior; rather, the task itself is of vital importance, even between two cognitively similar tasks. We also show that a simple model of individual behavior, when run in simulation on our networks, can qualitatively capture this behaviorally observed phenomenon.

Turning to aspects of individual rather than collective behavior, we also introduce natural notions of a player’s influence on their neighbors and the outcome of an experiment, and study the amount and origin of such influences. We find that the variation in influence across players is beyond what can be explained by the variability in their network positions, and that this influence is only weakly correlated with topological properties of network position such as degree and centrality.

Taken together, our results highlight aspects of collective behavior in network science that have been considered before (2, 3), but are perhaps deemphasized recently in favor of purely structural studies: namely, the potential primacy of task and agent details in social networks.

Related Work

Decentralized coordination is a problem of long standing interest. There are a number of game-theoretic models of coordination, in which players receive a positive payoff if and only if they can jointly coordinate on one of a collection of joint action choices. An alternative classic model is a cooperative game, which studies how players form coalitions. See Osborne and Rubenstein (4) for well known examples. Of central interest to us are the dynamics of the process by which players reach coordinated choice and the role of networks in this process; neither is informed by purely game-theoretic considerations.

While coordination games and cooperation in Prisoners Dilemma and other games have been extensively studied with human subjects over the years (5, 6–8), behavioral studies of coordination on networks are more recent. Kearns et al. (1, 9) study coloring and related problems on networks, although they do not focus on a particular parameterized family of networks as we do here. McCubbins et al. (10) and Kearns et al. (1) both observe that adding connections makes the coloring problem easier.

Experimental Methodology

The work described here continues a line of research at the University of Pennsylvania in controlled human-subject experiments on strategic behavior in social networks (1, 9, 13). In such experiments, each subject sits at a networked workstation with only a local (network neighborhood) view of the collective activity, and has a financial incentive to contribute to a global solution.

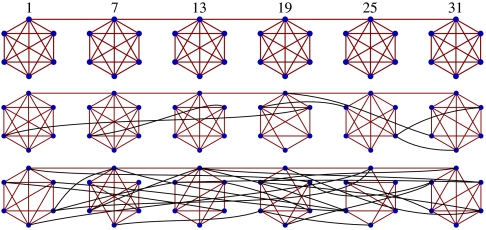
In the coloring and consensus experiments we shall describe, the networks used in each experiment were chosen from a stochastic generative model whose baseline network is a chain of six cliques (complete subnetworks) of six vertices each, for a total of 36 vertices. The model has a single parameter, a probability q∈[0,1]. For any fixed value of q, each edge not connecting two cliques in the baseline network is independently “rewired” with probability q. To rewire an edge, one endpoint is randomly selected to be replaced by another, chosen uniformly at random from among the remaining 35 network vertices; thus regardless of the value of q, the total number of edges is always preserved. See Fig. 1 for details and sample networks drawn from this stochastic model. Like many similar models from the literature (2), this model allows us to smoothly move between highly clustered, “tribal” network topologies with only loose interclique communication (q = 0) to networks that are essentially random and unstructured, and dominated by “long-distance” links (q = 1). Compared to earlier experiments (1, 9), which employed more heterogenous network structures, our parametric model here also permits aggregating data from experiments with similar values of q, which increases the statistical resolution of some of our tests.

Fig. 1.

Three sample networks used in the experiments. The top one is the baseline network, being a chain of cliques with q = 0, from which all other networks were derived by random edge rewiring. The second network had q = 0.1, and the third had q = 0.2. The six numbered vertices are called “connectors,” and the five edges connecting them were retained in all networks.

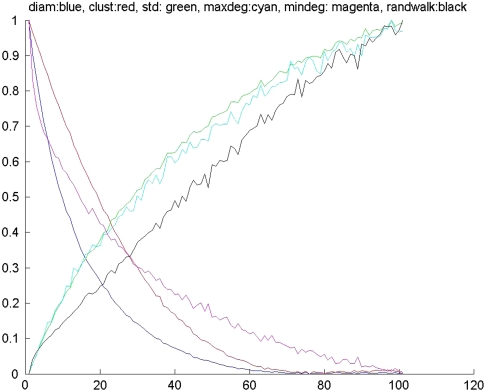
For the experiments, we used values of q∈{0,0.1,0.2,0.4,0.6,1}. These values were chosen so as to sample “interesting” networks with respect to a number of commonly studied structural properties of networks such as diameter and clustering coefficient; see Fig. 2. For each of these six values for q, three independent networks were generated from the rewiring model, and each network used in one coloring and one consensus experiment; thus both tasks were performed on an identical set of 18 networks.

Fig. 2.

Structural properties of networks vs. rewiring parameter q. For each of many values of q (x-axis) ranging from 0–1 (corresponding to x = 100), we sampled 100 random networks from our generative model using that value of q, and computed a variety of structural measures. In order to permit plotting on common axes, each quantity is normalized by its maximum and minimum values across all q to lie between 0 and 1. The quantities network diameter (blue plot), clustering coefficient (red) and minimum degree (magenta) all decrease rapidly with increasing q; while the quantities maximum degree (cyan), standard deviation of degree (green) and ratio of largest to smallest degree (black, and which can be interpreted as the ratio of the largest to smallest probability in the stationary distribution of a random walk on the network) all increase rapidly with q. This plot permitted us to sample “interesting” values of q for our experiments. In particular, the response to all quantities is greater at smaller q, so we sampled more densely there.

In the consensus experiments the collective objective was to color all vertices the same color within three minutes. In the coloring experiments, the collective objective was to color all vertices with a color that was different from those of any of its neighbors. Note that for coloring, there is a well defined minimum number of colors required for a solution to exist (the so-called chromatic number of the particular network in question), and this was the number provided in each experiment. For consensus, there is no obvious analogue, and one would generally expect the problem to become more difficult the more colors are provided; we arbitrarily allowed nine colors in each consensus experiment.

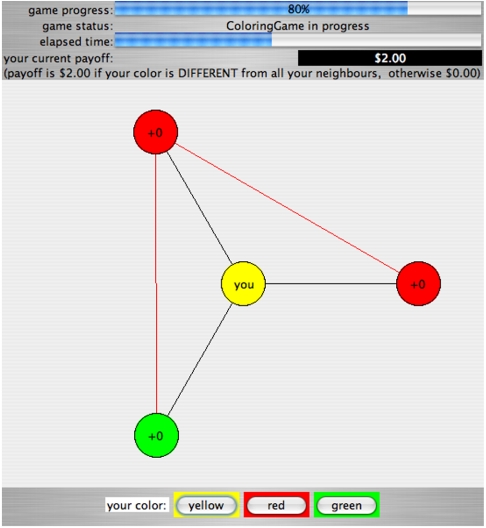
In the consensus experiments each subject received two dollars if a global (unanimous) consensus to any single color was reached, and zero dollars otherwise. In the coloring experiments subjects received two dollars if a valid global coloring was reached, and zero dollars otherwise. The subjects were given three minutes to reach a solution, although an experiment would terminate as soon as a solution was reached (thus, most experiments took less than three minutes). Each player was given only a local (neighborhood) view of the network. A screenshot of the Graphical User Interface is shown in Fig. 3.

Fig. 3.

The Graphical User Interface for the coloring game showing a typical local neighborhood; interfaces for the consensus game were similar in every detail except the statement of the payoffs, and the number of color buttons available.

All experiments were held in a single session lasting a total of several hours with 36 University of Pennsylvania students as subjects. Each experiment had a fixed network in which subjects were randomly assigned to vertices. The session was closely proctored and physical partitions were erected to ensure no communication between subjects, other than permitted by the system. In order to eliminate coordination based on previous experimental outcomes (particularly important for the consensus games), a random permutation between the colors chosen by a subject and the corresponding number of integer indices was chosen before each experiment, and the integer indices used to determine global state and solutions; thus what appears red to one player might appear blue to another, even though all players have a locally consistent view of the global state at all times. This randomization destroys the possibility of establishing social conventions across experiments, and renders any potential side communication about colors or buttons meaningless.

Collective Behavior and Network Structure

Whether the two problems could be solved in the allotted time, and how long it would take to reach solutions, was a central question. All 18 coloring experiments ended with a global solution, as did 17 of the 18 consensus experiments. Thus overall collective performance was strong, a finding consistent with our previous experiments on other problems and network structures (1, 9).

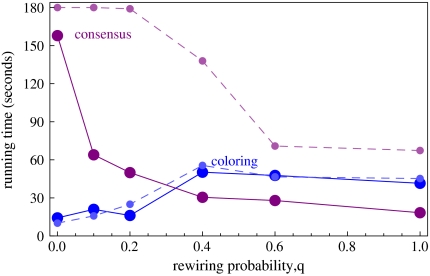
Turning next to the effects of network structure, our first main result is shown in Fig. 4, which plots average solution time against the rewiring parameter q. The key finding is that the coloring and consensus tasks induce qualitatively opposite collective performance as a function of q: consensus appears to be much harder at low values of q, and got easier as q increased. In contrast, the coloring problem was easiest at low q. When the coloring and consensus solution times are aggregated separately for q∈{0,0.1,0.2} (low q) and q∈{0.4,0.6,1} (high q), four separate one-sided pairwise t-tests confirmed the statistical significance of these claims: with confidence levels all at P < 0.02, coloring was harder for high q than low q, consensus was harder for low q than high q, and low q was harder for consensus than coloring; with P < 0.07 confidence level high q was harder for coloring than consensus. These tests simply confirm the significance of the qualitative shapes and crossing point of the curves in Fig. 4. We remark that we looked for learning trends in the performance data and found very little; the correlation between solution time and experiment index number was actually positive, but it was not statistically significant.

Fig. 4.

Average solution times (solid lines) for consensus and coloring experiments. The dashed lines are from a behavioral model described in the text.

It is natural to ask whether the observed collective behavior can be at least qualitatively replicated in simulations of simple behavioral models on the same network structures. We investigated a myopic heuristic for each vertex that selects a color resulting in the fewest immediate conflicts (defined as being opposite colors in consensus, or the same color in coloring) with neighbors. Updates of vertices are made asynchronously at probabilistically chosen times. The dashed lines in Fig. 4 show that such simple models do indeed broadly approximate the human collective behavior we observed: in both game types, the models qualitatively track collective behavior over the full domain of q, including the reversal of the relative difficulty of the two problems. Our simulations for the consensus game echo findings of Watts (2) on what he calls the “density classification” problem. We also remark that finding simulation models providing numerically better fits proved difficult, despite the investigation of regressions permitting a number of behavioral state variables. Given our limited data, we were unable to discover models balancing simplicity with numerically accurate fits to both game types.

To further elucidate the behavioral dynamics of these games, in Fig. 5 we present four visualizations of actual subject play in consensus experiments for small values of the rewiring parameter q (thus, the highly clustered structure of the baseline network is largely intact). In all images, we can observe that the subjects rather quickly converge on just two or three of the nine available colors, and most of the duration of the experiments involves a protracted network battle between the colors of different cliques, which each reach internal solutions rather quickly. A variety of interesting collective and individual behaviors can be seen in these visualizations; see the caption for detail.

Fig. 5.

Progression of vertex colors in four consensus experiments. The x-axis measures experiment duration (thus image width is proportional to time to completion), and there is a horizontal row for each of the 36 players showing its current color at each moment of the experiment. The first two images are for rewiring parameter q = 0, and the last two for q = 0.1. Players in the same clique (before any rewiring) are in six consecutive rows, thus explaining the overall tendency for such blocks of six to change colors in approximate unison. In the (successful) leftmost experiment, we see a rapid reduction from 9 to 3 and then just 2 colors used by the population; a long stalemate between two halves of the network is gradually broken by yellow cliques adopting brown. The second image shows the only consensus experiment out of 18 total to not successfully complete. Again we see a rapid reduction to 3 and then 2 colors, but this time the dynamics are much richer; shortly before the halfway mark, we see that blue is chosen by the vast majority of the subjects but there remains an orange holdout clique. A short while later, this clique has adopted blue, but not before causing a cascade of orange to ripple through the network, where it then proceeds to take hold and in fact constitute the majority near the end of the time limit. The rightmost two images (where q = 0.1) complete significantly faster (consistent with the reported overall effect of q on consensus games), and show similar overall dynamics but with more mixing and experimentation by subjects. The images also reveal interesting acts of individual behavior, including attempts at signalling and apparently “irrational” experimentation such as playing a color not chosen by anyone else in the network.

Individual Behavior and Influence

Thus far we have reported performance results from a collective viewpoint, but ultimately collective behavior is a result of interactions between individual human subjects. Given the nature of our experiments, where a desired global state must be reached through local network interactions, it is natural to focus on measures of influence that subjects exert on their neighbors and on the collective outcome. The subject of individual influence is important enough to have spawned a substantial literature, particularly in the context of adoption cascades in networks (11, 12) where a decision maker is seeking out the most influential agents. Traditionally, the focus has been on identifying the relationships between influence and network position measures such as degree and centrality, viewing network position rather than individual human actors as the primary force. In contrast, below we argue that in our experiments it is people who are the primary conduits of influence in networks, and thus that human factors, often understudied in modern network science, may have much to do with influence and the success or failure of cascades.

We studied two distinct notions of influence in our experiments. The first, which we shall call neighborhood influence, attempts to measure the extent to which the actions of a player apparently cause changes in the actions of his neighbors. Fix a vertex i in a given network, and suppose that at some time t₀ this vertex or player changes their color to c, and that their next color change to c^′ ≠ c comes at time t₁ > t₀. Now suppose that a network neighbor j of i changes their color to c at some time t lying in the interval [t₀,t₁]. Then we will credit i with an amount of influence equal to 1/(t - t₀). The intuition here is that j has adopted the current color of i, and that the amount of influence we credit i with should diminish the longer this adoption took. Note that under this definition, j could contribute more than one influencing event to i (for instance, if j toggled back and forth between c and another color during the interval [t₀,t₁]), and the same color change by j could contribute influence credit to more than one neighbor (for instance, if j had another neighbor i^′ who was also color c at time t). However, neither of these phenomena diminishes the fact that the notion captures apparent temporal influences between neighboring players.

In order to filter out potentially coincidental color changes, we only credit i in the manner described if t - t₀ is at least 1 s, an approximation of human reaction time combined with system display update latency (which was less than 100 ms). Finally, we define the overall neighborhood influence of a player in a given experiment to be the sum of all the influence credits as described, divided by its degree and number of color changes; thus the measure is already normalized to compensate for either a large number of neighbors or players who change color frequently.

Our second measure of influence is called outcome influence, and is simply the amount of time elapsed between a player’s final color change and the end of the experiment. We thus attribute the most credit to those players who anticipate the eventual global solution, and thus may have participated in its creation. Under this definition, the outcome influence of the last player to complete a global solution is zero. Note that neighborhood influence depends intimately on network structure, while outcome influence does not do so in any obvious or direct way.

Influence Variation by Subject and Position.

Armed with these two notions of influence, our first interest is to examine whether the influence of an agent can be understood as arising primarily from their position in the network, or is to a significant extent a property of the actual human subject. In our experimental methodology, human subjects are randomly assigned to vertices at the beginning of each experiment. This policy helps to separate the effect of the human from the effect of the vertex (network position).

For each of our two notions of influence, we use a standard ANOVA test to detect whether variability of average influence among the 36 human subjects exceeds the variability of influence due to experimental conditions, such as random assignments of subjects to network vertices.

For neighborhood influence, we find that human subject variability is significant in coloring games (with P < 0.001), but not consensus games; while for outcome influence, human variation is significant with P < 0.05 in both game types. We conclude that overall, influence is not a product of just an agent’s network position, but arises from their intrinsic human behavioral patterns as well.

Correlates of Influence.

Our two measures of influence quantify the (apparent) effects of a player or vertex on other players or vertices. We now examine a number of correlates of influence that are determined only by a player’s own actions, or their apparent reaction to their neighbors.

For instance, consider the change rate or instability of a player or position, which is the number of color changes per second in an experiment. For this measure we again find that human variation is significant under a standard ANOVA test, and furthermore that the change rate of a human subject is strongly negatively correlated with both their neighborhood and outcome influence in both game types (correlations ranging from -0.40 to -0.51 depending on the influence and game type, all with P < 0.02). We thus conclude that more stable players exhibit greater influence. Note that this finding is not obvious a priori, since neighborhood influence is already normalized for change rate, and for outcome influence the least stable players may still settle on their final color relatively early.

We also examined the notion of stubbornness, defined as the proportion of time that a player or vertex chooses a “noncompliant” color. In consensus, a color is noncompliant if there is another played by more neighbors. In coloring, a color is noncompliant if there is another played by fewer neighbors. As with change rate, we find stubbornness variation among subjects to be significant, and stubbornness is strongly negatively correlated with both influence types (-0.45 for neighborhood influence, -0.50 for outcome influence, both with P < 0.02) in consensus games (but not in coloring games). Thus it appears that rather than causing others to react to or coalesce around their noncompliant choices, stubborn players reduce their impact on their neighbors and the outcome of experiments.

Despite the fact that human variation in influence cannot be explained by network position alone, and that there appear to be a number of other behavioral traits that strongly correlate with influence, it remains reasonable to ask what purely structural properties of network position still have some explanatory value. The degree of a vertex is only weakly correlated with influence in consensus games (0.21 for neighborhood influence, 0.10 for outcome influence, both with P < 0.03). Also, degree is not significantly correlated with either type of influence in coloring games. Vertex centrality (average inverse shortest path distance to all other vertices) is significantly correlated only with outcome influence in consensus games (0.26 with P < 0.03). The clustering coefficient of a vertex, which can be viewed as a measure of connectivity in a vertex’s neighborhood, is significantly correlated only with outcome influence (0.086, P < 0.05 in coloring, -0.22, P < 0.001 in consensus). Similarly, being one of the “connector” vertices between cliques in the baseline network before rewiring is correlated only with neighborhood influence in consensus games (0.17, P < 0.03). The evidence again suggests that influence seems more determined by the behavioral characteristics of actual human subjects than by the abstract properties of network position.

An interesting related question is to what extent influence, as well as the measures of individual behavior above, correlate with the time the subjects took to reach a global solution. Stubbornness and change rate (averaged for each experiment) both exhibit strong negative correlation with running time in both games (correlations ranging from -0.81 to -0.66 with P < 0.005); stubbornness and instability seem to adversely affect decentralized coordination. On the other hand, we did not find significant correlation between running time and neighborhood influence in either game.

Conclusion

The results presented here have shown that simple and systematic changes in social network structure can elicit opposing effects on collective performance in two similar coordination tasks, and that the intrinsic behavioral traits of human actors may play a stronger role in their relative influence than purely structural properties of their network position. Both findings suggest the potential benefits of broadening the current emphasis of network science on topology. We would further note that our controlled experimental methodology—allowing us to systematically vary network structure across the same pool of human subjects—was crucial to the findings, since it placed the same subject in many different network positions throughout the session. Empirical field studies measuring only the structure and behavior within a single, fixed social network are handicapped in this regard.