Abstract
Behavioral demonstrations of reciprocal interactions among the dimensions of space, number, and time, along with evidence of shared neural mechanisms in posterior parietal cortex, are consistent with a common representational code for general magnitude information. Although much recent speculation has concerned the developmental origins of a system of general magnitude representation, direct evidence in preverbal infants is lacking. Here we show that 9-month-olds transfer associative learning across magnitude dimensions. For example, if shown that larger objects were black with stripes and smaller objects were white with dots, infants expected the same color/pattern mapping to hold for numerosity (i.e., greater numerosity: black/stripes; smaller numerosity: white/dots) and duration (i.e., longer-lasting objects: black/stripes; shorter-lasting objects: white/dots). Cross-dimensional transfer occurred bi-directionally for all combinations of size, numerosity, and duration. These results provide support for an early-developing and pre-linguistic general magnitude system, whereby representations of magnitude information are (at least partially) abstracted from the specific dimensions.
Introduction
Magnitude information comes in many forms, including the dimensions of space, number, and time. When reasoning about predators, for example, we can judge their size, the number of them present, and the time it may take them to reach us. Although much research has focused on the processing of magnitude dimensions each in isolation, recent work has investigated their associations. In the case of space and number, perhaps the classic demonstration of an association is known as the SNARC (Spatial-Numerical Association of Response Codes) effect, which highlights the left-to-right organization of increasing numerical values (Dehaene, Bossini, & Giraux, 1993; also: Fischer et al., 2003; Gevers et al., 2006). Other evidence for a spatial-numerical association comes from findings that judgments of number are faster when digits and physical size are congruent (e.g., 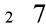 ) rather than incongruent (e.g.,
) rather than incongruent (e.g., 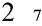 ) (Henik & Tzelgov, 1982; also: Hurewitz, Gelman, & Schnitzer, 2006). For space and time, greater distances are associated with longer durations (Sarrazin et al., 2004; also: DeLong, 1981); for example, perceived distance increases with temporal separation for sequentially-presented stimuli and perceived duration increases with spatial separation. For number and time, the classic demonstration is that rats appear to treat numerical and temporal stimuli interchangeably, with one second approximately equal to a count of five (Meck & Church, 1983). In humans, recent evidence for a numerical-temporal association comes from comparisons of Arabic numerals presented in varying durations; adults’ duration judgments were biased by numerical value such that small numbers were underestimated in duration and larger numbers overestimated (Oliveri et al., 2008). The pervasive nature of these behavioral associations, together with evidence of shared activation in posterior parietal cortex during spatial (Pinel et al., 2004; Sereno, Pitzalis, & Martinez, 2001), numerical (Dehaene et al., 1999; Piazza et al., 2007), and temporal (Leon & Shadlen, 2003; Maquet et al., 1996) processing, has led to the suggestion that magnitude is represented quite generally in a common representational format (Walsh, 2003).
) (Henik & Tzelgov, 1982; also: Hurewitz, Gelman, & Schnitzer, 2006). For space and time, greater distances are associated with longer durations (Sarrazin et al., 2004; also: DeLong, 1981); for example, perceived distance increases with temporal separation for sequentially-presented stimuli and perceived duration increases with spatial separation. For number and time, the classic demonstration is that rats appear to treat numerical and temporal stimuli interchangeably, with one second approximately equal to a count of five (Meck & Church, 1983). In humans, recent evidence for a numerical-temporal association comes from comparisons of Arabic numerals presented in varying durations; adults’ duration judgments were biased by numerical value such that small numbers were underestimated in duration and larger numbers overestimated (Oliveri et al., 2008). The pervasive nature of these behavioral associations, together with evidence of shared activation in posterior parietal cortex during spatial (Pinel et al., 2004; Sereno, Pitzalis, & Martinez, 2001), numerical (Dehaene et al., 1999; Piazza et al., 2007), and temporal (Leon & Shadlen, 2003; Maquet et al., 1996) processing, has led to the suggestion that magnitude is represented quite generally in a common representational format (Walsh, 2003).
Much recent speculation has concerned the origins of general magnitude representation, with particular interest in whether associations among space, number, and time exist early in human life (Feigenson, 2007; Walsh, 2003). Evidence consistent with, at least some, associations in children comes from early work by Piaget who reported effects of spatial extent on number (1965) and time (1969; also: Levin, 1977; Siegler & Richards, 1979) judgments. In the classic number conservation task, children judge that two unequal-lengthened rows of objects differ in numerical value, believing that a longer row is greater in numerosity, whether both are numerically identical or the longer row actually contains fewer objects. Evidence consistent with associations in infants comes from habituation/dishabituation studies showing that similar Weber ratios mediate discrimination sensitivity for different dimensions. Six-month-olds differentiate stimuli differing by 2:1 – but not 3:2 – ratios for size (Brannon, Lutz, & Cordes, 2006), numerosity (Xu & Spelke, 2000), and duration (van Marle & Wynn, 2006). Furthermore, this sensitivity appears to increase in parallel over the first year of life for numerical (Lipton & Spelke, 2003) and temporal (Brannon, Suanda, & Libertus, 2007) information. Parallel discrimination functions, though consistent with general magnitude representation, could result from developmental changes in perception, memory, or attention, none of which is specific to magnitude or a shared representational code for space, number, and time. In addition, discrimination functions have been observed for a restricted range of intensities, making it unclear whether they would generalize to non-tested intensities, and it is known that range differences exist for number discrimination; for example, infants differentiate 2 versus 3 objects (Cordes & Brannon, 2009) but not 8 versus 12 (Xu & Spelke, 2000), despite identical ratios.
Present Study
To test directly whether associations among space, number, and time exist in preverbal infants, we modeled our approach on that of Meck and Church (1983), in which rats trained to discriminate two durations spontaneously generalized learning to number discriminations. We ‘taught’ preverbal infants an arbitrary mapping between one magnitude dimension and color/pattern cues (e.g., larger size: black/stripes; smaller size: white/dots). In the initial (habituation) phase, infants were shown stimuli depicting the mapping until their looking times decreased to a criterion. Infants were then presented with novel stimuli during the test phase, which either maintained (congruent trials) or violated (incongruent trials) the mapping between magnitude and color/pattern presented during habituation. In Experiment 1, habituation and test trials involved the same magnitude dimension. In Experiment 2, magnitude dimensions varied between habituation and test. If infants learn the color/pattern mapping, they should dishabituate to the incongruent stimuli, looking longer during incongruent than congruent test trials, whether these trials involve the same (Experiment 1) or different (Experiment 2) dimensions.
Experiment 1: Within-Dimension Discrimination
We conducted a first experiment to determine whether 9-month-olds are capable of learning arbitrary color/pattern mappings for different magnitude cues: size, numerosity, and duration. In the Size condition, for example, infants might see that the larger rectangle in a pair was always black with white stripes and the smaller rectangle was always white with black dots. Numerosity and Duration conditions were similarly structured except that stimulus pairs varied either with respect to the number of rectangles or the time rectangles remained visible on screen.
Method
Participants
Thirty-six full-term 9-month-olds (M = 9.2, SD = 0.47) participated, 12 (6 girls) in each of three conditions: Size, Numerosity, or Duration. Eleven additional infants failed to complete the experiment due to fussiness (Size: 4; Numerosity: 2; Duration: 5).
Stimuli and Procedure
On each trial, infants saw pairs of stimuli featuring a mapping between magnitude and color/pattern. In each condition, there were three stimulus pairs. Pairs varied in magnitude (e.g., size) by a ratio of at least 2:1, which even 6-month-olds have been shown to discriminate for size (Brannon et al., 2006), numerosity (Xu & Spelke, 2000), and duration (van Marle & Wynn, 2006); see Supplemental materials for stimulus values. In the Numerosity condition, both arrays in each set (e.g., 2 vs. 4) were equivalent in cumulative perimeter and surface area, ensuring that discriminations were based on number rather than spatially-related cues (for discussion, see: Mix, Huttenlocher, & Levine, 2002). In the Duration condition, equal-sized rectangles, which varied in presentation time (e.g., 1 vs. 2 s), were presented in repeating loops with a 0.5 s inter-stimulus-interval (ISI).
Stimuli were presented using Habit X 1.0 software (Cohen, Atkinson, & Chatput, 2004) and rear-projected onto a screen (92 by 67 cm). Infants sat on their parent’s lap, approximately 90 cm from the screen. Parents kept their eyes closed so as to not influence infants’ behaviors. Trials began with a beeping target to attract infants’ attention. Trials continued until infants looked for at least 2 s, and ended after looking time totaled 30 s or infants looked away for a continuous 2 s. An experimenter (blind to condition) recorded looking times via a hidden camcorder, and recordings were confirmed off-line by another experimenter (also blind to condition). Inter-observer agreement (calculated across trials at 100-ms intervals for each infant) was high (Size: 91%; Numerosity: 93%; Duration: 93%).
Habituation trials involved two stimulus pairs, with a third pair retained for test trials (counterbalanced across infants). For example, in the Numerosity condition, infants might be habituated to displays showing arrays of 2 versus 4 and 3 versus 6, and tested with 5 versus 10. For each pair, two trial types were formed by varying the left/right positions of items, creating four unique habituation trials. During habituation, magnitude information varied systematically according to color/pattern (e.g., Size condition; larger size: black/stripes, smaller size: white/dots), with the magnitude and color/pattern mapping counterbalanced across infants. Trial order was randomized with the constraint that each of the four unique trials was presented once before repetition. The habituation phase ended when the average looking time for four consecutive trials was less than 50% of the average for the first four trials, or after 24 trials, whichever came first. Following habituation, infants were presented with four test trials involving the third stimulus pair (left/right positions of items counterbalanced across trials). Test trials alternated between congruent (i.e., magnitude and color/pattern mapping maintained) and incongruent (i.e., magnitude and color/pattern mapping violated) types (order counterbalanced across infants).
Results and Discussion
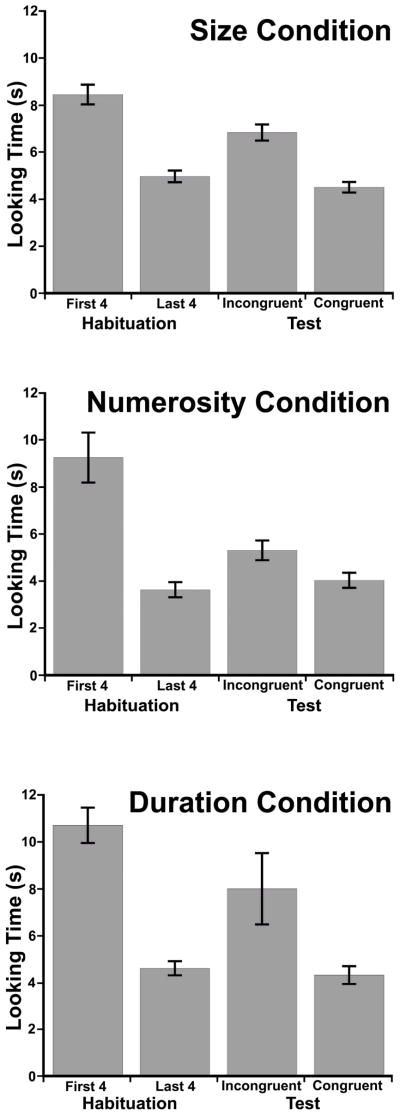
The mean number of habituation trials was 14.1, 13.8, and 13.4 in Size, Numerosity, and Duration conditions, respectively. Analyses of habituation trials (first four vs. last four) revealed that infants in each condition showed significant decreases in looking time (Size: t(11)= 4.75; Numerosity: t(11)= 7.26; Duration: t(11)= 12.60; all ps < .001; see Figure 1). All infants met the habituation criterion.
Figure 1.
Results for each condition in Experiment 1. Mean looking time (seconds) is reported for habituation and test phases; error bars represent standard errors.
An analysis of variance (ANOVA) conducted on looking times during test – with condition (Size, Numerosity, Duration), stimulus pair (one of three possible pairs used in test; see above and Supplemental materials), test order (congruent or incongruent first) as between-subjects variables and type of test trial (congruent vs. incongruent) as the within-subjects variable – revealed a significant main effect of test trial type, F(1, 18)= 12.21, p < .01, but no other significant main effects or interactions (ps > .2). Follow-up ANOVAs conducted separately on each condition revealed that infants in all conditions looked significantly longer on incongruent than congruent test trials, as judged by the average for each trial type (Size: F(1, 11)= 4.97; Numerosity: F(1, 11)= 4.88; Duration: F(1, 11)= 6.15; all ps < .05; Figure 1), or the first test trial of each type (Size: F(1, 11)= 7.34; Numerosity: F(1, 11)= 5.43; Duration: F(1, 11)= 5.57; all ps < .05), with the majority of infants looking longer at incongruent than congruent test trials (Size: 10/12; Numerosity: 9/12; Duration: 10/12). Additional analyses comparing average looking times during test to the end of the habituation phase (average of last four trials) confirmed dishabituation to incongruent (Size: t(11)= 2.13, p = .057; Numerosity: t(11)= 3.38, p < .01; Duration: t(11)= 2.21, p < .05) but not congruent (Size: t(11)= −0.80; Numerosity: t(11)= 0.91; Duration: t(11)= −0.51; ps > .3) test trials. These data show that infants learned the arbitrary mapping between magnitude (whether size, numerosity, or duration) and color/pattern (see Supplemental materials).
Experiment 2: Between-Dimension Discrimination
Having shown that 9-month-olds can learn an arbitrary mapping between magnitude information and color/pattern, we turned to the critical question: does information related to one dimension of magnitude generalize to other magnitude dimensions? If infants represent magnitude more generally across space, number, and time, they might expect the color/pattern mapping learned for one dimension to hold for other dimensions. We examined this issue by habituating infants to stimuli from one dimension (e.g., size), but then presenting them with stimuli for another dimension (e.g., numerosity or duration) during the test phase. Infants were tested with all possible pairing combinations of size, numerosity, and duration.
Method
Participants
Seventy-two full-term 9-month-olds (M = 9.3, SD = 0.33) participated, 24 (12 girls) in each of three conditions: Space & Number, Space & Time, and Number & Time. Twenty-three additional infants did not complete the experiment due to fussiness (Space & Number: 8; Space & Time: 7; Number & Time: 8).
Stimuli and Procedure
The major difference from the previous experiment was the change in magnitude dimension between habituation and test phases, with dimensions presented during habituation and test counterbalanced across infants, for two groups per condition (Space & Number: size-to-numerosity, numerosity-to-size; Space & Time: size-to-duration, duration-to-size; Number & Time: numerosity-to-duration, duration-to-numerosity).
Habituation trials involved two sets of stimulus pairs, whereby relative magnitude information mapped systematically onto color/pattern. As in Experiment 1, pairs varied in magnitude by a ratio of at least 2:1. Additional variation (e.g., orientation of items), which could not be used to distinguish subsequently presented congruent and incongruent test trials, was used to increase the salience of the mapping (see Figures 2, 3, and 4, top panels, and Supplemental materials). There were eight unique habituation trials, presented randomly and with no repetitions until each was sampled once. Habituation ended when the average looking time for four consecutive trials was less than 50% of the average for the first four trials, or after 32 trials, whichever came first. ‘Congruent’ and ‘incongruent’ test trials were based on the mapping between magnitude and color/pattern during habituation. For example, if, in the size-to-numerosity group, larger-sized rectangles mapped onto black/stripes and smaller ones onto white/dots during habituation, then congruent test trials involved larger numerical arrays mapped onto black/stripes (smaller numerosity onto white/dots), and incongruent test trials involved larger numerical arrays mapped onto white/dots (smaller numerosity onto black/stripes). There were six test trials (left/right positions of items counterbalanced across trials), alternating between congruent and incongruent types (order counterbalanced across infants). Looking times were recorded as in Experiment 1, and inter-observer agreement (calculated at 100-ms intervals) was high (Space & Number: 92%; Space & Time: 91%; Number & Time: 93%).
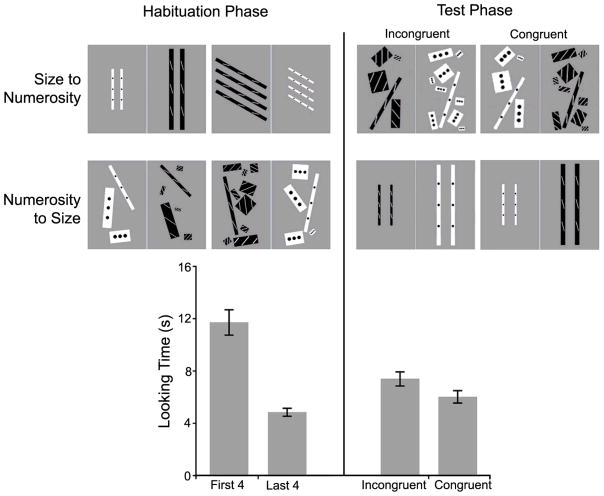
Figure 2.
Space & Number condition in Experiment 2. Examples of stimuli for habituation and test phases for both groups (top panels). Mean looking time (seconds) is reported for habituation and test (bottom panel); error bars represent standard errors. Results are collapsed across group (size-to-numerosity and numerosity-to-size), as statistical analyses revealed no significant differences related to group (see Main text).
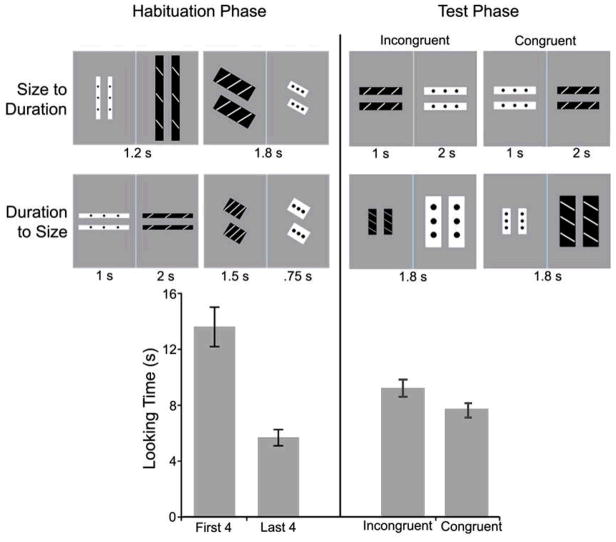
Figure 3.
Space & Time condition in Experiment 2. Examples of stimuli for habituation and test phases for both groups (top panels). Mean looking time (seconds) is reported for habituation and test (bottom panel); error bars represent standard errors. Results are collapsed across group (size-to-duration and duration-to-size), as statistical analyses revealed no significant differences related to group (see Main text).
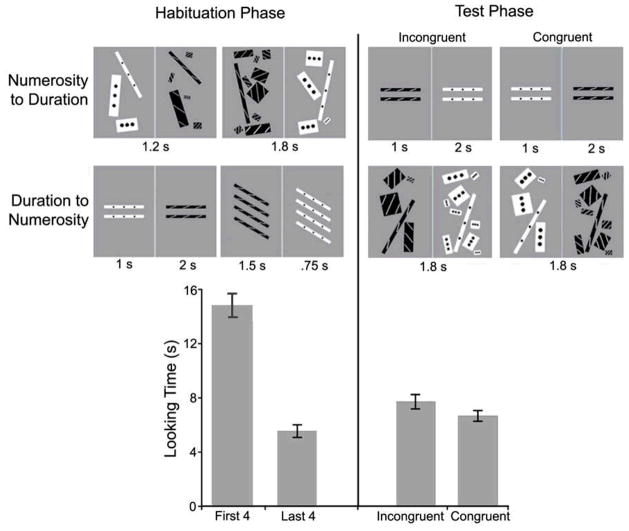
Figure 4.
Number & Time condition in Experiment 2. Examples of stimuli for habituation and test phases for both groups (top panels). Mean looking time (seconds), collapsed across group, is reported for habituation and test (bottom panel); error bars represent standard errors. Results are collapsed across group (numerosity-to-duration and duration-to-numerosity), as statistical analyses revealed no significant differences related to group (see Main text).
Space & Number
In the size-to-numerosity group, habituation trials involved pairs of larger versus smaller rectangles, which, across trials, were presented in sets of two or four rectangles (number within trial held constant). Test trials involved a larger- versus smaller-number set, equivalent in cumulative perimeter and surface area. Equating extraneous spatial variables across number arrays ensured that generalizations occurred between size and numerosity rather than size and other spatially-related information1. In the numerosity-to-size group, habituation trials involved pairs of larger versus smaller number arrays. Cumulative perimeter and surface area were varied orthogonal to numerosity and color/pattern mappings such that on half the trials the larger number array was smaller in cumulative perimeter and area than the smaller number array, and on the other half it was larger. Varying perimeter and area in this way ensured that infants habituated to number and that generalization was not supported by spatially-related variables. Test trials involved a larger- versus smaller-sized set, equivalent in number. See Supplemental materials for stimulus values and Figure 2 (top panels) for an illustration of both groups.
Space & Time
In the size-to-duration group, habituation trials involved pairs of larger versus smaller rectangles, which, across trials, were presented in repeating loops of 1.2 or 1.8 s (0.5 ISI; duration within trial held constant). Test trials involved a longer- versus shorter-duration set, equivalent in size. In the duration-to-size group, habituation trials involved pairs of longer versus shorter durations, which, across trials, were presented with sets of different-sized rectangles (size within trial held constant). Test trials involved a larger- versus smaller-sized set, equivalent in duration. See Supplemental materials for stimulus values and Figure 3 (top panels) for an illustration of both groups.
Number & Time
In the numerosity-to-duration group, habituation trials involved pairs of larger versus smaller number arrays, as in numerosity-to-size. Number arrays were presented in repeating loops, as in size-to-duration. Test trials involved a longer- versus shorter-duration set, equivalent in number, as in size-to-duration. In the duration-to-numerosity group, habituation trials involved pairs of longer versus shorter durations, which, across trials, were presented in sets of two or four rectangles (number within trial held constant), as in size-to-numerosity. Test trials involved a larger- versus smaller-number set, equated for cumulative perimeter and surface area, as in size-to-numerosity, and also for duration, as in duration-to-size. See Supplemental materials for stimulus values and Figure 4 (top panels) for an illustration of both groups.
Results and Discussion
The mean number of habituation trials was 14.8, 18.0, and 16.8 in the Space & Number, Space & Time, and Number & Time conditions, respectively. Analyses of habituation trials (first four vs. last four) revealed significant decreases in looking time in each condition (Space & Number: t(23)= 9.01; Space & Time: t(23)= 7.33; Number & Time: t(23)= 9.76; all ps < .0001; see Figures 2, 3, and 4, bottom panels). The habituation criterion was met by all but six infants (Space & Time: 3; Number & Time: 3).
An ANOVA was conducted on average looking times during test with condition (Space & Number, Space & Time, Number & Time) and order (congruent or incongruent first) as the between-subjects variables, and test trial type (congruent vs. incongruent) as the within-subjects variable. There was a significant main effect of test trial type, F(1, 66)= 29.32, p < .0001, but no other significant main effects or interactions (ps > .1). To test for possible asymmetrical associations, separate ANOVAs were conducted for each condition with habituation dimension as the between-subjects variable. Looking times were significantly longer to incongruent than congruent trials in all conditions: Space & Number: F(1, 22)= 9.60; Space & Time: F(1, 22)= 10.50; Number & Time: F(1, 22)= 7.85; all ps < .05 (Figures 2, 3, and 4, bottom panels), with the majority of infants showing longer looking to incongruent trials (Space & Number: 18/24; Space & Time: 19/24; Number & Time: 16/242). There were no main effects of habituation dimension (ps > .1) and no interactions of test trial type and habituation dimension (ps > .3), suggesting that the transfer between magnitude dimensions was generally symmetrical.
Infants discriminated congruent and incongruent test trials, providing evidence for the generalization of arbitrary color/pattern mappings across size, numerosity, and duration. Generalizations occurred bi-directionally for all pairings, regardless of which dimension was presented during habituation, demonstrating that infants extended learning from one dimension to another, despite not having previously seen color/pattern variations for the test dimension. A possible explanation for these generalizations is that infants may have actually failed to discriminate between dimensions. One account of general magnitude representation argues for largely overlapping dimensions (a “one-bit” representation) such that space, number, and time might be used interchangeably (Walsh, 2003). Analyses of first test trials would seem to argue against this possibility, however. Relative to the end of habituation (average of last four trials), infants in all conditions looked significantly longer on the first test trial, whether it was congruent (Space & Number: t(23)= 4.66; Space & Time: t(23)= 4.96; Number & Time: t(23)= 3.43; all ps < .01) or incongruent (Space & Number: t(23)= 4.10; Space & Time: t(23)= 6.28; Number & Time: t(23)= 4.36; all ps < .001). That infants dishabituated to both types of test trials indicates that they detected the change in stimuli across habituation and test phases, and, yet, still generalized learning concerning the color/pattern mapping across dimensions.
We have suggested that infants in our study transferred learning about the dimension presented during habituation (e.g., duration) to the dimension seen at test (e.g., size). Another possibility, however, is that generalizations occurred because of misperceptions at early stages of processing. It is possible that viewing one dimension of magnitude led to illusory experiences concerning other magnitude dimensions. Consider the duration-to-size group. If shorter and longer durations during habituation were additionally experienced as smaller and larger sizes, respectively, the novel test stimuli might be compared to the previous illusory size information rather than the durations. As stimuli in our study were always presented visually, we cannot exclude this possibility. Although such misperceptions would also provide support for associations among space, number, and time (i.e., general magnitude representation), future research should test for generalizations with magnitude information from different modalities (e.g., vision and audition). If transfer of learning supports generalization, similar patterns of performance should be observed across modalities (see General Discussion). If illusory experiences explain behavior, then generalizations should be less likely with different modalities.
General Discussion
The present findings provide evidence for general magnitude representation early in human life. In our task, information related to one dimension of magnitude influenced preverbal infants’ expectations about other magnitude dimensions. Infants appeared to expect, for example, that if black/striped objects are large in size, they ought also to be more numerous and longer lasting. To our knowledge, these findings provide the first direct evidence of shared representations for space, number, and time in preverbal infants, suggesting early, pre-linguistic, origins of a general magnitude system.
In the case of number, infants have been shown to match numerosities across different sensory modalities (vision and audition), a phenomenon known as cross-modal number matching (e.g., Jordan & Brannon, 2006; Starkey, Spelke, & Gelman, 1983; but see: Mix, Levine, & Huttenlocher, 1997). Although those findings suggest an abstract representation of number, not tied to a particular modality, the present findings of cross-dimensional magnitude generalization suggest that number is merely one component of a still more abstract system, not tied to specific dimensions. Within a single sensory modality (vision), infants in our study generalized associative learning across magnitude dimensions. Although the exact relation between these two phenomena is unknown, it is an intriguing possibility that magnitude reasoning is, at least partially, independent of both dimension (e.g., size vs. number) and modality (e.g., vision vs. audition). Some authors have argued that specific associations may be cognitively privileged, for example, between number and time (van Marle & Wynn, 2006). Our findings, however, showed that generalizations held across all combinations tested, suggesting that the relation between number and time is only one type of association in a more general system of magnitude representation.
In recent years, much debate has concerned the origins and development of numerical reasoning. Whereas some researchers argue that young infants use ’cognitive‘ numerical information to make discriminations and to perform arithmetic operations such as addition and subtraction (e.g., Brannon, Abbott, & Lutz, 2004; Wynn, 1992; Xu & Spelke, 2000), others argue that these abilities are supported by more ’perceptual‘ spatial and temporal cues such as area and contour length, as well as rate, rhythm, and duration (e.g., Clearfield & Mix, 1999; Mix et al., 2002). This debate presupposes that space, number, and time are dissociable, with distinct underlying mechanisms (cf. Castelli, Glaser, & Butterworth, 2006). The present results, however, suggest that such an assumption may not be entirely accurate. Although the distinctions among magnitude dimensions may be salient to researchers, they may be less so from the perspective of the infant.
For any dimension of magnitude, pairs of unequal values involve an item that is ‘more than’ or ‘less than’ another. By drawing on a common language of measurement, namely, the ordered property of unequal values, a general magnitude system may facilitate comparisons across multiple dimensions. In extant models, shared processing resources are rooted in the need to represent co-variance in the physical world, as well as to structure relevant action sequences (Gallistel & Gelman, 1992; Walsh, 2003). In a world such as ours where spatial, numerical, and temporal cues are highly correlated, representing different dimensions with a shared vocabulary may constitute a powerful learning mechanism, allowing information related to one dimension to be used in making predictions, and evaluating variation, in other dimensions. But just how general is general magnitude representation? Research with children and adults suggests that any information which can be conceptualized in ordinal (more/less) terms may share representational resources. Among the possible candidates are speed (Siegler & Richards, 1979; Levin, 1977), loudness (Smith & Sera, 1992), luminance (Smith & Sera, 1992; Levin, 1977; Pinel et al., 2004), and even less prototypical sources of magnitude information such as emotional expression (Holmes & Lourenco, 2009).
Supplementary Material
Acknowledgments
The authors would like to thank Dede Addy, Supria Batra, Lindsey Chapman, Kathy Choi, Gillian Glauber, Shaina Gordon, Carissa Romero, and Lily Stutman for help with stimulus preparation, testing, and reliability coding. The authors would also like to thank Kevin Holmes, Susan Levine, and Philippe Rochat for comments on an earlier draft of this manuscript. This research was supported by award number R03HD059993 from the Eunice Kennedy Shriver National Institute of Child Health & Human Development (NICHD) to Stella F. Lourenco.
Footnotes
Although it was not possible to systematically control for particular density cues, namely, inter-element distances in the arrays presented during test, we attempted to ensure that smaller and larger distances were represented in both arrays across test trials. Nevertheless, the greater the number of items in an array, the smaller the inter-element distances on average. It is unlikely, however, that differences in inter-element distances can account for differences in looking times during congruent and incongruent test trials since the size stimuli presented during habituation involved equal inter-element distances.
By group for each condition, the number of infants showing longer looking times to the incongruent test trials compared to the congruent test trials were as follows: size-to-numerosity = 10/12, numerosity-to-size = 8/12; size-to-duration = 10/12, duration-to-size = 9/12; numerosity-to-duration = 7/12, duration-to-numerosity = 9/12.
References
- Brannon EM, Abbott S, Lutz DJ. Number bias for the discrimination of large visual sets in infancy. Cognition. 2004;93:B59–B68. doi: 10.1016/j.cognition.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Lutz D, Cordes S. The development of area discrimination and its implications for number representation in infancy. Developmental Science. 2006;9:F59–F64. doi: 10.1111/j.1467-7687.2006.00530.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Suanda S, Libertus K. Temporal discrimination increases in precision over development and parallels the development of numerosity discrimination. Developmental Science. 2007;10:770–777. doi: 10.1111/j.1467-7687.2007.00635.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castelli F, Glaser DE, Butterworth B. Discrete and analogue quantity processing the parietal lobe: A functional MRI study. Proceedings of the National Academy of Sciences, USA. 2006;103:4693–4698. doi: 10.1073/pnas.0600444103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clearfield MW, Mix KS. Number versus contour length in infants’ discrimination of small visual sets. Psychological Science. 1999;10:408–411. [Google Scholar]
- Cohen LB, Atkinson DJ, Chatput HH. Habit X: A new program for obtaining and organizing data in infant perception and cognition studies. 1.0. Austin, TX: University of Texas; 2004. [Google Scholar]
- Cordes S, Brannon EM. The relative salience of discrete and continuous quantity in young infants. Developmental Science. 2009;12:453–463. doi: 10.1111/j.1467-7687.2008.00781.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, Giraux P. The mental representation of parity and number magnitude. Journal of Experimental Psychology: General. 1993;122:371–396. [Google Scholar]
- Dehaene S, Spelke ES, Pinel P, Stanescu R, Tsivkin S. Sources of mathematical thinking: Behavioral and brain-imaging evidence. Science. 1999;284:970–974. doi: 10.1126/science.284.5416.970. [DOI] [PubMed] [Google Scholar]
- DeLong AJ. Phenomenological space-time: Toward an experiential relativity. Science. 1981;213:681–683. doi: 10.1126/science.7256273. [DOI] [PubMed] [Google Scholar]
- Feigenson L. The equality of quantity. Trends in Cognitive Sciences. 2007;11:185–187. doi: 10.1016/j.tics.2007.01.006. [DOI] [PubMed] [Google Scholar]
- Fischer MH, Castel AD, Dodd MD, Pratt J. Perceiving numbers causes spatial shifts of attention. Nature Neuroscience. 2003;6:555–556. doi: 10.1038/nn1066. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Gevers W, Verguts T, Reynvoet B, Caessens B, Fias W. Numbers and space: A computational model of the SNARC effect. Journal of Experimental Psychology: Human Perception and Performance. 2006;32:32–44. doi: 10.1037/0096-1523.32.1.32. [DOI] [PubMed] [Google Scholar]
- Henik A, Tzelgov J. Is three greater than five: The relation between physical and semantic size in comparison tasks. Memory and Cognition. 1982;10:389–395. doi: 10.3758/bf03202431. [DOI] [PubMed] [Google Scholar]
- Holmes KJ, Lourenco SF. Spatial organization of magnitude in the representation of number and emotion. In: Taatgen NA, van Rijn H, editors. Proceedings of the 31th Annual Conference of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2009. [Google Scholar]
- Hurewitz F, Gelman R, Schnitzer B. Sometimes area counts more than number. Proceedings of the National Academy of Sciences, USA. 2006;103:19599–19604. doi: 10.1073/pnas.0609485103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan KE, Brannon EM. The multisensory representation of number in infancy. Proceedings of the National Academy of Sciences, USA. 2006;103:3486–3489. doi: 10.1073/pnas.0508107103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leon MI, Shadlen MN. Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron. 2003;38:317–327. doi: 10.1016/s0896-6273(03)00185-5. [DOI] [PubMed] [Google Scholar]
- Levin I. The development of time concepts in young children: Reasoning about duration. Child Development. 1977;48:435–444. [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: Large-number discrimination in human infants. Psychological Science. 2003;14:396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Maquet P, Lejeune H, Pouthas V, Bonnet M, Casini L, et al. Brain activation induced by estimation of duration: A PET study. NeuroImage. 1996;3:119–126. doi: 10.1006/nimg.1996.0014. [DOI] [PubMed] [Google Scholar]
- Meck WH, Church RM. A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes. 1983;9:320–334. [PubMed] [Google Scholar]
- Mix KS, Levine SC, Huttenlocher J. Numerical abstraction in infants: Another look. Developmental Psychology. 1997;33:423–428. doi: 10.1037//0012-1649.33.3.423. [DOI] [PubMed] [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Multiple cues for quantification in infancy: Is number one of them? Psychological Bulletin. 2002;128:278–294. doi: 10.1037/0033-2909.128.2.278. [DOI] [PubMed] [Google Scholar]
- Oliveri M, Vicario CM, Salerno S, Koch G, Turriziani P, et al. Perceiving numbers alters time perception. Neuroscience Letters. 2008;438:308–311. doi: 10.1016/j.neulet.2008.04.051. [DOI] [PubMed] [Google Scholar]
- Piaget J. The child’s conception of number. Oxford: W. W. Norton & Company; 1965. [Google Scholar]
- Piaget J. The child’s conception of time. NY: Ballantine Books; 1969. [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Pinel P, Piazza M, Le Bihan D, Dehaene S. Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron. 2004;41:983–993. doi: 10.1016/s0896-6273(04)00107-2. [DOI] [PubMed] [Google Scholar]
- Sarrazin JC, Giraudo MD, Pailhous J, Bootsma RJ. Dynamics of balancing space and time in memory: Tau and kappa effects revisited. Journal of Experimental Psychology: Human Perception and Performance. 2004;30:411–430. doi: 10.1037/0096-1523.30.3.411. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Pitzalis S, Martinez A. Mapping of contralateral space in retinotopic coordinates by a parietal area in humans. Science. 2001;294:1350–1354. doi: 10.1126/science.1063695. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Richards DD. Development of time, speed, and distance concepts. Developmental Psychology. 1979;15:288–298. [Google Scholar]
- Smith LB, Sera MD. A developmental analysis of the polar structure of dimensions. Cognitive Psychology. 1992;24:99–142. doi: 10.1016/0010-0285(92)90004-l. [DOI] [PubMed] [Google Scholar]
- Starkey P, Spelke ES, Gelman R. Detection of intermodal numerical correspondence by human infants. Science. 1983;222:179–181. doi: 10.1126/science.6623069. [DOI] [PubMed] [Google Scholar]
- van Marle K, Wynn K. Six-month-old infants use analog magnitudes to represent duration. Developmental Science. 2006;9:F41–F49. doi: 10.1111/j.1467-7687.2006.00508.x. [DOI] [PubMed] [Google Scholar]
- Walsh V. A theory of magnitude: Common cortical metrics of time, space and quantity. Trends in Cognitive Sciences. 2003;7:483–388. doi: 10.1016/j.tics.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Wynn K. Addition and subtraction by human infants. Nature. 1992;358:749–750. doi: 10.1038/358749a0. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.