Relative Location of Inhibitory Synapses and Persistent Inward Currents Determines the Magnitude and Mode of Synaptic Amplification in Motoneurons

Abstract

In some motoneurons, L-type Ca²⁺ channels that partly mediate persistent inward currents (PICs) have been estimated to be arranged in 50- to 200-μm-long discrete regions in the dendrites, centered 100 to 400 μm from the soma. As a consequence of this nonuniform distribution, the interaction between synaptic inputs to motoneurons and these channels may vary according to the distribution of the synapses. For instance, >93% of synapses from Renshaw cells have been observed to be located 65 to 470 μm away from the cell body of motoneurons. Our goal was to assess whether Renshaw cell synapses are distributed in a position to more effectively control the activation of the L-type Ca²⁺ channels. Using compartmental models of motoneurons with L-type Ca²⁺ channels distributed in 100-μm-long hot spots centered 100 to 400 μm away from the soma, we compared the inhibition generated by four distributions of inhibitory synapses: proximal, distal, uniform, and one based on the location of Renshaw cell synapses on motoneurons. Regardless of whether the synapses were activated tonically or transiently, in the presence of L-type Ca²⁺ channels, inhibitory synapses distributed according to the Renshaw cell synapse distribution generate the largest inhibitory currents. The effectiveness of a particular distribution of inhibitory synapses in the presence of PICs depends on their ability to deactivate the channels underlying PICs, which is influenced not only by the superposition between synapses and channels, but also by the distance away from the somatic voltage clamp.

INTRODUCTION

The strength of a synaptic input may depend as much on the intrinsic properties of the postsynaptic neuron to which the synapse is apposed to as on the characteristics of the synapse itself. The electric and morphological properties of the postsynaptic dendritic tree play a large role in determining the efficacy of signal transmission and the electrical distance that the signal must travel (Rall 1977). The interaction of a synaptic input with other postsynaptic conductances also influences the strength of a particular input. Coactivation of ligand-gated conductances leads to mutual changes in driving potential that can increase or decrease the amount of synaptic current injected (Koch et al. 1983). Activation or deactivation of active conductances can lead to increases or decreases in the excitability of the postsynaptic neuron. In light of these possible interactions, a very important element in determining the efficacy of a synaptic input may be its location on the dendritic tree, which sets the distance that the synaptic currents signal must travel to interact with other conductances.

The inhibition produced by Renshaw cells via recurrent motoneuron axons is usually described as weak (Hamm et al. 1987; Lindsey and Binder 1991; Maltenfort et al. 2004; Wind-horst 1996). However, the strength of Renshaw cell inhibition has been reexamined in light of an emergent intrinsic property of motoneurons. In the presence of neuromodulatory agents such as monoamines, membrane depolarization can activate persistent inward currents (PICs) (Heckman et al. 2003; Hounsgaard et al. 1988; Lee et al. 2003; Li and Bennett 2003). PICs are composed of Ca²⁺ and Na⁺ currents mediated respectively by L-type Ca²⁺ channels (Ca_V1.3 subtype; Carlin et al. 2000; Hounsgaard and Kiehn 1989) and persistent sodium channels (Li and Bennett 2003) whose exact identity has not been determined. Their activation serves as a mechanism for amplification of excitatory synaptic inputs. In a complementary manner, their deactivation is a mechanism by which inhibitory synaptic inputs can increase their ability to dampen the excitability of the motoneuron (Kuo et al. 2003). In the absence of PICs, the hyperpolarization generated by recurrent inhibition is weak (Hamm et al. 1987; Lindsay and Binder 1991). Lindsay and Binder estimated that the steady-state reduction in medial gastrocnemius motoneuron firing frequency in response to stimulation of the lateral gastrocnemius nerve was in the order of 1 to 2 Hz. Hultborn et al. (2003) showed that, in the presence of PICs, the activation of Renshaw cells could reduce the firing of motoneurons by 30 Hz.

According to anatomical evidence, the synapses of Renshaw cells are located in the proximal dendritic region of motoneurons, where >93% of these synapses were located within 65 to 470 μm from the soma (Fyffe 1991). A similar distribution was estimated through a mathematical analysis of the conductance change in motoneurons generated by activation of Renshaw cells (Maltenfort et al. 2004). Electrophysiological observations indicate that L-type Ca²⁺ channels are located on the dendrites of motoneurons (Bennett et al. 1998; Carlin et al. 2000). More recent studies have suggested that L-type Ca²⁺ channels are functionally distributed in discrete regions (hot spots) on the motoneuron dendritic tree. ElBasiouny et al. (2005) concluded that these hot spots were located 300 to 850 μm from the soma. Bui et al. (2006) placed the hot spots more proximally, 100 and 400 μm from the soma. Grande et al. (2007) reconciled these two sets of observations by showing that the distribution of the channels could be correlated with the size of the motoneurons. Importantly, in both cases there was a considerable overlap between the location of the inhibitory synapses from Renshaw cells and that of the L-type Ca²⁺ channels.

Our goal was to determine whether the superposition of inhibitory synapses and inward conductance optimizes the amplification of inhibitory inputs active in the presence of an inward current. The arrangement of Renshaw cell synapses and L-type Ca²⁺ channels on the dendrites of motoneurons lends itself well to achieving this goal. We used compartmental models to determine the effective synaptic current delivered to the soma by a set of inhibitory synapses that matched the distribution of synapses from Renshaw cells in the absence and presence of L-type Ca²⁺ channels. These currents were compared with the currents generated by the same number and type of synapses, but distributed in other regions of the dendritic tree. These distributions included: inhibitory synapses that were proximal to the location of Renshaw synapses, distal to the location of Renshaw synapses, or uniform throughout the dendritic tree. Two sets of simulations were performed. In the first set of simulations, inhibitory synapses were modeled as tonic conductance change. In the second set of simulations, inhibitory synapses were modeled as a conductance change similar to that observed in motoneurons following the activation of Renshaw cells (Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004). Our results show that the relative effectiveness of the different distributions depends on the absence or the presence of L-type Ca²⁺ channels. In the absence of these channels, the proximal distribution of inhibitory synapses is the most effective. In the presence of L-type Ca²⁺ channels, inhibitory synapses distributed according to the Renshaw cell distribution are the most effective among the distributions studied.

METHODS

Animal preparation

All cells examined were selected from a collection of feline motoneurons stained in previous experiments (Rose and Neuber-Hess 1991; Rose et al. 1995). The experimental protocols were conducted in compliance with approved institutional protocols (Queen’s University Animal Care Committee and Wright State University) and in accordance with Canadian Council of Animal Care and National Institutes of Health guidelines.

Compartmental modeling

Construction of the motoneuron compartmental models has been described previously (Bui et al. 2003; Rose and Cushing 2004). Briefly, biventer cervicis and complexus motoneurons were anti-dromically identified using stimulating electrodes placed on C2 and C3 nerves. The intracellular staining of motoneurons was performed using beveled electrodes filled with 20% horseradish peroxidase in 0.1–0.5 M Tris/0.2–0.5 M KCl (pH 7.4). Their three-dimensional structure was mapped using a neuron tracing system (Eutectic Electronics). This structure was segmented into short (<30 μm) compartments of uniform diameters and each compartment was converted into a parallel resistor–capacitor circuit. Each compartment was joined to adjacent compartments by resistors. The value of the resistors and capacitors was determined by the length and the diameter of the individual compartments and by specific membrane and cytoplasmic properties that were assumed to be constant throughout the dendritic tree. The following values were used to set the passive properties of the motoneuron models. The value of the specific resistivity of the cytoplasm (R_i) was set to 70 Ω·cm. The value of the specific membrane resistivity (R_m) was set to 15,000 or 5,000 Ω·cm². The specific membrane capacitance (C_m) was set to 1 μF/cm² (Hille 2001).

Simulations were performed using Saber, a mixed-signal simulator software package (Synopsys, Mountain View, CA) (Carnevale et al. 1990). To calculate the total synaptic current that reaches the soma, the membrane potential of the cell body was clamped to −55 mV to simulate the average membrane potential during repetitive firing (Koch et al. 1995). This is analogous to the experimental technique developed by Heckman and Binder (1988) and subsequently used by Binder and colleagues (e.g., Lee and Heckman 1996, 1998, 2000; Powers and Binder 1995, 2000) to calculate the effective synaptic current generated by tonic activation of synaptic inputs to motoneurons.

Distribution of L-type Ca²⁺ channels

In a previous modeling study we replicated the electrophysiological experiments of Bennett et al. (1998) showing that the threshold of PIC activation changed with the presence of excitatory and inhibitory synaptic activity. Based on these models, we concluded that L-type Ca²⁺ channels were distributed in discrete regions, located in the dendrites (Bui et al. 2006). The best fits were obtained when the L-type Ca²⁺ channels were distributed in 100-μm hot spots that were centered about 100–400 μm away from the cell body.

Number and distribution of inhibitory synapses

Four distributions of synaptic inhibitory inputs were modeled. The “uniform distribution” was defined by synapses that were distributed at a constant density with respect to membrane surface area throughout the dendritic tree. The “proximal distribution” was defined by a set of synapses that were also arranged at a constant density with respect to membrane surface area, but included dendrites that were only <65 μm from the cell body. Synapses in the “distal distribution” were also distributed at a constant density with respect to membrane surface area, but were restricted to dendrites ≥470 μm away from the cell body. The final distribution, “Renshaw synapse distribution,” was based on the observed anatomical distribution of Renshaw cell synapses on α-motoneurons (Fyffe 1991). In this distribution, synapses were distributed at a constant density from 65 to 470 μm away from the cell body. No synapses were distributed elsewhere in the dendritic tree.

A single series of simulations consisted of four runs, one for each synapse distribution. Within each series of simulations, the number of synapses was the same. To determine this number, we calculated the number of synapses distributed according to the Renshaw synapse distribution using a density of one synapse/1,000 μm². At this density, the current reaching the cell body during inhibitory synaptic activity resembling experimental activation of Renshaw cells is within the range reported in the literature (see Modeling of synapses; Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004). For the motoneuron models—LAD5-4, LVN2-1, and LVN4-1—the numbers of inhibitory synapses were 113, 98, and 91, respectively. For the remaining distributions, the synaptic density was adjusted to keep the number of synapses the same. With this density of inhibitory synapses, the steady-state component of the transient composite recurrent inhibitory postsynaptic currents (IPSCs) was 0.80, 0.62, and 0.54 nA for LAD5-4, LVN2-1, and LVN4-1, respectively. These values are within the experimentally observed values reported for recurrent IPSCs following motor axon stimulation at a frequency >50 Hz (Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004).

Number and distribution of excitatory synapses

The number of synaptic inputs to neck motoneurons has been estimated to be about one synapse/14.3 μm² of surface membrane area throughout the dendritic tree, corresponding to a uniform density of 7 synapses/100 μm² (Rose and Neuber-Hess 1991). Assuming that the ratio of excitatory to inhibitory synapses is 1:1, we distributed excitatory at a density of 3.5 synapses/100 μm². In our simulations, we activated 32% of these excitatory synapses, which is 1.1 excitatory synapses/100 μm². This level of activity activated a high level of PICs in all three motoneuron models to permit an assessment of the relative effectiveness of the four distributions of inhibitory synapses studied.

Modeling of synapses

The current injected by the activation of a synapse is determined by the following equation

$$I(t)=g(t)(V_{\text{m}}-E_{\text{r}})$$ (1)

The synapses were tonically activated and the time course was time-averaged. If the conductance is modeled as a single alpha function, then according to Bernander et al. (1991), the time-averaged conductance g change is equal to

$$\overline{g}=g_{\text{peak}}{et}_{\text{peak}}f$$ (2)

where g_peak is the peak conductance, t_peak is the time to peak of the conductance change, and f is the frequency. For the excitatory synapses, g_peak was set to 5 nS, t_peak was set to 0.2 ms, and f was set to 50 Hz. The values of g_peak and t_peak are based on data obtained for unitary glutamatergic synaptic current in motoneurons (Finkel and Redman 1983).

Inhibitory synapses were modeled as glycine/GABAergic synapses based on experimentally observed dual glycinergic and GABAergic unitary IPSCs on motoneurons (Jonas et al. 1998) as well as dual glycinergic and GABAergic inhibitory postsynaptic potentials (IPSPs) on Renshaw cells (Schneider and Fyffe 1992). In Bui et al. (2005), we modeled unitary glycine/GABAergic changes as consisting of a single time constant and a dual-component decay with two time constants. Transient unitary conductance changes were modeled as a piecewise function

$$g_{\text{gly}/\text{GABA}}(t)=\left\{\begin{array}{ll}\frac{g_{\text{peak}}{\mathit{ete}}^{-t/t_{\text{peak}}}}{t_{\text{peak}}}\hfill & t<t_{\text{peak}}\hfill \\ g_{\text{peak}}[\text{A}{e}^{-(t-t_{\text{peak}})/{\tau }_1}+\text{B}{e}^{-(t-t_{\text{peak}})/{\tau }_2}]\hfill & t>t_{\text{peak}}\hfill \end{array}\right\}$$ (3)

where the peak conductance g_peak is 12.2 nS; the time-to peak t_peak is 0.32 ms; the two decay time constants, τ₁ and τ₂, are 2.7 and 12.2 ms, respectively; and the two constants A and B, associated with each decay component, are 0.74 and 0.26, respectively. The conductance change due to tonic activity of glycine/γ-aminobutyric acid (GABA) synapses can be modeled as the time average of the conductance change described in Eq. 3 (Bernander et al. 1991)

$$\begin{array}{l}{g}_{\text{gly}/\text{GABA}}=\int g_{\text{gly}/\text{GABA}}(t)={\int }_0^{t_{\text{peak}}}\frac{g_{\text{peak}}{\mathit{ete}}^{-t/t_{\text{peak}}}}{t_{\text{peak}}}\text{d}t+{\int }_{t_{\text{peak}}}^{\infty }{g}_{\text{peak}}[\text{A}{e}^{-(t-t_{\text{peak}})/{\tau }_1}+\text{B}{e}^{-(t-t_{\text{peak}})/{\tau }_2}]\text{d}t\\ =g_{\text{peak}}{et}_{\text{peak}}\left[\frac{-2}{e}+1\right]+g_{\text{peak}}[\text{A}{\tau }_1+\text{B}{\tau }_2]\end{array}$$ (4)

The conductance change of n synapses activated tonically at a frequency f is

$${\overline{g}}_{\text{syn}}={\overline{g}}_{\text{gly}/\text{GABA}}fn$$ (5)

The glycine/GABA synapse mediates a chloride-mediated current with a reversal potential value of −81 mV as calculated by Stuart and Redman (1990) for glycinergic IPSCs in in vivo motoneurons.

Some IPSCs produced by repeated stimulation (>1 s) of motor axon collaterals at frequencies >50 Hz have a fast rising phase that decays to a sustained plateau (Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004), reminiscent of unitary IPSCs. To simulate IPSCs produced by this method of stimulation, we modified the unitary conductance change described in Eq. 3 by increasing t_peak, τ₁, and τ₂ to values (in ms) of 100, 50, and 1,400, respectively. These changes converted the unitary glycine/GABAergic conductance into a composite recurrent IPSC, composed of an initial rising transient component followed by a decay to a sustained component, which resembled experimentally recorded IPSCs produced by repeated stimulations of motor axon collaterals (see Bui et al. 2007).

RESULTS

In three compartmental models of motoneurons—LAD5-4, LVN2-1, and LVN4-1 (from here on, we will refer to these motoneurons in this order)—we examined the influence of synapse distribution on the effectiveness of inhibitory inputs. Four different distributions of glycine/GABAergic inhibitory synapses were tested. The number of inhibitory synapses located within 0.1λ of the L-type Ca²⁺ hot spots is listed in Table 1. The greatest amount of superposition between L-type Ca²⁺ channel hot spots and inhibitory synapses occurred when the synapses were distributed according to the Renshaw distribution. Between the three cells, the number of synapses distributed according to the Renshaw distribution that was within 0.1λ of the L-type Ca²⁺ hot spots was significantly different only between LVN2-1 and LVN4-1 (P < 0.05). In the three cells, there was a small amount of superposition between channels and synapses when the synapses were distributed uniformly, and in LVN2-1 and LVN′4–1 there was also some superposition between channels and synapses when the synapses were distributed proximally. Regarding the number of excitatory synapses within 0.1λ of the L-type Ca²⁺ hot spots, there was a greater number on LVN2-1 than LVN4-1 or LAD5-4, although these differences were not significantly different (Mann–Whitney test: LVN2-1 vs. LAD5-4, P > 0.30; LVN2-1 vs. LVN4-1, P > 0.12).

TABLE 1.

Average number of synapses within 0.1λ (R_m = 5,000 Ω·cm², R_i = 70 cm) of each L-type Ca²⁺ hot spot

	LAD5-4	LVN2-1	LVN4-1
Renshaw	2.1 ± 1.1	2.6 ± 1.1	1.9 ± 0.9
Proximal	0.0	0.2 ± 0.0	0.9 ± 0.1
Distal	0.0	0.0	0.0
Uniform	0.4 ± 0.0	0.6 ± 0.0	0.4 ± 0.0
Excitatory synapses	24.2 ± 15.5	33.1 ± 19.4	25.0 ± 10.4

Values are means ± SD.

Simulations of tonic synaptic activity

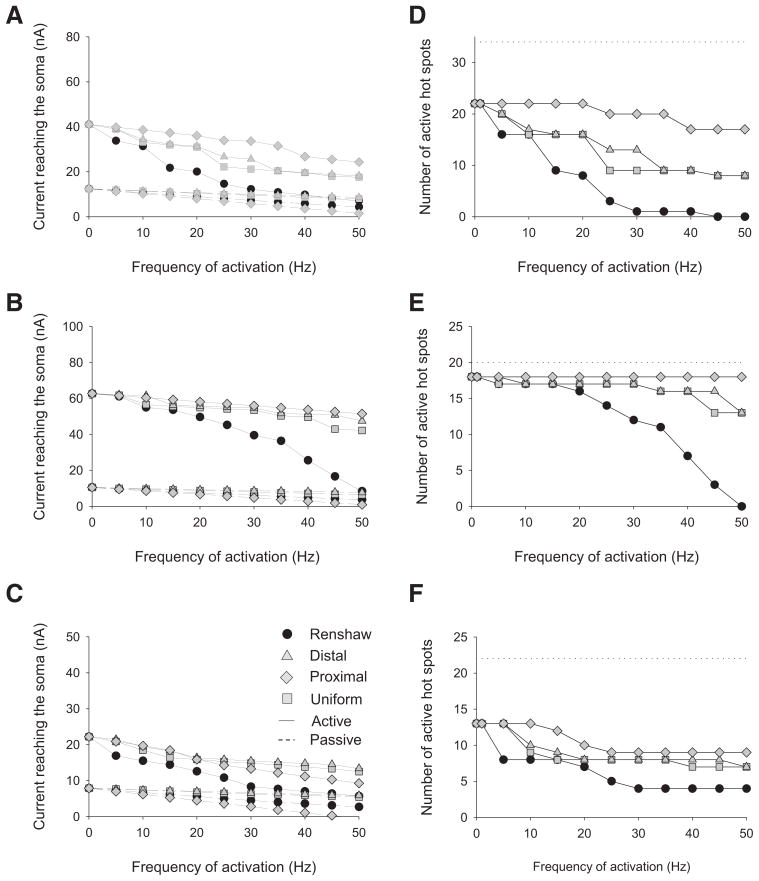
The membrane resistivity was initially set to 15,000 Ω·cm². Since the repetitive firing of action potentials produces a quasi-voltage clamp of the somatic membrane potential as described by Koch et al. (1995), the membrane potential of the soma was clamped to −55 mV. The current reaching the cell body in response to different frequencies of inhibitory synaptic activity was measured. Excitatory synapses were distributed uniformly at a density of 1.1 synapses/100 μm² and activated at 50 Hz in all simulations. In the first set of simulations, we activated the inhibitory synapses in motoneuron models with no active conductances (dashed lines in Fig. 1, A–C). In all three passive motoneuron models, the relationship between current reaching the cell body and the frequency of inhibitory synaptic activation was linear for all distributions of inhibitory synapses. For the three motoneuron models, the current reaching the cell body in the absence of any inhibitory synaptic activity was 17.8, 15.4, and 11.7 nA, respectively. At the maximal frequency of inhibitory synaptic activity simulated, the average effective inhibitory current (current reaching the cell body with synaptic inhibition – current reaching the cell body in the absence of inhibition) produced by the inhibitory synapses distributed according to the Renshaw synapse distribution, the proximal distribution, the distal distribution, and the uniform distribution was −8.1 ± 1.6, −9.9 ± 1.2, −4.6 ± 1.3, and −5.2 ± 1.2 nA, respectively. For all three motoneurons, the order of inhibitory effectiveness of the four distributions, from greatest to least effective, was proximal, Renshaw, uniform, and distal.

FIG. 1.

Current reaching the cell body and number of active L-type Ca²⁺ channel hot spots for 3 motoneuron models with 4 distributions of inhibitory synapses activated at various frequencies and a specific membrane resistivity (R_m) of 15,000 Ω·cm². The cell body was clamped at −55 mV and excitatory synaptic inputs were activated at 50 Hz. Current reaching the cell body for LAD5-4 (A), LVN2-1 (B), and LVN4-1 (C). Solid lines indicate simulations with L-type Ca²⁺ channels distributed in hot spots. Dashed lines indicate simulations with no L-type Ca²⁺ channels present. D–F: number of active L-type Ca²⁺ channel hot spots for LAD5-4 (D), LVN2-1 (E), and LVN4-1 (F). A hot spot is defined as active if the open probability of its channels is >0.5. Dotted lines indicate the total number of L-type Ca²⁺ channel hot spots in each model. In E, the total number of L-type Ca²⁺ channel hot spots is 20.

In a second set of simulations, L-type Ca²⁺ channels were incorporated in motoneuron models as hot spots according to previously estimated distributions (Bui et al. 2006). Both the distribution and the frequency of activation of excitatory and inhibitory synaptic activity were the same as in the passive setting. For the three motoneuron models, LAD5-4, LVN2-1, and LVN4-1, the current reaching the cell body in the absence of any inhibitory synaptic activity was 73.5, 81.0, and 45.4 nA, respectively. If we subtract the current reaching the cell body that was measured in the absence of L-type Ca²⁺ channels, then we can conclude that the presence of L-type Ca²⁺ channels thus led to an increase of 55.7, 55.6, and 33.7 nA, respectively, to the current reaching the cell body. In this active setting, the reduction in the current reaching the cell body in response to synaptic inhibition distributed under the four different distributions differed considerably from the passive setting (solid lines in Fig. 1, A–C). Qualitatively, the relation between the frequency of inhibitory synaptic activation and the current reaching the cell body was not linear, but exhibited stepwise decreases. At the maximal frequency of inhibitory synaptic activity simulated, across the three motoneurons the average effective inhibitory current produced by the inhibitory synapses distributed according to the Renshaw synapse distribution, the proximal distribution, the distal distribution, and the uniform distribution was −34.8 ± 14.1, −12.3 ± 0.7, −14.9 ± 9.1, and −18.5 ± 5.5 nA, respectively. For LAD5-4 and LVN4-1, the order of inhibitory effectiveness of the four distributions, from greatest to least effective, was Renshaw, uniform, distal, and proximal. For LVN2-1, the order of inhibitory effectiveness of the four distributions, from greatest to least effective, was Renshaw, uniform, proximal, and distal.

To assess whether the differences in the effectiveness of the four distributions of inhibitory synapses in the presence of L-type Ca²⁺ channels were due to disparities in the ability of the synaptic inhibition to deactivate the L-type Ca²⁺ channels, we examined the number of active hot spots at different levels of synaptic inhibition (Fig. 1, D–F). A hot spot is considered active if the probability of channel activation is >0.5. Overall, the decrease in the number of active hot spots in response to varying frequencies of synaptic inhibition closely reflected the decrease in the current reaching the cell body. For all three motoneurons, at maximal frequency of synaptic activation the order of inhibitory effectiveness as assessed by the smallest number of active hot spots remaining was, from greatest to least effective, Renshaw, uniform, distal, and proximal. Inhibitory synapses distributed under the proximal distribution were able to deactivate L-type Ca²⁺ channels only in LVN4-1. Note that in LVN2-1, inhibitory synapses distributed under the proximal and the distal distributions were unable to deactivate any hot spots. This absence of hot spot deactivation by both distributions, which occurred only in LVN2-1, explains why proximal inhibition is more effective than distal distribution for LVN2-1, whereas the reverse order was observed for both LAD5-4 and LVN4-1.

The preceding simulations were repeated with an R_m lowered to 5,000 Ω·cm² (Fig. 2) to simulate conditions involving background synaptic activity (Bernander et al. 1991) and/or activation of resting leak potassium currents (Cameron et al. 2000; Campbell and Rose 1997). Lowering R_m led to a decrease in the current reaching the cell body due to a decrease in the membrane depolarization produced by the synaptic excitation (compare the initial current reaching the cell body with and without L-type Ca²⁺ channels with no inhibitory activity in Figs. 1, A–C and 2, A–C) and the resulting smaller activation of the L-type Ca²⁺ channels (compare the initial number of activated hot spots with no inhibitory activity in Figs. 1, D–F and 2, D–F). Similar to the case where R_m was set to 15,000 Ω· cm², for all three motoneurons the order of inhibitory effectiveness of the four distributions, from greatest to least effective, was proximal, Renshaw, uniform, and distal in the absence of L-type Ca²⁺ channels. In the presence of L-type Ca²⁺ channels, the inhibition distributed according to the Renshaw synapse distribution was, once again, the most effective. For LAD5-4 and LVN2-1, the order of inhibitory effectiveness, from greatest to least effective, was Renshaw, uniform, distal, and proximal. For LVN4-1, the proximal inhibition was relatively more effective when R_m was lowered as the order of inhibitory effectiveness, from greatest to least effective, was Renshaw, proximal, uniform, and distal. Note that in some cases, the ability of the inhibition distributed under the Renshaw distribution to deactivate the hot spots is stronger with a lower R_m. For instance, in LVN2-1, synapses distributed according to the Renshaw synapse distribution are able to deactivate 100% of the hot spots when R_m is 5,000 Ω·cm²(Fig. 2E), which is not the case when R_m is 15,000 Ω·cm² (Fig. 1E). This suggests that lowering R_m decreases the sustainability of self-regenerative current through L-type Ca²⁺ channels by decreasing the membrane depolarization generated by either the somatic quasi-voltage clamp, the excitatory synaptic inputs, or the L-type Ca²⁺ channels themselves.

FIG. 2.

Current reaching the cell body and number of active L-type Ca²⁺ channel hot spots for 3 motoneuron models with 4 distributions of inhibitory synapses activated at various frequencies and an R_m of 5,000 Ω·cm². The cell body was clamped at −55 mV and excitatory synaptic inputs were activated at 50 Hz. Current reaching the cell body for LAD5-4 (A), LVN2-1 (B), and LVN4-1 (C). Solid lines indicate simulations with L-type Ca²⁺ channels distributed in hot spots. Dashed lines indicate simulations with no L-type Ca²⁺ channels present. D–F: number of active L-type Ca²⁺ channel hot spots for LAD5-4 (D), LVN2-1 (E), and LVN4-1 (F). A hot spot is defined as active if the open probability of its channels is >0.5. Dotted lines indicate the total number of L-type Ca²⁺ channel hot spots in each model.

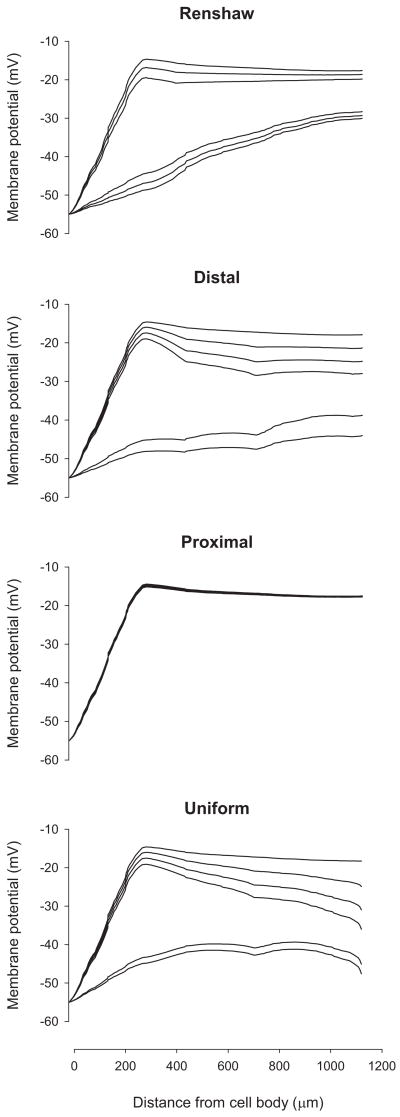
To assess whether the quasi-linear decreases in the current reaching the cell body with increasing frequencies of synaptic inhibition resulted from a graded deactivation of L-type Ca²⁺ channels or the complete deactivation of these channels at different frequencies, we examined the membrane potential profiles of a dendritic path from cell body to terminal end of LAD5-4 (Fig. 3). At low frequencies of synaptic inhibition, the membrane potential profiles showed a steep rise from the cell body to about 250 μm and then a plateau or small decrease out to the terminal end. The peak of the profile corresponds to the location of the L-type Ca²⁺ channel hot spot for this particular path (centered at 258 μm). As the frequency of inhibition increased, however, profiles corresponding to the membrane potential under Renshaw, distal, and uniform inhibition exhibit sharp declines corresponding to the complete deactivation of the L-type Ca²⁺ channel hot spots. The profiles corresponding to the membrane potential under proximal inhibition does not change with increasing frequency due to the proximity of the inhibition to the somatic voltage clamp. For each motoneuron, we examined profiles for at least a quarter of the hot spots that were deactivated and each profile exhibited sharp declines in the membrane potential associated with deactivation of the hot spot. Thus the graded decrease in current reaching the cell body with increasing frequency of synaptic inhibition is not a product of graded deactivation of all L-type Ca²⁺ channel hot spots but rather the complete deactivation of select L-type Ca²⁺ channel hot spots at different frequencies of synaptic inhibition.

FIG. 3.

Membrane potential profile of a dendritic path from cell body to terminal end of LAD5-4 during different levels of steady-state inhibitory synaptic activity under the 4 different distributions. R_m was set at 5,000 Ω·cm². The cell body was clamped at −55 mV and excitatory synaptic inputs were activated at 50 Hz. For each set of membrane potential profiles corresponding to a particular distribution of inhibitory synaptic activity, the profiles from top to bottom depict the responses to steady-state inhibition at frequencies of 0, 10, 20, 30, 40, and 50 Hz, respectively.

Simulations of transient synaptic activity

IPSCs in motoneurons in response to repetitive Renshaw cell activation often display a rapid rise followed by a rapid decay to a small plateau (Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004). Electrophysiological recordings suggest that amplification of the IPSCs in the presence of L-type Ca²⁺ channels is sometimes accompanied by a change in the time course of the IPSC characterized by a larger plateau relative to the initial peak (Bui et al. 2007). This pleomorphic amplification is due to the persistent deactivation of the channels underlying the PICs by the synaptic inhibition. An alternate form of IPSC amplification by PICs does not involve a change of shape. This isomorphic amplification is due to an increase in the inhibitory driving potential by the depolarizing effects of PICs with an absence of persistent channel deactivation. The results from the simulations of tonic synaptic activity suggest that inhibitory inputs distributed according to the Renshaw synapse distribution would more likely be amplified in a pleomorphic fashion by the presence of PICs whereas, conversely, proximally distributed inhibitory inputs would more likely be amplified in an isomorphic fashion.

Tonically active inhibitory synapses were replaced by a transiently active set of inhibitory synapses that produce composite IPSCs that resemble those produced by Renshaw cell activity in motoneurons. Inhibitory synapses were activated at 50 Hz and the somatic membrane potential was clamped at −55 mV. L-type Ca²⁺ channels were again activated by a combination of the somatic voltage clamp and the activation of excitatory synapses (50 Hz). IPSCs were first generated in a passive model where L-type Ca²⁺ channels were absent. IPSCs were activated after 500 ms of L-type Ca²⁺ channel activation (Fig. 4A). As a reminder, the current injected by the voltage clamp is the inverse of the current reaching the cell body. Therefore upward deflections in the traces indicate hyperpolarizing currents. The average peak values of the IPSC and of the time average of the last 500 ms of the IPSCs under the different distributions of inhibitory inputs for the three motoneuron models are found in Table 2. For the three motoneuron models, the largest IPSCs (as assessed by the peak of the IPSC or by the time average of the last 500 ms of the IPSC) were generated by inhibitory synapses distributed, from largest to smallest, proximally, according to Renshaw synapses, uniformly, and distally. This order seems to be a reflection of the average distance of the synapses from the cell body. When the IPSCs were normalized to the peak of the largest IPSC for each motoneuron, the shapes of the IPSCs were virtually indistinguishable (Fig. 4B).

FIG. 4.

Transient inhibitory postsynaptic currents (IPSCs) generated by synapses distributed according to Renshaw, proximal, distal, and uniform synapse distribution with membrane potential clamped at −55 mV and tonically activated excitatory synapses for motoneuron models LAD5-4 (left), LVN2-1 (center), and LVN4-1 (right). R_m was set to a value of 5,000 Ω·cm². Currents are injected by a somatic voltage clamp; therefore downward currents are depolarizing and upward currents are hyperpolarizing. A: IPSCs in motoneurons with no L-type Ca²⁺ channels. The current reaching the soma in the absence of any inhibition is denoted to the left of each trace. B: IPSCs from A normalized to the peak of the largest IPSC in each model. C: IPSCs in motoneurons with L-type Ca²⁺ channels included in the models. The current reaching the soma in the absence of any inhibition is denoted to the left of each trace. D: IPSCs from C normalized to the peak of the largest IPSC in each motoneuron.

TABLE 2.

Average IPSCs during transient activity

	Renshaw	Uniform	Proximal	Distal
Peak without L-type Ca2+ channels, nA	3.7 ± 0.8	6.6 ± 1.0	1.6 ± 0.6	1.9 ± 0.6
Peak with L-type Ca2+ channels, nA	9.0 ± 2.1	7.8 ± 0.5	3.4 ± 1.2	4.3 ± 0.7
Time-average of last 500 ms without L-type Ca2+ channels, nA	0.7 ± 0.1	1.2 ± 0.1	0.3 ± 0.1	0.3 ± 0.1
Time-average of last 500 ms with L-type Ca2+ channels, nA	4.1 ± 2.6	1.4 ± 0.1	0.7 ± 0.2	1.0 ± 0.3

The simulations were repeated with L-type Ca²⁺ channels included in the models (Fig. 4C). IPSCs generated by every distribution of inhibitory synapses were amplified by the presence of L-type Ca²⁺ channels (Table 2). The level of amplification could be measured either as the ratio of the peak of the IPSC in the presence of L-type Ca²⁺ channels to the peak of the IPSC in the absence of L-type Ca²⁺ channels (i.e., amplification of transient component) or, alternatively, as the ratio of the time average of the last 500 ms of the IPSC in the presence of L-type Ca²⁺ channels to the time average of the last 500 ms of the IPSC in the absence of L-type Ca²⁺ channels (i.e., amplification of steady-state component). Across the three motoneurons, the average amplifications of the transient component for the Renshaw, proximal, distal, and uniform distributions were 2.4 ± 0.5, 1.2 ± 0.1, 2.2 ± 0.5, and 2.4 ± 0.9, respectively. The average amplifications of the steady-state component for the Renshaw, proximal, distal, and uniform distributions were 6.2 ± 3.5, 1.3 ± 0.2, 2.5 ± 0.5, and 3.2 ± 2.0, respectively. For LAD5-4 and LVN4-1, the IPSC produced by inhibition distributed according to the Renshaw synapse distribution was the largest in terms of peak and time average of the last 500 ms. For LVN2-1, the IPSC produced by inhibition distributed according to the proximal distribution was the largest in terms of peak; the IPSC produced by inhibition distributed according to the Renshaw distribution was the largest in terms of time average of the last 500 ms. Indeed, despite undergoing the least amount of amplification the IPSCs from proximally distributed inhibitory synapses in the simulations of transient activity were not the smallest. Instead, the IPSCs from distally distributed inhibitory synapses were the smallest in terms of peak and time average of the last 500 ms in all three motoneuron models with L-type Ca²⁺ channels.

To determine the form of amplification (isomorphic vs. pleomorphic) of the IPSCs by L-type Ca²⁺ channels, the IPSCs were normalized to the peak of the IPSC of the largest IPSC for each motoneuron (Fig. 4D). For LVN2-1, the normalized IPSCs from the four distributions of inhibitory synapses were virtually identical (Fig. 4D, center). This suggests that inhibition produced by synapses distributed under the four distributions considered were not able to deactivate any of the L-type Ca²⁺ channels. This is consistent with the results from the steady-state simulations where there was little deactivation of the L-type Ca²⁺ channels. In the absence of any channel deactivation, amplification of the IPSC is determined by shunting where the activation of L-type Ca²⁺ channels is maintained by the somatic voltage clamp and the membrane depolarization caused by the excitatory synapses. Thus in LVN2-1, inhibitory synapses distributed under all distributions considered undergo isomorphic amplification due to the inability to deactivate the L-type Ca²⁺ channels. Inhibitory synapses distributed according to the Renshaw synapse distribution undergo pleomorphic amplification in LAD5-4 and LVN4-1, as seen by a larger plateau relative to the initial peak of the IPSCs (Fig. 4D, left and right panels). This indicates that inhibitory synapses distributed according to the Renshaw synapse distribution have a greater ability to persistently deactivate the L-type Ca²⁺ channels, as suggested by the steady-state simulations. Uniformly distributed inhibitory synapses also undergo pleomorphic amplification in LVN4-1, but not LAD5-4, suggesting that their ability to deactivate the L-type Ca²⁺ channels is smaller compared with that of the inhibitory synapses distributed according to the Renshaw synapse distribution.

Properties of L-type Ca²⁺ channel hot spots

Considering that there were differences in how synaptic inhibition was amplified by the L-type Ca²⁺ channels in the three cells studied, we measured the electrotonic distance and the local passive input resistance of their hot spots (Table 3). The electrotonic distance and the local passive input resistance of the hot spots were significantly larger in LAD5-4 than those in LVN2-1 (Mann–Whitney test, P < 0.05). Although the electrotonic distance of the hot spots was not significantly different between LVN2-1 and LVN4-1 (Mann–Whitney test, P > 0.98), the local passive input resistance of the hot spots of these two cells was significantly different (Mann–Whitney test, P < 0.05). There were no significant differences in the electrotonic distance (Mann–Whitney test, P > 0.14) or the local passive input resistance (Mann–Whitney test, P > 0.84) of the hot spots between LAD5-4 and LVN4-1.

TABLE 3.

Properties of L-type Ca²⁺ channel hot spots

	LAD5-4 (n = 34)	LVN2-1 (n = 20)	LVN4-1 (n = 22)
Electronic distance from the cell body	0.32 ± 0.07	0.27 ± 0.06	0.31 ± 0.14
Local input resistance, MΩ	27.3 ± 21.6	14.7 ± 9.6	23.6 ± 15.9

Values are average ± SD; n = number of hot spots.

DISCUSSION

The effectiveness of inhibitory synapses distributed according to the Renshaw synapse distribution

We simulated four different distributions of inhibitory synapses, including a distribution that was based on anatomical observations of Renshaw cell synapses to motoneurons (Fyffe 1991), in models of three motoneurons with and without the presence of L-type Ca²⁺ channels. In the absence of active conductances, inhibitory synapses distributed as Renshaw cell synapses were not the most effective distribution of inhibitory inputs during tonic and transient simulations. However, in the presence of L-type Ca²⁺ channels, the Renshaw cell synapses underwent the greatest amount of amplification and generated the largest IPSCs not only in terms of current reaching the cell body during tonic activity, but also in terms of the IPSC peak or the time average of the last 500 ms of the IPSC during transient synaptic activity.

Determinants of the strength of inhibitory synaptic inputs in the presence of L-type Ca²⁺ channels

In the presence of active depolarizing conductances such as PICs, these three components are critical in determining the strength of inhibitory synaptic inputs: the ability to deactivate the channels, the increase in the driving potential of the inhibitory synapses, and the proximity of the synapses to the cell body. The latter determines the synaptic current as measured at the cell body by influencing the amount of current generated at the site of synaptic activity through the spatially extended actions of the somatic voltage clamp and the efficacy of current transmission from the synapse to the cell body (Rall 1977). In the absence of a sufficient membrane hyperpolarization by synaptic inhibition, the channels underlying PICs cannot be deactivated and the amplification of inhibitory current is due to an increase in the driving potential of inhibitory synapses. When a sufficient membrane hyperpolarization is applied by synaptic inhibition, amplification of inhibitory current is due to the deactivation of the channels but not an increase in the driving potential of the inhibitory synapses since the deactivation of the channels precludes the generation of a depolarizing current by the channels. In simulations of tonic synaptic activity during activation of L-type Ca²⁺ channels, inhibitory synapses distributed according to the Renshaw synapse distribution were the most potent synapses, whereas proximally distributed synapses were the weakest. This was due to the inability of proximally distributed synapses to deactivate the L-type Ca²⁺ channels in contrast to the ability of the other distributions to deactivate the channels.

However, in simulations of transient synaptic activity that were designed to mimic the experimental activation of Renshaw cells (Bui et al. 2007; Lindsay and Binder 1991; Maltenfort et al. 2004), inhibitory synapses distributed proximally or according to the Renshaw synapse distribution were the two most potent. Inspection of the shape of the IPSCs in the absence and the presence of L-type Ca²⁺ channels reveals that during transient activity, many of the IPSCs generated, including all of the IPSCs generated by proximal synapses, did not undergo a change of shape following L-type Ca²⁺ channel activation. This suggests that during transient activity, a greater amount of amplification of IPSCs occurs due to an increase in inhibitory driving potential. This preponderance of amplification attributed to an increase in inhibitory driving potential was likely due to the decay of the IPSCs that decreased the membrane hyperpolarization below a sufficient amount to deactivate the L-type Ca²⁺ channels (Bui et al. 2007). Therefore in the absence of any channel deactivation, the effective inhibitory current will be determined by the increase in the driving potential by the presence of a persistent inward current and the location of the synapse. Amplification of proximal synapses was the least of the four distributions (1.2 ± 0.1 compared with >2 for the other distributions). Thus the proximal inhibitory synapses appear to be disadvantaged by the relatively small change in driving potential due to the nearby influence of somatic voltage clamp, although this disadvantage is largely offset by their proximity to soma and the small loss of synaptic current that occurs en route to the soma.

The Renshaw synapse distribution and the uniform distribution were the only distributions that were able to deactivate the L-type Ca²⁺ channels in transient simulations. Renshaw synapse distribution was able to deactivate the L-type Ca²⁺ channels in transient simulations for two of three motoneurons and the uniform distribution deactivated the L-type Ca²⁺ channels in transient simulations in one of three motoneurons, further supporting the benefits of the relative proximity of the Renshaw inputs to the L-type Ca²⁺ channels. Also, the distribution based on Renshaw synapses generated much larger IPSCs than did the uniform distribution. This difference is due in part to the more distal location of the average synapse in the uniform synapse distribution and the resultant greater loss of current en route to the soma.

Methodological considerations

SIZE OF CA²⁺ PICS

In our simulations, the activation of excitatory synapses led to the activation of L-type Ca²⁺ channels. The size of the current generated by these channels was, in one cell, >60 nA. In electrophysiological recordings of motoneurons, PICs have been measured to be as large as 35 nA (cf. Fig. 3B of Kuo et al. 2003). Several factors may explain the discrepancy between the Ca²⁺ PICs generated in our model and those measured in motoneuron recordings. First, activation of L-type Ca²⁺ channels in motoneuron recordings is often made by the use of a somatic voltage clamp (Kuo et al. 2003; Lee et al. 2003), whereas in our models their activation is produced by the combination of a somatic voltage clamp and the activation of excitatory synapses. Due to their dendritic location, a greater number of channels may be activated by the combination of somatic and dendritic sources of membrane depolarization rather than by the application of a somatic voltage clamp alone. The latter is limited in its ability to depolarize the dendrites due to the electrotonic properties of motoneuron dendrites (Heckman and Binder 1988; Müller and Lux 1993). Second, in motoneurons, outward currents are activated at depolarized membrane potentials that may mask the true amount of current generated by PICs (Heckman et al. 2005; Powers and Binder 2003; Schwindt and Crill 1980). Our models do not include active outward conductances. It is thus possible that the Ca²⁺ PICs generated in our models are close to the Ca²⁺ PICs generated in motoneurons.

DISTRIBUTION OF L-TYPE CA²⁺ CHANNELS AS HOT SPOTS

In our models, the effectiveness of inhibitory synapses distributed according to the Renshaw synapse distribution benefited from their overlap with L-type Ca²⁺ channels. Therefore the distribution of L-type Ca²⁺ channels used in the present simulations is critical to our results. Immunohistochemical studies have reported that L-type Ca²⁺ channels on motoneurons are located on the soma and proximal dendrites of rat and cat motoneurons (Westenbroek et al. 1998; Zhang et al. 2006), at branch points of proximal dendrites of mice motoneurons (Carlin et al. 2000), in local zones >1,000 μm from the soma in feline motoneurons (Ballou et al. 2006), and throughout the dendritic tree on turtle motoneurons (Simon et al. 2003). Thus the exact distribution of L-type Ca²⁺ channels on motoneurons based on anatomical techniques is unclear.

In the present study, the distribution of L-type Ca²⁺ channel as hot spots was derived using analytical methods based on the observation that the somatic threshold of plateau potentials varies with synaptic activity (Bennett et al. 1998). Models with L-type Ca²⁺ channels distributed as hot spots replicate this observation (Bui et al. 2006; ElBasiouny et al. 2005). However, estimations of the distribution of hot spots based on computational techniques also lack consensus. ElBasiouny et al. (2005) concluded that the hot spots were 300 to 850 μm from the soma. In contrast, we found that L-type Ca²⁺ channels were distributed in hot spots 100 to 400 μm from the soma (Bui et al. 2006). A more recent study by Grande et al. (2007) reconciled these observations. Motoneurons with larger dendritic trees, like the one studied by ElBasiouny et al. (2005), have hot spots 650 to 900 μm from the soma, whereas smaller motoneurons, like those used in the studies of Bui et al. (2006), have hot spots closer to the soma, typically 200 to 350 μm from the soma. Assuming that the distribution of Renshaw cell synapses on motoneurons is invariant with motoneuron type, Renshaw cell synapses on large motoneurons would be proximal to the hot spots. This would greatly reduce their relative effectiveness, as suggested by our simulations. Indeed, observations made in human studies suggest that recurrent inhibition is stronger in motoneurons responsible for weak contractions (i.e., small motoneurons) than that in motoneurons responsible for strong contractions (i.e., large motoneurons) (Pierrot-Deseilligny and Burke 2005). The magnitude of IPSCs in the absence of PICs does not vary with motor unit type in the absence of PICs (Lindsay and Binder 1991). Therefore the differences in the strength of recurrent inhibition across motor unit type in the presence of PICs may indeed be due to the presence or lack of superposition between the channels underlying PICs and inhibitory synapses from Renshaw cells.

Note that the distribution of available L-type Ca²⁺ channels may depend on the distribution of neuromodulation (e.g., 5-HT, noradrenaline) that facilitate the activation of these channels. Therefore the effectiveness of Renshaw cell inputs in deactivating L-type Ca²⁺ channels may also depend on the particular neuromodulatory state of the neuron.

Differences between three motoneurons

The interactions between the four distributions of synaptic inhibition and the L-type Ca²⁺ channels differed between the three motoneurons modeled. There was a greater amount of hot spots deactivated by synaptic inhibition, across the four distributions of inhibition in LAD5-4 in steady-state and transient simulations whereas, conversely, there was the least amount of deactivation by synaptic inhibition in LVN2-1. Based on our analysis of the properties of hot spots, it would seem that the passive local input resistance and the electrotonic distance of hot spots from the cell body were the critical distinguishing factors between LAD5-4 and LVN2-1. However, in our previous study, the number of synapses within 0.1λ was identified as a major determinant of whether a hot spot is deactivated (Bui et al. 2007), and yet LAD5-4 and LVN2-1 did not differ in the number of synapses within 0.1λ. It would seem then that the susceptibility of the hot spots of a cell to deactivation results from a combination of factors that determine the balance between the local membrane depolarization and hyperpolarization produced by intrinsic properties and synaptic activity.

Conclusions

In the absence of an intrinsic source of persistent depolarizing current in the form of PICs modulated by monoamines, the inhibition produced by Renshaw cells is weak, as measured by the voltage changes or current reaching the cell body (Hamm et al. 1987; Hultborn et al. 1988; Lindsey and Binder 1991; Maltenfort et al. 2004; Windhorst 1996). The simulations presented in the study suggest that not only is the strength of Renshaw cells significantly increased in the presence of L-type Ca²⁺ channels, but the location of Renshaw cell synapses in relation to the calcium channels underlying PICs may make them the most effective source of inhibition in the presence of PICs. The connections from Renshaw cells to motoneurons are not the only set of inhibitory synapses that may be weak, when measured in a passive context, and yet prove to play a greater role in the control of neuronal activity. In Purkinje cells, the synaptic inhibition from stellate cells is weak when measured somatically, although it exerts a very powerful control of the spread of Ca²⁺ transients in the dendrites in response to climbing-fiber stimulation (Callaway et al. 1995). Both of these sets of synaptic inputs have in common a dendritic location that limits their effectiveness in a passive setting but places them in a strategic position to control the activation of active inward conductances. This further highlights the need to describe the distribution of active conductances and their spatial relations to synaptic inputs to accurately assess the strength of a particular synaptic input. This is of particular relevance to motoneurons that receive inhibitory inputs from two different classes of neurons that are distributed differently. The synaptic inputs from Ia inhibitory interneurons to motoneurons are believed to be distributed more proximally than those from Renshaw cells (Burke et al. 1971). Reciprocal inhibition from Ia inhibitory interneurons has also been shown to be amplified in the presence of PICs (Hyngstrom et al. 2007; Kuo et al. 2003). Our results predict that the amplification of the reciprocal inhibition by PICs is mainly due to a shunting effect based on the somatic nature of their inputs to motoneurons. These predictions could be tested by assessing the impact of PICs on single IPSCs generated by reciprocal inhibition.