Mechanisms of short-term plasticity at neuromuscular active zones of Drosophila

Abstract

During short bursts of neuronal activity, changes in the efficacy of neurotransmitter release are governed primarily by two counteracting processes: (1) Ca²⁺-dependent elevations of vesicle release probability and (2) depletion of synaptic vesicles. The dynamic interplay of both processes contributes to the expression of activity-dependent synaptic plasticity. Here, we exploited various facets of short-term plasticity at the Drosophila neuromuscular junction to dissect these two processes. This enabled us to rigorously analyze different models of synaptic vesicle pools in terms of their size and mobilization properties. Independent of the specific model, we estimate ∼300 readily releasable vesicles with an average release probability of ∼50% in 1 mM extracellular calcium (∼5% in 0.4 mM extracellular calcium) under resting conditions. The models also helped interpreting the altered short-term plasticity of the previously reported mutant of the active zone component Bruchpilot (BRP). Finally, our results were independently confirmed through fluctuation analysis. Our data reveal that the altered short-term plasticity observed in BRP mutants cannot be accounted for by delocalized Ca²⁺ channels alone and thus suggest an additional role of BRP in short-term plasticity.

Synapses are specialized intercellular contact sites, which serve as the communication link between neurons and their partner cells. At chemical synapses, calcium-ion (Ca²⁺) influx triggers the fusion of transmitter-laden vesicles with the presynaptic membrane at a specific subcellular region termed the active zone. Transmitter substances released by this process then diffuse across the synaptic cleft and are sensed by the postsynaptic reception apparatus to convey signal transduction. The discovery that synaptic transmission is not only highly dynamic but that its strength also crucially depends on the recent history of presynaptic activity, has attracted decades of considerable scientific interest, and has identified synapses as key regulators of complex brain processes. Activity-dependent changes in synaptic function can last from milliseconds to hours or days, and this plasticity enables synapses to filter, modify, or integrate information. In appropriate neural networks, synaptic plasticity gives rise to processes such as sensory adaptation, rhythm generation, or learning and memory.

During short-term plasticity, the postsynaptic response to brief bursts of presynaptic activity may increase (facilitation) or decrease (depression) over time. Besides postsynaptic changes that contribute to these phenomena, the main presynaptic influences appear to be exerted by two counteracting processes: hand-in-hand with the proposal of the quantal nature of transmitter release, went the suggestion that depression was brought about by a depletion of transmitter “parcels,” whereas facilitation was caused by an elevated probability of their release (del Castillo and Katz, 1954a, 1954b). Derived from this, the postsynaptic response can be expressed as the product of quantal size (q, usually taken as the postsynaptic sensitivity), the number of synaptic vesicles available for release (N, or alternatively: the number of available release sites multiplied by their probability of occupancy), and the probability of transmitter release from a vesicle (p or p_r).

Regarding p, the calcium hypothesis proposed that the release of neurotransmitter is triggered by elevations of the Ca²⁺ concentration in the presynaptic terminal (Katz and Miledi, 1965). This in turn, led to the suggestion that facilitation of release during closely spaced stimuli was caused by the intracellular build-up of residual Ca²⁺ (Katz and Miledi, 1968).

To address N and to describe the depletion of the store of transmitter during synaptic depression, the concept of functionally distinct vesicle pools, with respect to their release and mobilization properties, was adopted (Liley and North, 1953; Elmqvist and Quastel, 1965). In particular, the idea that a “readily releasable pool” (RRP, Birks and Macintosh, 1961) of synaptic vesicles is supplied by a larger storage pool has been used to explain short-term plasticity phenomena, such as paired-pulse facilitation or depression, in terms of either a change in the size of the RRP or a change in the release probability of the vesicles comprising this pool.

The various expression patterns of short-term plasticity observed at different synapses, in various Ca²⁺ concentrations, and during different frequencies of activity, appear to mainly stem from distinct changes in the influence of p and N on release. And in this respect, we are essentially still faced with the difficulty first formulated by del Castillo and Katz (1954a). To accurately dissect changes in p and N, we need to know “[…] more about the molecular nature of the reaction whose probability we are considering.”

In the present study, we addressed this challenge, by making use of recent advances in our understanding of molecular aspects of presynaptic function. The work was carried out at the larval neuromuscular junction (NMJ) of Drosophila. This synaptic system is highly accessible to genetic manipulations, which can be employed to give insight into molecular mechanisms of synaptic communication. Our approach was based on applying different stimulation protocols in several extracellular Ca²⁺ concentrations ([Ca²⁺]_e) to sample a broad range of synaptic plasticity. We then utilized several previously reported, independent models of activity-dependent facilitation (Tsodyks and Markram, 1997; Trommershäuser et al., 2003). By focusing mainly on a mechanistic description of the relationship between vesicle release probability and Ca²⁺ dynamics (Trommershäuser et al., 2003), information was gained regarding p. This was then used to examine the behavior of various vesicle pool concepts during plasticity and to resolve N. Based on their ability to faithfully reproduce the experimental data, the pool concepts were evaluated and their implications for active zone function at the Drosophila NMJ were interpreted. Additionally, the resting parameters determined in this manner were independently supported by nonstationary fluctuation analysis.

Finally, the models were applied to analyze the physiology of synapses lacking the active zone component Bruchpilot (BRP, Kittel et al., 2006b; Wagh et al., 2006). Our results indicate that BRP mutant active zones are not only affected by a reduced release probability but also by impaired trafficking of synaptic vesicles.

RESULTS

Measurements of short-term plasticity

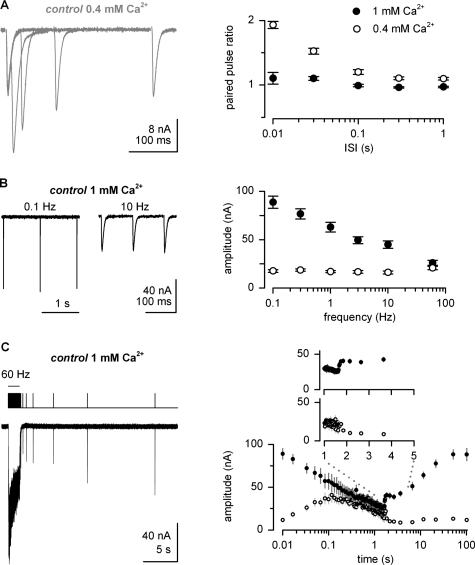
A broad range of short-term plasticity (STP) was evoked through prototypical stimulation protocols and sampled via the peak amplitude of excitatory postsynaptic currents (EPSCs) in voltage clamped muscles. Under conditions of low release probability (0.4 mM [Ca²⁺]_e) paired-pulse stimulation [Fig. 1A] led to prominent facilitation, which subsided at higher p_r (1.0 mM [Ca²⁺]_e) due to simultaneously occurring depression. Assuming that facilitation is based on a build-up of residual Ca²⁺ in the nerve terminal, the time course of paired-pulse facilitation (PPF) in low [Ca²⁺]_e (i.e., with little contribution by depletion) should correspond to the decay of the residual Ca²⁺ concentration. A mono-exponential fit to the PPF revealed a time constant of 57 ms, which is in good agreement with the previously recorded decay of residual Ca²⁺ (τ=60 ms, Macleod et al., 2002). The models of facilitation used in this study therefore assume that residual Ca²⁺ decays with τ=60 ms.

Figure 1. Measurements of short-term plasticity.

(A) Superimposed EPSCs recorded in TEVC mode in response to paired-pulse stimulation in 0.4 mM [Ca²⁺]_e and average paired-pulse ratios plotted against interstimulus intervals (ISI; filled symbols: 1.0 mM [Ca²⁺]_e, n=9 (Kittel et al., 2006b, open symbols: 0.4 mM [Ca²⁺]_e, n=8). (B) Examples of steady-state EPSCs and summary of average amplitudes versus frequency (1 mM [Ca²⁺]_e, n⩾10 (Kittel et al., 2006b), 0.4 mM [Ca²⁺]_e, n=6). (C) Example of 100 stimuli applied at 60 Hz followed by stimuli at increasing intervals. The stimulation protocol is illustrated above the current trace (left). The average peak amplitudes are plotted on a logarithmic time scale (1 mM [Ca²⁺]_e, n=6, 0.4 mM [Ca²⁺]_e, n=5). Inset: average EPSC amplitudes plotted on a linear time scale to illustrate the initial phase of recovery. In 1.0 mM [Ca²⁺]_e, recovery after the train is biphasic whereas in low [Ca²⁺]_e EPSC amplitudes decrease during the first 100 ms after the train.

Next, we measured the amplitude maintained under steady-state conditions at different stimulation frequencies [Fig. 1B]. In high [Ca²⁺]_e depression became dominant at increased frequencies while under conditions of low p_r high-frequency stimulation was capable of increasing the steady-state level (SSL) of EPSC amplitudes via elevated facilitation.

Finally, a complex stimulation protocol was investigated, consisting of a train of 100 pulses at 60 Hz followed by test pulses at increasing intervals [Wu et al., 2005; Fig. 1C]. During the 60 Hz, the tetanus residual glutamate likely accumulates in the synaptic cleft, thereby mediating a “tonic” current [see, e.g., Sakaba (2006)]. In this study we concentrated on the “phasic” component and used the peak EPSC amplitude as a measure for synchronous release. We determined time courses for the facilitation and depression during the train and for the recovery thereof. EPSC amplitudes in high and low [Ca²⁺]_e were similar after the first ∼10 pulses [Fig. 1C]. Recovery of EPSCs after the train critically depends on [Ca²⁺]_e. In 1.0 mM [Ca²⁺]_e, a biphasic recovery process was discernible (Wu et al., 2005), characterized by a fast initial component during which EPSC amplitudes increased almost twofold within the first ∼100 ms and a slow subsequent phase lasting ∼50 s. In contrast, low [Ca²⁺]_e led EPSC amplitudes to decrease during the first 100 ms after the train, which is most likely attributable to the decay of residual Ca²⁺ in the terminal and with that, cessation of facilitation.

Comparing mechanistic models of short-term plasticity

The observed STP results from the complex interplay of facilitation and depression, which in turn are both subject to specific constraints. Thus for example, a model of facilitation must be capable of describing the twofold PPF at short intervals in low [Ca²⁺]_e [Fig. 1A]. We focused on implementing a mechanistic model for facilitation proposed by Neher and co-workers (Neher, 1998; Trommershäuser et al., 2003), which is based on detailed investigations of Ca²⁺ fluxes and Ca²⁺ buffer saturation in the vicinity of Ca²⁺ channels. This work provides estimations of Ca²⁺ concentrations by assuming that microdomains arising from individual Ca²⁺ channels add up linearly (Neher, 1998). While several parameters of this model were experimentally determined at the calyx of Held synapse, here, two (or three) free parameters were implemented to allow faithful descriptions of the experimental data: (1) the parameter α is related to the distance between Ca²⁺ channels and the Ca²⁺ sensor for vesicle fusion and thereby critically determines p_r (a large value for α corresponds to a high p_r). (2) The parameter γ characterizes the saturation of Ca²⁺ buffers and thus sets the strength of facilitation. (3) If heterogeneity in p_r is assumed, the parameter η defines the difference in p_r between vesicle populations (Trommershäuser et al., 2003).

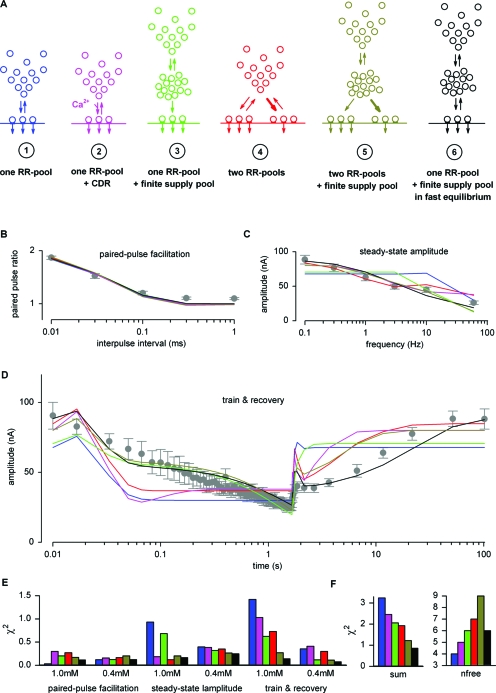
The model of facilitation was then combined with several frameworks describing the kinetics of vesicle trafficking to active zone release sites. Six of such “vesicle pool models” are illustrated in Fig. 2A. The free parameters of these concepts (including the free parameters of the facilitation model) were now systematically varied to simultaneously describe PPF, SSL, and STP during and after the train in both [Ca²⁺]_e. The predictions of the models are superimposed on the experimentally recorded data in Figs. 2B, 2C, 2D and the best-fit parameters are given in Supplementary Table S1 (see Supplementary Figs. S1 and S3 for more details and further models). The deviation of the model predictions is expressed as the difference between the data and the predictions (χ²) and is plotted in Fig. 2E for all sets of stimulation protocols. As illustrated in Fig. 2F, vesicle pool model 6 (black) delivered the best description of the experimental data using only six free parameters.

Figure 2. Comparison of mechanistic models of short-term plasticity.

To investigate the mechanisms underlying STP, we compared different vesicle pool models. (A) Simple schemes of six models (for more details, see Supplementary Fig. S1). Note the color code used hereafter. Average values for PPF (B) in 0.4 mM [Ca²⁺]_e, SSL (C), and train plus recovery (D) experiments in 1.0 mM [Ca²⁺]_e superimposed with model predictions (note that the models also had to fit the corresponding STP experiments in 1 and 0.4 mM [Ca²⁺]_e). The free parameters of each model were optimized to give the best description of the experimental findings (see Supplementary Table S1 for values). (E) The deviation of predictions from the experimental data is plotted as χ² for each set of experiments and for each model. (F) Sum of all six χ²-values and the number of free parameters used by each model.

Properties of the vesicle pool models

One RR-pool: We started with a model based on the idea that a number of vesicles are readily releasable (RR) and that after release, new RR vesicles are supplied from a reserve pool of vesicles (Fig. 2, model 1, blue; Liley and North, 1953; Elmqvist and Quastel, 1965; Betz, 1970). The release probability of a vesicle in the RR-pool changes during the train according to the implemented model of facilitation (Trommershäuser et al., 2003). The best description of the data was obtained with 262 RR vesicles (N_RR, see Supplementary Table S1) with a p_r of 0.41 in 1.0 mM [Ca²⁺]_e, a recovery time constant of 83 ms (τ_RR), and a facilitation parameter, γ, of to 2.74 μM⁻¹. This resulted in an increase in p_r from 0.41 to 0.97 based on the rise of residual Ca²⁺ from 0.1 μM to ∼1 μM during the train (see Supplementary Fig. S1 and Table S1 for model rates). After the initial pulses of the train, the number of vesicles released per action potential equals the number of vesicles newly supplied in between stimuli. On average 30 RR vesicles exist in this steady-state condition (see Supplementary Fig. S1A).

One RR-pool+CDR: It has been suggested that the supply of vesicles is accelerated after stimulation (Worden et al., 1997; Wang and Kaczmarek, 1998; Sakaba and Neher, 2001a; Hosoi et al., 2007). Especially the rate of vesicle mobilization from the reserve pool to the RR-pool was assumed to be accelerated when residual Ca²⁺ is increased (Weis et al., 1999; Dittman et al., 2000; Zucker and Regehr, 2002; Hosoi et al., 2007). Consistently, introducing such Ca²⁺ dependent recovery (CDR) led to an improved description of the STP found at the Drosophila NMJ (Fig. 2, model 2, pink). The best description was obtained with 386 RR vesicles that recover with a time constant of 5.2 s under resting conditions (see Supplementary Table S1). During the train, residual Ca²⁺ accumulates and the mobilization rate increases, elevating the steady-state level. After the train, the mobilization rate drops back to its resting value, resulting in slow refilling of the RR-pool.

One RR-pool+a finite supply pool: The implemented infinite reserve pool is used as an approximation of a large pool of vesicles whose depletion does not limit the supply of vesicles to the release sites. Abandoning this simplification leads directly to model 3, which incorporates an intermediate supply pool (Fig. 2, green). This model was recently applied to cerebellar mossy fiber bottoms (Saviane and Silver, 2006). At the Drosophila NMJ the best description of the data was obtained with 224 RR vesicles, which are supplied with a time constant τ_RR of 20 ms by 6941 supply vesicles (N_suppl), which in turn, are refilled with a time constant τ_suppl of 9 s from the reserve pool. The delayed depression of EPSC amplitudes during the train, which is especially apparent in logarithmic plots, can be interpreted with this model. Since each vesicle in the supply pool is able to refill a depleted RR vesicle, a decreased number of vesicles in the supply pool leads to a proportionally slowed supply of vesicles to the RR-pool. In between stimuli this results in fewer RR vesicles available per action potential. As the intervals between stimuli increase after the end of the train, the RR-pool is refilled quite rapidly from the only partially depleted supply pool. In summary while the depression during the train is captured accurately, the fast monophasic recovery predicted by this model is obviously incorrect.

Two RR-pools: A possible interpretation of the observed biphasic recovery could be that two populations of RR vesicles exist, which recover with different kinetics (Fig. 2, model 4, red). In fact, the calyx of Held synapse appears to harbor one population of vesicles that posses a high p_r but recover slowly and another population that has a low p_r and recovers rapidly (Wu and Borst, 1999; Neher and Sakaba, 2001; Sakaba and Neher, 2001b; Sakaba and Neher, 2001a). At the Drosophila NMJ the data are described best by a population of 181 vesicles that recover with a time constant of 44 ms and a population of 163 vesicles that recover with a time constant of 3.7 s. During the train, the slowly recovering vesicles are completely depleted and transmission is sustained by the rapidly recovering pool. However, the delayed depression during the train is not captured by this model and, in contrast to the expectation derived from the findings at the calyx, the data demand similar release probabilities (p_r=0.44 and p_r=0.36) for both populations of vesicles.

Two RR-pools+a finite supply pool: Our aforementioned results indicated that heterogeneous vesicle populations could explain the biphasic recovery after the train and that a finite supply pool of vesicles captured the build-up of depression during the train. We therefore investigated a combination of both mechanisms (Fig. 2, model 5, brown). It turned out that while this model was capable of describing all of the experimental findings (see also Supplementary Fig. S1 and Table S1), some of its properties seemed suspicious. (1) The model predicts a very small population of 82 RR vesicles with a high p_r. Estimates from anatomical investigations suggest that about 500 synapses mediate the EPSCs studied here (Atwood et al., 1993), which implies that only 16% of the synapses would posses a vesicle from this population. (2) The predicted p_r (∼0.80) of these vesicles is surprisingly high and the remaining vesicles have a p_r of ∼0.40, which is similar to the estimated p_r in the other models (see Supplementary Table S1). According to the results obtained at the calyx of Held, we would expect the high p_r pool to posses a release probability of ∼0.5 and that these vesicles should dominate the results acquired through fluctuation analysis under resting conditions (Fig. 5). The low p_r pool was expected to have a much lower release probability (p_r<0.1) and to operate preferentially during the train. We therefore addressed whether simpler models might also be able to explain our data appropriately.

Figure 5. Independent verification of the model parameters.

(A, B) Differential-interference contrast image of larval longitudinal muscles 6 (red) and 7 (blue), superimposed with a confocal image of motoneurons expressing GFP. For STP protocols the two-electrode voltage clamp recording configuration was used (A) while data for fluctuation analysis (C-F) were collected with a focal electrode. In both cases a suction electrode triggers action potentials in the innervating nerve. (C) Example EPSCs from BRP mutants (blue) and control animals (black), recorded at the indicated [Ca²⁺]_e (ten traces superimposed. (D) Peak EPSC amplitude versus [Ca²⁺]_e. The data were fitted with a Hill equation and show a right-shift of BRP mutants in the Ca²⁺-dependency of release (controls: n=5, BRP mutants: n=7). (D) Example of a mean-variance relationship of the peak current amplitude [same experiments as in (A)]. (F) From the parabolic fits, the binominal parameters N, the number of release sites, and p_r, the release probability in 1 mM [Ca²⁺]_e, were extracted. Plots show mean ± SEM (controls: n=5, BRP mutants: n=8).

One RR-pool in fast equilibrium with a finite supply pool: It emerged that our synaptic recordings could be described by a model consisting of an RR-pool, which is in fast equilibrium with a finite supply pool (Fig. 2, model 6, black, see also Zucker and Regehr, 2002). The most satisfactory fit to the data was obtained with 299 RR vesicles, 11 075 supply vesicles, and an equilibrium time constant of 47 ms. Both the time course of depression during the train, attributable to depletion of the supply pool, and the biphasic recovery thereafter are adequately captured. The initial fast recovery stems from the fast equilibrium between RR vesicles and the supply pool. Since vesicles are able to rapidly leave the RR-pool, its replenishment, in turn, depends on the refilling of the supply pool. Thus, the later phase of recovery follows the slow refilling kinetics of the supply pool.

In summary, the parameters of diverse models were quantified and several of the investigated models were able to reproduce the facets of STP recorded in high and low [Ca²⁺]_e. Notably, several parameters appeared comparably robust despite the substantially different mechanisms assumed by the models (compare, e.g., N_RR, N_suppl, and p_r of different models in Supplementary Table S1).

Next, we investigated several assumptions underlying the data presented up to this point. First, the implemented model of facilitation, which is based on detailed mechanistic interpretations of calcium dynamics in the terminal (Neher, 1998; Trommershäuser et al., 2003), uses parameters determined at the calyx of Held to describe facilitation at the Drosophila NMJ. In addition, we therefore applied an alternative, phenomenological model of facilitation developed at neocortical pyramidal neurons (Tsodyks and Markram, 1997; Markram et al., 1998). Using such an entirely different description of facilitation (see Materials and methods section) to drive vesicle pool models delivered essentially identical results (see Supplementary Table S1B).

Second, we tested how postsynaptic mechanisms of STP would influence our conclusions. To this end, a strong but realistic degree of postsynaptic depression was assumed with kinetic properties based on previous investigations. Again, similar results were obtained (Supplementary Table S1).

Prolonged stimulation

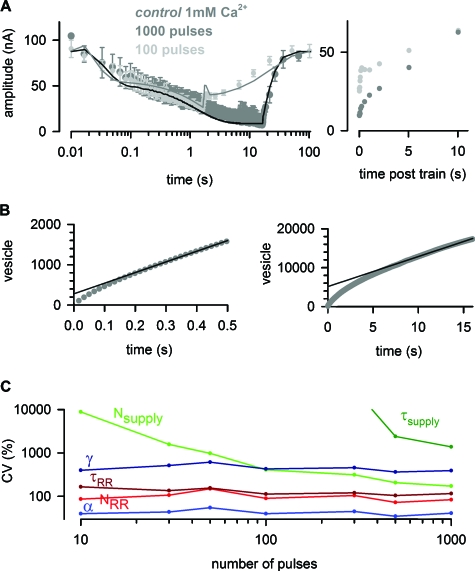
The analysis of STP critically depended on the information gained from the time course of recovery after depression [e.g., Fig. 2D]. The different pool models predict very different recovery behavior and only those models with a supply pool (models 3, 5, and 6) would predict an altered recovery after trains with more stimuli. Fig. 3A shows the average EPSC amplitudes during and following trains with 1000 stimuli at 60 Hz (dark gray) and, for comparison, the 100 pulse train (light gray). Fitting model 6 to the train of 1000 stimuli including the recovery (black line) gives very similar parameters as estimated using the aforementioned protocols (see legend of Fig. 3 for values). The more rapid recovery of the supply pool may be due to CDR of the supply pool from the reserve pool (Zucker and Regehr, 2002). Notably, model 6 accurately describes the mono-exponential nature of the recovery from 1000 stimuli, whereas model 4, for instance, would predict an unaltered biphasic recovery independent of the train duration.

Figure 3. Prolonged stimulation.

(A) A train of 1000 stimuli was applied at 60 Hz (EPSC amplitudes in dark gray, superimposed with EPSCs during 100 stimuli in light gray). Consistent with the prediction of model 6 (black line), depression during the train was biphasic while recovery after the train was mono-exponential. The right panel depicts the first 11 s of the recovery phase on a linear time scale. The parameters of the fit to the average 1000 pulses were: N_suppl=10500, τ_suppl=9.3 s, N_RR=276, τ_RR=40.0 ms, α=24.9 μM, and γ was fixed to 2.85 μM⁻¹. (B) The cumulative EPSC amplitude of the 60 Hz train of 1000 stimuli was converted to the number of released vesicles assuming a miniature EPSC amplitude of 0.63 nA (see Materials and methods section). Back-extrapolation of linear fits from 0.3 s to 0.5 s (left) and from 10 s to 16 s (right) resulted in pool estimates of 280 vesicles and 5200 vesicles, respectively. (C) The accuracy of the parameters estimated by model 6 is plotted as the CV versus the number of stimuli within a train. The accuracy of N_supply and τ_supply critically depends on the number of pulses. Here, only the train and not the time course of recovery is taken into account.

As an additional approach to gain information about vesicle pools and their mobilization rates, a linear extrapolation of the cumulative EPSC amplitude was performed [Schneggenburger et al., 1999; Fig. 3B]. Focus on the first 30 EPSCs of a 60 Hz train suggested ∼300 RR vesicles. However, when all 1000 EPSCs of a long 60 Hz train were taken into account ∼5000 vesicles were estimated. Besides indicating that back-extrapolation of cumulative EPSC amplitudes should be interpreted cautiously (as the results depend heavily on the identified SSL), these data also clearly highlight that complex mechanisms (as, e.g., several pools of synaptic vesicles) are involved in the depression during trains of stimuli.

Finally, we addressed how well the parameters of a model were defined depending on the number of stimuli within the train. Focusing on model 6, EPSC amplitudes during 60 Hz trains of 10–1000 stimuli were simulated and subsequently used as data to extract the parameters of the model. The calculated errors of the parameters (square roots of the diagonal elements of the covariance matrix; Colquhoun et al., 2003) were expressed as coefficients of variation (CV) and indicate how well each parameter could be estimated. The values for the supply pool (especially τ_supply) could be estimated only poorly from the depression during the train [Fig. 3C]. However, when the same calculations were repeated with trains of stimuli including 14 pulses during recovery [as in the experiments lasting ∼100 s; compare with Fig. 1C] all parameters could be determined very reliably and almost independently of the number of stimuli within the train (CV<100%; data not shown). These results indicate that the parameters of the model can be estimated reliably as long as the information contained in the time course of recovery is included.

The Bruchpilot mutant

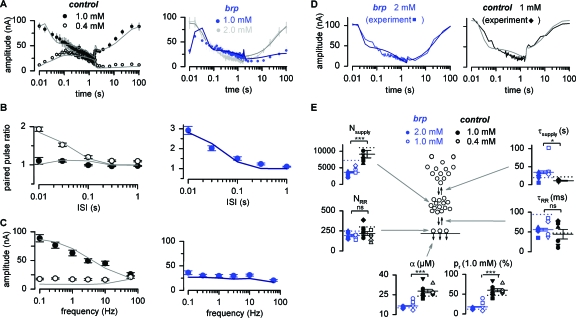
Bruchpilot (BRP) is an integral component of the Drosophila active zone cytomatrix where it helps clustering presynaptic Ca²⁺ channels at vesicle fusion sites to ensure adequate release probability (Kittel et al., 2006a, 2006b; Wagh et al., 2006; Fouquet et al., 2009). The modeling study presented here was partially motivated by findings made at BRP null mutant synapses. In particular, the strongly altered recovery of BRP mutants after a train [Fig. 4A] prompted us to develop quantitative models of active zone function that would allow us to interpret the complex observations.

Figure 4. The Bruchpilot mutant.

Average EPSCs during trains plus recovery (A), PPF (B), and at SSL (C), in controls (left column) and BRP mutants (right column), overlaid with descriptions of the experimental data by model 6 (solid lines). (D) Examples of single experiments in controls and BRP mutants to confirm the reliability of model parameters (symbols identify single experiments in the summary). (E) Summary of model parameters. Values from single experiments are given by symbols and their averages by solid lines±SEM (n=6 and 5 for 1 mM and 0.4 mM [Ca²⁺]_e in controls, n=5 and 4 for 2 mM and 1 mM [Ca²⁺]_e in BRP mutants). The parameters obtained from fitting all STP protocols in both [Ca²⁺]_e are denoted by dotted lines. According to model 6, BRP mutant active zones have a low p_r [defined by α (Trommershäuser et al., 2003)], less supply vesicles (N_supply), and refill the supply pool (τ_supply) more slowly than controls.

Figures 4A, 4B, 4C (right column) shows the PPF, the SSL, and the train plus recovery recorded at BRP mutant neuromuscular synapses in 1.0 mM [Ca²⁺]_e (blue). The train experiments were also performed in 2 mM [Ca²⁺]_e [light gray, Fig. 4A] in order to give roughly the same p_r as experienced by control animals in 1 mM [Ca²⁺]_e [compare initial values of trains in Fig. 4A]. By applying model 6 to the STP data of BRP mutants and by optimizing all six free parameters, we were able to obtain good fits to the experimental observations [dark blue and dark gray lines in Figs. 4A, 4B, 4C]. Figure 4E summarizes the parameters used by the model to fit both controls (black dotted lines) and mutants (blue dotted lines).

Importantly, the modeling approach captured the previously reported low p_r of BRP mutants (Kittel et al., 2006a). However, while the number of RR vesicles appeared unaltered, BRP mutant active zones were described as possessing a significantly smaller supply pool with slower refilling kinetics [compare with Fig. 4E].

To confirm the reliability of the extracted parameters, we fitted single experiments of the train with subsequent recovery and estimated the variability of the parameters form one experiment to the next (Figs. 4D, 4E and Supplementary Fig. S2). The data were acquired separately under conditions of low and high release probability (0.4 mM and 1 mM [Ca²⁺]_e for controls; 1 mM and 2 mM [Ca²⁺]_e for BRP mutants) and model 6 was utilized to fit the results. The available information was now strongly reduced compared to the previous approach of simultaneously fitting the averages of PPF, SSL, and train plus recovery in both Ca²⁺ concentrations. Nevertheless, in 1 mM [Ca²⁺]_e the single trains sufficed to extract most of the model parameters. The parameter γ critically depends on PPF and was therefore fixed to the value estimated previously (2.74 μM⁻¹). In addition, vesicle release in 0.4 mM [Ca²⁺]_e is so moderate that it was not significantly limited by the size and the kinetics of the supply pool. For single experiments in low [Ca²⁺]_e the number of supply vesicles and their refilling kinetics were therefore fixed to the previously obtained values (Fig. 4E, see Supplementary Table S1). The reproducibility of the individual parameters [open and filled symbols in Fig. 4E] supports the validity of the investigated model (Colquhoun and Sigworth, 1995).

In addition, we tested model 2 (Wang and Kaczmarek, 1998; Hosoi et al., 2007) and assumed that the miniature amplitude was decreased by 1% per action potential with a recovery time constant of τ=1.5 s, resembling, e.g., postsynaptic receptor saturation, desensitization, or Ca²⁺-dependent Ca²⁺ channel inactivation (Forsythe et al., 1998; Hennig et al., 2008; see Supplementary Fig. S3). Although this model assumes different mechanisms it also highlighted that the BRP mutant phenotype cannot be accounted for by lower release probability alone (compare the changes in k and k_1,b in Supplementary Fig. S3)

Independent verification of the model parameters

Fluctuation analysis can be used to determine the three quantal parameters N, p, and q under resting conditions (Silver et al., 1996; Quastel, 1997; Meyer et al., 2001; Scheuss and Neher, 2001) and independently of the modeling approach. To increase the signal to noise ratio, all EPSCs used forfluctuation analysis were recorded with a focal electrode [Fig. 5B], whereas the two-electrode voltage clamp method had been applied for STP protocols to prevent muscle contractions [Fig. 5A]. Elevating [Ca²⁺]_e increased the peak amplitude of EPSCs such that similar values were reached by BRP mutants and controls in high [Ca²⁺]_e [Figs. 5C, 5D]. The variance of EPSC amplitudes rose with increase in [Ca²⁺]_e, reached a maximum at intermediate values, and then decreased again. To obtain the number of RR vesicles (N), the quantal size (q), and the release probability (p_r), mean-variance plots were generated and stationary fluctuation analysis was used [Fig. 5E]. Consistent with earlier work (Kittel et al., 2006b) and confirming the modeling results, p_r was reduced to 0.08±0.02 in BRP mutants compared to 0.29±0.06 in controls (P<0.01) while N was unchanged [Fig. 5F]. The absolute value obtained for N is smaller in focal recordings because the two-electrode voltage clamp technique (TEVC), applied for STP protocols samples a larger number of synapses (Fig. 5; see also Materials and methods section). Furthermore, the absolute values obtained for p_r with fluctuation analysis are smaller compared to the values determined through STP experiments because the fluctuation analysis was performed at 18 °C (to prevent muscle contraction in the focal recording configuration) and not at 22 °C as for the TEVC recordings. Assuming a temperature coefficient Q₁₀ of 4 (Hille, 2001), a p_r of 0.29 at 18 °C would correspond to a p_r of 0.50 at 22 °C. This is in good agreement with the model estimates based on TEVC recordings (see Supplementary Table S1).

DISCUSSION

To gain insight into the mechanisms underlying short-term plasticity at neuromuscular active zones of Drosophila, we compared several mechanistic models and quantified their parameters. Through utilization of these models we were then able to further analyze the function of the active zone protein BRP. Finally, the basic parameters under resting conditions were confirmed independently for both control animals and BRP mutants via fluctuation analysis.

In this study, we focused on the peak EPSC amplitude and related it linearly to the number of vesicles released per action potential. While linear summation of quanta has been demonstrated over a wide range of release probabilities at, e.g., cerebellar mossy fiber synapses (Sargent et al., 2005), a number of mechanisms could corrupt this assumption. For instance, increased asynchronous release may change the time course but not necessarily the peak amplitude of EPSCs (see, e.g., Sakaba 2006). However, deconvolving EPSCs during 60 Hz trains with templates of recorded miniature EPSCs (single quanta) resulted in very similar time courses of vesicle release per stimulus (data not shown). Also, the similar release probabilities estimated for both RR-pools of models 4 and 5 is consistent with recent data, which indicates that asynchronous release contributes little to the peak EPSC amplitude at the calyx of Held (Sakaba, 2006).

Furthermore, Ca²⁺-dependent Ca²⁺ channel modulation (Forsythe et al., 1998; Hennig et al., 2008; Mochida et al., 2008) and action potential broadening have been reported to influence STP (Geiger and Jonas, 2000). It is thus also conceivable that the increased p_r during the train may be influenced by such mechanisms in addition to buffer saturation (Trommershäuser et al., 2003). Postsynaptic depression is an obvious mechanism that contributes to STP (Scheuss et al., 2002; Zucker and Regehr, 2002; Taschenberger et al., 2005; Scheuss et al., 2007). Therefore, both fluctuation analysis in high [Ca²⁺]_e (Fig. 5) and investigations of SSLs and trains (Figs. 1234) could be distorted by, e.g., postsynaptic receptor desensitization or saturation. This would underestimate the number of RR vesicles and thereby overestimate p_r. However, implementing strong postsynaptic depression in our simulations did not affect the presented conclusions (see Supplementary Table S1C, Materials and Methods Section). Since the time course of recovery differs after 100 versus 1000 pulses [Fig. 3A] it appears unlikely that postsynaptic mechanisms elicit the biphasic recovery after 100 pulses (as by this time a steady-state situation concerning the glutamate concentration in the cleft and receptor saturation and desensitization should already have been attained (Adelsberger et al., 1997; Heckmann and Dudel, 1997; Pawlu et al., 2004). Instead, it appears more likely that a steady-state is not reached after 100 stimuli because the depletion of vesicles has not yet been completed.

Previous work has described variations in p_r across active zones formed on the same axon or innervating the same target (Wojtowicz et al., 1994; Murthy et al., 1997; Marrus and DiAntonio, 2004; Wairkar et al., 2009). Similarly, our estimations of p_r most likely reflect a mean value given by a broad distribution. As the neuromuscular preparation is innervated by two motoneurons differing in their physiological properties (Kurdyak et al., 1994), it will be interesting to examine whether these contribute heterogeneously to vesicle pool models.

Taking into account how many active zones (AZs) are present in this preparation (∼500, as estimated from serial electron-microscopic images of larval longitudinal muscle 6 (Atwood et al., 1993), our estimated rate of vesicle recruitment during sustained release is ∼15∕s per AZ (N_supply×k_RR=10,000×0.7∕s per 500 AZs (model 6) and k_1,b+ΔCa²⁺×k=0.2∕s+1 μM×15∕(μM s) per AZ [modified model 2 in Supplementary Fig. S3)]. Hence, an AZ requires about 70 ms to recruit a vesicle during sustained release. This is faster than previous calculations at the Drosophila NMJ (500 ms, Delgado et al., 2000; Kidokoro et al., 2004) but within the range of recent estimates at other synapses (12 ms, Saviane and Silver, 2006), 250 ms (Hosoi et al., 2007). Our model 6 assumes a fast equilibrium between RR and supply vesicles. Such a mass-action model was previously suggested for the Drosophila NMJ in order to account for the delayed depression during the train (Li and Schwarz, 1999). However, the estimated undocking rate of RR vesicles at central synapses (Murthy and Stevens, 1999) is lower than the high transition rate of vesicles from the RR to the supply pool described by model 6 (21.1 s⁻¹).

While these differences may be reconciled by distinct functional specializations present at different synapses, the aim of our modeling approach was to generate experimentally testable hypotheses for further analysis. For each investigated model a set of parameters was determined and several of these estimates appeared relatively independent of the underlying vesicle pool model (compare, e.g., N_RR, N_suppl, and p_r of different models in Supplementary Table S1). Together with additional experimental confirmations, such as through fluctuation analysis, this increases the confidence in the parameter estimates. Finally, both models 6 and 2 identified defective trafficking of vesicles to BRP mutant active zones (Fig. 4 and Supplementary Fig. S3). Examining the precise molecular mechanisms underlying this supply defect will be of great interest.

MATERIALS AND METHODS

Genetics

As control animals we used the genotype w¹ and the genotype of Bruchpilot null mutants was brp⁶⁹∕df(2R)BSC29 (Kittel et al., 2006b).

Electrophysiology

TEVC recordings of EPSCs were obtained at room temperature from late third instar male Drosophila larvae (ventral longitudinal muscle 6, segments A2 and A3, and Fig. 5), essentially as previously described (Kittel et al., 2006b). For the TEVC experiments, both mutants and control animals carried a copy of either elav-GAL4 or ok6-GAL4 to ensure comparability with a previous study (Kittel et al., 2006b). The composition of the extracellular hemolymph-like saline (HL-3, Stewart et al., 1994) was (in mM): NaCl 70, KCl 5, MgCl₂ 20, NaHCO₃ 10, trehalose 5, sucrose 115, HEPES 5, CaCl₂ as indicated, and pH adjusted to 7.4. Recordings were made from cells with an initial V_m between −50 mV and −70 mV (holding potential at −60 mV) using intracellular electrodes with resistances of 10–32 MΩ, filled with 3 M KCl. Train stimulation protocols consisted of either 100 or 1,000 pulses applied at 60 Hz. The recovery was assessed by evoking APs at (in ms following the last pulse in the train): 25, 50, 100, 200, 500, 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 (Wu et al., 2005). EPSCs reflect the compound response to stimulation of both motoneurons innervating muscle 6, and care was therefore taken to ensure their stable recruitment. Infrequently observed recruitment failures were linearly interpolated. Only cells that recovered at least 70% of their initial EPSC amplitude following tetanic stimulation were included in the analysis. The recordings were analyzed with pClamp 9 (now Molecular Devices, Sunnyvale, CA, USA) and the peak amplitude was determined as the difference between the peak value of the EPSC and the baseline value before onset of that EPSC. The amplitude of the second response in 10 ms interpulse recordings was measured from the peak to the point of interception with the extrapolated first response.

EPSCs for fluctuation analysis were recorded with a focal electrode from third instar larvae (Fig. 5), in HL-3 essentially as reported (Pawlu et al., 2004). For each [Ca²⁺]_e, more than ∼20 EPSC were recorded at 0.2 Hz, after a steady-state amplitude was reached. The bath temperature was kept within 18 °C±0.5 °C with a Peltier element (27 W, Conrad Electronic, Hirschau, Germany) glued to the bath inflow with heat-conductive paste (Fischer Elektronik, Lüdenscheid, Germany). Focally recorded EPSCs were analyzed with Igor Pro 5.04 (WaveMetrics, Lake Oswego, OR). EPSCs were digitally filtered at 3 kHz (Gaussian filter), baseline subtracted, and the average of all failures was subtracted from the currents. Whether action potentials had been initiated was assessed by the presence of the current resulting from action potential invasion of the nerve terminal (Dudel, 1981). The peak amplitude of the EPCSs was determined within a 5-ms-window after the presynaptic action potential. The average peak amplitude of the failures was subtracted from the peak amplitude of the EPSCs.

To plot the relationship between EPSC amplitudes and [Ca²⁺]_e, [Fig. 5D], the EPSC amplitudes of each experiment were first normalized to the amplitude in 1 mM [Ca²⁺]_e. The normalized values were then averaged across experiments and subsequently the average was rescaled with the average amplitude of all experiments in 1 mM [Ca²⁺]_e. The data were fitted with a Hill equation according to I([Ca²⁺]_e)=I_max[1+(EC₅₀∕[Ca²⁺]_e)^slope]⁻¹, where I_max=10.6 and 9.5 nA, EC₅₀=1.5 and 2.2 mM, and slope=2.1 and 2.8 for controls and BRP mutants, respectively.

To calculate the variance (and the variance of the variance) we followed the procedures described by Neher and co-workers (Meyer et al., 2001; Scheuss and Neher, 2001; Scheuss et al., 2002). For a set of N peak amplitudes x_i (i=1,…,N) recorded at a certain [Ca²⁺]_e, the sample variance was calculated as the average of the sample variance of overlapping segments of size two. The variance of the variance was calculated as the standard error of the mean (SEM) of all sample variances (Meyer et al., 2001).

Stationary EPSC fluctuation analysis was performed as formerly reported (Meyer et al., 2001; Scheuss and Neher, 2001; Silver, 2003). Based on a binomial model for synaptic transmission, the variance of the EPSC amplitude depends on the quantal size (q), the number of release sites (N), and the probability of release at each site (p_r), resulting in a parabolic dependence of the EPSC variance on the average EPSC amplitude. The variance-mean plots were fitted with $\text{Var}\left(I\right)={}_{\tilde{q}}I-I^2{∕}_{\tilde{N}}$ and weighted with the reciprocals of Var(Var) and constrained to pass the origin. To correct for the variability in q, we corrected for intrasite variance (CV_QI) and intersite variance (CV_QII). The apparent $\tilde{q}$ and $\tilde{N}$ estimates are related to the true parameters by (Frerking and Wilson, 1996; Meyer et al., 2001; Scheuss and Neher, 2001; Silver, 2003)

$$q=\tilde{q}{\left(1+\text{CV}_{QI}{}^2+\text{CV}_{QII}{}^2\right)}^{-1}$$ (1)

$$N=\tilde{N}\left(1+\text{CV}_{QII}{}^2\right)$$ (2)

The experimentally determined variance of q at theDrosophila NMJ [Pawlu et al., 2004; CV_Q=0.30=(CV_QI²+CV_QII²)^0.5] in combination with the assumption of CV_QI=CV_QII (Frerking and Wilson, 1996; Meyer et al., 2001; Scheuss and Neher, 2001; Silver, 2003) results in $q=0.92\tilde{q}$ and $N=1.05\tilde{N}$.

Modeling

The simulations were based on a biophysical interpretation of facilitation described in Trommershäuser et al. (2003). In brief, a linear build up of residual calcium (ΔCa²⁺) was assumed, where each AP leads to a constant increase in ΔCa²⁺ by x₀=0.4 μM and decays mono-exponentially with τ_x=60 ms. Instead of 100 ms (Helmchen et al., 1997; Trommershäuser et al., 2003) we used 60 ms since (1) recent data indicate τ_x≈30 ms for undialysed Calyces (Müller et al., 2007); (2) measurements at the Drosophila NMJ indicated τ_x=60 ms (Macleod et al., 2002); and (3) a mono-exponential fit of the paired pulse facilitation versus interval duration recorded in 0.4 mM extracellular Ca²⁺ concentration ([Ca²⁺]_e) gave τ=57 ms.

Two types of readily releasable vesicles can be considered (Trommershäuser et al., 2003): vesicles close to Ca²⁺ channels (pool2) and vesicles further away from Ca²⁺ channels (pool1). The corresponding peak local Ca²⁺ concentration at a release site of pool j, [Ca²⁺]_j, can be expressed as (Trommershäuser et al., 2003):

$${\left[{\text{Ca}}^{2+}\right]}_j={\left[{\text{Ca}}^{2+}\right]}_{gl}+J\left({\left[{\text{Ca}}^{2+}\right]}_e\right)\alpha \left[{\delta }_{j,2}+\eta \left(1+\gamma \Delta {\text{Ca}}^{2+}\right)\right]$$ (3)

where δ_j,2 is the Kronecker symbol, which has the value 1 for j=2 and 0 for j=1. The local [Ca²⁺] at the release site is related to the probability of release according to a fourth power relationship with a half-maximal release at K_1∕2=42.5 μM (Trommershäuser et al., 2003). The global Ca²⁺ concentration ([Ca²⁺]_gl) is elevated above the resting Ca²⁺ concentration ([Ca²⁺]_r) by the residual Ca²⁺ concentration. The Ca²⁺ influx (J) depends on [Ca²⁺]_e as described by a Michaelis–Menten saturation equation

$$J\left({\left[{\text{Ca}}^{2+}\right]}_{\text{out}}\right)=J_{\text{max}}\frac{{\left[{\text{Ca}}^{2+}\right]}_e}{{\left[{\text{Ca}}^{2+}\right]}_e+{\text{EC}}_{50}}$$ (4)

with half-maximal Ca²⁺-influx at an EC₅₀ of 2.61 mM [Ca²⁺]_e and a dimensionless quantity J_max=2.31 (Schneggenburger et al., 1999; Trommershäuser et al., 2003). In addition, the increase per AP (x₀) was scaled according to

$$x_0\left({\left[{\text{Ca}}^{2+}\right]}_{\text{out}}\right)=0.4\mu \text{M}\frac{{\left[{\text{Ca}}^{2+}\right]}_e}{{\left[{\text{Ca}}^{2+}\right]}_e+{\text{EC}}_{50}}$$ (5)

The parameter α is proportional to the inverse of the distance between Ca²⁺ channels and the vesicles (Trommershäuser et al., 2003) and defines the resting release probability. The parameter η determines the difference in release probability between pool1 and pool2. The parameter γ quantifies facilitation.

The free parameters (α, η, and γ) were used to fit the experimental data of control animals including paired-pulse plasticity, frequency-dependent steady-state levels, and the response to and recovery from a train of 100 pulses at 60 Hz, in 0.4 mM and 1.0 mM [Ca²⁺]_e (Fig. 2). In models with only one pool of readily releasable vesicles (e.g., model 6), only the vesicles close to Ca²⁺ channels (pool2) were simulated (compare Sakaba, 2006; Hosoi et al., 2007) and η was fixed to the value in Trommershäuser et al. (2003). Due to the degree of facilitation required to reproduce the twofold paired pulse facilitation at short intervals in low [Ca²⁺]_e, γ was (2.74 μM⁻¹). When individual experiments (train plus recovery) were fitted [Fig. 4D and Supplementary Fig. S2], γ was fixed to 2.85 μM⁻¹ because the paired-pulse ratio in low Ca²⁺ critically constrained the degree of facilitation. For fitting individual train-experiments in 0.4 mM [Ca²⁺]_e, in addition, N_supply, τ_supply, and τ_RR (model 6, Fig. 4D, and Supplementary Fig. S2) and α, k_1.b, and k (model 2, see Supplementary Fig. S3D) were fixed to the values obtained from the average data [Fig. 4E and Supplementary Fig. S2].

Starting with analytically calculated steady-state values, the number of vesicles in each pool was numerically calculated with a fifth-order Cash–Karp Runge–Kutta method with adaptive stepsize control (Cash and Krarp, 1990). For computational speed, global calcium [Ca²⁺]_gl(t) was calculated as an array with a temporal resolution of 100 μs. For steady-state EPSC amplitude, 10, 30, 50, 70, 100 and 150 stimuli were simulated at a frequency of 0.1 Hz, 0.3 Hz, 1 Hz, 3 Hz, 10 Hz, and 60 Hz, comparable to the experiments. The last EPSC of the simulated sweep was taken as the steady-state level at the corresponding frequency. The predicted number of released vesicles was converted to a current assuming a miniature EPSC amplitude of 0.63 nA for controls and 0.87 nA for BRP mutants (based on 0.84 nA for controls and 1.17 nA for BRP mutants recorded at −80 mV holding potential (Kittel et al., 2006b) and scaled to −60 mV, assuming 0 mV reversal potential and a linear current voltage relation).

For parameter optimization, all free parameters were varied with a simplex algorithm as described (Press et al., 2002). The deviations of the model predictions from the experimental data were measured as the sum of squared differences, χ², as follows: first, the number of data points obtained from the train and recovery experiments (100 during the train+13 from the recovery) was reduced by exponential sampling to 28 values (15 during the train+13 from the recovery). Second, the six values from the steady-state and the five values from paired-pulse plasticity were weighted fivefold. Finally, the χ² values from the steady-state and train plus recovery were scaled by the inverse of the squared average current amplitude under resting conditions. This resulted in six χ² values of similar size for the paired-pulse plasticity, the steady-state level, and the train plus recovery at both 0.4 mM and 1.0 mM [Ca²⁺]_e [compare with Fig. 2E].

Subsequently, the model predictions and the experimental data were plotted superimposed using MATHEMATICA 5.0 (Wolfram Research, Champaign, IL, USA) for visual inspection. Simulation and plotting lasted only several seconds on a conventional 2.7 GHz dual core computer, which allowed us to gain a better understanding of the reliability and the constraints of the parameters. After the fit was completed, internal estimates of the errors of the best-fit parameters were calculated as the square roots of the diagonals of the covariance matrix [Colquhoun et al., 2003; compare with Fig. 3C]. To confirm that the global minimum was reached, the best-fit parameters were shown to be independent of the starting values within a plausible range. In addition, the reproducibility of the best-fit parameters to individual experiments, as performed in the analysis of single channel recordings (Colquhoun et al., 2003; Hallermann et al., 2005), indicated that the global minimum was reached (Colquhoun and Sigworth, 1995).

Statistical analysis

The nonparametric Mann–Whitney rank sum test was used for statistical analysis. The data are reported as mean±SEM, n indicates the sample number and P denotes the significance (^*P<0.05, ^**P<0.01, and ^***P<0.001).