Effect of Registration on Cyclical Kinematic Data

Abstract

Given growing interest in Functional Data Analysis (FDA) as a useful method for analyzing human movement data, it is critical to understand the effects of standard FDA procedures, including registration, on biomechanical analyses. Registration is used to reduce phase variability between curves while preserving the individual curves shape and amplitude. The application of three methods available to assess registration could benefit those in the biomechanics community using FDA techniques: comparison of mean curves, comparison of average RMS values, and assessment of time-warping functions. Therefore, the present study has two purposes. First, the necessity of registration applied to cyclical data after time normalization is assessed. Second, we illustrate the three methods for evaluating registration effects. Masticatory jaw movements of 22 healthy adults (2 males, 21 females) were tracked while subjects chewed a gum-based pellet for 20 seconds. Motion data were captured at 60 Hz with two gen-locked video cameras. Individual chewing cycles were time normalized and then transformed into functional observations. Registration did not affect mean curves and warping functions were linear. Although registration decreased the RMS, indicating a decrease in inter-subject variability, the difference was not statistically significant. Together these results indicate that registration may not always be necessary for cyclical chewing data. An important contribution of this paper is the illustration of three methods for evaluating registration that are easy to apply and useful for judging whether the extra data manipulation is necessary.

1. Introduction

Functional data analysis (FDA) is an advanced statistical method for assessing data that change continuously over time (Ramsay and Silverman, 2005). FDA can be used for exploratory and hypothesis driven analyses (e.g., Loehr and Palmer, 2009; Ramsay, 2000; Page et al., 2006; Ramsay and Silverman, 2002). It offers the advantage of retaining information in continuous signals, such as changes in joint angles or in landmark positions during a movement task, by representing movement patterns as a function of time rather than reducing the signal into discrete variables (Levitin et al., 2007). FDA techniques have been used to study back pain (Page et al., 2006), osteoarthritis (Deluzio and Astephen, 2007; Landry et al., 2007), lifting (Wrigley et al., 2006), load carrying(Lee et al., 2009), developmental differences in gait kinetics (Chester and Wrigley, 2008), the role of knee flexors and extensors in gait (Sadeghi et al., 2002, 2000), as well as age, gender, and speed effects on walking (Røislien et al., 2009).

FDA begins by transforming raw continuous data into functional observations. Typically, the functions are then registered to reduce phase variability while preserving the curves shape and amplitude (Ramsay and Silverman, 2005). The registration is useful, because when both phase and amplitude variation is present between curves, they cannot be easily compared, and representative curve features are dampened in a group average (Robertson and Caldwell, 2004; Ramsay and Silverman, 2002). In this regard, registration (Ramsay and Silverman, 2002, 2005; Ramsay et al., 2009), accomplishes a similar goal as time normalization.

Prior to beginning any FDA procedures the trial duration must be standardized. For discrete movements, one possibility for creating a common time interval is to pad the end of each trial (See Page et al., 2006). However, this technique creates artifacts in cyclical data that affect the interpretation of the behavior. Therefore, when studying cyclical movement, time normalization methods are necessary prior to any FDA procedures. Because tools for registration are available in open source packages, such as the R fda library, understanding the complex mathematical procedures is not a prerequisite to the application of registration. However, it is necessary to evaluate the effect of registration, particularly after related methods such as time normalization have been applied, and to determine whether the additional data processing is justified. Thus, criteria for determining whether registration offers an advantage are needed.

The application of three methods available to assess registration could benefit those in the biomechanics community using FDA techniques: comparison of mean curves, comparison of average RMS values, and assessment of time-warping functions. Therefore, the present study has two purposes. First, the necessity of registration applied to cyclical data after time normalization is assessed. Second, we illustrate the three methods for evaluating registration effects.

2. Materials and methods

2.1. Subjects

Twenty-two healthy adults (2 males, 20 females) between ages 19 and 58 (mean + SD = 31 + 12.0) participated in the study. No participants had removable prostheses, and all had functional natural anterior and posterior dentitions. None had chronic dental pain, headaches, or temporo-mandibular disorder signs or symptoms. Prior to participation, participants reviewed and signed an informed consent approved by the university review board.

2.2. Data collection protocol

The experimental protocol is described in detail in Gerstner and Parekh (1997). Nine 2-mm retroreflective markers used to track jaw, chin, and head movements were attached to dark planer surfaces. To track head movement, three markers were attached to safety glasses, which were secured with surgical tape to the bridge of the nose. Jaw movements were tracked with three markers attached to the lower left canine. These markers were attached to an orthodontic bracket, and orthodontic cement was used to attach the bracket to the facial surface of the tooth. To track chin movement, three markers were mounted below the lip using double-sided adhesive tape.

Participants were asked to chew a gum base pellet (~ 8-10 mm, Wrigley’s, Chicago, IL) for ~ 2 minutes before the experiment began. Next, they were asked to chew only on their right side for 20 seconds, then only on the left side for 20 seconds, while the motion was captured at 60 Hz with two gen-locked video cameras (Panasonic 5100 HS camera, Panasonic AG 4700 SVHS recorder, Panasonic AG 455 camcorder, Peak Performance event synchronization unit, Peak Performance Technologies, Inc. Englewood, CO).

2.3. Data processing

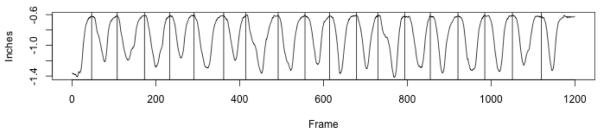
Each 20-second chewing sequence was standardized in the vertical axis so maximum close occurred at y = 0. Next each sequence was divided into individual chewing cycles (Figure 1), defined as beginning and ending at maximum closing in the vertical axis. Although each chewing sequence was standardized to zero, it is important to note that not all individual chewing cycles within a sequence had maximum closings that reached zero.

Figure 1.

Representative 20 second chewing sequence of motion in the y axis from one subject. Vertical lines indicate points of maximum closing.

Cycles were time normalized to 101 points per cycle. 10 representative cycles were selected for each trial based on a quantitative measure of curve similarity, eliminating cycles confounded by swallowing or activity related to positioning the gum (Wintergerst et al., 2004), and an average curve was created for each chewing sequence.

3. Registration analysis

The dataset included 22 curves (one average curve per participant). The registration analysis involved three steps. First, the 22 curves were smoothed, creating a function for each curve. Next, the functions were registered to reduce inter-subject variability. Smoothing and registration are described in Appendices A and B. Finally, the unregistered and registered sets of curves were compared. We refer to the set of time normalized functions as unregistered and the set of time normalized and registered functions as registered. R library fda was used for analyses.

3.0.1. Effect of registration process

To assess registration effects, mean unregistered and registered curves were compared, RMS values of unregistered and registered curves were compared, and time-warping functions were assessed. Since registration can reduce inter-subject variability, it could solve a main problem in human movement analysis, which is to obtain a representative mean pattern of motion for a given group. Therefore, the mean functions of the unregistered and registered sets of curves were compared (e.g., Ramsay and Silverman, 2005; Sadeghi et al., 2000), since it is expected that registration affects the average curve. To further quantify the comparison, the Pearson product-moment correlation coefficient was calculated.

Next, a t-test was used to compare average RMS values of the unregistered curves to the registered curves. RMS values were calculated between the mean curve and the individual curves for each group (See Sadeghi et al., 2000). Finally, time-warping functions were assessed for nonlinearity. Page and Epifanio (2007) found that time normalization adequately reduces phase variability when a linear relationship between individual phase durations and total movement duration exists. Therefore, if warping functions are linear, then registration may not offer any additional advantage over time normalization.

4. Results

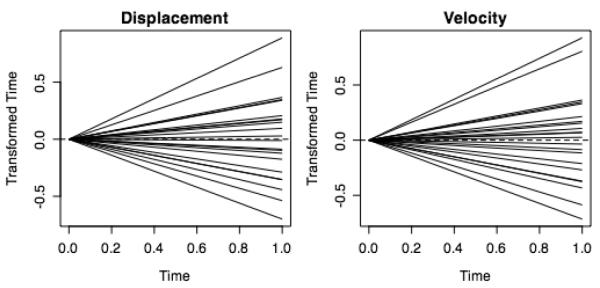
Registration did not create significantly greater peaks and valleys, as would be expected if time normalization alone did not sufficiently align the curves (figure 2 c & f). The Pearson product-moment correlation coefficient confirms the similarity between unregistered and registered curves for both displacement (ρ = .9998) and velocity (ρ = .9984). The average decrease in RMS associated with registration was 18.6% and 20.3% for displacement and velocity, respectively. However, neither decrease was statistically significant (displacement p=.2249, velocity p=.0726). The time-warping functions illustrate that all transformations were linear (figure 3).

Figure 2.

Effect of registration. a and d show the time normalized data that have been transformed into functional observations. b and e show the registered functional observations. c and f show the comparison of mean curves. The dashed line represents the time normalized mean, while the solid line represents the registered mean.

Figure 3.

Warping functions associated with registering displacement and velocity curves.

5. Discussion & Conclusions

This study used three outcome measures to evaluate the necessity of registration on cyclical data applied after time normalization: comparison of mean curves, comparison of RMS values, and the assessment of time-warping functions. Unregistered and registered mean curves were nearly identical and warping functions were linear. Although registration decreased the RMS, indicating a decrease in inter-subject variability, the difference was not statistically significant. Together these results indicate that registration may not always be necessary for cyclical chewing data. In contrast to Sadeghi et al.’s (2000) recommendation to register curves prior to gait analysis, our findings indicate that registration may not always be a necessary adjunct to analyses of cyclical movement patterns. Therefore, the important point of this paper is that simple and easily checked measures should be used to determine whether registration is recommended.

Based on the results of the current analysis, we consider when registration may be justified. When an average curve is needed to represent a population, the similarity of the unregistered and registered mean curves indicates the extra data processing may not be justified. That is, registration did not change the interpretation of the behavior. However, when methods such as functional ANOVA or functional PCA are included in the analysis protocol, inter-subject variability decreases within a homogenous group (e.g., the 18.6% and 20.3% RMS decreases), even if the average curve is unaffected, indicate registration may be justified. In this case, the chance of finding significant differences between two or more populations increases.

Two important methodological considerations should be considered prior to registration. First, although displacement is regularly used in biomechanics studies, derivatives such as velocity may provide better curve alignment (Ramsay and Silverman, 2005). Effectiveness of registration tends to improve with clear maxima, minima, inflection points, and zero-crossings, features that are more prevalent in derivatives. Second, prior to registration it must be considered whether the set of curves is indeed from a homogenous group; if not, important differences between curves related to phase variation will be removed, affecting the outcome of the analysis.

In conclusion, techniques for assessing registration are available and simple to apply. Therefore, these methods should be used to help determine whether the extra data processing is justified prior to analysis.