Abstract
Mouse hearts have a diversity of action potentials (APs) generated by the cardiac myocytes from different regions. Recent evidence shows that cells from the epicardial and endocardial regions of the mouse ventricle have a diversity in Ca2+ handling properties as well as K+ current expression. To examine the mechanisms of AP generation, propagation, and stability in transmurally heterogeneous tissue, we developed a comprehensive model of the mouse cardiac cells from the epicardial and endocardial regions of the heart. Our computer model simulates the following differences between epicardial and endocardial myocytes: 1) AP duration is longer in endocardial and shorter in epicardial myocytes, 2) diastolic and systolic intracellular Ca2+ concentration and intracellular Ca2+ concentration transients are higher in paced endocardial and lower in epicardial myocytes, 3) Ca2+ release rate is about two times larger in endocardial than in epicardial myocytes, and 4) Na+/Ca2+ exchanger rate is greater in epicardial than in endocardial myocytes. Isolated epicardial cells showed a higher threshold for stability of AP generation but more complex patterns of AP duration at fast pacing rates. AP propagation velocities in the model of two-dimensional tissue are close to those measured experimentally. Simulations show that heterogeneity of repolarization and Ca2+ handling are sustained across the mouse ventricular wall. Stability analysis of AP propagation in the two-dimensional model showed the generation of Ca2+ alternans and more complex transmurally heterogeneous irregular structures of repolarization and intracellular Ca2+ transients at fast pacing rates.
Keywords: cardiac myocytes, action potential, computer modeling, alternans
the mouse is an important animal for the study of the physiology of the heart and various pathophysiological and proarrhythmic conditions such as heart failure. The development and study of genetically modified mice have often led to unexpected or counterintuitive results in cardiac electrophysiology. The resolution of complex interactions often turned to the use of comprehensive models of mouse cardiac myocytes to explain experimental observations of action potential (AP) generation, propagation, Ca2+ dynamics, and arrhythmias (14, 35, 42, 44, 50, 56, 58, 67). Spatial diversity of molecular heterogeneity is now understood to be an important factor in arrhythmogenesis. One difference of key importance is thought to be the difference between endocardial and epicardial tissues (8, 18). In this article we develop models of epicardial and endocardial mouse myocytes, using our previous models of cells from the apex and septum regions of the heart (3, 4, 6) as a starting point. The new epicardial and endocardial cell models have different membrane current densities and distinct Ca2+ handling properties based on recent data from the different regions of the mouse heart (8, 18). These models reproduced the fundamental differences in the two cell types including some unexpected phenotypes. The model cells were coupled together into two-dimensional (2-D) tissues to explore the consequences of a transmural gradient on the stability of APs and Ca2+ transients.
Transmural heterogeneity is of critical importance in the generation of arrhythmias and ECG abnormalities in larger mammals. This has been less clear in the mouse, in part because of the absence of models that distinguish between epicardial and endocardial cells based on experimental data. Recently, voltage-clamp studies of major repolarization currents and Ca2+ handling in the mouse ventricular myocytes from two other regions of the mouse heart, epicardium and endocardium, have shown that there are differences in K+ repolarization currents and in Ca2+ handling mechanisms (8, 18). We have used these data to reproduce dynamic experimental studies of AP shape and duration from the isolated myocytes, epicardial and endocardial tissues (2, 8, 32). The model simulations of differences in AP shape and durations were predominantly due to the differential expression of three major K+ repolarization currents: rapidly inactivating transient outward K+ current (IKto,f), ultrarapidly activating K+ current (IKur), and noninactivating steady-state K+ current (IKss) (8). These current differences were capable of sustaining functional heterogeneity of repolarization in a 2-D sheet, roughly approximating the thickness of the left ventricular wall.
In contrast to our previous model of apex and septal cells, the new models incorporated experimental findings on the differences in transmural Ca2+ handling (18). These differences include diastolic and systolic intracellular Ca2+ concentration ([Ca2+]i), and [Ca2+]i transients, which are higher in paced endocardial and lower in epicardial myocytes, a Ca2+ release rate that is about two times larger in endocardial than in epicardial myocytes, and a Na+/Ca2+ exchanger turnover rate that is greater in epicardial than in endocardial myocytes. This allowed us to examine the interaction between membrane currents and intracellular Ca2+ handling as a mechanism for transmural differences in Ca2+ handling and the consequences of the interaction of heterogeneity of both Ca2+ and AP in a 2-D system.
Perturbation of the key components of the Ca2+ handling system revealed that intracellular components as opposed to sarcolemmal ion channel differences are the most sensitive factors regulating the differences in Ca2+ transient magnitude and behavior between the two myocyte types. Simulated pacing of isolated epicardial and endocardial myocytes revealed that there was a more complex response of the epicardial cells at rapid rates compared with endocardial cells. We also studied the consequences of transmurally inhomogeneous 2-D ventricular tissue that contained models of epicardial and endocardial myocytes. This multicellular modeling reproduced experimentally observed propagation velocities and predicted that rapid pacing rates would yield the development of Ca2+ alternans, irregular APs, and a complex transmurally inhomogeneous structure of [Ca2+]i transients. These studies suggest that molecular and electrotonic interactions can produce unexpected complex behavior related to potential arrhythmogenic mechanisms. These models should be a useful tool for others in understanding the complex interactions that occur during disease processes such as heart failure that are frequently studied on a molecular level in transgenic mice.
METHODS
We investigated a transmural 2-D model tissue consisting of the mouse ventricular myocytes modified from Ref. 6 (Fig. 1A). Two different types of cells were developed to simulate AP propagation and Ca2+ handling in transmurally inhomogeneous model tissue: the epicardial and the endocardial cells. These cells differ in the set of K+ currents and Ca2+ handling systems. They are based on the model of Bondarenko et al. (6) with differences in parameters that are outlined in Table 1.
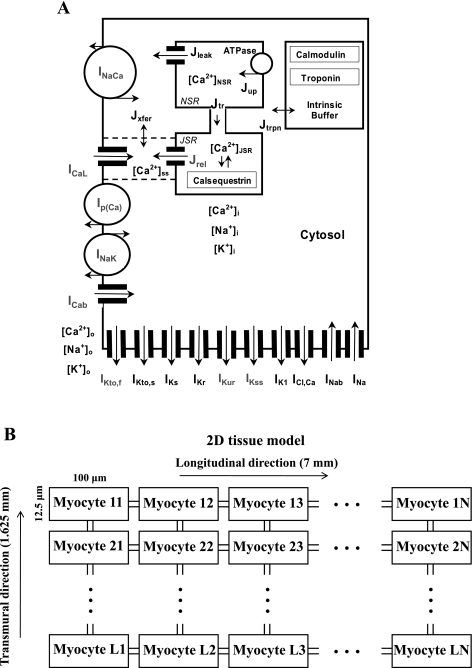
Fig. 1.
A: schematic diagram of the mouse model ionic currents and Ca2+ fluxes. Transmembrane currents are as follows: the fast Na+ current (INa), the L-type Ca2+ current (ICaL), the sarcolemmal Ca2+ pump [Ip(Ca)], the Na+/Ca2+ exchanger (INaCa), the rapidly recovering transient outward K+ current (IKto,f), the slowly recovering transient outward K+ current (IKto,s), the rapid delayed-rectifier K+ current (IKr), the ultrarapidly activating delayed-rectifier K+ current (IKur), the noninactivating steady-state voltage-activated K+ current (IKss), the time-independent K+ current (IK1), the slow delayed-rectifier K+ current (IKs), the Na+-K+ pump (INaK), the Ca2+-activated chloride current (ICl,Ca), and the Ca2+ and Na+ background currents (ICab and INab, respectively). Istim, external stimulation current; NSR, network sarcoplasmic reticulum; JSR, junctional sarcoplasmic reticulum; [Ca2+]i, [Na+]i, and [K+]i, intracellular Ca2+, Na+, and K+ concentrations, respectively; [Ca2+]o, [Na+]o, and [K+]o, extracellular Ca2+, Na+, and K+ concentrations, respectively. The Ca2+ fluxes within the cell are as follows: uptake Ca2+ from the cytosol to the network sarcoplasmic reticulum (SR) (Jup), Ca2+ release from the junctional SR (Jrel), Ca2+ flux from the network to junctional SR (Jtr), Ca2+ leak from the SR to the cytosol (Jleak), Ca2+ flux from the subspace volume to the bulk myoplasm (Jxfer), and Ca2+ flux to troponin (Jtrpn). The model includes Ca2+ buffering by troponin and calmodulin in the cytosol and by calsequestrin in the SR. Current systems changed from the apex/septum model of Bondarenko et al. (6) are shaded gray. B: geometry of two-dimensional (2-D) multicellular tissue used in this study. The transmural 2-D model tissue consists of 9,100 mouse ventricular myocytes, a rectangular sheet of 130 myocytes × 70 myocytes (L = 130, N = 70), which is equivalent to the rectangle with 7 mm length and 1.625 mm width.
Table 1.
Differences between current model and model from Bondarenko et al. (6)
| Current Model | Model from Bondarenko et al. (6) | ||
|---|---|---|---|
| Both cell types | |||
| This condition is removed | PRyR set to 0.0 during each stimulus pulse Istim | ||
| Kpc,max = 0.11662 ms−1 | Kpc,max = 0.23324 ms−1 | ||
| Kpc,half = 10.0 μM | Kpc,half = 20.0 μM | ||
| Kpcf = 2.5 ms−1 | |||
| Epicardial cell | |||
| ν1 = 1.5 ms−1 | ν1 = 4.5 ms−1 | ||
| kNaCa = 292.8 pA/pF | kNaCa = 292.8 pA/pF | ||
| GCab = 0.000165 mS/μF | GCab = 0.000367 mS/μF | ||
| GKto,f, = 0.3362 mS/μF | GKto,f, = 0.4067 mS/μF (apex) | ||
| GKur = 0.2056 mS/μF | GKur = 0.160 mS/μF (apex) | ||
| GKss = 0.0491 mS/μF | GKss = 0.050 mS/μF (apex) | ||
| Endocardial cell | |||
| ν1 = 2.9 ms−1 | ν1 = 4.5 ms−1 | ||
| kNaCa = 146.4 pA/pF | kNaCa = 292.8 pA/pF | ||
| GCab = 0.0001 mS/μF | GCab = 0.000367 mS/μF | ||
| GKto,f = 0.1939 mS/μF | GKto,f = 0.4067 mS/μF (apex) | ||
| GKur = 0.1405 mS/μF | GKur = 0.160 mS/μF (apex) | ||
| GKss= 0.0445 mS/μF | GKss= 0.050 mS/μF (apex) |
See methods and Fig. 1 legend for definitions of abbreviations.
K+ currents.
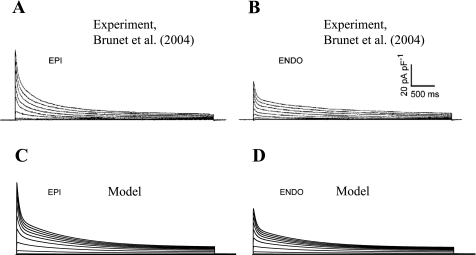
Epicardial and endocardial ventricular myocytes have different expression of K+ currents. These K+ channel expression levels are mainly responsible for differences in AP duration (APD) (8). Experimentally, differences were described in the magnitudes of three major repolarization currents: IKto,f, IKur, and IKss (8). We adjusted the values of the maximal current conductances for these currents to fit the experimental values of the current densities without changing the kinetic parameters (Table 1). Experimental data from Ref. 8 for the inactivation of total voltage-activated K+ currents are shown in Fig. 2, A and B. They compared well with the corresponding simulations for epicardial and endocardial model cells (Fig. 2, C and D).
Fig. 2.
Total depolarization-activated K+ currents from different regions of mouse heart. A and B: epicardial (Epi) and endocardial (Endo) whole cell currents from Ref. 8. C and D: simulated currents from the model epicardial and endocardial cells. Experimental currents were recorded in response to 4.5-s voltage steps to test potential between −40 and +40 mV from holding potential of −70 mV. Simulated currents were elicited by a 4.5-s depolarizing step to between −70 and +50 mV in 10-mV increments from a holding potential of −70 mV.
Ca2+ dynamics.
The first step in modeling the differences in Ca2+ dynamics between epicardial and endocardial cells was to “tune” the previous model (6) and address some of the limitations to this portion of the system. The previously published models of apical and septal cells have been criticized as having disproportional levels of Ca2+ extrusion by the Na+/Ca2+ exchanger (INaCa) relative to the Ca2+ pump (6, 43). This limitation in the previous model has been addressed in the current model by a significant reduction of the maximum Ca2+ pump current from 1.0 pA/pF in the previous model to 0.17 and 0.085 pA/pF in the current model for epicardial and endocardial myocytes, respectively (Table 1). We also reduced the maximal conductance for the Ca2+ background current (Table 1) that played a compensatory role for Ca2+ extrusion via Ip(Ca) in the apical and septal cell models (6, 43).
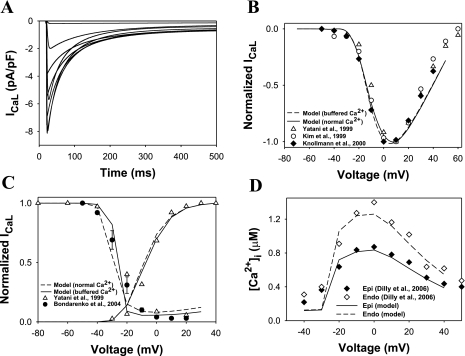
We also improved the Markov model for the L-type Ca2+ current (ICaL) (Fig. 4 in Ref. 6) by simplifying the voltage dependence of the rate constants and tuning them to match the experimental data. While the model of the Ca2+ current in Ref. 6 matched the data, it had some arbitrary voltage dependence for the activation rate constant α(V) that had no biophysical interpretation. The Markov model structure was not changed. The rate constant for activation [α(V) and β(V)] and inactivation [γ(Ca2+) and Kpcf] were adjusted to match experimental data (6, 31, 33, 75). Simulated ICaL traces obtained by depolarization for 5 s to between −70 and +40 mV (in 10 mV increments) from a holding potential of −80 mV and under heavy buffer conditions (5–10 mM EGTA) are shown in Fig. 3A (simulations in Fig. 3, A–C, are shown for epicardial cells, which are not noticeably different from those for endocardial cells). They are similar to the corresponding current traces observed experimentally under similar conditions (41, 75). Normalized peak current-voltage relationships for ICaL are shown in Fig. 3B for normal (without buffer) and heavy buffer conditions by solid and dashed lines, respectively. For normal conditions, we used the same voltage-clamp protocol as for the heavy buffer conditions, except for the duration of the first pulse P1 (250 ms). Both simulations show similar voltage dependences for normalized peak current amplitude and compare well to the experimental data (31, 33, 75). The corresponding absolute maximum peak current amplitudes (7.9 and 8.1 pA/pF) are well centered within the range of experimental values 5.1–11.6 pA/pF as well (29, 53, 70). Markov models for ICaL were improved to fit not only steady-state inactivation relationships, as in our previous model (6), but also the voltage dependence of normalized ICaL conductance G/Gmax (Fig. 2C), which should reflect steady-state activation.
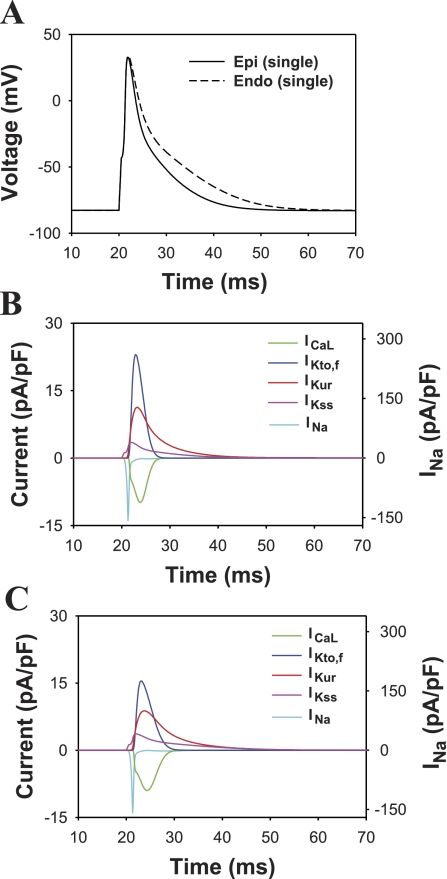
Fig. 4.
Simulated action potentials (APs) and underlying currents of the mouse ventricular myocyte model. A: the epicardial (solid line) and endocardial (dashed line) APs. B: currents underlying the epicardial AP. C: currents underlying the endocardial AP. The scale for the relatively large INa is given on the right-hand axis in B and C. All other currents are scaled to the left axis. Pacing frequency was 1 Hz. APs and ionic currents are shown for the 10th stimulation basic cycle length (BCL).
Fig. 3.
ICaL and [Ca2+]i transients. A: a family of simulated current traces. A 5-s depolarizing first pulse (P1) to between −70 and +40 mV (in 10-mV increments) was applied from a holding potential of −80 mV. This was followed by a second 500-ms pulse to +10 mV. For clarity, only first 500 ms are shown. Raw current simulations were performed to match the experimental conditions of Masaki et al. (41) and Yatani et al. (75) in which [Ca2+]i was buffered with 5 mM EGTA (BAPTA) and SR was depleted with 10 μM ryanodine (no Ca2+ release). Simulated inactivation time constants at +20 mV τf = 27.1 ms (Af = 42.3%) and τs = 96.7 ms (Af = 57.7%) were similar to the experimental values from Ref. 41 τf = 26.1 ± 2.7 ms (Af = 54.4 ± 11.3%) and τs = 96.1 ± 18.8 ms (Af = 45.6 ± 11.3%). B: Peak ICaL current-voltage relationships for simulated and experimental data. The solid line shows data from simulations under normal physiological extracellular ion concentrations, and the dashed line connects data simulating the experimental conditions of Yatani et al. (75). Experimental results are shown by white circles (31), white triangles (75), and black diamonds (33). C: normalized channel conductance G/Gmax and steady-state inactivation relationships for 500-ms P1 pulse simulations (dashed lines) and 5-s P1 pulse simulations with buffered Ca2+ (solid lines). Black circles are our data from 5-s P1 pulses and [Ca2+]i buffered with 5 mM EGTA (6). White triangles are from the experimental measurements of Yatani et al. (75) where Ca2+ was buffered with 5–10 mM EGTA (BAPTA). D: voltage dependence of simulated (solid and dashed lines for endocardial and epicardial cells, respectively) and experimental [black and white diamonds for endocardial and epicardial cells, respectively (18)] [Ca2+]i.
While the gating properties of the ICaL in isolation are similar for epicardial and endocardial myocytes, there are differences between them because of the amplitudes of the [Ca2+]i transients. These differences in transients are due to differences in Ca2+ handling mechanisms (18). The modeling of increased release is based on the experimental observation that the expression level of ryanodine receptors is about twofold higher in endocardial than in epicardial myocytes (18). To simulate this difference with our model, we used Ca2+ release rates ν1 = 1.5 and 2.9 ms−1 for epicardial and endocardial cells, respectively (Table 1). These values for ν1 were also chosen to match differences both in [Ca2+]i and to reproduce the average integrated experimental Ca2+ release efflux of about 39 ± 3 μM (40). The resulting simulations for the voltage dependences of peak [Ca2+]i are shown in Fig. 3D by solid and dashed lines for epicardial and endocardial myocytes, respectively. Corresponding experimental data (18) are shown in Fig. 3D by black and white diamonds. Relationships between voltage dependences of peak [Ca2+]i and ICaL reproduce graded Ca2+ release.
In addition to the differences in Ca2+ release as described above, epicardial and endocardial cells possess distinct diastolic Ca2+ levels and rates of Ca2+ extrusion by INaCa (18). Experimental data show that epicardial myocytes have a smaller level of diastolic Ca2+ during stimulation and about a twofold faster rate of Ca2+ extrusion via INaCa. However, both cell types have the same resting values of [Ca2+]i (18). To simulate these differences, we used two different scaling factors kNaCa for the Na+/Ca2+ exchanger in the epicardial and endocardial cell models, 292.8 and 146.4 pA/pF, respectively (Table 1). These values produced slightly different diastolic resting [Ca2+]i in the two myocyte models, 0.124 and 0.136 μM for epicardial and endocardial cells, respectively, which are close to the corresponding experimental resting values 0.150 ± 0.019 and 0.156 ± 0.021 μM (18).
The transmural 2-D model tissue consists of 9,100 mouse ventricular myocytes, a rectangular sheet of 130 myocytes × 70 myocytes (nx = L = 130, transmural direction; ny = N = 70, longitudinal direction, Fig. 1B). The number of cells and dimensions of 2-D tissue were chosen to match the experimental measurements of the mouse ventricle, with a length and thickness of about 7 and 1.6 mm, respectively (28, 59). Taking into account the cell volume 3.8×104 μm3 (cytosol volume is 2.584×104 μm3, or 68% of the total cell volume) (6, 39), we chose the cell length of 100 μm, the cell width of 30.4 μm, and the cell thickness of 12.5 μm (Fig. 1B). These myocyte dimensions are close to those obtained in different experimental studies (12, 45, 52, 55). As a result, our 2-D model represents the rectangular surface with a 7 mm length and 1.625 mm width. Each model myocyte is described by the equations from Ref. 6 with corresponding modifications (Table 1) and initial conditions plus intercellular currents:
| (1) |
where i is the cell number, Cm,i is the membrane capacitance of the ith cell, Vi is the membrane potential, Imemb,i is the total membrane ion current (Ref. 6 and Table 1), Istim,i is the stimulus current, Igap,i = ggap,xi (−Vi−1 + 2Vi − Vi+1) + ggap,yi (−Vi−nx + 2Vi − Vi+nx), where ggap,xi and ggap,yi are the gap conductances along axes x and y, respectively. Note that for the model myocytes on the tissue perimeter, the expression for Igap,i contains only two or three intercellular currents from the neighboring cells. In this article, we used values of ggap,xi = ggap,x and ggap,yi = ggap,y for all myocytes. The conductances in two directions were chosen to yield experimentally measured AP propagation velocities in the mouse hearts, ggap,x = 500 nS/pF (0.36 m/s) and ggap,y = 25 nS/pF (0.62 m/s) (27, 68). When we take into account that the mouse ventricular myocyte capacitance is about 100 pF (7, 8), these numbers correspond to resistances of ∼0.02 and 0.4 MΩ, respectively. Since there are no explicit measurements of transmural propagation velocity in the mouse heart, we assumed that this value is close to the measured minimal velocity, 0.36 m/s, measured for larger animals where transmural velocity varies from 0.33 to 0.41 m/s (47, 48, 73).
For the isolated myocytes, Istim was 60 pA/pF. In all cases, the stimulus pulse duration was equal to 0.5 ms. The amplitude of the stimulus current Istim,i for 2-D tissue was varied from 180 to 2,000 pA/pF to be equal approximately to 150% of the threshold value, depending on the intercellular conductance. Stimulation protocols will be described in detail in the text or in the figure legends. Inhomogeneous 2-D tissues consist of 65 columns of epicardial and 65 columns of endocardial cells. We also used the approximation that all conduction delay occurs at the gap junctions. This approximation was validated for model multicellular cardiac tissue in the detailed study of Shaw and Rudy (61).
Model equations were solved by a fourth-order Runge-Kutta method, with a time step of 0.0001 ms. Steady-state initial conditions were obtained by running the models until changes in all variables did not exceed 0.01%. The AP of the single ventricular myocyte, voltage-clamp experiments, and bifurcation diagrams were simulated on single processor (3.2 GHz Intel Xeon “Irwindale”). Thirty-six processors were used to simulate 2-D model activity: one of them was used for data input-output, and the remaining 35 processors performed numerical simulations, 260 model myocytes on each processor.
RESULTS
Models of AP and Ca2+ handling in epicardial and endocardial ventricular myocytes.
In this study, we developed models for epicardial and endocardial mouse ventricular myocytes. These models used our previously published model of the mouse apical ventricular myocyte (6) as a starting point. There are five major differences between epicardial and endocardial cells: 1) APD is longer in endocardial and shorter in epicardial myocytes; 2) diastolic and systolic [Ca2+]i and [Ca2+]i transients are higher in paced endocardial and lower in epicardial myocytes; 3) Ca2+ release rate is about two times larger in endocardial than in epicardial myocytes; 4) Na+/Ca2+ exchanger rate is greater in epicardial than in endocardial myocytes (18); and 5) epicardial and endocardial cell have different conductances for IKto,f, IKur, and IKss (8).
Simulated APs from epicardial and endocardial myocytes and the corresponding major repolarization currents are shown in Fig. 4. As expected from voltage-clamp data of K+ currents, the APD for the model epicardial cell is shorter than that for the endocardial cell [APD at 50% of repolarization (APD50) is equal to 3.7 and 5.4 ms, for epicardial and endocardial cells, respectively, Table 2]. Simulations of the time course of the major repolarization currents (Fig. 4, B and C) demonstrate that significantly larger outward K+ currents in epicardial myocytes produce a smaller APD. These data correspond reasonably well to the experimental APD50 that range from 2.6 to 6.2 for epicardial and from 4.5 to 9.9 ms for endocardial myocytes, respectively (Refs. 2, 8, 32, and Table 2). Similarly, simulated values for APD at 90% of repolarization (APD90) are close to the experimental values for isolated cardiac myocytes (8); however, they are somewhat smaller than the APD90 obtained from the mouse left ventricular tissues (2, 32). Such relative APD prolongation in cardiac tissue was also noted previously and may be due to reduced K+ repolarization currents (4). Other possibilities include difficulties associated with measuring APD90 under different experimental conditions (2, 8, 32).
Table 2.
Experimental and simulated APDs for epicardial and endocardial mouse ventricular myocytes
| Simulation | Ref. 2 | Ref. 32 | Ref. 8 | |
|---|---|---|---|---|
| Epicardial cell | ||||
| APD30, ms | 2.2 | 3.6 ± 0.9 | ||
| APD50, ms | 3.7 | 3 ± 0.3 | 6.2 ± 1.9 | 2.6 ± 0.1 |
| APD70, ms | 7.7 | 10 ± 1 | 32 ± 10 | |
| APD90, ms | 14.8 | 36 ± 3 | 61 ± 12 | 15.8 ± 2.5 |
| Endocardial cell | ||||
| APD30, ms | 3.0 | 6.2 ± 1.0 | ||
| APD50, ms | 5.4 | 8 ± 0.4 | 9.9 ± 2.1 | 4.5 ± 0.7 |
| APD70, ms | 11.7 | 15 ± 0.7 | 32 ± 8 | |
| APD90, ms | 22.2 | 37 ± 3 | 62 ± 9.1 | 18.0 ± 2.8 |
Values are means ± SE. APD30, APD50, APD70, APD90, action potential duration at 30%, 50%, 70%, and 90% of repolarization, respectively.
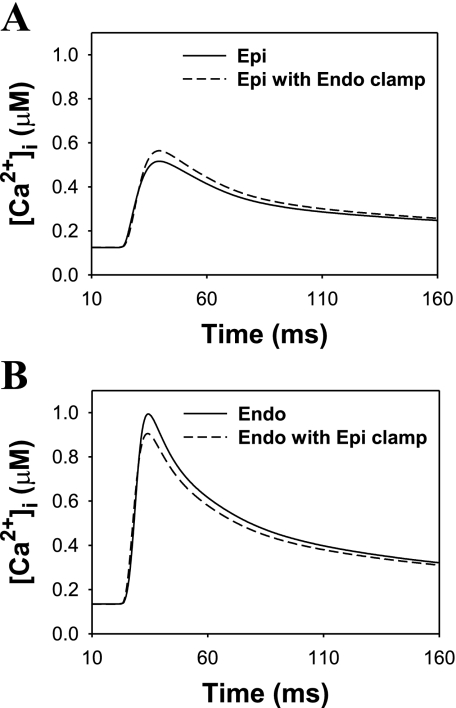
To evaluate the relative contribution of AP waveform into [Ca2+]i, Dilly et al. (18) depolarized epicardial and endocardial ventricular myocytes with the stored endocardial and epicardial waveforms, respectively, with a stimulation frequency of 1 Hz. If the differences in [Ca2+]i were due exclusively to AP waveform, then [Ca2+]i transients of epicardial cell stimulated with endocardial AP waveform would resemble that of an endocardial cell. Similarly, [Ca2+]i transients of endocardial cell stimulated with an epicardial AP waveform would resemble that of an epicardial cell. Dilly et al. (18) found that this was not the case. While AP waveform contributed to the changes in [Ca2+]i transients, these changes were relatively small. We also stimulated epicardial and endocardial model cells with endocardial and epicardial AP waveforms, respectively, with a basic cycle length (BCL) of 1,000 ms. Simulation results shown in Fig. 5 demonstrated small changes in peak [Ca2+]i in clamped epicardial and endocardial myocytes. Simulated peak [Ca2+]i obtained from the epicardial cell model alone and from the epicardial cell model stimulated with endocardial AP waveform (Endo clamp) were 0.516 and 0.564 μM, respectively. These values were comparable with the experimental peak [Ca2+]i obtained for epicardial myocytes, 0.478 ± 0.078 and 0.707 ± 0.059 μM, respectively (18). Simulated peak [Ca2+]i obtained from the endocardial cell model alone and from the endocardial cell model stimulated with an epicardial AP waveform (Epi clamp) were 0.996 and 0.906 μM, respectively; they are close to the corresponding experimental values 0.886 ± 0.078 and ∼0.8 μM (18). Thus our simulations and the experimental data (18) show that the AP waveforms contribute to, but do not account for differences in, [Ca2+]i transients between epicardial and endocardial ventricular myocytes. The major contribution was due to differences in Ca2+ handling systems of these two myocyte types (18).
Fig. 5.
Simulated intracellular Ca2+ transients for the epicardial (A) and endocardial (B) cells. Pacing frequency was 1 Hz. A: [Ca2+]i transients in epicardial cell induced by epicardial AP (solid line) and by endocardial AP clamp (dashed line). B: [Ca2+]i transients in endocardial cell induced by endocardial AP (solid line) and by epicardial AP clamp (dashed line). The data show the contribution of AP shape into differences between [Ca2+]i transients in epicardial and endocardial cells.
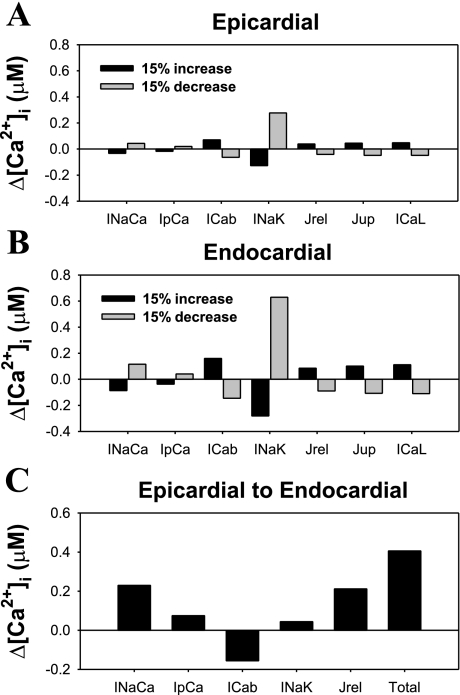
To determine the mechanisms underlying the differences in [Ca2+]i transients between epicardial and endocardial cells, we performed a sensitivity analysis, i.e., dependence of [Ca2+]i transients on changes in INaCa, Ip(Ca), the Na+/K+ pump (INaK) rates, background Ca2+ current (ICab), or ICaL, amplitudes, ryanodine release channel density (Jrel), or increased sarcoplasmic reticulum (SR) Ca2+ pump activity (Jup) (54, 64). We simulated changes in [Ca2+]i transients in response to a 15% increase and a 15% decrease in one of the components of the Ca2+ handling system (Fig. 6). In the myocyte model (epicardial or endocardial), we first increased (or decreased) one of the components of the Ca2+ handling system and then ran the perturbed model until steady state was achieved without stimulation. The myocyte model was then stimulated with a BCL of 1,000 ms, and the steady-state [Ca2+]i transient amplitude was calculated as the difference between its systolic and diastolic values. The difference between this [Ca2+]i amplitude and the [Ca2+]i amplitude for control epicardial or endocardial myocyte was plotted in Fig. 6, A and B. [Ca2+]i transient amplitudes are most sensitive to changes in Na+-K+ pump or Na+/Ca2+ exchanger activity, or ICab amplitude. However, a smaller but nonetheless significant contribution to changes in [Ca2+]i occurs in response to the variation of Ca2+ release or uptake rates or by changes in amplitude of ICaL.
Fig. 6.
Sensitivity analysis of epicardial and endocardial model cells and contribution of key elements of Ca2+ handling system to differences in [Ca2+]i transients in epicardial and endocardial myocytes. A: changes in the amplitude of [Ca2+]i transients (Δ[Ca2+]i) in response to a 15% increase (black bars) or a 15% decrease (gray bars) of the indicated current or Ca2+ flux for epicardial cell. B: same as in A for endocardial cell. C: changes in the amplitude of [Ca2+]i transients in epicardial model cell when the indicated model current (Ca2+ flux) changed its value to that corresponding to the endocardial model cell. Total increase in the amplitude of [Ca2+]i transient (“Total” bar) is close to the sum of partial contributions from the currents and a flux changed.
To evaluate the absolute contribution of the particular component of the Ca2+ handling system to the difference in [Ca2+]i between the two myocyte types, we also calculated Δ[Ca2+]i for the epicardial cell when INaCa, Ip(Ca), ICab, INaK, or Jrel was changed from its epicardial to endocardial value (Fig. 6C). Our finding shows that there are three major players that are responsible for the difference: INaCa, ICab, and Ca2+ release rate from the SR (Jrel). The total increase in [Ca2+]i (“Total” bar in Fig. 6C) is equal to the sum of partial changes resulted from the changes of INaCa, Ip(Ca), ICab, INaK, and Jrel plus the contribution of Δ[Ca2+]i from the difference in APD between the two myocyte types (0.406 μM + 0.048 μM = 0.454 μM). This value is close to the Δ[Ca2+]i between epicardial and endocardial myocytes (0.470 μM). The result of this analysis suggests that each component of Ca2+ handling in the mouse ventricular myocyte contributes to the change in [Ca2+]i in a nearly additive fashion relative to the changes in the other components, at least near its normal operating point.
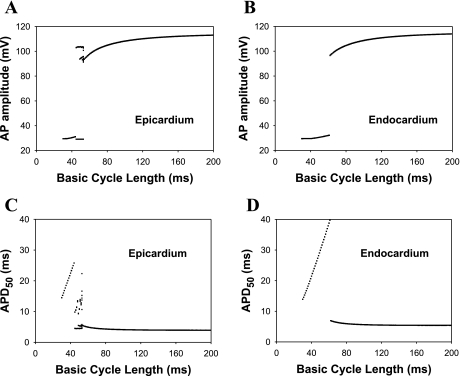
Epicardial and endocardial ventricular myocytes also showed different responses to changes in stimulation rate. Figure 7 shows AP amplitudes and APD50 for the epicardial and endocardial myocyte models as functions of the BCLs for the same stimulus amplitude Istim = 60.0 pA/pF (τstim = 0.5 ms). The AP amplitudes and APD50 were calculated after 48 s of stimulations over a 2-s time interval. The epicardial cell model showed a cascade of bifurcations in AP amplitude and APD50 with a decrease in BCL (Fig. 7, A and C). First, periodic activity became irregular when the BCL decreased from 54 to 53 ms. At a BCL of 52 ms, this chaotic activity was replaced by APs with four different APD50, i.e., period 4 locking. Further decreasing BCL to 51 and 48 ms yielded activities with three and two different APD50, respectively. Finally, at a BCL of 44 ms, the model epicardial cell failed to generate full-scale APs at all. Interestingly, this cascade of bifurcations for APD50 was accompanied by the same bifurcation scenario for [Ca2+]i, with identical BCLs for the transition from one type of activity to another. In contrast, the endocardial myocyte model showed only a single transition from periodic full-scale APs to low-amplitude perturbations of the membrane potential at a BCL of 61 ms (Fig. 7, B and D).
Fig. 7.
Simulated frequency dependence (bifurcation diagrams) of AP amplitude (A and B) and AP duration (APD) at 50% of repolarization (APD50; C and D) for epicardial (A and C) and endocardial (B and D) ventricular myocytes. BCL as a bifurcation parameter was varied from 30 to 200 ms. The bifurcation diagrams for epicardial cells show complex behavior when the pacing frequency increases.
A distinctive and unusual property of mouse ventricular AP restitution is an increase in APD at the early stages of repolarization (APD at 30% of repolarization) when BCL decreases (34). Our model was able to reproduce this feature for the both myocyte types. As seen from Fig. 7, C and D, the APD50 increases gradually with the shortening BCL. Eventually, this trend is terminated in the epicardial cell when it starts to bifurcate and show complex behavior. In contrast, the increase in APD50 is terminated by a sharp decrease in endocardial cells. In addition, the amplitude of AP in both myocyte types gradually decreases when APD50 increases. The longer APD50 values at faster pacing rates are related to the recovery of major repolarization K+ currents in mouse ventricular myocytes (4). During a shorter BCL, the K+ currents do not recover completely and become decreased in amplitude. This causes the prolongation of APD50. The decrease of AP amplitude (Fig. 7, A and B) is due to the incomplete recovery of the Na+ current (4). The last effect is also observed experimentally (34).
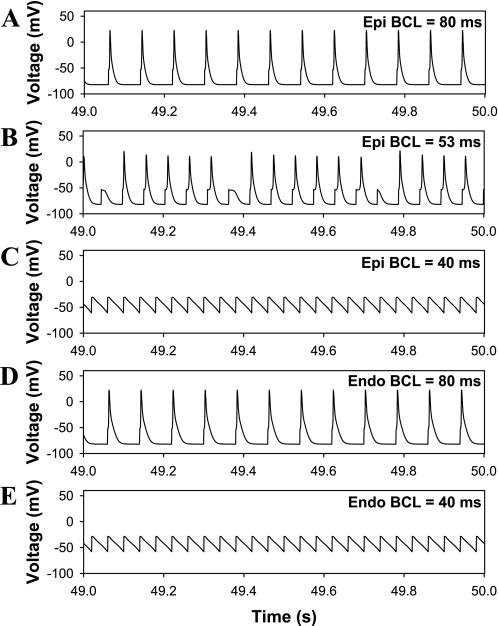
Figure 8 shows the time dependence of the membrane potential for epicardial (Fig. 8, A–C) and endocardial (Fig. 8, D and E) myocytes. At a relatively long BCL of 80 ms, both cells demonstrate full-scale APs (Fig. 8, A and D). Epicardial cells have an interval of BCLs with irregular AP; the time-dependent behavior of one of them is shown in Fig. 8B. At relatively fast pacing rates with a BCL of 40 ms, both cells are unable to generate full-scale APs but only low-amplitude APs (Fig. 8, C and E). Such low-amplitude APs differ from the full-scale AP by considerably smaller excitatory currents that are unable to overcome the activation barrier for a full-scale AP but still maintain depolarization and by relatively small repolarization currents, such as IKto,f and IKur, which are active but need a longer time to cause repolarization. Such low-amplitude APs with increased depolarization can potentially be proarrhythmic for cardiac tissue.
Fig. 8.
Simulated APs: expansions of the action potentials corresponding to critical regions of Fig. 7. A–C: epicardial myocytes. D and E: endocardial myocytes. A and D: BCL = 80 ms. C and E: BCL = 40 ms. B: irregular APs from epicardial cells stimulated with a BCL of 53 ms.
Transmural gradients of repolarization and [Ca2+]i transients in heterogeneous mouse ventricular tissue.
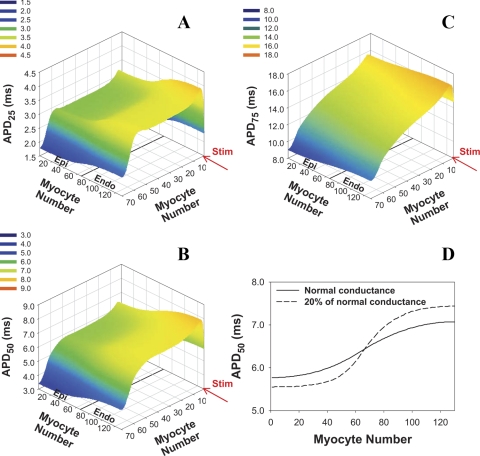
We used our new models to investigate AP propagation and stability in a 2-D cardiac tissue model designed to mimic the transmural heterogeneity described for the ventricular wall of the mouse heart. Figure 9 shows a simulated distribution of APDs at 25%, 50%, and 75% of repolarization across the mouse ventricular wall. The APs in cardiac tissue are more prolonged than those for isolated epicardial and endocardial myocytes, consistent with experimental observations (2, 8, 32). Despite the small thickness of the ventricular wall in the mouse heart (∼1.6 mm), there is a predicted transmural gradient of repolarization at levels of 25% and 50% that is predominantly defined by the cellular properties. However, at 75% of repolarization, the gradient is mainly determined by the site of stimulation. This gradient is regulated by intercellular coupling (Fig. 9D): the reduction of transmural conductances increased the differences in APDs between epicardial and endocardial regions.
Fig. 9.
APDs in 2-D model of transmurally heterogeneous tissue. Model tissue consists of 9,100 cells (130 columns, 70 cells in each column), 65 columns contain epicardial cells (columns 1–65), and 65 columns contain endocardial cells (columns 66–130). Stimulus (Istim = 900 pA/pF, τstim = 0.5 ms, shown by red arrow) is applied for the first row with pacing frequency of 4 Hz. APDs were determined after 16 stimuli. A: APD at 25% of repolarization (APD25). B: APD50. C: APD at 75% of repolarization (APD75). D: transmural distribution of APD50 in row 35 of the 2-D tissue with normal intercellular conductances (ggap,l = 25 nS/pF, ggap,tr = 500 nS/pF, solid line) and with intercellular conductances reduced by factor 5 (dashed line).
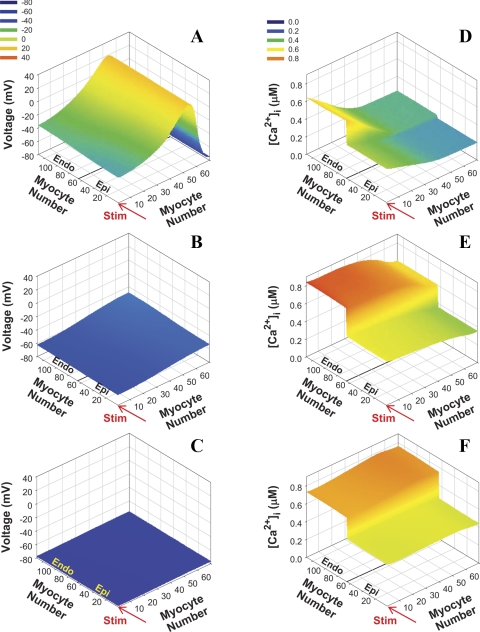
The small dimensions of the mouse heart and short APDs lead to some peculiarities in AP propagation and excitation-contraction coupling. One of them is that the [Ca2+]i transient is very delayed relative to the AP both in experiments and in our simulations (6, 49, 60). Figure 10 shows snapshots of AP and [Ca2+]i in 2-D transmurally heterogeneous tissue at three time points (10, 20, and 30 ms after Istim). The AP waveform at 10 ms showed a heterogeneity of repolarization with a relatively smooth transition from the epicardial to the endocardial region (Fig. 10A). The AP had already passed through the whole mouse ventricular tissue by 10 ms, whereas [Ca2+]i was still on the rising phase in the region of tissue experiencing the earliest excitation (Fig. 10D). By 30 ms, when repolarization is complete (Fig. 10C), we observed a maximum in simulated [Ca2+]i transients and significant differences in the magnitudes between epicardial and endocardial regions (Fig. 10F). Unlike the membrane potential, [Ca2+]i showed a relatively sharp transition between the two myocyte types and was determined predominantly by differences in Ca2+ handling mechanisms such as differences in SR Ca2+ load, Ca2+ extrusion rate, and the Ca2+ release rate, however, with some modulation by APD. Such differences are important for the stability of [Ca2+]i transients.
Fig. 10.
2-D plots of APs and [Ca2+]i transients in transmurally heterogeneous model tissue with normal conductances at different times after the stimulation was applied. Stimulation (Istim = 900 pA/pF, τstim = 0.5 ms) is applied to the first row with pacing frequency 4 Hz (shown by red arrows). Data are shown for 16th stimulus. A–C: APs. D–F: [Ca2+]i transients. A and D: 10 ms after stimulus. B and E: 20 ms after stimulus. C and F: 30 ms after stimulus. Note that all cells show maximal [Ca2+]i transients in the whole tissue simultaneously (F).
Stability of AP and [Ca2+]i transients in heterogeneous mouse ventricular tissue.
To investigate the stability of AP propagation and [Ca2+]i transients, we paced inhomogeneous 2-D model tissues with different BCLs. One set of simulations was with control intercellular conductances, ggap,x = 500 nS/pF and ggap,y = 25 nS/pF, and the second was where the intercellular conductances were reduced by factor 5 (ggap,x = 100 nS/pF, and ggap,y = 5 nS/pF). The two tissues, as well as isolated cardiac myocytes, demonstrated different susceptibilities to rapid pacing (Table 3). Epicardial myocytes showed a transition to irregular behavior of both APs and [Ca2+]i transients near threshold BCL, but endocardial cells failed to generate full-scale AP and [Ca2+]i below the threshold BCL. The threshold pacing rates in multicellular simulations were different (Table 3). When epicardial and endocardial myocytes were connected into inhomogeneous 2-D tissue, the thresholds for the instabilities of AP and [Ca2+]i transients in the tissue became different (Table 3). Alternans in [Ca2+]i transients appeared at relatively slower pacing rates (74 ms for normal and 76 ms for reduced conductances, respectively). APs during these stimulations do not show significant changes. However, when the BCLs were reduced to 64 and 67 ms for normal tissue and tissue with lowered conductances, respectively, the APs became unstable and demonstrated irregular behavior (Table 3).
Table 3.
Threshold basic cycle lengths for instability of AP and [Ca2+]i transients in 2-D transmurally inhomogeneous mouse cardiac tissue and isolated ventricular myocytes
| AP Instability Type and Threshold |
[Ca2+]i Instability Type and Threshold |
|||
|---|---|---|---|---|
| Object | Normal conductance, ms | Conductance reduced by factor 5, ms | Normal conductance, ms | Conductance reduced by factor 5, ms |
| Isolated epicardial myocyte | 53 (irregular AP) | 53 (irregular [Ca2+]i transients) | ||
| Isolated endocardial myocyte | 61 (low-amplitude AP) | 61 (no Ca2+ release) | ||
| Inhomogeneous 2-D cardiac tissue | 64 (irregular AP) | 67 (irregular AP) | 74 ([Ca2+]i alternans) | 76 ([Ca2+]i alternans) |
Irregular action potentials (APs) refer to generation of full-scale and low-amplitude APs with APDs that change irregularly. Low-amplitude APs have upstrokes that are predominantly determined by the stimulus current and which show delayed and incomplete repolarization. Generation of the low-amplitude APs is due to significant inactivation of the major ionic currents during rapid pacing. [Ca2+]i, intracellular Ca2+ concentration; 2-D, two-dimensional.
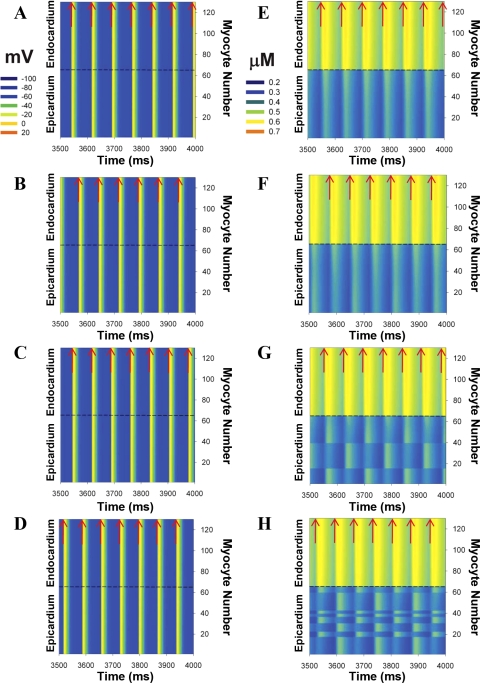
The spatiotemporal development of [Ca2+]i alternans and corresponding behavior of APs are shown in Fig. 11 for row 35 in 2-D tissue with normal conductances (ggap,x = 500 nS/pF, and ggap,y = 25 nS/pF). At relatively long BCLs (≥75 ms), both APs and [Ca2+]i transients demonstrated periodic behavior (Fig. 11, A and E). A reduction of the BCL to 74 ms resulted in the appearance of [Ca2+]i alternans in the epicardial zone only, whereas the corresponding APs did not show significant changes (Fig. 11, B and F). The alternans are in phase in a whole epicardium. A further decrease in BCL to 72 ms also produced spatial differences in [Ca2+]i alternans, when the epicardium was divided into three clusters of cells within which [Ca2+]i transients oscillate in the same phase (Fig. 11G). However, the neighboring clusters of cells show the maxima and minima of [Ca2+]i in different stimulus cycles. At a smaller BCL of 70 ms, the number of such clusters increases and they create an irregular structure in the epicardium (Fig. 11H). Thus changes in the pacing rate resulted in the development of spatiotemporal [Ca2+]i alternans in multicellular cardiac tissue, which increased in complexity as the BCL decreased. It is interesting that the APs both in the epicardium and in the endocardium do not show a significant deviation from the periodic behavior at the same pacing rates (Fig. 11, A–D).
Fig. 11.
Spatiotemporal organization of APs (A–D) and [Ca2+]i transients (E–H) in row 35 of 2-D model of the mouse inhomogeneous multicellular cardiac tissue, consisting of 65 epicardial and 65 endocardial myocytes. Stimulus currents (Istim = 900 pA/pF, τstim = 0.5 ms) were applied at pacing periods of 75 (A and E), 74 (B and F), 72 (C and G), and 70 (D and H) ms to row 1. Red arrows show time moments at which stimuli were applied. Intercellular connection strengths ggap,x = 500 nS/pF and ggap,y = 25 nS/pF in transmural and longitudinal directions, respectively.
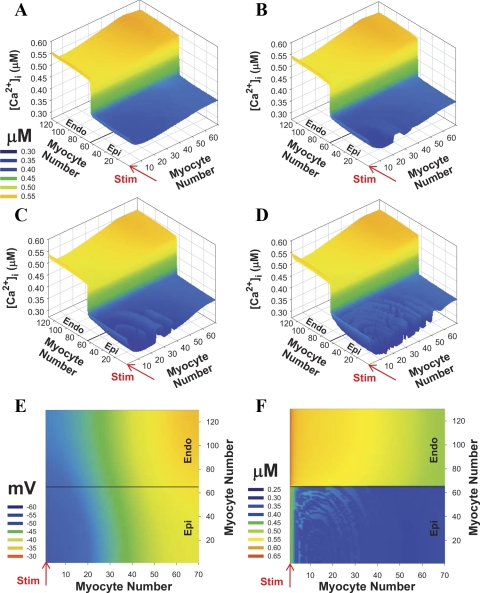
The spatial distributions of [Ca2+]i transients in 2-D transmurally inhomogeneous tissue at different pacing BCLs were particularly interesting. Figure 12, A–D, shows snapshots of simulated [Ca2+]i transients at 40 ms after the stimulus current was applied. At a BCL of 76 ms, [Ca2+]i showed different amplitudes in epicardial and endocardial regions, but without complex spatial structure, except for slightly larger values at the site of stimulation (Fig. 12A, row 1). During faster stimulation with a BCL of 74 ms (Fig. 12B), [Ca2+]i in the epicardial half demonstrated spatial (or discordant) alternans, in which two neighboring regions oscillate in opposite phases. Further decreasing BCL to 72 and 70 ms led to more complex curved spatial transmural structures of [Ca2+]i transients (Fig. 12, C and D). This spatial structure tends to center on the region near the site of the stimulation where the magnitude of [Ca2+]i is the smallest, and the structure did not appear in the endocardial region where [Ca2+]i transients were larger (Fig. 12, B and C).
Fig. 12.
[Ca2+]i transient alternans in transmurally heterogeneous 2-D model tissue with normal conductances at different BCLs. Stimulation (Istim = 900 pA/pF, τstim = 0.5 ms) is applied for the first row (shown by red arrows). A–D: three-dimensional view of [Ca2+]i transient alternans at 40 ms after stimulus was applied. A: BCL = 76 ms. B: BCL = 74 ms. C: BCL = 72 ms. D: BCL = 70 ms. E and F: 2-D view of AP and [Ca2+]i transients at BCL = 70 ms and at 20 ms after stimulus was applied. Data are obtained after at least 50 stimuli.
To elucidate the mechanism of this transmural inhomogeneity of [Ca2+]i, we analyzed the spatial structure of AP amplitude and the duration along with [Ca2+]i transients (Figs. 9A and 12, E and F) based on the results of our previous study related to the stability of Ca2+ handling in mouse ventricular myocytes (4). The spatial distribution of the membrane potentials and APD at 25% of repolarization showed a gradient between epicardial and endocardial regions and within epicardial region itself (Figs. 9A and 12E). In the endocardial region, where [Ca2+]i values are relatively large, they produced stable ryanodine receptor gating and Ca2+-induced Ca2+ release from the SR (4). In the epicardial region, the Ca2+ release became unstable at small BCLs because of the smaller amount of released Ca2+ and shorter APD, compared with the endocardial region (Figs. 3 and 5). The Ca2+-induced Ca2+ release magnitude is determined by cellular mechanisms (there are no longitudinal Ca2+ fluxes between cardiac myocytes in the tissue) and by the Ca2+ influx through L-type Ca2+ channels, which are modulated by APD. Because the APD showed a spatial curvilinear structure in the epicardial region of the tissue (Figs. 9A and 12E), it modulated Ca2+ influx, Ca2+ release, and ultimately [Ca2+]i transients and their stability to the same degree along these curves (compare Fig. 12E and Fig. 12F). As result, a complex transmurally inhomogeneous spatial structure of [Ca2+]i transients emerged (Fig. 12F).
DISCUSSION
Differences in APs and Ca2+ handling in isolated epicardial and endocardial ventricular myocytes.
The diverse range of ventricular myocyte models reflects in large part the diversity of the different species (9, 13, 57). They are distinct in AP shape and duration, set of repolarization currents, and Ca2+ handling and reflect in part the different constraints imposed by size on cardiac function. Mouse ventricular myocytes are at the extreme end of the spectrum because of the very short APDs they generate. These short APs reflect the magnitude and types of repolarization currents (8, 26). There is further diversity in the different APs and ionic current densities in cells from different regions of the mouse heart as well (8, 74).
Ionic channel heterogeneity may be critical to the timing and spread of repolarization. Previously, we developed models of mouse ventricular myocytes from the apical and septal regions of the heart (6). Apical ventricular myocytes predominantly express Kv4 and Kv1.5 channels that encode the largest IKto,f, and IKur, IKto,f, and IKur define short apical APD50 of 4.0 ms (6, 74). In septal ventricular myocytes, the magnitude of IKto,f is considerably smaller than in apical myocytes that lead to the prolongation of APD (APD50 = 7.6 ms). These differences in repolarization led to functionally significant effects on the spatial distribution of refractoriness and Ca2+ transients from septum to apex. Similarly, IKto,f and IKur are larger in mouse epicardial than in endocardial ventricular myocytes, which manifest in shorter epicardial APD50 of 3.7 ms compared with endocardial APD50 of 5.4 ms (Table 2, Fig. 4, and Ref. 8). However, the magnitude and functional significance of such differences have not been clear.
It may seem surprising that abrupt discontinuities in AP properties occurred in the bifurcation analysis of the different cell types. However, such discontinuities are predicted because of the “all or none” threshold nature of full-scale AP generation. There have been relatively few attempts to reproduce such diagrams in living heart cells or tissues (see, for example, review in Ref. 5). The study of sheep and canine Purkinje fiber AP dynamics by Chialvo et al. (11) also shows small-amplitude APs and abrupt discontinuities in behavior. Thus the abrupt discontinuities are predictions that are consistent with observations in other species.
The small-amplitude electrical activity in Figs. 7 and 8 is not, properly speaking, an AP. The “upstroke” is predominantly due to the stimulus, but the repolarizing response is not a simple passive decay; inward and outward currents are both active, resulting in the slow repolarization, which fails to completely repolarize before the next stimulus. Such states can potentially be achieved during high-frequency stimulation of isolated cells or pathophysiologically during tachycardia in the heart, in which a repetitive stimulated region of tissue may become depolarized and “undulate” in response to electrotonic current flow (10, 62). This is also qualitatively similar to consistent stimulation during an EAD or with the development of reentrant arrhythmias because of programmed stimulation.
Two major functionally distinct regions are usually described for the transmural structure of the mouse ventricle, epicardium and endocardium. These differences arise from differential expression of not only K+ currents but also distinct Ca2+ handling (2, 8, 18, 32). In contrast, larger species have been described with a more complex structure of the ventricular wall that includes epicardial, endocardial, and midmyocardial layers (1, 19, 63). The mouse heart may also have these three distinct layers, but the resolution of these layers may lie beyond current experimental resolution.
Transmural heterogeneity of Ca2+ handling in the heart is less studied than the differences in AP and repolarization currents. However, regional differences in [Ca2+]i transients, ryanodine receptor, sarco(endo)plasmic reticulum Ca2+-ATPase (SERCA) pump, and Na+/Ca+ exchanger expression have been reported between epicardial and endocardial cells in different species (15, 18, 36). Several factors determine the magnitude of [Ca2+]i transients, such as APD, SR load, SR release rate, and SERCA pump activity. Our simulations for mouse ventricular myocytes show that the longer APD in endocardial cells slightly contributes to [Ca2+]i; however, the major contributing factors are about twofold larger SR release and slower Ca2+ extrusion by INaCa in endocardial cells compared with epicardial cells. The last contributes to an increase in [Ca2+]i transient through an increased SR Ca2+ load, resulting from the slower Ca2+ extrusion from the cell (20, 21, 66). The contributions of APD, Na+/Ca2+ exchanger rate, and Ca2+ release rate into [Ca2+]i transient magnitudes in mouse ventricular myocytes are similar to those determined experimentally (18). SR load is also larger in endocardial than in epicardial cells during pacing, both in experiments (18) and our simulations, in particular, at rapid pacing rates. Smaller SR load and larger Na+/Ca+ exchanger expression in epicardial than endocardial ventricular myocytes were also described for rats (23).
The mouse cellular models, therefore, are qualitatively similar in diversity to larger species, such as canine, where differences were observed in SERCA pump expression and activity, which were larger in the epicardial ventricular myocytes. However, no differences were found in ICaL and [Ca2+]i transient magnitudes and Na+/Ca+ exchanger expression (15, 36, 37) although a separate study (69) measured significantly larger ICaL in endocardial canine cells. Thus it is unclear to what extent heterogeneity in the Ca2+ handling systems in mice are analogous to those found in larger animals.
Transmural heterogeneity of repolarization in ventricular tissue.
Experimental data from the mouse hearts and from the hearts of other species show that the transmural heterogeneity of repolarization and Ca2+ handling is maintained in ventricular tissues (2, 16, 32, 36). The heterogeneity of repolarization and Ca2+ handling was also predicted by our simulation in the 2-D model of the mouse ventricular wall despite the very small wall thickness (about 1.6 mm) and is consistent with our previous simulations for apical and septal cell types (4). This is a critical point of contention since simulations of APs in the whole mouse heart using a model based on a modified rat AP did not predict significant transmural gradients of repolarization (59).
Electrotonic interactions are important in the mouse heart. Our simulations showed a prolongation of APD in ventricular myocytes in the propagating tissue model compared with isolated cells (Figs. 4 and 9). Experimentally, longer APDs were reported in mouse ventricles compared with isolated ventricular myocytes (2, 8, 32). Despite significant electrotonic interactions, both experimental data and our simulations demonstrate the existence and potential functional importance of heterogeneity of repolarization across the mouse ventricular wall. This supports the point of view that the APD is determined predominantly by the intracellular ionic currents. Changes in expression of major repolarization currents across the ventricle, i.e., IKto,f and IKur, determine the AP shape and duration across the wall. While APD contributes to the magnitude of [Ca2+]i transients, this contribution was not sufficient to account for the large differences in Ca2+ handling between epicardial and endocardial cells. Unlike APs, the sharp transition region for [Ca2+]i transients is maintained in simulated 2-D cardiac tissue (Figs. 9 and 10), and it is only weakly modulated by a relatively smooth transition for APs across the wall.
This weak modulation by electrotonic forces in an inhomogeneous cellular environment can influence cellular Ca2+ handling especially when integrated over several cycles. By influencing repolarization morphology and duration, Ca2+ entry and extrusion can be altered. This is particularly important at fast pacing rates and is predicted by our simulations to result in rate dependent Ca2+ instabilities arising out of heterogeneity.
The transmural distribution of [Ca2+]i transients in the mouse ventricle has not been reported. However, transmural [Ca2+]i transients have been investigated for the hearts of the other species (22, 36). Laurita et al. (36) concluded that the transmural heterogeneity of Ca2+ handling is most likely an intrinsic property of the cell, which is similar to the mechanism demonstrated in our simulations. In rats, [Ca2+]i transients across the ventricular wall had peak systolic and diastolic [Ca2+]i that were larger in paced endocardium than in epicardium (22). However, the magnitude of [Ca2+]i transients were similar, suggesting similar Ca2+ release rates in epicardial and endocardial rat myocytes. In mouse ventricular myocytes, the Ca2+ release rates differ by twofold and suggest larger [Ca2+]i transients in endocardial than in epicardial cells (18). However, the diastolic [Ca2+]i were larger in stimulated endocardial versus epicardial regions [both in rats and in mice (18, 22)], and these findings are matched by our simulations of paced 2-D mouse ventricular tissue.
Ca2+ alternans and stability of AP propagation in the 2-D model.
Our simulations of 2-D mouse ventricular tissue showed that the transmural heterogeneity of repolarization and Ca2+ handling can lead to different stability properties across the mouse ventricle. APs and [Ca2+]i transients in cardiac myocytes incorporated into a multicellular tissue demonstrated an increased susceptibility to instabilities and alternans compared with isolated myocytes (Table 3). Isolated epicardial and endocardial ventricular myocytes have the same threshold BCL for instability of both AP and [Ca2+]i, i.e., both Ca2+ and AP instabilities occurred concurrently in their respective cell types. However, when myocytes were connected in 2-D tissue, they developed [Ca2+]i alternans followed by AP instability with further reduction of BCL (Fig. 12, and Table 3). Ca2+ alternans first appeared in the epicardial region of the tissue where APD and [Ca2+]i transients are smaller because of instability of Ca2+ handling at the cellular level that was perturbed by electrotonic interactions (4). The fivefold reduction of intercellular conductances increased susceptibility to the alternans when paced with the same stimulus. This increase in threshold BCL for Ca2+ alternans was due to the increase in gradient of repolarization in 2-D tissue with the reduced intercellular coupling (Fig. 9D).
Our simulations of the relationship between cell-to-cell coupling and susceptibility to alternans are supported in part by experimental data on alternans of [Ca2+]i transients in rats and TNF-α transgenic mice (17, 38). Rat hearts that have had partial ryanodine-sensitive release inhibition show increased instability in Ca2+ transients (17). The phenotype of TNF-α-overexpressing transgenic mice is characterized by a more prolonged AP, smaller magnitude [Ca2+]i transients, and slower Ca2+ sequestration into the SR compared with wild-type littermates (38). In TNF-α mice, rapid heart pacing yielded significantly smaller conduction velocities and larger susceptibility to Ca2+ alternans compared with wild-type mice (38). Our simulations predict qualitatively similar results in the 2-D tissue with reduced conductances (smaller AP propagation velocity). Our simulations also show that Ca2+ alternans appears in a region with smaller [Ca2+]i transients (Fig. 12). While other contributions to the proarrhythmic behavior in the hearts from TNF-α mice play a role, our simulations are consistent with these experiments and provide a plausible mechanism for the development of alternans because of impaired Ca2+ handling (see also Ref. 4).
This mechanism of Ca2+ alternans is different from that thought to commonly occur in the larger species, where Ca2+ overload is an important proarrhythmic condition (30, 36, 46, 51). In the larger species, APDs are much longer than those for the mice and rats. Consequently, [Ca2+]i transients and APs largely overlap in time, and APD and [Ca2+]i are regulated by the magnitude and inactivation of ICaL, which, in turn, depend on [Ca2+]i. In adult mice, APD is not affected by ICaL to the similar extent, as in species with more prolonged APDs, and ryanodine receptors are the major players for alternans development (4, 17). In neonatal mouse hearts, however, the duration of the AP is significantly larger and Ca2+ channel inactivation may play a role (71). In contrast, in canine cardiac muscle, ICaL significantly inactivates during long APD and in addition because of a larger [Ca2+]i transient (24). During the next AP, this results in smaller ICaL amplitude, smaller APD, and smaller Ca2+ release. In humans, the importance of Ca2+ channel inactivation is underscored by the rare disease, Timothy Syndrome, in which a defect in the voltage-dependent component of the L-type Ca2+ channel inactivation leads to profound QT prolongation, arrhythmias, and sudden cardiac death at a young age (65).
The development of Ca2+ alternans occurs both in time and in space, yielding concordant and discordant alternans (72), and has several underlying mechanisms for development (see recent review in Ref. 25). The simulations of epicardial and endocardial muscle show that the discordant Ca2+ alternans can form complex 2-D structure, both in the transmural and in the longitudinal directions in the mouse ventricle. The transmural 2-D structure of the discordant alternans is largely determined by the heterogeneity of AP repolarization (Fig. 12), since APD is an important factor in alternans development in mouse tissue (4). Our simulations show that the complex structures of repolarization and [Ca2+]i transients can appear through instabilities of AP generation and Ca2+ handling that have cellular origin and are modulated by the heterogeneities in cardiac channel expression.
GRANTS
This work was supported in part by National Heart, Lung, and Blood Institute Grant R01-HL-59526 and National Science Foundation Knowledge and Distributed Intelligence Grant DBI-9873173 (to R. L. Rasmusson); Pittsburgh Supercomputer Center Grant MCB010020P; and a seed grant from Brain and Behavior Program at Georgia State University (to V. E. Bondarenko).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
ACKNOWLEDGMENTS
This work was performed in part at the State University of New York's Buffalo's Center for Computational Research.
REFERENCES
- 1.Antzelevitch C, Shimizu W. Cellular mechanisms underlying the long QT syndrome. Curr Opin Cardiol 17: 43–51, 2002 [DOI] [PubMed] [Google Scholar]
- 2.Anumonwo JM, Tallini YN, Vetter FJ, Jalife J. Action potential characteristics and arrhythmogenic properties of the cardiac conduction system of the murine heart. Circ Res 89: 329–335, 2001 [DOI] [PubMed] [Google Scholar]
- 3.Bondarenko VE, Rasmusson RL. Re-entry in a multicellular model of mouse ventricle (Abstract). Biophys J 90: 547A, 2006 [Google Scholar]
- 4.Bondarenko VE, Rasmusson RL. Simulations of propagated mouse ventricular action potentials: effects of molecular heterogeneity. Am J Physiol Heart Circ Physiol 293: H1816–H1832, 2007 [DOI] [PubMed] [Google Scholar]
- 5.Bondarenko VE, Rasmusson RL. Suppression of cellular alternans in guinea pig ventricular myocytes with LQT2: insights from the Luo-Rudy model. Int J Bifurcat Chaos 17: 381–425, 2007 [Google Scholar]
- 6.Bondarenko VE, Szigeti GP, Bett GC, Kim SJ, Rasmusson RL. Computer model of action potential of mouse ventricular myocytes. Am J Physiol Heart Circ Physiol 287: H1378–H1403, 2004 [DOI] [PubMed] [Google Scholar]
- 7.Brouillette J, Clark RB, Giles WR, Ficet C. Functional properties of K+ currents in adult mouse ventricular myocytes. J Physiol 559: 777–798, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brunet S, Aimond F, Li H, Guo W, Eldstrom J, Fedida D, Yamada KA, Nerbonne JM. Heterogeneous expression of repolarizing, voltage-gated K+ currents in adult mouse ventricles. J Physiol 559: 103–120, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cabo C, Boyden PA. Heterogeneous gap junction remodeling stabilizes reentrant circuits in the epicardial border zone of the healing canine infarct: a computational study. Am J Physiol Heart Circ Physiol 291: H2606–H2616, 2006 [DOI] [PubMed] [Google Scholar]
- 10.Cerrone M, Noujaim SF, Tolkacheva EG, Talkachou A, O'Connell R, Berenfeld O, Anumonwo J, Pandit SV, Vikstrom K, Napolitano C, Priori SG, Jalife J. Arrhythmogenic mechanisms in a mouse model of catecholaminergic polymorphic ventricular tachycardia. Circ Res 101: 1039–1048, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chialvo DR, Gilmour RF, Jr, Jalife J. Low dimensional chaos in cardiac tissue. Nature 343: 653–657, 1990 [DOI] [PubMed] [Google Scholar]
- 12.Clark RB, Tremblay A, Melnyk P, Allen BG, Giles WR, Ficet C. T-tubule localization of the inward-rectifier K+ channel in mouse ventricular myocytes: a role in K+ accumulation. J Physiol 537: 979–992, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Clayton RH, Holden AV. Propagation of normal beats and re-entry in a computational model of ventricular cardiac tissue with regional differences in action potential shape and duration. Prog Biophys Mol Biol 85: 473–499, 2004 [DOI] [PubMed] [Google Scholar]
- 14.Collis LP, Meyers MB, Zhang J, Phoon CK, Sobie EA, Coetzee WA, Fishman GI. Expression of a sorcin missense mutation in the heart modulates excitation-contraction coupling. FASEB J 21: 475–487, 2007 [DOI] [PubMed] [Google Scholar]
- 15.Cordeiro JM, Greene L, Heilmann C, Antzelevitch D, Antzelevitch C. Transmural heterogeneity of calcium activity and mechanical function in the canine ventricle. Am J Physiol Heart Circ Physiol 286: H1471–H1479, 2004 [DOI] [PubMed] [Google Scholar]
- 16.Cordeiro JM, Malone JE, Di Diego JM, Scornik FS, Aistrup GL, Antzelevitch C, Wasserstrom JA. Cellular and subcellular alternans in canine left ventricle. Am J Physiol Heart Circ Physiol 293: H3506–H3516, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Diaz ME, Eisner DA, O'Neill SC. Depressed ryanodine receptor activity increases variability and duration of the systolic Ca2+ transient in rat ventricular myocytes. Circ Res 91: 585–593, 2002 [DOI] [PubMed] [Google Scholar]
- 18.Dilly KW, Rossow CF, Votaw VS, Meabon JS, Cabarrus JL, Santana LF. Mechanisms underlying variations in excitation-contraction coupling across the mouse left ventricular free wall. J Physiol 572: 227–241, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Drouin E, Charpentier F, Gauthier C, Laurent K, Le Marec H. Electrophysiologic characteristics of cells spanning the left ventricular wall of human heart: evidence for presence of M cells. J Am Coll Cardiol 26: 185–192, 1995 [DOI] [PubMed] [Google Scholar]
- 20.Eisner DA, Choi HS, Diaz ME, O'Neill SC, Trafford AW. Integrative analysis of calcium cycling in cardiac muscle. Circ Res 87: 1087–1094, 2000 [DOI] [PubMed] [Google Scholar]
- 21.Eisner DA, Trafford AW, Diaz ME, Overend CL, O'Neill SC. The control of Ca release from the cardiac sarcoplasmic reticulum: regulation versus autoregulation. Cardiovasc Res 38: 589–604, 1998 [DOI] [PubMed] [Google Scholar]
- 22.Figueredo VM, Brandes R, Weiner MW, Massie BM, Camacho SA. Endocardial versus epicardial differences of intracellular free calcium under normal and ischemic conditions in perfused rat hearts. Circ Res 72: 1082–1090, 1993 [DOI] [PubMed] [Google Scholar]
- 23.Fowler MR, Naz JR, Graham MD, Bru-Mercier G, Harrison SM, Orchard CH. Decreased Ca2+ extrusion via Na+/Ca2+ exchange in epicardial left ventricular myocytes during compensated hypertrophy. Am J Physiol Heart Circ Physiol 288: H2431–H2438, 2005 [DOI] [PubMed] [Google Scholar]
- 24.Fox JJ, McHarg JL, Gilmour RF., Jr Ionic mechanism of electrical alternans. Am J Physiol Heart Circ Physiol 282: H516–H530, 2002 [DOI] [PubMed] [Google Scholar]
- 25.Garfinkel A. Eight (or more) kinds of alternans. J Electrocardiol 40: S70–S74, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guo W, Xu H, London B, Nerbonne JM. Molecular basis of transient outward K+ current diversity in mouse ventricular myocytes. J Physiol 521: 587–599, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gutstein DE, Morley GE, Tamaddon H, Vaidya D, Schneider MD, Chen J, Chien KR, Stuhlmann H, Fishman GI. Conduction slowing and sudden arrhythmic death in mice with cardiac-restricted inactivation of connexin43. Circ Res 88: 333–339, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jiang Y, Pandya K, Smithies O, Hsu EW. Three-dimensional diffusion tensor microscopy of fixed mouse hearts. Magn Reson Med 52: 453–460, 2004 [DOI] [PubMed] [Google Scholar]
- 29.Jones LR, Suzuki YJ, Wang W, Kobayashi YM, Ramesh V, Franzini-Armstrong C, Cleemann L, Morad M. Regulation of Ca2+ signaling in transgenic mouse cardiac myocytes overexpressing calsequestrin. J Clin Invest 101: 1385–1393, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Katra RP, Oya T, Hoeker GS, Laurita KR. Ryanodine receptor dysfunction and triggered activity in the heart. Am J Physiol Heart Circ Physiol 292: H2144–H2151, 2007 [DOI] [PubMed] [Google Scholar]
- 31.Kim SJ, Yatani A, Vatner DE, Yamamoto S, Ishikawa Y, Wagner TE, Shannon RP, Kim YK, Takagi G, Asai K, Homcy CJ, Vatner SF. Differential regulation of inotropy and lusitropy in overexpressed Gsα myocytes through cAMP and Ca2+ channel pathways. J Clin Invest 103: 1089–1097, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Knollmann BC, Katchman AN, Franz MR. Monophasic action potential recordings from intact mouse heart: validation, regional heterogeneity, and relation to refractoriness. J Cardiovasc Electrophysiol 12: 1286–1294, 2001 [DOI] [PubMed] [Google Scholar]
- 33.Knollmann BC, Knollmann-Ritschel BE, Weissman NJ, Jones LR, Morad M. Remodelling of transgenic mice overexpressing calsequestrin. J Physiol 525: 483–498, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Knollmann BC, Schober T, Petersen AO, Sirenko SG, Franz MR. Action potential characterization in intact mouse heart: steady-state cycle length dependence and electrical restitution. Am J Physiol Heart Circ Physiol 292: H614–H621, 2007 [DOI] [PubMed] [Google Scholar]
- 35.Landeen LK, Dederko DA, Kondo CS, Hu BS, Aroonsakool N, Haga JH, Giles WR. Mechanisms of the negative inotropic effects of sphingosine-1-phosphate on adult mouse ventricular myocytes. Am J Physiol Heart Circ Physiol 294: H736–H749, 2008 [DOI] [PubMed] [Google Scholar]
- 36.Laurita KR, Katra R, Wible B, Wan X, Koo MH. Transmural heterogeneity of calcium handling in canine. Circ Res 92: 668–675, 2003 [DOI] [PubMed] [Google Scholar]
- 37.Li GR, Lau CP, Ducharme A, Tardif JC, Nattel S. Transmural action potential and ionic current remodeling in ventricles of failing canine hearts. Am J Physiol Heart Circ Physiol 283: H1031–H1041, 2002 [DOI] [PubMed] [Google Scholar]
- 38.London B, Baker LC, Lee JS, Shusterman V, Choi BR, Kubota T, McTiernan CF, Feldman AM, Salama G. Calcium-dependent arrhythmias in transgenic mice with heart failure. Am J Physiol Heart Circ Physiol 284: H431–H441, 2003 [DOI] [PubMed] [Google Scholar]
- 39.Luo CH, Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res 74: 1071–1096, 1994 [DOI] [PubMed] [Google Scholar]
- 40.Maier LS, Zhang T, Chen L, DeSantiago J, Brown JH, Bers DM. Transgenic CaMKIIδC overexpression uniquely alters cardiac myocyte Ca2+ handling: reduced SR Ca2+ load and activated SR Ca2+ release. Circ Res 92: 904–911, 2003 [DOI] [PubMed] [Google Scholar]
- 41.Masaki H, Sato Y, Luo W, Kranias EG, Yatani A. Phospholamban deficiency alters inactivation kinetics of L-type Ca2+ channels in mouse ventricular myocytes. Am J Physiol Heart Circ Physiol 272: H606–H612, 1997 [DOI] [PubMed] [Google Scholar]
- 42.Mørk HK, Sjaastad I, Sande JB, Periasamy M, Sejersted OM, Louch WE. Increased cardiomyocyte function and Ca2+ transients in mice during early congestive heart failure. J Mol Cell Cardiol 43: 177–186, 2007 [DOI] [PubMed] [Google Scholar]
- 43.Noble D, Sarai N, Noble PJ, Kobayashi T, Matsuoka S, Noma A. Resistance of cardiac cells to NCX knockout: a model study. Ann NY Acad Sci 1099: 306–309, 2007 [DOI] [PubMed] [Google Scholar]
- 44.Noujaim SF, Pandit SV, Berenfeld O, Vikstrom K, Cerrone M, Mironov S, Zugermayr M, Lopatin AN, Jalife J. Up-regulation of the inward rectifier K+ current (IK1) in the mouse heart accelerates and stabilizes rotors. J Physiol 578: 315–326, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Olsson MC, Palmer BM, Stauffer BL, Leinwand LA, Moore RL. Morphological and functional alterations in ventricular myocytes from male transgenic mice with hypertrophic cardiomyopathy. Circ Res 94: 201–207, 2004 [DOI] [PubMed] [Google Scholar]
- 46.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation 99: 1385–1394, 1999 [DOI] [PubMed] [Google Scholar]
- 47.Poelzing S, Akbar FG, Baron E, Rosenbaum DS. Heterogeneous connexin43 expression produces electrophysiological heterogeneities across ventricular wall. Am J Physiol Heart Circ Physiol 286: H2001–H2009, 2004 [DOI] [PubMed] [Google Scholar]
- 48.Poelsing S, Roth BJ, Rosenbaum DS. Optical measurements reveal nature of intercellular coupling across ventricular wall. Am J Physiol Heart Circ Physiol 289: H1428–H1435, 2005 [DOI] [PubMed] [Google Scholar]
- 49.Pott C, Philipson KD, Goldhaber JI. Excitation-contraction coupling in Na+-Ca2+ exchanger knockout mice. Reduced transsarcolemmal Ca2+ flux. Circ Res 97: 1288–1295, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pott C, Ren X, Tran DX, Yang MJ, Henderson S, Jordan MC, Roos KP, Garfinkel A, Philipson KD, Goldhaber JI. Mechanism of shortened action potential duration in Na+-Ca2+ exchanger knockout mice. Am J Physiol Cell Physiol 292: C968–C973, 2007 [DOI] [PubMed] [Google Scholar]
- 51.Pruvot EJ, Katra RP, Rosenbaum DS, Laurita KR. Role of calcium cycling versus restitution in the mechanism of repolarization alternans. Circ Res 94: 1083–1090, 2004 [DOI] [PubMed] [Google Scholar]
- 52.Raju SV, Zheng M, Schuleri KH, Phan AC, Bedja D, Saraiva RM, Yiginer O, Vandegaer K, Gabrielson KL, O'Donnell CP, Berkowitz DE, Barouch LA, Hare JM. Activation of the cardiac ciliary neurotropic factor receptor reverses left ventricular hypertrophy in leptin-deficient and leptin-resistant obesity. Proc Natl Acad Sci USA 103: 4222–4227, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ritter M, Su Z, Xu S, Shelby J, Barry WH. Cardiac unloading alters contractility and calcium homeostasis in ventricular myocytes. J Mol Cell Cardiol 32: 577–584, 2000 [DOI] [PubMed] [Google Scholar]
- 54.Romero L, Pueyo E, Fink M, Rodriguez B. Impact of ionic current variability on human ventricular cellular electrophysiology. Am J Physiol Heart Circ Physiol 297: H1436–H1445, 2009 [DOI] [PubMed] [Google Scholar]
- 55.Rota M, Hosoda T, De Angelis A, Arcarese ML, Esposito G, Rizzi R, Tillmanns J, Tugal D, Musso E, Rimoldi O, Bearzi C, Urbanek K, Anversa P, Leri A, Kajstura J. The young mouse heart is composed of myocytes heterogeneous in age and function. Circ Res 101: 387–399, 2007 [DOI] [PubMed] [Google Scholar]
- 56.Royer A, Demolombe S, El Harchi A, Le Quang K, Piron J, Toumaniantz G, Mazurais D, Bellocq C, Lande G, Terrenoire C, Motoike HK, Chevallier JC, Loussouarn G, Clancy CE, Escande D, Charpentier F. Expression of human ERG K+ channels in the mouse heart exerts anti-arrhythmic activity. Cardiovasc Res 65: 128–137, 2005 [DOI] [PubMed] [Google Scholar]
- 57.Rudy Y, Silva JR. Computational biology in the study of cardiac ion channels and cell electrophysiology. Q Rev Biophys 39: 57–116, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sabir IN, Fraser JA, Killeen MJ, Grace AA, Huang CL. The contribution of refractoriness to arrhythmic substrate in hypokalemic Langendorff-perfused murine hearts. Pflügers Arch 454: 209–222, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sampson KJ, Henriquez CS. Electrotonic influences on action potential duration dispersion in small hearts: a simulation study. Am J Physiol Heart Circ Physiol 289: H350–H360, 2005 [DOI] [PubMed] [Google Scholar]
- 60.Santana LF, Chase EG, Votaw VS, Nelson MT, Greven R. Functional coupling of calcineurin and protein kinase A in mouse ventricular myocytes. J Physiol 544: 57–69, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Shaw RM, Rudy Y. Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ Res 81: 727–741, 1997 [DOI] [PubMed] [Google Scholar]
- 62.Shimizu W, Antzelevitch C. Effects of a K+ channel opener to reduce transmural dispersion of repolarization and prevent Torsade de pointes in LQT1, LQT2, and LQT3 models of the long-QT syndrome. Circulation 102: 706–712, 2000 [DOI] [PubMed] [Google Scholar]
- 63.Sicouri S, Antzelevitch C. A subpopulation of cells with unique electrophysiological properties in the deep subepicardium of the canine ventricle. The M cell. Circ Res 68: 1729–1741, 1991 [DOI] [PubMed] [Google Scholar]
- 64.Sobie EA. Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys J 96: 1264–1274, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Splawski I, Timothy KW, Sharpe LM, Decher N, Kumar P, Bloise R, Napolitano C, Schwartz PJ, Joseph RM, Condouris K, Tager-Flusberg H, Priori S, Sanguinetti MC, Keating MT. Cav1.2 calcium channel dysfunction causes a multisystem disorder including arrhythmia and autism. Cell 119: 19–31, 2004 [DOI] [PubMed] [Google Scholar]
- 66.Trafford AW, Diaz ME, Sibbring GC, Eisner DA. Modulation of CICR has no maintained effect on systolic Ca2+: simultaneous measurements of sarcoplasmic reticulum and sarcolemmal Ca2+ fluxes in rat ventricular myocytes. J Physiol 522: 259–270, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Tranquillo JV, Hlavacek J, Henriquez CS. An integrative model of mouse cardiac electrophysiology from cell to torso. Europace 7: S56–S70, 2005 [DOI] [PubMed] [Google Scholar]
- 68.Vaidya D, Morley GE, Samie FH, Jalife J. Reentry and fibrillation in the mouse heart. A challenge to the critical mass hypothesis. Circ Res 85: 174–181, 1999 [DOI] [PubMed] [Google Scholar]
- 69.Wang HS, Cohen IS. Calcium channel heterogeneity in canine left ventricular myocytes. J Physiol 547: 825–833, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang L, Feng ZP, Duff HJ. Glucocorticoid regulation of cardiac K+ currents and L-type Ca2+ current in neonatal mice. Circ Res 85: 168–173, 1999 [DOI] [PubMed] [Google Scholar]
- 71.Wang LJ, Sobie EA. Mathematical model of the neonatal mouse ventricular action potential. Am J Physiol Heart Circ Physiol 294: H2565–H2575, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Watanabe MA, Fenton FH, Evans SJ, Hastings HM, Karma A. Mechanisms for discordant alternans. J Cardiovasc Electrophysiol 12: 196–206, 2001 [DOI] [PubMed] [Google Scholar]
- 73.Wu J, Zipes DP. Transmural reentry during acute global ischemia and reperfusion in canine ventricular muscle. Am J Physiol Heart Circ Physiol 280: H2717–H2725, 2001 [DOI] [PubMed] [Google Scholar]
- 74.Xu H, Guo W, Nerbonne JM. Four kinetically distinct depolarization-activated K+ currents in adult mouse ventricular myocytes. J Gen Physiol 113: 661–678, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Yatani A, Frank K, Sako H, Kranias EG, Dorn GW., 2nd Cardiac-specific overexpression of Gαq alters excitation-contraction coupling in isolated cardiac myocytes. J Mol Cell Cardiol 31: 1327–1336, 1999 [DOI] [PubMed] [Google Scholar]