Stochastic Emergence of Groupthink

Abstract

Oscillations in the synthesis and release of a chemical signal synchronize the behavioral response of a cell population.

Oscillations are found at nearly every level of biology. From the dynamic instability of cytoskeletal elements in an individual cell to the circadian rhythms that regulate a multitude of operations at the organismal level, it is clear that periodicity is an essential characteristic of living systems. On page 1021 of this issue, Gregor et al. (1) describe how cell aggregation and development of the amoeba Dictyostelium discoideum is guided by emergent rhythmic behavior arising from the stochastic pulsing of individual cells with a chemical cue. By combining experimental and computational approaches, the authors present the exciting story of the dynamical onset of collective behavior in this organism. The findings raise the question of whether biology uses oscillations to solve problems typically assumed to have static or unidirectional solutions.

D. discoideum is a “social” amoeba in that it transitions from a collection of unicellular organisms to a multicellular slug and finally to a fruiting body during its life cycle (see the figure). Cell aggregation and the commitment to form a fruiting body are regulated through cell-to-cell signaling by the small molecule cyclic adenosine mono-phosphate (cAMP). With the rhythmic synthesis and release of the chemoattractant cAMP, D. discoideum coordinates its collective behavior by aggregating to the region of highest cell density and initiating the formation of a fruiting body only when sufficient accumulation of cAMP is achieved. Before this threshold is met, cells act independently and do not aggregate. This marked synchronization, called dynamical quorum sensing, occurs when individual oscillators are coupled through a common field, often comprising extracellular signaling molecules in biological settings (2, 3). This highly dynamic process ensures that the cell population behaves efficiently and differentiates only when conditions are desirable. Whether this synchronized behavior is initiated and governed by the activities of a few specialized cells or is an emergent collective phenomenon has been an open question.

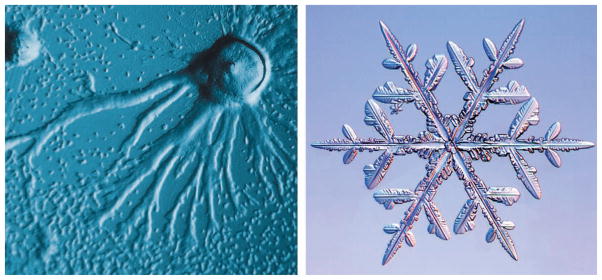
Emergent phenomena.

The social amoeba D. discoideum is a single-cell organism that, when collected together at sufficiently high density, exhibits emergence in its cellular aggregation (left). A common example of emergent phenomena in nature is the snowflake, where the macroscopic shape is dictated by the molecular geometry of the water molecule (right).

In the study by Gregor et al., individual cells and populations were observed in a perfusion chamber to study their dynamics in a controlled environment. A fluorescence resonance energy transfer (FRET)–based sensor monitored the amount of cytosolic cAMP directly. The authors probed the behavior of the system under varying amounts of extracellular cAMP, measuring the oscillatory frequency of intracellular cAMP production by cells each time. It is this precise variation of parameters that permits the analysis of a complex system such as the D. discoideum collective. Gregor et al. found that intracellular oscillations in cAMP concentration could occur even when the environmental concentration of cAMP was held constant and far above the saturation level of the cAMP receptors, demonstrating that the origin of oscillations is internal to the cell and does not require extracellular cAMP to be periodically cleared. By driving the internal cAMP oscillation system with periodic fluctuations in extracellular cAMP, the authors identified a single dominant frequency of internal cAMP oscillation above and below which the population-level oscillation diminished over time. This natural frequency is determined by the intracellular oscillation machinery and provides an internal timekeeping mechanism. Future biochemical studies on the origin of oscillations may use this frequency as a starting point in thinking about the types of biological processes that match the time scale.

In their computational modeling, Gregor et al. used a phase equation to describe the oscillatory state of a single cell. Equations like this are sometimes called “theta models” because the state of the system is given by a periodic variable θ, often represented as an angle on a circle. Such models naturally lend themselves to cyclical processes and have been used to describe oscillations in a variety of engineering and biological contexts such as the synchronization of flashing in fireflies. Upon coupling many of these single-cell models together computationally via the common field (cAMP), the behavior of the single-cell models began to synchronize and dynamical quorum sensing emerged. The population of single-cell models switched to a synchronized oscillatory state when a critical cell density was reached, as observed experimentally. They reproduced the experimentally measured relationship between cell density and frequency of collective cAMP oscillation only when the stochastic pulsing of individual cells in response to low, subthreshold concentrations of extracellular cAMP was included in the model. This is perhaps the most intriguing result because it confirms that random pulses of cAMP production at subthreshold levels of extracellular cAMP can affect the collective interactions of individual cells and initiate rhythmic synthesis of cAMP across a population. That is, organized group behavior originates from random individual behavior. When the population is at very low density, individual cells are “excited” by external cAMP infrequently and randomly without regard for their neighboring cells. With each pulse of excitation by extracellular cAMP, cAMP is synthesized intracellularly and secreted, increasing the local probability of excitation and creating chain reactions that produce patches of synchronized cAMP synthesis. These synchronized patches continue to excite nearby cells, producing a snowball effect. Multiple oscillatory patches can arise in this way, and a competition between them ensues. Those that produce more cAMP can “pulse” (synthesize cAMP) at higher frequencies, entraining and attracting patches that pulse at lower frequencies. As each new patch is conquered, the size and oscillatory frequency of the victorious patch increases. A single dominant frequency is ultimately reached, coordinating the behavior of the population.

In addition to providing a beautiful description of collective behavior in D. discoideum, the work of Gregor et al. offers new insights into the underlying mechanisms of control in living systems. It provides a detailed look at emergent biological phenomena—unpredictable, complex behaviors arising from a large number of relatively simple interactions. Although the mechanism of oscillation remains elusive, clues may be found in recent synthetic circuits that produced similar emergent behavior (4). Using simple gene circuits, emergent oscillatory behavior was achieved by a population of cells with a common extracellular signaling molecule, N-acyl homoserine lactone (AHL), which performs the dual roles of activating the genes necessary for intracellular oscillations of AHL and mediating the coupling between cells (4). It may be that cAMP acts similarly in D. discoideum.

Cellular aggregation and differentiation are behaviors critical to the survival of an organism, and yet the work of Gregor et al. demonstrates that random, decentralized processes initiate them in D. discoideum. It may seem surprising that biology would take this approach rather than leaving this decision in the hands of specialized pacemaker cells with more elaborate timekeeping and nutrient-sensing mechanisms. Is such stochasticity merely limited to lower organisms, or might it be an underlying property that guides all of biology? If so, how can this be reconciled with the homeo-static picture we observe macroscopically? Contending with these questions may reveal new fundamental properties of living cells and their methods of control.