Online Interactive Teaching Modules Enhance Quantitative Proficiency of Introductory Biology Students

Abstract

There is widespread agreement within the scientific and education communities that undergraduate biology curricula fall short in providing students with the quantitative and interdisciplinary problem-solving skills they need to obtain a deep understanding of biological phenomena and be prepared fully to contribute to future scientific inquiry. MathBench Biology Modules were designed to address these needs through a series of interactive, Web-based modules that can be used to supplement existing course content across the biological sciences curriculum. The effect of the modules was assessed in an introductory biology course at the University of Maryland. Over the course of the semester, students showed significant increases in quantitative skills that were independent of previous math course work. Students also showed increased comfort with solving quantitative problems, whether or not they ultimately arrived at the correct answer. A survey of spring 2009 graduates indicated that those who had experienced MathBench in their course work had a greater appreciation for the role of mathematics in modern biology than those who had not used MathBench. MathBench modules allow students from diverse educational backgrounds to hone their quantitative skills, preparing them for more complex mathematical approaches in upper-division courses.

INTRODUCTION

Consensus is growing within the scientific and academic communities that undergraduate biological science curricula are in need of substantial reform (National Research Council [NRC], 2003, 2009; Steen, 2005; Project Kaleidoscope, 2006). Interdisciplinary and multidisciplinary approaches now dominate the forefront of biological sciences research at every level, from nanobiotechnology to ecosystem dynamics, but undergraduate curricula remain essentially disciplinary in nature. Mathematics and quantitative approaches in particular clearly constitute a key tool for modern life scientists, yet the undergraduate curriculum fails to help students appreciate the important relationships between mathematics and modern biology (Gross, 2000; Ewing, 2002; Hastings and Palmer, 2003; Cohen, 2004; Hoy, 2004; Jungck, 2005; Steen, 2005). Biology courses remain largely qualitative and descriptive rather than rigorously quantitative. Lack of quantitative training among our biology majors weakens students at a practical level, whether they plan to analyze environmental impacts (e.g., minimum viable population size) or pursue a career in medicine (e.g., nonlinear drug dose responses, Yuan, 2005).

Currently, biology undergraduates at many four-year institutions have few requirements relative to mathematics, far fewer than those in other sciences such as physics or chemistry. Although biology majors typically take math through calculus, these courses often use nonbiological examples or abstractions (Gross, 1994) and rarely teach other mathematical skills essential for modern biology (NRC, 2003). Many institutions have addressed this by developing special courses (capstone courses, advanced undergraduate seminars, or special research tracks) that introduce elite students to quantitative biology. Such courses undoubtedly produce excellent cutting-edge scholarship, but they are limited to only the strongest students and thus do not help to transform the culture of biology teaching and learning. A stronger approach, and one that is more likely to heal the damaging disjunction between mathematics and biology, is to infuse math throughout the entire undergraduate biology curriculum for all students (Gross, 2004; Labov et al., 2010).

Online modules (free-standing instructional elements, often Web-based, that can be used by multiple instructors and revisited throughout a course sequence) have become a key educational tool to integrate mathematics and biology. MathBench Biology Modules were designed to integrate quantitative approaches and mathematics more deeply into the introductory biology curriculum in a way that would reinforce biological concepts, increase math literacy, and prepare students to be receptive to more complicated mathematical approaches in upper-level courses (Nelson et al., 2009). The MathBench suite consists of 37 self-contained learning modules that use an informal tone to combat math anxiety and leverage the students' pre-existing knowledge of math. We developed the modules in alignment with generally accepted best practices in online instruction, including embedding concepts within storylines (Parker and Lepper, 1992; Mayer, 2008), using informal language (Ross, 1983; d'Ailly et al., 1997; Moreno and Mayer, 2000), proving opportunities for self-calibration (Hannafin and Sullivan, 1996), and striking a balance between demonstrating solutions to problems and allowing students to practice finding the solutions themselves (Hannafin and Sullivan, 1996). Each MathBench module consists of 8–30 interlinked, well-illustrated Web pages focusing on a single quantitative theme (e.g., diffusion, Punnett squares, data visualization, log transformations) plus interactive problems, interactive graphics, and quizzes to measure student comprehension. The quiz questions can be drawn randomly from a larger bank of test questions, allowing for individualized grading opportunities even in large-enrollment classes. MathBench modules are freely available online at mathbench.umd.edu.

MATERIALS AND METHODS

The impact of MathBench Biology Modules on undergraduate student quantitative skills was evaluated during the fall 2009 semester in a large introductory biology course at the University of Maryland, College Park. The course was BSCI 105 Principles of Biology 1: Cell and Molecular Biology, with a total enrollment of 614 students. The course was subdivided into five separate lecture sections of between 42 and 155 students, each taught by a different faculty member. Each lecture section was further subdivided into laboratory sections of approximately 20 students each, which met once each week for 3 h. Although BSCI 105 is designed for biology majors, it is also required in several other degree programs (e.g., chemistry, kinesiology, nutrition) and is taken by students from a wide variety of majors to fulfill medical school application requirements.

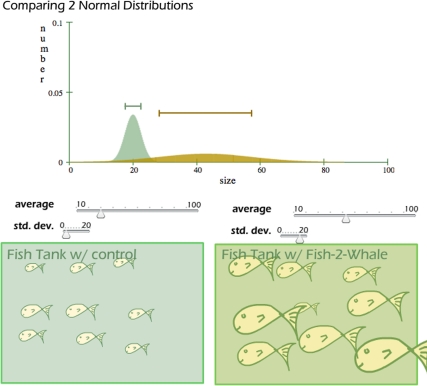
A series of nine MathBench modules was incorporated into the BSCI 105 laboratory curriculum. The modules were designed to introduce and reinforce specific quantitative skills and concepts that were identified by our faculty as being important for success in modern biology (Table 1). Modules covered topics such as basic lab techniques (metric system and use of the micropipetor), developing standard curves, logarithmic functions (particularly with respect to understanding pH), calculating molar weight, visualizing three-dimensional structures in two dimensions, probability calculations necessary for understanding BLAST searches, basic graphing (bar graphs, log), and simple statistical analyses. For example, the module entitled “Normal Distributions and the Scientific Method” begins with a brief overview of hypothesis testing, emphasizing the need for measuring outcomes, replicating measurements, and making comparisons. The module then uses a fanciful hypothetical scenario (the role of Fish2Whale fish food in increasing body length of tropical fish) to introduce students to the idea of characterizing variable traits within a population, such as organism size, using mean and SD. An interactive applet imbedded within the module allows students to manipulate these parameters and watch the effect of these manipulations directly on a virtual population of fish and graphically on a distribution of fish body lengths. Students are guided through their explorations with a systematic series of questions. At the conclusion of the module, students have the opportunity to manipulate means and standard deviations independently for two groups of virtual fish, representing control and treatment groups, allowing them to see the impact of these parameters on a scientist's ability to draw robust conclusions from an experiment (Figure 1).

Table 1.

MathBench modules used and specific quantitative skills and concepts emphasized in each

	Distill biology into math	Use equations	Use graphs	Fundamental equations	Magnitude	Unit conversions	Probability	Statistics	Model structure/iteration	Rates and equilibrium
Measurement
Basic lab techniques	X	X	X	X		X				X
Straight lines/standard curves	X	X	X	X						X
Logs and pH	X	X		X	X					X
Calculating molar weight	X	X				X
Visualization
A graphing primer	X	X	X							X
Log transformations	X	X	X	X	X
Probability and statistics
Normal distributions and the scientific method	X		X				X	X	X
Bar graphs and SEs	X	X	X					X
BLAST and (im)probability	X				X	X	X

Figure 1.

Screen shot from the “Normal Distributions and the Scientific Method” module.

Students were assigned modules at predetermined intervals throughout the fall semester. Each of the nine modules was developed to complement a specific laboratory exercise, so that students made immediate practical use of what they had learned. Modules were completed as homework, outside of class time. Each module was followed by a quiz, which was administered online through the campus course management system. Student quiz scores in total constituted 16% of the laboratory course grade.

Quantitative Skill Survey Design and Administration

To measure changes in quantitative skills over the course of the semester, we developed an 18-question pretest instrument that touched upon nine of our 10 specific quantitative skills (Table 1). We did not create specific questions for the skill “Distill biology into math,” as it represented the overarching goal of the project and would presumably be reflected in changes in total scores between the pretest and the posttest. The questions were crafted to allow each quantitative skill to be evaluated along a cognitive spectrum (Mayer, 2002), with one question designed to measure basic understanding and the other designed to reflect a more sophisticated understanding. For each question, students could select one of four multiple-choice options, or they could answer “I do not know how to approach this problem.” The “I do not know…” option was included as a way of assessing the students' degree of comfort with solving quantitative problems, whether or not they ultimately arrived at the correct answer. Before its use in this study, the instrument was piloted in introductory biology and genetics classes to establish internal consistency, criterion validity, and content validity (Garson, 2007). A second version, with the same 18-question structure but differing only slightly in numerical details, was created to serve as a posttest. The posttest also asked students to reflect on whether their quantitative skills had improved as a result of the introductory biology course and, if so, which components of the course curriculum were responsible for the improvement. The posttest also contained two open-ended questions that allowed students to provide feedback on the modules and their implementation.

Students in BSCI 105 were asked to complete the pretest during the first two weeks of the semester, before the first MathBench module was assigned. At the end of the semester, following the completion of all MathBench modules and quizzes, they were asked to complete the posttest. Analyses of changes over the course of the semester included only those students who completed both the pretest and the posttest (n = 204). Analyses of self-reported assessments of improvement in quantitative skill used all students who completed the posttest (n = 396).

Survey of Attitudes in Graduates

In an effort to assess longer-term impacts of the MathBench initiative on student attitudes regarding the relationship between math and biology, we added several questions to an existing survey routinely administered to all graduating seniors in the College of Chemical and Life Sciences. Between 2005 and 2009, MathBench modules had been gradually introduced into selected sections of four introductory-level courses typically taken in the first two years of the biological sciences curriculum (Principles of Biology I, II, and III, and Principles of Genetics). Spring 2009 graduates (n = 307) were first asked whether they had used MathBench modules in any of their courses. Because MathBench had only been integrated into the curriculum fairly recently and had not yet been fully implemented, we expected that a large proportion of the graduating seniors would not have encountered it as part of their course work. They were then asked to select the statement that most closely represented their attitude toward math (“I hate math and try to avoid it,” “I don't like math but I can cope with it,” “I don't care about math one way or another,” “I like math but I don't seek it out,” or “I like math and enjoyed having course work that included math”) and to describe their attitude regarding the relationship between math and biology (“Math is not relevant to biology,” “Math can be useful in biology but it's not really necessary,” “Math is helpful in biology,” “Math is essential in biology if you want to do cutting-edge work,” or “Math is essential for doing any biology, cutting-edge or not”). Attitudes of students who had encountered MathBench in their course work were then compared with those who had not.

Data Analysis

Pre- and posttest data were matched for all students completing both tests. We augmented the data set with the students' math eligibility level (determined by a math eligibility test administered by the university at orientation and completion of college mathematics course work) and whether or not they were concurrently enrolled in a math class. All statistical tests (multiple analysis of variance [MANOVA], Pearson product-moment correlation, Chi-square) were performed using JMP version 8.0.2.

RESULTS

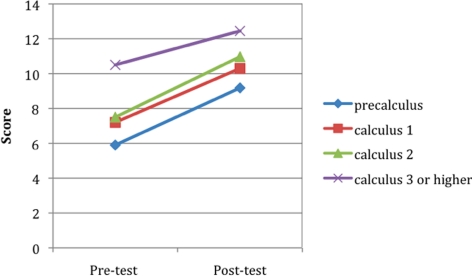
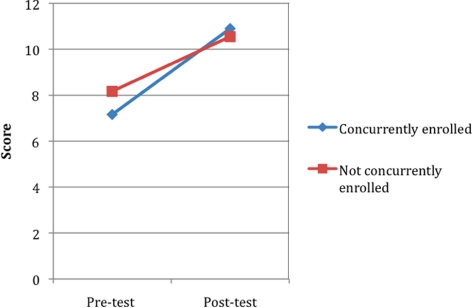
Students showed significant improvement in quantitative skills over the course of the semester (pretest x = 7.3 correct out of 18, posttest x = 10.4 correct; repeated measures MANOVA F₁₁₉₆ = 125.4040, p < 0.0001). There was a significant effect of math eligibility on pre- and posttest scores, with students eligible for precalculus having the lowest scores and students eligible for calculus 3 or higher having the highest scores (F₃₁₉₆ = 11.0634, p < 0.0001; Figure 2). Nonetheless, the magnitude of improvement in scores between the pre- and posttest was independent of math eligibility (F₃₁₉₆ = 0.4764, NS). Students who were concurrently enrolled in a math class showed slightly, but significantly, greater improvements in scores than those not concurrently enrolled in math (F₁₁₉₆ = 6.2077, p < 0.05; Figure 3). Overall, the improvement in score from pre- to posttest was negatively correlated with pretest score, indicating that students with lower initial scores made more dramatic gains (Pearson product-moment correlation, r = −0.657, n = 204, p < 0.0001).

Figure 2.

Changes in scores across the semester on an 18-item quantitative assessment for introductory biology students eligible for different levels of mathematics classes (precalculus, n = 51; calculus 1, n = 85; calculus 2, n = 53; or calculus 3 or higher, n = 15).

Figure 3.

Changes in scores across the semester on an 18-item quantitative assessment for introductory biology students concurrently enrolled in a math class (n = 79) or not concurrently enrolled in a math class (n = 125).

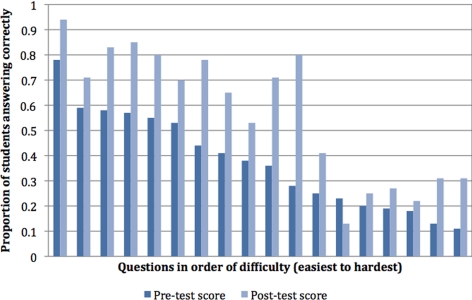
Students did not show uniform improvement across all questions. When the questions were sorted by the proportion of students who answered them correctly, the largest gains were seen in the 12 questions that were most likely to be answered correctly on the pretest (i.e., the “easiest” questions; Figure 4). Little or no improvement was seen on the six questions that the students were least likely to have answered correctly on the pretest (the “hardest” questions).

Figure 4.

Proportion of students answering correctly on the pre- and posttests for each of 18 questions on a quantitative skills assessment, with questions sorted by the proportion of students answering correctly on the pretest.

Math eligibility significantly affected level of risk aversion, as measured by the frequency with which students responded “I don't know how to approach this problem.” Overall, 75% of students answered “I don't know…” to at least one pretest question, whereas 29% so answered on the posttest. Students having low math eligibility were most risk averse (repeated measures MANOVA F₃₁₉₆ = 5.6801, p < 0.01). As a whole, students were less risk averse after completing the MathBench modules, as evidenced by a significant decrease in the frequency of “I don't know…” responses between the pre- and the posttests (F₁₁₉₆ = 80.578, p < 0.0001). The greatest decreases in risk aversion were seen in the students with the lowest math eligibility (F₃₁₉₆ = 4.7257, p < 0.005) and those concurrently enrolled in a math course (F₁₁₉₆ = 4.0114, p < 0.05).

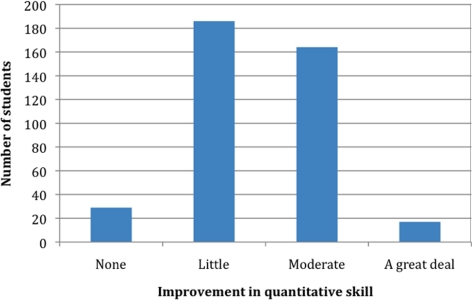
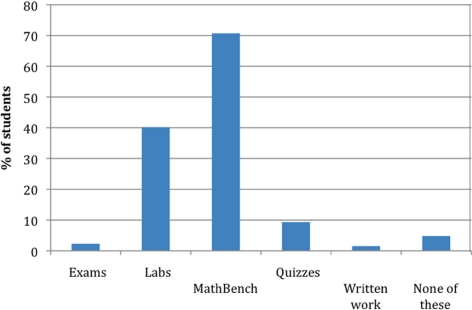
In the posttest, students were asked whether they had experienced an improvement in quantitative skills as a result of the course. Most students indicated that they had experienced “little” or “moderate” improvement (Figure 5). Of the students who reported improvement in quantitative skills (367 of 396, or 93% of students who completed the posttest), 71% attributed this improvement to the MathBench modules (Figure 6).

Figure 5.

Self-reported improvement in quantitative skills across the fall 2009 semester by students enrolled in introductory biology BSCI 105 (n = 396).

Figure 6.

Student perceptions of BSCI 105 course components that contributed to improvement in quantitative skills (n = 367; percentages sum to >100% because students could select multiple answers).

Student comments to the open-ended question, “What role did the MathBench modules have in the development of your scientific content knowledge and quantitative skills?” were overwhelmingly positive (83% of responses). Many students (31%) indicated that the modules helped them refresh their understanding of material learned in previous courses and high school. “The MathBench Biology Modules helped my content knowledge and quantitative skills by reviewing previous math skills I learned and elaborating on these skills to take my understanding of science-related math to another level.” A small percentage of students (9%), largely those with more advanced mathematics backgrounds, found the modules too informal and simplistic. However, there were many positive comments from other students who appreciated those features (e.g., “its humorous style of writing and funny images make it easier to study without any pressure,” “MathBench modules improved my quantitative skills because they made it very easy to see what the math was, they had good examples and explained all the math visually which really helped me”). Specific design features that students found helpful were its interactivity, opportunities for practice, immediate self-assessment feedback, and the ability of students to proceed at their own pace. “It helped to have interactive examples within the modules that allowed me to test my knowledge throughout the lesson.” “I found it easier to go at my own pace with the modules rather than being in a classroom setting where I find it difficult to comprehend the material as quickly as the other students.” Some indicated that the modules increased their level of engagement with the class (e.g., “I enjoyed the MathBench modules because during the week it kept me constantly active with the Bio class”). Many students specifically mentioned that they had a greater appreciation for the role of math in the biological sciences (e.g., “I now better understand the connection between math and Biology”).

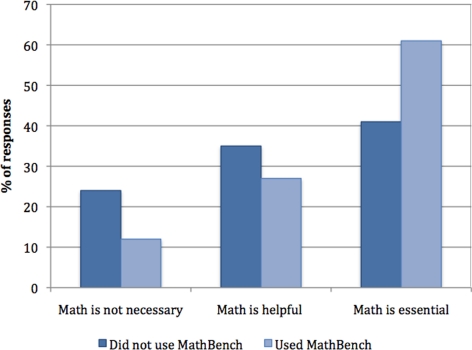
About half (51%) of the Spring 2009 graduates had encountered the modules in their course work. Regardless of their exposure to MathBench, a large majority of graduates (74%) either enjoyed or actively sought mathematical content in their course work. Graduates who had used MathBench were significantly more likely to describe the relationship between math and biology as “essential to cutting-edge biology” or “essential for all fields of biology” (χ² = 13.7, df = 2, p < 0.001; Figure 7).

Figure 7.

Responses of 2009 biological sciences graduates (n = 307) to a survey question regarding their attitude regarding the relationship between math and biology.

DISCUSSION

MathBench Biology Modules were effective in introducing and reinforcing quantitative concepts and skills into a large-enrollment introductory biology course. Over the course of the semester, students showed significant increases in quantitative skill that were independent of previous math course work. Specific attributes that students felt contributed to the development of their quantitative skills included interactivity, use of humor and informal language, opportunities for practice, immediate self-assessment feedback, and the ability of students to proceed at their own pace. This integration of mathematical approaches into biology courses appears to have lasting effects on student attitudes, as graduating seniors who encountered MathBench in their introductory course work reported a greater appreciation of the essential role of mathematics in the biological sciences than those who had not used MathBench.

Our findings are consistent with previous research that indicates that computers facilitate active learning and increase student interest and motivation, allowing them to gain a deeper understanding of complex technical information (American Association for the Advancement of Science, 1993, Weglinsky, 1998; Mayer, 2002; NRC, 2003). Computer-assisted instruction may be particularly advantageous for certain groups of otherwise disadvantaged students (Cotton, 1991), such as low-achieving students (Edwards et al., 1975; Bangert-Drowns et al., 1985; Roblyer et al., 1988) and economically disadvantaged students (Ragosta et al., 1982). These gains seem to come from the ability of students to work at their own pace and receive as much assistance as they require (Robertson et al., 1987).

These techniques are also thought to help the approximately one-third of college students who have trouble with quantitative work because of “math anxiety” (Betz, 1978). In our study, students with less-well-developed quantitative skills at the beginning of the semester (i.e., low math eligibility) were significantly more likely than those with stronger quantitative skills to avoid answering specific problems on the quantitative assessment. By the end of the semester, they showed increased comfort with solving quantitative problems, whether or not they ultimately arrived at the correct answer. Many of their comments on the open-ended assessment questions indicated that they felt more confidence in applying math to biological problems. This is heartening, especially in light of recent data that show that students with weak quantitative skills are wary of attempts to infuse mathematical approaches into introductory biology courses (Matthews et al., 2009).

Although students showed improvement across a range of quantitative skills and concepts, little to no improvement was seen in the “hardest” items on the assessment instrument. This result is not entirely surprising, given that the modules evaluated in this study were developed specifically for use in an introductory level course and therefore were designed to provide a basic level of conceptual understanding. It remains an open question whether this online modular approach is similarly effective in deepening quantitative understanding in more advanced course work. There is some evidence that the effectiveness of various pedagogical techniques differs depending on whether the intended audience is composed mainly of “novice” or “expert” learners, with many best practices shifting markedly for a more experienced audience (the so-called “expertise reversal effect,” sensu Clark and Mayer, 2008).

Online modules are now widely used in quantitative biology. Some were written before technological tools for interactivity were widespread. Others, (e.g., ESTEEM and COMAP) include minimal explanatory text, couch explanations in formal language, and are best suited for upper- division students. MathBench modules differ in their approach, using simple, clear, and intuitive explanations of the math involved to help students bridge the gap between biology and mathematical formalism. As such, MathBench modules are complementary with many existing modules—indeed, other modules largely begin where MathBench leaves off. The modules' easy accessibility makes it possible for them to be disseminated widely in a variety of educational contexts, and their design is inclusive of diverse learning styles and educational backgrounds, making them a useful tool for preparing students for the complex mathematical approaches that have become essential to modern biology.