Refolding the Engrailed Homeodomain: Structural Basis for the Accumulation of a Folding Intermediate

Abstract

The ultrafast folding pathway of the engrailed homeodomain has been exceptionally well characterized by experiment and simulation. Helices II and III of the three-helix bundle protein form the native helix-turn-helix motif as an on-pathway intermediate within a few microseconds. The slow step is then the proper docking of the helices in ∼15 μs. However, there is still the unexplained puzzle of why helix docking is relatively slow, which is part of the more general question as to why rearrangements of intermediates occur slowly. To address this problem, we performed 46 all-atom molecular dynamics refolding simulations in explicit water, for a total of 15 μs of simulation time. The simulations started from an intermediate state structure that was generated in an unfolding simulation at 498 K and was then quenched to folding-permissive temperatures. The protein refolded successfully in only one of the 46 simulations, and in that case the refolding pathway mirrored the unfolding pathway at high temperature. In the 45 simulations in which the protein did not fully fold, nonnative salt bridges trapped the protein, which explains why the protein folds relatively slowly from the intermediate state.

Introduction

The homeodomain superfamily has been of special interest in the development of theories and the application of methods to protein folding. The engrailed homeodomain (EnHD) is a three-helical bundle protein (helices HI, HII, and HIII), and its native state is barely stable with ΔG_D-N = 2.5 kcal/mol (1,2). It folds via a proven on-pathway folding intermediate (1–3) that is formed at ∼300,000 s⁻¹ and rearranges at ∼50,000 s⁻¹ at 42°C (t_1/2 = 15 μs at 25°C). At the time these rate constants were reported, they were the fastest yet observed for a protein (2,4), which made EnHD a prime target for real-time molecular dynamics (MD) simulation (2,4–6). Further, the folding pathway can be blocked at the rearrangement step by protein engineering to ensure that the intermediate is stable under physiological conditions and its structure can be solved by NMR (3). It contains the HII-turn-HIII motif in the native structure, but the helices are not docked. The motif is in fact an independently folding domain (7).

MD simulation predicted the complete description of the folding pathway in reverse by simulating unfolding, and was later benchmarked and validated by experiment (2,4–6). For example, the high-temperature simulation we used as a starting point for the study presented here is in excellent agreement with experiment: the MD-predicted transition state (TS) is in quantitative agreement with experiment, and the MD predictions (4) were published 3 years before the experimental work (2,6). The MD-predicted intermediate is also in agreement with experiment (4,5) and the MD-generated structure was confirmed through direct NMR experiments (3) 5 years after the prediction. Coarse-grained refolding models and atomic-level Monte Carlo methods have also reproduced structures on EnHD's folding pathway (8–10). Thus, this is a well-characterized system for protein folding studies.

Nevertheless, there remains an unresolved problem: Why, when a folded helix-turn-motif is formed in a few microseconds, does simple docking of the helices take 15 μs? This is part of a more general question as to why the major structural parts of a protein can be formed rapidly but the final formation of the native structure occurs slowly (11). To address this problem for EnHD, we conducted MD simulations of refolding starting from the folding intermediate, which was generated at high temperature and then quenched to folding permissive conditions by lowering the temperature. Here, we report 46 independent MD quench simulations in explicit water at 37°C, 41°C, and 46°C (310, 314, and 319 K) totaling nearly 15 μs of simulation time completed over ∼8 years of computer time. The starting structure came from the experimentally verified 498 K unfolding simulation discussed above (2,4,5) (Fig. 1). Experimentally, the intermediate state is the denatured state under folding conditions, that is, the intermediate is the starting point for folding (1–4). Consequently, we chose a snapshot from the thermal unfolding simulations corresponding to the native end of the intermediate ensemble as the starting structure for multiple independent quench simulations.

Figure 1.

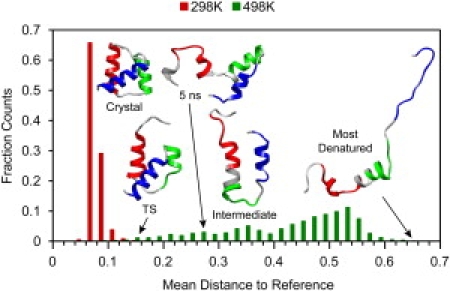
Reaction coordinate for high-temperature denaturation simulation. The mean Euclidean distance in our 35-dimensional property space was calculated to the reference set for each structure in the 298 K native set (N = 30,888) and 498 K unfolding simulation (N = 5932), and a histogram of those distances is shown here. The reference set was each structure in the 298 K native simulation, so more native-like structures have a lower mean distance to reference. The crystal structure is shown to represent the 298 K reference set, and the following structures are shown with their mean distance to reference in 35-dimensional property space: TS (0.16); 5 ns structure, which is the starting structure for the quench simulations (0.27); folding intermediate ensemble (∼0.24–0.40); and most denatured structure (0.66). EnHD is colored by helix: HI residues 10–22, HII 28–38, and HIII 42–55. The color version of the figure can be viewed online.

The use of a large number of parallel simulations is a convenient method for studying first-order reactions because such processes are stochastic and a small number N of the total processes N_T will have gone to completion in a short period of time (δt): N/ N_T = δt / t_1/2 (12). For this reason we performed 46 simulations with an average simulation time of 326 ns, which yields δt/t_1/2 = 326 ns / 15,000 ns = 0.0217, given the experimental t_1/2 for I → N. Thus, from this simple analysis, we would expect only one of the simulations to refold. The problem is that short simulations might become trapped in on- or off-pathway events by the formation of transiently stable structures.

Determining whether a protein has refolded in simulation is another important, though less appreciated, challenge. Previous studies used any individual properties or pairs of properties, including the radius of gyration, Cα root mean-square deviation (RMSD), native contacts, and solvent-accessible surface area (SASA), to determine whether a protein had refolded. These properties, when considered individually, are insufficient to prove that the protein has reached the native state. For example, proteins may achieve a native-like Cα RMSD and radius of gyration, yet make few native contacts. However, many properties in combination can provide satisfying proof that a protein has refolded.

Here, we found that 45 of the 46 simulations explored off-pathway events, and one folded successfully. Our previous unfolding simulations captured the reverse of productive folding pathways, as described above, and the productive refolding simulation presented here mirrors the previously simulated unfolding pathway. In addition, the single simulated refolding process observed here is consistent with our earlier study in which we observed microscopic reversibility directly for EnHD at its T_m (13). Furthermore, the unproductive refolding simulations captured off-pathway events that explain why the docking reaction is slowed down.

Materials and Methods

Simulation protocol

The starting structure for all of the quench simulations was obtained from a thermal denaturation simulation at 498 K, which was previously verified against experimental data (2,4–6). The 5 ns structure was strategically chosen from the native end of the intermediate state ensemble, as it was poised for refolding and therefore did not require computational resources to simulate a portion of the folding pathway that was not directly of interest. This was done because we wanted to begin from the same state as experimental folding studies, and the intermediate is the denatured state under folding conditions. The native simulations began from the crystal structure of EnHD (PDB ID: 1enh (14)). We used our in-house-developed MD software, in lucem molecular mechanics (ilmm) (15), with the all-atom force field of Levitt et al. (16), for all simulations. The starting structure was minimized for 150 steps for the MD-derived starting structure and 1000 for the crystal. The minimized structure was solvated in a box of F3C water molecules (17) with 8–10 Å of padding between the protein and edge of the periodic box, and the water density was set based on the simulation temperature according to the experimentally determined liquid-vapor coexistence curve (298 K: 0.997 g/mL; 310: 0.993; 314: 0.992; 319: 0.990 (18)). Standard protocols were used to complete preparation of the system and for the production run (19). The NVE microcanonical ensemble was employed with 2 fs timesteps and structures written out every 1 ps. Nonbonded interactions were truncated at 8 Å with a force-shifted cutoff (20), and the nonbonded list was updated every two steps.

The fastest experimental folding rate constant for EnHD was measured at 51,000 s⁻¹ around 42°C (315 K) (4). Accordingly, we chose to run our quench simulations at 310, 314, and 319 K. Forty-six simulations were run at these three temperatures for varying lengths of time, resulting in a total simulation time of 14.996 μs. The average simulation time was 326 ns, and the longest was 793 ns. The simulations are listed in Table S1 and Table S2 in the Supporting Material. We employed various computing clusters, including Intel, AMD, and Power5 architectures. The total wall-clock time for the quench simulations was nearly 8 years.

Analyses

The Cα RMSD was monitored over time for the core residues (residues 8–53) since the N- and C-termini have large fluctuations that are not representative of the general structure and dynamics of the protein. The SASA of the core residues and Trp⁴⁸, a fluorescence probe of folding, was calculated using our in-house-developed implementation of the Lee and Richards algorithm (21), and secondary structure was calculated with our in-house implementation of the DSSP algorithm (22).

Eleven contacts between HIII and the HI-HII scaffold were identified previously as key indicators of foldedness (13), and an additional five contacts between HI and HII were also selected. Residues were considered to be in contact if they contained atoms that met at least one of the following criteria: 1), carbon-carbon distance < 5.4 Å; 2), hydrogen bond acceptor-hydrogen distance < 2.6 Å and donor-hydrogen-acceptor angle within 45° of linearity; or 3), heavy atom-heavy atom distance < 4.6 Å for atoms that do not satisfy criterion 1 or 2. The distance between the center of mass (COM) of each residue was also calculated for all 16 pairs. Contacts were monitored over all residues in the protein and categorized based on whether they were present in the crystal structure (native, otherwise nonnative) and whether the contact pair consisted of main-chain atoms, side-chain atoms, or both. Contact lifetimes were also calculated at 1 ps granularity. Carbon atoms were classified as nonpolar, and all other atoms were considered polar. Two residues were considered in contact if the distance between a heavy atom from each residue fell below a cutoff of 5.4 Å for carbon-carbon pairs and 4.6 Å for all other pairs.

Experimental nuclear Overhauser effect (NOE) values were obtained from the Biological Magnetic Resonance Data Bank, entry 15536 (23). An NOE was considered satisfied in our simulations if the r⁻⁶ weighted distance between the closest protons during the simulation was ≤5.5 Å, which was the maximum cutoff employed by Religa (23) in building his NMR structure.

Property space and reaction coordinate

A total of 35 physical properties of the protein were selected to create a multidimensional property space and are listed with their average values and standard deviations in Table S3 of the Supporting Material. The properties were calculated at 10 ps granularity and were normalized over the simulations being compared. The principal components of this space were calculated for the 498 K denaturing simulation and all of the 298 K native simulations, and each property's contribution to the first principal component is reported in Table S3.

The distance in property space between any two time points was calculated as the average Euclidean distance between the 35-dimensional points. The average distance in property space between one point and a set of points was calculated as the sum of the distance between the point of interest and each point in the set divided by the number of points in the set. For a detailed explanation, see Beck and Daggett (24) (in particular their Eqs. 1 and 2), as well as the original work by Kazmirski et al. (25) that introduced property space analysis and principal component analysis (PCA) of MD trajectories.

We created a one-dimensional reaction coordinate by calculating the mean distance in property space from each time point in the simulation of interest to a reference set as described above and in more detail by Toofanny et al. (26). The reference set for a given temperature was made up of all time points from the native simulations at that temperature during which EnHD was in the native state.

TS selection

The mean distance to the 298 K reference set in property space was used to select TS ensembles in the native simulations. The TS was defined as the final time point that fell below a cutoff defined based on the simulation's distribution on the reaction coordinate. This method is a variation on the method described by Toofanny et al. (26).

Three-dimensional projection using multidimensional scaling of the all-against-all Cα RMSD matrix for the quench simulation was performed using the statistical package, R (27). TS ensembles were selected as the native cluster exit and preceding 5 ps for unfolding, and as the native cluster entry and subsequent 5 ps for refolding, as described previously (13,28,29).

The S-value, a residue-based measure of structure comparable to experimental Φ-values, is a product of the extent of native secondary structure (S_2°) and native and nonnative tertiary contacts (S_3°) in a given residue in the TS ensemble relative to the crystal structure (30). S_3° was reported only for residues Phe⁸, Leu²⁶, and Leu⁴⁰, as described previously (6).

Results

We first discuss simulations of EnHD at 298–319 K and the stability of the native state. Next, we validate a 35-dimensional property space and use it to identify states in a high-temperature unfolding simulation. Finally, we discuss our refolding (or quench) simulations, which we compared with the native simulations using our property space. One of the 46 quench simulations was found to successfully refold, and that simulation is described in detail. Additionally, we identify the interactions that inhibited the other 45 quench simulations from refolding to the native state.

Native simulations

We constructed a reference set for native EnHD from the native simulations at 298, 310, 314, and 319 K (see Table S1 and Table S2). Note, however, that many of these native simulations are intentionally at elevated temperature, where both the folding and unfolding rates are high. Overall, EnHD was stable in the native state with a core (residues 8–53) Cα RMSD of 2.27 ± 0.60 Å (Table S3) and on average 86% ± 2% NOE crosspeaks were satisfied (Table S1). The residues that consistently had the most violations were Phe²⁰ (HI) and Leu²⁶ (HI-HII loop), which both pack into the hydrophobic core. When EnHD is in the nearly native (N′) state (13), HIII translates toward the N-terminus, which breaks ∼75% of the native contacts made by Phe²⁰ and Leu²⁶. N′ involves reorientation of HIII along HI and HII without exposing the hydrophobic core, and it becomes more prevalent as the temperature rises (298 K, 6% population; 310, 28%; 314, 21%; 319, 33%), and since the NOEs were measured at 278 K, we expect such NOE violations.

Property space reaction coordinate

A multidimensional-embedded, one-dimensional reaction coordinate based on the physical properties of the protein was calculated for the high-temperature unfolding simulation using the 298 K native simulations as the reference (Fig. 1; see Materials and Methods for details). The reaction coordinate for the high-temperature unfolding shows that the TS selected previously (2,4–6) falls at 0.16 along the reaction coordinate, just outside the reference distribution (Fig. 1), as would be expected for this method. The intermediate and denatured populations form broad, connected peaks in the 498 K distribution. The intermediate spans a mean distance to reference of ∼0.24–0.40, and the starting structure for the quench simulations is 0.27. The starting structure contains the HII-HIII helix-turn-helix motif (Fig. 1), and it is 10.5 Å Cα RMSD from the crystal structure or 8.0 Å over core residues. A more detailed discussion of the property space for the native state and unfolding simulations is available in the Supporting Material.

A PCA was run on this dataset to determine which properties contributed most to the reaction coordinate, and the resulting weights are listed in Table S3. Nearly all of the properties had weights above 0.90, and the highest weights were observed for core Cα RMSD (0.99) and total native contacts (0.97). The COM distances between the five residue pairs between HI and HII all had very high weights, as did the various types of native contacts. The lowest weights were observed for the Trp⁴⁸ SASA and COM distances of residues in or near the HII-HIII turn.

Quench simulations: successful refolding

The property space analysis indicated that one of the 46 quench simulations refolded. This simulation was run at 319 K for 698 ns. A reaction coordinate was calculated using the native portions of the 319 K native state simulations as the reference set (with the native state at 0.169 ± 0.019 along this 319 K reaction coordinate; Fig. 2). Boundaries for the TS ensembles were chosen at 122.210 ns (+ 5 ps) for refolding and at 394.596 ns (− 5 ps) for the subsequent unfolding. The refolding and unfolding TS ensembles were more native-like than expected (0.194 and 0.170 mean distance to reference for refolding and unfolding, respectively, Fig. 2 a), which probably resulted from the broad native state population at 319 K.

Figure 2.

Reaction coordinate for the successful quench simulation. (a) The mean distance to the 319 K reference set in 35-dimensional property space is plotted over time for the quench simulation. The folded portion spans 122.210–394.596 ns with a mean distance to reference = 0.19 ± 0.02 (N = 27,239), and the denatured portion has a mean distance to reference of 0.24 ± 0.03 (N = 42,559). (b) The distribution of the mean distance to reference for the 319 K reference set (0.17 ± 0.02, N = 31,960; see Table S1) is shown along with the folded portion of the quench simulation and the denatured portion of the quench simulation. The folded portion of the quench simulation falls within the 319 K native state distribution, which indicates that the folded portion of the quench simulation is as similar to the native state as the native state is to itself. The color version of the figure can be viewed online.

The semiquantitative structure index (S-value) is a residue-based measure of secondary and tertiary structure that can be compared with experimental Φ-values (30). Both typically range from zero to one, and higher values reflect increased local structure in the TS ensemble. The correlation between our S-values and experimental Φ-values was 0.79 for the refolding TS ensemble and 0.54 for the subsequent unfolding TS ensemble (see Materials and Methods for details). The correlation between S and Φ was low for the unfolding TS ensemble (394 ns) due to a different motion of HIII relative to HI and HII than is usually observed for EnHD. The unfolding TS ensemble was characterized by HIII pulling away from the core by first rotating such that it became parallel to HI and HII. However, the N-terminus of HIII pulled away from HI and HII with the HII-HIII loop acting as a hinge for the refolding TS identified here and the previously observed TSs (2,4–6). As a result, the following residues in the unfolding TS ensemble had more contacts with HII and thus a higher S-value than expected: Phe⁸ (N-term), Leu¹³ (HI), Leu¹⁶ (HI), Phe²⁰ (HI), and Leu²⁶ (HI-HII loop).

Several properties were plotted over the course of the quench simulation (Fig. 3) to determine the order of events. Only one of the five HI-HII key contacts (Arg³⁰-Glu¹⁹) was present in the starting structure (Figs. 3 c and 4). The next contact formed was Leu³⁴-Leu¹⁶ at 0.5 ns, followed by Glu³⁷-Arg¹⁵ at 4.8 ns, and Leu³⁴-Arg¹⁵ at 13.9 ns. In the successful quench simulation, these residues came in contact at 102 ns. The N-terminal end of HIII reformed α-helix at 4 ns, the N-terminal end of HII at 52 ns, and the N-terminal end of HI at 111 ns (Fig. 3 b). In the 39 simulations where EnHD maintained the Arg³⁰-Glu¹⁹ contact, the Leu³⁴-Leu¹⁶ contact always formed first, and it formed very early in the simulation. Glu³⁷-Arg¹⁵ and Leu³⁴-Arg¹⁵ formed next in the seven simulations where they formed at all. The last HI-HII contact, Leu³⁸-Gln¹², formed only in the presence of the previous four contacts in five of our simulations, including the successful one.

Figure 3.

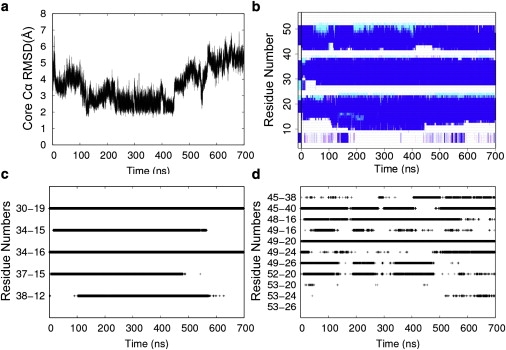
Selected properties from the successful quench simulation. (a) Cα RMSD of the core residues (residues 8–53) to the minimized crystal structure; N = 698,699. (b) DSSP showing the secondary structure for each residue over time: α-helix (blue), π-helix (cyan), and 3/10-helix (magenta), N = 68,970. (c) HI-HII contacts, N = 273,759. (d) HIII-core contacts, N = 229,394. For c and d, a cross (+) was plotted at each time point when the two residues were in contact. The color version of the figure can be viewed online.

Figure 4.

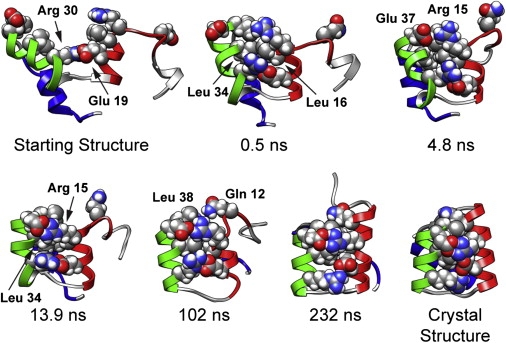
Structures from the successful quench simulation showing the order of HI-HII contacts. Arg³⁰-Glu¹⁹ was present in the starting structure. Leu³⁴-Leu¹⁶ formed at 0.5 ns, followed by Glu³⁷-Arg¹⁵ at 4.8 ns, and Leu³⁴-Arg¹⁵ at 13.9 ns. Finally, Leu³⁸-Gln¹² formed at 102 ns. The crystal structure and the best structure from the quench simulation are also shown for comparison. The color version of the figure can be viewed online.

The formation of these contacts and helices is apparent in the structures of EnHD over the time course of the quenched refolding simulation (Fig. 4 and Fig. S4). HI and HII snapped together in the first 2 ns of the simulation. Around 100 ns, the N-terminus of HI developed α-helix and the final HI-HII contact formed. For the next 20 ns, HIII reoriented on the HI-HII scaffold. EnHD passed through the TS at 122 ns with HIII docking in the native orientation. At 232.260 ns, EnHD achieved its lowest mean distance to reference of 0.15 and a core Cα RMSD of 2.30 Å. After the unfolding TS at 394 ns, HIII continued reorienting over the HI-HII scaffold, and HI and HII came apart at ∼570 ns.

The core Cα RMSD of EnHD is plotted for three simulations in Fig. 5. The structure from 5 ns into the 498 K unfolding simulation was quenched at 319 K. Eventually it attained a core Cα RMSD that would be expected for a protein in the native state at 319 K.

Figure 5.

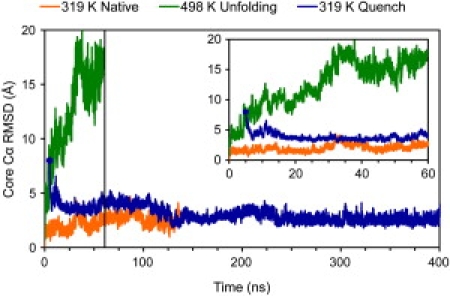
Core (residues 8–53) Cα RMSD to the minimized crystal structure is plotted for a 319 K native (137 ns, N = 13,735), 498 K unfolding (60 ns, N = 5,933), and 319 K quench (395 ns, N = 20,000) simulation. The structure from 5 ns into the 498 K unfolding simulation (8 Å core Cα RMSD, emphasized on the plot) was quenched to 319 K, and after an additional 122 ns (at 127 ns on this plot) refolded to the native state for 272 ns (it unfolded at 399 ns on this plot). The inset shows the detail of the first 60 ns. The color version of the figure can be viewed online.

Quench simulations: factors preventing refolding

We identified several common motifs that prevented folding from proceeding by analyzing the 45 simulations (14 × 10⁶ structures, 14.2 μs of sampling) that did not refold. Many nonnative salt bridges formed in the unsuccessful quench simulations that kept residues involved in native contacts from finding each other. For example, Arg¹⁵ (in HI) often formed a salt bridge with Glu¹⁹ (HI), which prevented Arg³⁰ (HII) and Glu¹⁹ (HI) from adopting their native arrangement (Fig. 6 a). This nonnative salt bridge also kept Arg¹⁵ (HI) from finding Glu³⁷ (HII) and pulling HI and HII into their parallel native orientation. Arg²⁹ (HII) often formed salt bridges with Glu³⁷ (HII), again deterring the native Arg¹⁵ (HI)-Glu³⁷ (HI) salt bridge from forming and also kinking the N-terminal end of HII (Fig. 6 a). The placement and orientation of the N-terminus (residues 3–10) had a strong influence over whether the N-terminus of HI would form α-helix. For example, Lys¹⁷ (HI) often interacted with the carbonyl groups in the backbone of Phe⁸ (N-term) and Ser⁹ (N-term), which along with a number of salt bridges that often formed beween either Arg³ (N-term) or Arg⁵ (N-term) and Glu²² (HI), locked the N-terminus to HI and made it impossible for the N-terminus of HI to adopt native ϕ/ψ angles and backbone hydrogen-bonding patterns or the native Leu³⁸ (HII)-Gln¹² (HI) contact to form (Fig. 6, b and c).

Figure 6.

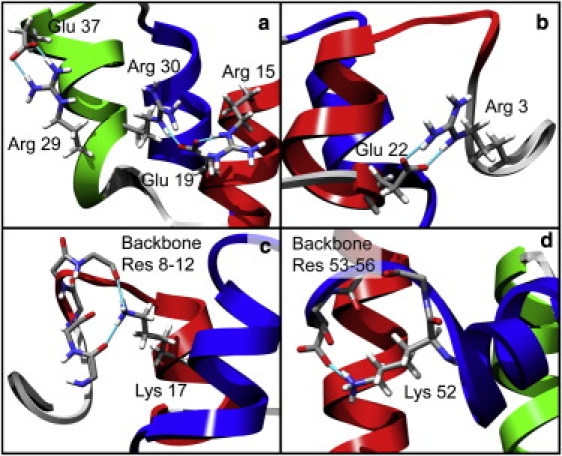
Structures of nonproductive salt bridges (shown in sticks) in several unsuccessful quench simulations. (a) Glu³⁷-Arg²⁹ and Arg³⁰-Glu¹⁹-Arg¹⁵ salt bridges inhibited the native Arg³⁰-Glu¹⁹ contacts from forming, and caused HI and HII to skew relative to each other. (b) The Glu²²-Arg³ salt bridge is an example of several salt bridges that formed between the N-terminus and Glu²² and kept HI from fully forming. (c) Lys¹⁷ coordinated the backbone carbonyl groups of Phe⁸, Ser⁹, and Gln¹², which stabilized the N-terminus in a nonnative orientation. (d) Lys⁵² formed a salt bridge with the C-terminus, kinking the end of HIII.

Even in the few cases in which all five of the native HI-HII contacts formed, HIII never packed exactly correctly against the HI-HII scaffold. The C-terminus of HIII never fully formed α-helix, usually because a salt bridge between Lys⁵² and the carboxy group of the C-terminal residue made it impossible to pack all of the core residues from the C-terminus into the core (Fig. 6 d). In one case, a salt bridge between Arg²⁸ (HII) and Lys⁴⁶ (HIII) caused the HII-HIII turn to kink, and it disrupted the α-helix at the N-terminus of HIII as well as the orientation of HIII relative to HI and HII.

Whenever long-lived, long-range, nonnative nonpolar interactions occurred, they were always accompanied by polar interactions (Fig. S5). However, these polar interactions, particularly salt bridges, were often present in the absence of nonpolar interactions. In contrast, whenever long-lived nonpolar interactions occurred, they were always accompanied by longer-lived polar interactions, particularly salt bridges.

Discussion

Refolded native state

A drop in mean distance to reference to 0.193 ± 0.019 (Fig. 2 a), and a drop in core Cα RMSD to 2.69 ± 0.39 Å (Fig. 3 a) were observed upon refolding. For comparison, the reference native state at 319 K had a mean distance to reference of 0.169 ± 0.019 (Fig. 2 b) and a core Cα RMSD of 2.20 ± 0.60 (Table S3). The refolded native state kept all five native HI-HII contacts and had intermittent HIII-core contacts (Fig. 3, c and d), as did the reference native state (data not shown). However, HIII was more variable in the refolded native state, in terms of both the fraction of helix and the position relative to HI and HII (Fig. S4). HIII spent more time in alternate orientations than the two seen primarily in the reference native state. The first is characterized by HIII lying diagonally across HI and HII as in the crystal structure (Fig. S4), and the second by HIII moving ∼10 Å toward the N-terminus, although other arrangements were observed as well (13). The mobility of HIII is apparent in Fig. 3 d, which shows the residues between HIII and the core going in and out of contact.

The refolded native state had a slightly lower fraction α-helix (0.61 ± 0.04; Fig. 3 b) than the reference native state (0.68 ± 0.04; Table S3), which was due to fraying at the C-terminus of HIII. This fraying was also apparent in the NOE satisfaction calculated from simulation: 77% of the NOEs were satisfied in the refolded native state, compared with 86% in the reference native state (Table S1). The most severe violations were in the C-terminus, since the last turn of HIII never formed due to a stable salt bridge between Lys⁵² and the C-terminal carboxyl group; however, this is consistent with experimental data. The C-terminus has higher B-factors in the crystal structure (27 ± 15 Ų) than the core of the protein (19 ± 11 Ų) (14), and NMR experiments have shown higher J-couplings and lower backbone order parameters in the C-terminus, attributed to helix fraying (23). Otherwise, the violations were due to Leu²⁶, which did not have all of its NOEs satisfied in the native simulations either. Additionally, due to the orientation of the N-terminus, Phe⁸, which accounted for many of the violations, interacted with other residues in the N-terminus rather than residues in HI and HIII as in the native simulations.

Comparison of one successful folding trajectory and 45 unsuccessful trials

We performed 46 independent refolding simulations beginning from the EnHD intermediate state, which is the starting point for experimental folding under physiological conditions (1,2). We generated the intermediate by unfolding the protein at 498 K and quenching it at experimentally determined refolding temperatures. In addition to providing an atomic-level description of aspects of the folding pathway, our quench simulations give insight into the energy traps the protein might encounter as it navigates the energy landscape between the denatured and native states. For the most part, EnHD got stuck in nonproductive conformations due to the formation of nonnative salt bridges, although in some cases these interactions were stabilized by nonpolar interactions. EnHD contains nine Arg, four Lys, and six Glu residues, for a total of 19 of 54 residues, or 35%. The native salt bridges stabilized the native state, and their formation contributed to key steps along the folding pathway (e.g., Arg³⁰-Glu¹⁹ initiating HI and HII zipping together); however, EnHD can form many more nonnative salt bridges that can stabilize nonnative conformations (Fig. 6). Salt bridges were the strongest and longest-lived noncovalent interaction in our simulations (Fig. S5). Therefore, once a favorable nonnative interaction formed, it often did not break on the timescale of our shorter simulations. In the longer unproductive quench simulations, nonnative salt bridges gave way to native interactions, and we expect that if the simulations were extended, more of them would eventually refold to the native state.

Misfolding traps in the intermediate slow refolding

The protein correctly refolded in just one of the simulations, but in all 46 of our quench simulations the zipping together of HI and HII was a common initial event. The order of contact formation between HI and HII observed in the productive refolding simulation was representative of other quench simulations: Arg³⁰-Glu¹⁹ was present in the starting structure, Leu³⁴-Leu¹⁶ formed early on, Leu³⁴-Arg¹⁵ and Gly³⁷-Arg¹⁵ were formed next, and Leu³⁸-Gln¹² was the last to form (Figs. 3 c and 4). All five contacts formed at the same time in only five of the quench simulations. The Leu³⁴-Leu¹⁶ contact was the second to form in all 39 quench simulations when the Arg³⁰-Glu¹⁹ contact remained intact. Additionally, both Leu¹⁶ and Leu³⁴ are highly conserved among all 84 homeodomains in Drosophila melanogaster (31). The consistent order of contact formation and the evolutionary conservation of these two Leu residues suggest that the Leu³⁴-Leu¹⁶ contact is critical for folding. If this is true, and EnHD is unable to form this contact, folding would be halted in the intermediate state. Indeed, when Leu¹⁶ is mutated to the smaller Ala, EnHD preferentially populates the folding intermediate (1,3).

The trapped intermediate states were characterized by HIII never being completely correctly packed onto the HI-HII scaffold. The C-terminus of HIII never fully formed α-helix, usually because of a salt bridge between its terminal carboxy group and Lys⁵². Indeed, Gianni et al. (6) showed that removing this interaction via mutation of Lys⁵² to Ala leads to faster folding: 6.4 × 10⁴ s⁻¹ vs. 3.8 × 10⁴ s⁻¹ for wild-type. These data are consistent with the implication from the simulations that there is an interaction involving Lys⁵² competing with productive folding. For comparison, α₃D, a designed three-helical bundle protein, folds faster than EnHD and does not populate an intermediate (32). For α₃D, folding rates of 3.1 × 10⁵ s⁻¹ were measured at 49°C (t_1/2 ≈ 4.8 μs at 25°C) at a pH of 2.2. Because folding took place at low pH, all Asp and Glu residues were protonated, and nonnative salt bridges could not cause bottlenecks in the folding pathway.

In another study of three-helical bundle protein folding, the R16 and R17 domains of α-spectrin were shown to fold ∼3 orders of magnitude more slowly than the R15 domain due to the internal friction of the proteins (33). Based on Φ-value analysis and measurement of the internal friction of the three proteins and several variants, the authors proposed that transient misdocking of the helices slowed folding in the cases of R16 and R17. Similarly, the nonnative interactions seen in our refolding simulations kept the helices from packing correctly (Fig. 6) and slowed folding.

Accordingly, our MD simulations strongly imply that the intermediate refolds slowly because of diversions, and such transient off-pathway traps prevent the protein from finding productive folding pathways on the timescale of our simulations. The combination of unfolding simulations with many parallel folding simulations has been shown to be very powerful (12). Unfolding simulations mirror productive, on-pathway folding events measured experimentally (2,4,6), and refolding simulations detect both on-pathway folding directly (described here and in simulations at the T_m (13,34)) as well as off-pathway events in the nonproductive refolding simulations. The results of these quench simulations resolve the question of why the folding intermediate folds relatively slowly: the transient off-pathway traps slow the reaction by 1–2 orders of magnitude.

Microscopic reversibility

Considering that protein folding and unfolding have been shown to follow the same pathway for EnHD and CI2 at their melting temperatures (13,34), it is interesting to consider the order in which the HI-HII contacts were gained in the quench simulations compared with the order in which they were lost in the high-temperature unfolding direction, noting that unfolding and folding occurred under different conditions. The order of loss for the five contact pairs in the high-temperature denaturation simulation was Leu³⁴-Arg¹⁵ (0.2 ns), Leu³⁸-Gln¹² (1.2 ns), Glu³⁷-Arg¹⁵ (3.0 ns), Leu³⁴-Leu¹⁶ (4.2 ns), and Arg³⁰-Glu¹⁹ (8.4 ns). The order in which the contacts were gained in the successful quench simulation was Arg³⁰-Glu¹⁹ (present at start), Leu³⁴-Leu¹⁶ (0.5 ns), Glu³⁷-Arg¹⁵ (4.8 ns), Leu³⁴-Arg¹⁵ (13.9 ns), and Leu³⁸-Gln¹² (102 ns; Figs. 3 c and 4). The order of gain and loss is nearly identical, with the only exception being swapping of the Leu³⁴-Arg¹⁵ and Leu³⁸-Gln¹² interactions, although they together occurred first in unfolding and last in folding. We note that this comparison is subject to the caveat that we obtained only one successful refolding trajectory. However, when these five key HI-HII contacts formed in the 45 simulations that never fully refolded, they were gained in the same order as the successful quench simulation, even though all five contacts only formed in four of the unsuccessful simulations.

The formation of the HI-HII scaffold is a critical step in the folding pathway for EnHD and must be completed before HI and HIII can dock in their native orientation. The scaffold forms in a stepwise manner beginning with contacts forming near the HI-HII loop, including the critical Leu³⁴-Leu¹⁶ contact, and continuing with combined HI helix formation and the zipping together of HI and HII.