Predicting Ion Binding Properties for RNA Tertiary Structures

Abstract

Recent experiments pointed to the potential importance of ion correlation for multivalent ions such as Mg²⁺ ions in RNA folding. In this study, we develop an all-atom model to predict the ion electrostatics in RNA folding. The model can treat ion correlation effects explicitly by considering an ensemble of discrete ion distributions. In contrast to the previous coarse-grained models that can treat ion correlation, this new model is based on all-atom nucleic acid structures. Thus, unlike the previous coarse-grained models, this new model allows us to treat complex tertiary structures such as HIV-1 DIS type RNA kissing complexes. Theory-experiment comparisons for a variety of tertiary structures indicate that the model gives improved predictions over the Poisson-Boltzmann theory, which underestimates the Mg²⁺ binding in the competition with Na⁺. Further systematic theory-experiment comparisons for a series of tertiary structures lead to a set of analytical formulas for Mg²⁺/Na⁺ ion-binding to various RNA and DNA structures over a wide range of Mg²⁺ and Na⁺ concentrations.

Introduction

RNAs are highly charged polyanions. Metal ions, which can bind to RNAs to mediate the electrostatic interactions, are critical for RNA stability. Therefore, quantitative predictions for the ion-binding properties are essential for understanding the ion-dependent RNA folding thermodynamics and kinetics (1–17). RNA folding is often hierarchical (1,2): the secondary structural segments (helices, loops) are formed first, followed by the formation of tertiary contacts in the presence of Mg²⁺ or high monovalent salt (1,2). Most thermodynamic measurements for RNAs have been focused on the folding of secondary structural segments at a fixed standard salt condition, i.e., 1 M Na⁺ (18–23). These parameters have led to accurate predictions for RNA secondary structures and folding stabilities (18–23). More recent experimental and computational studies have extended the helix and loop thermodynamic parameters to different ionic conditions (19,24–27).

In contrast, our ability to predict the ion-dependent stability for tertiary structural folding is relatively limited (2–17). One of the difficulties comes from the fact that ion-RNA interactions are much more complicated for tertiary structural folding. The folding of a tertiary structure involves very high buildup of RNA backbone. The massive buildup of negative charges in the nucleotide backbone leads to significant binding of the counterions around RNA. The high concentration of the counterions around RNA causes strong coupling (correlation) between the ions, i.e., ions form a network due to the strong Coulomb interactions and, hence, the discrete distributions (instead of the mean-field distribution) of the ions become important. The effect can be quite significant for multivalent ions such as Mg²⁺ ions, which involve strong Coulomb interactions. The results from several experiments have suggested the potential significance of ion correlation for the binding of multivalent to nucleic acids (6,28).

The strong ion correlation prevents the use of any mean-field type of treatment for the multivalent ions. In general, there have been two major types of polyelectrolyte theories: the counterion condensation theory (29) and the Poisson-Boltzmann (PB) theory (30–34). Both theories have been quite successful in predicting a variety of electrostatic properties for nucleic acids and proteins (29–33). However, they both neglect the ion correlation effect, which can be important for multivalent ions such as Mg²⁺ (17,35–40). For example, the PB theory assumes the mean fluidlike ion distribution and thus ignores ion-ion correlation and ion fluctuation. Moreover, the counterion condensation theory is based on the simplified line-charge model and double-limit law, and thus is not applicable for complex nucleic acid structures with finite size in a solution of finite ion concentration.

Recently, motivated by the importance of ion correlation and fluctuation effects, we developed the tightly bound ion (TBI) model (37). The model takes into account the correlations between bound ions and the ion-binding ensembles (37). Experimental comparisons showed that the inclusion of ion correlations and binding ensembles in the TBI model leads to the improved predictions on salt-dependent thermodynamics of DNA/RNA helices/hairpins (25–27) and DNA helix assembly/bending (38–41). However, the model is based on simplified coarse-grained structures (37,42) originally developed for DNA helices. Because an RNA tertiary fold involves structural complexity far beyond helices, the coarse-grained model (for helices) cannot treat RNA tertiary folds. Therefore, we need a model that can handle the ion effects with ion correlations for RNA tertiary folds at the all-atom level.

The model developed here may lead to significant applications to the quantitative prediction of the ion effects in RNA tertiary structural folding, such as the folding of RNA kissing loop complex. Kissing loop complex is a tertiary structural motif (2,43) formed by basepairing between two hairpin loops. The motif is a highly frequently one occurring in RNA tertiary folds (2,44–46,48–50). The formation of a kissing complex involves significant buildup of the nucleotide backbone charges. As a result, the folding stability and kinetics of kissing loop complex critically depends on the ion-mediated electrostatic interactions. For example, Mg²⁺ ions can alter the unfolding and refolding rates by a factor of 10²–10³ and the saturating Mg²⁺ ions can cause a large change ΔG ∼10 k_BT in the folding stability of a kissing loop (44,45), where k_B is the Boltzmann constant and T is the temperature.

To date, no computational model has been developed to quantitatively predict the ion binding properties by considering the ion correlation effect for RNAs at the level of atomic structures. Here we develop an atomistic TBI model that can treat complex atomic nucleic acid structures, and employ the atomistic TBI model to predict the Na⁺/Mg²⁺-binding to RNA and DNA structures and the ion-dependent folding stability of HIV-1 DIS-type RNA kissing complex in Na⁺/Mg²⁺ solutions. Throughout the article, we emphasize the comparisons between the theoretical predictions and the experimental data. Furthermore, based on the theoretical predictions and the theory-experiment comparisons, we will derive analytical formulas for the Na⁺/Mg²⁺-binding. Such formulas may be practically useful for data analysis, experimental design, and quantitative predictions for the ion-dependence of RNA folding.

Methods

Structural model

The study covers a range of nucleic acid structures, including DNA and RNA duplexes, RNA pseudoknots, tRNAs, and the folded and unfolded forms of RNA kissing loop complexes. Below we describe how these structures are generated in the computational study.

For the canonical A-RNA and B-DNA duplexes, we use the software X3DNA (51) to construct the structure. For the native structure of the beet western yellow virus (BWYV) pseudoknot (Protein Data Bank (PDB) code: 437D) (52), the 58-nucleotide (nt) fragment of ribosomal RNA (rRNA, PDB code: 1HC8) (53), and the yeast tRNA^Phe (PDB code: 1TRA) (54), we adopted the Protein Data Bank structure (see Fig. 1). For the HIV-1 dimerization initiation signal (DIS)-type kissing complexes (KC-1 and KC-2 in Fig. 1 G), because the wide-type HIV-1_Lai sequence and the KC-1 and KC-2 kissing complexes show high similarities in basepairing patterns in the kissing interface and in the hairpins (49,50,55) and the kissing complexes generally have the similar coaxially stacked structures, we can use the wide-type HIV-1_Lai (55,56) (PDB code: 2B8S) structure to model the three-dimensional all-atom structures of KC-1 and KC-2 kissing complexes (55,56).

Figure 1.

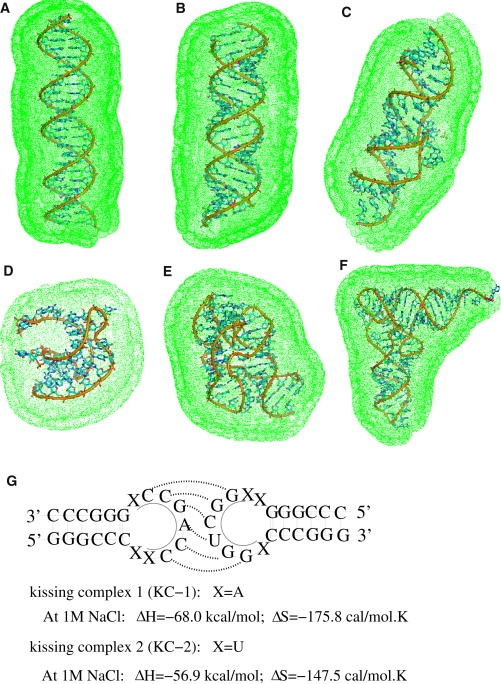
(A–F) The tightly bound regions in 0.1 M Mg²⁺ solution: (A) A 24-bp DNA duplex (structure produced from X3DNA (51)). (B) A 24-bp RNA duplex (structure produced from X3DNA (51)). (C) HIV-1 DIS kissing complex (PDB code: 2B8S) (55). (D) Beet Western yellow virus (BWYV) pseudoknot fragment (PDB code: 437D) (52). (E) A 58-nt ribosomal RNA (rRNA) fragment (PDB code: 1HC8) (66). (F) Yeast tRNA^Phe (PDB code: 1TRA) (54). The figure for the three-dimensional structures is generated by the software PyMol (http://pymol.sourceforge.net/). (Green dots) Boundary of the tightly bound regions defined in the TBI model (37–40). (G) Illustration of the HIV-1 DIS type RNA loop-loop kissing complexes (KC-1 and KC-2) used in the calculations. The thermodynamic parameters for KC-1 and KC-2 at 1 M NaCl are taken from the experimental measurements (49,50). (Shaded lines) Basepairs at the kissing interface.

Tightly bound ion model at all-atom level

The original tightly bound ion (TBI) model was based on coarse-grained structures (37–40). Here we develop a new TBI model that can treat all-atom nucleic acid structures.

For multivalent ions such as Mg²⁺ ions, the higher charge and the resultant strong Coulomb interaction between the ions can cause strong coupling (correlation) between the ions. To treat such an effect, according to the correlation strength, we classify the counterions into two types (37–41): the strongly and weakly correlated ions, denoted as the tightly bound and diffusive ions, respectively. Correspondingly, the space occupied by these ions is denoted as the tightly bound region and diffusive region, respectively (see Fig. 1 for examples of the tightly bound regions for the different structures). For the diffusive ions, we use the mean-field (PB) approach, while for the tightly bound ions, we must consider discrete modes of ion distributions to account for the ion-ion correlation effect. For a mixed monovalent and multivalent ion solution, because the correlation effect for the monovalent ions is negligible, monovalent ions can be treated as diffusive ions that form a background for multivalent ion binding.

Evaluation of ion correlation requires enumeration of the discrete distributions of the tightly bound ions and calculation of the free energy of the system for each given ion distribution mode. To enumerate the discrete ion distributions, for an N-nucleotide (nt) RNA, we divide the tightly bound region into N cells, each around a phosphate. There exist a large number of modes (i.e., binding modes) of ion distributions represented as the different ways to partition the tightly bound ions into the different cells. A tightly bound cell contains the phosphate and the groove space that surrounds the respective phosphate. The tightly bound ions move inside the respective cells. The total partition function Z is given by the summation over all the possible binding modes M,

$$Z=\sum _M{Z}_M\text{,}$$ (1)

where Z_M is the partition function for a given binding mode M (37–40),

$$Z_M=Z^{\left(id\right)}{\left(c_z\right)}^{N_b}\left(\int \prod _{i=1}^{N_b}d{\mathbf{R}}_i\right)e^{-\left(\Delta G_b+\Delta G_d+\Delta G_b^{pol}\right)/k_{\text{B}}T}\text{.}$$ (2)

Here Z^(id) is the partition function for the uniform ion solution (without the polyelectrolyte). The value c_z is the concentration of z-valent counterions. The value N_b is the number of tightly bound ions and

$$\int \prod _{i=1}^{N_b}d{\mathbf{R}}_i$$

is the volume integral for the N_b tightly bound ions. The value ΔG_b is the mean Coulombic interaction energy between the tightly bound charges (including the phosphate groups and the tightly bound ions). The value ΔG_d is the sum of the free energy for the electrostatic interactions between the diffusive ions, and among the diffusive ions and the tightly bound charges and the entropic free energy of the diffusive ions. The expression ΔG_b^pol is the (Born) self-polarization energy for the tightly bound charges (40). The calculations for ΔG_b, ΔG_d, and ΔG_b^pol are described in the Supporting Material and also in Tan and Chen (40).

Based on the partition function Eq. 1, the electrostatic free energy for RNA in ion solutions is computed by

$$G_{\text{E}}=-k_{\text{B}}T\ln \left(Z/Z^{\left(id\right)}\right)$$

and other electrostatic properties can also be computed (17).

Computation procedure and atomistic parameter sets

In both the TBI model and the PB calculations, for an atomistic nucleic acid structure (e.g., from the Protein Data Bank or the Nucleic Acid Database), the different types of atoms are treated as spheres with the radii determined by the respective van der Waals radii which has been tabulated in Table S1 in the Supporting Material. Each phosphate (P) atom is considered to carry one unit negative charge at its center, while other types of atoms (C, O, N, etc.) are treated as neutral spheres. The molecular van der Waals boundary defines the dielectric boundary. The computational process of the TBI model is briefly described as follows:

During the first step, for the given all-atom structure, we solve the PB equation to obtain the counterion distributions, from which we determine the tightly bound region for the multivalent counterions (37–40).

During the second step, we compute the pairwise potentials of mean force Φ₁(i) and Φ₂(i, j) and Born energy Φ₀(i); see the Supporting Material. To account for the dielectric discontinuity, we apply the generalized Born model for the calculations of the pairwise charge-charge interactions and the self-polarization energy of discrete charges (57–59). The Born radii for discrete charges are estimated from the pairwise method proposed by Hawkins et al. (58), and the scaling parameters for atoms are taken the values in Liu et al. (59); see Table S2. The volume exclusion between ions and nucleic acid atoms are accounted for by a truncated Lennard-Jones potential,

$$U=u_0\left(\frac{1}{r^{12}}-\frac{1}{r^6}\right)\text{,}$$

for r < 1 or U = 0 for r > 1, where r is the distance between an ion and an atom in the unit of the sum of their radii. The parameter u₀ is taken as 0.35 because the exclusion between the hydrated ions and the molecular atoms are soft due to the soft H-atom exclusion (60). The calculated potentials of mean force Φ₁(i) and Φ₂(i, j) and the Born energy Φ₀(i) are tabulated and stored for the following calculations of the partition function.

During the third step, we enumerate the possible binding modes. For each mode, we calculate ΔG_b, ΔG_d, and ΔG_b^pol (Eq. 2). The sum over the binding modes gives the total partition function Z (Eq. 1) (17,37,38), from which we can calculate the electrostatic free energy.

The ions are hydrated and the ionic radii are equal to 3.5 Å for Na⁺, 4.5 Å for Mg²⁺, and 4 Å for K⁺ (37–40), respectively. We also use a smaller divalent ion (with radius ∼3.5 Å) for the purpose of examining the ion size effect in the PB calculations. Here, the dielectric constant ɛ of nucleic acid interior is set to be 20, and ɛ of solvent is set as the value of water (37–40). In the PB calculation, a thin charge-free layer of thickness of a cation radius is added to the molecular surface to account for the excluded volume layer of the cations (37–40). The detailed parameter sets are given in the Supporting Material.

Results and Discussion

In the following sections, we apply the atomistic TBI model to investigate the properties of Mg²⁺ binding to the different nucleic acid structures, including duplexes and tertiary folds in mixed Na⁺/Mg²⁺ solutions. We will then compute the ion-dependent folding stability of HIV DIS type RNA kissing complex for a broad range of Na⁺/Mg²⁺ concentrations. All the theoretical predictions will be compared with the available experimental data. Furthermore, to examine the significance of ion correlation effect, the TBI-predictions will also be compared against the PB results. Based on the systematic quantitative predictions, we will derive a set of analytical formulas to for the estimation of the Na⁺/Mg²⁺ binding to nucleic acids.

Mg²⁺/Na⁺ binding to RNA/DNA

In the TBI model, the number of the so-called bound ions includes both the tightly bound Mg²⁺ ions and the diffusively bound ions (in the excess of bulk concentrations). Thus, the number of the bound Mg²⁺ and Na⁺ ions per nucleotide, f_Mg²⁺ and f_Na⁺, can be calculated according to the Boltzmann distribution of the diffusive ions (26)

$$\begin{array}{c}{f}_{{\text{Mg}}^{2+}}=\overline{f_b}+\frac{1}{N}\int \left[c_{{\text{Mg}}^{2+}}\left(\mathbf{r}\right)-c_{{\text{Mg}}^{2+}}^0\right]d^3\mathbf{r};\\ f_{{\text{Na}}^{+}}=\frac{1}{N}\int \left[c_{{\text{Na}}^{+}}\left(\mathbf{r}\right)-c_{{\text{Na}}^{+}}^0\right]d^3\mathbf{r},\end{array}$$ (3)

where $\overline{f_b}$ is the mean fraction of the tightly bound Mg²⁺ per nucleotide, which is given by the average over all the possible tightly bound modes M:

$$\overline{f_b}=\frac{1}{NZ}{\sum }_M{N}_b{Z}_M\text{.}$$

Here, N_b is the number of the tightly bound ions for mode M, Z_M is the partition function for mode M, Z is the total partition function given by Eq. 1, and N is the number of the phosphates (nucleotides) of the RNA. We note that the fractions of bound ions can be measured for the different nucleic acids. Therefore, in our theory-experiment comparisons, we adopt the data directly from the experimental literature (12,28,61–68).

We applied the TBI model to predict the properties of ion binding to different structures from short and long helices to complex RNA tertiary folds. Because the competition behaviors between Mg²⁺ and Na⁺ binding to different nucleic acids share some general features, in the following, we will first discuss the general behavior in Na⁺/Mg²⁺-binding and then analyze the specific features for different RNA/DNA structures.

General features in Mg²⁺/Na⁺-binding

We calculated the amount of Mg²⁺- and Na⁺-bound ions for a 24-bp DNA duplex, a 40-bp RNA and the DNA duplexes, a BWYV pseudoknot fragment, a 58-nt rRNA fragment, and the yeast tRNA^Phe, respectively. From Figs. 2 and 3, we can see the following general features for various RNAs/DNAs.

Figure 2.

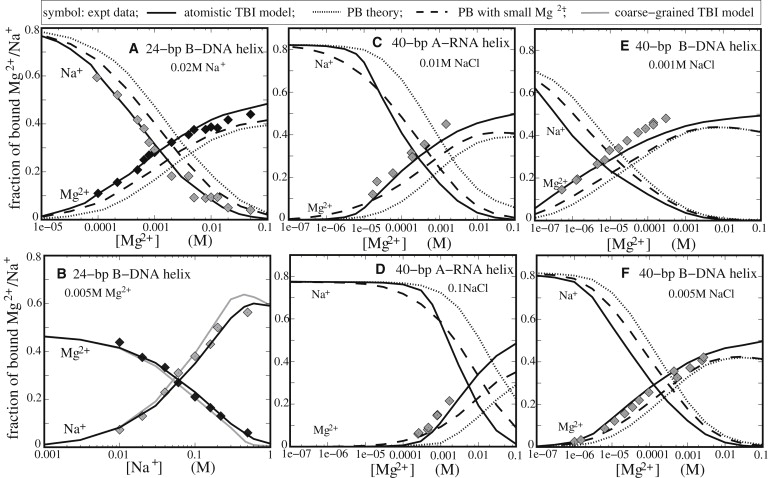
The Mg²⁺ and Na⁺ binding fractions per nucleotide for oligomeric DNA and RNA helices as functions of [Mg²⁺] or [Na⁺]. (Symbols) Experimental data. (Solid lines) Atomistic TBI predictions. (Dotted lines) PB predictions. (Dashed lines) PB predictions with a smaller Mg²⁺ radius (≃3.5 Å). (Shaded lines) TBI predictions on a coarse-grained DNA duplex. (A) A 24-bp B-DNA duplex in 20 mM Na⁺ (28,63). (B) A 24-bp B-DNA duplex in 5 mM Mg²⁺ (28,63). (C and D) A 40-bp RNA duplex in 10 mM [Na⁺] and 100 mM [Na⁺], respectively. The experimental data are for poly(A.U) (64). (E and F) A 40-bp DNA duplex in 1 mM [Na⁺] and 5 mM [Na⁺], respectively. The experimental data are for calf thymus DNA (65).

Figure 3.

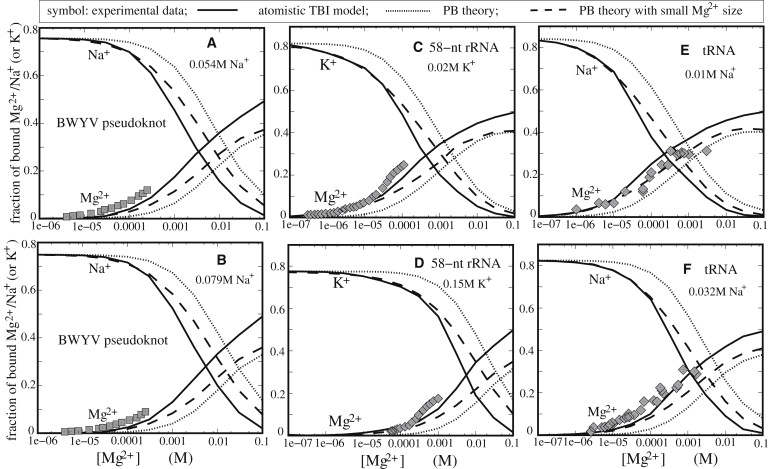
The Mg²⁺ and Na⁺ (or K⁺) binding fractions per nucleotide for various RNA tertiary structures. (Symbols) Experimental data. (Solid lines) Atomic TBI predictions. (Dotted lines) PB predictions. (Dashed lines) PB predictions with a smaller Mg²⁺ radius (≃3.5 Å). (A and B) BWYV pseudoknot fragment at different Na⁺ concentrations: 54 mM Na⁺ and 79 mM Na⁺, respectively. The experimental data are adopted from Soto et al. (12). (C and D) A 58-nt rRNA fragment at different K⁺ concentrations: 20 mM K⁺ and 150 mM K⁺, respectively. The experimental data are from Grilley et al. (66). (E and F) Yeast tRNA^Phe at different Na⁺ concentrations: 10 mM Na⁺ and 32 mM Na⁺, respectively. The experimental data was taken from Rialdi et al. (67) and Römer and Hach (68) for panels A for panels B, respectively.

Mg²⁺-binding and Na⁺-binding are competitively coupled, i.e., the increase of [Mg²⁺] ([Na⁺]) enhances Mg²⁺(Na⁺)-binding and suppresses Na⁺(Mg²⁺)-binding. Mg²⁺ has higher valency than Na⁺. Therefore, the same level of charge neutralization for RNA backbone requires a smaller number of bound Mg²⁺ ions and hence a smaller cost of the translational entropy upon ion binding, causing a stronger preference of Mg²⁺ binding than Na⁺.

For both Mg²⁺ and Na⁺ binding, the TBI predictions agree well with the experimental data for a variety of nucleic acid structures over a wide range of [Mg²⁺] and [Na⁺]. The PB theory, which ignores ion correlation, underestimates the amount of the bound Mg²⁺, especially at high [Mg²⁺]. This is because the Coulomb correlation (coupling) between the bound ions causes the ions to self-organize and reach low-energy states. Such correlation-induced low-energy states cannot be accounted for by a mean-field theory such as PB.

For very low [Mg²⁺], however, the TBI model gives the same results as the PB. This is because the number of bound Mg²⁺ is small and the average distance between the bound ions is large at low [Mg²⁺]; therefore, the interion correlation is weak.

The above findings are also in accordance with the results from the Monte Carlo study (61).

The high level of ion binding for Mg²⁺ at lower (millimolar) ion concentration than Na⁺ goes beyond the effect of the ionic strength. For example, for a 24-bp DNA duplex, 0.4 mM and 5 mM [Mg²⁺] are equivalent to 20 mM and 160 mM [Na⁺] (shown in Fig. 2, A and B), respectively, i.e.,

$$2f_{{\text{Mg}}^{2+}}\simeq f_{{\text{Na}}^{+}}\text{.}$$

The unusually efficient role of the Mg²⁺ may come from the higher ionic charge of Mg²⁺, which results in the stronger ability of the Mg²⁺ ions in RNA backbone neutralization and the stronger Coulomb correlation between the bound ions. The Coulombic correlation between the bound ions can significantly enhance the stability of the ion-RNA system (8).

In general, a smaller ionic radius can enhance the ion-RNA interaction and ion binding. Indeed, the use of a small Mg²⁺ size in the PB calculation (by decreasing the width of ion exclusion layer (30); see Methods) can improve the PB-based predictions on Mg²⁺-binding. However, such improvement is not sufficient to offset the difference between the PB prediction and the experimental data. Therefore, the theory-experiment difference for the PB may not just come from the effect of the ionic radius.

In addition to the above general features, the TBI model also predicts the differences in the ion binding properties for a great variety of different nucleic acid structures.

24-bp DNA duplex

Experiments based on the direct counting of the number of the bound ions (62) for a 24-bp DNA duplex (28,63) suggested that PB underestimates the Mg²⁺-binding and correspondingly overestimates the Na⁺-binding (28). The predictions from our TBI model, which explicitly accounts for the ion correlation and complete ensemble of ion distribution, show significant improvement for the predictions for both Na⁺ and Mg²⁺ binding over a wide ranges of ion concentrations (see Fig. 2, A and B). We note that Chu et al. (63) developed a size-modified PB theory to quantify the ion binding using adjustable effective ion sizes. Their method works well for mixed monovalent ion solution while the results are not completely satisfactory for Mg²⁺ solution (63). In contrast, the excellent agreement between the experimental data and the TBI predictions and the imperfect agreement between experiment and the PB/size-modified PB suggest that the interion Coulombic correlations and ion-binding ensembles may be important for the binding of multivalent ions such as Mg²⁺.

40-bp RNA and DNA duplexes

To examine the ability of the atomistic TBI model to treat long helices, we apply the model to treat the Mg²⁺- and Na⁺-binding to a 40-bp RNA duplex and a 40-bp DNA duplex. As shown by the theory-experiment comparisons in Fig. 2, C–F (64,65), TBI gives much more reliable predictions than PB, which tends to underestimate the binding of Mg²⁺. Similar to our conclusions for the ion-binding to the 24-bp DNA, we find that Mg²⁺ is much more efficient than Na⁺ in neutralizing the 40-bp duplexes. For example, for the 40-bp RNA duplex, 0.09 mM and 2.5 mM Mg²⁺ can approximately cause the same neutralization as 10 mM and 100 mM Na⁺, respectively. The overall agreements between the TBI predictions and the experimental data in Fig. 2, C–F, show that the helix-end effect for Mg²⁺-binding to the 40-bp duplexes is minor, in accordance with the previous analysis on Mg²⁺-binding to a DNA helix (40).

BWYV pseudoknot fragment

Fig. 3, A and B, shows the Mg²⁺ and Na⁺ binding fractions for a BWYV pseudoknot fragment predicted by the TBI model and the PB theory, along with the experimental data (12). The concentration dependence of Mg²⁺ and Na⁺ binding shows a trend similar to the one in Fig. 2. Theory-experiment comparison indicates that the TBI model gives reliable predictions for this 29-nt complex RNA tertiary structure (12). As shown in Fig. 3, A and B, 1.6 mM and 2.5 mM Mg²⁺ have about the same effect on RNA backbone neutralization as the 54 mM and 79 mM Na⁺, respectively. For the same RNA, a previous PB calculation yields ion binding slightly lower than the experimental results (12). We note that the PB calculation was based on an ion-exclusion layer of 2 Å, effectively corresponding to a small radius of 2 Å for both Mg²⁺ and Na⁺ ions. Small ion size results in enhancement of ion binding predicted by PB, and partially offsets the deficiency in ion binding caused by the neglect of ion correlation for the Mg²⁺ ions.

58-nt ribosomal RNA fragment

To investigate the ion-binding in a mixed Mg²⁺/K⁺ solution, we model K⁺ as a monovalent ion with a hydrated radius 4 Å, slightly larger than 3.5 Å for Na⁺. Fig. 3, C and D, shows that TBI gives reliable predictions for the Mg²⁺ and K⁺ binding to a 58-nt rRNA fragment (66). In contrast, the PB theory underestimates the Mg²⁺ binding and overestimates the K⁺ binding. Moreover, Mg²⁺ shows much higher efficiency in ion-binding and charge neutralization than K⁺. Specifically, 0.17 mM and 2.8 mM Mg²⁺ have the same effect in backbone charge neutralization as 20 mM and 150 mM K⁺, respectively. In contrast, we note that a previous PB calculation for the system involves much smaller radii for the (hydrated) ions (through the 2 Å ion-exclusion layer) for both K⁺ and Mg²⁺ (66).

Yeast tRNA^Phe

To extend the TBI analysis to larger and more complex structures, we investigated the ion-binding properties for yeast tRNA^Phe. We quantify the Na⁺-Mg²⁺ competition in the binding to yeast tRNA^Phe (54). Fig. 3, E and F, shows that, as compared with the experimental data (67,68), the TBI model gives better predictions than the PB theory, which underestimates the Mg²⁺ binding. Decreasing the Mg²⁺ size in the PB calculations would improve the prediction. However, the improvement is not sufficient to make up the deficiency in the PB prediction presumably caused by the neglect of the correlation effect. For neutralizing the tRNA^Phe, 0.07 mM and 0.4 mM Mg²⁺ have the same effect as 10 mM and 32 mM Na⁺, respectively.

Atomistic TBI versus coarse-grained TBI

By considering correlated ion distributions, the previous coarse-grained TBI model is able to give reliable predictions for the ion effects for simple nucleic acid structures such as DNA and RNA helices (25,26), DNA and RNA hairpin stability (27), and DNA helix assembly/bending (38–40). However, the coarse-grained model, originally derived for helices, cannot treat single-stranded regions of the structure and other, more-complex structures such as the tertiary packing of loops and helices. Therefore, a TBI model that can handle atomic structures of RNAs becomes indispensable for the study of ion effect in tertiary structural folding. As shown above by the theory-experiment comparisons, our atomistic TBI model can indeed give reliable predictions for Mg²⁺/Na⁺-binding properties for complex RNA tertiary folds such as BWYV pseudoknot, rRNA fragment, and yeast tRNA.

It is important to note that the previous coarse-grained model cannot represent the above tertiary folds in a reliable way, therefore, for the tertiary folds, a direct comparison between the present atomic TBI model and the previous coarse-grained TBI model is not possible. However, such a direct comparison is possible for simple nucleic acid helices (see Fig. 2 B).

Fig. 2 B shows the Mg²⁺/Na⁺-binding as a function of [Na⁺] for a 24-bp DNA helix immersed in a solution with 5 mM Mg²⁺. Detailed comparisons between the present atomic TBI and the previous coarse-grained TBI models and experimental data show the following results:

• 1.Both models give overall reliable predictions.
• 2.In the Mg²⁺-dominating region (low [Na⁺]), the two models give nearly identical predictions.
• 3.In the Na⁺-dominating region (high [Na⁺]), the coarse-grained model slightly overestimates (underestimates) the Na⁺-binding (Mg²⁺-binding).

The very slight discrepancy between the two models might come from the molecular shape and volume which directly influence the accumulations of Na⁺ ion cloud near the DNA surface. In addition, for the 24-bp duplex, the atomic TBI model costs about twice the computational time as the coarse-grained model because the all-atomic structure considers more atoms (spheres) than the coarse-grained one.

In the TBI calculations, we also examined the sensitivity of the TBI predictions to the ion sizes. We have previously shown that smaller ions are more efficient in ionic neutralization and stabilization of the folded (or compact) structures (25,26,40). Here, for a 24-bp DNA helix in 20 mM Na⁺ and 10 mM Mg²⁺, the atomic TBI predicts that the decrease of Mg²⁺ size from 4.5 Å to 4 Å would cause the decrease in electrostatic free energy by ∼10% and the increase in tightly bound Mg²⁺ number by ∼4%. The decrease in Na⁺ size also enhances the Na⁺ binding, but the effect is not as strong as for Mg²⁺.

Na⁺-binding versus Mg²⁺-binding: analytical formulas

Charge neutralization

The TBI model allows us to systematically compute the mean number of bound ions per nucleotide $f_{{\text{Mg}}^{2+}}$ and $f_{{\text{Na}}^{+}}$ for the different RNA structures and different ion concentrations in a mixed Na⁺/Mg²⁺ solution. Based on the TBI calculations, equating $2f_{{\text{Mg}}^{2+}}$ and $f_{{\text{Na}}^{+}}$ (i.e., equal charge neutralization) leads to the following empirical conversion formula between the ion concentrations,

$$\log {\left[{\text{Na}}^{+}\right]}_{\text{Mg}}=A\log \left[{\text{Mg}}^{2+}\right]+B,$$ (4)

where [Na⁺]_Mg and [Mg²⁺] are the concentrations in millimolar (mM). Physically, for a nucleic acid in a mixed Na⁺/Mg²⁺ solution with a specific [Mg²⁺], such [Mg²⁺] can achieve the same ionic neutralization as the [Na⁺]_Mg defined by Eq. 4. Our data for a variety of RNA structures discussed in the preceding sections suggest that, as an approximation, the chain length (N-nt) and the radius of gyration (R_g) of RNA backbone may be the two (low-resolution) determinants for parameters A and B,

$$\begin{array}{l}A=0.65+\frac{4.2}{N}{\left(\frac{R_g}{R_g^0}\right)}^2,\\ B=1.8-\frac{9.8}{N}{\left(\frac{R_g}{R_g^0}\right)}^2,\end{array}$$ (5)

where R_g⁰ is the radius of gyration for the corresponding A-form N-nt RNA helix. Equations 4 and 5 partially reflect the effects of the number N of the phosphate charges and the compactness R_g of RNA backbone. It is important to note that the R_g²-dependence reflects the effect of RNA surface charge density on ion-binding.

We calculated R⁰_g for RNA duplexes with N nucleotides and found R_g⁰ = 0.406N + 130/(N + 11), where N ≳ 10-nt. As shown in Fig. S5 in the Supporting Material, Eq. 4 fits the results from the exact calculations quite well for both RNA duplexes and complex RNA tertiary structures.

Ion-binding profile in a mixed Mg²⁺/Na⁺ solution

Based on Eq. 4, we can derive an analytical formula for the [Na⁺]/[Mg²⁺]-dependent ion-binding profiles,

$$\begin{array}{l}{f}_{{\text{Mg}}^{2+}}=\frac{{\left[{\text{Na}}^{+}\right]}_{\text{Mg}}}{{\left[{\text{Na}}^{+}\right]}_{\text{Mg}}+\left[{\text{Na}}^{+}\right]}{f}_{{\text{Mg}}^{2+}}^0,\\ f_{{\text{Na}}^{+}}=\frac{\left[{\text{Na}}^{+}\right]}{{\left[{\text{Na}}^{+}\right]}_{\text{Mg}}+\left[{\text{Na}}^{+}\right]}{f}_{{\text{Na}}^{+}}^0,\end{array}$$ (6)

where [Na⁺]_Mg is given by Eq. 4 and $f_{{\text{Mg}}^{2+}}^0$ and $f_{{\text{Na}}^{+}}^0$ are the mean numbers of bound ions per nucleotide for pure Mg²⁺ (i.e., [Na⁺] = 0) and pure Na⁺ (i.e., [Mg²⁺] = 0, [Na⁺]_Mg = 0) solutions, respectively. Strictly, $f_{{\text{Mg}}^{2+}}^0$ and $f_{{\text{Na}}^{+}}^0$ depend on the charge density of nucleic acids and ion concentration. From the calculations over the extensive nucleic acid molecules, $f_{{\text{Mg}}^{2+}}^0$ and $f_{{\text{Na}}^{+}}^0$ only changes slightly for various molecules, as shown in Figs. 2 and 3. Here, for simplicity, we approximately use the constants of $f_{{\text{Mg}}^{2+}}^0\sim 0.47$ and $f_{{\text{Na}}^{+}}^0\sim 0.8$ for the extensive RNA and DNA molecules.

Extensive tests based on the experimental data for various RNA (and DNA) structures show that the analytical formulas above (Eqs. 4 and 6) are quite accurate over a wide range of ionic conditions (see Fig. S6 in the Supporting Material).

Ion-dependent stability of RNA loop-loop kissing complex

We model the folding stability of RNA kissing complex based on a two-state model: the kissing complex and the unkissed state (i.e., two dissociated hairpins) (see Fig. 1 G). The difference in the charge distributions of the kissing and the unkissed states leads to the ion-dependence of the folding stability of the kissing complex.

The stability of the kissing complex can be quantified by the free energy difference ΔG^o_T between the two states:

$$\Delta G_T^o=G_T^o\left(\text{kissing}\right)-G_T^o\left(\text{unkissed}\right)\text{.}$$ (7)

As an approximation, ΔG^o_T is decomposed into two parts: the electrostatic contribution $\Delta G_T^{\text{el}}$ and the nonelectrostatic (chemical) contribution $\Delta G_T^{\text{nel}}$ (25,26),

$$\Delta G_T\left({\text{Na}}^{+}/{\text{Mg}}^{2+}\right)=\Delta G_T^{\text{el}}\left({\text{Na}}^{+}/{\text{Mg}}^{2+}\right)+\Delta G_T^{\text{nel}}\text{,}$$ (8)

$$=\Delta G_T^{el}\left({\text{Na}}^{+}/{\text{Mg}}^{2+}\right)+\left[\Delta G_T\left(1\text{M}{\text{Na}}^{+}\right)-\Delta G_T^{el}\left(1\text{M}{\text{Na}}^{+}\right)\right]\text{,}$$ (9)

where the electrostatic free energies ΔG^el_T (Na⁺/Mg²⁺) and ΔG^el_T (1 M Na⁺) are calculated from the polyelectrolyte theory (the TBI model) and ΔG^o_T (1 M Na⁺) is obtained from experimental measurement. From ΔG_T, the melting temperature T_m can be computed for a given strand concentration C_S (19,26).

We focus on two specific kissing complexes (KC-1 and KC-2 in Fig. 1). With the TBI model, we calculate the free energy change ΔG₃₇ at 37°C and the melting temperature T_m as functions of Na⁺ and Mg²⁺ concentrations.

ΔG₃₇ for KC-1 and KC-2 in Na⁺ solution

Fig. 4 A shows the folding free energy ΔG₃₇ as a function of [Na⁺] for KC-1 and KC-2. The increase of [Na⁺] causes the decrease of ΔG₃₇, indicating that Na⁺ favors the formation of the kissing complex over the unkissed state. This is because Na⁺-binding causes reduced Coulomb repulsion between the backbone charges and a lower free energy, and such Na⁺-induced stabilizing force is more significant for a more densely charged state—the kissing complex.

Figure 4.

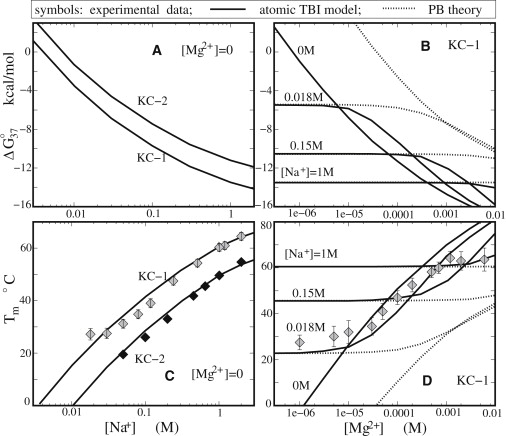
The free energies ΔG₃₇ (A and B) and melting temperature T_m (C and D) as functions of the Na⁺ concentration (A and C) and the Mg²⁺ concentration (B and D). (C) The experimental data for KC-1 and KC-2 are from Weixlbaumer et al. (49) and Lorenz et al. (50), respectively. (D) The experimental data are from Weixlbaumer et al. (49). (Solid lines) TBI predictions. (Dotted lines) PB predictions.

T_m for KC-1 and KC-2 in Na⁺ solution

In accordance with the Na⁺-dependence of ΔG₃₇, the melting temperatures T_m increases with increasing [Na⁺], as shown in Fig. 4 C, indicating the higher stability at high [Na⁺]. Theory-experiment comparison shows that the TBI predictions agree well with the experimental data for both complexes (49,50).

ΔG₃₇ for KC-1 in mixed Na⁺/Mg²⁺ solution

In a pure Mg²⁺ solution ([Na⁺] = 0), the increase of [Mg²⁺] causes the decrease in ΔG₃₇ and higher stability of the complex (see Fig. 4 B), which is similar to the trend for the Na⁺-dependence. However, Mg²⁺ is much more efficient than Na⁺ to achieve the same folding free energy. For example, 0.4 mM Mg²⁺ and 100 mM Na⁺ cause approximately the same free energy ΔG₃₇ (∼−10 kcal/mol) for KC-1. The efficient role of Mg²⁺ is due to the higher ionic charge of Mg²⁺ and the possible ion correlation effect, as discussed above. For a pure Mg²⁺ solution, the PB theory predicts much higher ΔG₃₇ than the TBI calculations, which is in accordance with the predictions on the Mg²⁺-binding for other structures discussed in the preceding sections.

In a mixed Na⁺/Mg²⁺ solution, there are apparently three regions in the ΔG₃₇ curves as a result of the interplay between the Na⁺ and Mg²⁺ binding (26,27): Mg²⁺ dominant, Na⁺-Mg²⁺ competitive, and Na⁺ dominant regions. When [Mg²⁺] is high (relative to [Na⁺]), Mg²⁺ dominates the system. In this case, ΔG₃₇ is close to the value for the corresponding pure Mg²⁺ solution and PB underestimates the Mg²⁺-induced stabilization. With the addition of Na⁺, Na⁺ begins to compete against Mg²⁺ in ion-binding and pushes Mg²⁺ away from the RNA surface, resulting in a weakened effect of Mg²⁺. Because the (divalent) Mg²⁺ is much more efficient than the (monovalent) Na⁺ in stabilizing the folded RNA, the weakened Mg²⁺-binding (and the enhanced Na⁺-binding) could lead to (slight) destabilization of the kissing complex. When [Na⁺] becomes high enough, Na⁺ would dominate the ion effect. In this case, ΔG₃₇ becomes close to the value of the pure Na⁺ and the TBI model and the PB theory give the same results.

T_m for KC-1 in a mixed Na⁺/Mg²⁺ solution

The salt dependence of the melting temperature T_m in mixed Na⁺/Mg²⁺ is in accordance to ΔG₃₇, as shown in Fig. 4 D. For the Na⁺- or Mg²⁺-dominated regime, T_m is close to the value of the corresponding pure Na⁺ or Mg²⁺. For the Na⁺-Mg²⁺ competing regime, the addition of Na⁺ causes slight increase in the T_m as compared with the pure Mg²⁺. As discussed above and previously (26,27), this is because the addition of Na⁺ counteracts the efficient role of Mg²⁺.

Fig. 4 D also shows that the TBI predictions are in good agreement with the available experimental data (49), while the PB theory underestimates T_m for the concentration range where Mg²⁺ ions play a role. The significant deviation between the PB prediction and the experimental data may be attributed to the neglect of ion-ion correlations and ion-binding ensemble, as discussed above.

Kissing complex versus duplex

The salt (Na⁺ and Mg²⁺)- dependence of T_m for the kissing complexes is stronger than that for the corresponding duplex with the same kissing and terminal mismatch sequences (26,49) (see Fig. 1). This is because the kissing complex involves much higher charge buildup, and hence, a much stronger ion dependence than the duplex.

At high salt (1M NaCl), the kissing complex has higher stability than the corresponding duplex. The higher stability may come from two contributions. First, because the initial unkissed state (dissociated hairpins) has a much smaller entropy than free single-strand chains (27), the formation of the kissing complex from the unkissed hairpins involves a smaller conformational entropy loss than the formation of the duplex from single-stranded chains. Second, the two hairpin stems are coaxially stacked in the kissing complex (49,50,55), and can further enhance the stability of the complex.

Kissing complexes KC-1 versus KC-2

T_m values of KC-1 and KC-2 have the similar [Na⁺]-dependence and very different [Mg²⁺]-dependence (49,50). The experimental Mg²⁺-dependence of T_m for KC-2 is weaker than that for KC-1 (49,50) (not shown here). This may be attributed to the sequence-dependent specific binding of Mg²⁺, while Na⁺ ions have negligible contribution to the specific binding. Experiments suggest that the uronic acid (U)-rich sequence of KC-2 would help the Mg²⁺ specific binding through the attraction between the negatively charged O atom (in U) and the positively charged Mg²⁺ (55), and the effect may be even more pronounced for the dangling U-sequence near the kissing interface (55); see KC-2 in Fig. 1. As a result, [Mg²⁺]-dependence of T_m for KC-2 is weaker due to the (weakly [Mg²⁺]-dependent) neutralization by the specific binding of Mg²⁺ (50).

Conclusions

This tightly bound ion model (TBI) enables all-atom treatment for the ion correlation and ion fluctuation effects which can be important for multivalent ions such as Mg²⁺ ions in RNA folding. The availability of the high-resolution all-atom RNA/DNA structures motivates the development of an all-atom model for the TBI theory. Based on the atomistic TBI model, we systematically quantify the Na⁺/Mg²⁺-binding to different nucleic acid structures as well as the salt-dependent RNA kissing complex stability. Our main conclusions are the following.

• 1.Mg²⁺ is much more efficient in ionic neutralization than Na⁺, and such high efficiency goes beyond the mean-field electrostatic effect such as the ionic strength. The high efficiency of Mg²⁺ is stronger for compact tertiary folds than for extended states.
• 2.
  The Mg²⁺ binding and Na⁺ binding are competitively coupled in a mixed Na⁺/Mg²⁺ solution. There exist approximately three distinctive regimes for the Na⁺-Mg²⁺ competitive binding:

  • I.
    For [Mg²⁺] > > [Na⁺], Mg²⁺ binding is dominant and Na⁺ binding is suppressed. In this case, the PB underestimates the Mg²⁺-binding possibly due to the neglect of the ion correlation and fluctuation effects. In contrast, the TBI model gives much improved predictions.
  • II.
    As [Na⁺] increases, Na⁺-Mg²⁺ competition becomes stronger. Because of the high efficiency of Mg²⁺-binding, Mg²⁺-binding may still outcompete Na⁺-binding; thus, PB may still underestimate the Mg²⁺-binding.
  • III.
    [Na⁺] >> [Mg²⁺], Na⁺-binding becomes dominant. In this case, PB and TBI give the same predictions.
• 3.There exists a reliable analytical formula for the Mg²⁺/Na⁺-binding as a function of [Mg²⁺] and [Na⁺], the chain length, and the structure compactness of nucleic acids.
• 4.The kissing complex formation is electrostatically highly unfavorable because of the strong Coulombic repulsion. Na⁺ and Mg²⁺ can effectively reduce such repulsion and make the complex formation less unfavorable. The Na⁺/Mg²⁺-dependence of kissing complex is very strong. The TBI model gives reliable predictions for the ion-dependent folding stability of the kissing loop complexes.

The excellent agreement between the TBI predictions and the experimental data for ion-binding properties and folding free energies indicates that the model is quite reliable. However, the model has several limitations.

In the TBI model and the PB calculations, we assume that each phosphate has one negative unit charge and treat all other types of atoms as neutral ones without considering the detailed partial charges.

The nonideality of the ionic solution is neglected and ions are assumed to be completely dissociated from each other. The nonideality effect of the solution, which can become important at high salt concentrations, may contribute to the overestimation of ion-binding (at high salt concentration) (47).

We ignore the effect of specific ion binding. The contribution of the specific binding to the global ion-dependence of the folding stability might not be significant. However, specific ion-binding may be important for the sequence-sensitive features of the ion effect for many tertiary folds such as the KC-2 kissing complex.

In the TBI model, the interactions in the tightly bound region are calculated as the sum of the pairwise potentials of mean forces where multibody effects are neglected. The experimental comparisons for the binding curves suggest that the TBI model generally tends to overestimate ion binding at high (divalent) ion concentrations.

All the above approximations (ideality of the ionic solution, pairwise potential of mean force) can contribute to such theory-experiment discrepancy. Further development of the model should include the improvement for the above approximations. A possible way for further development of the model may involve a combination of the present TBI theory and computer simulations. For ion-binding properties to RNAs, computer simulations (48,69) can be highly valuable in providing detailed ion distributions, sequence effects, and the ion-related dynamics. Detailed simulations can also provide effective tests and validations for many theoretical predictions such as the empirical formula that we derived in this study.