Exploring the Paths of (Virus) Assembly

Abstract

Assembly of viruses that have hundreds of subunits or folding of proteins that have hundreds of amino acids—complex biological reactions—are often spontaneous and rapid. Here, we examine the complete set of intermediates available for the assembly of a hypothetical viruslike particle and the connectivity between these intermediates in a graph-theory-inspired study. Using a build-up procedure, assuming ideal geometry, we enumerated the complete set of 2,423,313 species for formation of an icosahedron from 30 dimeric subunits. Stability of each n-subunit intermediate was defined by the number of contacts between subunits. The probability of forming an intermediate was based on the number of paths to it from its precedecessors. When defining population subsets predicted to have the greatest impact on assembly, both stability- and probability-based criteria select a small group of compact and degenerate species; ergo, only a few hundred intermediates make a measurable contribution to assembly. Though the number of possible intermediates grows combinatorially with the number of subunits in the capsid, the number of intermediates that make a significant contribution to the reaction grows by a much smaller function, a result that may contribute to our understanding of assembly and folding reactions.

Introduction

Many viruses spontaneously assemble from purified components. In this way, they are analogous to proteins that spontaneously fold. In both cases, everything required for the reaction is contained in the primary structure (1). Though virus capsids may have hundreds of individual subunits, they assemble with high fidelity in a biologically relevant time frame; thus, they have found a way to simplify the immense number of paths available to them, overcoming the equivalent of the Levinthal paradox (2).

In the development of any general model of virus self-assembly, it is important to consider biological examples of the reaction. Viruses show structural diversity, evident in the details of their assembly, but common underlying physics. In vitro assembly has been investigated with bacteriophage P22 (3), hepatitis B virus (4), cowpea chlorotic mottle virus (CCMV) (5,6), bacteriophage MS2 coat protein homodimers (7,8), and papillomavirus (9), to name a few examples. In general, assembly is driven by weak interactions connecting polyvalent subunits (10). The pairwise association energy between subunits is on the order of 2–4 kcal/mol (11–14). Assembly reactions for most viruses show sigmoidal kinetics, where intermediates are observed only transiently (6,9,15–17).

Models of such complex reactions are required to interpret experimental data and are powerful tools for generating new hypotheses. Modeling of virus capsid assembly has taken many approaches, from master equations (18–23) to discrete events (24) to molecular dynamics (25–27). Each approach has advantages and limitations. Dynamics approaches allow self-selection of intermediates based on molecular interactions but are sensitive to parameterization (especially in coarse-grained simulations) and limited sampling due to computational overhead. Master equations have more modest computational requirements, facilitating examination of a broad range of assembly conditions, but this approach requires explicit descriptions of intermediates and paths between them (18,19). In the simplest biological applications, master equation models have followed a single path of the most stable intermediates from subunit to complete capsid (20,21). Because of its relevance to biology and to developing more relevant master equations, describing assembly paths has been the subject of considerable effort. Paths for assembly of geometric molecules have been developed from graph theory and applied to small molecules and viruses to show the diversity of paths (18,19). Assembly paths for polyomaviruses and papillomaviruses have been suggested based on tiling (22,28–30). Based on thermodynamic considerations, likely paths were suggested for human rhinovirus, poliovirus, southern bean mosaic virus, and black beetle virus (31,32).

Although such paths are plausible, their selection is based on specific assumptions. Here, we enumerate all possible intermediates in the assembly of a generic geometric model, a 30-subunit icosahedron assembled from dimers. With these data, we are able to examine the probability or kinetic accessibility of a species (i.e., the number of forward paths available to generate a structure), which is likely to be a critical factor in situations where assembly is essentially unidirectional. We also can evaluate the thermodynamic stability of a species, a feature that is likely to be a critical factor where species are approaching equilibrium. By both of these criteria, we find very small and extensively overlapped sets of intermediates, notable for their compact form. These are the only species that contribute substantially to assembly, and appear to be all that are required for assembly simulations that recapitulate the behavior of a much larger database.

Methods

ENUMERATOR is a suite of programs for describing the intermediates of capsid assembly. A manual and source code, including input files, is supplied in the Supporting Material; here, we give a brief overview.

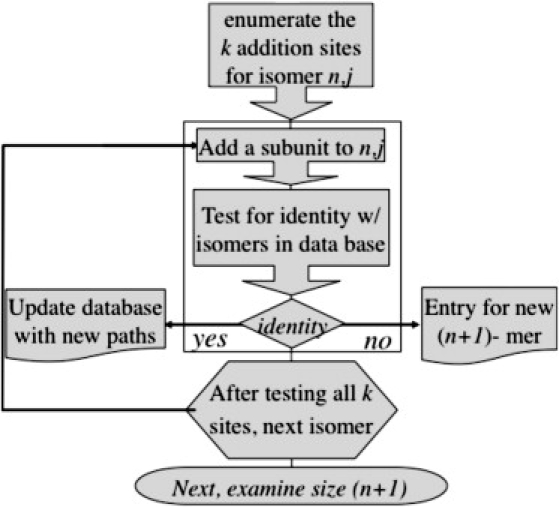
The three elements of ENUMERATOR are the input file, PRELOAD, and LOAD (Fig. 1). The input file for PRELOAD includes a description of the final particle, the subunit(s), and the seed subunit(s). The input file specifies the geometry of the model in terms of vertices, edges, turns along subunit outlines, and the unique faces (synonymous with subunit in ENUMERATOR's syntax), all based on a unit sphere. The seed is defined by the subunits. Edges are defined as traversing from one vertex to another. They require a starting vertex, an ending vertex, and the name of the adjacent seeds. Turns are defined as starting from one edge and ending at a destination vertex. Each turn has a name and a reference to its associated edge.

Figure 1.

A schematic of ENUMERATOR.

PRELOAD generates a complete geometric description of the model in two distinct processes. The first process creates abstracts of the geometric components with the exception of the vertex. It labels all the components with their given names. After the seed, faces are defined implicitly by their relation to other components. Each vertex is defined by Cartesian coordinates. The abstract edges are defined in terms of vertices and faces. They reference two vertices and the names of the adjacent faces. The abstract turn builds on this, referencing the interior angle between two joined edges. PRELOAD defines all the specific components. It enumerates each edge, turn, and face of the model and assigns a numerical reference to each. This process starts by defining a face that includes the starting edge identified by the input file. A queue starts with this edge, where for each edge in this queue all possible turns are explored, generating new edges in the queue, eliminating duplication. By convention, the next edge follows the sharpest left turn, giving edges associated with the current face higher priority. Each edge is assigned its start and end vertex at this time. When the face is complete, the next edge in the queue starts a new face. The queue is empty when the last face has been defined.

LOAD performs the build-up procedure. It starts with a specified face or faces to seed the process, placing the available build-up sites into a source queue. The elements in this queue are processed one by one. For the current intermediate, one subunit is added at a time to every open binding site and written to a database. The collection of new intermediates, from all the recently processed intermediates, forms the basis of the next source queue. This process stops when a new subunit cannot be added. LOAD enumerates every possible intermediate, its stability (e.g., the number of intersubunit contacts), the paths for its assembly, and paths of disassembly (assuming that both assembly and disassembly reactions proceed one subunit at a time). Each species is given a unique identifier, (n,j), where n is the number of subunits and j is an arbitrary index. As each structure is generated, it is compared to a growing list of like-sized polymers so that each (n,j) remains unique and an accurate count is kept of paths to and from it. The vast majority of the time required to run ENUMERATOR is devoted to testing for redundancy. To minimize detailed examination of intermediates, comparisons are filtered by coarse criteria starting with size, number of intersubunit contacts, path around the perimeter, and number of holes within the contiguous complex. Thus, a complete run for a 20-subunit, 2600-intermediate icosahedron takes on the order of 10–15 min, whereas it took on the order of 3600 CPU hours to compile the 2.4-million-intermediate database for a 30-mer.

The list of species is compiled in a flat file database. Other programs can output that data in a variety of forms including a PostgreSQL database. One of the outputs from ENUMERATOR is a list of differential equations for kinetic simulations. Simulations were accomplished by the numerical integration program BERKELEY MADONNA (http://www.berkeleymadonna.com/), implementing a fourth-order Runge-Kutta integration scheme. The much smaller single-path simulations could be treated as stiff equations and integrated by the method of Rosenbrock, as implemented in MADONNA. Schematically, equations are of the form

$$d\left[n,j\right]/dt=\sum \left(\text{assembly}\text{from}\left(\text{n}-\text{1},\mathit{j}\right)\right)-\left(\text{assembly}\text{from}\left(\text{n},\mathit{j}\right)\right)-\left(\text{dissociation}\text{of}\left(\mathit{n},j\right)\right)+\sum \left(\text{dissociation}\text{of}\left(\mathit{n}+1,\mathit{j}\right)\right)\text{.}$$ (1)

Each forward reaction is described by a microscopic forward rate constant, k_f, modified by a statistical factor, s_n,j,κ (the number of paths toward the intermediate of n subunits and arbitrary index j from the n − 1 intermediate with index κ) (20). Backward rates are based on KD = k_back/k_f, where KD is based on the integral number of contacts made or broken also modified by a statistical factor, sb_n,j,κ. For example, Eq. 2 shows (n,j) = (6,6),

$$d\left[6,6\right]/dt=k_{\text{f}}\left[1,1\right]\left(s_{6,6,2}\left[5,2\right]+s_{6,6,3}\left[5,3\right]+s_{6,6,4}\left[5,4\right]\right)-s_{7,1,6}{k}_{\text{f}}\left[1,1\right]\left[6,6\right]-s{b}_{6,6,1}{k}_{\text{f}}K{D}_{6,6,1}\left[6,6\right])+k_{\text{f}}(s{b}_{7,2,6}K{D}_{7,2,6}\left[7,2\right]+s{b}_{7,3,6}K{D}_{7,3,6}\left[7,3\right]+s{b}_{7,9,6}K{D}_{7,9,6}\left[7,9\right]+s{b}_{7,24,6}K{D}_{7,24,6}\left[7,24\right]+s{b}_{7,25,6}K{D}_{7,25,6}\left[7,25\right]+s{b}_{7,26,6}K{D}_{7,26,6}\left[7,26\right]+s{b}_{7,27}K{D}_{7,27,6}\left[7,27\right]+s{b}_{7,28,6}K{D}_{7,28,6}\left[7,28\right])\text{.}$$ (2)

The differential equation for [1,1], the monomer concentration, is particularly unwieldy because it is affected by every assembly and disassembly reaction.

The statistical factors modifying the forward rates, if normalized over all reactions of (n − 1) ⇒ n, would be equivalent to Markov transmission factors. The probability of a species of size n and index j, P(n,j), is calculated over all n-mers and takes into account the probability of preceding species. P(n,j) is thus a function of the statistical factors (20,23) multiplied by the probability of the κ preceding species and normalized over all j species. As described later in the text, in some cases, a factor μ (0 ≤ μ < 1) is included to downweight the probabilities of the (n,j) products of (n − 1,κ) unstable species; there is no weighting when μ = 1.

$$\text{P}\left[n,\kappa \right]=\frac{\sum _{\kappa }{s}_{n,j,\kappa }\text{P}\left[n-1,\kappa \right]{\mu }_{n,j,\kappa }}{\sum _j\sum _{\kappa }{s}_{n,j,\kappa }\text{P}\left[n-1,\kappa \right]{\mu }_{n,j,\kappa }}$$ (3)

Results

Our choice of model for these investigations is an icosahedral 30-mer (Fig. 2, inset). In the context of this capsid, each dimerlike subunit is tetravalent and has twofold symmetry. The subunits are analogous to those found in many viruses, including hepatitis B virus, CCMV, Brome mosaic virus, and bacteriophage MS2. The 30-mer is computationally tractable for our purposes but still allows a diversity of assembly paths not available in smaller assembly models (e.g., a dodecahedron constructed from pentagons (23)). We consider assembly by the addition of only one subunit at a time, because the concentrations of intermediates will be extremely small compared to the concentration of subunit, except under the exceptional conditions that lead to kinetically trapped reactions (13,24).

Figure 2.

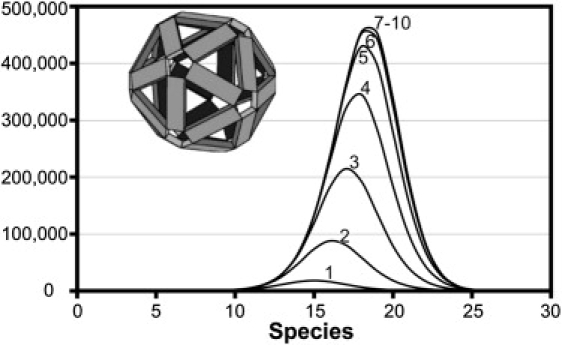
All possible intermediates for assembly of a 30-mer. The 30-mer itself (taken from Keef et al. (30)) is shown in the inset. The individual lines in this histogram are based on the number of holes in a growing oligomer, from one hole (the open edge of a growing oligomer) to 10 holes. The lines for 7–10 holes are very close, so that they are all obscured by the thick line used for the 10-hole histogram. There are 2.4 million species overall.

Census of intermediates

For an N = 30 capsid, there are a total of 2,423,323 possible species, including monomer and capsid. Most species in this population have two or more holes in them, where a hole is defined as a gap of one or more subunits from the complex, so that all incomplete complexes have, by definition, at least one hole. There are only 97,741 species with a continuous surface of subunits (≤1 hole). For ≤1 hole, the population of species has a normal distribution centered on N/2 = 15 (Fig. 2); the distribution of sizes is symmetrical, because the continuous complex of subunits is exactly mirrored by a continuum of missing subunits. However, the overall population maximum is distinctly skewed by the many species with two or more holes to a maximum of 452,327 for 18-mers.

The population was evaluated for stability (Fig. 3, A and B). For simplicity, we equated stability with the number of intersubunit contacts, ignoring the small statistical/entropic contribution to stability. The three lowest energy levels (i.e., the most contacts for a given size species) are comprised of 141, 1016, and 5147 total species, including monomer and capsid. For these lowest energy levels, the number of contacts correlates with compactness. The lowest energy level population is symmetrically distributed, with 1–15 species in each size range (Fig. 3 A). As shown later in this article, a critical feature of the lowest energy level is that the number of examples of an n-mer jumps up and down from 1 to 16. When additional energy levels are included in the histogram, the population distribution becomes asymmetric with multiple holes in some larger particles. The number of species in the first three energy levels is relatively modest, but the number increases sharply as this constraint is relaxed.

Figure 3.

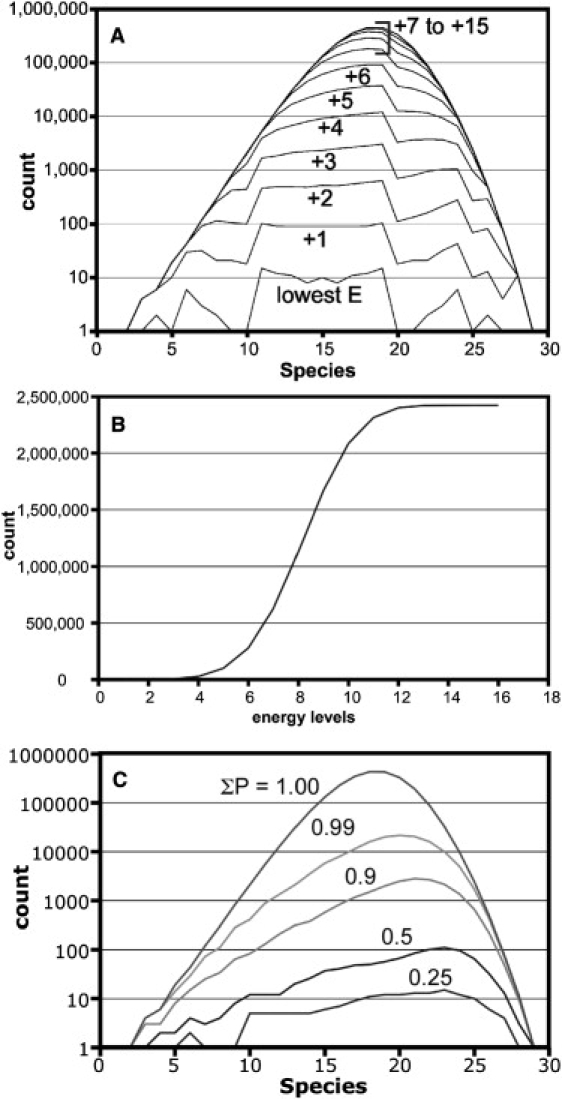
Parsing intermediates by stability and probability. (A) A histogram of intermediates, analogous to Fig. 2 but on a log scale and with individual lines based on stability—the number of intersubunit contacts in a given intermediate. There are as many as 15 energy levels. There are only 141 species in the lowest energy level of 2.4 million total species. (B) Only a small fraction of species are in the lowest four energy levels. (C) A histogram of species (as in A) based on the probability of intermediates. The probability here is calculated based on the total population, where each intermediate makes only a very small contribution to the total.

Another way to parse the database of particles is in terms of probability (Eq. 3). A reaction where every intermediate is at equilibrium will be populated by the most stable species; the probability of a given species forming is the characteristic of a reaction where there is no equilibration between species. Probability would be the only factor in truly unidirectional reaction, but it is also the dominant factor at early, preequilibrium times in a reversible reaction. Again, we find that a small number of particles account for a high fraction of probability (Fig. 3 C). For probability cutoffs of 0.25, 0.5, and 0.9, the populations are 168, 917, and 19,688, respectively.

Examining assembly paths

The energies and probabilities viewed over the whole database are broadly distributed. There is no obvious discrete cutoff. The number of intermediates considered in an assembly reaction can be markedly decreased by selecting intermediates according to specific criteria during the build-up procedure and eliminating those that do not fit the criteria (Fig. 4). This approach has previously been used to define likely paths in complex reactions (33) and assembly paths based on the most stable intermediates (31,32). Here, we consider criteria of stability, probability (Eq. 3, μ = 1), and probability weighted by stability (Eq. 3) to make sparse data sets of the most important species. The physical rationale for the selection rules will be described in the Discussion section.

Figure 4.

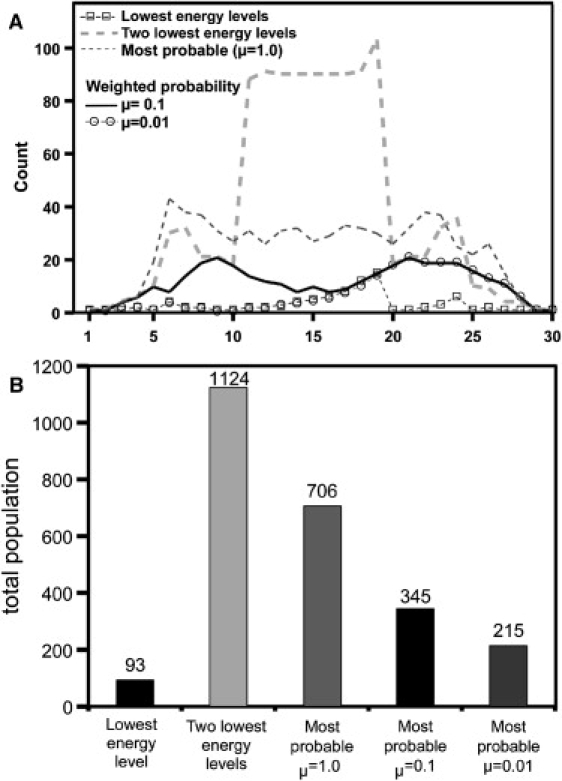
Selection rules segregate very small pools of intermediates. Selection rules are based on the lowest energy level, two-lowest-energy-levels, most-probable-90%, and the most-probable-90% with two different weighting factors to minimize contribution of the least stable intermediates. (A) The distribution of species for each selection rule shows that stability-based rules tend to incorporate steep minima and maxima in their populations. Note that three of the populations extensively overlap. (B) The total populations of sparse models for simulations based on different selection rules. The two largest populations (two-lowest–energy-levels and most–probable-90%) include <0.05% of the total possible number of species.

The simplest selection rule is to generate a path using only the lowest energy species, pruning off paths leading to higher energy intermediates. This lowest-energy level includes 93 out of the 141 possible lowest-energy-level species. There is only a single lowest energy species for n = 5, 9, 10, and 20, which results in a defect in this set of assembly paths that is inherent to the build-up approach: Most of the fifteen 19-mers in this subset are on dead-end paths. Only four are on a direct path to the sole 20-mer. From the perspective of a scientist making a continuous path for a simulation, it may be desirable to eliminate the dead-end 19-mers from consideration. However, except in hindsight, there is no structural reason or basis in a Markov path to exclude the dead ends.

The second continuous path is comprised of the two lowest energy levels. The 1124 members of this subset include almost all 1197 species in the two lowest energy levels of the complete data set. This set of intermediates has a broad maximum from 11-mers to 19-mers, with a median of 90 species of each. There are no dead ends in this subset.

The coefficients used to calculate probability (Eq. 3) reflect the degeneracy and number of forward paths to that n-mer. Probability-based rules were surprisingly effective in constraining the number of species, especially considering how probability had a much less definitive cutoff than energy when viewed over the whole database (Fig. 4). This effect is attributed to the probability calculation being multiplicative, so that the progeny of the least likely species have a vanishingly small probability.

For the subset identified by the probability-based selection rule (Eq. 3, μ = 1), we included intermediates to account for at least 90% of probability. All species for n = 1–6 are included. However, for n = 7, only 38 out of 119 possible structures are included. The multiplicative effect and the large number of low-probability species for n ≥ 7 has the effect of concentrating probability in a relatively constant number of intermediates, 32 ± 5, from n = 6 to n = 26. There are only 706 species for the μ = 1 probability rule. This is only 0.03% of the total of 2.4 million species and only 4% of the 90%-probability cutoff of the whole database (Fig. 4 C). The probability selection rule includes a few particles with two or more holes, but excludes species that are snakelike chains of subunits. This data set includes almost all the lowest-energy selection rule and many in the second-lowest energy level. Nonetheless, for almost every size of n from 2 to 27, there are species in which at least one subunit is associated by a single contact.

We considered two other probability-based selection rules to take into account the stability of intermediates. The probability calculation (Eq. 3) includes an instability penalty, μ < 1, for species where their progenitor has a subunit associated by a single contact. The μ = 0.1 weighted probability rule has 345 species and μ = 0.01 only 215. Predictably, for μ < 1, the data sets lost intermediates associated by a single contact where more stable alternatives are available. For μ = 0.1, there are monovalent associations for n = 2–12 but none for larger species. For μ = 0.01, there are only eight monovalent associations in the whole data set—a dimer, two types of tetramer, four types of hexamer, and one type of 11-mer. The μ = 0.1 and μ = 0.01 subsets largely overlap the μ = 1 subset.

Assembly simulations

We compared assembly simulations based on 1), a single path comprised of 30 species; 2), the 93 species in the lowest-energy-level path; 3), the 1124 species in the path comprised by the two lowest levels; 4), the 706-species most probable path; 5), the 345 species in the μ = 0.1 weighted probability path; and 6), the 215 species in the μ = 0.01 weighted probability path (Fig. 5).

Figure 5.

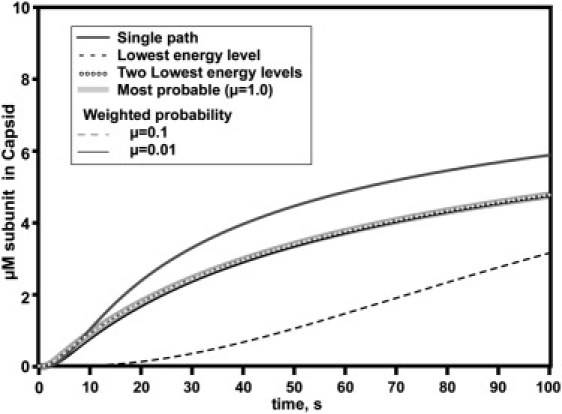
Kinetic trajectories for capsid formation for different selection rules. The most stable species simulation is much slower than the other simulations due to kinetic traps. The single-path simulation follows distinctly different kinetics than any of the multipath systems. The two-lowest-energy-levels model and the three probability models show very similar kinetics. In all cases, the conditions are the same: 10 μM initial subunit, k_nuc = 80 M⁻¹ s⁻¹, k_elong = 8000 M⁻¹ s⁻¹, and K_D = 10^−3.5 M.

With parameters that would be expected to result in high yields of capsid in the single-path simulations, most of the multipath simulations yield essentially identical results, though different from the single-path simulation (23). The lowest-energy-level path was an outlier due to the large number of kinetically trapped 19-mers, as anticipated from the population distribution. This kinetic trap slowly resolved as fresh monomer became available from dead-end 19-mers shedding subunits, and the resulting 18-mers entered a productive route. The single-path assembly model is appreciably faster than the other models, probably because the many intermediates in the multipath models create a sink for free monomer, decreasing the concentration of monomer and the net forward flux of the reaction.

Discussion

The number of possible unique intermediates for capsid grows approximately combinatorially with the number of subunits, N. Because there is no reliable function to guide extrapolation to larger values of N, it is impossible to make a rigorous approximation of the number of virus intermediates. However, a lower limit for hepatitis B virus, which is constructed from 120 dimers, based on a semilog extrapolation (12 species for an octahedron, 73 for a dodecahedron, 2649 for an icosahedron, and 2.43 × 10⁶ for a 30-mer) suggests that the actual number will be orders of magnitude greater than 10²⁶. Since a typical in vitro reaction only has 10¹⁴ dimers as starting material, the vast majority of intermediates are never realized; in vivo concentrations are probably similar but with much smaller volumes, further decreasing the diversity of intermediates. In our efforts to identify subsets of important intermediates, we found that the most stable species, which will be dominant for most of the reaction, starting as the assembly approaches steady state (13,21,23), and the most probable, kinetically favored species, dominant at the earliest stages in the reaction (23,34), are actually overlapping subsets of compact species. The 706 most probable species include 87 of the 93 lowest-energy-level species; 435 members of the two-lowest-energy-levels subset also overlap with the most probable set. This result recapitulates MD simulations of the assembly of a 20-subunit icosahedron where < 50 of 2649 possible species were observed (25).

With the large database of species available for an N = 30 capsid, the selection rules based on different arguments, from kinetics (probability) to thermodynamics (stability), picked out a surprisingly small, heavily overlapping subset of intermediates. Careful consideration of the selection rules explains this redundancy. The stability-based rules specifically select for intermediates with the greatest number of subunit-subunit contacts, which necessarily are those species that are most compact. The unweighted probability rule selected the most highly traveled paths without regard to stability. For the smallest species (e.g., trimers), where there is a branch between extended and compact structures, there is only a small probabilistic difference between paths. However, there are many ways for these small extended structures to progress to a more compact form. Compact structures tend to have redundant paths to the next size intermediate and convergent paths to even larger intermediates, whereas extended structures can only arise from a series of extended predecessors, following a very limited number of paths. The additivity of probability due to redundancy/symmetry coupled with the multiplicativity of probability over a path results in high probabilities for the few compact structures and negligible probabilities for the many extended structures. The unlikelihood of the extended structures is further compounded by their inherent instability.

Extrapolating from the observations presented in this article, assembly reactions for any spherical virus will depend on a small group of intermediates. The number of compact structures is a necessarily small fraction of N for any oligomer. The most compact n-mers are roughly discs of area n with the maximal number of intersubunit contacts. There are few arrangements that satisfy these criteria. The structural details of the compact states will vary from virus to virus, but as long as 1), stability scales with the number of intersubunit contacts and 2), assembly paths to compact states are not specifically excluded, the importance of the relatively rare compact and degenerate intermediates is expected to be general.

Since we are drawing conclusions based on comparing the different subsets of particles, it is important to consider the biophysical rationale of each selection rule. The single-path model, in which each step from monomer to capsid is represented by one species, would be expected for assembly directed by a one-dimensional scaffold, such as the genome of the virus. Recent studies suggest that bacteriophage MS2 assembly preferentially proceeds directionally along the viral RNA (35). A defined path would also result from a specific sequence of binding sites: studies with hepatitis B virus suggest that assembly proceeds by induced fit, which could, in theory, support a specific assembly path (36).

The most-probable-species rule is based on kinetic selection of intermediates. As shown with smaller oligomers (23), at early times in the reaction, probability is the critical predictor for the presence of a given species. We can expect that these species will also be heavily represented in kinetic traps. At later times, the relative population shifts to the most stable species. The renormalization of probability and the 90% cutoff for each species eliminate a huge number of species. For n = 7, only 38 species accounted for 90% probability; the missing 71 species were thus rare at the earliest times in the reaction and essentially absent by the time the time intermediates were approaching steady-state concentrations, driven by stability, and capsids began to accumulate (23). The most probable species would be expected to strongly overlap species observed in stochastic simulations. The forward reaction coefficients are directly analogous to probabilistic Markov transmission coefficients useful for simulations of stochastic reactions by a Gillespie algorithm as in discrete event simulations (24,33). However, with master equations, we describe the distribution of a large population of molecules, as would be found in an in vitro reaction.

The weighting schemes imposed on the probability selection rule have the practical effect of eliminating the least stable species and their progeny from the resulting data sets. The physical rationale for these selection rules is to approximate the effect of entropically attenuating the association constant for subunits bound to an intermediate by a single contact, crudely approximating a dynamic effect. We were surprised to find that even the modest μ = 0.1 penalty eliminated the majority of such intermediates and their progeny from the subset.

The most stable intermediates selection rule was an obvious choice with a counterintuitive result. As successful assembly simulations proceed, the concentrations of intermediates approach a steady state of the most stable intermediates (20,21,23), consistent with reversible reactions (37). However, the dead ends in the most-stable species subset provide an unexpected view of off-path assembly. In a more complete master equation simulation, these dead ends could return on path through higher-energy intermediates; in a dynamic simulation, subunits might actually rearrange. This subset resembles the behavior of a reversible reaction with an off-path shunt. It has been predicted (38–40) that once virus assembly goes off path due to (meta)stable interactions, it is likely to remain trapped off-path. In vitro, assembly-misdirecting small molecules provide an example of this effect (41). However, self-assembling viruses are naturally selected for fidelity with reversible intermediate reactions, so off-path monsters are observed only where assembly is artificially diverted (42–44).

Expanding the lowest-energy-level subset to the two lowest-energy-levels incorporated the majority of the intermediates found in the probability-based pathways. This selection rule generated a data set with a swollen array of midsized species like the complete set of intermediates, testing the effect of a very large number of species centered at N/2.

Master-equation approaches to kinetic simulations describe large populations. They are appropriate models for in vitro reactions. The statistical factors modifying the rate constants in the simulations are essentially Markov probabilities, such that simulations are equivalent to stochastic simulators integrated over an infinite number of experiments (24,33). Of course, the master-equation simulations ignore the concentration fluctuations of small populations. In a similar way, dynamic effects (e.g., off-path assembly and nuances of geometry) can only be emulated by the choice of intermediates. Coarse-grained dynamic studies allow critical investigation of such effects, in a manner that reflects parameterization of subunit-subunit interactions.

As with any model, the species and the paths connecting them are biased by critical assumptions. The two most obvious assumptions are that assembly proceeds one subunit at a time, and that disassembly proceeds one subunit at a time. Association one subunit at a time is reasonable, as the most common reactant in any mixture is free subunit. The exceptions to this assumption occur when there is association by oligomers dictated by the biology/biophysics of the system that imposes a strong preference for a specific intermediate (as in CCMV (6)). Otherwise, we only observe substantial concentrations of oligomer reactions that are deliberately pathological as a result of fast nucleation compared to subsequent elongation (24) and/or high association energy (45). Dissociation one subunit at a time is computationally convenient but not necessarily reasonable. This limitation should actually increase the role of extended structures in assembly simulations. However, the small contribution of such extended chains is minimized and/or excluded by probability- and stability-based selection rules.

Deterministic differential equations for modeling virus assembly impose three other interrelated assumptions: all subunits associate with perfect geometry; all microscopic forward rates are the same; and all intersubunit contacts are equivalent. These assumptions are reasonable for describing bulk behavior. However, they are all related to the limitation of master equations. The absence of dynamic effects eliminates off-path interactions and intramolecular rearrangements to improve geometry. This caveat is most important for kinetically trapped and aberrant assembly, as may be found with mutants and small-molecule assembly effectors; caution must be used in interpreting aberrant assembly reactions with these simple models (41,46–49). The authors know of no examples of off-path assembly for wild-type viruses in vivo. In vitro, aberrant assembly and accumulation of kinetically trapped oligomers can easily be avoided by choosing appropriately mild conditions. Also, in vitro, the large numbers of reactants minimize the importance of concentration fluctuations that are evident in stochastic simulations. Thus, although these assumptions of bulk behavior may affect the details of paths, they have little effect on our overall conclusion that the major traffic of assembly involves a small number of compact intermediates on largely redundant paths.

Finally, we return to the analogy between virus assembly and protein folding. We have observed that assembly overwhelmingly follows a path of compact intermediates because of geometry, not some predetermined path. By analogy, we suggest that the early stages of protein folding, often characterized by a collapse to a compact state followed by relaxation to a lowest-energy conformation (50–52), may have a geometric basis in addition to a chemical basis. The structural collapse is directly analogous to the preference for compact intermediates in capsid assembly. There are simply more ways to make a compact structure, and such structures are more stable than the more numerous extended alternatives. Because compact structures are more stable, there is also an increased likelihood to create misfolded traps, as happens all too frequently in protein expression systems. The critical difference between assembly of empty capsids, as developed in this article, and protein folding is that the subunits (i.e., amino acids) of a protein chain are covalently linked, creating geometric constraints and a much more difficult calculation. The effect of having the subunits linked on a chain in proteins may be mirrored in viruses when assembly is facilitated by interaction between subunits and the viral genome to be encapsidated, a subject of continuing research.