Influence of Hydrophobic Mismatch and Amino Acid Composition on the Lateral Diffusion of Transmembrane Peptides

Abstract

We investigated the effect of amino acid composition and hydrophobic length of α-helical transmembrane peptides and the role of electrostatic interactions on the lateral diffusion of the peptides in lipid membranes. Model peptides of varying length and composition, and either tryptophans or lysines as flanking residues, were synthesized. The peptides were labeled with the fluorescent label Alexa Fluor 488 and incorporated into phospholipid bilayers of different hydrophobic thickness and composition. Giant unilamellar vesicles were formed by electroformation, and the lateral diffusion of the transmembrane peptides (and lipids) was determined by fluorescence correlation spectroscopy. In addition, we performed coarse-grained molecular-dynamics simulations of single peptides of different hydrophobic lengths embedded in planar membranes of different thicknesses. Both the experimental and simulation results indicate that lateral diffusion is sensitive to membrane thickness between the peptides and surrounding lipids. We did not observe a difference in the lateral diffusion of the peptides with respect to the presence of tryptophans or lysines as flanking residues. The specific lipid headgroup composition of the membrane has a much less pronounced impact on the diffusion of the peptides than does the hydrophobic thickness.

Introduction

Biological membranes are composed of a large variety of lipid species and membrane proteins of diverse functions and structures. The diversity in molecular species can result in lateral heterogeneity. The presence of domains with a lipid (and protein) composition different from that of the bulk of the membrane has been suggested to have functional importance (1–3). The different lipid composition of membrane domains and the accompanying difference in properties in comparison with the bulk membrane can serve as a platform for assembly and/or workspaces of some membrane proteins.

The function of proteins in the membrane depends on hydrophobic and polar interactions of their transmembrane domains and hydrophilic segments with the surrounding lipids. When the hydrophobic stretches of the proteins do not match with the acyl core of the membrane lipids, there will be a so-called hydrophobic mismatch (4). As a consequence, the lipids and/or the proteins in the membrane may adapt their conformation to avoid the exposure of hydrophobic domains to the aqueous phase. Proteins may tilt their helices, change their overall conformation, or self-associate/aggregate, whereas lipids may stretch, compress, or distort their acyl chains to match with the proteins (5). Here, we studied the diffusion behavior of model peptides in synthetic membranes to obtain a mechanistic understanding of the consequences of hydrophobic mismatch. We used peptides, known as WALP and KALP series, with hydrophobic stretches from 9 to 25 residues. Previous studies (6,7) have shown that the longer peptides can tilt in response to a too-thin hydrophobic membrane core, which will give rise to a larger Stokes radius of the peptide. Peptides with a too-short hydrophobic stretch have been shown to distort the membrane (8). WALP peptides in the fluid phase remain as single entity in the membrane; however, increasing the peptide/lipid ratio beyond threshold values will ultimately result in self-association of the molecules (9). It is evident that hydrophobic mismatch influences lipid-peptide interactions and can affect their organization in the membrane, but how this affects the lateral mobility of the molecules has not been determined in detail.

In this work, our goal was to understand the basic principles of lateral diffusion of molecules in membrane systems in which the hydrophobic cores of the proteins and lipids do not match. We used model peptides designed to allow systematic variation of peptide properties such as the length and hydrophobicity of the hydrophobic stretch, and the nature of the flanking residues. The peptides were incorporated into fluid bilayers of unsaturated phospholipids with different thicknesses. The experimental data are compared with the results of coarse-grained (CG) MD simulations. The influence of hydrophobic (mis)match and electrostatic interaction between peptides and membrane is discussed.

Materials and Methods

Materials

For the experiments in this work, 1,2-dimyristoleoyl-sn-glycero-3-phosphocholine (di-C14:1PC), 1,2-dipalmitoleoyl-sn-glycero-3-phosphocholine (di-C16:1PC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (di-C18:1PC), 1,2-dieicosenoyl-sn-glycero-3-phosphocholine (di-C20:1PC), 1,2-dierucoyl-sn-glycero-3-phosphocholine (di-C22:1PC), and 1,2-dioleoyl-sn-glycero-3-phosphoglycerol (di-C18:1PG) were purchased from Avanti Polar Lipids (Alabaster, AL) as lyophilized powders and used without further purification. The peptides Cys-WALP15–Cys-WALP31, Cys-KALP23, Cys-KALP27, and Gly-Cys-WLP23 were synthesized using Fmoc/tBu peptide solid-phase synthesis as described elsewhere (10). The peptide sequences are given in Table 1.

Table 1.

Amino acid sequences of peptides labeled with AF488

Peptide	Sequence
Cys-WALP 15–31	Acetyl-C∗GWW(LA)4-12LWWA-amide
Cys-KALP23	Acetyl-C∗GKKLALALALALALALALALKKA-amide
Cys-KALP27	Acetyl-C∗GKKLALALALALALALALALALALKKA-amide
Gly-Cys-WLP23	Acetyl-GC∗GWWLLLLLLLLLLLLLLLLLWWA-amide

^∗Cysteine labeled with AF488 C₅-maleimide.

The fluorescent probes Alexa Fluor 488 (AF488 C5-maleimide) and DiD-C18:0 (DiIC₁₈(5) solid 1,1′-dioctadecyl-3,3,3′,3′-tetramethylindodicarbocyanine, 4-chlorobenzene-sulfonate salt) were purchased from Molecular Probes/Invitrogen (Carlsbad, CA). All other chemicals used were of analytical grade. The water used was deionized and purified with a Milli-Q Gradient purification system from Millipore (Billerica, MA). Indium-tin oxide (ITO)-coated microscope cover slides (thickness #1, 0.13–0.16 mm; 15–30 ohms) were obtained from SPI Supplies/Structure Probes (West Chester, PA).

Peptide labeling with AF488

To label the peptides with AF488, ∼0.5 mg of each peptide was weighed into an Eppendorf tube and dissolved in 200 μL trifluoroethanol. Subsequently, 10 μL of H₂O were added. The peptide solution was then deoxygenized by bubbling with N₂ gas for several minutes. While the peptide solution was kept under N₂ atmosphere, 2 μL of triethylamine and 1.25 (peptide) equivalents of AF488 label, dissolved in methanol and purged with N₂, were added. After the reaction mixture was stirred in the dark for 3 days at 4°C, the peptides were precipitated in 10 mL of cold methyl tert-butyl ether/n-hexane (1:1, stored at −20°C) to remove unbound AF488 label. The precipitate was collected by centrifugation, the supernatant containing the unreacted AF488 label was decanted, and the precipitate was washed once again with methyl tert-butyl ether/n-hexane (1:1). The AF488 labeling of all peptides was verified by matrix-assisted laser desorption/ionization time-of-flight mass spectrometry using α-cyano-4-hydroxycinnaminic acid as the matrix.

Sample preparation

Stock solutions of ∼5 mM lipids in chloroform were prepared by weight, and their precise lipid concentration was determined by the Rouser phosphorus assay (11). Subsequently, the stock solutions were diluted to reach a 0.5 mM concentration. Stock solutions of AF488-labeled WALP23 peptides were prepared at a concentration of ∼10 μM in TFE. The peptide concentration was determined by absorption spectroscopy using an extinction coefficient of 22,400 M⁻¹cm⁻¹ at 280 nm for WALP23. Peptide-bound AF488 absorption at 280 nm was corrected for by subtracting the 280 nm absorbance of free label, which was scaled to equal intensity at the main absorbance band around 488 nm. From the peptide absorption spectra, a typical labeling efficiency of 80–90% was estimated.

For each tested bilayer composition, samples containing ∼200 nmol of lipids were prepared by mixing appropriate amounts of phospholipids and AF488-labeled peptides at a peptide/lipid molar ratio of ∼1:100,000. Additionally, the fluorescent lipid dye DiD-C18:0, dissolved in methanol, was added to the bulk lipids at a molar ratio of 1:153,000. After thorough mixing, the organic solvents were evaporated under a stream of N₂ gas and further removed under vacuum overnight (∼1 × 10⁻² mbar). The sample was redissolved in 40 μL of chloroform/methanol (1:1 v/v), and ∼4 μL of the mixture was applied in small droplets onto an ITO-coated microscope slide stored on a warm plate of ∼50°C. The solvents were allowed to evaporate for 5–10 min on the warm plate.

The in-house-made electroformation setup was assembled using a second ITO-coated coverslip, and the electroformation chamber was filled with buffer (10 mM potassium phosphate, pH 7.0) warmed to 50°C. Subsequently, an alternating current with frequency 10 Hz of 2 V (corresponding to ∼400 V/m) was applied using a function generator (FG 100; Digimess). Electroformation was allowed for at least 2 h, while the chamber was kept on the warm plate, to prepare sufficient numbers of homogeneous and equal-sized giant unilamellar vesicles (GUVs) without inclusions. For fluorescence correlation spectroscopy (FCS) measurements, the electroformation setups were directly mounted on the sample stage of the laser-scanning confocal microscope.

The use of conducting microscope slides has the additional advantage of allowing GUVs to be grown in reach of the short focus of the objective of the laser-scanning microscope. This allowed us to measure the fluorescence intensity fluctuations on GUVs that were still attached to the microscope slide at the bottom, which minimized movements of GUVs within the long observation time of 8 s for each measurement. Furthermore, we observed a noticeable reduction of the low-frequency oscillations on the membrane when more GUVs were growing in direct proximity, probably due to a dampening effect of the surrounding GUVs on microflows in the sample chamber.

FCS measurements

FCS measurements were performed on a dual-color laser scanning confocal microscope. The laser scanning confocal microscope is based on an inverted microscope Axiovert S 100 TV (Zeiss, Jena, Germany) in combination with a galvanometer optical scanner (model 6860; Cambridge Technology, Watertown, MA) and a microscope objective nanofocusing device (P-721; Physik Instrumente, Germany). The laser beams were focused by a Zeiss C-Apochromat infinity-corrected 1.2 NA 40× water immersion objective. A blue laser (488 nm, argon ion laser; Spectra Physics) and a red laser (633 nm He-Ne laser; JDS Uniphase) were used to excite the AF488 fluorophore and the lipid dye DiD-C18:0, respectively.

The fluorescence was collected through the same objective, separated from the excitation beams by a beam-pick off plate (BSP20-A1; Thor-Labs) and directed through emission filters (HQ 535/50 and HQ675/50; Chroma Technology) and pinholes (30 μm diameter) onto two avalanche photodiodes (SPCM-AQR-14; EG&G). The fluorescence signal was digitized, and the autocorrelation curve was calculated using a multiple τ algorithm. The autocorrelation curves were fitted to a model of two-dimensional Brownian motion (12). The setup was calibrated by evaluating autocorrelation curves for AF488 and Alexa Fluor 633 in water and using a diffusion coefficient D = 380 μm²/s (13). The lateral radius w_xy of the detection volume depends on the wavelengths of the light and was estimated to be 195 nm for AF488, and 264 nm for DiD-C18:0.

For the FCS measurements, the focal volume was always positioned at the upper pole of a GUV. For this purpose, we searched the samples for qualified GUVs under the microscope, using white light or a fluorescence lamp. An xy scan was performed and the focus was centered to a suitable GUV, followed by a z scan that was used to position the focus to the membrane. For each tested condition, the fluorescence intensity fluctuations of ∼10 different GUVs were recorded for up to 10 periods, each lasting 8 s. For each combination of peptide and bilayer, FCS measurements were performed on different days on at least 15 selected GUVs with a diameter of 5–20 μm. The triplet-state formation was excluded from the fitting model, as the τ of peptides and DiD were not influenced by the photophysics of fluorophore. A calibration factor of 1.25 was used for the calculation of the diffusion coefficients of the lipid probe, DiD (see Ramadurai et al. (14) for detailed information on this procedure).

Molecular-dynamics simulations

Methods

All molecular-dynamics (MD) simulations were carried out with the Gromacs package (v. 4.0.5) (15). The MARTINI CG force field was used, in which on average ∼4 heavy atoms (and associated hydrogen atoms) are mapped onto a single CG bead (16,17). An integration time step of 25 fs was applied together with the standard settings for the nonbonded interactions (16). Systems were simulated at constant particle number, pressure, and temperature (NpT ensemble) using periodic boundary conditions. The temperature was kept constant by coupling to a heat bath at 300 K (τ_T = 0.3 ps) (18). The systems were semiisotropically coupled to a pressure bath at 1 bar (τ_p = 3 ps) (18). In a several previous applications (19,20), the CG MARTINI force field has been used to efficiently simulate peptide/lipid systems.

Simulation setup

Three different WALP peptides (WALP16, WALP23, and WALP27) were embedded into five different phosphatidylcholine (PC) bilayers. These bilayers matched the ones used in the experiments (see above) in that they all contained singly unsaturated PC lipids. MARTINI lipid models with tail lengths varying between two and six tailbeads were used to vary the thickness of the bilayers between 1.8 and 4.0 nm. All PC lipid models (except the two-tailbead model) contain a C3-type bead, which together with the appropriate bonded parameters models a double bond (16). The C3-type bead is located at the second position along the tail in the three-tailbead model, at the third position in the four- and five-tailbead models, and at the fourth position in the six-tailbead model.

To generate starting structures for the MD simulations, single WALP transmembrane peptides were inserted into preequilibrated bilayers comprised of 512 PC lipids. Lipid and water molecules overlapping with the peptides were removed, and the systems were energy minimized (steepest descent, 1000 steps). Subsequently, the bilayers were relaxed through 1 ns of MD simulation with positional restraints on the peptide (force constant 1000 kJ mol⁻¹ nm⁻²), followed by extended free MD simulations. The first 200 ns of each simulation were considered equilibration time and discarded from data collection. The helicity of the WALPs was maintained during the simulations by means of dihedral restraints (17). Depending on the system details, the final systems consisted of a single WALP embedded into ∼500 lipids, solvated by ∼6800 CG water beads (with one CG water bead representing four real water molecules). The individual simulation times were 4 μ-s for the the four-, five-, and six-tailbead bilayers, and 8 μ-s for the two- and three-tailbead bilayers, respectively; the total simulation time amounts to 84 μ-s.

Lateral diffusion

The lateral diffusion coefficient was calculated from the long time mean-square displacement (MSD) over time according to

$$D_{lat}=\underset{t\to \infty }{\lim }\frac{\langle {|r\left(t+t_0\right)-r\left(t_0\right)|}^2\rangle }{4t}\text{,}$$ (1)

where r is the center of mass vector of the peptide backbone or lipid molecule in the membrane plane. The time window averaging was done over all initial time origins t₀. The overall center of mass motion was removed. The obtained MSD curves are to a good approximation linear over a time interval between 10 and 100 ns (simulation time). Lateral diffusion coefficients were obtained from linear fits to the MSD curves in this time interval. Statistical errors were estimated by taking the difference between the diffusion coefficients obtained by separately analyzing the two halves of the trajectories.

Results

Experimental system

We investigated the influence of peptide composition on the diffusion of model peptides mimicking transmembrane segments of integral membrane proteins. For this purpose, we synthesized transmembrane peptides with different lengths and sequences of the hydrophobic stretch, and with different flanking residues (for peptide sequences see Table 1). The flanking amino acids chosen were the aromatic residue tryptophan and the positively charged lysine, which both have a preference for locations at the membrane-water interface (21). A cysteine was added to the N-terminus of each peptide to attach a maleimide-functionalized AF488 label. The AF488-labeled peptides were inserted into bilayers made of unsaturated phospholipids with hydrocarbon chain lengths varying from 14 to 22 carbons, corresponding to hydrophobic thicknesses of 2.38–3.70 nm (22).

For FCS measurements, the GUVs were formed by electroformation and visualized with the confocal microscope (Fig. 1 A). The resulting images confirm that at optical resolution the peptides are homogeneously distributed in the membrane. Fig. 1 B depicts typical autocorrelation functions of peptides diffusing in bilayers of different thicknesses. The obtained autocorrelation functions, G(τ), could be fitted reasonably well to a one-component, two-dimensional diffusion model, yielding values for the diffusion coefficients of the peptides and DiD molecules.

Figure 1.

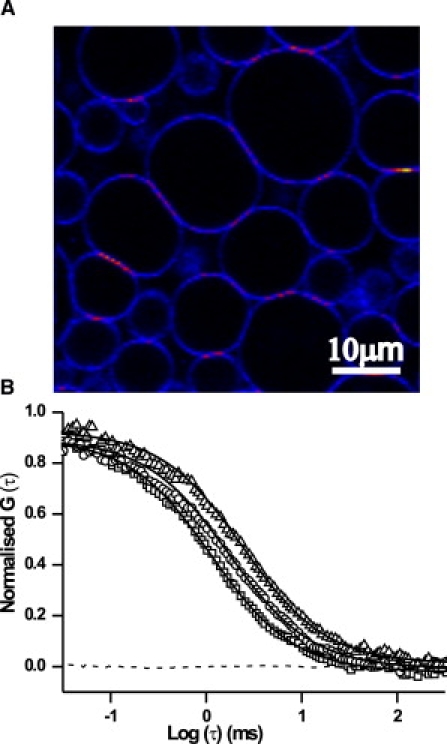
(A) GUVs prepared from AF488-labeled WALP23 and di-C18:1PC at a molar ratio of 1:100,000. In many instances, the fluorescence intensity was increased at the contact sites between GUVs. (B) Normalized autocorrelation curves of AF488-labeled WALP19 in di-C14:1PC (□), di-C18:1PC (○), and di-C22:1PC (▵). The solid line is a fit to the one-component, two-dimensional diffusion model; the dashed line indicates the residuals of the fit.

Peptide diffusion as a function of bilayer thickness

The diffusion coefficients measured for the peptides in different types of bilayers are plotted against bilayer thickness in Fig. 2 A and summarized in Table 2. The results obtained from our MD simulations are presented in Fig. 2 B and Table 3. The diffusion coefficients obtained from the FCS experiments and MD simulations agree, and show a linear decrease with increasing bilayer thickness. For all peptides investigated, the measured diffusion coefficient drops by a factor of ∼2 over the membrane thickness range of 2.38–3.7 nm, and the diffusion coefficients obtained from the MD simulations display a similar behavior. An analogous relationship between the diffusion coefficients and the thickness of the bilayer was observed for the diffusion of lipid probes in pure lipid bilayers (22), which be explained by an increased viscosity of thicker bilayers due to an increased number of van der Waals interactions between the lipid hydrocarbon chains. The larger viscosity of thicker bilayers would limit the diffusion of transmembrane peptides. For a quantitative comparison of the diffusion coefficients from CG MD simulations and FCS experiments, one must account for an artificial speed-up in the simulations. Since (part of) the friction due to motion of the atoms is removed, the energy landscape of CG models is smoother and the dynamics is faster compared to the atomistic level. For the MARTINI model, we found that a time conversion factor of 4 was adequate to match the simulated and experimental diffusion coefficients of both bulk water and DPPC lipids in a bilayer. Due to the coupling of peptide and lipid diffusion, a similar factor of 4 also matched the peptide lateral diffusion times from our FCS experiments and the CG MD simulations. Therefore, we used a global time scaling factor of 4 to convert simulation times to real times in this work and did not attempt to individually match the diffusion of the different peptides to the experimental data.

Figure 2.

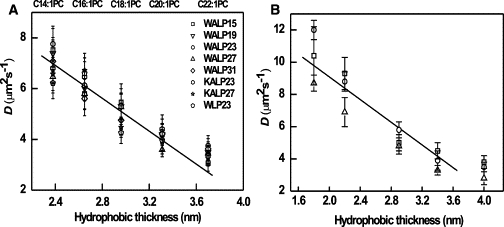
(A) Diffusion coefficient of different AF488-labeled model peptides. The error bars refer to the standard deviation of the diffusion measurements, obtained from ∼20 GUVs and at least two independent sets of measurements. The bilayer thickness was derived from Kucerka et al. (22). (B) Diffusion coefficient of WALP peptides in lipid membranes of different hydrophobic thicknesses, as calculated from CG simulations. The symbols are the same as in panel A, except that the open square symbol is now used for WALP16.

Table 2.

Experimentally determined peptide diffusion coefficients (D)

Thickness (nm)	2.38	2.65	2.96	3.31	3.70
Peptides Lipids	di-C14:1PC	di-C16:1PC	di-C18:1PC	di-C20:1PC	di-C22:1PC
WALP15 D (μm2/s)	7.5 ± 0.8	5.8 ± 0.8	5.5 ± 0.7	4.20 ± 0.7	3.1 ± 0.3
WALP19	7.4 ± 0.6	6.0 ± 0.5	5.3 ± 0.7	4.2 ± 0.2	3.5 ± 0.4
WALP23	7.8 ± 0.7	6.1 ± 0.6	5.3 ± 0.5	4.2 ± 0.4	3.8 ± 0.4
WALP27	6.5 ± 0.6	5.8 ± 0.6	5.3 ± 0.5	3.6 ± 0.3	3.5 ± 0.3
WALP31	7.1 ± 0.8	5.6 ± 0.4	4.8 ± 0.5	4.2 ± 0.4	3.6 ± 0.4
KALP23	6.8 ± 0.6	6.5 ± 0.5	5.4 ± 0.4	4.4 ± 0.4	3.4 ± 0.4
KALP27	6.6 ± 0.6	6.7 ± 0.6	4.5 ± 0.4	3.9 ± 0.4	3.3 ± 0.3
WLP23	6.2 ± 0.6	6.6 ± 0.5	4.3 ± 0.4	4.0 ± 0.4	3.4 ± 0.4

Mean and standard deviations were obtained from at least 15 GUVs; bilayer thickness was derived from Kucerka et al. (22).

Table 3.

Diffusion coefficients (D) of peptides from CG MD simulations

Peptides Thickness (nm)	1.8 nm	2.2 nm	2.9 nm	3.4 nm	4.0 nm
WALP16 D (μm2/s)	10.4 ± 1.8	9.3 ± 1.0	5.0 ± 0.5	4.5 ± 0.5∗	3.8 ± 0.4∗
WALP23	12.0 ± 0.6	8.8 ± 0.6	5.8 ± 0.5	3.9 ± 0.6	3.5 ± 0.3
WALP27	8.7 ± 0.5	6.9 ± 0.9	4.8 ± 0.5	3.3 ± 0.3	2.8 ± 0.4

A factor of 4 was used to convert simulation times to real times. The bilayer thickness was determined from the density profiles along the membrane normal, as observed in the simulations.

^∗Peptide motion with respect to the leaflet comprising the peptide was analyzed, and the simulations were continued for 4 μs (simulation time) after the peptide adopted the flat orientation.

During the MD simulations, the WALP peptides stayed in their initial transmembrane orientations, with one exception: In the simulations of the bilayers with five or six tailbeads (bilayer thickness = 3.4 and 4.0 nm, respectively), WALP16 was not stable in its transmembrane orientation; rather, it adopted a flat orientation at the membrane interface (after 1.5 μs and 0.2 μs simulation time, respectively). Since in the flat orientation the friction between peptide and membrane does not depend on the bilayer thickness, the diffusion coefficients of WALP16 in the two thickest bilayers were the same within the statistical error (Table 3). Obviously, the hydrophobic mismatch of the short WALP16 helix in the two thickest bilayers was too large to maintain the transmembrane orientation. A similar effect was not observed in the experiments, possibly because the bilayers in the GUVs span a smaller thickness range than those in the MD simulations.

Influence of the peptide composition

Within the experimental error of 10%, the peptides WALP15–WALP31, KALP23, KALP27, and WLP23 displayed similar diffusion coefficients in all bilayers tested (values summarized in Table 2). The simulation data also show that the length and composition of the peptides did not have a significant effect on the diffusion rate (MD simulation data summarized in Table 3). Furthermore, the experimental data show that the diffusion coefficients of the tryptophan-flanked WALP and lysine-flanked KALP peptides were similar. Thus, even though KALP peptides are effectively shorter than WALP peptides, with the same length of leucine-alanine stretch, this (small) difference was not reflected in the diffusion coefficients.

Peptide diffusion as a function of surface charge

Next, we studied the influence of electrostatic interactions between charged (KALP) and neutral (WALP) peptides with charged membranes. For this, KALP23 and WALP23 peptides were incorporated into DOPG-DOPC lipid bilayers of varying composition. The measured diffusion coefficients are plotted in Fig. 3. The diffusion coefficients of KALP23, WALP23, and DiD were almost constant over the entire range of DOPG concentrations in the membrane (and DOPC was decreased accordingly), suggesting that the electrostatic interactions do not play a prominent role.

Figure 3.

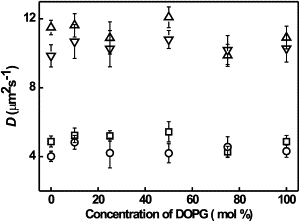
Diffusion coefficient of AF488-labeled WALP23 (□), KALP23 (○), and DiD (▵ for WALP23, ▿ for KALP23) as a function of increasing concentration of DOPG in the GUVs. The lipid probe DiD was incorporated at a 1:153,000 (mol/mol) ratio and the peptide/lipid ratio was 1:100,000.

Discussion

The aim of this study was to elucidate whether differences in the structure of transmembrane peptides influence the lateral diffusion of the molecules in lipid bilayers. The lateral diffusion of peptides was slowed down in thicker bilayers due to stronger van der Waals interactions between the lipid acyl chains, in similarity to what was previously observed for lipids by Kahya and Schwille (23). Lateral diffusion of transmembrane peptides of different hydrophobic lengths and amino acid composition decreased linearly with the hydrophobic thickness of the lipid bilayer. Of importance, very short (WALP15) and very long (WALP31) peptides, which are expected to have maximum hydrophobic mismatch in thick and thin membranes, respectively, have similar lateral mobilities. For peptides like WALP31, which are significantly tilted in thin membranes (6), the hydrodynamic radius will be larger than that of a peptide in which the hydrophobic stretch matches the acyl chain region of the membrane.

Before trying to explain the data in detail, let us first consider the factors that determine the diffusion speed and discuss them according to the widely accepted continuum hydrodynamic model of Saffman and Delbrück (24). In this model, the diffusion coefficients of transmembrane proteins or peptides moving along the bilayer plane are weakly (logarithmically) dependent on the hydrodynamic radius of the diffusing object and strongly (approximately linearly) dependent on the bilayer thickness, according to the equation

$$D=\frac{k_{\text{B}}T}{4\pi \mu h}\left(\ln \left(\frac{\mu h}{{\mu }^{\prime }R}\right)-\gamma \right)\text{,}$$ (2)

where k_B is the Boltzmann constant, T is the absolute temperature, h is the thickness of the bilayer, μ is the viscosity of the membrane, μ′ is the viscosity of the outer liquid, and γ is Euler's constant. Indeed, our recent work indicates that the diffusion coefficients of integral membrane proteins and peptides scale with ln(1/R) (14), which means that diffusion is only weakly dependent on the hydrodynamic radius. For example, the hydrodynamic radius of the peptide (lateral radius of ∼0.5 nm) would have to increase by a factor of 7 (e.g., as a result of tilting and/or aggregation) for one to observe a ∼1.5-fold decrease in diffusion coefficient.

Hydrophobic mismatch

Several adaptations can occur in response to an increase in the hydrophobic mismatch between a transmembrane peptide or protein and the surrounding bilayer lipids. In positive mismatch situations (the hydrophobic thickness of the peptides exceeds that of the membrane lipids), a peptide may tilt, aggregate, or distort the bilayer, as illustrated in Fig. 4. In the case of negative mismatch, the peptide may aggregate or distort the bilayer. In addition to structural changes in the peptides, the lipids surrounding the peptide or protein may also adapt, i.e., they may stretch or be compressed depending on the mismatch. Most likely, multiple mechanisms of adaptation may play a role. However, at the low peptide/lipid ratios used in this study, the WALP peptides did not show a tendency to self-associate, and thus can be expected to exist as monomers (9), ruling out aggregation as a possible adaptation mechanism.

Figure 4.

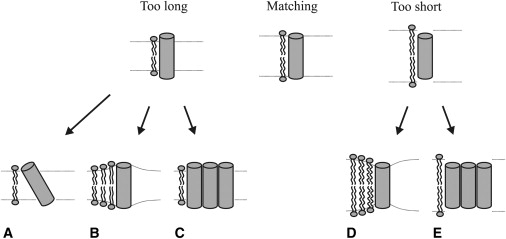
Possible adaptations to hydrophobic mismatch in the case of too-short transmembrane peptides ((A) peptide tilting, (B) bilayer distortion, and/or (C) peptide aggregation) or too-long transmembrane peptides ((D) bilayer distortion and/or (E) peptide aggregation).

The transmembrane peptides can tolerate a certain extent of hydrophobic mismatch. With increasing hydrophobic mismatch, the effects will progressively become larger because more extensive adaptations will be required to accommodate the peptide in the membrane. Owing to the dynamic character of bilayers in combination with the inherent flexibility of the lipid acyl chain, local thickening or thinning of the bilayer in the vicinity of the peptide may occur (Fig. 4, B and D). Under conditions of large hydrophobic mismatch, more distant lipid layers around the peptide may also need to adapt to still accommodate the peptide, which would increase the effective hydrodynamic radius. Also, transmembrane peptides may tilt more when experiencing a positive hydrophobic mismatch (Fig. 4 A), with the same effect on the hydrodynamic radius. Thus, in principle, large changes in hydrodynamic radius may occur as a consequence of mismatch. Our data suggest that such changes are very small; at least they are not detected in our measurements. This is consistent with previous studies that reported small adaptations (tilt angles as well as stretching of the lipids (7,25)). Nevertheless, significant deformations may occur due to mismatch. Such deformations would affect peptides and lipids differently, since the peptides form the center of any deformations, and the lipids represent bulk lipid. To test the occurrence of membrane deformations, we calculated the ratio of the diffusion coefficients for peptides and lipids, DiD (Fig. 5 A). The normalized diffusion coefficient D_N (i.e., the ratio of diffusion coefficients of peptides and lipids) excludes the apparent thickness dependence and possible variation in membrane viscosity. Fig. 5 A shows that the D_N is almost constant in bilayers of different thicknesses. Even in the high hydrophobic mismatch condition, we do not observe a change in the D_N. A similar trend was observed in our CG simulations (Fig. 5 B). The diffusion of the lipids was ∼2-fold faster than that of the peptides, consistent with our previous work (14) and other published data (26,27). Overall, our analysis indicates that hydrophobic mismatch has a negligible effect on the lateral mobility of peptides in the membrane. The data suggest that the membrane distortions caused by the peptides must be small, which may be why the WALP peptides do not aggregate.

Figure 5.

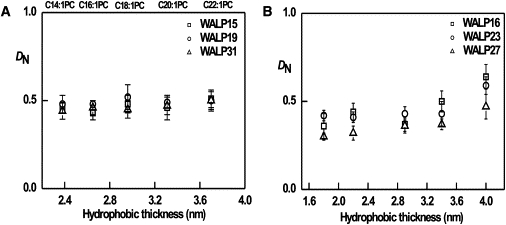
(A) Ratio of experimental diffusion coefficients of peptides and lipids, D_N (=D_P/D_L), plotted against the hydrophobic thickness of the phosphatidylcholine bilayer. (B) D_N (=D_P/D_L) obtained from CG simulations.

A recent study on the diffusion of transmembrane peptides of different hydrophobic lengths, inserted into an artificial membrane system, demonstrated that the diffusion coefficient reached a maximum value under hydrophobic matching conditions (28). A complicating factor in this case is that the bilayer system consisted of penta-monododecylether (a nonionic surfactant), and that the hydrophobic thickness was modulated by the addition of dodecane, which incorporates in-between the layers of surfactant. The surfactants and solvent used rather than genuine lipids in this artificial bilayer system give rise to unknown effects on the diffusion coefficients of the transmembrane peptides.

Charge interactions

Biological membranes contain negatively charged phospholipids such as phosphatidylglycerol, cardiolipin, and phosphatidylserine, which are essential for the activity of many membrane proteins (29). The functional activity of the proteins depends on hydrophobic interactions with the acyl chains of the surrounding lipids, as well as on interactions of protein residues with interfacial and headgroup regions of the lipids. Structural studies on transmembrane proteins suggest that two types of amino acids in particular—aromatic tryptophans and charged residues (e.g., lysine and arginine)—prefer to interact with the interfacial regions of the lipids. Positively charged residues interact with the negatively charged phospholipids and are predominantly positioned at the cytoplasmic side of the membrane, according to the positive inside rule, and this electrostatic interaction may play a role in the orientation of membrane proteins (30). The interfacial interactions of lipids with the WALP and KALP peptides have been studied in phosphocholine membranes. The tryptophan residues prefer to locate at the polar/apolar interface, whereas lysine residues prefer to localize near the phosphate group region or outward toward the aqueous phase (they tend to stay in the polar regions) (10). The lysine residues involved in anchoring transmembrane helices do so by ionic interaction or hydrogen bonds (31). Such interfacial interactions might be expected to contribute to diffusion. However, in our analysis of the diffusion of Lys- and Trp-flanked peptides as a function of increasing concentration of DOPG in the membrane (increasing surface charge), we did not observe significant differences in the diffusion coefficients of KALP23, WALP23, and DiD.

Conclusions

The membrane diffusion coefficient of peptides of different hydrophobic lengths and amino acid composition is determined mainly by the hydrophobic thickness of the bilayer. The adaptation of peptides to the surrounding lipid environment and a distortion of the annular lipids will affect the effective hydrodynamics radius of the peptides. Yet, we observed no such effect on diffusion in either the experiments or the simulations. This is because, as a result of the logarithmic dependence of the diffusing species' radius on the lateral mobility, adaptations of the peptides and lipids are not readily reflected in their mobilities. Of importance, our experimental data correlate perfectly with the MD simulations. Our studies suggest that lateral diffusion measurements will provide information on the bulk properties of the membrane, rather than on peptide-peptide or lipid-peptide interactions, because they are relatively insensitive to such associations. We stress that our measurements were done in relatively simplified fluid membranes without segregated lipid domains, which is different from the situation in real cell membranes. Nevertheless, this work now opens the way to achieving a more thorough, physics-based understanding of biomolecular motion in crowded environments such as cells.