Abstract
Presented here is a quantitative model of the wrapping and unwrapping of the DNA around the histone core of the nucleosome that suggests a mechanism by which this transition can be controlled: alteration of the charge state of the globular histone core. The mechanism is relevant to several classes of posttranslational modifications such as histone acetylation and phosphorylation; several specific scenarios consistent with recent in vivo experiments are considered. The model integrates a description based on an idealized geometry with one based on the atomistic structure of the nucleosome, and the model consistently accounts for both the electrostatic and nonelectrostatic contributions to the nucleosome free energy. Under physiological conditions, isolated nucleosomes are predicted to be very stable (38 ± 7 kcal/mol). However, a decrease in the charge of the globular histone core by one unit charge, for example due to acetylation of a single lysine residue, can lead to a significant decrease in the strength of association with its DNA. In contrast to the globular histone core, comparable changes in the charge state of the histone tail regions have relatively little effect on the nucleosome's stability. The combination of high stability and sensitivity explains how the nucleosome is able to satisfy the seemingly contradictory requirements for thermodynamic stability while allowing quick access to its DNA informational content when needed by specific cellular processes such as transcription.
Introduction
The important role of chromatin organization in key cellular processes such as DNA replication, repair, transcription, and epigenetic inheritance (i.e., inheritance that is not coded by the DNA sequence), is now well recognized (1). The principle component for DNA compaction in eukaryotic organisms is the nucleosome which consists of 146–147 basepairs of DNA wrapped ≈1.75 superhelical turns around a roughly cylindrical core of eight histone proteins (2,3) (Fig. 1).
Figure 1.
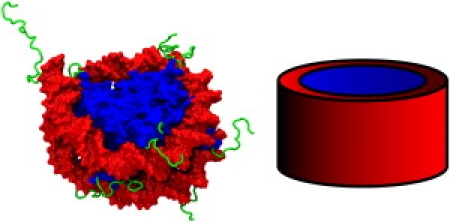
(Color online) (Left) The atomic-resolution x-ray structure of an isolated nucleosome (2,3) used here as the basis for the fine-grained representation of the system. The molecular surface is shown. (Red) DNA. (Blue) Globular histone core. The histone proteins, H2A, H2B, H3, and H4, are either part of two dimers (H2A–H2B) or one tetramer (H3–H4)2. We use a previous definition (8) of the globular histone core which includes residues 13–119 of H2A, 24–122 of H2B, 27–135 of H3, and 20–102 of H4. (Green) Histone tail regions. The wrapped DNA covers almost all of the side surface of the globular histone core, with the tails primarily protruding into the solvent. (Right) The coarse-grained representation of the isolated nucleosome. The DNA is represented as a smooth concentric cylinder surrounding the globular histone core. The left image was created using the VMD software package (80) with the Tachyon renderer (81).
The nucleosome in vivo has two competing properties: it must be highly stable, preserving its unique spatial structure, while simultaneously allowing for easy retrieval of the DNA's information content when needed by the cell. Modulation of the nucleosome's stability is implicated as a mediator of chromatin function (1,4–6). However, the underlying principles that govern the stability of the system in vivo remain unclear.
A great variety of reversible structural modifications to the components of chromatin are known to occur, such as acetylation, methylation, or phosphorylation of specific amino acids of the histone proteins. However, to our knowledge, it is still a mystery as to which types of modifications are the most important for the intrinsic stability of the nucleosome. Until very recently, experimental research focused exclusively on modifications in the histone tail regions (Fig. 1). However, evidence is now mounting that these modifications, although likely to be important for the compaction of higher level chromatin structures (7), may have relatively little effect on the nucleosome's stability (2,8–10). Conversely, the role of the globular histone core (GHC) (shown as the blue region in Fig. 1), which was once believed to be limited to guiding the DNA folds, clearly needs reassessment. A number of posttranslational modifications (PTMs) in this region have recently been discovered (4,11). Their associated biological functions have so far been investigated in only a handful of cases (12–20). There is a pressing need for a clear quantitative understanding of the relative roles of the various histone regions in controlling the nucleosome's stability (21). However, presently developing such a detailed understanding is difficult. A large part of the difficulty is that no unifying quantitative, causal model exists that connects PTMs with the stability of the nucleosome. As the amount of diverse data on PTMs will undoubtedly increase, the absence of such a unifying model could hamper progress toward development of a detailed understanding of the nucleosome dynamics and its connection with the biological function. In the long term, such a model might serve as a conceptual centerpiece for building a larger framework for understanding the much more complex structure-dynamics-function relationships in chromatin (4).
Here we describe the construction, validation, and predictions of a model that provides a quantitative and causal connection between the nucleosome's stability and a class of PTMs that directly affect the charge of the histones (such as acetylation or phosphorylation). We show how the model can help us gain insights into key structure-function relationships in the nucleosome. Our guiding principle is that the underlying physics behind some of the robust mechanisms that control the stability of the nucleosome in vivo can be revealed by in vitro experiments in conjunction with carefully crafted theoretical models.
Experiments have implicated electrostatic interactions to be the dominant factor that controls the nucleosome's overall stability, which is consistent with the highly charged nature of both the histone core and the DNA. Several physical-chemical experiments have studied the response of the nucleosome to changes in parameters (e.g., salt and pH) that directly affect the strength of electrostatic interactions (22–36). The results of these experiments provide the critical advantage of validating a model based on the electrostatic interactions in the nucleosome against the diverse quantitative experimental data accumulated over almost three decades.
Several physics-based models focusing on various aspects of the nucleosome's dynamics have become available recently. These models can be roughly divided into two broad categories according to the level of approximation used to represent the nucleosome's structure. Coarse-grain models based on highly idealized geometries (37–45) drastically simplify the electrostatic problem that needs to be solved, which greatly facilitates the investigation of the phase diagram and various parameter regimes of the system. The more complex, fine-grain models are based on the detailed molecular geometry of the nucleosome (46) and are more restrictive in this sense, but they provide a greater degree of physical realism.
A unique feature of our approach is that it uses a hybrid model in which an analytically solvable, coarse-grain model based on an idealized geometry structure of the nucleosome is integrated with a fine-grain numerical model based on its fully atomistic description. The model yields qualitative insights into the physics of nucleosome stability combined with quantitative free energy estimates of the effects of a wide class of charge-altering PTMs in both the globular core and tail regions. To our knowledge, these insights and predictions are, as yet, unavailable experimentally, and should be useful for rationalizing and guiding the experiment.
Methods
The section describes the key methods and computational procedures; however, extra details, including the derivations, numerical constants used, and dimensions of the nucleosome, are presented in the Supporting Material.
Model based on idealized geometry
We represent the nucleosome as a two-state system: the wrapped state in which the DNA is fully wrapped around the histone core, and the unwrapped state with the DNA completely separated from the histone core (Fig. 2). Experimental evidence suggests that transitions in the nucleosome induced by altering the charge-charge interactions are indeed two-state, at least when effected through changes in ionic strength of the environment in the physiologically relevant range (22) in vitro. Although in vivo conformational transitions in the system may be more complex, we show that our main conclusion—the biologically relevant strong dependence of the nucleosome's stability on the charge of its GHC—is robust to the assumptions of the model.
Figure 2.
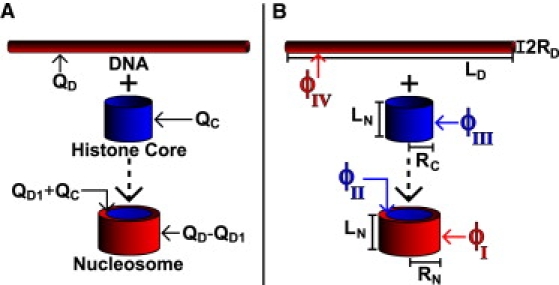
(Color online) The two states of the nucleosome in the idealized geometry model: the fully wrapped nucleosome core particle and the globular histone core plus free DNA. The computed stability, ΔG, corresponds to the unwrapped state→wrapped state transition (Large dashed arrows pointing from top to bottom). (A) The charge distribution of the idealized geometry model. For all cylinders, the total charge is uniformly distributed on the side surface; the top and bottom surfaces are excluded. The labels QC, QD1, and QD correspond to the total charge of the globular histone core, the charge of the DNA not exposed to the solvent, and the total charge of the DNA. (B) The potentials and geometric dimensions used in the model. The labels RN, LN, RC, LC, RD, and LD correspond to the radii and lengths of the nucleosome, histone core, and DNA, respectively. The value ϕI specifies the potential at the external surface of the nucleosome. The value ϕII is the potential at the interface between the histone core and DNA. The value ϕIII represents the potential at the external surface of the histone core, and the value ϕIV is the potential at the external surface of the unwrapped DNA. See Eqs. 6–9 for the exact forms of these potentials.
The geometry and the associated surface charge distributions for the coarse-grained model are shown in Fig. 2. All charges are assumed uniformly distributed on the respective surfaces. The values used for all the input parameters (see Supporting Material) come from the experiment or previously used and accepted values in theoretical calculations (2,45,47–49). In particular, the fraction of the DNA charge exposed to the solvent is determined by the actual geometry of the nucleosome core particle (NCP), from its atomic-resolution structure.
Electrostatic contribution to ΔG
We used the Linearized Poisson-Boltzmann equation (LPBE) to compute the electrostatic potential ϕ(r) produced by a molecular charge distribution ρ(r),
| (1) |
where ε(r) is the position-dependent dielectric constant, and the electrostatic screening effects of monovalent salt enter via the Debye-Hückel screening parameter κ.
The electrostatic free energy of building a given charge distribution within the linear Poisson-Boltzmann theory is given by (50)
| (2) |
For the uniform surface charge distributions present in our model, Eq. 2 reduces to
where ϕ(R) is the potential at the given surface charge, and Q is the total charge that is uniformly distributed on the surface.
The wrapped state has one cylinder, the NCP, containing two surface charges, and we refer to the electrostatic free energy of this state as Wwrapped. However, the unwrapped state contains two independent cylinders, the GHC and the free DNA, each with a surface charge. The combined electrostatic free energy of the GHC and the free DNA is referred to as Wunwrapped. Using the notation of Fig. 2, the electrostatic free energy of the NCP folding,
is given by
| (3) |
To obtain a closed form expression for ΔGelectro, we approximate all ϕ(R) values by the exact infinite cylinder solutions of the LPBE. The electrostatic potential at the exterior surface, ϕext(R), of an infinitely long cylinder of radius R in a solvent with monovalent salt is (51,52)
| (4) |
where K0 and K1 are modified Bessel functions of the second kind, εout is set to 80 for water, Q is the total charge on the surface of the cylinder, and L is the length of the cylinder. We expand upon Eq. 4 by incorporating ion exclusion effects with a standard Stern radius b by R → R + b (53) for any surfaces exposed to the solvent.
The values of the potential at three of the four charged surfaces are determined by Eq. 4. The other charged surface is inside the concentric cylinder of the wrapped state and has the following form for the potential,
| (5) |
where C is a constant, and εin is set to 15 to account for the water trapped between the two wrapped helices of DNA being more ordered than free water (54,55). Thus, the potentials at the surface of the various cylinders defined in Fig. 2 are
| (6) |
| (7) |
| (8) |
| (9) |
The corresponding total ΔGelectro from Eq. 3 is
| (10) |
Equation 10 is the main result of the derivation and serves as the foundation for the results discussed below. The first two terms in Eq. 10 correspond to the wrapped state and the last two terms correspond to the unwrapped state of the nucleosome. The critical term with respect to a dependence on the charge state of the GHC is the one proportional to the total charge at the interface between the GHC and DNA, (QC + QD1)2/εin. Implications on how this term affects the nucleosome's stability are discussed below and in the Supporting Material.
The approximation of using the infinite cylinder solutions for finite cylinders is limited to ionic strengths such that the associated Debye length is less than that of the shortest object. The shortest length-scale associated with the model is the length of the nucleosome, LN = 57 Å, which corresponds to a monovalent salt concentration of ∼0.0028 M. For lower salt concentrations, we can only expect general qualitative trends to be correct. The low-salt and high-salt limits for Eq. 10 are discussed in the Supporting Material.
The full atomistic structure of the nucleosome, PDB ID 1KX5 (3), with only the residues forming the GHC (Fig. 1, left panel), was used to compute the parameters of the model. We excluded the tails because they have little effect on the stability of individual nucleosomes (2). We estimated the nucleosome's total charge state by the charge states of the ionizable amino acids within the GHC at pH 7.5 which is appropriate for the nucleus (56), via the H++ server (57,58), which employs the standard continuum electrostatics methodology for determining the pK values of amino-acid residues (59).
For DNA, the electrostatic free energies computed with the LPBE are in a reasonable agreement with the full nonlinear PB equation—the associated relative errors are expected to be a few percent (53) in the most relevant ionic strength regime κRD ≥1, where RD ∼10 Å is the DNA radius (45,48). The LPBE was also successfully used in the past to describe DNA's A→Z transition (51). Our calculations also agreed with previous experiment and theory in a similar context in the low-salt limit of Eq. 10 ((60–63) and see this article's Supporting Material). Furthermore, significant approximations were already made in the conversion from the full atomistic model to an idealized geometry model of the nucleosome, and there was an inherent uncertainty of at least 10% (49) in the DNA radius, which corresponded to a ±7 kcal/mol uncertainty in the calculated stability of the nucleosome; thus, we did not see a clear justification for the use of the nonlinear PB equation within our model.
Nonelectrostatic contribution
In addition to the nonelectrostatic component of the DNA elastic energy, ΔGnon includes the free energy of binding between the DNA strands and the GHC. The size and complexity of the nucleosome make a first-principles calculation of the nonelectrostatic contributions (ΔGnon) impractical (64). We instead estimate ΔGnon from the experimentally known midpoint of the salt-induced wrapping transition (ΔG(κref) = 0) (22). A similar approach previously led to correct quantitative predictions in the context of the pH dependence of protein stability (65). This method assumes that all nonelectrostatic contributions lack salt dependence, which allows us to write and solve for . From experiment, (22,66), which gives Incorporating the difference between the nucleosome density in vitro and in vivo (67) leads to a modest correction, (see Supporting Material).
Model based on full atom-level structure
We represented the wrapped state with the full (including the tails) atomic structure of the nucleosome (see Fig. 1, left panel); protonation states of the ionizable residues are set using the methodology specified above. The unwrapped state was represented by the same structure with the DNA removed; the free DNA conformation in the unwrapped state does not affect ΔΔG as defined below.
A numerical solver for Eq. 1, APBS (68), was employed to compute changes in the nucleosome's stability, ΔΔG, due to changes in charge states of the histones. We referred to the total free energy of the state without any modifications to the GHC charge as ΔG(native). Any states where PTMs, e.g., acetylation, were applied have an associated total free energy of ΔG(PTM). We defined , and computed this quantity for the acetylation of a select number of lysines shown in Table 1. We assumed that the effect of the PTMs on ΔGnon was negligible compared to its effect on ΔGelectro, so that . Because there are two copies of each histone protein in the core, we applied the PTMs in pairs, e.g., acetylation of K56 on both H3 histones.
Table 1.
The destabilization (ΔΔG) of the nucleosome due to selective acetylation (neutralization) of each of the two lysines in the globular histone core and in the tails
| Acetylated lysines | Destabilization ΔΔG (kcal/mol) |
|---|---|
| (1) Core H3K56 | 8.7 |
| (2) Core H4K91 | 7.2 |
| (3) Tail H2BK5 | 1.8 |
| (4) Tail H3K4 | 0.07 |
The ΔΔG values are computed based on the full atomic level structure of the nucleosome using the numerical Poisson-Boltzmann solver. The labels from 1 to 4 are the same as in Fig. 4.
APBS was used with the following parameters: the internal dielectric set to 4, the external dielectric set to 80, and the monovalent salt concentration set to 145 mM with an ion radius of 2.0 Å. The boundary between the two dielectrics was set to be the molecular surface as determined by a probe radius of 1.4 Å. The grid spacing of 0.75 Å with 4803 grid points was used. We also verified that the use of the nonlinear solver, with the same settings as used with the linear solver, does not affect our key conclusions.
Specifically, the relative effect on ΔΔG due to the acetylation of residues in the GHC versus residues in the tails shown in Table 1 is preserved. In Table 1, the largest ΔΔG from the core comes from the acetylation of H3K56, and the largest ΔΔG from the tails comes from the acetylation of H2BK5. The nonlinear solver shows 93% agreement to the linear solver when comparing the ratio (core versus tail) of these two ΔΔGs. Similarly, when comparing the ratio (core versus tail) of the other two residues, H4K91 and H3K4, the nonlinear solver shows 65% agreement with the linear solver. The values from the nonlinear solver can be found in Table S2 of the Supporting Material.
Results and Discussion
We compute the free energy associated with the wrapping and unwrapping transition of the DNA from the globular histone core (GHC). Our self-consistent estimates are based on two distinct representations of the nucleosome structure (see Methods). The coarse-grain representation is based on an idealized geometry in which the nucleosome and its wrapped DNA are represented as coaxial cylinders of appropriate dimensions (see Fig. 2) while the fine-grain model corresponds to the full atomic resolution structure of the nucleosome (see Fig. 1).
The physics of the nucleosome wrapping/unwrapping
In Fig. 3, we present the calculated stability phase diagram of the nucleosome with respect to the two most commonly used variables in experiments that study the nucleosome's stability in vitro—the salt concentration of the solution and the total charge of the GHC. Remarkably, we observe that all of the trends where a phase boundary is crossed or approached (shown as red arrows) agree quantitatively or at least semiquantitatively with experiment ((22,24–26,29–32), and see Supporting Material for details). The horizontal red arrows show that in either direction of salt change, the wrapped state destabilizes. The vertical red arrow shows that an increase in core charge initially increases the stability of the wrapped state but then destabilizes the system. The observation that is perhaps the most relevant to biology is that even a slight decrease of the GHC charge from its physiological value should generally destabilize the nucleosome (see Fig. 3).
Figure 3.
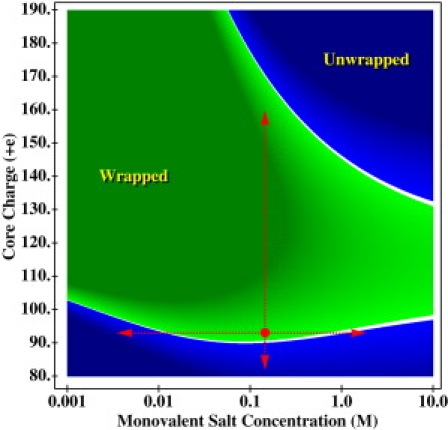
(Color online) Phase diagram of the nucleosome two-state system as a function of globular histone core charge and monovalent salt concentration of the surrounding solution. The interior region represents the wrapped state, ΔG < 0. The darker the interior region, the more stable the system is. The exterior region represents the unwrapped state, ΔG > 0. The darker the exterior region, the more unstable the system is. (White band) Interface between the two states is defined as |ΔG| < 5 kcal/mol. (dot, lower region of the graph) Physiological conditions at which the predicted stability of the nucleosome is ΔG = –38 ± 7 kcal/mol. (dashed arrows) Predicted trends that agree with experiment as conditions are changed from the physiological conditions.
The physical origin of this effect is primarily in the destabilizing free energy of the electric field trapped inside the low dielectric bulk of the DNA; it is revealed by the analysis of the analytical expressions for ΔGelectro available within the idealized geometry model (see the Supporting Material). Essentially, a large portion of the electric field flux from the GHC goes through the low dielectric environment of the DNA wrapped around the histone core. At physiological conditions, the charge of the GHC is such that this flux is (nearly) canceled by the opposite field due to the charge on the surface of the DNA in contact with the core. The existence of this strong trapped field is the consequence of the peculiar topology of the wrapped conformation (Fig. 1), and will be absent from any model that treats DNA as a zero-thickness thread.
Specifically, a decrease in the GHC charge increases the destabilizing energy associated with the trapped field and reduces the natural electrostatic attraction between the nucleosomal DNA and histone core. This synergistic effect is what amplifies the nucleosome's sensitivity to slight decreases in the total GHC charge. The fundamental question of how this effect may be used for precise control of the nucleosome's stability is discussed below. (Note that the trapped field effect is also responsible for the counterintuitive decrease in the nucleosome's stability when a large increase in the GHC charge occurs; see Fig. 1. As the magnitude of the GHC charge increases, the destabilizing energy associated with the trapped field rapidly builds up in the low dielectric bulk of the DNA, eventually overwhelming other stabilizing contributions to ΔG and thus driving the system towards the unwrapped state.)
Implications to the nucleosome's stability control in vivo
Stability versus accessibility
Predictions of the model immediately suggest how the nucleosome's stability-versus-DNA accessibility dilemma may be resolved by the nucleosome and suggest specific mechanisms for biologically relevant control of the stability of the nucleosome. At physiological conditions, our model predicts the absolute stability, |ΔG|, of a single isolated nucleosome to full unwrapping of its DNA to be 38 ± 7 kcal/mol which lies within experimental rough estimates for the upper and lower bounds of |ΔG| (34,69–71). However, the system lies very close to the phase boundary between the wrapped state and unwrapped state (Fig. 3). The borderline position of the system means that small variations of the proper control parameters can significantly loosen the structure, or unwrap it completely if needed for a specific biological function. Our model provides insights into how this control can be effected.
As can be seen from the phase diagram, the monovalent salt concentration is unlikely to be used by the cell in vivo to control the stability of the nucleosome—the phase boundary along the salt axis is almost flat. The changes in [NaCl] that would have to occur in the nucleus during the cell cycle for this kind of stability control would be 10-fold, which is biologically unreasonable. Although the addition of multivalent ions could shorten the boundary along the salt axis, the analysis of their effects on the nucleosome's stability is beyond the scope of this work. Regardless, these effects of changing ionic strength are inherently nonlocal; generic changes in equilibrium ionic strength cannot be confined to individual nucleosomes.
Globular histone core charge as stability control parameter
In contrast to ionic strength modulations, change in the GHC charge offers a possibility to exert selective control over the stability of an individual nucleosome. Notice that within our model, ΔG is very sensitive to changes in the GHC charge (Fig. 3): according to our calculations based on the idealized geometry model, a change in one unit charge can cause a ∼15 kcal/mol change in the stability of the nucleosome at physiological conditions. Therefore, a decrease of the GHC charge by only a few unit charges can cause a complete unwrapping of the DNA. A careful analysis of the analytical model (see Supporting Material) shows that the system owes its extreme sensitivity to changes in the charge of the GHC to the same destabilizing effect of the trapped field described above, which increases rapidly as the system moves away from the physiological conditions. In fact, among the many contributions to the derivative of the total free energy with respect to the GHC charge, the main contribution comes from the trapped field term unique to the wrapped state of the nucleosome. Thus, as long as the unwrapped state(s) break the unique topology of the wrapped state in which the DNA fully encloses the histone core on the sides, we can still expect ΔG to be sensitive to the GHC charge. This is why the two-state assumption made in this work may not be entirely necessary for its main result. See a detailed discussion in the Supporting Material.
Application to histone acetylation: core versus tails
The analytical solutions based on an idealized geometry model of the nucleosome have given us valuable insights into the physics of the nucleosome's stability. In what follows, we verify our key conclusions using the full atomic resolution structure of the nucleosome in conjunction with accurate numerical solutions of the Poisson-Boltzmann equation (see Methods). The goal is to mimic histone acetylation experiments and compute the effect of the charge change in the GHC on the nucleosome's stability. To this end, we purposely selected a set of four pairs of lysine residues that have known biological significance and are located in very different regions within the nucleosome (Fig. 4). To mimic acetylation, we neutralize each of the selected lysines by changing its charge distribution accordingly (72) (the overall charge changes from +1 to 0 (see Supporting Material) and compute the relative impact of the change on the stability of the nucleosome, estimated as ΔΔG per neutralized lysine (see Methods). (Within the idealized model, the acetylation of any pairs of residues is mapped to one and the same location in Fig. 3: two charges down from the dot representing in vivo conditions.) These impacts are qualitatively illustrated in Fig. 4; the numerical ΔΔG estimates are provided in Table 1.
Figure 4.
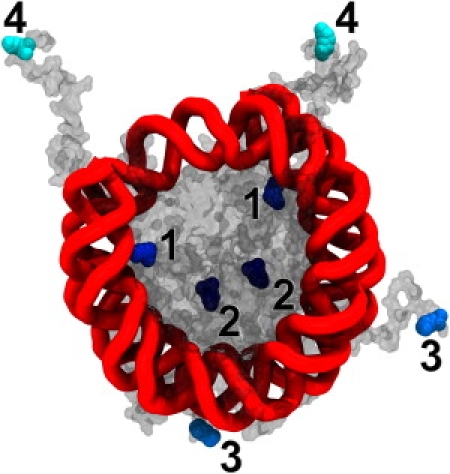
(Color online) The location of each of the acetylated (neutralized) lysine residues and its relative impact on nucleosome's stability, ΔΔG. The relative intensity of the residue color roughly corresponds to the computed ΔΔG values shown in Table 1: the darker the color, the stronger the effect. Each lysine pair is labeled from 1 to 4 as in Table 1 for the ease of identification. This image was created using the VMD software package (80) with the Tachyon renderer (81).
We note that the analytical coarse-grained model should not be expected to yield highly accurate quantitative estimates of the ΔΔG value associated with specific GHC residues because the dependence on their relative location inside the GHC is not accounted for within this model, which is its main limitation. The model predicts the (ΔΔG = 30.8 kcal/mol) for acetylation of any pair of residues inside the globular histone core and zero for any tail residue. What is important, however, is that the key prediction holds—the system is sensitive to small changes in the GHC charge, regardless of the precise location of the change. This is in contrast to the minimal effect the tail charges are predicted to have on the nucleosome's stability, and is in agreement with the experimental observations discussed above (8). The physics behind the difference is simple: the tail charges lie in the high dielectric solvent, outside of the DNA shell wrapped around the core.
Specific predictions and examples
Targeted acetylation of lysines or phosphorylation of serines or threonines within the GHC is one way to decrease its charge with minimal disruption to the overall nucleosome structure. For example, consider a situation when loosening of the nucleosome structure is required for a specific biological process, such as transcription (or initiation of it). Within our model, the latter will be facilitated by acetylation of GHC lysines. And vice versa: deacetylation of these lysines will hamper transcription because deacetylation increases the charge of the GHC. Accordingly, recent experimental genome-wide evidence suggests that acetylation of K56 of histone H3 is necessary for efficient gene transcription (73) in vivo. A similar observation has been made for acetylation of K36 of H3 (74). Moreover, acetylation of K56 also enables DNA replication and prevents epigenetic silencing (17,19), consistent with a looser state of the nucleosome acetylated at H3K56, as predicted by our model. Conversely, deacetylation of K56 of histone H3 tightens the nucleosome structure, thereby facilitating compaction of heterochromatin (12). This finding is also consistent with the predictions of our model: deacetylation of a site in the GHC at physiological conditions increases its charge by one unit, thus increasing the stability of the wrapped state of the nucleosome (Fig. 3). Also consistent with the model is the observation that acetylation of lysine 91 on histone H4 results in a disruption of the chromatin structure and increases the system's sensitivity to DNA damage and un-silences many genes near the telomeres (15). As further evidence that these changes came primarily from the relative charge change, an experiment was conducted in which H4K91 was replaced with a glutamine to mimic the acetylated state and then replaced with an arginine to mimic the original charged state. The mutant with the glutamine showed similar phenotypes as the acetylated lysine and the mutant with the arginine showed similar phenotypes to the wild-type (nonacetylated lysine) (15). Another piece of supporting, in vivo evidence comes from previous assays on chicken erythrocytes showing that phosphorylation of serine 28 (located in the GHC) destabilized the nucleosome while phosphorylation of serine 10 (located on a tail) did not appreciably affect the stability of the nucleosome. The same study also showed that phosphorylation of serine 28 on the H3 histone was predominantly in active/competent regions of the chromatin (16), which is where one would expect the DNA accessibility to be higher, with lower stability of the associated nucleosomes. Finally, phosphorylation of threonine 45 on the H3 residue has been associated with DNA replication in Saccharomyces cerevisiae (75) and with apoptosis in human neutrophil cells (76).
In addition to histone acetylation and phosphorylation, other electrostatics-based mechanisms for changing the nucleosome's stability may exist that are consistent with our model. For example, small changes in ambient pH around the physiological value may also have the desired effect of altering the charge of the GHC. However, similar to changing the ionic strength, this effect would be nonlocal and therefore may only be suitable to controlling spatially extended regions of chromatin rather than individual nucleosomes. To exert selective control at the level of individual nucleosomes, one may consider a scenario in which a charged protein binds to the exposed face of the nucleosome GHC (Fig. 1), thereby loosening the structure. Recent experimental work has suggested such a mechanism (77,78).
Implications for nucleosome assembly
Our model can also give insight into how the nucleosome assembly process might work. The process would begin with the system initially being just outside the phase boundary in the unwrapped state (Fig. 3). The nucleosome would then be driven across the boundary to the wrapped state by a gradual increase of the effective charge on its histone core. Indirect evidence that in vivo systems may need to use slow adjustment of the electrostatic interactions to assemble the nucleosome comes from in vitro experiments where the process of reconstituting the nucleosomes from free DNA and histone cores is based on gradually turning on the electrostatic attraction between the core and the DNA by slow dialysis from high salt down to physiological ionic strength (79). It is known that simply mixing the components at physiological conditions results in improperly wrapped nucleosomes. This suggests a kinetic trap brought on by strong electrostatic attraction that rapidly brings the DNA and histone core together before the DNA has a chance to properly wrap around the core. The trap is not unexpected, given the complex topology of the nucleosome structure and the depth of the folding funnel manifested by the high ΔG of formation predicted by our model. Assuming that such a trap also exists in vivo, gradual turning on of the interactions through core charge increase would be one way to circumvent it.
Although only a handful of in vivo studies have so far investigated the link between charge state of the GHC and chromatin assembly (13–15), the observations made in these works appear to be consistent with this model. For example, acetylation of free histone H3 at lysine 56 promotes subsequent (replication-independent) chromatin assembly (13), implying that the assembly process indeed starts with a lower charge state of the GHC. At the same time, the existing assembled chromatin is driven toward the disassembled state by a decrease in the GHC charge via H3K56 acetylation (14); recall that, according to our model, such decrease reduces the stability of the wrapped state of the nucleosome.
Limitations of the model
We emphasize that within our model the simple and straightforward relationship between changes in the charge of the GHC and corresponding changes in the nucleosome's stability holds only when the stability change ΔΔG is dominated by the electrostatic contribution. This is likely to be true for pointlike alterations such as acetylation and phosphorylation and protonation and may be possible for some mutations, and even binding of some proteins to the exposed surface of the nucleosome. At the same time, there are many situations where this condition is not expected to hold. PTMs that significantly affect the structure of the GHC are one such example. Changes in amino-acid composition that may accompany histone substitution with a variant form, e.g., H2A → H2A.Z, may also bring about large unknown changes in the nonelectrostatic component of the total free energy. In the cases where there are large changes in the nonelectrostatic component of the total free energy, the model should not be expected to yield accurate predictions unless one can account for these changes.
The main conclusion of our study is that cells may utilize the sensitivity of the nucleosome's stability to the charge of the globular histone core (GHC) for effective loosening or tightening of the structure when needed by specific biological processes. Given the dominant role of electrostatics in the thermodynamic stability of the nucleosome, and agreement of our model's predictions with a variety of in vitro and recent in vivo experiments focused on the role of charge-altering PTMs of residues within the globular histone core (such as H4K91, H3K36, H3K56, H3T45, and H3S28) in various cellular functions, we believe that the proposed electrostatics-based mechanism of its control is an important one, although it is probably not the only one. We emphasize that alternative explanations for the in vivo observations cannot be completely excluded at this point. Although it would be naive to expect a first-principles, physics-based model such as the one presented here to provide a comprehensive description of structure-function connections in the nucleosome in vivo, the model may nevertheless be expected to correctly describe the overall causal trends within its bounds of applicability. As such, it may serve as a useful general guide to experimentalists.
Acknowledgments
Alexey Onufriev thanks Victoria Lunyak for the initial motivation and many subsequent discussions, and Maxim Frank-Kamenetskiǐ for helpful discussions at the early stages of the project. The authors also thank Jonathan Widom, Joel Gottesfeld, Igor Sharakhov, Alexander Konev, and Jessica Tyler for many helpful comments and suggestions.
This work was supported in part by the National Institutes of Health R01 grant No. GM076121. A.T.F. acknowledges partial support from the EIGER project at Virginia Tech under National Science Foundation Integrative Graduate Education and Research Traineeship grant No. DGE-0504196.
Supporting Material
References
- 1.Henikoff S. Nucleosome destabilization in the epigenetic regulation of gene expression. Nat. Rev. Genet. 2008;9:15–26. doi: 10.1038/nrg2206. [DOI] [PubMed] [Google Scholar]
- 2.Luger K., Mäder A.W., Richmond T.J. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 3.Richmond T.J., Davey C.A. The structure of DNA in the nucleosome core. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- 4.Cosgrove M.S., Boeke J.D., Wolberger C. Regulated nucleosome mobility and the histone code. Nat. Struct. Mol. Biol. 2004;11:1037–1043. doi: 10.1038/nsmb851. [DOI] [PubMed] [Google Scholar]
- 5.Giresi P.G., Gupta M., Lieb J.D. Regulation of nucleosome stability as a mediator of chromatin function. Curr. Opin. Genet. Dev. 2006;16:171–176. doi: 10.1016/j.gde.2006.02.003. [DOI] [PubMed] [Google Scholar]
- 6.Mariño-Ramírez L., Kann M.G., Landsman D. Histone structure and nucleosome stability. Expert Rev. Proteomics. 2005;2:719–729. doi: 10.1586/14789450.2.5.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robinson P.J., An W., Rhodes D. 30 nm chromatin fiber decompaction requires both H4–K16 acetylation and linker histone eviction. J. Mol. Biol. 2008;381:816–825. doi: 10.1016/j.jmb.2008.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gottesfeld J.M., Luger K. Energetics and affinity of the histone octamer for defined DNA sequences. Biochemistry. 2001;40:10927–10933. doi: 10.1021/bi0109966. [DOI] [PubMed] [Google Scholar]
- 9.Widlund H.R., Vitolo J.M., Hayes J.J. DNA sequence-dependent contributions of core histone tails to nucleosome stability: differential effects of acetylation and proteolytic tail removal. Biochemistry. 2000;39:3835–3841. doi: 10.1021/bi991957l. [DOI] [PubMed] [Google Scholar]
- 10.Dorigo B., Schalch T., Richmond T.J. Chromatin fiber folding: requirement for the histone H4 N-terminal tail. J. Mol. Biol. 2003;327:85–96. doi: 10.1016/s0022-2836(03)00025-1. [DOI] [PubMed] [Google Scholar]
- 11.Zhang K., Tang H., Burlingame A.L. Identification of acetylation and methylation sites of histone H3 from chicken erythrocytes by high-accuracy matrix-assisted laser desorption ionization-time-of-flight, matrix-assisted laser desorption ionization-postsource decay, and nanoelectrospray ionization tandem mass spectrometry. Anal. Biochem. 2002;306:259–269. doi: 10.1006/abio.2002.5719. [DOI] [PubMed] [Google Scholar]
- 12.Xu F., Zhang Q., Grunstein M. Sir2 deacetylates histone H3 lysine 56 to regulate telomeric heterochromatin structure in yeast. Mol. Cell. 2007;27:890–900. doi: 10.1016/j.molcel.2007.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen C.-C., Carson J.J., Tyler J.K. Acetylated lysine 56 on histone H3 drives chromatin assembly after repair and signals for the completion of repair. Cell. 2008;134:231–243. doi: 10.1016/j.cell.2008.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Williams S.K., Truong D., Tyler J.K. Acetylation in the globular core of histone H3 on lysine-56 promotes chromatin disassembly during transcriptional activation. Proc. Natl. Acad. Sci. USA. 2008;105:9000–9005. doi: 10.1073/pnas.0800057105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ye J., Ai X., Parthun M.R. Histone H4 lysine 91 acetylation a core domain modification associated with chromatin assembly. Mol. Cell. 2005;18:123–130. doi: 10.1016/j.molcel.2005.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sun J.-M., Chen H.Y., Davie J.R. Phosphorylated serine 28 of histone H3 is associated with destabilized nucleosomes in transcribed chromatin. Nucleic Acids Res. 2007;35:6640–6647. doi: 10.1093/nar/gkm737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller A., Yang B., Kirchmaier A.L. Proliferating cell nuclear antigen and ASF1 modulate silent chromatin in Saccharomyces cerevisiae via lysine 56 on histone H3. Genetics. 2008;179:793–809. doi: 10.1534/genetics.107.084525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Masumoto H., Hawke D., Verreault A. A role for cell-cycle-regulated histone H3 lysine 56 acetylation in the DNA damage response. Nature. 2005;436:294–298. doi: 10.1038/nature03714. [DOI] [PubMed] [Google Scholar]
- 19.Downs J.A. Histone H3 K56 acetylation, chromatin assembly, and the DNA damage checkpoint. DNA Repair (Amst.) 2008;7:2020–2024. doi: 10.1016/j.dnarep.2008.08.016. [DOI] [PubMed] [Google Scholar]
- 20.Cook P.J., Ju B.G., Rosenfeld M.G. Tyrosine dephosphorylation of H2AX modulates apoptosis and survival decisions. Nature. 2009;458:591–596. doi: 10.1038/nature07849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cosgrove M.S., Wolberger C. How does the histone code work? Biochem. Cell Biol. 2005;83:468–476. doi: 10.1139/o05-137. [DOI] [PubMed] [Google Scholar]
- 22.Yager T.D., McMurray C.T., van Holde K.E. Salt-induced release of DNA from nucleosome core particles. Biochemistry. 1989;28:2271–2281. doi: 10.1021/bi00431a045. [DOI] [PubMed] [Google Scholar]
- 23.Khrapunov S.N., Dragan A.I., Zagariya A.M. Mechanisms of stabilizing nucleosome structure. Study of dissociation of histone octamer from DNA. Biochim. Biophys. Acta. 1997;1351:213–222. doi: 10.1016/s0167-4781(96)00199-6. [DOI] [PubMed] [Google Scholar]
- 24.Libertini L.J., Small E.W. Effects of pH on low-salt transition of chromatin core particles. Biochemistry. 1982;21:3327–3334. doi: 10.1021/bi00257a013. [DOI] [PubMed] [Google Scholar]
- 25.Mangenot S., Leforestier A., Livolant F. Salt-induced conformation and interaction changes of nucleosome core particles. Biophys. J. 2002;82:345–356. doi: 10.1016/S0006-3495(02)75399-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ni X., Cole R.D. Effects of various salts and pH on the stability of the nucleosome in chromatin fragments. Biochemistry. 1994;33:9276–9284. doi: 10.1021/bi00197a031. [DOI] [PubMed] [Google Scholar]
- 27.Bashkin J., Hayes J.J., Wolffe A.P. Structure of DNA in a nucleosome core at high salt concentration and at high temperature. Biochemistry. 1993;32:1895–1898. doi: 10.1021/bi00059a002. [DOI] [PubMed] [Google Scholar]
- 28.Almagor M., Cole R.D. In physiological salt conditions the core proteins of the nucleosomes in large chromatin fragments denature at 73°C and the DNA unstacks at 85°C. J. Biol. Chem. 1989;264:6515–6519. [PubMed] [Google Scholar]
- 29.Libertini L.J., Small E.W. Effects of pH on the stability of chromatin core particles. Nucleic Acids Res. 1984;12:4351–4359. doi: 10.1093/nar/12.10.4351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Karpenchuk K.G., Minchenkova L.E., Mizabekov A.D. Unfolding of core nucleosomes induced by chemical acetylation of histones. Molekulyarnaya Biologiya. 1983;17:855–867. [PubMed] [Google Scholar]
- 31.Ausio J., van Holde K.E. Histone hyperacetylation: its effects on nucleosome conformation and stability. Biochemistry. 1986;25:1421–1428. doi: 10.1021/bi00354a035. [DOI] [PubMed] [Google Scholar]
- 32.Oliva R., Bazett-Jones D.P., Dixon G.H. Histone hyperacetylation can induce unfolding of the nucleosome core particle. Nucleic Acids Res. 1990;18:2739–2747. doi: 10.1093/nar/18.9.2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Brower-Toland B., Wacker D.A., Wang M.D. Specific contributions of histone tails and their acetylation to the mechanical stability of nucleosomes. J. Mol. Biol. 2005;346:135–146. doi: 10.1016/j.jmb.2004.11.056. [DOI] [PubMed] [Google Scholar]
- 34.Brower-Toland B.D., Smith C.L., Wang M.D. Mechanical disruption of individual nucleosomes reveals a reversible multistage release of DNA. Proc. Natl. Acad. Sci. USA. 2002;99:1960–1965. doi: 10.1073/pnas.022638399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Li G., Levitus M., Widom J. Rapid spontaneous accessibility of nucleosomal DNA. Nat. Struct. Mol. Biol. 2005;12:46–53. doi: 10.1038/nsmb869. [DOI] [PubMed] [Google Scholar]
- 36.Tomschik M., Zheng H., Leuba S.H. Fast, long-range, reversible conformational fluctuations in nucleosomes revealed by single-pair fluorescence resonance energy transfer. Proc. Natl. Acad. Sci. USA. 2005;102:3278–3283. doi: 10.1073/pnas.0500189102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kunze K.K., Netz R.R. Salt-induced DNA-histone complexation. Phys. Rev. Lett. 2000;85:4389–4392. doi: 10.1103/PhysRevLett.85.4389. [DOI] [PubMed] [Google Scholar]
- 38.Kunze K.K., Netz R.R. Complexes of semiflexible polyelectrolytes and charged spheres as models for salt-modulated nucleosomal structures. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;66:011918. doi: 10.1103/PhysRevE.66.011918. [DOI] [PubMed] [Google Scholar]
- 39.Schiessel H. The physics of chromatin. J. Phys. Condens. Matter. 2003;15:699–774. doi: 10.1088/0953-8984/27/6/060301. [DOI] [PubMed] [Google Scholar]
- 40.Manning G.S. Is a small number of charge neutralizations sufficient to bend nucleosome core DNA onto its superhelical ramp? J. Am. Chem. Soc. 2003;125:15087–15092. doi: 10.1021/ja030320t. [DOI] [PubMed] [Google Scholar]
- 41.Manning G.S. Simple model for the binding of a polyelectrolyte to an oppositely charged curved surface. J. Phys. Chem. B. 2003;107:11485–11490. [Google Scholar]
- 42.Cherstvy A.G., Winkler R.G. Complexation of semiflexible chains with oppositely charged cylinder. J. Chem. Phys. 2004;120:9394–9400. doi: 10.1063/1.1707015. [DOI] [PubMed] [Google Scholar]
- 43.Korolev N., Lyubartsev A.P., Laaksonen A. Electrostatic background of chromatin fiber stretching. J. Biomol. Struct. Dyn. 2004;22:215–226. doi: 10.1080/07391102.2004.10506997. [DOI] [PubMed] [Google Scholar]
- 44.Kulić I.M., Schiessel H. DNA spools under tension. Phys. Rev. Lett. 2004;92:228101. doi: 10.1103/PhysRevLett.92.228101. [DOI] [PubMed] [Google Scholar]
- 45.Arcesi L., La Penna G., Perico A. Generalized electrostatic model of the wrapping of DNA around oppositely charged proteins. Biopolymers. 2007;86:127–135. doi: 10.1002/bip.20711. [DOI] [PubMed] [Google Scholar]
- 46.Beard D.A., Schlick T. Modeling salt-mediated electrostatics of macromolecules: the discrete surface charge optimization algorithm and its application to the nucleosome. Biopolymers. 2001;58:106–115. doi: 10.1002/1097-0282(200101)58:1<106::AID-BIP100>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 47.Dickerson R.E., Drew H.R., Kopka M.L. The anatomy of A-, B-, and Z-DNA. Science. 1982;216:475–485. doi: 10.1126/science.7071593. [DOI] [PubMed] [Google Scholar]
- 48.Lyubartsev A., Nordenskiöld L. Monte Carlo simulation study of DNA polyelectrolyte properties in the presence of multivalent polyamine ions. J. Phys. Chem. B. 1997;101:4335–4342. [Google Scholar]
- 49.Schellman J.A., Stigter D. Electrical double layer, ζ-potential, and electrophoretic charge of double-stranded DNA. Biopolymers. 1977;16:1415–1434. doi: 10.1002/bip.1977.360160704. [DOI] [PubMed] [Google Scholar]
- 50.Sharp K.A., Honig B. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 1990;94:7684–7692. [Google Scholar]
- 51.Frank-Kamenetskiǐ M.D., Anshelevich V.V., Lukashin A.V. Polyelectrolyte model of DNA. Sov. Phys. Usp. 1987;30:317–330. [Google Scholar]
- 52.Stigter D. The charged colloidal cylinder with a Gouy double layer. J. Colloid Interface Sci. 1975;53:296–306. [Google Scholar]
- 53.Stigter D. Evaluation of the counterion condensation theory of polyelectrolytes. Biophys. J. 1995;69:380–388. doi: 10.1016/S0006-3495(95)79910-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Randall G.L., Pettitt B.M., Zechiedrich E.L. Electrostatics of DNA-DNA juxtapositions: consequences for type ii topoisomerase function. Phys. Condens. Matter. 2006;18:S173–S185. doi: 10.1088/0953-8984/18/14/S03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yang L., Weerasinghe S., Pettitt B.M. Dielectric response of triplex DNA in ionic solution from simulations. Biophys. J. 1995;69:1519–1527. doi: 10.1016/S0006-3495(95)80022-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Seksek O., Bolard J. Nuclear pH gradient in mammalian cells revealed by laser microspectrofluorimetry. J. Cell Sci. 1996;109:257–262. doi: 10.1242/jcs.109.1.257. [DOI] [PubMed] [Google Scholar]
- 57.Gordon J.C., Myers J.B., Onufriev A. H++: a server for estimating pKas and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005;33(Web Server issue):W368–W371. doi: 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Myers J., Grothaus G., Onufriev A. A simple clustering algorithm can be accurate enough for use in calculations of pKs in macromolecules. Proteins. 2006;63:928–938. doi: 10.1002/prot.20922. [DOI] [PubMed] [Google Scholar]
- 59.Bashford D., Karplus M. pKa's of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 60.Mascotti D.P., Lohman T.M. Thermodynamics of single-stranded RNA and DNA interactions with oligolysines containing tryptophan. Effects of base composition. Biochemistry. 1993;32:10568–10579. doi: 10.1021/bi00091a006. [DOI] [PubMed] [Google Scholar]
- 61.Lohman T.M., Mascotti D.P. Thermodynamics of ligand-nucleic acid interactions. Methods Enzymol. 1992;212:400–424. doi: 10.1016/0076-6879(92)12026-m. [DOI] [PubMed] [Google Scholar]
- 62.Record M.T., Jr., Lohman M.L., De Haseth P. Ion effects on ligand-nucleic acid interactions. J. Mol. Biol. 1976;107:145–158. doi: 10.1016/s0022-2836(76)80023-x. [DOI] [PubMed] [Google Scholar]
- 63.Record M.T., Jr., Anderson C.F., Lohman T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 64.Swanson J.M., Henchman R.H., McCammon J.A. Revisiting free energy calculations: a theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004;86:67–74. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Honig B., Yang A.S. Free energy balance in protein folding. Adv. Protein Chem. 1995;46:27–58. doi: 10.1016/s0065-3233(08)60331-9. [DOI] [PubMed] [Google Scholar]
- 66.Ausio J., Seger D., Eisenberg H. Nucleosome core particle stability and conformational change. Effect of temperature, particle and NaCl concentrations, and crosslinking of histone H3 sulfhydryl groups. J. Mol. Biol. 1984;176:77–104. doi: 10.1016/0022-2836(84)90383-8. [DOI] [PubMed] [Google Scholar]
- 67.Weidemann T., Wachsmuth M., Langowski J. Counting nucleosomes in living cells with a combination of fluorescence correlation spectroscopy and confocal imaging. J. Mol. Biol. 2003;334:229–240. doi: 10.1016/j.jmb.2003.08.063. [DOI] [PubMed] [Google Scholar]
- 68.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Thåström A., Gottesfeld J.M., Widom J. Histone-DNA binding free energy cannot be measured in dilution-driven dissociation experiments. Biochemistry. 2004;43:736–741. doi: 10.1021/bi0302043. [DOI] [PubMed] [Google Scholar]
- 70.Polach K.J., Widom J. Mechanism of protein access to specific DNA sequences in chromatin: a dynamic equilibrium model for gene regulation. J. Mol. Biol. 1995;254:130–149. doi: 10.1006/jmbi.1995.0606. [DOI] [PubMed] [Google Scholar]
- 71.Garcia H.G., Grayson P., Wiggins P.A. Biological consequences of tightly bent DNA: the other life of a macromolecular celebrity. Biopolymers. 2007;85:115–130. doi: 10.1002/bip.20627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Onufriev A., Smondyrev A., Bashford D. Proton affinity changes driving unidirectional proton transport in the bacteriorhodopsin photocycle. J. Mol. Biol. 2003;332:1183–1193. doi: 10.1016/s0022-2836(03)00903-3. [DOI] [PubMed] [Google Scholar]
- 73.Xu F., Zhang K., Grunstein M. Acetylation in histone H3 globular domain regulates gene expression in yeast. Cell. 2005;121:375–385. doi: 10.1016/j.cell.2005.03.011. [DOI] [PubMed] [Google Scholar]
- 74.Morris S.A., Rao B., Strahl B.D. Identification of histone H3 lysine 36 acetylation as a highly conserved histone modification. J. Biol. Chem. 2007;282:7632–7640. doi: 10.1074/jbc.M607909200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Baker S.P., Phillips J., Grant P.A. Histone H3 Thr 45 phosphorylation is a replication-associated post-translational modification in S. cerevisiae. Nat. Cell Biol. 2010;12:294–298. doi: 10.1038/ncb2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Hurd P.J., Bannister A.J., Kouzarides T. Phosphorylation of histone H3 Thr-45 is linked to apoptosis. J. Biol. Chem. 2009;284:16575–16583. doi: 10.1074/jbc.M109.005421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Shlyakhtenko L.S., Lushnikov A.Y., Lyubchenko Y.L. Dynamics of nucleosomes revealed by time-lapse atomic force microscopy. Biochemistry. 2009;48:7842–7848. doi: 10.1021/bi900977t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lorch Y., Maier-Davis B., Kornberg R.D. Mechanism of chromatin remodeling. Proc. Natl. Acad. Sci. USA. 2010;107:3458–3462. doi: 10.1073/pnas.1000398107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Dyer P.N., Edayathumangalam R.S., Luger K. Reconstitution of nucleosome core particles from recombinant histones and DNA. Methods Enzymol. 2004;375:23–44. doi: 10.1016/s0076-6879(03)75002-2. [DOI] [PubMed] [Google Scholar]
- 80.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14 doi: 10.1016/0263-7855(96)00018-5. 33–38. 27–28. [DOI] [PubMed] [Google Scholar]
- 81.Stone, J. 1998. An efficient library for parallel ray tracing and animation. Master's thesis, Computer Science Department, University of Missouri-Rolla, Rolla, MO.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


