Sequence dependence of DNA bending rigidity

Abstract

For many aspects of DNA–protein interaction, it is vital to know how DNA bending rigidity (or persistence length, a) depends on its sequence. We addressed this problem using the method based on cyclization of short DNA fragments, which allows very accurate determination of a. Our approach was based on assigning specific values of a to each of 10 distinct dinucleotide steps. We prepared DNA fragments, each about 200 bp in length, with various quasi-periodic sequences, measured their cyclization efficiencies (j factors), and fitted the data by the theoretical equation to obtain the values of a for each fragment. From these data, we obtained a set of a for the dinucleotide steps. To test this set, we used it to design DNA sequences that should correspond to very low and very high values of a, prepared the corresponding fragments, and determined their values of a experimentally. The measured and calculated values of a were very close to one another, confirming that we have found the correct solution to this long-standing problem. The same experimental data also allowed us to determine the sequence dependence of DNA helical repeat.

The value of DNA persistence length, a, closely related to the bending rigidity of the double helix, is very important for quantitative analysis of many aspects of DNA functioning. Many different methods were applied over the last decades to determine this value and its dependence on ionic conditions (1). These studies showed that under near physiological ionic conditions the value of a is close to 50 nm (1–3). They also showed that, in a good approximation, the value of a does not depend on DNA sequence, because many studies that use different DNA molecules gave very close values of a. However, the sequence dependence of DNA bending rigidity is vital for many aspects of DNA–protein interaction, and is particularly important for understanding how nucleosomes position along DNA molecules (4, 5). Despite its importance, the problem has formerly remained unsolved, although a few research groups have tried various approaches (6–8). The data that are generally considered most reliable were obtained from statistical analysis of DNA–protein crystal structures (9, 10). The large volume of available structural data allowed this group of researchers to present a very detailed picture of the sequence dependence of DNA conformational properties. This analysis, however, is based on the assumption that variations of the DNA bend angles in the crystals correspond to the amplitudes of thermal fluctuations of these angles in solution. It is hard to justify this assumption.

The major obstacle in determining the sequence dependence of a is the necessity of highly accurate measurements of a for different sequences. The majority of methods applied for the measurements of a do not provide the necessary level of accuracy. The only known method that allows one to measure a with the required accuracy is based on cyclization of short DNA fragments by DNA ligase (2, 3, 11, 12). It is also very important in addressing the problem that short DNA fragments can be prepared with any desired sequence. Thus, the method is perfectly suited for the determination of the sequence dependence of DNA bending rigidity. We applied it in the current study.

We determined the values of a for different DNA fragments with specially designed sequences. Using these data, we found the bending rigidities associated with various dinucleotide steps. To test the obtained set of rigidity constants, we used it to design DNA fragments with very low and very high values of a, made these fragments, and determined their actual persistence lengths. The measured values are in very good agreement with the prediction, confirming the validity of the obtained set of bending rigidity constants. The experimental data also allowed us to evaluate the sequence dependence of DNA helical repeat and to test the validity of this result. These results provide a base for reliable calculation of the bending rigidity and the helical repeat of a DNA segment with a known sequence. They show that, with a good accuracy, sequence dependence of DNA conformational properties is specified by the properties of the dinucleotide steps. The data represent an important step in developing a way to calculate the energy of elastic deformation for a specific DNA conformation set by a DNA–protein interaction.

Results

Theoretical Analysis.

It is known that both thermal fluctuations and equilibrium intrinsic bends contribute to the measurable persistence length, a (3, 13–15). In general, both of these contributions are sequence dependent, which greatly complicates the problem. It was shown, however, that the contribution of intrinsic bends to measured values of a is very small (shown in ref. 3 and confirmed in the current study). This conclusion is true under the condition that DNA fragments do not contain A tracts and/or GGGCCC motifs that are associated with substantial intrinsic curvature (16–20). The latter sequence elements were excluded from the DNA fragments used in the current study, which allowed us to ignore the contribution of intrinsic bends to the measured persistence length. Therefore, in the subsequent analysis, we assume that contribution of intrinsic curvature to DNA bending is negligibly small. Under this assumption, the measured value of a for a DNA fragment and its average bending rigidity, g, differ by the Boltzmann temperature factor (21), kT:

[1]

Below, for convenience, we will mainly use persistence lengths rather than bending rigidity constants converting one to another according to Eq. 1.

We addressed the problem using the dinucleotide approximation. Thus, the total bending energy, E, of DNA fragment of n base pairs in length is specified as

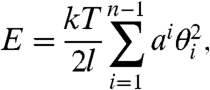[2]

where kTaⁱ/l is the bending rigidity of dinucleotide step i, θ_i is the bend angle between base pairs i and i + 1, and l is the length of the dinucleotide step. Eq. 2 is the generalization of the discrete worm-like chain model usually used for analysis of DNA conformational properties (22–24). It is assumed in Eq. 2 that DNA bending rigidity is isotropic. Theoretical studies and analysis of DNA–protein crystals show that the bending rigidity in the direction of the grooves is essentially smaller than in the perpendicular direction (9, 25). Though this anisotropy is important for DNA–protein complexes, it cannot be addressed in the macroscopic approach used in this study. However, this anisotropy is self-averaged over very short distances during conformational calculation of DNA properties (26). So, the values of aⁱ in Eq. 2 correspond to the average values of two bending rigidity constants for the perpendicular directions of bending (21).

In our experimental approach, we measured persistence lengths of DNA fragments or their average bending rigidities. In the dinucleotide approximation, the average bending rigidity of a fragment, kTa, is expressed through the rigidity constants of the dinucleotide steps:

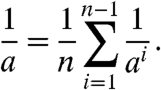[3]

Eq. 3 holds under the condition that the value of a is many times larger than the length of one dinucleotide step, which is definitely held for double-stranded DNA.

There are 10 different dinucleotide steps in DNA double helix that specify 10 different persistence lengths: a^AA/TT, a^AC/GT, a^AG/CT, a^AT, a^CA/TG, a^GA/TC, a^CC/GG, a^CG, a^GC, and a^TA. Therefore, performing the determination of a_k for a set of DNA fragments with different sequences, we generate the equations

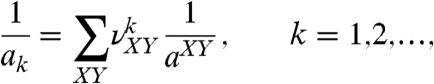[4]

where 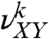is the fraction of the dinucleotide step XY in the fragment k, and summation in the equations is performed over all 10 types of steps.

It is known, however, that the rank of the matrix produced by Eqs. 4 cannot exceed eight for circular or very long linear DNA (27, 28). Therefore, only eight linear combinations of 1/a^XY can be found from this approach. On the other hand, these eight linear combinations, which will be called invariants, are sufficient for unambiguous calculation of the average a for any given circular or sufficiently long linear DNA.

Determination of a for a fragment generates one equation in the system of Eqs. 4. A set of DNA fragments that forms the system is called the elemental set below. To determine eight independent variables, the system of Eqs. 4 has to include at least eight equations. We used two elemental sets in this study, because the first one brought very disappointing results. If the system of Eqs. 4 contained eight equations, it was solved directly; if it consisted of more than eight equations, we applied the nonlinear numerical method to minimize the deviations between the measured and calculated rigidity constants for each fragment of the elemental set (see Materials and Methods).

Determination of Bending Rigidity Constants and DNA Helical Repeats.

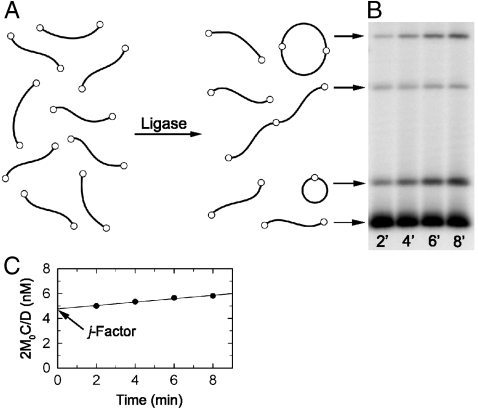
To determine the values of a_k for individual DNA fragments, we measured their j factors and fitted the measured values with the theoretical equation (see Materials and Methods for details). The j factor is the effective concentration of one end of the fragment in the vicinity of the other (12, 29). Its value can be determined in the ligation experiment (2, 3, 11, 12). In the presence of DNA ligase, the fragments form circular monomers, linear and circular dimers, trimers, and so on (Fig. 1A). The ligation products are separated by gel electrophoresis to measure relative amounts of circular monomers, C(t), and linear and circular dimers, D(t) (Fig. 1B). The value of j factor is calculated as

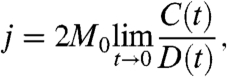[5]

where M₀ is the initial concentration of the fragment and t is the reaction time (2). To perform extrapolation of C(t)/D(t) to zero reaction time, the ratio has to be measured for a few values of t. A typical quantitation of such an experiment is shown in Fig. 1C.

Fig. 1.

Determination of j factor for a DNA fragment with short sticky ends. (A) Diagram of the fragment ligation. The sticky ends are shown via small open circles at the fragment ends. (B) Separation of the ligation products by agarose gel electrophoresis. (C) Extrapolation of 2M₀C(t)/D(t) to zero ligation time to obtain the value of j factor.

The value of j factor for a DNA fragment depends on its persistence length, a, the helical repeat, γ, and its torsional rigidity, C. To obtain all three parameters from the fitting, we performed the measurements for a set of fragments with a chosen sequence with lengths covering the interval from 196 to 206 bp.

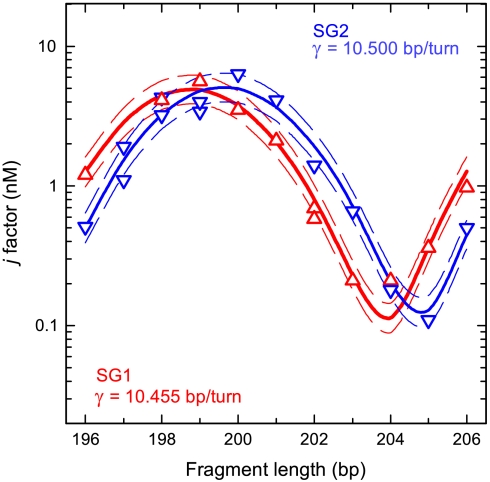
First, we used this method to test if the bending rigidity can be well specified by the dinucleotide approximation that is the base of our approach. We designed two DNA sequences, SG1 and SG2, with the same dinucleotide composition but different tri- and tetranucleotide compositions (the sequences are shown in SI Text), made the corresponding fragments, and measured their j factors (Fig. 2). One can see from the figure that the best fits of the data for two sequences correspond to identical values of a and C but slightly different values of γ. We conclude from this comparison that the dinucleotide model provides reasonably good approximation for DNA rigidity constants and helical repeats, although we see that the model accuracy has its limits.

Fig. 2.

The test of the dinucleotide model for DNA bending rigidity (specified by the persistence length a) and its helical repeat, γ. The measured j factors of two sets of fragments with the same dinucleotide composition but different tri- and tetranucleotide compositions are shown by red (SG1) and blue (SG2) triangles. The data were fitted by the theoretical equation for j factor by adjusting the values of γ, torsional rigidity, C, and a. The best fits (solid lines) correspond to a = 48.5 nm, C = 2.9 × 10^-19 erg·cm for both sets, but slightly different values of γ, 10.455 and 10.500 bp/turn. The dashed lines show the theoretical dependencies for a of 47.5 and 49.5 nm and the same values of γ and C. The latter lines do not fit to the data, showing that the method allows determination of a with 2% accuracy.

It is important that the values of j factors for the fragments of different length can be fitted unambiguously by the theoretical equation, because each parameter of the equation specifies a particular feature of the j-factor length dependence (2, 12). The amplitude of the j-factor oscillations depends mainly on the value of C, the fragment length that corresponds to the local maxima of j factor depends on the value of γ, and the value of j factor at the maximum is specified by the value of a. An example of the fit shown in Fig. 2 proves that this method of the persistence length determination provides approximately 2% accuracy in the determination of a.

It should be noted that the solution to Eq. 4 is very sensitive to statistical error in the determined values of a_k, if the fragments of the elemental set have close fractions of different dinucleotide steps. Therefore, to diversify the dinucleotide composition in the fragments of the elemental set 1, we designed the fragments with sequences containing a minimum number of different dinucleotide steps: d(G)_n·d(C)_n, d(AT)_n·d(AT)_n, d(AC)_n·d(GT)_n, etc. (see SI Text for details). The regular sequence patterns had only rare interruptions to facilitate the cloning of these fragments. We tested, by polyacrylamide gel electrophoresis, that the fragments of the set do not have notable intrinsic curvature (Fig. S1). Using this elemental set of fragments we obtained the values of all eight invariants (Table S1). In order to test the found solution, we used the obtained values of the invariants to design the fragments with very low and very high predicted values of a, 39.5 nm, and 52.2 nm (LPL1 and HPL1). We prepared the corresponding fragments and determined their values of a. To our disappointment, the obtained values were 48.0 ± 1 nm and 48.5 ± 1 nm for LPL1 and HPL1, correspondingly.

To explain the failure, we suggested that the dinucleotide approximation does not work well for DNA fragments with very short sequence repeats, duplexes containing all purines in one strand, or extreme GC content (27). It is known, for example, that d(A)_n·d(T)_n polynucleotide has a helical structure that is different from canonical B form (30–32). If such is the case, one has to use fragments with longer repeating sequence motifs for the elemental set. Thus, we designed elemental set 2 consisting of fragments with longer repeating motifs, like AGAT, CAGT, CAACTT, and so on, and fragments LPL1 and HPL1 (see SI Text). We confirmed by gel retardation analysis that the new fragments do not have a notable intrinsic curvature (Fig. S2). We also added two fragments with trinucleotide repeats from elemental set 1 to the new elemental set, so the total number of fragments was equal to 11. Clearly, using a larger elemental set reduces the statistical error of parameter determination. We found, however, that eliminating CAA fragment from the set does not change the results. The measured j factors were fitted by the theoretical dependence to obtain the values of a for all new fragments (Fig. S3). Using these data, we obtained the values of eight invariants of a^XY.

The obtained results also provide information on the sequence dependence of DNA helical repeat, γ. We analyzed the data on the helical repeats in exactly the same way as we did for the bending rigidity constants. Thus, we obtained the values of eight invariants of helical repeats associated with the individual dinucleotide steps, γ^XY.

Testing the Obtained Solution.

To test the solution based on elemental set 2, the values of eight invariants were again used to design the fragments with very low and very high persistence lengths, named as LPL2 and HPL2. The predicted values of a were equal to 43.9 and 55.7 nm, so they were outside of the range of a_k found for the fragments of the elemental set (Fig. S3). Using the data obtained for the helical repeats we found that γ_LPL and γ_HPL should be substantially different for the two fragments as well, 10.55 for LPL2 and 10.40 for HPL2. We made the fragments and determined their values of a and γ (Fig. S4). The obtained values of a, 45.5 ± 1 nm and 54.0 ± 1 nm for LPL2 and HPL2, correspondingly, were in very good agreement with the prediction. Similar agreement was obtained for the fragment helical repeats, which were equal to 10.58 ± 0.02 and 10.42 ± 0.02, respectively. We extended the testing to other available data and found very good agreement between determined and predicted values of a and γ (Table 1). It is worth noting that predictions based on elemental set 1, also shown in Table 1, do not fit the experimental data. This comparison shows that the values of the invariants based on elemental set 2 give accurate solution of the problem. To further refine this solution, we included fragments LPL2 and HPL2 in the elemental set 2 and obtained slightly improved values of the invariants. These values are shown in Table 2, together with the original values obtained from elemental set 2 without the latter extension.

Table 1.

Comparison of the experimentally determined and predicted values of a and γ for different fragments

Fragment	Exp. a, nm	Predicted a from elemental set 2	Predicted a from elemental set 1	Exp. γ, bp/turn	Predicted γ from elemental set 2	Predicted γ from elemental set 1
HPL1	48.5	—	52.2	10.43	—	10.47
LPL1	48.0	—	39.5	10.53	—	10.45
HPL2	54.0	55.7	49.7	10.42	10.40	10.46
LPL2	45.5	43.9	45.8	10.58	10.55	10.48
λ DNA frag.	48.0	48.4	47.2	10.50	10.49	10.48
IS	49.5	49.4	45.8	10.50	10.49	10.48
SG1	48.5	49.1	46.1	10.455	10.46	10.47
602	47.9	48.5	46.6	—	—	—

The predictions are based on elemental sets 1 and 2 of 8 and 11 fragments, correspondingly. The measured values for λ DNA and IS (intrinsically straight) fragments were taken from ref. 3. The value of the bending rigidity for Widom’s fragment 602 (48), expressed over a in the table, was determined by fitting the computed j factor to the measurement assuming 11° and 15° bend angles in two A tracts of the fragment. The computations followed the procedure described in ref. 49.

Table 2.

The values of invariants of DNA persistence lengths and helical repeats obtained from elemental set 2 extended by fragments HPL2 and LPL2

Invariant combination of aXY or γXY; symbol r corresponds to a or γ	Persistence length, a, nm	Helical repeat, γ, bp/turn
rAA/TT	50.4 (50.3)	10.27 (10.26)
rCC/GG	41.7 (40.5)	10.76 (10.73)
2/(1/rAT + 1/rTA)	42.7 (42.3)	10.62 (10.61)
2/(1/rGC + 1/rCG)	49.6 (50.3)	10.39 (10.36)
2/(1/rAC/GT + 1/rCA/TG)	50.7 (50.7)	10.59 (10.59)
2/(1/rAG/CT + 1/rGA/TC)	52.6 (53.2)	10.39 (10.40)
3/(1/rAT + 1/rGA/TC + 1/rCA/TG)	46.7 (45.8)	10.51 (10.51)
3/(1/rAC/GT + 1/rCG + 1/rGA/TC)	55.3 (57.4)	10.43 (10.42)

The values of the invariants obtained from elemental set 2 without the extension are shown in parenthesis.

If one wants to calculate the average persistence length or the helical repeat of a fragment, it is convenient to have the values of a^XY and γ^XY rather than their linear combinations. The values of a^XY and γ^XY are not uniquely defined in our approach and can be specified in different ways (27, 28, 33–35). We used a method based on symmetry properties of DNA bases (34). The values of a^XY and γ^XY based on this method are given in Table S2.

Discussion

The results obtained in this study provide accurate data for the sequence dependence of DNA bending rigidity. The values of a^XY invariants (Table 2) span from 41.7 nm for CC/GG step to 55.3 nm for the combination of AC/GT, CG, and GA/TC steps. Using these data, we can calculate the persistence length of the “average” DNA molecule with equal fractions of each nucleotide. The resulting value, 48.5 nm, is in good agreement with many other measurements of DNA persistence length. The maximum deviation from this value for the simple sequences corresponding to a^XY invariants constitutes nearly 15%. Still, the variations of the values of a over various sequences are essentially smaller than was suggested in many earlier studies. Our result shows, however, that the variations of a over DNA molecules with different sequences may be sufficiently large to affect DNA biological activity. The variations can substantially affect the binding affinity of DNA to proteins in cases where the DNA segment is strongly bent, first of all the binding affinity to the nucleosome core. For a simple estimation of the possible effect, we can calculate the component of the binding constant that depends on the bending energy, K_b, for a DNA segment with the radius of the induced curvature R and length L. Using Eqs. 1 and 2, we obtain

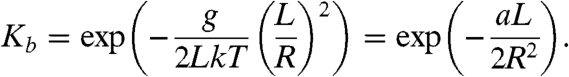[6]

Substituting the values of L and R corresponding to the nucleosome structure (36) we can obtain from Eq. 6 that variation of a by 2.1 nm changes K_b by factor of 10. Clearly, this simple estimation shows that the found sequence variations of DNA bending rigidity may be sufficient to explain the selectivity of nucleosome binding on long DNA molecules.

Our data allow one calculating average bending rigidity and average helical repeat for a DNA segment with any chosen sequence. These average values can be used to evaluate the sequence-dependent energy of DNA deformation in short loops which are involved in transcription regulation (37–39). In such loops, where DNA is constrained at its ends only, the double helix fluctuates around the conformation with the minimum energy of elastic deformation, similar to the situation in the minicircles used in this study. Our data show that in such cases the knowledge of the average bending rigidity and helical repeat is sufficient to calculate the free energy of DNA deformation. However, our results do not allow for calculation of the energy of elastic deformation for a specific DNA conformation that can be imposed by DNA–protein interaction. In the latter case, all angles in the dinucleotide steps are set to some specific values, and to calculate the energy of DNA deformation, we need to know the anisotropic parameters for the individual dinucleotide steps. These parameters cannot be determined by our approach. In particular, the energy of DNA deformation in the nucleosome structure cannot be evaluated from the data presented in Table 2. Still, our data can be used to analyze certain correlations between the sequence of DNA segments and their affinity for the nucleosome core. For example, it has been found that CC/GG steps have a pronounced periodicity of 10 bp in the nucleosomes in vivo (40). This observation correlates well with low bending rigidity of CC/GG step (see Table 2). Strong periodicity was also found for TA step in a pool of synthetic random sequences with strong nucleosome forming ability (41). Our study does not provide the bending rigidity for TA step, although the assumption about its softness is consistent with the results shown in Table 2.

It should be noted that the observable persistence length can be affected by intrinsic bends associated with A tracts. The fragments used in this study do not contain such tracts (with exception of Widom’s 602 fragment used in Table 1). Still, for fragments containing A tracts any conformational property (like j factor or the probability of loop formation) can be calculated with good accuracy by using the obtained invariants and the values, locations, and directions of the intrinsic bends.

It follows from our data that the average value of γ for DNA with a random sequence with GC content of 50% is 10.50. One can see from Table 2 that γ varies substantially for different invariants, from 10.27 to 10.76. The values in the table correlate very well with solution data obtained on circular DNA for AA/TT and GG/CC dinucleotide steps, and d(AT)_n segments (30, 31, 42). Our data on the sequence dependence of DNA helical repeat show that variations of this parameter can also affect the DNA–protein binding energy. We can estimate the possible effect assuming that specific values of helix rotation angles are set by the structure of a DNA–protein complex. If these angles are different from the equilibrium ones for the dinucleotide steps participating in the complex, the DNA torsional deformation contributes to the binding energy. The estimation shows, however, that the effect of these variations on the binding constant should be essentially smaller than the effect of the variations of a.

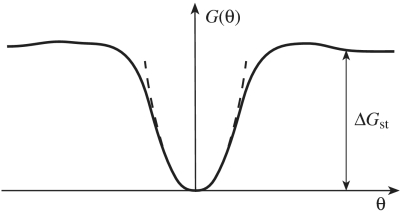
There were suggestions that the sequence dependence of DNA bending rigidity correlates to the free energy of stacking between adjacent base pairs, ΔG_st (4, 8). We compared our results with the data on the sequence dependence of ΔG_st obtained recently (43, 44). The latter data show, in particular, that the average stacking interaction between GC base pairs is essentially stronger than between AT base pairs. Using the data in Table 2, we calculated the average values of a for DNA molecules with random sequences as a function of GC content. The calculation showed that DNA molecules with random sequences consisting of only AT base pairs are slightly more stiff than the molecules made from only GC base pairs, first of all due to the low bending rigidity of GG/CC dinucleotide step (Fig. S5). This result clearly shows that there is no correlation between the sequence dependences of a and ΔG_st. This is not surprising, if we take into account that a and ΔG_st specify two different features of the bending potential between adjacent base pairs, G(θ) (Fig. 3). The value of bending rigidity is specified by the shape of the potential at small values of θ and corresponds to the quadratic term of the Taylor expansion of G(θ) at θ = 0 (linear term equals zero, because we assume that the potential has a minimum at θ = 0). The value of ΔG_st, on the other hand, corresponds to the height of the potential plateau.

Fig. 3.

Diagram of bending potential between adjacent base pairs. The bending rigidity, g, corresponds to the quadratic approximation of the potential for small values of θ, which is shown by the dashed line. The value of g hardly correlates with the free energy of stacking, ΔG_st, which is specified by the height of the potential plateau.

It is interesting to compare our results with the data obtained from statistical analysis of angles between adjacent base pairs in the crystals of DNA–protein complexes (10). For this comparison, we renormalized the data from ref. 10 to obtain a of 48.5 nm for DNA with random sequence and calculated the values of a and γ for all fragments of elemental set 2. The comparison with our data shows that there is some correlation between the two sets of data (Table S3), although there are very substantial discrepancies as well. We also found no clear correlation between our data and the results of statistical analysis of oligonucleotide crystal structures (45).

Our results proved that the dinucleotide approximation for DNA bending rigidity constants and helical repeats works well for DNA molecules with typical sequences, strongly suggesting that the approximation is also good for other conformational parameters of the double helix. A few exceptions from the rule have to be mentioned, however. First, the dinucleotide approximation fails for intrinsically curved fragments containing A tracts and/or GGGCCC motifs. It also does not work well for DNA molecules with long repeats of very short sequence elements, like d(AG)_n·d(CT)_n, as we see from our unsuccessful attempt to extract the dinucleotide parameters from this type of DNA fragments. Our data suggest that the dinucleotide approximation works well if the length of the repeats does not exceed 8–14 nucleotides, although further investigation is needed to reliably establish this limit.

Materials and Methods

DNA Preparation.

The sets of DNA fragments with chosen sequences were obtained by chemical synthesis of subfragments, assembling them in solution, and cloning into pSP73 vector (Promega). First, a common part for all fragments of a set (≈160 bp) was inserted between the PstI and HindIII sites of the vector. The new plasmid was used as a vector for cloning the variable parts of the set, about 40 bp in length, which were inserted between PstI and XbaI sites. Each of the latter inserts also contained a HindIII site near their left end which was needed to release the fragments from the vector. The sizes of the variable inserts diminished in 1 bp steps. All plasmids were maintained in Escherichia coli DH5α cells. The QIAGEN Miniprep Purification Kit was used to extract DNA from the cells. The sequences of each set of fragments were checked directly by Genewiz. The concentrations of purified DNAs were determined using a Hitachi Gene Spec I spectrophotometer.

The desired fragments were obtained by treating the plasmids with HindIII restriction endonuclease [New England Biolabs (NEB)]. Each digested DNA was 5′-end-labeled with ³²P by OptiKinase (USB Corporation) in a 20-μL total volume, containing 5 μL of [γ-³²P]ATP [10 mCi/mL, 6,000 Ci/mmol (1 Ci = 37 GBq); PerkinElmer]. The DNA concentrations were 2.5–10 nM. The labeling was carried out at 37 °C for 90 min, followed by heat inactivation of HindIII and DNA kinase at 65 °C for 20 min.

Ligation Time Course.

The plasmid vectors remained in solution, along with the excised ≈200 bp fragments, during the subsequent labeling and the ligation time course. Leaving the vector DNA in the reaction mixture does not affect the ratio of circular monomers and dimeric forms of the insert formed at the early stage of ligation while greatly facilitating sample preparation. Ligation experiments were performed in 100–200-μL volumes, using T4 DNA ligase (NEB) and its standard ligation buffer at 21 °C. The final concentrations of DNA substrates in ligation buffer were 0.25–0.5 nM, depending on the expected value of the j factor. Each reaction was initiated by the addition of ligase diluted from stock with its standard buffer just before the ligation experiments. The concentration of DNA ligase in the reaction mixture was 5–20 NEB units/mL which satisfies the method requirement (11, 12, 46). Aliquots of the ligation mixtures were withdrawn at specific time intervals and quenched with EDTA at a 40 mM final concentration. Unincorporated [γ-³²P]ATP from the ligation samples was removed with Performa Spin columns (Edgebio) before the gel electrophoresis.

Gel Electrophoresis.

Ligation products were separated on 2.4% MetaPhor agarose gel (Lonza) in TBE buffer (89 mM Tris borate/2 mM EDTA, pH 8.3). Under continuous circulation of TBE electrophoresis buffer, the gels were run at room temperature at 5.5 V/cm, for 7 h. After electrophoresis, the gels were dried and quantified using Storm PhosphorImager and ImageQuant software (Amersham Bioscience). For the gel retardation test, we use 4–12% gradient Novex polyacrylamide gels (Invitrogen) which were run at 100 V in TBE buffer at 8 °C for 3 h.

Theoretical Calculation of j Factor.

The theoretical value of j factor was calculated as a product of two components j_wlc and j_tw. For the first component, j_wlc, we used analytical approximation obtained by Shimada and Yamakawa (SY) for the worm-like chain (23). We tested that SY solution gives very accurate results for DNA fragments 150–250 bp in length (see SI Text and Fig. S6). Thus, j_wlc (in moles) was calculated as

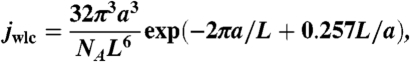[7]

where N_A is Avogadro’s number, and a and L are measured in decimeters.

The second component of j factor, j_tw, reflects the requirement of the torsional alignment of the fragment ends for their ligation. It was calculated similar to what has been described earlier (12). Detailed information on the j_tw calculation is given in SI Text.

Determination of a^XY from the Persistence Lengths of DNA Fragments.

To obtain the values of a^XY from a set of n measured persistence lengths, a₁,…,a_n, when n > 8, we used numerical minimization of the function

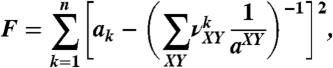[8]

where 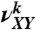are the fraction of dinucleotide step XY in the fragment k. The minimization was performed by the gradient descent algorithm (47). Although we found that the variation of the starting point for the minimization procedure in reasonable limits did not affect the results, the procedure usually started from the point where all a^XY were equal to 48 nm.