Dynamical organization of the cytoskeletal cortex probed by micropipette aspiration

Abstract

Bleb-based cell motility proceeds by the successive inflation and retraction of large spherical membrane protrusions (“blebs”) coupled with substrate adhesion. In addition to their role in motility, cellular blebs constitute a remarkable illustration of the dynamical interactions between the cytoskeletal cortex and the plasma membrane. Here we study the bleb-based motions of Entamoeba histolytica in the constrained geometry of a micropipette. We construct a generic theoretical model that combines the polymerization of an actin cortex underneath the plasma membrane with the myosin-generated contractile stress in the cortex and the stress-induced failure of membrane-cortex adhesion. One major parameter dictating the cell response to micropipette suction is the stationary cortex thickness, controlled by actin polymerization and depolymerization. The other relevant physical parameters can be combined into two characteristic cortex thicknesses for which the myosin stress (i) balances the suction pressure and (ii) provokes membrane-cortex unbinding. We propose a general phase diagram for cell motions inside a micropipette by comparing these three thicknesses. In particular, we theoretically predict and experimentally verify the existence of saltatory and oscillatory motions for a well-defined range of micropipette suction pressures.

The dynamical properties of the actin cytoskeleton (CSK) and its interaction with the plasma membrane (PM) control crucial aspects of cellular shape change and motility. Actin-based motility can result from the polarization of the cell, with actin polymerization at the leading edge, in a flat cellular extension called lamellidopium, and myosin contraction at the rear end of the cell (1). Renewed attention is currently being paid to an alternative form of actin–myosin-based cell motility, where the contraction of the actomyosin cortex leads to cortex unbinding from the PM and the pressure-driven inflation of micron-size spherical membrane protrusions called “blebs” (2). Blebs are often the sign of apoptotis, but are also used for motility by several cell types, including amoebae and possibly cancer cells (3–5).

The life cycle of a bleb is a remarkable illustration of the highly dynamical interplay between the CSK and the PM. Blebs are usually initiated by local rupture of the CSK cortex (6) or its local detachment from the PM (7), followed by the inflation of a CSK-free membrane blister. A new actin cortex containing myosin often repolymerizes under the bare membrane, and myosin contraction brings the bleb and the cell body back together. Blebbing generally occurs in a stochastic fashion and may be harnessed for cell motility through the cell’s interaction with the external matrix. This example illustrates the importance of the mechanical interaction between the CKS and the PM for the conversions of a contractile stress into forward cellular protrusion in bleb-based motility. More generally, it calls for a quantitative understanding of the role of membrane-cortex cohesion in dictating many of the cell morphological changes.

In this work, we combine theoretical modeling and micropipette manipulation of Entamoeba histolytica to study the mechanical response of the cell to a controlled perturbation in a controlled geometry. Our model includes actin polymerization and depolymerization, coupled to actomyosin contraction within the cytoskeletal cortex, as well as the dynamical nature of the CSK-PM interactions. We show that cortical activity may generate sufficient lateral tension to unbind the cortex from the cell membrane, leading to the observed fast-forward movements of the cell inside the micropipette. We provide a phase diagram that matches the various types of cell motion observed experimentally, including remarkable spontaneous oscillations where phases of cell retraction due to cortical contraction alternate with phases of forward movement following cortex detachment.

Model

Micropipette manipulation is a widely used technique to measure the mechanical properties of giant unilamellar vesicles (GUV) and cells. The micropipette setup, which allows us to quantify the relationship between strain (the system’s deformation inside the pipette) and stress (the pipette suction pressure), has provided a definitive description of the mechanical properties of lipid bilayers as a combination of molecular and entropic elasticity (8, 9). When applied to cells, it reveals a complex dynamical response dominated by the properties of the active CSK, constantly converting chemical energy into mechanical forces (10–14). Broadly speaking, cells exhibit a viscoelastic response characterized by an elastic behavior at short times and a viscous behavior at long times, including active contraction and/or crawling. Generically, the cell mechanical response not only depends on the time and length scales at which it is probed, but also on the active state of the cell (15).

Strong pipette suction can force the PM detachment from the CSK, thereby mimicking the initiation of a bleb (10, 12, 13). Micropipettes have also been used to study the growth of membrane blebs artificially nucleated by ablating part of the cellular cortex (16). Here, we propose a self-consistent model that includes the CSK dynamical properties and its kinetic coupling with the PM to explore the complexity of the cell’s response to a controlled mechanical perturbation.

Micropipette Aspiration of Vesicles and Cells.

Laplace law states that at mechanical equilibrium, the pressure drop across a curved interface is equal to the interfacial tension times its curvature. A cell or a GUV subjected to micropipette suction (suction pressure ΔP and pipette radius R_p) deforms until the Laplace law is satisfied both inside and outside the pipette. Calling γ^f and γ^r the interfacial tensions in the front (inside the pipette) and at the rear of the object, and R the radius of curvature of the rear, static equilibrium requires 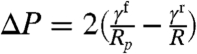(9).

For GUVs, the only tension resisting pipette suction is the membrane tension γ_mbr, which is roughly uniform throughout the membrane. For cells, the interfacial tension also includes a contribution from the CSK attached to the membrane. This cortical tension depends on the activity of the CSK through actin polymerization and depolymerization, the on-off kinetics of actin cross-linking proteins, and the contractile activity of myosin microfilaments. Fig. 1 presents a sketch of the cortex properties that are included in the model. The cortical tension γ_c is modeled as the sum of a passive viscoelastic tension γ_el and an active (contractile) tension due to myosin activity γ_myo. The motion of the cell inside the pipette is characterized by the position of the cell front L measured from the pipette entrance. The position and curvature of the rear may be obtained assuming volume conservation. The equation of motion follows by equating the difference between the driving and restoring forces (the suction pressure and the membrane and cortex tensions) to a dissipative force:

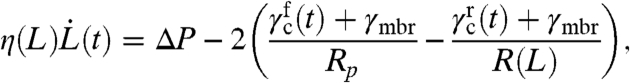[1]

with γ_c = γ_el + γ_myo and f and r designing the front and the rear of the cell. The dissipative force is assumed to be linear with the tongue velocity, and characterized by a friction η(L). It originates from membrane and cytosol flow, but not CSK flow and friction with the pipette walls, which is included in γ_c (see below). Although Eq. 1 is valid for slowly moving cells with a uniform inner pressure, the front and the rear of cells undergoing fast deformations such as blebbing are expected to be fairly uncoupled (17). Because the rear cell radius is typically larger than the pipette radius (R≫R_p), the rear cortical stress should have a marginal influence on the tongue velocity, and we neglect its contribution in the following.

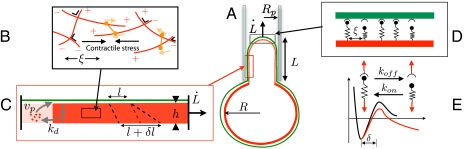
Fig. 1.

Sketch of the mechano-kinetic model for a cell inside a micropipette. (A) A cell is drawn inside a micropipette (of radius R_p) by a pressure difference, forming a cylindrical tongue with an hemispherical cap (L is the length of the tongue and 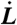the velocity of its front). The PM is in green and the actin cortex in red. (B) The cortex is a gel of cross-linked actin filaments (red), of mesh size ξ, and contractile myosin microfilaments (orange). (C) The cortical actin layer (of thickness h) is constantly being renewed by polymerization (of velocity v_p) near the membrane and depolymerization (with a rate k_d), leading to treadmilling. An element of cortex (of initial length l when it is formed at the PM) is stretched by the extension of the tongue and reaches a length l + δl before being depolymerized. (D) The cortex is attached to the PM by dynamical molecular linkers. (E) Linkers have association and dissociation rates dependent on their energy landscape (black curve). When a force is applied on the bond, its energy landscape and associated rates are modified (red curve).

Membrane Elasticity.

The stress-strain relationship of pure lipid membranes is well understood as a crossover from a soft entropic regime to a stiff lipid stretching regime with increasing strain, the latter being characterized by a stretching modulus k_γ ∼ 0.2 N/m (9). The elasticity of the PM is much more complex, and its tension γ_mbr is regulated by membrane invaginations (18) and by trafficking (19). Here, we adopt a simple linear relationship between the tension and membrane area γ_mbr = γ_mrb0 + k_γR_pL/(2R²) and choose k_γ ∼ 0.8 mN/m. An extensive discussion of our choice of all parameter values can be found in SI Text.

Cortical Stress.

Coarsed-grained mechanical models of arbitrary complexity can be used to try to reproduce the rich features of cellular response to mechanical perturbations (20). While linear viscoelastic models have shown their limitations (15, 21), they constitute a valuable starting point to investigate the complex dynamics of PM-CSK interaction. Here, we adopt the simplest description of a viscoelastic medium that displays short-time elastic response and long-time viscous flow, which is characterized by a bulk elastic modulus (Young’s modulus) E and a single relaxation time τ^∗. The viscoelastic nature of the cortex stems both from the transient binding of actin cross-linking proteins such as filamin and α-actinin and from the constant renewal of actin filaments by polymerization and depolymerization (15). Actin polymerization is thought to occur predominantly at the PM [which contains actin nucleator complexes (1)], whereas depolymerization is thought to take place throughout the cortex, leading to a constant flow of actin away from the membrane (treadmilling). In our model, the unique CSK relaxation time is the result of all these effects, which are regulated by a host of proteins (formin, profilin, Arp2/3) and lipids (PIP₂) (22). In the micropipette geometry, and assuming for simplicity that the cortex stress does not propagate outside the pipette (23), the evolution of the viscoelastic cortical tension γ_el is given by the Maxwell-like equation

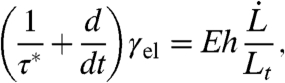[2]

where the length L_t involved in the strain rate 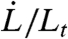characterizes the extent of cortex perturbation near a moving cellular tip. This length initially increases with time to account for the renewal of the actin cortex and eventually saturates to a length L_f controlled by the amount of friction between the cortex and the pipette walls (24).

Actomyosin contraction also participates in the cortical stress. As a first approximation, one may assume that this active tension increases linearly with the cortex thickness: γ_myo = σ_myoh, where σ_myo is the stress produced by myosin microfilaments within the cortex and is assumed constant for simplicity (see ref. 25 for a more advanced description). Our experiments (see below) show that Entamoeba histolytica is able to retract against pipette suction pressures larger than ΔP = 1 kPa in a pipette of R_p = 5 μm radius, which indicates a cortical tension larger than 2.5 mN/m, in agreement with measurements on another amoeba: Dictyostelium (11). Actin staining experiments suggest a cortex thickness of order 1 μm (see SI Text), leading to a myosin stress of order σ_myo ≃ 5 kPa, consistent with the literature (see SI Text). We note that the precise value of the cortex thickness bears no direct relevance to our model. Only the contractile tension γ_myo( ∼ 5 mN/m), which is also controlled by myosin and actin density, is relevant.

Dissipative Force.

Dissipation is thought to mostly originate from the viscous flow of membrane through the dense mesh of CSK-PM linkers (26): η(L) ∼ η_b(1 + L/R_p), where the effective membrane friction η_b includes friction with the pipette walls. The value η_b = 130 Pa s/μm evaluated in SI Text predicts a bare membrane velocity consistent with our observations (∼μm/s for ΔP = 1 kPa).

Membrane-Cytoskeleton Attachment.

The PM-CSK attachment involves a complex network of kinetic interactions between proteins and lipids (22). This is implemented here by a collection of dynamical molecular bonds (Fig. 1D) characterized by mechanosensitive on/off rates. The unbinding rate, in particular, is expected to increase exponentially with the force per bond (27). A higher force thus results in a lower density of attached bonds, hence to a further increase of force per bonds. Such a collection of force-sharing dynamical bonds displays a dramatic collective unbinding (28, 29) beyond a critical bond force 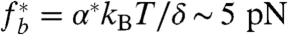(δ is a molecular length characteristic of the bond’s energy landscape (Fig. 1E), and α^∗ is a numerical factor—of order unity—that depends on the ratio of binding to unbinding rates under no force. The force density on the bonds is the total cortex tension (the sum of elastic and active tensions) times the curvature C_urv of the cell interface. One can thus expect the global failure of PM-CSK attachments beyond a critical cortical tension satisfying

[3]

where ρ is the linkers density. We assume the linker density to be correlated with the actin density in the cortex (ρ ∼ 1/ξ²), but one should bear in mind that this parameter can be independently regulated by the cell. The salient features of this model are that PM-CSK unbinding can be achieved by a thick cortex with large myosin activity or by a cortex with high curvature. Beyond a critical (myosin-dependent) membrane curvature 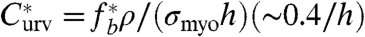, the internal myosin stress is sufficient to detach the cortex. Fluctuations of the myosin activity, the cell shape, or any parameter appearing in Eq. 3 may cause cell blebbing even below this critical condition. Note also that the rupture of the cortex itself, which may also cause blebbing, is another dramatic event that can be accounted for by introducing a critical cortical stress for cortex rupture (30).

Results

The complex response of a cell to micropipette suction is a direct illustration of the active mechanics of the CSK and the dynamical nature of PM-CSK interaction. The motion of a cortex-bound membrane inside the micropipette satisfies the force-balance equation, Eq. 1. It reflects the viscoelasticity of the cytoskeleton (short-times elastic response and long-times viscous response, Eq. 2), and the presence of active force generators (contractile myosin microfilaments). The cortical stress is directly transmitted to the PM-CSK linkers, which collectively rupture (i.e., they detach faster than they can bind) if the cortex stress reaches a critical value given by Eq. 3. Below, we analyze the conditions under which the cortex becomes unstable, and we study the ability of a new cortex to reform under a moving membrane.

Cortex Response to a Dynamical Perturbation.

Under a constant suction pressure, a cell may reach a static mechanical equilibrium satisfying the static force balance (Eq. 1 with 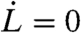), with a static cortical tension mostly provided by myosin contraction: γ = γ_mbr + σ_myoh, because the viscoelastic tension relaxes after a time τ^∗ (Eq. 2). This situation is stable provided the cell is not entirely swallowed inside the pipette (R(L) > R_p), and the PM remains attached to the CSK, below a critical value of σ_myoh/R_p (Eq. 3). If the myosin activity is too large, or if the pipette radius is too small, myosin contractility is sufficient to unbind the cortex from the PM.

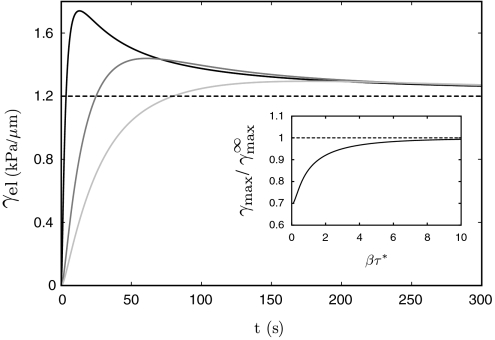
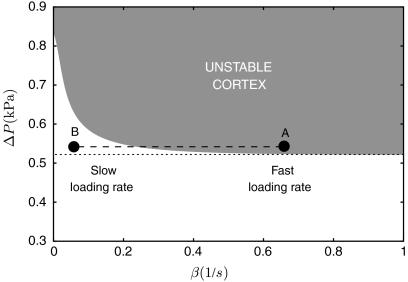
Experimentally, the pipette pressure is always applied over a finite time, thereby probing the viscoelastic nature of the cortex. Fig. 2 shows the evolution of the cortical tension of a cell subjected to a pressure ramp ΔP_t growing from zero to a finite value ΔP with a finite loading rate β: [we use ΔP_t = ΔP(1 - e^-βt)]. The tension initially increases during the short-times elastic response of the cortex and relaxes to a value controlled by the cortex viscous flow after a time τ^∗ (Eq. 2). Because of cortex renewal by polymerization, the strain actually decreases with increasing tongue length in the viscous regime, eventually reaching an asymptotic value controlled by the friction between the cortex and the pipette walls. The maximum amount of elastic tension transiently stored in the cortex increases with the loading rate and saturates to an asymptotic value for fast loading rates (β → ∞). By comparing the maximum elastic tension with the critical tension for cortex unbinding (Eq. 3), one obtains a stability diagram for the CSK-PM cohesion under a given pressure ramp, Fig. 3. The loading rate dramatically affects the membrane-cortex stability. For the same final pressure, the cortex may remain attached for small rates, but detaches for large rates.

Fig. 2.

Numerical solution for the evolution of the cortical elastic tension with time (Eqs. 1 and 2) under a pipette pressure ramp (ΔP = 1 kPa) with different loading rates (β = 1, 0.05, and 0.22 s^-1). The asymptotic value of the tension is controlled by friction with the pipette. (Inset) Maximum tension as a function of the loading rate, normalized by the tension under infinite loading rate, controlled by the membrane viscous dissipation. Parameters are E = 10³ Pa, τ^∗ = 15 s, h = 1 μm, L_f = 10 μm, and η_b = 130 Pa s/μm.

Fig. 3.

Variation of the critical suction pressure for membrane-cytoskeleton unbinding with the loading rate β, obtained by comparing the maximal cortical tension (Fig. 2) with the critical tension for linkers unbinding, Eq. 3. For the same suction pressure, the membrane may detach from the cortex if the pressure is applied quickly (dot A, e.g., when the cell first contact the micropipette), while being stable for slow loading rate (dot B, e.g., during the myosin-driven cell retraction; see text). For a large suction pressure, the cortex detaches even at very slow rate (β → 0) because of the stress caused by friction with the pipette. The critical force per bond is 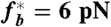(see SI Text), with other parameters as in Fig. 2.

Membrane detachment (if it occurs) is followed by a fast and transient extension of the membrane tongue inside the pipette. The tongue is then often seen to stop and possibly to retract back toward the cell body (see Movies S1 and S2 and ref. 12). Two possible mechanisms may contribute to stopping the membrane tongue: an increase of membrane tension or the polymerization of new actin cortex. The former mechanism stabilizes micropipetted GUV and might play a role in cells as well. Its physiological relevance depends mostly on the membrane stress–strain relationship γ_mbr(L). Retraction, however, must involve the contractile activity of the cortex.

Can Actin Stop a Moving Membrane?

Although a fairly detailed description of the life cycle of a cellular bleb has been obtained with fluorescent microscopy (7), one pending question is whether bleb inflation is stopped by the polymerization of a new actin cortex, or by other factors such as a (possibly local) decrease of internal pressure or increase of membrane tension. In what follows, we establish the conditions for cortex repolymerization under a moving membrane, and we discuss its ability to retract the cell tongue.

Generically, the growth of the new cortex may be described by a kinetic equation for the variation of the cortex thickness h(t): ∂_th = v_p - k_dh. It accounts for the velocity v_p of actin polymerization (at the PM, promoted by membrane-bound actin nucleators) and the rate of actin depolymerization k_d (throughout the cortex). A stationary cortex thickness is reached when depolymerization balances polymerization (h = v_p/k_d). The rate of actin depolymerization is thought to increase under stress (31), so the cortex under the membrane of an advancing tongue, which develops tensile stress, should have a reduced stationary thickness. A proper actin meshwork can form only if the stationary thickness is larger than the gel mesh size ξ, controlled by such factors as the densities of nucleators and cross-linking proteins. This sets the criterion v_p/k_d > ξ for the formation of the cortex, which can be formalized by assuming a Kramers statistics for the depolymerization rate (25, 27): 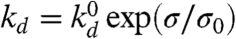, where σ is the local mechanical stress in the cortex, σ₀ characterized the mechanosensitivity of depolymerization, and 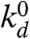is the stress-free depolymerization rate. The stress can be estimated as σ ∼ Eδl/l, where the strain δl/l (see Fig. 1C) is of the order of the strain rate times the lifetime of a piece of gel: 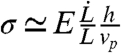. The condition for proper cortex growth under the moving membrane tongue thus reads

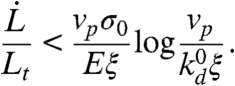[4]

The growth of a new cortex thus requires a subcritical velocity (controlled by the pipette pressure). The transition to cortex growth could be fairly abrupt, because even a thin cortex will reduce the tongue velocity, and in turn favor further growth.

The retraction of the membrane tongue toward the cell body requires the myosin contractile tension to overcome the pressure force (now assumed constant in time): σ_myoh > ΔPR_p/2 - γ_mbr [for R_p ≪ R(L)]. Tongue retraction should thus occur once the cortex reaches a critical thickness h_s. However, beyond yet another critical thickness h_b, the contractile tension destabilizes the membrane–cortex attachments and drives cortex unbinding, Eq. 3. There is thus a potentially narrow window of cortex thicknesses that permits retraction without leading to cortex unbinding. The critical thicknesses may be evaluated by neglecting the cortical tension of the cell outside the pipette [R_p ≪ R(L)], and in the limit of small tongue velocity, for which the viscoelastic stress can be neglected altogether compared to the contractile stress:

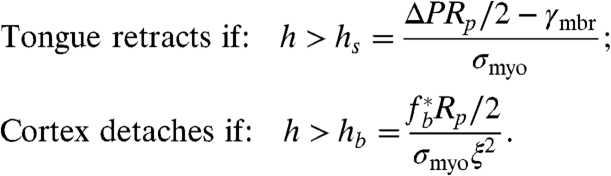[5]

The critical thickness for cortex detachment h_b solely depends on microscopic parameters, the myosin activity and the density (assumed ∼1/ξ²) and strength of the linkers, and on the pipette radius. With our choice of parameter, we find h_b ∼ 1 μm.

Discussion

Beyond its physiological importance for the motility of several cell types and its possible role in tumor cell invasion, the growth and retraction of cellular blebs reveal the complex dynamical interactions between the cytoskeleton and the plasma membrane. Below, we discuss important physical and physiological parameters controlling the dynamics of the cellular surface and ultimately regulating the bleb-based motility. We also quantitatively confront our model with the results of micropipette manipulations on Entamoeba histolytica.

Stability of the Membrane-Cortex Adhesion.

Strong micropipette suction is known to cause membrane-cortex detachment, creating a CSK-free membrane tongue extending inside the pipette (10, 12, 13). Tongue retraction under a sustained level of pipette pressure [e.g., in Dictyostelium (12)] is, however, still to be explained. Retraction, which requires the growth of a new cortex on the detached membrane, is somewhat counterintuitive. Indeed, whereas the preexisting cortex was unstable under a given pipette pressure, the new cortex is not only stable, but sufficiently contractile to counteract this pressure. It has been proposed that an increased density of CSK-PM linkers such as Talin (12) or other structural adjustments could strengthen the new cortex. Our theoretical analysis suggests an alternative explanation that relies solely on the viscoelastic nature of the cortex. As we show below, our picture consistently explains more complex (saltatory and oscillatory) types of cell deformation.

The cortex is a permeable filamentous meshwork that does not experience hydrostatic pressure. The pressure drop across the cell interface is thus mostly acting on the PM. It is not directly responsible for membrane-cortex detachment, and indeed, a perfectly compliant cortex would never detach from the membrane. Detachment occurs because the combination of cortex tension and curvature leads to a normal stress on the cortex-membrane protein linkers, increasing the linkers unbinding rate. Membrane-cortex adhesion is lost above a critical stress for which all linkers unbind (Eq. 3). The cortex being viscoelastic, its internal stress increases with the rate of mechanical perturbation as shown in Fig. 2. This rate is very fast during the initial contact between the cell and the micropipette, with a correspondingly large cortical stress. On the other hand, it is fairly low during retraction and set by a combination of actin polymerization, recruitment of myosin motors, and myosin-driven actin contraction. Little elastic stress is then built within the cortex, which effectively behaves as a fluid. Thus, a given level of micropipette suction can lead to membrane–cortex disruption during the initial contact between the pipette and the cell while allowing the slow active contraction of a stable renewed cortex with similar structural properties (Fig. 3).

Cell Deformation Under Controlled Perturbation.

While apoptotic cells and cells treated with specific drugs can show extensive blebbing (2), bleb-based motility is most efficient if blebs are generated one at a time, and cells using the bleb-based strategy generally show almost periodic cycles of blebbing and retraction (5). This requires a relatively fine tuning between the strength of PM-cortex attachment and the level of myosin contractile activity, so that myosin alone can generate the critical amount of stress needed for membrane detachment. We have experimentally studied the process in detail by micropipette manipulation of E. histolytica, which exhibited motility through blebbing (32). The micropipette setup is ideally suited for such an undertaking, since both the level of pressure and the morphology of the “bleb” (the cylindrical tongue inside the pipette) can be accurately controlled. The latter point is crucial, as the critical tension for membrane detachment is directly related to the curvature of the cell interface (Eq. 3).

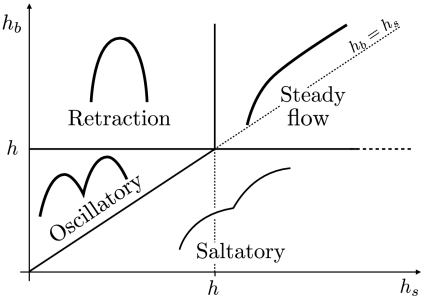
Based on our theoretical analysis, the motion of a cell subjected to pipette suction can be of four different classes, sketched in Fig. 4. If the cortex remains stably attached to the membrane, the cell flows inside the pipette, either up to a new equilibrium deformation (eventually stabilized by an increase of membrane tension), or until complete engulfment inside the pipette. If the pipette pressure is sufficient to unbind the cortex (Fig. 3), a bare membrane tongue quickly extends inside the pipette, under which a new cortex starts to grow when the condition, Eq. 4, is satisfied. The ensuing cell motion can be determined by comparing the cortex stationary thickness h, essentially controlled by polymerization and depolymerization, with two characteristic thicknesses corresponding to critical levels of cortical tension (Eq. 5). A cortex with a thickness larger than h_s generates enough contractile stress to counterbalance the pipette pressure and retract the tongue, whereas the stress generated by a cortex thicker than h_b is sufficient to tear it out from the membrane.

Fig. 4.

Predicted classes of cell motion inside a micropipette as a function of the critical cortex thicknesses for unbinding h_b and retraction h_s (Eq. 5). An arbitrary value of the stationary cortex thickness h is chosen. Depending on the value of h_s and h_b, we observe four different regimes: the retraction regime, corresponding to h_b > h > h_s; the oscillatory regime, corresponding to h > h_b > h_s; the saltatory regime (in which the membrane does not actually stop at any time), h_s > h > h_b; the steady flow regime, if h < (h_s,h_b).

If the critical unbinding thickness is not reached (h < h_b), the new cortex remains stably attached to the membrane. If h > h_s, the cortex tension eventually balances pipette suction and the cell retracts back to a new equilibrium position. Otherwise, the cell steadily flows inside the pipette as previously described. These two regimes have been reported for Dictyostelium (12), and we have observed the latter in E. histolytica as well. The former regime cannot be observed in motile E. histolytica cells, which naturally showed pronounced blebbing, indicating that the cortical stress alone can lead to membrane unbinding (h > h_b). In this case, and depending on pipette suction, the cortex may be able to partly retract the tongue before membrane unbinding (h_s < h_b). The cell then displays periodic oscillations where phases of tongue retraction, initiated by cortex polymerization, are terminated by cortex unbinding. For stronger suction (h_s > h_b), the tongue rather displays a (periodic) saltatory movement without true retraction (see Fig. 4). In principle, drugs targeting actin and myosin could allow us to explore the entire phase diagram for a single cell type by tuning the stationary cortex thickness h, density 1/ξ², and contractility σ_myo.

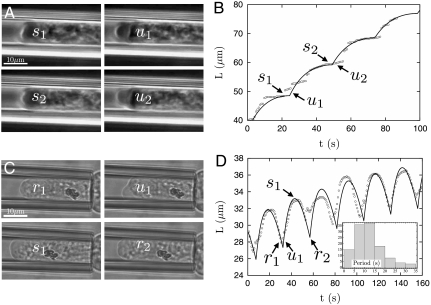
We have quantified the saltatory and oscillatory regimes experimentally in E. histolytica, and our model produced quantitatively accurate fits of the two types of motions, with the pipette pressure as the main switching parameter between the two regimes (see Fig. 5). In either case, the period of motion is controlled by the time needed to grow a cortex with the critical unbinding thickness: τ ∼ h_b/v_p. Remarkably, both v_p and h_b are controlled by cellular parameters (actin treadmilling, the density of actin nucleators and cross-linkers, and myosin activity) and by the pipette radius, but are insensitive to the pipette pressure. We observed an average oscillation period of 13 s (see Fig. 5), consistent with an actin polymerization velocity v_p ∼ 70 nm/s. As discussed in SI Text, the accuracy of the fits does not depend on the value of individual parameters, of which we only have an imprecise knowledge, but on particular combinations of them such as those given by Eq. 5 or discussed above. In the example shown for the oscillatory regime, the average tongue length slowly saturates, a likely signature that the cell membrane tension γ_mbr(L) increases with the cell deformation.

Fig. 5.

Representative motions of the E. histolytica inside the pipette in the Saltatory (A and B) and Oscillatory (C and D) pipette suction regimes. (see Movies S1 and S2). (A) and (C) Snapshots of the tip of the cell inside the pipette at different instants in time. (B) and (D) Corresponding tracking of the tip position with time, and theoretical fit (black lines). (D Inset) Histogram of the oscillation periods (from 147 oscillations observed on five different cells). The average period is 10–15 s. The fits are based on the force balance, Eq. 1, with a time-varying cortex thickness controlled by polymerization (v_p = 60 nm/s) and depolymerization (1/k_d = 25 s) and neglecting the rear cortical tension of the cell (see text). The cortex flow is assumed to be controlled by the friction with the pipette walls (L > L_f). The effects of membrane tension cancel out in the saltatory regime as the cell is entirely engulfed inside the micropipette. All parameters are discussed in SI Text and are the same as in Fig. 2, with a critical rupture force , giving an unbinding thickness h_b = 0.95 μm. The transition between the two regimes is solely driven by the pipette pressure ΔP (= 1.2 kPa—oscillatory and = 1.9 kPa—saltatory regime), corresponding to retraction thicknesses h_s = 0.6 μm (oscillatory) and 0.95 μm (saltatory).

We argue that cortex polymerization, combined with myosin contraction, is sufficient to stop and retract the membrane tongue. The retraction of the tongue could also be caused by the cell blebbing outside the pipette. Large variation of cell body shape, and even blebbing, is often observed concomitantly with tongue retraction, and it is experimentally difficult to determine which of the two is the consequence of the other (see Movies S1 and S2). The existence of a saltatory regime provides strong support for the direct role of the cortex in slowing down the membrane tongue. Furthermore, the cortex is sometimes seen to only partially cover the spherical cap of the tongue. In this case, the fraction covered is seen to slow down while the rest of the tongue typically moves past it (see Movie S1). This observation can be attributed to neither the increase of membrane tension nor the decrease of the cell inner pressure following blebbing outside the pipette, as both these phenomena would uniformly affect the tongue. Our observations thus provide strong evidence for cortex involvement in stopping large cellular protrusions. More direct confrontation with our theoretical predictions would require varying the pipette radius over a wide range, which is not easily feasible (cells tend to crawl out of pipettes with small radii). It is nevertheless quite remarkable that the oscillation periods recorded for different amoebae were always peaked around the same value, although different cells displayed oscillations for different pipette pressure.

Conclusions

In this work, we propose a self-consistent dynamical description for the mechanical properties of the plasma membrane and the cytoskeleton cortex attached to it. We have combined physical modeling and micropipette manipulation on E. histolytica to reach a quantitative characterization of the interfacial instability that gives rise to bleb-based cell motility. Even though we have used a fairly simple description for the individual players, their combination yields a rich dynamical behavior that reproduces different types of amoebae motion observed upon micropipette suction, including remarkable spontaneous oscillations of purely mechanical origin. The main ingredients of the model are the actin polymerization and depolymerization kinetics, which control the cortex thickness, the myosin contractility, and the on/off kinetics of the proteins linking the cortex to the cell membrane. Although the experimental focus was on micropipette manipulations, the conclusions of our model are of relevance for cell morphological changes in general, and cell motility in particular. These include the following:

• Membrane detachment from the cortex is strongly influenced by the viscoelastic properties of the cortex and is heavily dependent on the rate of perturbation. This explains in a self-consistent way previous observations on Dictyostelium (12).

• The growth of an actomyosin cortex can stop and retract a membrane protrusion moving at a subcritical speed.

• A contractile stress generated by the actomyosin cortex can provoke its own detachment from a sufficiently curved membrane.

Our theoretical predictions identify two important length scales: a cortex thickness that allows for the retraction of the protrusion and one for which the cortex contractility induces membrane detachment, Eq. 5. Even though we rely on simplifying assumptions in order to express these length scales in terms of physical and physiological parameters, their existence does not depend on the details of the model. Comparing these two length scales with the actual cortex thickness, controlled by actin treadmilling, produces a general phase diagram of possible cellular motions, which includes stable oscillations. Bleb-based motility usually occurs in the absence of an external mechanical driving force, the cortex contractility not only providing the normal stress that pulls the cortex inward, but also being responsible for the building of internal pressure that pushes the plasma membrane outward. We believe, however, that the periodic motions uncovered here are a clear illustration of how a combination of contractility and fragility within the cell can lead to extensive shape changes that serve as a basis for motility and that are forced into regular cycle by the constraining shape and pressure of a micropipette.

Materials and Methods

Cell Culture.

E. histolytica HM1-IMSS (33) wild-type strain is grown and resuspended before experiments in TY-SS3 medium.

Micropipette Experiments.

Sample chambers are made of two clean glass coverslips glued with vacuum grease, fixed with nail polish to an aluminum support (1 mm thick), and sealed with mineral oil to prevent water evaporation and limit oxygen entrance. The chamber is placed on the stage of an inverted microscope (Axiovert 200, Zeiss). Temperature is regulated by a homemade setup (water circulation around the objective, fluid temperature regulation performed by a thermostatic bath/circulator Lauda RE 107). The microscope is equipped with a 60X Olympus UPlanFl immersion oil objective (1.25 NA) and a 0.8-NA air condenser. Pipette manipulation is achieved with a homemade micromanipulator clamped on the microscope; a micropipette of about 10-μm diameter at the tip is connected to a mobile water tank. The phase-contrast images are collected by an analog CCD camera (XC-ST70CE, SONY) and recorded through a frame grabber (Picolo Pro 2) by the software Graph Edit.