Interplay of mechanical and binding properties of Fibronectin type I

Abstract

Fibronectins (FNs) are a major component of the extracellular matrix (ECM), and provide important binding sites for a variety of ligands outside and on the surface of the cell. Similar to other ECM proteins, FNs are consistently subject to mechanical stress in the ECM. Therefore, it is important to study their structure and binding properties under mechanical stress and understand how their binding and mechanical properties might affect each other. Although certain FN modules have been extensively investigated, no simulation studies have been reported for the FN type I (Fn1) domains, despite their prominent role in binding of various protein modules to FN polymers in the ECM. Using equilibrium and steered molecular dynamics simulations, we have studied mechanical properties of Fn1 modules in the presence or the absence of a specific FN-binding peptide (FnBP). We have also investigated how the binding of the FnBP peptide to Fn1 might be affected by tensile force. Despite the presence of disulfide bonds within individual Fn1 modules that are presumed to prevent their extension, it is found that significant internal structural changes within individual modules are induced by the forces applied in our simulations. These internal structural changes result in significant variations in the accessibility of different residues of the Fn1 modules, which affect their exposure, and, thus, the binding properties of the Fn1 modules. Binding of the FnBP appears to reduce the flexibility of the linker region connecting individual Fn1 modules (exhibited in the form of reduced fluctuation and motion of the linker region), both with regard to bending and stretching motions, and hence stabilizes the inter-domain configuration under force. Under large tensile forces, the FnBP peptide unbinds from Fn1. The results suggest that Fn1 modules in FN polymers do contribute to the overall extension caused by force-induced stretching of the polymer in the ECM, and that binding properties of Fn1 modules can be affected by mechanically induced internal protein conformational changes in spite of the presence of disulfide bonds which were presumed to completely abolish the capacity of Fn1 modules to undergo extension in response to external forces.

1 Introduction

In multicellular organisms, cells and tissues are components of force-baring networks, which provide a large degree of mechanical coupling between the cells. Such mechanical coupling not only determines adhesive properties and the mobility of a particular cell type, but also affects intracellular processes through modulating specific receptors. Forces applied to the surface receptors anchored to the cytoskeleton, for instance, may quickly propagate into deep regions of the cell interior, including the nucleus [1]. For example, it has been shown that tugging on particular integrin receptors at the surface of a living cell can trigger nearly instantaneous rearrangements in the nucleus, and that the cytoskeleton provides a mechanism for mechanical signal transduction rather than just a supporting structure [2]. The network outside the cell that provides the backbone for such intercellular communication is known as the extracellular matrix (ECM). Fibronectins (FNs) are essential components of the ECM where they play a key role in establishing and modulation of the mechanical and binding properties of the network.

FNs assemble into cross-linked fibrillar networks that bind to integrins on the cell surface, and, thus, are responsible for mechanical coupling of the cell to the ECM. These networks participate in a large number of physiological processes, such as embryonic development, wound healing, immune responses, and tumor metastasis [3–5]. Experimental studies have established that FNs are consistently subject to cell-generated tension, and thus, are highly stretched under normal conditions [6, 7]. Mechanical stress is known to have significant effects on the behavior of FNs; for example, stretching induced by integrin clustering on the cell surface has been shown to expose buried (cryptic) binding sites on FNs [8–10], which can then bind other protein modules in the ECM, e.g., neighboring FN modules as well as other peptide and protein ligands. The binding of FN modules through these binding sites is an essential step, e.g., in the FN matrix assembly.

There are three types of repeating protein modules in FN polymers: type I (Fn1), type II (Fn2), and type III (Fn3), all composed primarily of anti-parallel β strands. Fn1 and Fn2 modules contain highly conserved disulfide bonds that cross-link the β strands within individual modules, a feature that has been presumed to rigidify their structure and, thus, to prevent them from undergoing large protein conformational changes in response to tension in the ECM. Fn3 modules, on the other hand, do not contain disulfide bonds, and are thus expected to exhibit large structural transitions upon tensile loading. Possibly for this reason, mechanical properties of Fn3 modules have been extensively studied both experimentally and theoretically [11–14], and it has been suggested that along the unfolding path of Fn3, there are metastable intermediates that play physiologically important roles. Mechanical properties of Fn1 and Fn2 modules, on the other hand, have received much less attention.

Fn1 modules are important elements of FN polymers since they provide binding sites for other FN modules (both for other Fn1 modules in the ECM as well as for Fn3 modules), and, thus, play an important role in the FN matrix assembly [15–17]. Fn1 modules also provide binding sites for other ligands in the ECM, e.g., fibrin [18], heparin [19], and tenascin [20]. In addition, FN-binding proteins (FnBPs) of some bacteria, such as Staphylococcus aureus and Streptococcus pyogenes, bind to Fn1 modules [21]. FnBPs are anchored to the cell wall of these bacteria and their binding to Fn1 modules is suggested to constitute an essential step in bacterial invasion of host cells [22]. The structure of the complex of a bacterial FnBP peptide and the first two Fn1 modules (¹Fn1²Fn1) has been resolved using NMR spectroscopy [21]. We refer to the complex using the acronym FnBP-¹Fn1²Fn1.

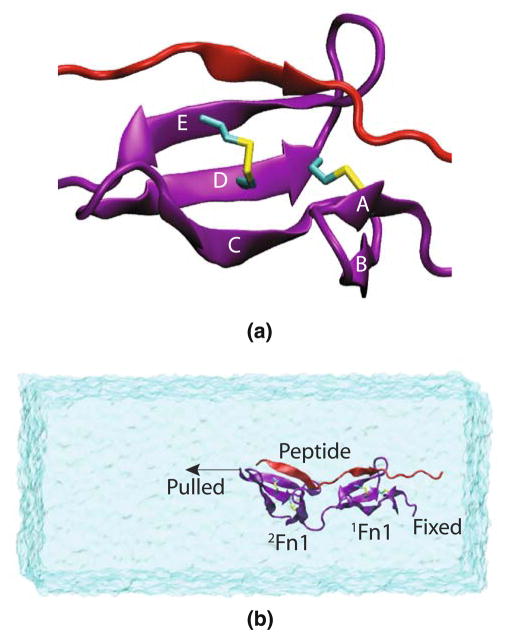
Fn1 modules are Ig-like (immunoglobulin-like) domains composed of five β strands, named A, B, C, D, and E, respectively (Fig. 1a), with β strands A/B and C–E forming two β-sheets, respectively. Two disulfide bonds connect β strands A and D, and D and E, respectively. In the FnBP-¹Fn1²Fn1 complex [21], the latter forms an additional anti-parallel β strand with both ¹Fn1 and ²Fn1 modules (Fig. 1). Since FNs are consistently under tension and highly stretched, it is relevant to study the structure of these modules under tension, and to investigate whether the binding of ligands to FN might be affected by tensile forces. Conversely, it is of relevance to understand how their mechanical properties might be affected by ligand binding. The FnBP-¹Fn1²Fn1 complex [21] provides us an ideal model system for such a study.

Fig. 1.

a Major structural features of Fn1 modules. An ¹Fn1 module (purple) with its five β strands, as well as a portion of the FnBP peptide (red) are shown. Two disulfide bonds connect β-strands A and D, and D and E, respectively. b A representative simulation system with ¹Fn1²Fn1 drawn in purple, the FnBP peptide in red and water in transparent surface representation. The binding peptide forms an additional β-strand with both ¹Fn1 and ²Fn1 modules. In pulling simulations, one end of ¹Fn1²Fn1 was fixed, while the other end was coupled to a constraint moving at a constant velocity. The water box is large enough to accommodate the stretching of the protein under tensile loading. Equilibrium simulations used a very similar setup, though with a smaller water box

In this paper, we investigate the mechanical properties of ¹Fn1²Fn1 under tension using steered molecular dynamics (SMD) simulations [23, 24] and study how these properties might be affected by binding of the FnBP peptide. SMD has been successfully employed previously in the investigation of mechanical properties of proteins and to interpret experimental measurements [23, 24]. With regard to the specific case of β-sheet proteins, SMD studies of titin [25–33] and Fn3 domains [11, 12, 34–37] present prominently successful cases of the combination of SMD and experimental force measurements in investigating mechanical properties of proteins. Our results show that, in spite of the presence of two disulfide bonds which one presumes to significantly confine the response of the Fn1 modules to external tension, individual Fn1 modules undergo significant internal structural changes under tension, and, thus, can contribute to the overall force-induced extension of the FN polymer in the ECM. The observed conformational changes of the Fn1 modules under tension give rise to changes in the accessibility of several residues, which might in turn modulate the binding properties of Fn1 modules. We also show that the FnBP peptide sustains the force applied and does not remain bound simultaneously to both the ¹Fn1 and ²Fn1 modules under large forces. Peptide binding, in turn, results in the rigidification of the linker region and stabilizes the inter-domain configuration. To our knowledge, this is the first simulation study investigating the mechanical properties of Fn1 modules.

2 Methods

2.1 Model building

The NMR structures of the FnBP-¹Fn1²Fn1 complex were obtained from the protein data bank (PDB code 1O9A) [21]. Among the 15 deposited structures in the pdb file, 14 are very similar. The last frame is different with regard to the inter-domain orientation. Frame 7, which is representative of the first 14 structures, was selected for this study. A peptide-free ¹Fn1²Fn1 was generated by removing the FnBP peptide from the FnBP-¹Fn1²Fn1 complex. The ¹Fn1²Fn1 with and without the peptide was solvated in a water box of size 70 Å in both the x and y directions and 160 Å in the z direction (Fig. 1b). The ¹Fn1²Fn1 was aligned along the z direction. To neutralize the system and maintain a physiological ionic concentration, Na⁺ and Cl⁻ ions were added to the system at a concentration of 100 mM. The total number of atoms in the system in the presence of the FnBP peptide is 73,472, including 23,878 water molecules, and 24 Na⁺ and 21 Cl⁻ ions.

2.2 MD simulations

All the molecular dynamics (MD) simulations were performed with the program NAnoscale Molecular Dynamics (NAMD) [38] with a time step of 1 fs, using the Chemistry at HARvard Molecular Mechanics (CHARMM27) parameter set [39] with TIP3P water [40]. The particle-mesh Ewald (PME) method [41] was used for computation of long-range electrostatic forces, and a cutoff with a switching function starting at 10 Å and reaching zero at 12 Å was used for van der Waals interactions. The temperature was maintained at 310 K via the Langevin dynamics with a damping coefficient, γ, of 0.5 ps⁻¹, and the pressure at 1 atm via the Langevin Nose–Hoover method [42, 43]. The systems were initially minimized for 5,000 steps and equilibrated for 0.5 ns with ¹Fn1²Fn1 and the FnBP peptide, if present, constrained to their initial NMR structure. Then the systems were further minimized for 5,000 steps and equilibrated for 10 ns without any constraints.

In pulling simulations, the equilibrated ¹Fn1²Fn1 systems were pulled from one end with the other end fixed (Fig. 1b) using steered MD [23, 24] to study their mechanical response. The direction of the force applied is consistent with tandem arrangement of Fn1 monomers in a FN polymer in which each monomer is connected to the previous and the next monomers by its N- and C-termini, respectively. Specifically, the C_α atom at the terminal residue on one end was subjected to a harmonic constraint with a force constant of 486 pN/Å (7 kcal/mol/Ų) that moved along the z (or −z) direction at a constant velocity of 0.005 Å/ps for 10–12 ns. The C_α atom of the terminal residue on the other end of the protein was fixed in space, in order to prevent net translocation of the protein in solvent during the pulling simulations. For the FnBP peptide-free system, only one pulling simulation was performed, in which the ¹Fn1²Fn1 was pulled from the ¹Fn1 end with the ²Fn1 end fixed. For the system with the FnBP peptide, four sets of pulling simulations were performed. In two, the system was pulled from the 1Fn1 end, and in the other two, from the ²Fn1 end.

2.3 Analysis

Root mean square displacement (RMSD) analysis was performed to examine structural deviation from the starting configurations, i.e., that of the NMR structure [21]. As a measure of availability for binding, surface exposure of individual residues and its variation in response to force-induced conformational changes of the Fn1 modules during the pulling simulations were calculated with two complementary methods: (1) solvent accessible surface area (SASA) [44] for each residue was calculated with VMD [45]; and (2) the number of water molecules within a radius of 3.5 Å of each residue was counted during the simulations. All the molecular images are made with VMD [45].

3 Results and discussion

3.1 Structural response of the Fn1 dimer to tension

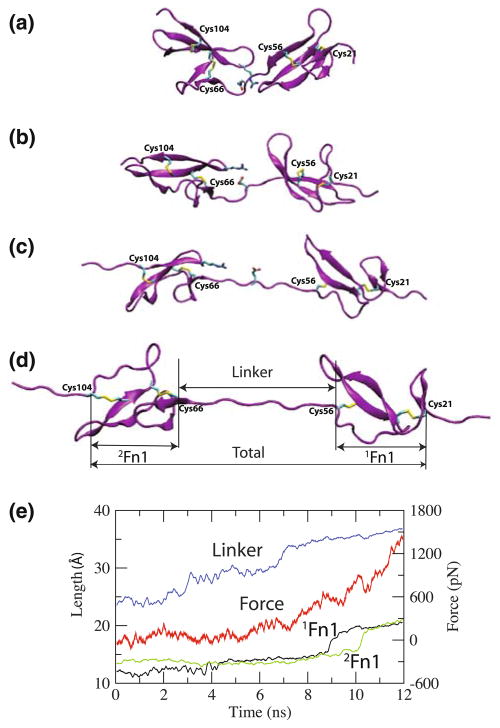
During the 10-ns equilibrium simulation, we did not observe any major intra-modular conformational deviation from the NMR structure for the individual ¹Fn1 and ²Fn1 modules. Backbone RMSDs of both ¹Fn1 and ²Fn1 plateau to a value of around 2.5 Å with respect to the initial NMR structure during the simulation. Application of tensile force, however, results in significant conformational changes of both modules. Figure 2 shows snapshots taken during the tensile loading of ¹Fn1²Fn1 in the absence of the FnBP peptide, monitoring the length of three distinct regions of ¹Fn1²Fn1 (Fig. 2d) used to characterize the elongation of the modules under the applied tensile force. Specifically, the length of ¹Fn1 is defined as the distance between the C_α atoms of CYS21 and CYS56, the length of ²Fn1 as the distance between the C_α atoms of CYS66 and CYS104, and the length of the linker as the distance between the C_α atoms of CYS56 in ¹Fn1 and CYS66 in ²Fn1. The total length of ¹Fn1²Fn1 is defined as the distance between the C_α atoms of CYS21 and CYS104, thus, excluding the floppy terminal regions from the analysis. The extensions of the three regions of ¹Fn1²Fn1 are shown in Fig. 2e, along with the corresponding applied force, as functions of the simulation time.

Fig. 2.

Stress-induced extension of ¹Fn1²Fn1. The snapshots are taken at a t = 0 ns, b t = 3 ns, c t = 9 ns, and d t = 11 ns of the pulling simulation. The extensions of the individual modules and that of the linker (the three distinct regions defined in d) are plotted in (e), along with the corresponding applied force, as functions of time. The disulfide bonds and a key salt bridge in the linker region are also shown

Under moderate forces (~300 pN, which is about half the force required to unfold Fn3 repeats under similar simulation conditions [12]), the extension mainly originates from the linker, which is not surprising due to the rather flexible nature of the unstructured linker region. At t = 7 ns, corresponding to a tensile force of 300 pN, we observe a sudden increase in the length of the linker (Fig. 2e), which is due to the disruption of a salt bridge between GLU61 in the linker and ARG99 on the D–E loop of ²Fn1 (Fig. 2). The breaking of this salt bridge, which represents the only major molecular event during the extension of the linker region, relaxes the system, and, thus, results in a drop in the applied force (Fig. 2e). At this point, the linker is almost fully extended and can only accommodate very limited additional extension. In contrast, the ¹Fn1 and ²Fn1 regions only show marginal extensions during this first stage of the pulling simulation.

During the later stages of the pulling simulation (Fig. 2e), significant increases in the length of both the ¹Fn1 and ²Fn1 modules take place. The observed extensions, interestingly, correspond to internal structural rearrangements of the two Fn1 modules. At the end of the simulation, a considerable alignment of the two disulfide bonds along the pulling direction is evident in both modules (Fig. 2d). Corresponding to the observed elongation, there are drops in the force profile (Fig. 2e). We note that these intra-modular conformational changes occur under a tensile force of 600–700 pN, which is comparable to the force required to fully unfold Fn3 repeats under similar simulation conditions [12]. Although SMD simulations usually result in overestimation of the required force to induce certain events, the comparable forces obtained in the present study to induce structural changes of the Fn1 modules and those to induce unfolding of the Fn3 modules in other simulations [12] under similar conditions suggest that these two molecular events might equally contribute to the extension of FN polymers in the ECM.

Here, we provide a more detailed picture of the events involved in internal structural rearrangement of the individual modules. During the pulling simulations, the applied force is sustained by β-strands A, D, and E, transmitted through the disulfide bonds connecting them (Figs. 1, 2). The β-strands B and C do not sustain force and are flexible to adjust their positions to form hydrogen bonds with β-strands A and D and thus help preserving the β-sheet conformation under tensile loading. However, the hydrogen bonds between β-strands D and E break in a two-stage process during the pulling. First, the hydrogen bonds in the region beyond the two disulfide bonds of each module break, and β-strands D and E partially separate (Fig. 2c). Due to the disulfide bonds, the breaking of the hydrogen bonds does not propagate into the region in between the two disulfide bonds of each module. During the second stage, upon further loading, the disulfide bonds that sustain the force align with the pulling direction and the hydrogen bonds between β strands D and E in the region between the disulfide bonds of each module break by relative shearing and separation of β-strands D and E, which are now connected only through the disulfide bonds (Fig. 2d). Significant internal conformational change of Fn1 modules in response to tensile loading is evident by comparing the structures of individual ¹Fn1 and ²Fn1 modules at the beginning (0 ns) and the end (11 ns) of the pulling simulation. Both modules exhibit clearly large conformational changes resulting in loss of some of the β-strand structures and alignment of the two disulfide bonds along the force direction.

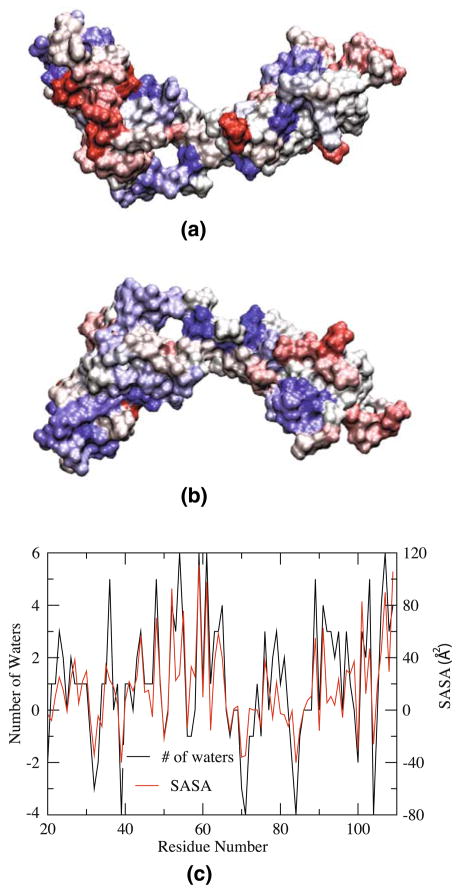
In order to assess how potential binding sites/motifs might be exposed by tensile loading, the change in solvent accessibility of the residues in ¹Fn1²Fn1 caused by the pulling was examined. An increased accessibility of a residue is an indication of its higher exposure to the surface, and, thus, its availability for binding. We counted the average number of water molecules within 3.5 Å of each residue over 100 ps of simulation at t = 11 ns and at t = 0 ns of the simulation. The differences in the number of water molecules for different residues are plotted in Fig. 3c and are also used to color the Fn1 dimer in Fig. 3a, b. We also calculated the solvent accessible surface area (SASA) [44] (Fig. 3c), and the results of the two methods are consistent. As expected, most residues become more accessible due to the tensile loading. However, and somewhat unexpected, there are also residues that exhibit reduced accessibility at the end of the pulling simulation. Since Fn1 modules play an important role in binding of a variety of ligands to FN polymers and in the assembly of FN matrix, the change in exposure of different residues in Fn1 induced by tension, which is an important, physiologically relevant aspect of the ECM, has direct implication in binding properties of the FN polymers.

Fig. 3.

Change in accessibility of residues in ¹Fn1²Fn1 upon tensile loading. The average surface accessibility (c) has been calculated using two complementary methods (resulting in similar conclusions): the number of water molecules within 3.5 Å of individual residues or the solvent accessible surface area (SASA). Both values are averaged over a period of 100 ps, at t = 11 ns and at t = 0 ns of the pulling simulation, and the differences are plotted in (c) and used to color the ¹Fn1²Fn1 molecule in front (a) and back (b) views, with residues that become exposed in blue and those that become buried in red

3.2 The effect of FnBP peptide binding on mechanical properties of ¹Fn1²Fn1

Similar to the peptide-free simulation, the individual ¹Fn1 and ²Fn1 modules were internally quite stable during the equilibrium simulation in the presence of the FnBP peptide (backbone RMSDs of ~2.5 Å). This observation is consistent with experimental data indicating that peptide binding does not affect the structure of individual Fn1 modules [21]. The binding of the FnBP peptide has a significant impact, both on the inter-modular dynamics of the Fn1 dimer and on its response to the applied force, as described in detail below.

In contrast to the peptide-free system, the peptide-bound Fn1 dimer shows a significantly smaller inter-domain fluctuation during the simulation. It appears that the FnBP peptide rigidifies the linker between the ¹Fn1 and ²Fn1 modules (Fig. 4). Using ¹Fn1 for the alignment of the individual frames, the average backbone RMSD of ²Fn1 is 12.6 Å in the absence of the FnBP peptide, and only 8.8 Å in presence of the peptide. The presence of the FnBP peptide appears to directly affect the dynamics of ¹Fn1²Fn1 through confining the bending motion of the linker region.

Fig. 4.

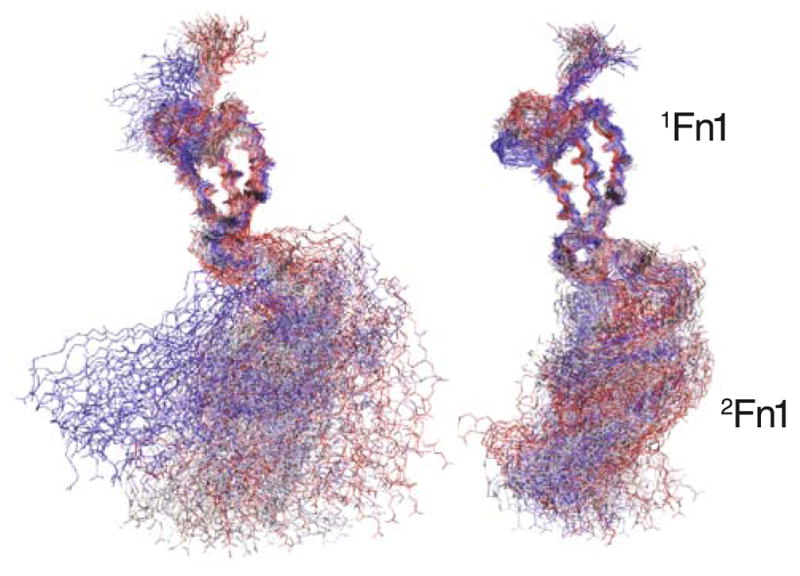
Linker rigidification induced by peptide binding. Shown are 100 frames of backbone structures of the ¹Fn1²Fn1 taken from the 10 ns of the equilibrium simulation with the ¹Fn1 modules used to align the frames. The results are shown for the peptide-free system (left), as well as for the peptide-bound system (right). The time interval between the frames is 100 ps, and ¹Fn1²Fn1 is colored according to the time steps, with the first step in red and the last one in blue

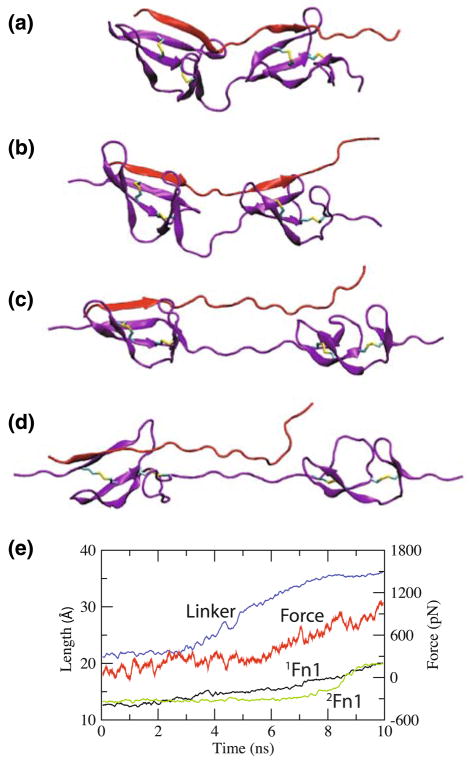
The effect of the binding of the FnBP peptide on mechanical properties of the dimer is also significant. Figure 5e shows the length of individual ¹Fn1 and ²Fn1 modules and that of the linker, along with the corresponding force, as functions of time, in one of the pulling simulations of ¹Fn1²Fn1 in the presence of the FnBP peptide. The pattern of extensions of the three regions is similar to those in the absence of the peptide. That is, during the initial stages of the pulling simulation, the extension mainly originates from the linker, while at later stages, it is furnished by the alignment of the disulfide bonds within individual modules along the pulling direction. Note, however, that the extensions occur more gradually due to the bound peptide. Very similar behaviors were observed in the other three pulling simulations of the FnBP-¹Fn1²Fn1 complex.

Fig. 5.

Stress-induced extension of ¹Fn1²Fn1 (purple) in the presence of the FnBP peptide (red). Snapshots of the FnBP-¹Fn1²Fn1 complex are taken at a t = 0 ns, b t = 3 ns, c t = 7 ns, and d t = 10 ns from one of the four pulling simulations; the extensions of the individual modules and the linker (defined in Fig. 2) are shown in e, along with the corresponding applied force, as functions of time

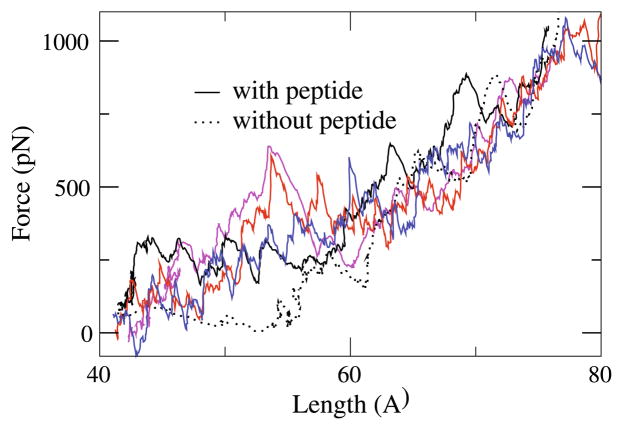
The main effect of the FnBP peptide on the mechanical behavior of ¹Fn1²Fn1 seems to be in the forces required to stretch ¹Fn1²Fn1. For a better comparison, in Fig. 6, we present the applied forces as a function of the total length of ¹Fn1²Fn1 (as defined in Fig. 2) for the system in the absence of the FnBP peptide (dotted line) along with the four independent simulation systems performed in the presence of the peptide. As shown, much larger forces are required to pull ¹Fn1²Fn1 in the presence of the FnBP peptide during the initial pulling stage, that is, the linker region is much more rigid with respect to moderate tensile force. Therefore, the binding of the FnBP peptide not only confines the linker with respect to its bending motion, as observed in the equilibrium simulation (Fig. 4), but also affects its response to tensile stretching. At later stages of pulling, the forces are comparable to those observed in the peptide-free simulation (Fig. 6). This is because during the initial pulling of ¹Fn1²Fn1, it is the FnBP peptide that mainly sustains the applied force, while during later stages, the peptide has detached from ¹Fn1²Fn1 and thus ceases to sustain the applied force. The ability of the FnBP peptide to sustain the force applied on ¹Fn1²Fn1 helps preserve the structure of the interface between ¹Fn1 and ²Fn1 under tensile force.

Fig. 6.

Force-extension profiles of ¹Fn1²Fn1. Applied forces as functions of the length of ¹Fn1²Fn1 during the pulling of ¹Fn1²Fn1 in the absence (dotted line) and four independent simulations in the presence of the FnBP peptide (solid lines)

3.3 Tension-induced unbinding of the FnBP peptide

The β-sheets formed between ¹Fn1²Fn1 and the FnBP peptide (Fig. 1) remain stable during the equilibrium simulation. In addition to backbone hydrogen bonds, van der Waals interactions between hydrophobic residues appear to be the main interaction between the FnBP peptide and ¹Fn1 [21]. On the other hand, side chain electrostatic attraction is found to constitute the main interaction between the peptide and the ²Fn1 module [21].

The binding of the FnBP peptide and the Fn1 dimer is affected by the tensile force, as observed in the pulling simulations. Figure 5 shows representative frames of the FnBP-¹Fn1²Fn1 complex taken from the first pulling simulation. The FnBP peptide is relatively short (Fig. 5a, b), and straightens (Fig. 5b) and sustains the applied force, upon stretching of ¹Fn1²Fn1. Then the hydrogen bonds between the backbone of the peptide and ¹Fn1 break one by one, resulting in the loss of the β-sheet connection between the two (Fig. 5c). The force required to break the β sheet connection is approximately 400 pN, which is also smaller than the force required to unfold Fn3 modules [12]. Upon further pulling, the peptide shears relative to ¹Fn1, and eventually detaches from it (Fig. 5d).

The FnBP peptide detaches from ¹Fn1 primarily due to its relatively short length, as it cannot accommodate the extension of the linker region of ¹Fn1²Fn1 (Fig. 5a, b). Upon stretching ¹Fn1²Fn1, the peptide straightens first due to its shorter length, and sustains the force applied to ¹Fn1²Fn1 due to its binding with both ¹Fn1 and ²Fn1. The linker region of ¹Fn1²Fn1 straightens and sustains the applied force only after the peptide shears and detaches from either ¹Fn1. Note, however, that the β-sheet connection between ²Fn1 and the peptide is preserved (Fig. 5d). This implies that the binding with ²Fn1 is not affected by the force applied to ¹Fn1²Fn1.

The pulling simulation was repeated with a slightly different starting configuration. Specifically, the equilibration was extended for 0.05 ns before the second pulling simulation. This time, the FnBP peptide detached from ²Fn1, in a similar manner to the first pulling simulation while remaining attached to ¹Fn1. Two other pulling simulations were also performed by pulling the ¹Fn1 end instead of the ²Fn1 end. Similarly, in one simulation the peptide detaches from ¹Fn1, and in the other from ²Fn1. The results suggest that under tensile loading of ¹Fn1²Fn1, the peptide detaches from either ¹Fn1 or ²Fn1 with approximately equal probabilities.

Based on the above observations and since while the FnBP peptide detaches from one module in ¹Fn1²Fn1, it usually preserves its binding with the other, we suggest that a peptide with a longer region between its two binding regions with ¹Fn1 and ²Fn1 could be engineered such that it does not have to sustain the force applied on ¹Fn1²Fn1, and thus remains bound to both ¹Fn1 and ²Fn1 simultaneously under tensile force in the ECM. Furthermore, in a FN polymer, the linkers between ²Fn1 and ³Fn1 [46], and between ⁴Fn1 and ⁵Fn1 [47] are much shorter than that between ¹Fn1 and ²Fn1. Based on the results of our simulations, we also suggest that these FN domains with shorter linkers between them might offer better binding sites for bacterial peptides in terms of resistance to force-induced unbinding.

4 Concluding remarks

The ECM plays a key role in mechanical coupling of the cell to its environment. Among the most important processes affected by mechanical stress are nuclear processes such as DNA sequestration, which can be controlled by mechanical signals from the ECM. Furthermore, the ECM also plays an important role in mobility of a cell, and, thus, an important player in metastasis. FNs provide important mechanical elements and key binding sites for various proteins in ECM. Due to the presence of cell-generated tensile force in the ECM, FNs are highly stretched. It is, therefore, important to study their structure and binding properties under mechanical stress and understand the interplay between their binding and mechanical properties. The present study constitutes the first simulation study on the mechanical properties of Fn1 modules investigating such aspects.

Fn1 modules were simulated in the presence or in the absence of a specific binding peptide, the FnBP peptide, under equilibrium conditions as well as under the effect of mechanical stress. The investigated Fn1 dimer was found to exhibit a significant elongation in response to tensile force, not only through the extension of the linker region between individual Fn1 modules, which was somewhat expected, but also due to internal structural changes of individual modules resulting in the alignment of disulfide bonds within individual modules along the pulling direction. The results provide evidence that despite the presence of disulfide bonds in individual Fn1 modules which make them appear as rigid modules, they might indeed undergo significant extension under tension, and, thus, contribute to the overall extension of FN polymers under tensile force in the ECM. The results of the present study encourage, and can be verified by, force-extension measurements of Fn1 modules, which are currently lacking.

One of the shortcomings associated with MD simulations of biomolecular systems is the limited time scale currently available to the method. Biological molecules, e.g., proteins usually operate on time scales that are on the order of at least microsecond or longer. Therefore, in order to induce processes that do not take place naturally during the time scales of simulations studies, one may resort to simulation methods, such as SMD, in which processes are accelerated. The method of SMD is a non-equilibrium method and interpretation of its results needs to be done cautiously. Often, the required forces are too large for the process at hand as the simulation time is too short for the biomolecule to sample the space along the reaction coordinate. In general, longer simulations and slower pulling schemes result in reduction of the force required to induce the process. In the present case, the fact that comparable forces were required to induce internal conformational changes (extensions) in Fn1 domains (present study) and Fn3 domains [12] under similar simulation conditions is indicative of similar mechanical properties of the Fn1 and Fn3 domains, despite the presence of disulfide bonds in the former. However, we note that the magnitude of the force required to induce the unfolding events in the present study are much larger than the physiological ones, and that only molecular processes observed here might be of relevance to the phenomena underlying natural unfolding of FN polymers under natural tensile forces.

We also find that mechanical stress can directly affect binding properties of the Fn1 modules. In the case of the FnBP peptide studied here, the primary effect of tension is mediated through the elongation of the linker region between the individual Fn1 modules which prevents the peptide from simultaneously interacting with both modules, and, thus, resulting in the separation of the peptide from one of the modules under tension. More importantly, structural rearrangements of the individual modules under force result in changes in the accessibility of a large number of residues that might be involved in binding of various ligands. Such sites that are exposed only under force, and thus made available for binding, have been referred to as cryptic sites in other FN modules. Our results suggest the possibility of the existence of such cryptic site also in Fn1 modules.