Abstract
When properly determined, spontaneous mutation rates are a more accurate and biologically meaningful reflection of the underlying mutagenic mechanism than are mutation frequencies. Because bacteria grow exponentially and mutations arise stochastically, methods to estimate mutation rates depend on theoretical models that describe the distribution of mutant numbers among parallel cultures, as in the original Luria-Delbrück fluctuation analysis. An accurate determination of mutation rate depends on understanding the strengths and limitations of these methods, and how to design fluctuation assays to optimize a given method. In this paper we describe a number of methods to estimate mutation rates, give brief accounts of their derivations, and discuss how they behave under various experimental conditions.
The purpose of this article is to provide experimental and mathematical methods for determining spontaneous mutation rates in bacterial cultures. Mutations are heritable changes in an organism's DNA (or RNA for RNA-based organisms). Spontaneous mutations are mutations that occur in the absence of an exogenous DNA damaging agent. These include DNA polymerase errors, mutations induced by endogenous agents, as well as deletions, duplications, and insertions. It is generally assumed that most spontaneous mutations that occur during growth are linked to DNA replication. Although we have not included mutations induced by DNA damaging agents in this article, the methods discussed also can be applied to mutations induced by DNA base analogues or by low, nonlethal doses of other mutagens.
We assume that our readers are interested in the mechanism of mutation, in mutation rates among natural isolates of bacteria, and/or in the influence of genetic background or environment on the mutational process. The alternative to determining a mutation rate is to determine a mutant frequency, that is simply to average the fraction of mutant bacteria in a few replicate cultures. There are two reasons for making the effort to determine a mutation rate instead of a frequency.
First, when properly determined, the mutation rate is more accurate and reproducible than the mutant frequency. This is, indeed, the fundamental fact that was exploited in the famous Luria and Delbrück experiment (1). During exponential growth every cell has a low but nonzero probability of sustaining a mutation during its lifetime, and this probability is what we call the mutation rate. After a cell sustains a mutation it produces a clone of mutants, and the size of this clone will depend on when during the growth of the population the mutation occurred. Thus, even though the growth of the population may be deterministic, the final number of mutants in the population reflects an underlying stochastic process. Because of the exponential growth of mutants, low probability events occurring early during the growth of a population have huge consequences. This makes mutant frequency, no matter how many cultures are averaged, inherently inaccurate. Furthermore, even if there were no element of chance and mutations occurred on a strict schedule, the resulting distribution of the number of mutants would not be normally distributed, and the mean would not be the best measure of the underlying mutational process.
Second, the mutation rate gives more information about biological processes than does the mutant frequency. Departures from the results expected from theory can be evaluated and their causes experimentally determined. Some examples of such departures and their causes will be discussed in this article.
There are two general methods for determining mutation rates. The first, mutant accumulation, is potentially accurate but experimentally arduous. During exponential growth of a bacterial culture, after the population reaches a size so that the mean probability of a mutation occurring is unity, the proportion of the cells that are mutants increases linearly (assuming no difference in growth rate between mutant and nonmutant). If the number of mutants, r, and the total number of cells, N, are determined at various points during the growth of the culture, then the mutation rate, μ, is simply the slope of the line of r versus the number of generations, assuming synchronous growth. Alternatively, by Eq. 5–9 of reference (2):
| Eq. [1] |
However, to accurately determine mutation rate in this way requires a very large number of cells and a very long period between N1 and N2. While serial dilutions potentially could solve these problems, every dilution introduces a sampling error that may be large compared to the mutation rate. The alternative is to grow the cells in continuous culture, but this not only requires equipment and expertise unknown to most researchers, continuous cultures are plagued by problems of periodic selection (3).
Therefore, we confine ourselves here to the second method, fluctuation analysis. A fluctuation assay consists of determining the distribution of mutant numbers in parallel cultures; the mutation rate is obtained from analyzing that distribution. We present and discuss below a variety of methods to achieve this end. While they differ in their calculations, they are all ways to estimate one parameter — the probable number of mutations per culture that gave rise to the distribution of mutants observed. We call this important parameter m, and emphasize that it is the number of mutations, not the number of mutants, per culture. The methods to calculate m are traditionally called "estimators". m will, of course, depend not only on the mutation rate, but also on the amount of cell growth (which will depend on the nature of the medium and the volume of the culture), so this parameter is itself of no biological interest. However, m is, to date, the only mathematically tractable parameter. As the mutation rate is the probability that a cell will sustain a mutation during its lifetime, m can be converted to the mutation rate by dividing it by some function of the number of cells at risk.
All methods to estimate m depend on the theoretical distribution of mutant clones, first partially described by Luria and Delbrück (1), and called the Luria-Delbrück distribution in their honor. The first method to calculate the distribution was provided by Lea and Coulson (4), and their model is the basis of the methods discussed below. The assumptions about the mutation process underlying this model are: (i) the probability of mutation is constant per cell-lifetime; (ii) the probability of mutation per cell-lifetime does not vary during the growth of the culture; (iii) the proportion of mutants is always small; (iv) the initial number of cells is negligible compared to the final number of cells; (v) the growth rates of mutants and nonmutants are the same; (vi) reverse mutations are negligible; (vii) death is negligible; (viii) all mutants are detected; and, (ix) no mutants arise after selection is imposed. How departures from the Lea-Coulson model affect the mutant distribution has been addressed by various theoreticians over the years. In general, a proper experimental protocol will meet most of the model's requirements, but some departures arise from real biological circumstances. We discuss below some of these and how to cope with them.
We are not mathematicians, and our approach has been to try to find the useful and biologically relevant outcomes of the theoreticians' modeling. This effort has been aided by a few well-written articles that present both theory and implications in a way understandable to the nonmathematician. For those interested, we recommend references (5–13).
EXPERIMENTAL METHODS
We describe here a general experimental outline for fluctuation assays that experimenters can adapt to their own systems. We assume that mutants will be selected on solid medium, but the p0 method can be used in liquid medium as well.
A fluctuation assay begins with a number of parallel cultures, each inoculated with a small number of identical cells (containing no mutants) that are then allowed to grow. At the end of growth the number of mutants in each culture is determined by plating the entire culture on a selective medium. The total number of cells is determined by plating an appropriate dilution on nonselective medium. The mutation rate is determined from the distribution of the numbers of mutants.
The first step in designing a fluctuation assay is to do some preliminary experiments to establish the range of the numbers of mutants obtained when a given number of cells are plated. A provisional m can be estimated from the median of these experiments (see Method 3 below). With this knowledge, the next step is to choose a method based on the factors discussed in the next sections. To minimize experimental manipulation and calculations, the obvious choices are the p0 method for low mutation rates and the method of the median for intermediate mutation rates. Although the calculations are more difficult, the MSS maximum-likelihood method is superior to both of these for all mutation rates, and by far the best choice for high mutation rates. If radically different mutation rates among strains or conditions are to be compared, it is probably best to choose one method and adjust the experimental conditions accordingly.
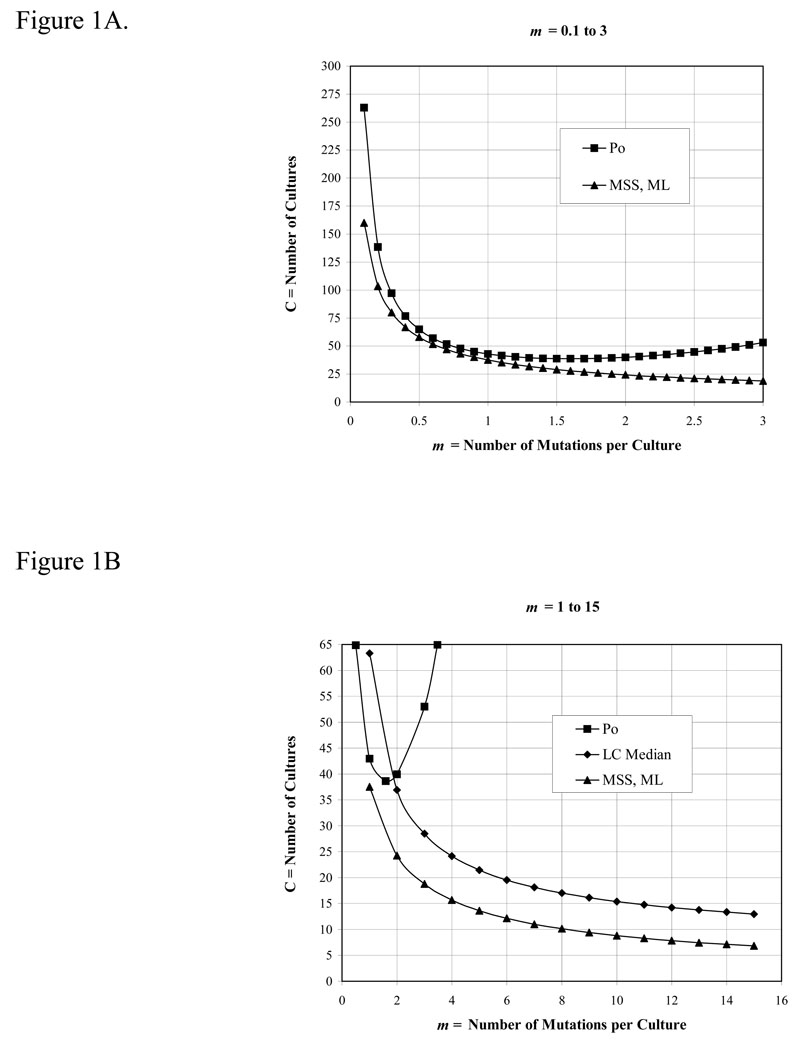
After deciding on a method, the first important parameter to consider is m, the expected number of mutations per culture. m should not be below 0.3 (unless a large number of cultures are used, see Figure 1A), and should be chosen to: (i) optimize the method being used, and, (ii) keep the number of mutants per plate within a countable range. For the p0 method, m should be between 0.3 and 2.3; for the method of the median, m should be between 1 and 15, although the performance of the median estimator is sub-optimal when m is below 4. Above m = 15, the MSS-maximum-likelihood method should be used. The desired m is achieved by adjusting the number of cells plated. We prefer to do this by limiting the carbon source during growth, but it is not recommended to use other growth factors, such as amino acids or vitamins, to limit growth (because the cell physiology may be distorted, and mutants that do not require the growth factor will be selected). The alternatives are to adjust the volume of the culture, or to plate aliquots of the cultures (although this introduces an error —see below). However, in all cases the initial number of cells, No, must be negligible compared to the final number of cells in the culture, Nt.
Figure 1.
The number of cultures required to achieve a theoretical precision of 20% using various estimators vs m, the number of mutations per culture. Precision is the coefficient of variation, (σm /m) × 100%, where σ was calculated from Eq. 35 and 41 of reference (4) for the p0 method and the Lea-Coulson method of the median, respectively, and from Eq. 1 of reference (12) for the MSS-maximum-likelihood method. These equations were solved for C, the number of cultures, by setting σm /m = 0.2
We let cultures grow to saturation before selecting for mutants. In some situations it may be desirable to use exponentially growing cells instead. However, it is extremely important that, when mutants are selected, Nt is the same in all the parallel cultures. Thus, before mutant selection, cell numbers should be monitored by optical density or counting (e.g. with a Petroff-Hausser chamber) and their numbers confirmed by plating dilutions on nonselective medium.
The second parameter to consider is the number of parallel cultures, C, to use. The precision of estimates of m is a function of both m and 1/√C, so more cultures is always better, but not always significantly so. Taking a precision level of 20% as acceptable for the estimate of m, the required number of cultures to achieve this level for the p0 (Method 1), median (Method 3), and MSS-maximum-likelihood (Method 8) methods are given in Figure 1. [For these calculation we used formulae for variances given in references (4) and (12); for another approach see reference (11)]. Note that precision is a measure of the reproducibility of an estimator, not a measure of its accuracy. Accuracy is how well an estimator estimates the actual m under the conditions of the experiment, and will be a function of the assumptions used in its derivation.
The third parameter to consider is the initial inoculum, No. The inoculum must not contain any preexisting mutants and must be negligible compared to Nt. At least for m ≤ 10, a 1/1000 ratio is sufficient (10) (although it is possible to adjust for the effect of larger inocula, the calculations are tedious). However, the smaller the inoculum, the longer it will take for the culture to grow, plus very small inocula often have poor viability. A good rule of thumb is that the inoculum should be about mNt/104 (this means the total number of cells inoculated, no matter what the volume of the culture into which they are inoculated).
It is common to inoculate each of the parallel cultures with a single colony of the strain being tested. However, this is not good practice because No will then vary among the cultures. In addition, a colony is equivalent to one tube in a fluctuation assay, so there is variation in the numbers of mutants among colonies. We recommend growing one culture, diluting it appropriately into fresh medium, and distributing this into the individual culture tubes.
After nonselective growth, it is best to plate the entirety of each culture on the selective medium so that all the mutants in each culture can be counted. Because of the nature of the Luria-Delbrück distribution, sampling introduces errors in the estimation of m. Sampling, or low plating efficiency, narrows the mutant number distribution, increasing the influence of small numbers and decreasing the influence of large numbers (8, 14). However, one often wants to assay for several mutant phenotypes, and these might have different mutation rates, making sampling required. Corrections can be applied if the p0 or the Jones methods are used (Methods 1 and 5) (see EVALUATION OF THE METHODS). Alternatively, one can divide the observed values by the fraction plated, and use these adjusted numbers to calculate m. Although this is not recommended, it is more accurate than using the observed values and then dividing the resulting m by the fraction plated.
If any mutations occur after plating on selective medium, the estimated m will be increased. This can be a problem with nonlethal selections involving, for example, reversion of an auxotrophy or mutation to utilize a carbon source. There are two possible sources of post-selection mutations: (i) the nonmutant cells can grow enough on the selective medium to produce mutations; and (ii) mutations occur in the absence of growth (adaptive mutations) (15). In the first case, the cells may grow because of contaminants in the medium or because they have a partial phenotype (i.e. their allele is "leaky"). This is detected as a lack of correlation between the number of cells plated and the number of mutants observed. One solution is to add to the plates an excess of scavenger cells that cannot mutate to the selected phenotype (e.g., because they are deleted for the relevant allele) (16). This will not prevent growth of "leaky" strains, however, in which case the only solution is to determine how long it takes a mutant to form a colony, and to count colonies at the earliest possible time after plating. The case of adaptive mutations will be addressed below.
CALCULATIONS
There are a number of different methods for estimating the mutation rate from the number of mutants per culture in a fluctuation assay. Although a closed, analytical solution of the Luria-Delbrück distribution does not yet exist (9), the observed distribution can be used to estimate the mean or the most likely number of mutations per culture, m. m is then used to calculate the mutation rate, μ. The methods to estimate m have improved with time, although with an increase in computational complexity. These methods are explained below with example calculations. The estimation of μ from m is discussed last. Comments about the uses and abuses of each method are presented briefly here and detailed in EVALUATION OF THE METHODS.
We have standardize the terms used in the equations below and our definitions are given in Table 1. The equations referred to below are given in Table 2. Many of these equations have been rearranged so that they are expressed in terms of r, the number of mutants observed, and m. Our m is other authors' μN. All the example calculations use the sample data given in Table 3 (although not all the methods are valid for this experiment). It is hoped that no one will be intimidated by the calculations, and that our examples will help people understand the details. The data in Table 3 are from a 52-culture fluctuation assay of strain FC40, a strain that can not utilize lactose but that reverts to lactose utilization (16). This is Exp. 2 in Table 4 and was also used in reference (13).
TABLE 1.
Definition of Terms
| Term | Definition |
|---|---|
| m | number of mutations per culture |
| μ | mutation rate = probability of mutation per cell per division or generation |
| r | observed number of mutants in a culture |
| r̄ | mean number of mutants in a culture |
| r̃ | median number of mutants in a culture |
| p0 | proportion of cultures without mutants |
| pr | proportion of cultures with r mutants |
| Pr | proportion of cultures with r or more mutants |
| C | number of cultures in experiment |
| N0 | initial number of cells in a culture = the inoculum |
| Nt | final number of cells in a culture |
| Q1 | value of r at 25% of the ranked series of r |
| Q2 | value of r at 50% of the ranked series of r = the median |
| Q3 | value at of r at 75% of the ranked series of r |
| S | sum in Eq. [11], Table 2 |
| a | 11.6 (in Lea–Coulson equations) |
| b | 4.5 (in Lea–Coulson equations) |
| c | 2.02 (in Lea–Coulson equations) |
| ln | natural logarithm (to the base e) |
| f | mutant fraction or frequency = r/N |
| z | dilution factor or sample of a culture plated |
TABLE 2.
Equations Used in the Calculation of m
| Method | Equation Number |
Equation | |
|---|---|---|---|
| 1. The p0 method | [2] | ||
| [3] | |||
| 2. The Luria-Delbrück method of the mean |
[4] | ||
| [5] | |||
| 3. The Lea-Coulson method of the median |
[6] |
|
|
| [7] |
|
||
| 4. The Drake formula | [8] |
|
|
| 5. The Jones median estimator |
[9] |
|
|
| 6. Koch's Quartiles method |
[10] | ||
| [11] |
|
||
| [12] | |||
| 7. The Lea-Coulson maximal likelihood method |
[13] |
|
|
| [14] | |||
| [15] | |||
| 8. The MSS-maximum likelihood method |
[16] |
|
|
| [17] |
where f(r|m)=pr from Eq. [16] |
TABLE 3.
Sample Data
| Number of Mutants Observed (r) |
Number of cultures with r mutants |
|---|---|
| 0 | 11 |
| 1 | 17 |
| 2 | 12 |
| 3 | 3 |
| 4 | 4 |
| 5 | 1 |
| 6 | 1 |
| 7 | 2 |
| 8 | 0 |
| 9 | 1 |
| Total | 52 |
TABLE 4.
Evaluation of the Methods with Experimental Data
| Description of the Experiments |
m = Number of Mutations per Culture |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp | Mutant | Cultures | Jackpots | Zeros | Mean | Median | Method | 1 | 2 | 3 | 4 | 5 | 7 | 8 |
| phenotype | LD | LC | Drake | Jones | LC, | MSS, | ||||||||
| p0 | mean | median | median | median | ML | ML | ||||||||
| 1 | Lac+ | 60 | 2 | 49 | 24 | 0 | m | 0.20 | 4.38 | 0.29 | 1.00 | UD | UD | 0.20 |
| −95%CL | 0.10 | NA | 0.11 | |||||||||||
| +95%CL | 0.36 | NA | 0.31 | |||||||||||
| 2 | Lac+ | 52 | 0 | 11 | 1.9 | 1 | m | 1.55 | 0.57 | 0.89 | 1.77 | 0.84 | 0.87 | 1.11 |
| −95%CL | 1.06 | 0.89 | 0.77 | |||||||||||
| +95%CL | 2.20 | 1.32 | 1.49 | |||||||||||
| 3 | RifR | 20 | 2 | 1 | 12.6 | 5.5 | m | 3.00 | 3.06 | 2.54 | 4.00 | 2.32 | 2.9 | 2.9 |
| −95%CL | 1.40 | 1.70 | 1.90 | |||||||||||
| +95%CL | 6.67 | 4.94 | 4.10 | |||||||||||
| 4 | RifR | 16 | 1 | 0 | 100 | 37.5 | m | NA | 17.7 | 10.4 | 14.2 | 9.2 | 11.2 | 11.0 |
| −95%CL | 7.6 | 8.1 | ||||||||||||
| +95%CL | 17.0 | 14.2 | ||||||||||||
| 5 | Lac+ | 30 | 1 | 13 | 2 | 1 | m | 0.84 | 0.67 | 0.89 | 1.77 | 0.84 | 0.44 | 0.71 |
| −95%CL | 0.47 | 0.29 | 0.39 | |||||||||||
| +95%CL | 1.37 | 0.89 | 1.09 | |||||||||||
| 6 | Lac+ | 30 | 3 | 6 | 15.3 | 1.5 | m | 1.61 | 3.32 | 1.14 | 2.08 | 1.04 | 1.04 | 1.23 |
| −95%CL | 0.96 | 0.89 | 0.76 | |||||||||||
| +95%CL | 2.56 | 1.69 | 1.77 | |||||||||||
| 5&6 | Lac+ | 60 | 4 | 19 | 8.6 | 1 | m | 1.15 | 1.84 | 0.89 | 1.77 | 0.84 | 0.72 | 0.95 |
| −95%CL | 0.80 | 0.89 | 0.67 | |||||||||||
| +95%CL | 1.59 | 1.32 | 1.27 | |||||||||||
UD = undefined; NA = not applicable; CL = Confidence limits. Lac+ = the ability to utilize lactose; RilR = resistance to rifampicin.
Method 1: The p0 Method
This method was first given by Luria and Delbrück [Eq. 5 in reference (1)], and is by far the simplest to calculate. Because the number of mutations (not mutants) per culture is Poissonally distributed, p0, the proportion of cultures without mutants, is the zero-term of this Poisson distribution, as given by Eq. [2] in Table 2. The p0 method should only be used when p0 is between 0.1 and 0.7 (m is between 2.3 and 0.3). Rearrangement of the terms gives the easily solvable Eq. [3] in Table 2.
From the sample data in Table 3, 11 of the 52 cultures had no mutants; thus, the p0 for this experiment is 11/52 = 0.212. From Eq. [3] in Table 2, m = −ln(0.212) = 1.55.
Method 2: Luria-Delbrück's Method of the Mean
The method of the mean, Eq. [4] in Table 2, was first presented by Luria and Delbrück [Eq. 8 in reference (1)]. The skewed distribution of mutant numbers often results in an elevated mutation rate calculated by this method, and thus this method is not recommended. Eq. [4] can be rearranged to Eq. [5] in Table 2, and solved by iteration, changing the value of m until Eq. [5] approaches zero. This is easily be accomplished on a spreadsheet as shown in Fig. 2A.
Figure 2.
Examples of methods to solve transcendental equations by iteration using a spreadsheet.
The mean of the sample data in Table 3 is 1.923. This value and the number of cultures substituted into Eq. [5] in Table 2 gives m × ln(m × 52) − 1.923 = 0. Using the spreadsheet illustrated Fig. 2A, an initial entry of m = 0.5 gave a value of − 0.29. Entering m = 0.6 gave a value of 0.14. After establishing this range, values of m were entered in 0.01 increments until a minimum value of 0.008 was found when m = 0.57.
Method 3: Lea-Coulson's Method of the Median
To avoid the overestimation of the method of the mean, the method of the median was introduced by Lea and Coulson (4). They observed that for m from 4 to 15, the distribution of the function [r/m – ln(m)] has a skewed distribution about a median of 1.24, as given by Eq. [6] in Table 2 [Eq. 37 in reference (4)]. Eq. [6] can be rearranged to Eq. [7] in Table 2 and solved for m by iteration on a spreadsheet, as illustrated in Fig. 2B.
The median of the data in Table 3 is 1 (with 52 values, the median is the 26th value of r when the r's are ranked). With r̃ = 1, Eq. [7] in Table 2 was solved by iteration as illustrated in the example above. A value of − 0.002 was obtained when m = 0.89.
Method 4: The Drake Formula using the median
The Drake formula has proved useful for comparing data from different sources; however, it introduces a serious bias in the calculation of m. Drake's equation using the median (17) has been rearranged to give Eq. [8] in Table 2, which can be solved by iteration as discussed above. Using the sample data in Table 3, with r̃ =1, Eq. [8] gave −0.006 when m = 1.77.
Method 5: The Jones Median Estimator
The Jones median estimator [Eq. 6 in reference (11)] is a newcomer in the field. Within our limited experience we have found it reliable. It has the advantage that the equation to calculate m, Eq. [9] in Table 2, is explicit. Using the sample data in Table 3, r̃ =1, and Eq. [9] is m = {1 − ln(2)}/{ln(1) − ln [ln(2)]} or (1 − 0.693)/[0 − (− 0.367)] = 0.836
Method 6: The Quartiles method
Determination of m by quartiles was first presented by Armitage (18) and expanded by Koch (6). This method calculates m1, m2 and m3, the mean number of mutations to give the observed r’s at the 25th, 50th and 75th position of the distribution by Eq. [10– 12] in Table 2 [Eqs. 3–5 in reference (6)]. The equations are valid over the range 2 ≤ m ≤ 14. Observed r’s, are ranked, and the number of mutants at the 25%, 50% and 75% points are determined. If (C + 1) is not exactly divisible by 4, then the two adjacent values are averaged to give the value at the quartile. These values are inserted into Eq. [10–12] in Table 2 to give m1, m2 and m3. If all three m’s are similar, then m has been determined. However, if the 3 values of m do not agree, this may indicate departures from the assumptions underlying the theoretical Luria-Delbrück distribution.
The experiment in Table 3 had 52 cultures, giving 13th, 26th, and 39th cultures as the 3 quartiles. From Table 3, Q1, Q2, and Q3 are 1, 1, and 2, respectively. Inserting Q1 into Eq [10] gave m1 = 1.7335 + (0.4474 × 1) − [0.002755 × (1)2 ] = 2.18; inserting Q2 into Eq [11] gave m2 = 1.43; and, inserting Q3 into Eq. [12] gave m3 = 0.96. [Note that for this experiment, m1 and m2 are larger than m3. The strain used has a high rate of post-selection "adaptive" mutations (16); because the pre-selection mutation rate is low, post-selection mutations increase the values of r falling in the lower quartiles.]
Method 7: Lea-Coulson's Maximal Likelihood Method
Maximum likelihood methods calculate the most probable m that would give the observed distribution of r. The Lea-Coulson method given here is for large values of r [Eqs. 48–50 of reference (4)]. The calculations are broken into 3 sections. First, using an estimate of m (e.g. from the median), x is calculated using Eq. [13] in Table 2 for each observed value of r. Second, the same value of m is then to used to calculate d by Eq. [14] in Table 2. Third, the values of x and d are put into Eq. [15] in Table 2 and summed for each value of x (from each r). The sum of Eq. [15] is evaluated, and adjacent values of m are then used to repeat the calculations until Eq. [15] approaches zero. Again, we do this on a spreadsheet.
The method of the median (see above) gave an estimate of m = 0.89 for the sample data in Table 3. Inserting this m into Eq. [13], x's were calculated for each value of r observed (the values of a, b and c are listed in Table 1). For example, for r = 0, xr=0 = {11.6/[(0/0.89) – ln(0.89) + 4.5]} − 2.02 = 0.49; for r = 1, xr=1 = {11.6/[(1/0.89) − ln(0.89) + 4.5]} − 2.02= 0.0009, etc. to r = 9. From Eq. [14], m = 0.89 gave d = [1 – 4.5 + ln(0.89)]/11.6 = − 0.312. Putting this d and all the values of the xr 's into Eq. [15] gave 0.819. This process was repeated with different values of m until Eq. [15] gave − 0.015 at m = 0.866.
Method 8: The MSS-Maximum-Likelihood Method
The MSS algorithm, Eq. [16] in Table 2 [Eq. 4 in reference (10)], is a recursive equation that efficiently computes the Luria-Delbrück distribution based on the Lea-Coulson generating function. To obtain a maximum likelihood estimation of m, Eq. [16] in Table 2 is used to calculate the probability, pr, of observing each of the experimental values of r for a given m. The likelihood function, Eq. [17] in Table 2, is the product of these pr's, [Eq. 7 in reference (13)]. As before, the first m evaluated is usually m estimated by the method of the median, then adjacent m's are used to recalculate the pr's until an m is identified that maximizes Eq. [17].
To obtain the pr's we use a spreadsheet that calculates all the pr's for r= 0 to 150 for a given m. As long as m ≤ 15, values of r greater than 150 contribute such a small proportion to the distribution that they can be lumped into the r = 150 value (13). Using this method, the r's that are not observed enter into the recursive calculation, i.e., a pr value must be calculated for each r in the series of possible observations of r, even if no actual values of a give r were observed. With a given m, p0 is calculated as in Eq. [3] in Table 2. Then, from Eq. [16], p1 = m/1 × (p0/2); p2 = m/2 × (p1/2 + p0/3); etc.
Using the sample data in Table 3 and starting with m = 0.89 as before, p0 = e(−0.89) = 0.411; p1 = 0.89/1 × (0.411/2) = 0.183; p2 = 0.89/2 × (0.183/2 + 0.89/3) = 0.102; etc, to p9. Eq [17] was evaluated as (p0)11 × (p1)17 × (P2)12 × (p3)3 × (p4)4 × (p5)1 × (p6)1 × (p7)2 × (p8)0 × (p9)1 = 4.29 × 10−47. [Note that p8 did not have to appear in this equation, but entering every pr facilitates the design of the spreadsheet.] This value and m = 0.89 were entered into a linear plot of m vs the value of Eq. [17]. Adjacent values of m's were used to recalculated the pr''s, which were entered into Eq. [17], and each value of m and Eq. [17] were entered into the plot. The value of the likelihood function vs m gives a smooth curve from which the maximum value is easily determined. For the sample data in Table 3, the maximum of the likelihood function was 11.8 × 10−47 when m = 1.11. [There are better ways to maximize the likelihood function than the one we have devised, but we present it here to show that it can be done with a spreadsheet on a personal computer.]
CALCULATING THE MUTATION RATE
The mutation rate is the probability of a cell sustaining a mutation during its lifetime, and is calculated by dividing m, the mean or most likely number of mutations per culture, by some measure of the number of cell-lifetimes at risk during the growth of the culture. There are three methods in common use, reflecting different assumptions about the mutational process. Luria and Delbrück (1) assumed that the probability of mutation is distributed evenly over a cell's division cycle. Because Nt bacteria will have arisen from Nt-1 divisions, they calculated the mutation rate per cell per generation as m/(Nt-1) ≈ m/Nt. This rate was also used by Lea and Coulson (4), and has been retained by most theoreticians.
However, bacterial growth is not synchronized and at any given time cells will be at various points in their division cycles. According to Armitage (18), because the mean generation time of an asynchronized population is ln(2)/(the growth rate), the number of generations that a population has undergone is Nt/ln(2). Thus, the mutation rate per cell per generation should be m × [ln(2)/Nt]. = m/(1.44 × Nt). Although the ln(2) correction depends on the assumption that the probability of mutation is evenly distributed over the division cycle, it was declared de rigor by Hayes (19) and has passed into common usage.
But, Armitage (18) went on to consider that mutations might occur only at the beginning or only at the end of the division cycle. In the first case the number of "at risk" points is the same as the total number of cells that ever existed in the culture, which is 2Nt. (This is because Nt cells had Nt/2 parents and Nt/4 grandparents, etc., and the sum of this series is 2Nt). This gives the mutation rate as m/2Nt (which is also called the mutation rate per cell per generation). In the second case, the number of "at risk points" is equal to the number of divisions that occurred, which is Nt, giving the mutation rate as m/Nt, the original Luria-Delbrück mutation rate, called the mutation rate per cell per division.
For the same m, the mutation rates calculated by these three methods will differ by 1:0.69:0.5. These differences are not trivial, but they are constant. So, the best procedure is to choose the method that you think best describes reality, and stick to it. And, most importantly, report what method you have used. Then your mutation rates can always be compared with mutation rates calculated by a different method. Note that, however calculated, the accuracy of a mutation rate is dependent on the accuracy of the estimate of Nt; thus, Nt should be determined to as high a level of accuracy as possible.
EVALUATION OF THE METHODS
Method 1
The p0 method, Eqs. [2] & [3] in Table 2. The p0 method is simple and reliable when properly used. Obviously, the absolute limits of its range are 1 > p0 > 0, but the precision of m estimated from p0 varies over this range (see Fig. 1). As no estimator of m is much good if m < 0.3 (unless a very large number of cultures are used), the useful range of the method is when p0 is between 0.7 and 0.1 (0.3 ≤ m ≤ 2.3). Like all the estimators, the precision of m estimated from p0 is a function of √C and therefore increases as C increases. But, compared to the median and maximum likelihood estimators, the p0 estimator becomes inefficient (i.e. requires more cultures for the same precision) when p0 < 0.3 (m ≥ 1.2) (20) (see Fig. 1A).
Because the p0 estimator does not depend on any experimental values other than zero, it is insensitive to certain deviations from the Lea-Coulson assumptions. For example, it is not affected if mutants grow more slowly than nonmutants as long as at least one member of every mutant clone produces a colony after selection. But, the p0 estimator is extremely sensitive to factors that increase p0, namely phenotypic lag, decreased plating efficiency, sampling, and post-plating mutations.
Phenotypic lag occurs when a mutant phenotype is not expressed until generations after the mutation occurs. As a result, mutations that occur in the last few generations of growth will produce no mutant cells, and the p0 will be inflated. Whether phenotypic lag is important in a given experiment can be evaluated with other estimators, as will be discussed below.
If mutants have a plating efficiency less that 100%, if only a portion of the culture is plated, or if mutants have a non-negligible death rate, then a fraction of every mutant clone will be lost. The p0 estimator is affected rather more than are other estimators because small clones will have a greater probability of being completely lost. If the fraction of mutants detected, z, is known (e.g. when z = the dilution factor or fraction plated), then the actual m can be estimated from the observed m by Eq. 41 in reference (8):
| Eq. [18] |
Because of the simplicity and reliability of the p0 method, researchers may wish to design their fluctuation assays so that 10 to 70% of the cultures have no mutants. As discussed above, this is best accomplished by limiting the growth of the cells or the volume of the culture. However, if required, the p0 can be adjusted by plating only a sample of each culture and using Eq. [18] to calculate that actual m. The Nt used to obtain μ would then be the Nt of the undiluted culture.
Method 2
The Method of the Mean, Eqs. [4] & [5] in Table 2. Mean estimators are based on the fact that when a population reaches a size large enough so that the probable number of mutations is unity, each generation will thereafter contribute μNt mutants to the final number (1). The required population size is 1/μ, and we will call the time after 1/μ is reached the "Luria-Delbrück period". The final mean number of mutants accumulated during the Luria-Delbrück period is r̄ = μNt log2(μNt), or r̄ = μ ln(μNt) if a continuous function is assumed (17). Taking μNt = m, this simplifies to r̄ = m ln(m). Luria and Delbrück (1) preferred to use the period after the population size of the whole experiment (i.e. all the cells in all the cultures) reaches the 1/μ point, and so their equation is r̄ = m ln(mC) (Eq. [4] in Table 2). Using Lea and Coulson's result that the median satisfies the relationship r̃ = m ln(m)+1.24, Armitage (18) corrected the Luria-Delbrück formula to r̄ = m ln(mC)+1.24, although the improvement is marginal (5).
Obviously, mean estimators cannot be used when Nt ≤ 1/μ (i.e. when m ≤ 1). In addition, these estimators require that mutations occur only during the Luria-Delbrück period, i.e. there are no jackpots. This is a false assumption in most experimental situations, particularly if the Luria-Delbrück period is only a small proportion of the total number of generations of the population. Thus, all mean estimators are subject to distortion by jackpots and will frequently overestimate mutation rates. The arbitrary use of the median instead of the mean improves their reproducibility (2), but not necessarily their accuracy. Note, however, that if a population could be purged of mutants at the start of the Luria-Delbrück period [e.g. with penicillin selection, or by techniques given in reference (21)], then these estimators would be more reliable.
Method 3
The Lea-Coulson Method of the Median, Eqs. [6] & Eq. [7] in Table 2. Lea and Coulson (4) found that, for r≫ 1, Pr, the probability that a culture has r or more mutants, is approximated by:
| Eq. [19] |
where F is some unknown function [Eq. 25 in reference (4)]. This is why we have rearranged equations into this format in Table 2. With values of m from 4 to 15, Lea and Coulson (4) showed that a plot of Pr vs [r/m − ln(m)] gives a smooth curve with a median [i.e. where Pr = 50%] = 1.24. Thus, their estimator is a good approximation for m over this range. And, indeed, Lea and Coulson's median estimator has been shown to be remarkably accurate in comparative tests using computer simulations (12, 13), which is borne out by experimental data (see Table 4). Although the method should not be pushed much beyond the limits for which it was devised, namely 4 ≤ m ≤ 15, (i.e. 10 ≤ r̃ ≤ 60), within these limits it is the method of choice baring maximum-likelihood methods. It is sensitive to deviations from the Lea-Coulson assumptions, although in a well designed experiment the r̃ should be large enough to be relatively unaffected by phenotypic lag. It's other major drawback is that little of the information from the fluctuation assay is used.
Method 4
Drake's formula, Eq. [8] in Table 2. Drake's formula (17) is an easy way to calculate mutation rates from frequencies, namely μ = f/ln(Ntμ), where f is the final mutant frequency. The derivation of this equation is the same as discussed above for the mean, i.e. mutations are assumed to occur only during the Luria-Delbrück period. Thus, taking f = r̄/Nt, and Ntμ = m, gives mln(m) = r̄, as above. However, to minimize the impact of jackpots, Drake uses the median f instead of the mean f, and thus the formula becomes Eq. [8] in Table 2. In this format it can be compared to the Lea-Coulson formula, making it obvious that Drake's method will often yield higher mutation rates. If m < 4, Drake's formula gives significantly higher estimates of m than the Lea-Coulson median or the maximum likelihood methods. Above m = 4, the m's from Drake's formula asymptotically approach those obtained with these other methods. For example, over the range r̃ = 10 to 60 (m = 4 to 15), Drake's formula yields m's 1.5 to 1.3 times that of the Lea-Coulson method of the median.
Method 5
The Jones Median Estimator, Eq. [9] in Table 2. As mentioned above, the Jones estimator is rather new. It has an interesting derivation. Jones et al. (11) calculated the hypothetical dilution that would be necessary to convert an observed distribution with a median of r̃ into a distribution with a median of 0.5, (i.e., a p0 of 0.5). Then, they used Eq. [18] above to calculate the mact from the observed r̃ and the hypothetical dilution factor, giving Eq. [9] in Table 2. For interested readers, we have attempted to put Eq. [9] into the format of Eq. [19], obtaining:
| Eq. [20] |
The Jones estimator has two great advantages. First, the equation for m is explicit. Second, because of its derivation, it readily accommodates dilutions [Eq. 5 of reference (11)]:
| Eq. [21] |
where z = the dilution factor. (This equation is the same as Eq. [9] in Table 2 if z = 1). mact is then divided by the real Nt to obtain the mutation rate. In a subsequent paper, Crane et al. (14) proposed that better estimations of m can be obtained if fewer cultures are grown to larger volumes, and then dilutions of these plated for mutants with m calculated by Eq. [21]. Part of the gain in precision from this procedure is artificial, i.e. the variance of mutant numbers will always be lower if there are fewer mutants. However, the real advantage of the procedure is that, with larger numbers of generations, more of these will be in the Luria-Delbrück period, increasing the contribution of the deterministic accumulation of mutants to the final distribution of mutant numbers.
Method 6
Koch's Quartiles method, Eqs. [10–12] in Table 2. Although the mean of the Luria-Delbrück distribution is almost useless, the quartiles of the distribution are fairly well behaved. The median quartile appears in the methods discussed above, but more of the results of an experiment can be used if the lower and upper quartiles also contribute to the estimation of m. Koch provided a graphical method and explicit equations to estimate m's from the values of r at the three quartiles. Eqs. [10–12] in Table 2 are based on the regressions of m vs the theoretical values at the quartiles for 2 ≤ m ≤ 14, whereas the graphs extend to m = 120(6). These are very useful because certain deviations from the Lea-Coulson assumptions will result in a lack of correspondence among the three m's, as discussed below.
Method 7
Lea-Coulson's maximal likelihood method, Eq. [13–15] in Table 2. Maximum likelihood methods use all the data from an experiment to estimate the m most likely to have produced the observed distribution. Thus, they are the gold-standard for estimating m. We have given Lea-Coulson's method for large values of r because it is somewhat computationally simpler than the MSS method (Method 8) (whereas Lea-Coulson's method for small values of r is more difficult than Method 8). Lea-Coulson's method depends on x, Eq. [13] in Table 2, being a normal deviate (i.e. having a mean of 0 and a standard deviation of 1), which is a reasonable assumption for 4 ≤ m ≤ 15 (4). [Note, Lea-Coulson's maximal likelihood method is not the same as the "Lea-Coulson estimator", which we have not included because it is seldom used today.]
Method 8
The MSS-maximum likelihood method, Eq. [16–17] in Table 2. As mentioned above, the MSS algorithm, Eq. [16] in Table 2, is a computationally efficient method to generate the Luria-Delbrück distribution from a given m (10). The MSS-maximum-likelihood method to estimate m consists essentially of working the algorithm backwards, i.e. using estimated m's to generate a provisional distribution, comparing that to the experimental values using the likelihood function, Eq. [17] in Table 2, and repeating until the best m is found. In addition to the advantage of using all the data, the m determined from the MSS-maximum likelihood method can be evaluated with more powerful statistics than m's obtained from other methods (see below). However, the MSS algorithm depends on the Lea-Coulson model, and is thus sensitive to deviations from the assumptions of this model.
The Behavior of the Estimators with Real Data
Most of our information about the behavior of the estimators is based on simulated data, e.g. see references (12, 13). However, readers may be interested in how these estimators behave with real data. Six fluctuations assays covering a range of mutation rates are given in Table 4 with the m's estimated by several of the methods discussed above. 95% confidence levels for some of these were obtained with the statistical methods discussed below. Jackpots are values that were clear outliers, but were not identified by any rigorous test. Exp.1 in Table 4 is an example of poor design combined with bad luck — too many cultures had no mutants and there were two jackpots, one with 30 and one with > 1000 mutants. The rest of the experiments are valid, although another large jackpot with ~ 1000 mutants occurred in Exp. 4. Exps. 5 and 6 were done with the same strain and the same Nt, and are included to show how reproducible fluctuation assays usually are. In the last entry they have been combined, as discussed below (see STATISTICAL EVALUATION OF MUTATION RATES)
COPING WITH DEPARTURES FROM THE LEA-COULSON ASSUMPTIONS
Interest in fluctuation analysis has recently been revived by the controversy surrounding the phenomenon known as "directed" or "adaptive" mutation (7). Part, but not all, of the evidence for post-selection mutation is that in a fluctuation assay the distribution of the numbers of mutants deviates from the Luria-Delbrück toward the Poisson. This has inspired new models describing the distribution of mutant numbers when one or another of the Lea-Coulson assumptions are not met (7, 8). We discuss a few of the more biologically relevant deviations here.
Phenotypic lag has the affect of shifting the time axis to a previous generation (corresponding to the duration of the lag) while increasing the variance of the final distribution of mutant numbers (6, 18). This affects the lower end of the distribution to a greater extent than the upper end, which can be detected with the quartiles method (Method 6) as lower values of m1, or m1 and m2, than m3. If phenotypic lag is suspected, Koch suggests estimating the duration of the lag in generations, n, and then calculating the three m's using the values of r obtained when the quartiles are set 2n-fold lower than actually observed. Different n's are tried until the three m's obtained are similar. The true m is the estimated m times (2n − 1).
Although it is usually a good assumption that mutants are not at a disadvantage during nonselective growth, this is not always true, especially in the case of certain antibiotic resistances. In particular, streptomycin-resistant mutants are usually enfeebled. If mutants grow more slowly than nonmutants during nonselected growth, the effect is the opposite from that of phenotypic lag — the upper end of the distribution is affected to a greater extent than the lower end, and the variance of the distribution is decreased (8). If selection against mutants is suspected, experimental results can be fit to the graphs of the values at the quartiles vs m that are given for a few relative growth rates in reference (6).
There are no other simple approaches to the problem of estimating m when there are deviations from the Luria-Delbrück distribution, and the next step is curve-fitting. The classical way of presenting the results of a fluctuation assay is to plot log(Pr) vs log(r), where Pr = the proportion of cultures that contain r or more mutants. As discussed above, during the Luria-Delbrück period mutants accumulate at a constant rate, giving Eq. 2 of reference (22):
| Eq. [22] |
With a perfect Luria-Delbrück distribution, a plot of log(Pr) vs log(r) (leaving out r = 0) yields a straight line with a slope of − 1. [The intercept of this curve at log(r) = 0 is log(2m); thus, this plot is a way of estimating m graphically.] Deviations from the Luria-Delbrück distribution can be detected as distortions of this curve. For example, post-selection mutations have a Poisson distribution, and so if mutations occur both during nonselective growth and after selection, the plot of log(Pr) vs log(r) will be a combination of the Luria-Delbrück and Poisson curves (7). Likewise, other factors, such as selection against mutants and low plating efficiency, will yield nonstandard distributions (8). The methods for modeling these distributions are beyond this article, but can be found in the references [but note that the MSS algorithm has supplanted older methods for generating the Luria-Delbrück distribution]. Fitting experimental data to the curves generated by these models provides a first test of whether observed deviations from the Luria-Delbrück distribution were caused by the factors modeled. Unfortunately, many of the modeled situations yield rather similar curves, so further experiments would have to be done to confirm that a given factor is distorting the distribution.
STATISTICAL EVALUATION OF MUTATION RATES
To compare mutation rates among different bacterial stains or conditions, one needs some idea of what confidence should be placed in the experimental determination of a mutation rate. Unfortunately, this is more difficult than it seems because normal statistics (that is, statistics based on a "normal" distribution) are not appropriate. It is obvious that the numbers of mutants per culture are not distributed normally. Less obvious is that estimates of m or of μ, whether determined from one or many experiments, also are not distributed normally. In addition, most of the estimators of m are biased; that is, no matter how many individual estimates of m are made, the mean of these will not approach the actual value of m under the given conditions (12). Therefore, it is statistically invalid to average such estimates or to use normal statistics to determine confidence limits for m or μ.
Statistical methods depend on knowledge of the variance and the shape of a distribution. The variance of a distribution is a measure of its dispersion, and can be calculated from any set of experimental values as Σ(yi−ȳ)2/n, where ȳ is the mean, yi is each value, and n is the number of values. The standard deviation (σ) is simply the square root of the variance. However, the variance does not reveal anything about the shape of the distribution. It may very well be outrageously skewed, and, indeed, the Luria-Delbrück distribution is, leaving us without a way to determine how the values are grouped. What is needed is the range in which some percentage (usually 95%) of the experimental values will fall, and a method to use this to establish confidence limits (CLs) for m. Below are described two general approaches, with examples, to approximating CLs for m.
If the distribution of the parameter used to calculate m can be defined, then this can be used to establish CLs for that parameter. [Note that it is the parameter, not m, that is assumed to have a defined distribution.] p0 can be considered a binomial parameter (4). If the number of cultures, C, is at least 10, 95% CLs for p0 can be calculated from the binomial distribution using standard statistical methods (23). Two new m's calculated from the 95% CLs for p0 are estimates of the 95% CLs for m determined by the po method (Method 1). When using the median to estimate m (Method 3), CLs for r̃ can also be obtained using standard methods if the number of cultures is 6 or greater (23). The 95% Cls for r̃ are then used to calculate two new m's, which are estimates of the 95% CLs for m (24). Because there is no defined distribution that describes the distribution of the mean, this method is not applicable when m is determined from r̄.
The second approach to setting CLs for m is to find a transforming function for m that gives an approximately normal distribution. The first of these was discovered by Lea and Coulson, (4), namely that x, as defined by Eq. [13] in Table 2, is approximately normally distributed about a mean of 0 with an σ = 1 for values of m from 4 to 15. For a normal distribution, 95% of the values lie within ±1.96σ of the mean. Thus, Eq. [13] could be used to calculate m at x = ±1.96, using the experimental values of r at these x's. However, in our experience this range exceeds the entire range of experimental values. A more useful transformation was given by Stewart (12) who observed that for estimates of m determined by the MSS-maximum likelihood method (Methods 9), the ln(m)'s are approximately normally distributed about their mean with a σ given by Eq. 1 in reference (12):
| Eq. [23] |
Thus, the 95% CLs for ln(m) can be estimated as ln(m) ± 1.96σ. However, the σ, m, and ln(m) to be used here are not the ones estimated from an experiment, but the unknown actual σ, m, and ln(m) of the population. Stewart (12) gives both transcendental equations and a graphical method to estimate the CLs. However, we have found that the CLs are closely approximated by using the estimated σ, m, and ln(m) in the following two equations
| Eq. [24] |
| Eq. [25] |
where σ is given by Eq. [23]. These approximations are based on the fact that the real and the estimated CLs differ by factors approximately equal to (e1.96σ)±0.315. 95% CLs for ln(m) can also be calculated using the t distribution as ln(m) ± to, where σ is the estimated σ, and the critical value of t is obtained at α(2) = 0.05 and (C-1) degrees of freedom. This is a conservative approach, as the CLs will be somewhat larger than those given by Stewart (12) or by Eqs. [24–25].
The methods described above give confidence limits for m. The simplest method to obtain the confidence limits for μ, the mutation rate, is to divide the m's at the CLs by Nt (or 2Nt, or Nt/ln2). However, this procedure ignores the fact that estimates of Nt are themselves normally distributed with a variance ≈ Nt. Given the inherent problems in determining m, it is probably justifiable to ignore this source of variation at the moment as long as Nt is determined to a high level of accuracy.
If fluctuation assays were done with the same Nt's, they can be statistically compared using the approaches outlined above. For example, whether two p0's or two r̃'s are significantly different can be tested using χ2 or the Fisher exact test. A more powerful alternative is the Mann-Whitney test because it uses all the observed values of r (23). But, none of these nonparametric procedures are as powerful as tests based on normal statistics. Stewart's observation (8) implies that normal statistics can be used with the ln(m)'s determined by the MSS-maximum-likelihood method. Thus, whether two ln(m)'s are significantly different could be determined by a standard t-test:
| Eq. [26] |
If the results of two or more fluctuation assays are homogeneous, i.e., they give the same m's and similar shaped distributions, they simply can be combined and a new m with new CL's calculated from the combined data. This is what we have done in Table 4 for Exps. 5 & 6. If the MSS-maximum likelihood method is used, the ln(m)'s can be averaged and the mean m is the geometric mean of the individual m's, which is emean[ln(m)]. CLs for the mean ln(m) can be obtained from the t distribution, using the combined σ and degrees of freedom as given in Eq. [26]. A more powerful treatment based on Bayesian procedures has been developed by Asteris and Sarkar (13).
Often one wishes to compare the results of fluctuation assays that did not use the same Nt's, or to compare mutation rates themselves. Unfortunately, statistical methods to accomplish this have not been developed. If the variance of Nt is ignored, then the methods discussed above for statistical treatment of ln(m)'s determined by the MSS-maximum-likelihood method might be applied to ln(μ)'s if they were also determined by the MSS-maximum-likelihood method. However, whether this method is valid is beyond our statistical expertise.
CONCLUSIONS
Recently developed mathematical models and new methods of calculating the theoretical Luria-Delbrück distribution have improved the estimation of mutation rates from fluctuation assays. The MSS-maximum likelihood method is superior to other methods over all ranges of mutation rates, but the p0 method and Lea-Coulson method of the median are adequate at low and intermediate mutation rates, respectively. However, the accurate estimation of mutation rates depends on designing fluctuation assays to optimize the validity of the estimator used. In addition, departures from the assumptions that underlie the theoretical Luria-Delbrück distribution must be evaluated. Still needed are better methods to deal with such departures and more robust statistical methods to evaluate mutation rates.
ACKNOWLEDGMENTS
We thank G. Asteris, J. Cairns, J. Drake, S. Sarkar, and F. Stewart for contributing to our understanding of mutation rates. Work in our laboratory was supported by Grant MCB 97838315 from the National Science Foundation and Grant GM5408 from the National Institutes of Health.
REFERENCES
- 1.Luria SE, Delbrück M. Genetics. 1943;28:491–511. doi: 10.1093/genetics/28.6.491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Drake JW. The molecular basis of mutation. San Francisco, CA: Holden-Day, Inc.; 1970. pp. 1–273. [Google Scholar]
- 3.Novick A, Szilard L. Proc. Natl. Acad. Sci. USA. 1950;36:708–719. doi: 10.1073/pnas.36.12.708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lea DE, Coulson CA. J. Genetics. 1949;49:264–285. doi: 10.1007/BF02986080. [DOI] [PubMed] [Google Scholar]
- 5.Armitage P. J. Hygiene. 1953;51:162–184. doi: 10.1017/s0022172400015606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Koch AL. Mutat. Res. 1982;95:129–143. [Google Scholar]
- 7.Cairns J, Overbaugh J, Miller S. Nature (London) 1988;335:142–145. doi: 10.1038/335142a0. [DOI] [PubMed] [Google Scholar]
- 8.Stewart FM, Gordon DM, Levin BR. Genetics. 1990;124:175–185. doi: 10.1093/genetics/124.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sarkar S. Genetics. 1991;127:257–261. doi: 10.1093/genetics/127.2.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sarkar S, Ma WT, Sandri GH. Genetica. 1992;85:173–179. doi: 10.1007/BF00120324. [DOI] [PubMed] [Google Scholar]
- 11.Jones ME, Thomas SM, Rogers A. Genetics. 1994;136:1209–1216. doi: 10.1093/genetics/136.3.1209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stewart FM. Genetics. 1994;137:1139–1146. doi: 10.1093/genetics/137.4.1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Asteris G, Sarkar S. Genetics. 1996;142:313–326. doi: 10.1093/genetics/142.1.313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Crane BJ, Thomas SM, Jones ME. Mutat. Res. 1996;354:171–182. doi: 10.1016/0027-5107(96)00009-7. [DOI] [PubMed] [Google Scholar]
- 15.Foster PL. Annu. Rev. Microbiol. 1993;47:467–504. doi: 10.1146/annurev.mi.47.100193.002343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cairns J, Foster PL. Genetics. 1991;128:695–701. doi: 10.1093/genetics/128.4.695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Drake JW. Proc. Natl. Acad. Sci. USA. 1991;88:7160–7164. doi: 10.1073/pnas.88.16.7160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Armitage P. J. R. Statist. Soc. B. 1952;14:1–40. [Google Scholar]
- 19.Hayes W. The Genetics of Bacteria and their Viruses. New York, NY: John Wiley & Sons Inc; 1968. pp. 1–925. [Google Scholar]
- 20.Koziol JA. Mutat. Res. 1991;249:275–280. doi: 10.1016/0027-5107(91)90154-g. [DOI] [PubMed] [Google Scholar]
- 21.Reddy M, Gowrishankar J. Genetics. 1997;147:991–1001. doi: 10.1093/genetics/147.3.991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Luria SE. Cold Spring Harbor Symp. Quant. Biol. 1951;16:463–470. doi: 10.1101/sqb.1951.016.01.033. [DOI] [PubMed] [Google Scholar]
- 23.Zar JH. New Jersey: Prentice Hall, Englewood Cliffs; 1984. Biostatistical Analysis; pp. 1–718. [Google Scholar]
- 24.Wierdl M, Greene CN, Datta A, Jinks-Robertson S, Petes TD. Genetics. 1996;143:713–721. doi: 10.1093/genetics/143.2.713. [DOI] [PMC free article] [PubMed] [Google Scholar]