Abstract
Spatial priors, such as probabilistic atlases, play an important role in MRI segmentation. However, the availability of comprehensive, reliable and suitable manual segmentations for atlas construction is limited. We therefore propose a method for joint segmentation of corresponding regions of interest in a collection of aligned images that does not require labeled training data. Instead, a latent atlas, initialized by at most a single manual segmentation, is inferred from the evolving segmentations of the ensemble. The algorithm is based on probabilistic principles but is solved using partial differential equations (PDEs) and energy minimization criteria. We evaluate the method on two datasets, segmenting subcortical and cortical structures in a multi-subject study and extracting brain tumors in a single-subject multi-modal longitudinal experiment. We compare the segmentation results to manual segmentations, when those exist, and to the results of a state-of-the-art atlas-based segmentation method. The quality of the results supports the latent atlas as a promising alternative when existing atlases are not compatible with the images to be segmented.
Keywords: Latent Atlas, Segmentation, MRI, Level-sets
1 Introduction
Volumes acquired via medical imaging modalities, such as MRI, are frequently subject to low signal-to-noise ratio, bias field and partial volume effects. These artifacts, together with the naturally low contrast between image intensities of some neighboring structures, make the automatic analysis of clinical images a challenging problem. Probabilistic atlases, typically generated from comprehensive sets of manually labeled examples, facilitate the analysis by providing statistical priors for tissue classification and structure segmentation (Ashburner and Friston, 2005; Fischl et al., 2002; Pohl et al., 2006, 2007a; Van Leemput et al., 1999). Yet, the limited availability of training examples that are compatible with the images to be segmented renders the atlas-based approaches impractical in many cases. While brain atlases of healthy human adult anatomy are widespread, reliable manual segmentations of newborn brains or of different body regions are not as common. Moreover, in the presence of pathologies where the diversity in structure and appearance is unpredictable, incorporating priors obtained from different subjects is error prone.
Recently, a few methods have been proposed to reduce or avoid the dependency on possibly incompatible atlases. Bazin and Pham (2007) proposed an atlas-based segmentation method that uses topological constraints to avoid possible bias introduced by the atlas. Yang and Duncan (2004) employed manually labeled structures to support automatic segmentation of neighboring structures within the same image. Tu et al. (2008) proposed a discriminative approach for segmentation of adjacent brain structures using a set of features learned from training examples. Lord et al. (2007) demonstrated a group-wise smoothing, segmentation and registration method for cross-sectional MR scans. They developed a level-set framework in which the evolving contours are spatially constrained by an image defined on a common domain, obtained from the ensemble via diffeomorphisms. Thus, the variability of the shapes in different images is captured by the deformation of the template. In contrast, our latent atlas explicitly models the variability of the shapes via a spatial distribution in the atlas space. Bhatia et al. (2007) adapted an initial atlas constructed from adult brain to newborns using combined groupwise segmentation and registration. In this framework, non-rigid groupwise registration is optimized by minimizing the Kullback-Leibler divergence between the average probability map of the group and the labeling probabilities of each image. Segmentation is improved iteratively based on the image intensity distributions. All of these methods with the exception of Bhatia et al. (2007) were demonstrated for healthy human brains of adults such that mild variations within the populations could be accommodated.
Segmentation becomes more challenging in the presence of pathologies where the appearance of the unhealthy tissues differs significantly from the norm and is patient-specific. Most of the existing methods for the detection of pathologies, rely heavily on priors such as shape, intensities, growth and expected evolution (Cuadra et al., 2004; Kaus et al., 2001; Jaume et al., 2001; Mohamed et al., 2006; Moon et al., 2002; Prastawa et al., 2003; Rey et al., 2002; Thirion and Calmon, 1999; Zacharaki et al., 2008). This prior information allows, for example, the generation of patient-specific atlases by iteratively refining the normal template model (Kaus et al., 2001; Moon et al., 2002; Prastawa et al., 2003). Alternatively, tumors and lesions were detected from differences between images acquired at different time points (Rey et al., 2002; Thirion and Calmon, 1999). A different approach uses a normal control training set or an atlas as a reference that allows detection of outliers suspected as pathological regions (Cobzas et al., 2007; Gering et al., 2002; Görlitz et al., 2007; Ho et al., 2002; Prastawa et al., 2004; Van Leemput et al., 2001; Wels et al., 2008). However, the variability of normal brain scans and the effects some tumors or lesions have on their surrounding healthy tissues lead to a high false positive detection rate. Moreover, mild anomalies can be wrongly classified as normal.
We propose and demonstrate a generative model for groupwise segmentation in which the evolving segmentation of the entire image set supports each of the individual segmentations. In contrast to the atlas-based approach that requires a set of training images or a probabilistic atlas for segmentation of a single image, we use at most a single manual segmentation to initialize segmentation of the entire image ensemble. This is made possible by iteratively inferring a subset of the model parameters, called the spatial parameters, as part of the joint segmentation processes. These spatial parameters are defined in the image domain and can be viewed as a latent atlas that is used as a spatial prior on the tissue labels.
Our latent atlas formulation is based on probabilistic principles, but we solve it using partial differential equations (PDEs) and energy minimization criteria. We describe a statistically driven level-set algorithm that expresses segmentation uncertainty via the logistic function of the associated level-set values, similar to Pohl et al. (2007b). We relate the image likelihood term to the region based constraint that relaxes the piecewise smoothness assumption of Mumford and Shah (1989), in the spirit of (Chan and Vese, 2001; Paragios and Deriche, 2002; Zhu and Yuille, 1996). We also draw a connection between a Markov Random Field (MRF) prior on the individual segmentations and two continuous-form energy terms: the commonly used smoothness constraint, originally proposed in Kass et al. (1988) and the spatial constraint, associated with the latent anatomy parameters.
We evaluate the latent atlas approach in two sets of experiments. In the first experiment we use a dataset of 39 MR brain volumes and their corresponding manual delineations. We segment six cortical and subcortical structures in the two hemispheres. We compare the segmentation results to the manual segmentations using the Dice measure of the volume overlap (Dice, 1945). We also evaluate these Dice scores by comparing them to the Dice scores obtained by the state-of-the-art atlas-based segmentation method in the Freesurfer software package (Freesurfer, 2009). The segmentation experiments on healthy brain images validate the algorithm, demonstrating segmentation accuracy that approaches the accuracy obtained with probabilistic atlases. In the second experiment we applied the algorithm to a longitudinal multi-modal patient-specific tumor dataset. The dataset consists of brain volumes acquired via six different modalities over several years. A sphere located around the tumor area in one of the volumes was used to initialize the segmentations of the images acquired at the first time point. Tumor segmentations at a given time point were then used to initialize the segmentations at the next time point for scans of corresponding modalities. In the absence of ground truth 3D segmentations we evaluate the segmentation results both visually and against the manual segmentation in a few tumor cross-sections. The accuracy of the results obtained for the tumor datasets further supports the latent atlas concept as a good alternative to atlas-based approaches when manual training labels or a probabilistic atlas are not available.
This paper extends the work previously presented in (Riklin Raviv et al., 2009b,a) by providing detailed derivations of the underlying mathematical model and thorough experimental validation and implementation details.
The remainder of the paper is organized as follows. Section 2 defines the problem of group-wise segmentation. In Section 3 we derive our level-set framework for fitting probabilistic model to image data. The alternating minimization algorithm is presented in Section 4. Section 5 provides implementation details and Section 6 reports the experimental results, followed by a discussion in Section 7.
2 Problem definition and probabilistic model
Our objective is to segment a particular structure or region of interest in N aligned MR images. Specifically, we consider the 2-partition problem where each voxel in image In (n = 1 … N) is assigned to either the foreground (structure of interest) or the background.
Let {I1 … IN} be the given set of aligned images that form the observed variable in our problem and let Γ = {Γ1 … ΓN} be the corresponding segmentations. In: Ω → ℝ+ is a gray level image with V voxels, defined on Ω ⊂ ℝ3, and Γn: Ω → {0, 1} is the unknown segmentation of the image In. We assume that each Γn is generated I.I.D. from a probability distribution p(Γ; θΓ) where θΓ: Ω → [0, 1] denotes the latent spatial model parameters. We also assume that Γn generates the observed image In, independently of all other image-segmentation pairs, with probability p(In|Γn; θI,n) where θI,n are the intensity parameters corresponding to image In. We assign an exclusive set of intensity parameters to each image since the acquisition conditions might vary across scans. Specifically, in the proposed framework θI are the parameters of the Gaussian Mixture Model (GMM) of the intensity distributions. The graphical model for our formulation is presented in Figure 1.
Fig. 1.
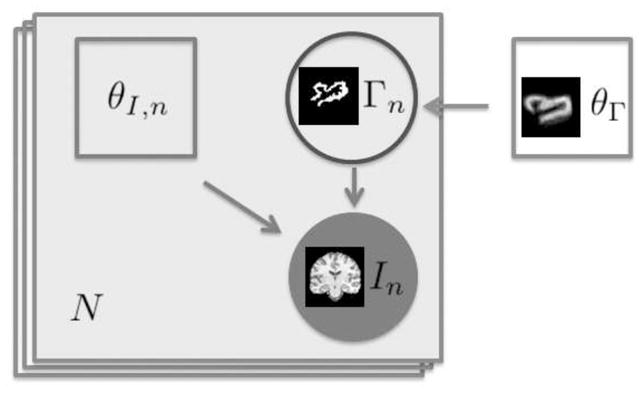
Graphical representation of the proposed generative segmentation model. The model parameters (θI,n, θΓ) are represented with squares, the random variables (Γn, In) are represented with circles. The shaded circle indicates the observed variable In. A subset of the variables (Γn, In and θI,n) is replicated N times, as indicated by the bounding box.
We start by presenting a probabilistic formulation of the problem. A comparison of the resulting expressions to the commonly used Expectation Maximization (EM) (Dempster et al., 1977) is unavoidable and is discussed in this section. However, here we replace the expectation step by a gradient descent process using a probabilistic level-set formulation. Our approach can be considered as an alternative way to model ‘soft’ assignments of the voxels in the segmentations.
The joint distribution p(I1 … IN, Γ1 … ΓN; Θ) is governed by the composite set of parameters Θ = {θΓ, θI,1 … θI,N}. Our goal is to estimate the segmentations Γ. This, however, cannot be accomplished in a straightforward manner since the model parameters are also unknown. A traditional way to approach this problem is to first construct a maximum likelihood (ML) estimate of the model parameters
| (1) |
and then compute the maximum a posteriori (MAP) estimates of the segmentations Γ:
| (2) |
The ML estimation of the model parameters requires marginalizing the joint probability distribution with respect to segmentations Γ1 … Γn:
| (3) |
One way to tackle the problem above is to use the EM algorithm which averages the log-likelihood over all possible segmentations. In this work, we propose to alternate between estimating the MAP segmentations and refining the model parameters. This could be viewed as replacing the sum in Equation (3) with the maximal contribution to the sum.
Formally, we jointly optimize for the segmentations Γ and the parameters Θ:
| (4) |
| (5) |
| (6) |
Equation (5) follows from the conditional independence of different images in the set. For a given value of the model parameters Θ̂, Equation (6) implies that the segmentations can be estimated by solving N separate MAP problems:
| (7) |
We then fix Γ̂ and estimate the model parameters Θ = {θΓ, θI,1, … θI,N} by solving the following ML problems:
| (8) |
| (9) |
Note that Equations (7), (8) can be solved for each image separately while Equation (9) uses all the segmentations to infer the atlas parameters. In the following sections we present a level-set framework that is motivated by this probabilistic model. We reformulate the estimation problem stated in Equation (7) such that the soft segmentations p(Γn), rather than the Γn, are estimated.
3 Probabilistic view of the level-set framework
Now we draw the connection between the probabilistic model presented above and the level-set framework for segmentation (Osher and Sethian, 1988). Let φn: Ω → ℝ denote a level-set function associated with image In. The zero level Cn = {x ∈ Ω|φn(x) = 0} defines the interface between the partitions of In. We choose to represent the binary segmentation Γn by the Heaviside function of φn:
| (10) |
The Heaviside function H(φn) partitions the image space Ω ∈ ℝ3 into two disjoint regions ω and Ω\ω by assigning positive levels of φn to the structure of interest and negative levels of φn to the background.
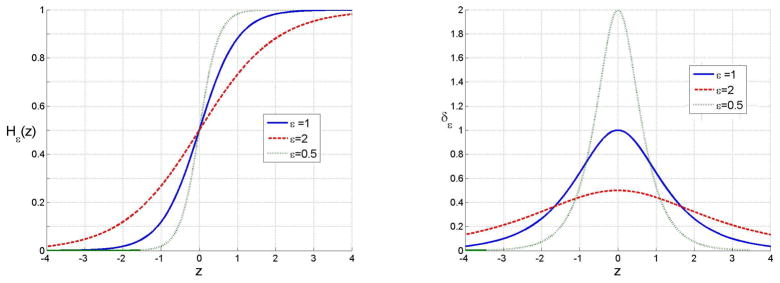
Since the Heaviside function as defined above is not differentiable, a regularized variant H̃ is used in practice. Chan and Vese (2001) propose to approximate the Heaviside function of φn by the sigmoid . Alternatively, we can use the hyperbolic tangent to achieve the same goal:
| (11) |
For ε = 1, the function H̃ε(·) becomes the logistic function. Similar to Pohl et al. (2007b), we define the level-set function φn using the log-odds formulation instead of the conventional signed distance function:
| (12) |
The scalar ε determines the scaling of the level-set function φn with respect to the ratio of the probabilities of the foreground and the background respectively. Substituting this definition into Equation (11) we obtain
| (13) |
which implies that the function H̃ε(φn(x)) can be viewed as the probability that a voxel at location x belongs to the foreground region. Specifically, the uncertainty in the labeling of the boundary voxels {x|φ (x) = 0} naturally stems from the equality H̃ε(φn(x)) = 1 − H̃ε(φn(x)) = 0.5. The functions H̃ε(φn(x)) and H(φn(x)) therefore represent soft and hard segmentations, respectively.
Figure 2 illustrates H̃ε and its derivative
Fig. 2.
(a) Smooth approximation of the Heaviside function H̃ε (Equation (11)) and (b) its derivative δ̃ε (Equation (14)) for different values of ε.
| (14) |
for several values of ε. To simplify the notation we omit the subscript ε in the rest of the paper.
3.1 Cost functional for segmentation
Joint estimation of the hidden variables Γn, or φn (using the level-set notation) and the unknown model parameters Θ (Equation (6)) can be solved as an energy minimization problem:
We now establish the correspondence between the log probability and the level-set energy terms.
3.2 Image likelihood term
Let us first consider the image likelihood term:
| (15) |
where pin and pout are the probability distributions of the foreground and background image intensities, respectively.
Let 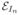 ≜ −β log p(In|Γn, θ̂I,n) define the energy term associated with the image likelihood term. Using the continuous level-set formulation, Equation (10) and the following approximations:
≜ −β log p(In|Γn, θ̂I,n) define the energy term associated with the image likelihood term. Using the continuous level-set formulation, Equation (10) and the following approximations:
we obtain
| (16) |
By replacing the binary labels H(φn) with soft assignments H̃ (φn), Equation (16) becomes a continuous approximation of the expectation of the image likelihood term in Equation (15).
When pin and pout represent normal density distributions, we get the familiar minimal variance term (Chan and Vese, 2001; Paragios and Deriche, 2002; Cremers et al., 2007). Here, we use a Gaussian mixture to model the background, as described later in the paper.
3.3 Spatial prior and length terms
In the atlas-based segmentation framework the spatial prior parameters θΓ are known and given in the form of a probabilistic anatomical atlas. In the problem at hand, such atlas does not exist. Instead, we estimate the spatial parameters by constructing a dynamically evolving probabilistic atlas. We define the prior probability p(Γn; θΓ) to be a MRF (Geman and Geman, 1984):
| (17) |
where Z(θΓ) is the partition function and 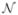 (v) are the closest neighbors of a voxel v.
(v) are the closest neighbors of a voxel v.
The corresponding energy functional 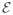 (Γn; θΓ) ≜ −α log p(Γn|θΓ) takes the form:
(Γn; θΓ) ≜ −α log p(Γn|θΓ) takes the form:
| (18) |
We first consider the pairwise interaction term in Equation (18). The function , is the penalty term for different assignments of neighboring voxels. The sum can be configured to act as a finite difference operator approximating the square of the gradient of Γn, i.e., . Specifically, if we let h be the grid resolution, then wv,v′ are set to either κ/h2 or 0, where κ is the relative weight of the pairwise term. Based on this connection, we approximate the pairwise clique potential term in Equation (18) with a continuous term
| (19) |
where γ = ακ. This smoothness term is related to the commonly used length regularizer in the level-set literature (Chan and Vese, 2001):
| (20) |
In practice, we used both terms, interchangeably, to constrain boundary smoothness, without any significant change in the overall quality of the results.
The mechanism of length-driven PDE evolutions on log odds representations of label probabilities was used in an atlas-based segmentation context by Pohl et al. (2007c). In that work, the derivation used a different strategy: a likelihood model was combined with a prior on segmentations that was in turn based on curve lengths; the resulting estimation problem was solved via the variational mean field method.
If we omit the pairwise term in Equation (18), the prior on segmentations p(Γn; θΓ) reduces to a Bernoulli distribution, where the parameters θΓ represent the probability map for the structure of interest. The introduction of the pairwise clique potentials complicates the model but encourages homogeneous labeling configurations.
We define the spatial energy term 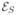 based on the singleton term in Equation (17). Using the continuous level-set formulation with soft segmentation, we obtain:
based on the singleton term in Equation (17). Using the continuous level-set formulation with soft segmentation, we obtain:
| (21) |
The spatial term in Equation (21) and the image likelihood term in Equation (16) have similar structures. The image likelihood term, the length term and the spatial prior term are derived directly from the generative probabilistic model. However, while the level-set formulations of the length and the likelihood terms are commonly used, the formulation of the spatial prior term, as defined in Equation (21) is novel.
Ignoring the partition function in the equations that follow Equation (18) has no effect on the estimation of Equation (7), but it changes Equation (9) to be maximum pseudo likelihood as in Besag (1975), rather than maximum likelihood.
3.4 Unified cost functional
We construct the cost functional for φ1 … φN and the parameters Θ by combing Equation (16), Equation (20) and Equation (21):
| (22) |
The weights are adaptively tuned such that the contributions of the energy terms ELEN, EI and ES to the overall cost are balanced. Subsection 5.3 describes the weight tuning heuristic we used in the experiments.
4 Gradient descent and parameter estimation
We optimize Equation (22) by a set of alternating steps. For fixed model parameters Θ, the evolution of each level-set function φn is determined by the following gradient descent equation:
| (23) |
where
is obtained from the first variation of 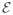 (φn, Θ). Using the Euler-Lagrange equations we get:
(φn, Θ). Using the Euler-Lagrange equations we get:
| (24) |
where δ(φn) is the derivative of H(φn) with respect to φn as defined in Equation (14). For fixed segmentations φn, the model parameters are recovered by differentiating the cost functional in Equation (22) with respect to each parameter.
4.1 Intensity parameters
We assume that the intensities of the structure of interest are drawn from a normal distribution, i.e., . Optimizing Equation (22) with respect to the distribution mean and variance of the foreground region of In, we obtain the following update rules:
| (25) |
The intensities of the background tissues are modeled as a K-Gaussian mixture:
where is the mixing proportion of the kth component in the mixture. When the images are brain scans and the ROIs are brain structures, K = 3 Gaussians are used to model the intensity distributions of the white and gray matters and the CSF. The Gaussian mixture model parameters are estimated using the EM method. In different applications, when there is less prior knowledge on the expected distribution, kernel density estimators over mixtures of Gaussians might be preferable (Cremers and Rousson, 2007).
4.2 Spatial parameters
We estimate the spatial function θΓ(x), constructing a dynamically evolving latent atlas, by optimizing the sum of the energy terms that depend on θΓ:
yielding,
| (26) |
5 Implementation details
5.1 Prior Registration of the Image Ensemble
Accurate alignment of the image ensemble is crucial to the success of the latent atlas method since the spatial constraint relies on voxel correspondences. In our experience, affine registration may not be sufficient to obtain the required correspondences. Instead we applied a non-rigid registration (Sabuncu et al., 2009b; Toussaint et al., 2007; Postelnicu et al., 2009). However, since the non-rigid registration procedure is applied to the entire images, sometimes small ROIs in some of the images are misaligned. To avoid those cases, we further aligned the ROIs using translation by integer pixel units. Since the images are cropped to accelerate the segmentation process, in practice, we used an exhaustive search to maximize the pairwise image intensity correlation between the cropped template image that includes the ROI (based on the known segmentation) and each of the other images in the ensemble.
5.2 Initialization and the stopping criterion
In the presence of at least a single manual segmentation of an image from the ensemble I1 … IN, we initialize the unknown segmentations φ1 … φN and the latent atlas as follows. We set φn,t=0 = φ0 (n = 1 … N), where φ0 is the signed distance function of the known segmentation. We also set θΓ,t=0 = θΓ0 where θΓ0 = H̃ (φ0 ★ Gσ) is the Heaviside function of φ0 smoothed with a Gaussian kernel of width σ (σ = .35 in our experiments). In cases where a manual segmentation is not available, the user provides an input that allows to initialize the level-set functions and the latent atlas. The user selects one of the volumes and identifies a single sagittal, axial or coronal slice where the region of interest is clearly seen. The user then marks (with a few mouse clicks) the approximate location of the ROI center and one of its boundary points. This input defines a sphere that is used to initialize the segmentations of all the volumes. In a longitudinal study, only the segmentations of the data acquired at the first time point are manually initialized. The segmentations of volumes acquired in consecutive time points are initialized from the final segmentations of the corresponding volumes acquired at the previous time points.
We run the segmentation algorithm for each image In until the changes in the segmentations are below a user-specified threshold:
Once this convergence criterion is met for a segmentation of an image In, the corresponding level-set function φn(t) is fixed, however φn(t) is used for the re-estimation of θΓ until the segmentations of the entire ensemble converges.
5.3 Parameter tuning
The optimal weights obtained in a leave-one-out analysis for a particular dataset may not be suitable for another dataset. We therefore do not optimize the weights prior to segmentation. Instead, in each iteration, we tune the weights such that the weighted magnitude of the contribution of each term in Equation (24) is normalized to one (Riklin-Raviv et al., 2008).
We set ε = 0.3 and Δt = 1. Both parameters should depend on the image size and resolution as well as the magnitude and shape of φ (we follow the classical definition of Osher and Sethian (1988) and represent φ by a signed distance function, such that |∇φ| = 1). The parameter ε determines the width of δε(φ) (Equation (14)). It controls the width of the band around the zero level of φ that is updated in every iteration (Equation (24). The parameter Δt, (Equation (23)) scales the contribution to the narrow band of φ. The product of δε and Δt, obtained by substituting Equation (24) into Equation (23) controls the evolution of the segmentation process. Therefore, tuning ε should be done with respect to Δt (or vice versa). Automatic estimation of these parameters and their influence on the convergence properties of the suggested algorithm are subject of future work.
5.4 Topological changes of the boundaries
The current framework does not control topological changes although it can be extended to include topology preservation (Han et al., 2003). In practice, the spatial constraint encourages preservation of the topology if the region of interest (ROI) is homogeneous and contiguous. In the brain tumor case, when the initial spatial constrain is weaker (sphere) one may expect topological changes to allow the segmentation of adjacent, yet not connected, regions with similar intensities.
5.5 Algorithm outline
Here we summarize the proposed latent atlas segmentation algorithm. The input consist of N aligned volumes {In}.
Initialize {φn} and θΓ (Section 5.2).
-
Repeat until convergence:
Calculate the background and foreground intensity parameters θI,n based on the current estimates of their corresponding level-set functions φn (Section 4.1).
Calculate the latent atlas parameters φΓ based on the current estimates of the level-set functions φn (Equation (26)).
Use Equation (24) (gradient descent) to evolve the level-set functions φn based on the current estimates of the respective intensity parameters θI,n and the spatial parameters θΓ.
5.6 Quantitative evaluation
We use the Dice measure (Dice, 1945) to quantify the overlap between the manual segmentations and the automatic segmentations. Let L̂: Ω → {0, 1} be a given manual labeling function (segmentation) and let L: Ω → {0, 1} be the corresponding automatic label map. The Dice score measures the volume overlap between the two segmentations:
where |·| is the size (cardinality) of the set, and ∩ denotes intersection of two sets.
5.7 Multi-label segmentation
The current framework considers binary segmentation in which the image is partitioned into a (semantically) single ROI and background. We ran the latent algorithm separately for each ROI with a single level-set function corresponding to each image. While partitioning images into multiple ROIs may not increase the computational efficiency, it allows handling of neighboring structures. The proposed method can be extended by using a region competition paradigm in which the contours between adjacent regions evolve to maximize the posterior probabilities (Zhu and Yuille, 1996; Tu and Zhu, 2002). A straightforward extension to multi-structure segmentation could be obtained by replacing the logit function for the binary case (Equation (12)) by the multi-label log-odds formulation as in Pohl et al. (2007b). In this implementation, multiple level-set functions compete for the ‘ownership’ of boundary voxels. The final partition is determined by the highest voxel assignment probabilities.
6 Experimental results
In this section, we present two sets of experiments. In the first experiment, we apply the proposed segmentation method to segment brain structures across a population. Our goal is to validate the method by comparing the automatic segmentations to expert delineations in a well studied problem. We also compared the resulting Dice scores to the Dice scores obtained by the state-of-the-art Freesurfer segmentation package (Freesurfer, 2009). In the second experiment, we demonstrate the algorithm by segmenting a brain tumor in application to a single-subject multi-modal longitudinal study. This application illustrates the benefits of our method in the case where no atlas is available to provide spatial priors for segmentation.
6.1 Brain structures segmentation
We test the proposed approach on 39 MR brain scans. Some of the subjects in this set were diagnosed with mild Alzheimer’s disease. The MR images (T1, 256 × 256 × 256 volume, 1mm3 isotropic voxel size) were acquired on a 1.5-T General Electric Scanner. All the pre-processing steps (gain-field correction and skull-stripping) were performed using the FreeSurfer tools (Freesurfer, 2009). In addition to the MR volumes, manual segmentations of hippocampus (HPC), thalamus (THL), caudate (CAD), putamen (PUT), pallidum (PAD), and amygdala (AMY) were available for these subjects. The images and the labels were aligned to a common template by applying the asymmetric image-template registration method (Sabuncu et al., 2009b). Based on the given manual segmentation of one of the images, the images were cropped such that for each image the entire region of interest resides within the cropped image. Due to significant misalignments of some of the small ROIs in some of the registered images, the initial registrations were adjusted by pixel-wise translation through the cropping procedure as described in Section 5.1.
We excluded the image associated with the given manual segmentation from the ensemble. In practice, we ran the latent atlas algorithm several times with 5 different randomly chosen manual initializations. The algorithm was implemented in Matlab. Execution time, and in particular the initial estimate of the background intensity distributions, depends on the size of the cropped images. Average CPU time for the segmentation of 38 corresponding structures ranged from approximately 10 mins (Amygdala, cropped image size: 38 × 40 × 38) to approximately 80 mins (Caudate, cropped image size: 42 × 36 × 100). Processing time includes the initial estimate of the GMM parameters and their update in consecutive iterations. Segmentation process converged in fewer than 10 iterations.
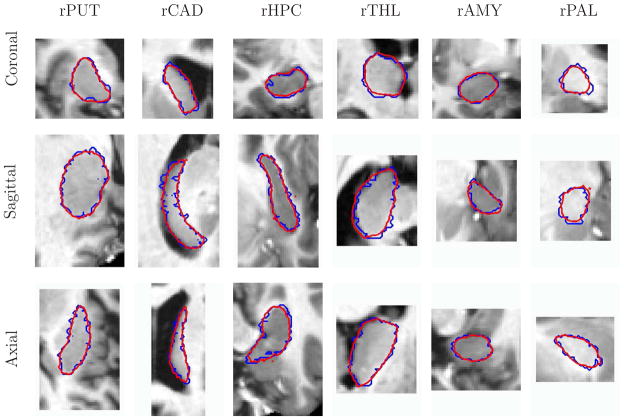
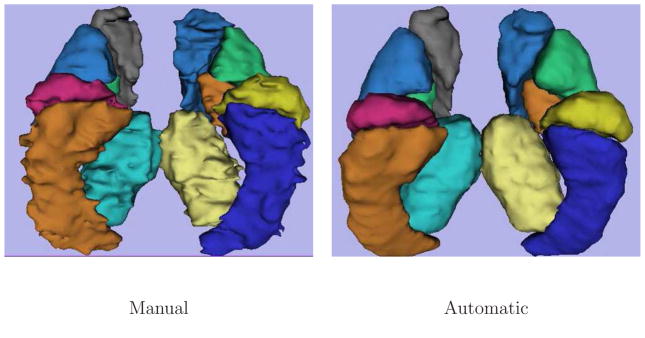
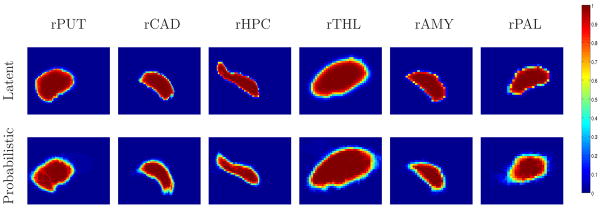
Figure 3 shows sagittal, axial and coronal cross-sections of the 3D segmentations of six structures in the right hemisphere in representative individual brains. We observe that the manual segmentations in Figure 3, and in particular the sagittal and axial slices, exhibit obvious jaggedness of the boundaries. This is due to the fact that the rater manually segments the structures slice-by-slice. Manual segmentation in one plane typically results in jagging boundaries in other planes (Yushkevich et al., 2006). In contrast, the automatic segmentation, estimated from the entire 3D structure is much smoother. Figure 4 presents 3D views of the automatic and the manual segmentations of the brain structures in one subject from the study. The structures are shown together for display purpose, yet each structure has been segmented independently. Cross-sections of the resulting 3D latent atlases and of the probabilistic atlases generated by averaging the manual expert segmentations are shown in Figure 5.
Fig. 3.
Three cross-sections of 3D segmentations of six brain structures in the right hemisphere. Automatic segmentation is shown in red. Manual segmentation is shown in blue.
Fig. 4.
3D views of the manual and the automatic brain structure segmentation in one subject.
Fig. 5.
Cross-sections of 3D atlases of six brain structures in the right hemispheres. Top row: Latent atlases generated as part of the proposed segmentation algorithm. Bottom row: probabilistic atlases. Each atlas is generated by averaging 39 corresponding manual labels of the input images.
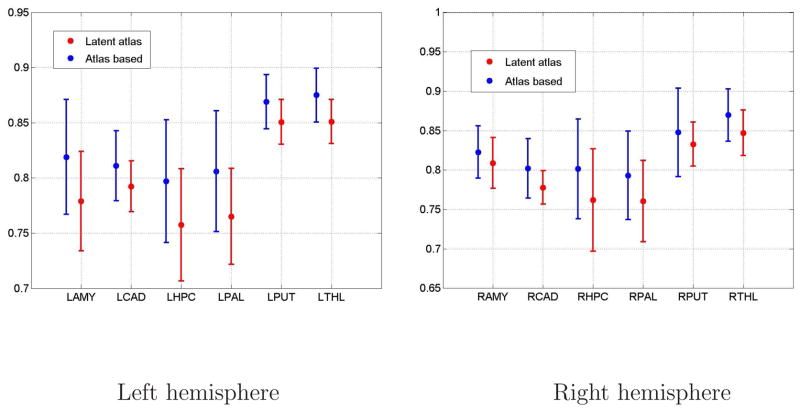
We used the Dice measure to quantitatively evaluate the segmentations as described in Section 5.6. We compared the Dice scores obtained by our Latent Atlas method (first row in Table 1) to the Dice scores obtained by the following baseline procedures:
Table 1.
A comparison of the Dice coefficients for 12 brain structures in the left and the right hemispheres averaged over the 39 volumes in the study. See text for detail.
| AMY | CAD | HPC | PAL | PUT | THL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | R | L | R | L | R | L | R | L | R | L | R | |
| Latent | .779 | .809 | .821 | .825 | .757 | .765 | .765 | .789 | .853 | .837 | .855 | .848 |
| FreeSurfer | .748 | .751 | .847 | .852 | .840 | .839 | .804 | .793 | .851 | .852 | .877 | .885 |
| Prob. | .818 | .828 | .837 | .833 | .801 | .801 | .806 | .803 | .864 | .852 | .875 | .872 |
| Single | .731 | .760 | .757 | .754 | .736 | .720 | .753 | .750 | .841 | .821 | .840 | .834 |
| Initial | .716 | .741 | .741 | .745 | .723 | .708 | .739 | .742 | .830 | .819 | .832 | .828 |
Initial (Last row in Table 1): The Dice scores calculated prior to segmentation. These initial Dice scores quantify the overlap between the initial segmentation (the known single segmentation of one of the subjects) and the true segmentation of the corresponding subject. These scores practically measure the quality of the alignments across scans. As expected, all of the noted segmentation methods obtain consistently better Dice scores than the initial Dice scores.
FreeSurfer (second row in Table 1): The Dice scores obtained by the Freesurfer tool for the same dataset (Sabuncu et al., 2009a). The Freesurfer is a widely used atlas-based segmentation approach and is considered state-of-the-art.
Prob. (third row in Table 1): The Dice scores obtained using an atlas-based approach implemented by using the described level-set framework where the dynamically estimated latent atlas is replaced by a fixed probabilistic atlas, in a leave-one-out manner.
Single (fourth row in Table 1): The Dice scores obtained by a level-set atlas-based approach similar to the one mentioned above, replacing the probabilistic atlas by a single known segmentation blurred by a Gaussian kernel. This single-label atlas remains fixed throughout the segmentation.
The Dice scores comparisons are summarized in Table 1 and in Figure 6. The Dice scores obtained by our method approach the atlas based segmentation results. Note also that the Dice scores obtained by our atlas-based implementation approach the Dice scores obtained by the FreeSurfer package. To exemplify the effectiveness of the latent atlas generated concurrently with the segmentation, we also show a comparison to the segmentation results obtained by using an atlas constructed from a single manual segmentation smoothed by a Gaussian kernel, without the update procedure. This method simulates the approach commonly used when only a single manual segmentation is available. The comparison supports the latent atlas approach as a preferred alternative when only a single segmentation is available.
Fig. 6.
The mean and standard deviation of the Dice scores calculated for all images in the ensemble for six brain structures in the left and the right hemisphere. The latent atlas segmentation (red) is compared to the atlas-based segmentation (blue).
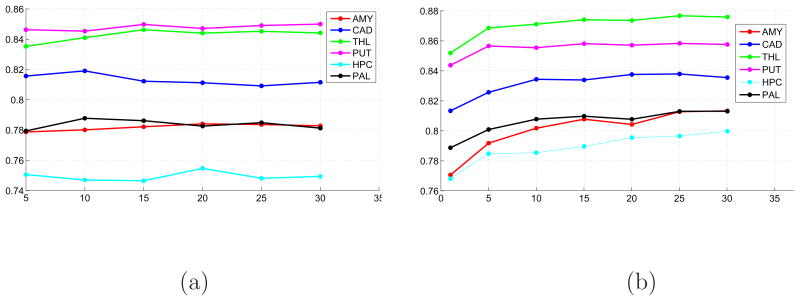
We conducted two additional experiments to test how the segmentation accuracy depends on the size of the image ensemble and on the number of manual segmentations used to initialize the latent atlas. We ran the latent atlas algorithm for 8 – 12 randomly chosen image subsets of 5, 10, 15, 20, 25 and 30 images for the six structures in both hemispheres. The results of both experiments are shown in Figure 7. While there is no clear dependency of the mean Dice scores on the ensemble size, the latent atlas scores approach the atlas-based results for a relatively small number of manual segmentations (5, 10) that are used for initialization.
Fig. 7.
(a) The mean Dice scores calculated for six brain structures in both hemispheres as a function of the number of images in the ensemble. (b) The mean Dice scores for six brain structures in both hemispheres as a function of the number of manual segmentations that initialize the latent atlas.
6.2 Tumor segmentation
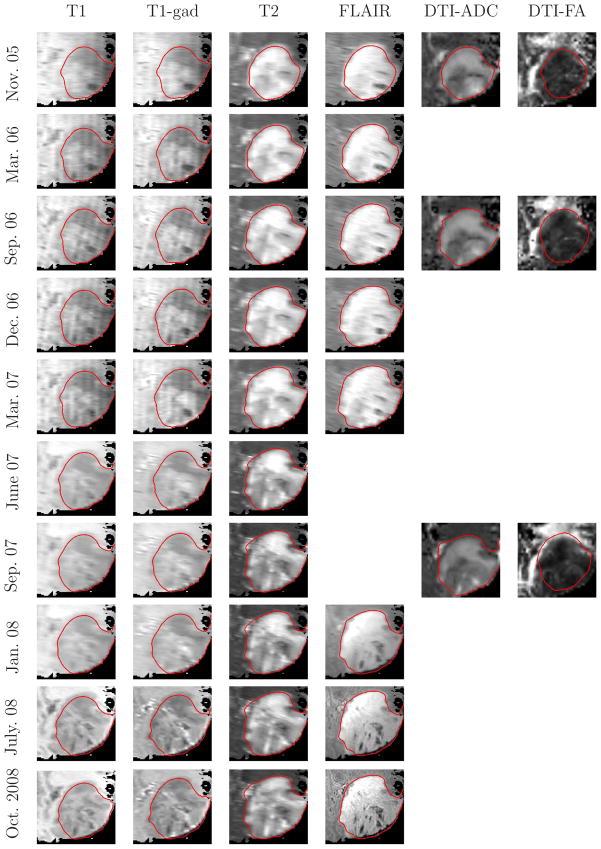
We also illustrate the proposed method on a set of 44 image volumes of a patient with histologically confirmed low-grade glioma. The volumes were acquired at 10 different time points at the German Cancer Research Center (Heidelberg, Germany) using 1.5T Siemens Magnetom and 3T Siemens TRIO MR scanners. Up to six imaging protocols: T1, T2, FLAIR, DTI, and contrast-enhanced T1 sequences (T1gd) were used, as shown in Figure 8. We aligned the images using the MedINRIA registration software (Toussaint et al., 2007). We calculated fractional anisotropy (FA) and apparent diffusion coefficient (ADC) maps from the diffusion tensor images (DTI) using the same software. In this experiment we applied the latent atlas method to every set of images acquired at a particular timepoint separately. In contrast to the multivariate approach (Van Leemput et al., 2001) that produces a single segmentation for a set of images, we obtained different segmentations corresponding to the different input images acquired by the different modalities. This output brings forth specific physical characteristics of the tumor that may be only seen in some (or one) of the modalities. Examples include differences in tissue water (T2, Flair-MRI), enhancement of contrast agents (post-Gadolinium T1-MRI), diffusion (DTI, DCE-MRI), or relative concentrations of selected metabolites (MRSI).
Fig. 8.
Axial slice of the tumor volumes and the automatic 3D segmentations (red outlines) across 6 modalities and 10 time points. Not all the modalities were acquired at each time point.
The individual delineation of the tumor areas can therefore facilitate quantitative analysis of tumor shape and evolution.
To enable quantitative evaluation, three manual segmentations of three orthogonal slices that pass through the center of the tumor were provided for each volume.
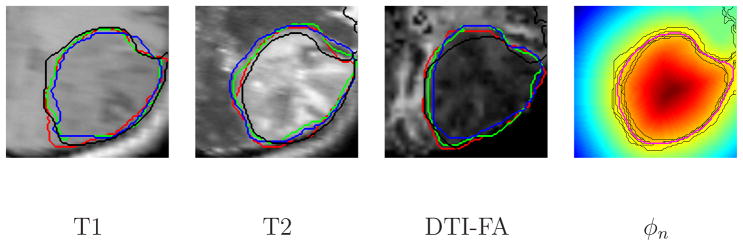
Figure 8 shows axial slices of the available image volumes together with the boundaries of the automatic 3D segmentation. Figure 9 shows the manual segmentations for three lateral slices through the tumor, together with the automatic segmentation. We observe that the segmentation error in the T2 image, due to the similarity in the intensities of the scanned tumor and the nearby healthy tissue, does not significantly affect the averaged level-set function (right panel of Figure 9), which corresponds to the latent atlas.
Fig. 9.
Manual segmentations (red, green, blue) and automatic segmentation (black) for lateral T1, T2 and DTI-FA images acquired at the same time point. The fourth image shows the corresponding section of the average of the associated 3D level-set functions. The zero level of the level-set functions average is shown in magenta. Tumor boundaries of all the modalities available for that time point are shown in black.
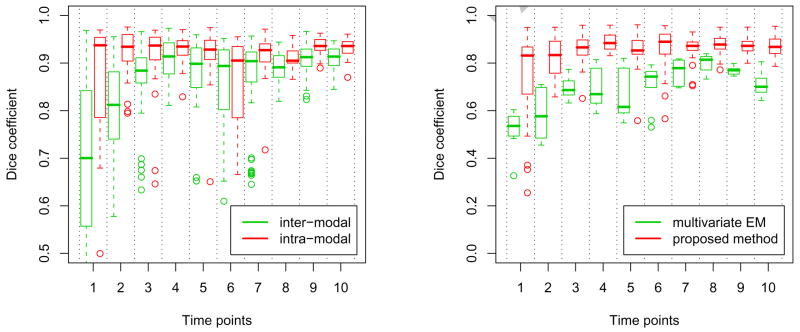
Table 2 provides quantitative evaluation of the overlap between the automatic and the manual segmentations as measured by the Dice coefficients. We compared the automatic segmentations with each manual segmentation in the corresponding triplets of manually segmented slices. The first number in each cell in Table 2 reports the mean and the standard deviation of these nine Dice scores. The second number in each cell in Table 2 reports the mean and the standard deviation of the Dice scores obtained by comparing one of the manual segmentations with the other two in the three slices. The overall average Dice score for the automatic segmentation is above 0.85 while the average Dice scores across the manual segmentations is 0.91. The top plot in Figure 10 reports the average Dice score over all modalities at a given time point obtained by our method and the Dice scores of the multivariate tissue classification according to Van Leemput et al. (2001). The plot shows that the Dices scores obtained via the latent anatomy method are consistently higher. The bottom plot in Figure 10 compares the overlap among the manual segmentations for each individual modality (‘intra-modal’) with the overlap among the manual segmentations for all the modalities together (‘inter-modal’). We define overlap as the mean Dice score among the three manual segmentations, as described above. This plot suggests that even the manual segmentations vary significantly across modalities for the same time point, justifying our approach of generating separate tumor segmentation for each volume.
Table 2.
Dice coefficients for 44 volumes in the study. The first and the second scores in each entry of the table are the mean and the standard deviation of the Dice scores between the automatic and the manual segmentations, respectively. See text for details.
| Acquisition date | T1 | T1gd | T2 | Flair | DA | ADC |
|---|---|---|---|---|---|---|
| Nov. 2005 | .71±.11 | .49±.14 | .87±.01 | .91±.03 | .84±.02 | .73±.08 |
| .80±.07 | .52±.15 | .95±.01 | .94±.02 | .94±.01 | .91±.07 | |
| March 2006 | .78±.04 | .77±.09 | .93±.02 | .84±.02 | ||
| .92±.02 | .85±.06 | .95±.02 | .96±.01 | |||
| Sep. 2006 | .87±.03 | .85±.08 | .84±.02 | .94±.01 | .88±.03 | .81±.04 |
| .90±.04 | .82±.12 | .95±.02 | .94±.02 | .94±.02 | .93±.03 | |
| Dec. 2006 | .87±.02 | .89±.03 | .93±.01 | .86±.02 | ||
| .91±.03 | .90±.04 | .95±.01 | .94±.01 | |||
| March 2007 | .84±.02 | .82±.11 | .93±.02 | .84±.02 | ||
| .91±.04 | .87±.11 | .94±.03 | .94±.01 | |||
| June 2007 | .81±.09 | .85±.09 | .93±.02 | |||
| .86±.11 | .81±.11 | .93±.03 | ||||
| Sep. 2007 | .87±.04 | .84±.08 | .87±.02 | .86±.03 | .87±.02 | |
| .92±.03 | .86±.07 | .94±.02 | .93±.01 | .94±.02 | ||
| Jan. 2008 | .88±.02 | .89±.02 | .91±.03 | .83±.04 | ||
| .90±.01 | .90±.02 | .91±.01 | .94±.02 | |||
| July 2008 | .87±.03 | .85±.02 | .91±.03 | .86±.03 | ||
| .93±.02 | .93±.02 | .94±.01 | .94±.02 | |||
| Oct. 2008 | .88±.03 | .85±.03 | .91±.03 | .84±.04 | ||
| .93±.03 | .93±.01 | .94±.01 | .93±.02 | |||
Fig. 10.
Left: comparison of the overlap in the manual segmentations for each individual modality (red) with the overlap in the manual segmentations for all the modalities together (green). Overlap is defined as the mean Dice score between the three manual segmentations. See text for details. Right: A comparison of the average Dice scores of the proposed latent anatomy method (red) and the Dice scores of the multivariate EM for lesion segmentation of Van Leemput et al. (2001) (green). The segmentation results obtained by the proposed latent anatomy method are consistently better.
7 Discussion and future directions
We presented a novel level-set framework for the segmentation of MR image ensembles that is motivated by a generative probabilistic model. Unlike most previous methods, spatial priors in the form of a probabilistic atlas are not employed. Instead, spatial parameters which form a dynamic atlas are inferred from the dataset through an alternating minimization procedure. The practical value of this work, as demonstrated by the experimental results, is to offer an alternative to standard segmentation methods when a suitable atlas is not available or when its reliability is questionable. The foremost advantage of the proposed method is therefore the potential saving of precious human hours that would be otherwise used to manually segment a large set of images for the generation of an atlas that fits a novel data of a non-standard population.
The essence of the theoretical contribution is the link between a statistical segmentation model and a variational active contour approach. We interpret the MAP estimation problem in statistical segmentation in terms of a level-set functional constructed for groupwise segmentation. The gradient descent procedure used to update the level-set functions, which can be viewed as soft segmentations of the ensemble, is alternated with the estimation of the model parameters. For fixed segmentations these unknown parameters are estimated by optimizing their likelihood, similar to the maximization step in EM procedure (Dempster et al., 1977). A comparison of the complete variational process to the EM approach is therefore interesting. Since not the labels themselves, but their probabilities are updated, each gradient descent iteration can be considered as one step toward the computation of the expectation step. With the existing variants of the standard EM approach (Neal and Hinton, 1998), the analogy between the two methods seems to be nearly complete. Nevertheless, the need to account for the regularization term derived from the pairwise interactions between neighboring voxels leads to a non-trivial problem, left for future work.
The probabilistic approach and the level-set framework are both commonly used methodologies. The connection between them adds a novel perspective to problems which could be solved with either of the two methods. While the gradient descent procedure, commonly used in level-set methods is a convenient way for optimization, it guarantees globally optimal convergence only for convex functionals (Cremers et al., 2008). The EM algorithm has attractive properties; it requires no ‘step size’ parameter, and will not oscillate around the optimum. However, there is no guarantee of global solutions. The proposed level-set functional is not necessarily convex, but it has the benefit of incorporating the image-likelihood, spatial and smoothness constraints in one coherent framework. In practice, the proposed level-set algorithm converges to the desired solutions in all the experiments.
Acknowledgments
We thank Bruce Fischl and Randy Buckner for the brain data used in the first experiment and Marc-andré Weber and Bram Stieltjes for the brain tumor data. We also thank Nicholas Ayache, Baba Vemuri and Nir Sochen for the fruitful discussions. This work was supported in part by NIH NIBIB NAMIC U54-EB005149, NIH NCRR NAC P41-RR13218, NIH NINDS R01-NS051826, NIH NCRR mBIRN U24-RR021382 grants and NSF CAREER Award 0642971. B. Menze was also supported in part by the Leopoldina Fellowship Programme (LPDS 2009-10). The work of K. Van Leemput was supported in part by the Academy of Finland, Grant No. 133611.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Tammy Riklin-Raviv, Email: tammy@csail.mit.edu.
Koen Van Leemput, Email: koen@nmr.mgh.harvard.edu.
Bjoern H. Menze, Email: menze@csail.mit.edu.
William M. Wells, III, Email: sw@bwh.harvard.edu.
Polina Golland, Email: polina@csail.mit.edu.
References
- Ashburner J, Friston K. Unified segmentation. NeuroImage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Bazin P, Pham D. Statistical and topological atlas based brain image segmentation. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2007. pp. 94–101. [DOI] [PubMed] [Google Scholar]
- Besag J. Statistical analysis of non-lattice data. The Statistician. 1975;24 (3):179–195. [Google Scholar]
- Bhatia K, Aljabar P, Boardman J, Srinivasan L, Murgasova M, Counsell S, Rutherford M, Hajnal J, Edwards A, Rueckert D. Groupwise combined segmentation and registration for atlas construction. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2007. pp. 532–540. [DOI] [PubMed] [Google Scholar]
- Chan T, Vese L. Active contours without edges. IEEE Transactions on Image Processing. 2001;10 (2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- Cobzas D, Birkbeck N, Schmidt M, Jagersand M, Murtha A. 3D variational brain tumor segmentation using a high dimensional feature set. Proceedings of the International Conference on Computer Vision; 2007. pp. 1–8. [Google Scholar]
- Cremers D, Rousson M, Deriche R. A review of statistical approaches to level set segmentation: Integrating color, texture, motion and shape. International Journal of Computer Vision. 2007;72 (2):195–215. [Google Scholar]
- Cremers D, Rousson M. Efficient kernel density estimation of shape and intensity priors for level set segmentation. In: Suri JS, Farag A, editors. Parametric and Geometric Deformable Models: An application in Biomaterials and Medical Imagery. Springer; May, 2007. [Google Scholar]
- Cremers D, Schmidt FR, Barthel F. Shape priors in variational image segmentation: Convexity, lipschitz continuity and globally optimal solutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Jun, 2008. [Google Scholar]
- Cuadra B, Pollo C, Bardera A, Cuisenaire O, Villemure J, Thiran J. Atlas-based segmentation of pathological brain MR images. IEEE Trans on Medical Imaging. 2004;23:1301–1314. doi: 10.1109/TMI.2004.834618. [DOI] [PubMed] [Google Scholar]
- Dempster A, Laird N, Rubin D. Maximal likelihood form incomplete data via the EM algorithm. Proceedings of the Royal Statistical Society. 1977;39:1–38. [Google Scholar]
- Dice L. Measure of the amount of ecological association between species. Ecology. 1945;26 (3):297–302. [Google Scholar]
- Fischl B, Salat D, Busa E, Albert M, Dieterich M, Haselgrove CAVDK, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale A. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33 (3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Freesurfer. 2009 URL Wiki. http://surfer.nmr.mgh.harvard.edu.
- Geman S, Geman D. Stochastic relaxation, gibbs distributions and the bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6 (6):721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Gering D, Grimson W, Kikinis R. Recognizing deviations from normalcy for brain tumor segmentation. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2002. pp. 388–395. [Google Scholar]
- Görlitz L, Menze B, Weber M, Kelm B, Hamprecht F. Semi-supervised tumor detection in magnetic resonance spectroscopic images using discriminative random fields. 2007. [Google Scholar]
- Han X, Xu C, Prince J. A topology preserving level set method for geometric deformable models. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003;25 (6):755–768. [Google Scholar]
- Ho S, Bullitt E, Gerig G. Level-set evolution with region competition: automatic 3D segmentation of brain tumors. Proceedings of the International Conference on Pattern Recognition; 2002. pp. 532–535. [Google Scholar]
- Jaume S, Ferrant M, Schreyer A, Hoyte L, Macq B, Fielding J, Kikinis R, Warfield S. Multiresolution signal processing on meshes for automatic pathological shape characterization. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2001. pp. 1398–1400. [Google Scholar]
- Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. International Journal of Computer Vision. 1988 Jan;1 (4):321–331. [Google Scholar]
- Kaus M, Warfield S, Nabavi A, Black P, Jolesz F, Kikinis R. Automated segmentation of MR images of brain tumors. Radiology. 2001;218:586–591. doi: 10.1148/radiology.218.2.r01fe44586. [DOI] [PubMed] [Google Scholar]
- Lord N, Ho J, Vemuri B. Ussr: A unified framework for simultaneous smoothing, segmentation, and registration of multiple images. Proceedings of the International Conference on Computer Vision; 2007. pp. 1–6. [Google Scholar]
- Mohamed A, Zacharakib E, Shena D, Davatzikos C. Deformable registration of brain tumor images via a statistical model of tumor-induced deformation. Medical Image Analysis. 2006;10:752–763. doi: 10.1016/j.media.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Moon N, Bullitt E, van Leemput K, Gerig G. Model-based brain and tumor segmentation. Proceedings of the International Conference on Pattern Recognition; 2002. pp. 528–531. [Google Scholar]
- Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics. 1989;42:577–684. [Google Scholar]
- Neal R, Hinton G. A view of the EM algorithm that justifies incremental, sparse, and other variants. Learning in Graphical Models. 1998:355–368. [Google Scholar]
- Osher S, Sethian J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics. 1988;79:12–49. [Google Scholar]
- Paragios N, Deriche R. Geodesic active regions: A new paradigm to deal with frame partition problems in computer vision. Journal of Visual Communication and Image Representation. 2002;13:249–268. [Google Scholar]
- Pohl K, Bouix S, Nakamura M, Rohlfing T, McCarley R, Kikinis R, Grimson W, Shenton M, Wells W. A hierarchical algorithm for MR brain image parcellation. IEEE Trans on Medical Imaging. 2007a;26 (9):1201–1212. doi: 10.1109/TMI.2007.901433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl K, Fisher J, Bouix S, Shenton M, McCarley R, Grimson W, Kikinis R, Wells W. Using the logarithm of odds to define a vector space on probabilistic atlases. Medical Image Analysis. 2007b;11 (6):465–477. doi: 10.1016/j.media.2007.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl K, Fisher J, Grimson W, Kikinis R, Wells W. A bayesian model for joint segmentation and registration. NeuroImage. 2006;31 (1):228–239. doi: 10.1016/j.neuroimage.2005.11.044. [DOI] [PubMed] [Google Scholar]
- Pohl K, Kikinis R, Wells W. Active mean fields: Solving the mean field approximation in the level set framework. Information Processing In Medical Imaging. 2007c:26–37. doi: 10.1007/978-3-540-73273-0_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postelnicu G, Zöllei L, Fischl B. Combined volumetric and surface registration. IEEE Trans on Medical Imaging. 2009;28 (4):508–522. doi: 10.1109/TMI.2008.2004426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prastawa M, Bullitt E, Ho S, Gerig G. A brain tumor segmentation framework based on outlier detection. Medical Image Analysis. 2004;8:275–283. doi: 10.1016/j.media.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Prastawa M, Bullitt E, Moon N, Van Leemput K, Gerig G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Academic Radiology. 2003;10:1341–1348. doi: 10.1016/s1076-6332(03)00506-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rey D, Subsol G, Delingette H, Ayache N. Automatic detection and segmentation of evolving processes in 3D medical images: Application to multiple sclerosis. Medical Image Analysis. 2002;6 (2):163–179. doi: 10.1016/s1361-8415(02)00056-7. [DOI] [PubMed] [Google Scholar]
- Riklin Raviv T, Menze B, Van Leemput K, Stieltjes B, Weber MA, Ayache N, Wells W, Golland P. Joint segmentation via patient-specific latent anatomy model. Proc. of MICCAI Workshop on Probabilistic Models for Medical Image Analysis.2009a. [Google Scholar]
- Riklin-Raviv T, Sochen N, Kiryati N. Shape-based mutual segmentation. International Journal of Computer Vision. 2008;79:231–245. [Google Scholar]
- Riklin Raviv T, Van Leemput K, Wells W, Golland P. Joint segmentation of image ensembles via latent atlases. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2009b. pp. 272–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabuncu M, Yeo B, Van Leemput K, Fischl B, Golland P. Non-parameteric mixture models for supervised image parcellation. Proc. of MICCAI Workshop on Probabilistic Models for Medical Image Analysis; 2009a. [PMC free article] [PubMed] [Google Scholar]
- Sabuncu M, Yeo B, Van Leemput K, Vercauteren T, Golland P. Asymmetric image template registration. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2009b. pp. 565–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirion J, Calmon G. Deformation analysis to detect and quantify active lesions in three-dimensional medical image sequences. IEEE Trans on Medical Imaging. 1999;18 (5):429–441. doi: 10.1109/42.774170. [DOI] [PubMed] [Google Scholar]
- Toussaint N, Souplet J, Fillard P. Medinria: Medical image navigation and research tool by inria. Proc. of MICCAI Workshop on Interaction in medical image analysis and visualization.2007. [Google Scholar]
- Tu Z, Narr K, Dollár P, Dinov I, Thompson P, Toga A. Brain anatomical structure segmentation by hybrid discriminative/generative models. IEEE Trans on Medical Imaging. 2008;27 (4):495–508. doi: 10.1109/TMI.2007.908121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu Z, Zhu S. Image segmentation by data-driven markov chain monte carlo. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002;24 (5):657–673. [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Colchester A, Suetens P. Automated segmentation of multiple sclerosis lesions by model outlier detection. IEEE Trans on Medical Imaging. 2001;20 (8):677–688. doi: 10.1109/42.938237. [DOI] [PubMed] [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE Trans on Medical Imaging. 1999;18 (10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- Wels M, Carneiro G, Aplas A, Huber M, Hornegger J, Comaniciu D. A discriminative model-constrained graph cuts approach to fully automated pediatric brain tumor segmentation in 3-D MRI. LNCS; Proceedings of International on Medical Image Computing and Computer-Assisted Intervention; Springer; 2008. pp. 67–75. [DOI] [PubMed] [Google Scholar]
- Yang J, Duncan J. Joint prior models of neighboring object for 3D image segmentation. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2004. pp. 314–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich P, Piven J, Hazlett H, Smith R, Ho S, Gee J, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. NeuroImage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Zacharaki EI, Shen D, Lee SK, Davatzikos C. Orbit: A multiresolution framework for deformable registration of brain tumor images. IEEE Trans on Medical Imaging. 2008;27 (8):1003–1017. doi: 10.1109/TMI.2008.916954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu S, Yuille A. Region competition: Unifying snakes, region growing, and bayes/MDL for multiband image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1996;18 (9):884–900. [Google Scholar]