Comparison of Spectral Fitting Methods for Overlapping J-Coupled Metabolite Resonances

Abstract

There is increasing interest in the use of two dimensional J-resolved spectroscopic acquisition (multi-echo) methods for in vivo proton MR spectroscopy due to the improved discrimination of overlapping J-coupled multiplet resonances that is provided. Of particular interest is the potential for discrimination of the overlapping resonances of glutamate and glutamine. In this study, a new time-domain parametric spectral model that makes use of all available data is described for fitting the complete two-dimensional multi-echo data, and the performance of this method was compared with fitting of one-dimensional spectra obtained following averaging multi-echo data (TE-averaged) and single-TE PRESS acquired spectra. These methods were compared using data obtained from a phantom containing typical brain metabolites and a human brain. Results indicate that improved performance and accuracy is obtained for the two-dimensional acquisition and spectral fitting model.

Introduction

Proton magnetic resonance spectroscopy (MRS) enables non-invasive detection of several brain metabolites and provides valuable information on neurochemistry that is complimentary to structural MRI in clinical studies. There is increasing interest in using MRS to map distributions of glutamate (Glu), a key neurotransmitter in the brain, and glutamine (Gln), the precursor and storage form of Glu, as their altered concentrations are linked to several neurodegenerative diseases, including multiple sclerosis, amyotrophic lateral sclerosis (ALS), Alzheimer's and Parkinson's diseases (1-4). However, spectral quantitation of the brain Glu signal obtained using standard spatially-localized acquisition sequences is problematic as its multiplet resonance patterns overlap significantly with the resonances from N-acetylaspartate (NAA) and the structurally similar Gln.

Model-based spectral fitting methods are commonly used for in vivo MRS quantitation and it has been shown that such methods benefit greatly from the incorporation of prior knowledge of the individual metabolite spectra, as observed with the specific acquisition sequence used (5). In this report, the parametric modeling approach is extended to fitting multi-echo data obtained using a 2D J-resolved spectroscopy acquisition (6-8), with 2D spectral model functions obtained by spectral simulation. This approach is compared to an alternative approach to processing the multi-echo data that limits the analysis to the so-called TE-averaged data (9), corresponding to the J=0 Hz spectrum, by summing spectra acquired at different echo times. Previous studies of Glu in the brain have largely used this method (10) or conventional (i.e. single-TE) acquisitions.

While multi-echo spectroscopy techniques theoretically improve detection of J-coupled metabolites by disentangling the overlapping spectral information via the indirectly-sampled spectral dimension, there is a lack of reported studies demonstrating the relative improvement in reliability over more conventional MRS methods for the in vivo measurements of Glu and Gln. A comparison of spectral fitting of single-TE and multi-echo spectra has been previously presented (11) and fitting of traditional TE-averaged spectra has also been described (10); however, to our knowledge, no direct comparison of these different fitting methods has been published.

In addition to the two-dimensional spectroscopy technique used in this study, there are other methodologies that have been used to improve the detection of Glu. This includes spectral editing techniques (12-15), which are based on refocusing of specific J-coupled resonances using additional pulses within the localization sequences. Such methods, however, typically sacrifice information from other resonances in the spectrum and hence have less clinical value. Optimization of conventional sequences have also been described, including a PRESS sequence with an intermediate echo time (TE) of 80 ms (16) and a STEAM sequence with optimal TE and TM times (16,17). These techniques simplify the overlapping spectral resonances, though at the expense of some signal loss resulting from both relaxation and J-modulation. Short echo STEAM or PRESS sequences have also been used, however suffered from strong overlap of Glu with other metabolites such as Gln, GABA, NAA and baseline from macromolecule resonances.

The two-dimensional spectroscopy techniques, such as the 2D J-resolved technique used in this study, consist of a series of acquisitions with different sequence timings to obtain an indirectly sampled spectral dimension that helps to resolve the overlapping spectral information. While these techniques preserve all metabolite information, they require longer minimum acquisition times and may involve a loss of sensitivity as longer TE values are typically used. Thus far, Glu has been mostly studied by the so-called TE-averaged method, by summing spectra acquired at different echo times. This approach provides considerable spectral simplification but at the expense of removing the information available from the J-evolution. It has been demonstrated that for data obtained at 3 T this approach greatly simplifies the glutamate resonance multiplet pattern and suppresses the overlapping multiplet resonances from Gln and NAA; however, this also makes the method unsuitable for measurement of Gln (10).

For this study, a multi-echo time-domain spectral fitting approach has been developed and the performance compared with one dimensional fitting of TE-averaged spectra and with fitting of conventional single-TE PRESS spectra for single-voxel data.

Methods

Data Acquisition

Data were acquired using an 8-channel phased-array head coil at 3 Tesla (Siemens Trio). The MR protocol consisted of anatomical and spectral data acquisitions. Anatomical MR images were used for voxel localization and comprised of an axial high-resolution T1-weighted MRI obtained with a magnetization-prepared rapid acquisition of gradient echo sequence (TR/TE= 2150/4.43 ms). Spectral data were acquired with a 2D J-resolved sequence implemented with TEs ranging from 30 to 180 ms in equal steps of 10 ms. This TE range was chosen to reduce signal contributions from short-T2 macromolecules to the baseline found at shorter TEs, while minimizing T2-weighting and signal intensity loss at longer TEs. With a repetition time of 2 s and 16 averages per TE, which incorporated a four-step phase cycling, the total acquisition was 9 minutes. The water signal was suppressed with a chemical shift selective saturation pulse. Prior to the MRS acquisition shimming was performed to optimize field homogeneity and water suppression was optimized with the automated routines provided by the manufacturer. A spectral sweep width of 1000 Hz and a data size of 1024 points were used. One additional acquisition was used to obtain a non-water suppressed spectrum at a TE of 30 ms. Data was also obtained using a conventional PRESS acquisition from the same voxel location, with a TR/TE of 2000/30 ms and matching the acquisition time of a 2D J-resolved sequence using 256 averages.

Data were acquired from an 8 cm³ voxel located at the precentral gyrus of the brain in a normal volunteer subject (37 year old male). The study was conducted under a human subject's research protocol approved by our Institutional Review Board and the volunteer gave written informed consent prior to participation in this study. The measurement was repeated 10 times, in 2 sessions on the same day with 5 scans in each session. During one of these repeated scans, one additional acquisition was used to obtain a non-water suppressed acquisition at multiple TE values. Additional data were collected from a phantom containing several brain metabolites at typical brain concentrations and all data were collected in one scanning session. For both in vitro and in vivo measurements the magnetic field shimming and water signal suppression for the selected volume was performed only for the first acquisition and kept the same for the subsequent acquisitions.

Data Processing and Spectral Fitting

Residual water signal was removed from each spectrum prior to spectral fitting using a low-pass finite impulse response filter. The zero-order phase of the water peak in the single water-unsuppressed acquisition was determined and this value applied to all the multi-TE data. Following Fourier transformation, the frequency shift between the acquired spectrum and the model function was determined for each TE data, and the corresponding frequency shift applied. The B0 shift was determined from the maximum of the cross-correlation of the real part of the data with an ideal spectrum created from the prominent singlet resonances of NAA, Cr, and Cho, at the chemical shift offsets defined in the prior information. Line-shape distortions caused by eddy currents were negligible, as seen from no phase variation in the water signal (result not shown).

The acquired MRS signal, S, that includes signals from metabolites, macromolecules, lipids and residual water, was modeled as

$$S=x(t)+b(\theta )+e$$ (1)

where x(t) is the metabolite part whose model is known, b(θ) the background signal whose model function is unknown, and e is Gaussian distributed noise. A time-domain model was used to determine the integrals of all metabolite resonances for both single-TE and multi-TE spectra. This model included independent amplitude, frequency, and T₂ terms for each metabolite, and a common frequency shift and zero order phase term. The whole multi-echo metabolite data set was modeled as the sums of exponentially decaying signals over time, t, for all metabolite resonances, with parametric optimization carried out to minimize |S − x(t)|, where:

$$x(t)=\sum _{\mathit{\text{TE}}}\sum _{n=1}^{N(m)}\sum _{m=1}^M{e}^{-\frac{t_{\mathit{\text{TE}}}}{T_{2_m}}}{a}_m{a}_n{e}^{i[({\omega }_m+{\omega }_n+{\Omega }_0)t+{\phi }_0+{\phi }_n]}{e}^{-(\frac{t}{T_a}+\frac{t^2}{T_b^2})}$$ (2)

where the terms indexed over m comprise the individual metabolites being analyzed in the spectrum and those over n comprises the prior information describing the resonance structures for each metabolite. For the multi-TE spectral fit, the sum over TE combines the full information from the whole data set, and the signal amplitude values returned correspond to the value at TE=0, i.e. unweighted by transverse relaxation. The prior metabolite signal information consists of amplitude, frequency and phase (a_n, ω_n, φ_n) for each resonance line, n, for metabolite, m. The variables a_m, ω_m, and T_2m indicate amplitude and common frequency shift and T2 values for all resonances in a metabolite. The parameter ω_m, accounted for frequency shifts relative to the signal model due to B0 field variations. This was implemented as an independent parameter for each metabolite to allow for potential metabolite-specific changes, but in practice resulted in essentially the same value for all metabolites. The common frequency shift, Ω₀, and phase term, φ₀, accounted for any residual variations remaining after the pre-processing frequency shift and phase correction, which was obtained from the first TE data and applied to all TE values. The lineshape model uses two parameters, T_a and T_b, which describe a combined Lorentz-Gauss lineshape. For the 2D fitting, T_a was set equal to T_2m.

For the single-TE spectral fitting the same parametric model was used except that the e^−t/T_2m term was removed, so that the signal integral value obtained corresponds to the time at the center of the spin echo and the Lorentz-Gauss lineshape is maintained. To enable direct comparison with the results obtained for the one- and two-dimensional fitting methods, the fitted metabolite amplitudes for the single-TE measurement were corrected for T₂ signal loss, using values of the T₂ obtained from the multi-echo fitting result.

Fitting of the MRS data started with the separation of the background from the metabolite signal. An initial metabolite estimate was first obtained using the time-domain data with a few initial sample points excluded from the signal, based on the fact that baseline components decay more rapidly than the metabolites (18). Using these “estimated” metabolite parameters, the time-domain data corresponding to those data points excluded in this initial optimization procedure were then determined, i.e. the data corresponding to the metabolite signal only was extrapolated to time t=0, and this was then subtracted from the raw data to obtain a function corresponding to the baseline. The resultant baseline-only signal was then subtracted from the complete time-domain signal to obtain the “background-free” metabolite signal and then a parametric least squares fitting of the metabolite signal was performed once again. It should be noted that the “background-free” metabolite signal contains more metabolite information than the initial metabolite estimate.

In practice, baseline estimation started with a small number of excluded time points, N_trunc, which was then iteratively increased until the background time-domain signal decayed into the noise. To ensure that not too many data points were excluded, a visual inspection was also performed verifying a smooth background and a good initial metabolite fit in the frequency domain following Fourier transformation. Because the baseline signal decays rapidly with increasing TE value, N_trunc was reduced with increasing TE. With the spectral prior information, the time-domain model used a constrained Levenberg-Marquardt optimization method written in Python (http://www.python.org) for determining the model parameters for the multi-echo, echo-averaged, and single-echo data. Among several statistical methods available, a coefficient of variation (CV) was chosen to characterize the precision. The reproducibility of each of the spectral fitting approaches was estimated by applying the fitting procedures on each of the 10 spectra and calculating a coefficient of variation for each of the metabolites in the spectrum. Following the methods of Bland and Altman (19), the CV was estimated by calculating the standard deviation of a particular metabolite amplitude value and dividing it by the mean value of the same metabolite, both provided by the different fitting methods.

Prior Information

Spectral prior information for the metabolites was generated using the GAVA program (20) which utilizes the GAMMA C++ spectral simulation library (21) and previously measured spectral parameters of the observed metabolites (22). For all spectral fitting, the prior information for each TE value consisted of the relative amplitude, frequency, and phase of every significant resonance for choline (Cho), creatine (Cr), Glu, Gln, myo-inositol (mI), and NAA. The amplitude term obtained by the spectral simulation was scaled to value 1.0 for a signal from one proton. For the TE-averaged spectral fitting, the prior information amplitudes for all resonances at each TE value were then modified to account for the T2 decay, using the metabolite T2 values determined from a previously-run 2D spectral fit, and then a vector summation of the data from all TEs performed to obtain the TE-averaged prior spectral information. As a result, the amplitude terms, a_m of Eqn. [2], for spectral fitting of the TE-averaged result was automatically corrected for T2 losses, i.e. corresponded to TE=0.

Results and Discussion

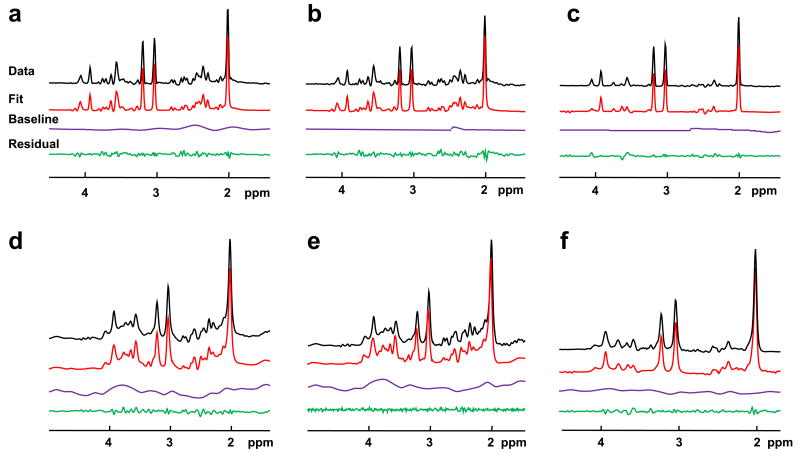
All MRS techniques produced good quality spectra and example data, spectral and baseline fits, and residuals for each of the spectral models are shown in Figure 1 for both in vitro and in vivo data. For the multi-echo fit (Figure 1 b and e), only the first echo data and fit results are shown. Typical frequency-domain signal-to-noise ratios for the in vivo measurements, taken as the peak NAA value to the noise, were 123 for the PRESS measurement and 36 for the first-TE of the multiple-TE measurement. Following processing for the TE-averaged result, a typical SNR result was 103.

Figure 1.

Fit results for in vitro and in vivo data. Shown are data, spectral and baseline fits and residual (a) conventional PRESS fit using in vitro data, (b) the first TE data from the multi-echo 2D model fit using in vitro data, (c) TE-averaged fit using in vitro data, (d) conventional PRESS fit using in vivo data, (e) the first TE data from the multi-echo 2D model fit using in vivo data, (f) TE-averaged fit using in vivo data.

Inspection of Figs. 1a and 1b indicates greater baseline signal in the result for the 1D analysis relative to the multi-TE analysis. Since the baseline for this in vitro data should be flat, this observation likely reflects the well-known difficulty of separating the wide tails resulting from multiple overlapping Lorentzian lines from a slowly-varying baseline model (23). It would appear that the inclusion of multiple TE values enables better separation of these signal components.

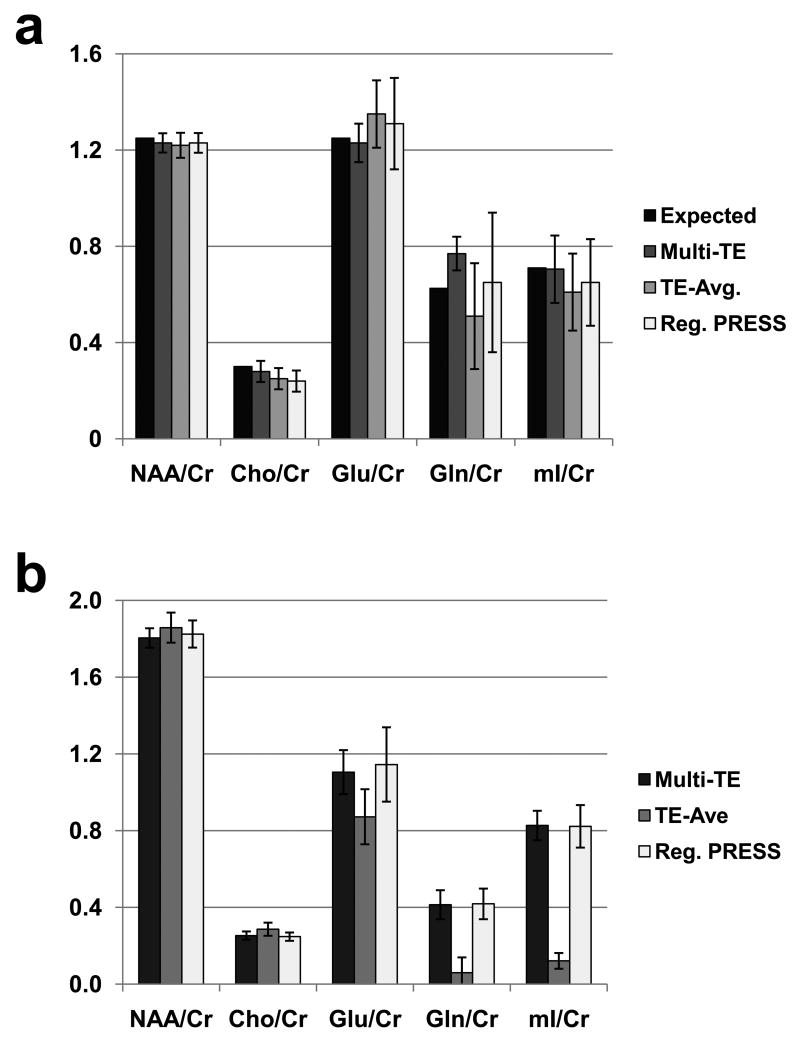
Both sets of data were first fit 10 times starting with only different starting amplitude values for each of the metabolites to test the stability of the fit. The resultant CV of 2% for both Glu and Gln indicated that the optimization was relatively insensitive to initial parameter estimates. Spectral fit results from each of the 10 separate in vitro and in vivo data sets were then obtained, using the same starting values for all fits. The mean and standard deviation of the resultant fitted metabolite amplitudes, expressed as the ratio to Cr, are shown in Figure 2. For the phantom measurement (Fig. 2a) the known metabolite ratio values are included for comparison. For the Glu/Cr in vitro data, the CVs of the fit results ranged from 7% for the multi-TE fitting to 15% for the 1D PRESS, and for the in vivo data from 10% to 17% respectively. For a stronger signal such as NAA, the CVs ranged between 3% and 4% for all methods and both sets of data. The CVs for all fitting methods are provided in Table 1. These results indicate that for measurement of Glu, decreased variance was obtained with the multi-TE acquisition relative to the conventional PRESS measurement, and that in addition the spectral fitting using the full multi-echo model shows improved performance in comparison to the TE-averaged result from the same multi-TE acquisition data.

Figure 2.

Summary of the fitting results, shown as ratios to Cr, for the in vitro (a) and in vivo data (b). For reference, the known ratio values are also shown for in vitro data. The error bars indicate the standard deviation over the 10 results.

Table 1.

Coefficient of Variance (CV) of the metabolite ratios for each fitting procedure and for the in vitro and in vivo data sets. Also shown are the T2 values of the individual metabolites obtained from the multi-TE acquisition and fitting procedure for the in vivo data.

Metab. Ratio	In Vitro CV (%)			In Vivo CV (%)			Metab.	T2 (ms)
	Multi-TE	TE-Ave	1D PRESS	Multi-TE	TE-Ave	1D PRESS
NAA/Cr	3.3	4.3	3.3	2.8	4.2	3.9	NAA	279 ± 19
Cho/Cr	15.7	17.6	18.3	8.5	11.9	8.8	Cho	237 ± 18
Glu/Cr	6.5	10.4	14.5	10.4	16.4	16.9	Glu	211 ± 21
Gln/Cr	9.1	43.1	44.6	18.3	n/a	19	Gln	225 ±24
mI/Cr	19.9	26.2	27.7	9.3	33.6	13.5	mI	84 ± 19
							Cr	177 ± 18

Results for Gln and mI show similar improvements for the multiple-echo acquisition and analysis relative to that of the PRESS acquisition and 1D analysis. For these metabolites, the TE-averaged approach is suboptimal since it involves a loss of signal associated with the summation over the multiple-TE data, and for this reason the value for Gln was not computed. Additionally the worse CV results may reflect both inaccuracies in the generation of the prior knowledge, for example from the absence of T2* in this calculation, as well as and absence of taurine from the signal model in the case of mI.

Measurement of metabolite T2 relaxation times is of potential value for investigating physiological and pathological processes. Although the T2 measurements of singlets are comparatively straightforward, measurement of T2 for coupled spin resonances must account for the complex J-coupling modulation. In order to reduce the number of fit parameters, the two-dimensional spectral model assumed that all resonance groups in each of the metabolites had the same T2 relaxation. The T2 values derived from the multi-echo model for the in vivo data were provided in Table 1. The Glu T2 of the present study was 211± 21 ms and that is also in good agreement with 194 ms as reported by Schubert et al. (24) for a voxel localized in the anterior cingulate and 201 ms as reported by Choi el al. (25) for a voxel in the prefrontal region.

The number of truncated data points is a sensitive parameter and it must be chosen to untangle the variable baseline and broad macromolecular resonances from the metabolite signals but must preserve as much as possible the metabolite information. The selection of the number of points to exclude remained a user-defined value and found to be no more than 15 points, which corresponds to 15 ms of data in the time-domain and a time from excitation to the first sample point of 45 ms, which is comparable with known T2 values of 40-50 ms for macromolecules (26,27).

In comparison to previous studies, the appearance of the Glu signal in our TE-averaged results was not as well defined as that shown by Hurd et al. (10) and the improvement measured with the multi-echo fitting procedure relative to the conventional PRESS acquisition was not as great as the 40% value determined by Schulte et al. (11). These differences may be related to different acquisition sequence parameters (Hurd et al. (10) collected data with TEs from 35-335ms, in steps of 2.5 ms, and Schulte et al. (11) collected data for TEs from 31 to 229 ms in steps of 2 ms). Additionally, the effects of RF inhomogeneity and chemical-shift displacement for the PRESS volume selection (28) could also contribute to these differences.

Limitations of the presented methods include that the spectral fit results are presented as ratios to Cr. This commonly used normalization approach takes into account instrumental instabilities and systematic data processing and analysis errors, however, assumes that Cr concentration remains stable. In general, calculating absolute concentration of metabolites using tissue-water reference signal of the same voxel will make comparisons between groups more robust, though such a procedure was not attempted in this study and the T1 relaxation times required for absolute quantitation were not obtained. In addition, the two-dimensional spectral model used a single T2 value for all resonance groups in each of the metabolites although, for example, previous studies have indicated different transverse relaxation for the NAA singlet and multiplet group at 2.6 ppm (15). Inclusion of a separate T2 for each molecular group of the metabolites in the model has not been further investigated. Finally, calculation of CV values has limitations as a measure of precision, the most important of which is the dependence on the magnitude of the measured value (19).

Conclusions

In this study, the performance of a multi-echo J-resolved acquisition and spectral model was compared against the conventional 1D spectral analysis approaches (single-echo and TE-averaged) for data obtained at 3 T. Decreased variance of spectral fitting results was obtained using the multi-TE acquisition and the two-dimensional spectral model, relative to one-dimensional spectral modeling of the conventional PRESS MRS and TE-averaged spectra. This finding is consistent across all metabolites, with the greatest benefit observed for the overlapping J-coupled metabolite resonances of Glu and Gln.