CLUSTERING OF LARGE CELL POPULATIONS: METHOD AND APPLICATION TO THE BASAL FOREBRAIN CHOLINERGIC SYSTEM

Abstract

Functionally related groups of neurons spatially cluster together in the brain. To detect groups of functionally related neurons from 3D histological data, we developed an objective clustering method that provides a description of detected cell clusters that is quantitative and amenable to visual exploration. This method is based on bubble clustering (Gupta and Gosh, 2008). Our implementation consists of three steps: (i) an initial data exploration for scanning the clustering parameter space; (ii) determination of the optimal clustering parameters; (iii) final clustering. We designed this algorithm to flexibly detect clusters without assumptions about the underlying cell distribution within a cluster or the number and sizes of clusters. We implemented the clustering function as an integral part of the neuroanatomical data visualization software Virtual RatBrain (http://www.virtualratbrain.org). We applied this algorithm to the basal forebrain cholinergic system, which consists of a diffuse but inhomogeneous population of neurons (Zaborszky, 1992). With this clustering method, we confirmed the inhomogeneity in this system, defined cell clusters, quantified and localized them, and determined the cell density within clusters. Furthermore, by applying the clustering method to multiple specimens from both rat and monkey, we found that cholinergic clusters display remarkable cross-species preservation of cell density within clusters. This method is efficient not only for clustering cell body distributions but may also be used to study other distributed neuronal structural elements, including synapses, receptors, dendritic spines and molecular markers.

1. Introduction

Understanding the functional architecture of the nervous system is contingent on recognizing the major statistical patterns in the spatial layout of different types of neurons and their connections (Stepanyants and Chklovskii, 2005; Chen et al., 2006). One of the most fundamental heuristics used when describing neuronal organization under the microscope is to isolate spatially localized clusters of neurons. Cell clusters are important not only because they allow compartmentalization of structures but also because cell clusters may reflect a functional link between the neurons, such as shared input, interaction via local axonal collaterals and/or shared common targets. The importance of detecting neuron clusters from large cell populations has been proven by a number of discoveries. High density areas like the columns in the cerebral cortex (Szentagothai, 1978: Mountcastle 1998), the striosome compartments in the striatum (Graybiel and Ragsdale 1978; Gerfen 1985), AChE patches in the superior colliculus (Chevalier and Mana 2000), cell clusters in the pontine nuclei (Bjaalie et al. 1991; Leergard and Bjaalie, 2007) and brain stem auditory nuclei (Malmierca et al. 1998) are thought to support special information processing streams. With current data acquisition methods we are able to collect data from thousands of neurons, and high-throughput processing pipelines are available for automated detection of neuronal somata (e.g. Oberlaender et al., 2009). Although cell clusters can be visualized by surface-rendering methods (Nadasdy and Zaborszky, 2001; Zaborszky et al., 2005) and analyzed using multivariate statistics (Bjaalie et al., 1991), the available programs are incapable of flexibly incorporating various types of data that can be used to explore the spatial configuration of clusters, such as the projection targets of cells, or superimpose other features, such as the presence/absence of specific transmitters.

Our first goal was to develop a clustering algorithm that (i) is cell density based, (ii) does not rely on any assumption about the topology and type of data distribution, (iii) keeps the number of predefined parameters minimal, (iv) allows neurons to be unassigned to any cluster, (v) is justifiable by immediate visual observation and (vi) is fast enough to give an instantaneous result. The algorithm is called “bubble clustering” (BC), a specific solution within a family of bubble clustering algorithms (Gupta and Gosh, 2008), and is described below. Our second goal was to implement the algorithm in a flexible visualization environment so that the clustering results could instantaneously validated by visual observation and quantified for further data processing. The algorithm was ported to the free cell clustering software tool “Virtual RatBrain” (VRB) for the neuroscience community (http://www.virtualratbrain.org).

For quantification and statistical analysis of cell clusters, the VRB software determines the number of cell bodies within a spherical volume around each neuron (cell-centered density approach) and allows users to observe them in an interactive 3D environment with rotation, zoom, and translation capabilities. The user also has the ability to detect spatial overlap between a found cluster and any given cell population defined by its transmitter or projection target. The software can be used in “batch” mode allowing users to call the clustering function from scripts or other programs (e.g., Matlab). In the Materials and methods section, first we introduce the formal algorithm that defines neurons that are in the “core” of clusters. Second we describe a software implementation specifically designed to analyze large populations of neurons. In the Results section we describe the application of the clustering algorithm for the basal forebrain cholinergic system. Our BC procedure consists of three main stages. An initial BC scan explores the data distribution and assesses whether the distribution is homogeneous or clustered (section 2.3). If the distribution is inhomogeneous we determine the optimal cluster diameter based on the initial scan (section 2.4). Then we apply the final BC (section 2.5). Although the first and third steps use the same BC clustering algorithm, the first algorithm explores the distribution by scanning the parameter space, whereas the second algorithm performs the actual clustering with the optimal parameters.

2. Materials and methods

2.1. Animals and tissue processing

The reconstructions and statistical analysis presented in this paper were prepared from four male SD rats (278–466 g) and two monkeys (Macaca mulatta). All animal procedures were in compliance with PHS policy on Humane Care and Use of Laboratory Animals and the NIH Guide for the Care and Use of Laboratory Animals and approved by the Rutgers University Institutional Review Board. Rats were perfused in deep anesthesia (sodium pentobarbital, 50 mg/kg i.p.), transcardially with 50 ml of saline, followed by 250 ml of an ice-cold solution containing 4% paraformaldehyde, 15% picric acid and 0.05% glutaraldehyde in 0.1M phosphate buffer (pH 7.4). Brains were removed immediately after perfusion and post-fixed in a similar fixative without glutaraldehyde for 4–12 h. Three rat brains (cases #96001, #96002, 04012) were cut into 50 µm coronal sections, brain #95124 was cut into 100 µm horizontal sections on an Oxford Vibratome^®. Sections were stained with an antibody against choline acetyltransferase (ChAT: 1:100, courtesy of Dr. F. Eckenstein, University of Washington). Additional processing of alternate sections of cases 96001 and 96002 is described in Zaborszky et al., (2005). Monkey brains fixed in 4% paraformaldehyde were cut on a freezing sliding microtome into 50 µm coronal sections and stained with an antibody against the low affinity NGF receptor; in monkey #1 sections immunostained were 300 µm, in monkey #2, 800 µm apart. Perfusion of the monkeys were performed aseptically and under general anesthesia as described in the publications of Siegel and Read, (1997) and Quraishi et al., (2007).

2.2. Data acquisition

For data acquisition, an image combining computerized microscope system and the Neurolucida® software package (MicroBrightField, Williston, VT) was used. Outlines of the sections, contours of structures and fiducial markers were drawn with a 5 x Plan-NEOFLUAR lens, immunostained, diaminobenzidine labeled cell bodies were mapped at a magnification of 20 x. For practical purposes, the left and right side of cases #96001 and #96002 were mapped and processed separately. In two cases (#95124, # 04012), cholinergic cells only in the right side of the brain were mapped. Similarly, in the two monkeys, only one side of the brain was used for mapping. Labeled cells were mapped from every 6^th sections in cases #96001 and # 96002; in one case using horizontal sections (#95124) all sections were mapped and in case # 04012 every fourth sections were mapped. Cells were detected by focusing through the entire depth of section. Recorded cells were represented in the Neurolucida® database by the x, y and z coordinates of the cell bodies, however the z input information was disabled. Thus all cells detected in each section were collapsed into a virtual plane, sharing the z coordinate of the upper layer of the section. Cells were mapped if the perikaryon is cut through the level of the nucleus that is a light area surrounded by a circular darkly stained cytoplasm. Neurons traced from each section were aligned to a common reference, e.g. the lowest midline point of the corpus callosum. The reference point defines the origin (0,0,0) of the Cartesian coordinate system that Neurolucida uses to represent the mapped data. Mapped sections were aligned using up to 99 alignment points for best-fit matching included in the Neurolucida software program. The database is composed of a stack of aligned sections. The user needs to set only the section distance based upon the cutting parameters and using the specific instructions for mapping serial sections. Sections were aligned at the midline where the imprecision of alignment was < 1 µm. Additionally, sections were aligned using fiducial markers like the corpus callosum, external capsule and rhinal sulcus.

2.3 Initial scan: exploration of inhomogeneity and definition of d

First we introduce a new algorithm to determine the optimal cluster diameter d. The algorithm of the initial scan is as follows. Assume a cell population is defined by the cell bodies b_i, where i=[1,‥,N], where N is the total number of cells and each cell body is defined by its x, y, z Cartesian coordinates. We would like to know whether the spatial distribution of cells is homogeneous or clustered. Here the “homogeneous” means uniform or monotonically changing density in all 3 dimensions. In contrast, we define the distribution to be clustered if the density has a non-monotonic change in any of the 3 dimensions. To determine which distribution category is appropriate, we perform the following procedure:

1. We assign a virtual bubble of d diameter to each neuron. The bubble must be smaller than the smallest possible cluster size, in our case twice the size of an average cholinergic cell body; i.e., 50 µm.

2. We count the number of cells within each bubble. Consequently, cells that are closer together than the bubble radius will be counted multiple times.

3. We define a reasonably small number n of cells as the threshold for clusters. The clusters we would like to see as results of the algorithm should contain at least this many cells.

4. We delete all bubbles that have less than n cells. The cells in the centers of remaining bubbles are defined as seeds (s). The number of seeds is equal to the number of bubbles.

5. We simply merge bubbles that share seed points. This is equivalent to tagging all the seeds with the same cluster ID that are less than a bubble radius apart. This step is done by the clustering algorithm (Chapter 2.5), which finds the shortest path between seeds, within which the distance between any two cells is less than the bubble radius.

6. We quantify two values. First, we count the number of bubbles (c) that cannot be merged further. Second, we quantify the total number of seeds. We plot these values (n, d and c on the x, y and z axes, respectively).

7. We increase the bubble diameter and iterate the steps (2–6) until we reach a bubble diameter that is larger than the largest reasonable cluster or larger than the space containing the majority of neurons.

2.4 Determining the optimal cluster size (d)

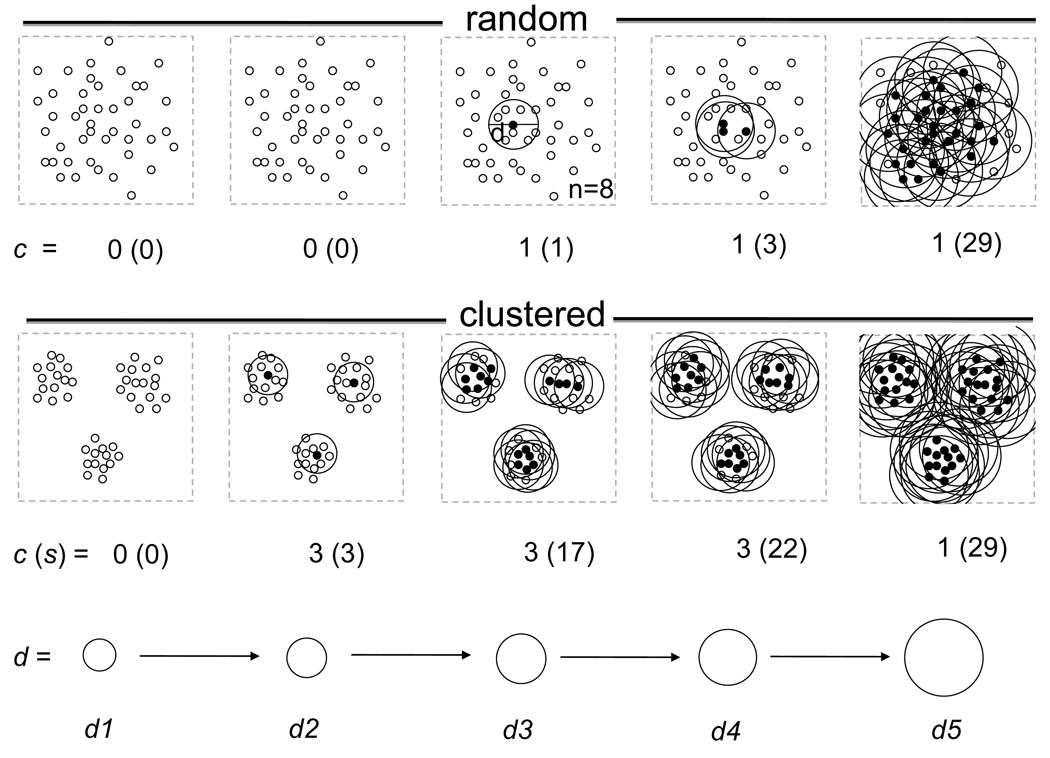
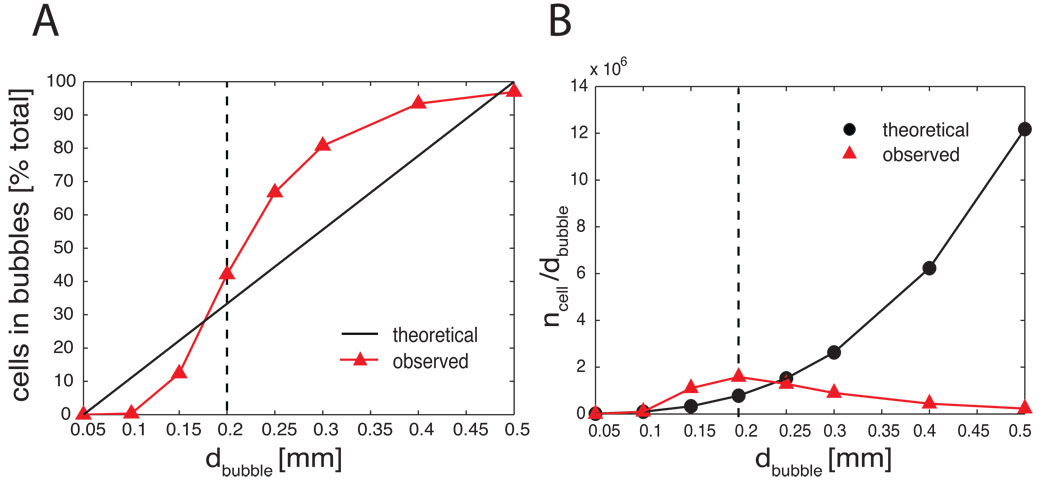
Figure 1 illustrates the algorithm in two different distributions. As a result we keep track of four important variables: independent variables d and n, and dependent variables, such as the number of seeds s in clusters and the number of clusters c. By each iteration of increasing d_i and n_i we obtain a s_ic_i parameter pair where i=[1…k] and k is the number of iterations. We determine the optimal d by plotting the c as a function of d and n. For a homogeneous random distribution, c changes between 0 and 1 (Fig. 1) and the number of cells divided by the bubble diameter increases exponentially as a function of d (Fig. 2B). In contrast, in a clustered distribution the number of clusters increases as a function of d, reaching a plateau, and then starts decreasing until all bubbles collapse into one cluster containing all the cells (Fig. 1 and Fig. 2B). The d at which the number of cells per bubble diameter is maximal (Fig. 2B, dashed line) is indicative of the cluster size that optimally represents the structure of the data. This d is also the diameter at which the largest increase in the % in-bubble cell population is observed (Fig.2A). The convergence of the two parameters strongly suggests an optimal d value for clustering. Given the optimal cluster size d_opt, the resulting cluster parameters c and s together with the cluster positions should correctly represent the data. In the Results section we will test this hypothesis on datasets of the BFCS collected from different individuals of the same and different species.

Figure 1.

Two-dimensional illustration differentiating between random and clustered distribution. The upper panel represents the space filled with randomly distributed cell bodies. Lower panel represents the clustered distribution. To quantify the difference between the two distributions we align a bubble of increasing diameter to each neuron (sub-panels from left to right) and we delete all bubbles which contain less than 8 cells bodies (n=8). After the deletion, the overlapping bubbles are merged and the number of isolated bubbles is determined. In the random distribution, as the diameter of bubbles increases, the number of cell bodies contained by bubbles increases exponentially while the number of bubbles after merging remains only one. In contrast, when we apply the same method for the clustered distribution (lower panel), the bubbles containing at least 8 cells quickly segregate into 3 bubble clusters. These clusters remain segregated after merging the bubbles despite the increasing diameter. The clusters only fuse when the bubble diameter exceeds the inter-cluster distance. Under the panels are the number of clusters and the number of cells contained by the clusters. Filled circles represent cells that are surrounded by 8 cells in the specified diameter (seeds). Small empty circles represent cell bodies for which this assumption is not fulfilled.

Figure 2.

Quantification of “clusteredness” on real and homogeneous random data. (A) The number of cell bodies within clusters (ordinate: % total) is a sigmoid function of the bubble diameter (abscissa). The cell count starts to increase from 0.1 mm diameter and reaches near maximum at d=0.5 mm. The characteristic cluster size d= 0.2–0.3 mm is the diameter at the steepest increase of cell count, containing approximately 40–70% of neurons. (B) Comparing the observed cell distribution with the homogeneous random distribution. Ordinate is the number of cells divided by the bubble diameter. Abscissa is the bubble diameter. As the bubble diameter increases the number of cells per diameter increases exponentially while the observed distribution from real data reaches a maximum at 0.2 mm, marking the putative average cluster size. This analysis is from a gapless series of 100 µm horizontal sections (n=34) stained for choline acetyltransferase containing about 15,700 cholinergic cell bodies (case 95124).

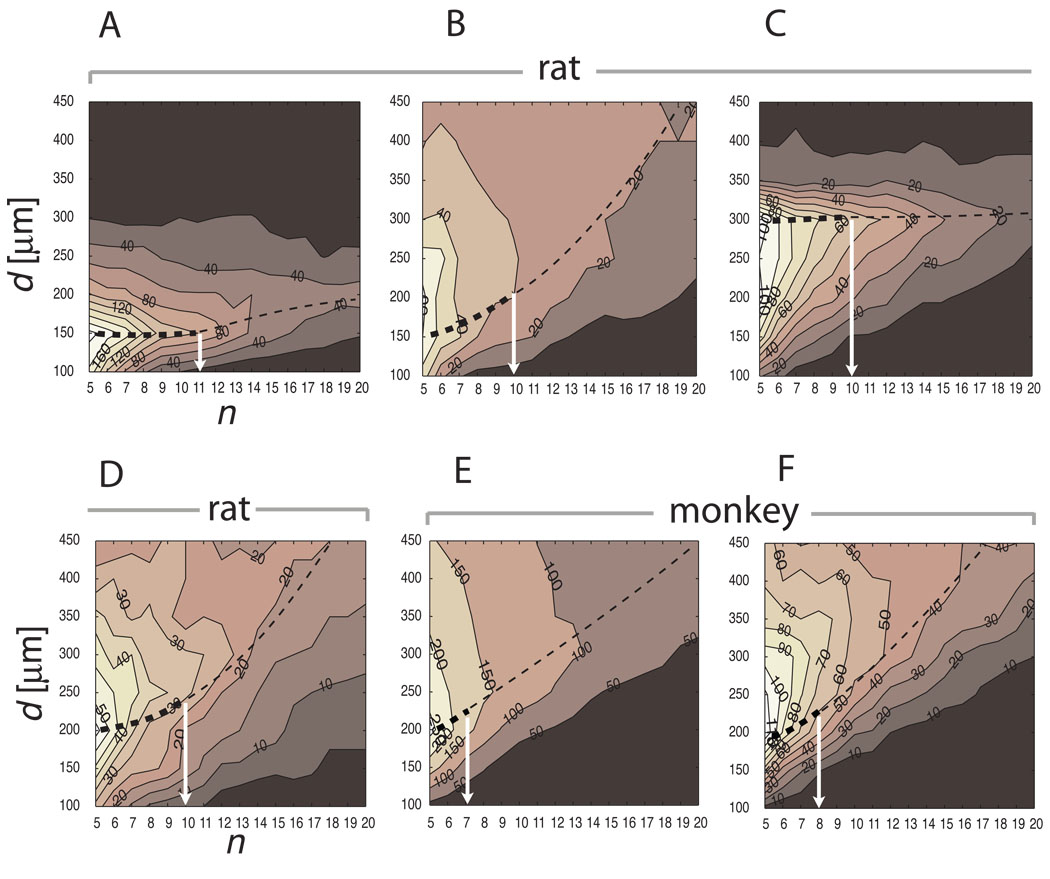
The technical definition of d relies on computing the first local maximum of c at the smallest d at each level of n, then connecting the points of local maxima over the range of n values (dashed lines in Fig. 3A–F). The critical number of neurons within clusters is defined by n where the largest negative gradient of c is observed between n and n+1 (white arrows in Fig. 3A–F).

Figure 3.

The parameter space reveals the characteristic cluster size. The basal forebrain cholinergic system of four rats (A–D) and two monkeys (E–F) were mapped and an initial cluster parameter scan was performed on the 3D cell body distribution. Each histogram depicts the number of clusters c as a function of bubble diameter d (ordinate), and minimum number of nearest neighbors n (abscissa). As the predefined bubble size d increases from 100 µm the number of clusters also increases at a broad range of cell density n. However, the number of clusters starts decreasing beyond a critical bubble size d. The characteristic bubble diameter corresponds the maximum d (thin dashed lines) at which the number of clusters c forms a plateau (thick dashed line) within a range of n-s (white arrows). (A) rat #95124 d=150 n=11 c=22; (B) rat #96001R d=200 n=10 c=9; (C) rat #04012 (VRB) d=300 n=10 c=21; (D) rat #96002R d=200 n=10 c= 8; (E) monkey #1 d=200 n=7 c=26; (F) monkey #2 d=200 n=8 c=5.

2.5 Clustering

Next, when the optimal d has been determined, we perform the clustering. For clustering we use a reduced set of steps assigning bubbles and merging them:

1. We align a bubble of a d diameter to each neuron’s cell body and we count the neighbors, i.e. the number of cell bodies within the enclosed volume. If the number of neighbors exceeds an arbitrary small value of n then we select the neuron as a seed (s).

2. We assign a c index to a set of seed points S if we can find a path P ⊂ S to any s_i , s_j Є S such that

   1. s_i , s_j Є P
   2. for any p_j Є P there is a p_k such that D(p_j, p_k) < d, where D represents the Euclidean distance metric.

3. Next, we compute the total count of s and the number of c used, where s is the number of seeds in clusters and c is the number of clusters. Each s cell will be assigned to its c cluster.

3. Results

3.1. Monte-Carlo simulations

First we investigated the quantitative features of the clusters obtained from the distribution of basal forebrain cholinergic (BFC) neurons relative to the theoretical homogeneous distributions. The database of BFC neurons from a rat brain contained approximately 15,700 cholinergic cell bodies mapped from a gapless series of 100 µm sections. (case #95124). We expressed the number of seeds as % total and the number of seeds per cluster diameter as function of bubble diameter (Fig. 2A, B, respectively). As one can see, the real distribution of % total seeds, i.e. the cells contained by bubbles of a given diameter, follows a sigmoid while the theoretical homogeneous random distribution is linear. The d where the slope of sigmoid is the steepest represents the largest increase of cells captured inside bubbles. Inflating the bubbles beyond this diameter yielded less and less extra cells until it reached a plateau. Therefore, this d is a good estimate of the cluster size in this dataset. This relationship between the theoretical homogenous and the actual data was confirmed when we plotted the total in-bubble cells per diameter ratios against the bubble diameters (Fig. 2B). The maximum of n/d was consistent with the steepest slope at d=0.2 mm in Figure 2A.

3.2. Determination of d and n

Not only we need to determine d but we also define the minimum number of cells n to create a bubble. Thus d and n are the two independent variables for clustering. Because the result of clustering (i.e. s and c) is critically dependent on d and n we must choose them carefully. Because cell density and cluster size varied between structures, animals and species, we could not define them a-priori. To define them for a given preparation we scanned the parameter space of the number of nearest neighbors n and d within a reasonable range of these variables and compute c. The reasonable range of our interest was d=100–450 µm with 10 µm steps and n=5–20 cells per bubble with step size 1. The example in Figure 3A represents the results of parameter scanning on the basal forebrain cholinergic cells from case #95124. The number of detected clusters (c), indicated by the numbers next to the iso-contour lines, monotonically decreases with increasing n. In contrast, c values form a peak at a narrow range around 150 µm. This peak represents an optimal bubble diameter for clustering because it is just large enough to incorporate the majority of cell bodies and just small enough to separate clusters before the bubbles start to fuse and c declines. This peak can be followed as a crest within a few decreasing steps of n until it declines. Therefore, we used the combination of d_j and n_i for which c is maximal, in rat case 95124 d=150 µm and n=11 (Fig. 3A, Fig. 4, Fig. 5).

Figure 4.

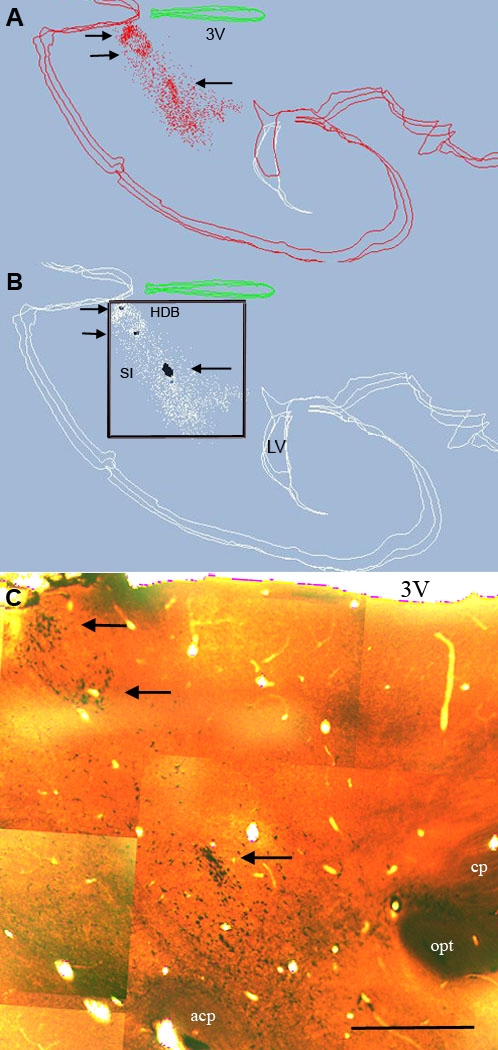
Distribution of cholinergic cells (red) from three plotted sections (A) and clusters as identified in the cluster program (B). For clarity cholinergic cells forming seeds in (B) are labeled in black all other cholinergic cells shown in white. Case #95124, sections 7–9. (C) Montage from one of the sections to compare the computed clusters with the location of high density cell aggregates (arrows). acp= anterior commissure; cp= cerebral peduncle; opt=optic tract; 3V= third ventricle HDB= horizontal limb of the diagonal band; SI=substantia innominata; LV=lateral ventricle. Two parallel arrows point to clusters in the HDB. Single arrow points a large cluster in SI. Bar scale: 1 mm.

Figure 5.

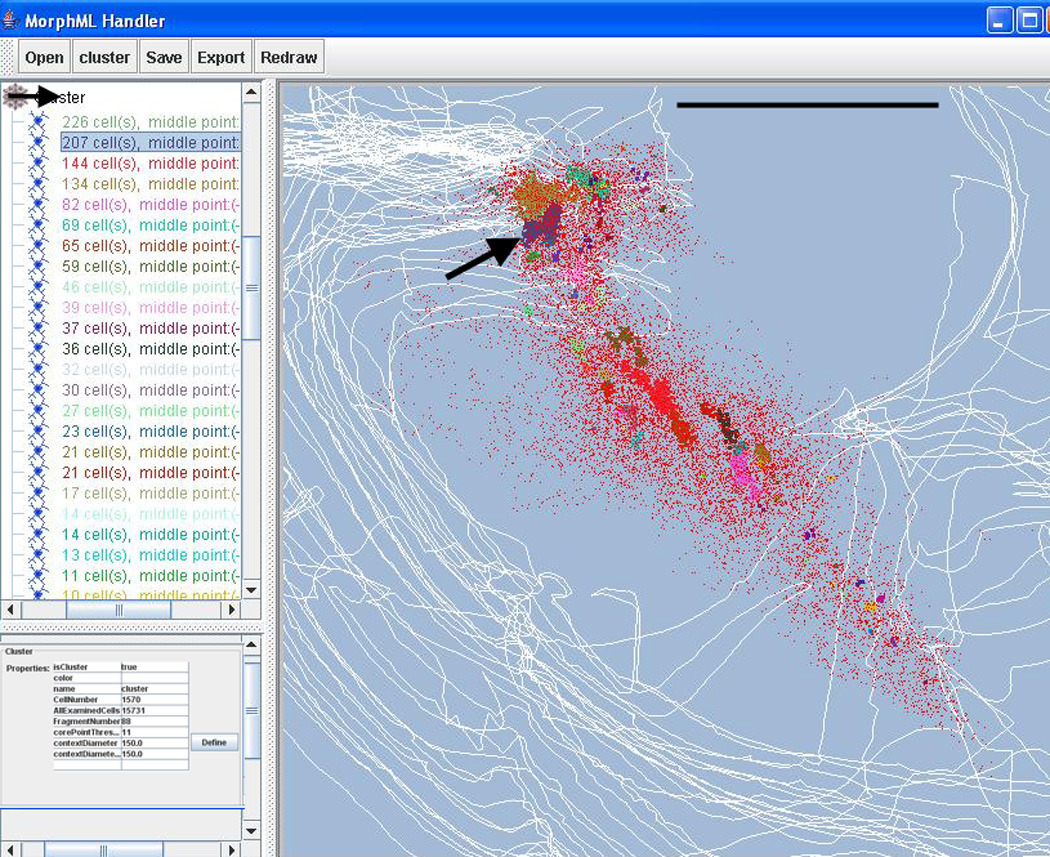
Screenshot of the VRB program during clustering. The tree displays the various clusters identified by their seed numbers. Arrow point to cluster with 207 seeds. The bottom form on the left displays the parameter used for clustering. The right window shows a dorsal view of the cholinergic cells, case #95124. The colors of the various clusters correspond to the colors of clusters as identified in the tree. Cluster with 207 seeds is marked with an arrow in the window. The parameters for cluster identification (lower left window) were: n=11; d=150 µm; c=22. Outlines of individual sections are in white. Bar scale: 2.5 mm

We computed the parametric cluster scans for eight individual basal forebrain cholinergic systems obtained from four rats (right and left sides are separately processed in cases #96001, #96002), and two monkeys. Figure 3 summarizes the results. Despite the difference in species, preparations of tissues, sectioning, and number of traced cells, the emerging pattern is that the sizes of clusters are relatively uniform (150 ≤ d ≤ 300 µm), and to capture them we need to look for at least n=7–11 neurons per bubble. The parameter that changes most dramatically between preparations and species was the number of clusters c, which varied between 5 and 26 (Fig. 3F and E, respectively). The main differences between these two preparations were the cell number (5,763; 14,041) and average cell density, which resulted in a larger number of small clusters in the higher cell density preparation than in the lower cell density preparation (Table 1). A closer inspection of all the histograms of within-clusters cell counts revealed a mixture of binomial and exponential distributions for each individual brain (not shown). The exponential part incorporated a large number of very small clusters containing less than 20 homogeneously distributed neurons. The binomial part reflected the larger clusters with at least 20 neurons in them, which were considered as the "true" structural clusters. Therefore, to filter out the large number of small clusters we applied a standard threshold of 20 seeds or more per cluster when quantifying the clusters for a given preparation.

Table 1.

Cholinergic cluster parameters in rat and monkey

Species/ID	plane	# of CH cells	Section distance (µm)	n	d	c	Mean s/c
96001L rat	coronal	3,427	300	10	200	11	59
96001R rat	coronal	3,259	300	10	200	9	70
96002L rat	coronal	3,269	300	10	200	10	53
96002R rat	coronal	2,975	300	10	200	8	68
04012 rat	coronal	5,181	200	10	300	21	49
95124 rat	horizontal	15,732	-0-	11	150	22	52
Monkey #1	coronal	14,041	300	7	200	26	52
Monkey #2	coronal	5,763	800	8	200	5	25

For definition of n, d and c, see Materials and methods. s=seed

3.3. Clustering in the VRB program from rat subjects

After the initial scan of the cluster parameter space and the definition of relevant cluster parameters we performed the third phase, the actual clustering of cholinergic neurons for each brain with the parameters individually tailored to that data. Figure 4 illustrates the cluster detection from a rat data base (rat #95124). The top panel represents the location of mapped cell bodies of cholinergic neurons within 3 sections. The middle panel identifies 3 high-density clusters (black markers). The montage made from one of the sections shows the distribution of cholinergic cell bodies and validates the cluster detection. The complete clustering of the same brain is seen on a screenshot from the VRB program in Figure 5. We ran the BC on rat #95124 using d=150 and n=11. The program detected c=87 clusters, from which 22 contained 20 or more seeds which are visually identified by labeling each seed neuron with a color specific for the given cluster. The left panel of the graphical user interface (GUI) lists the basic statistics of each cluster. Note that some clusters have spherical shapes while others are rather elongated. Nevertheless, the different cluster topologies are equally well recognized. Also note, that a significant number of cells remain unassigned to any cluster (red dots). This is an important feature that makes this algorithm favorable against a number of traditional clustering algorithms such as k-means, which assigns every point to clusters even if they are apparently not associated with any cluster core. Figure 6 shows the distribution of cholinergic clusters in four rat subjects viewed approximately from the same angle. Note, that case 95124 was cut in gapless horizontal series, while in the other three brains the coronal planes were taken from 200 µm or 300 µm series. Despite the differences in the section plane between animals the cluster sizes and statistics are similar (Table 1).

Figure 6.

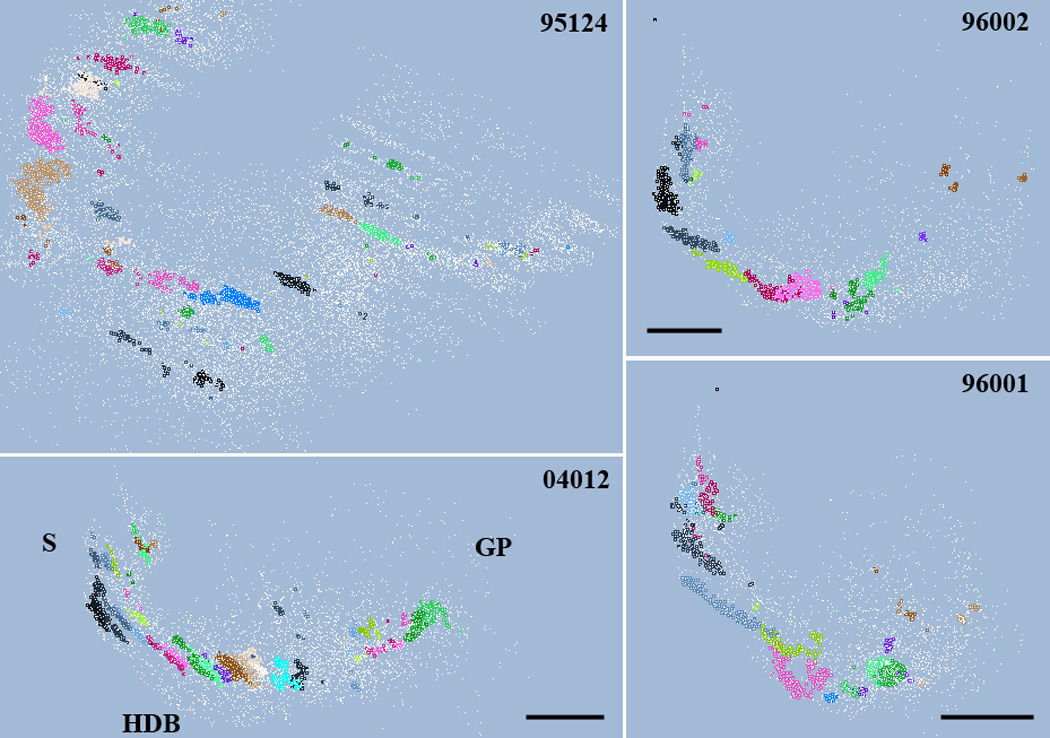
Distribution of cholinergic cells (unassigned in white) and clusters (in various colors) viewed from approximately the same angle in four different rats. Case 95124 were cut in horizontal plane; the three other brains were cut coronal. Cluster parameters are summarized in Table 1. The location of the septum (S), horizontal limb of the diagonal band (HDB) and globus pallidus (GP) are indicated. For better view of the clusters, section outlines are omitted. Scale in case #04012: 0.85 mm; case 96002: 1mm; case 96001: 1.5 mm.

3.4. Clustering in the VRB program from monkey subjects

Next, we investigated the effect of predefined bubble size on the clusters of a monkey cholinergic database (monkey #1, Table 1; Fig. 7). This is not part of the standard procedure and we only demonstrate it to signify the importance of choosing the optimal clustering parameters. We varied the bubble size between 100 and 700 µm while keeping the number of neurons per bubble the same (n=8). Figure 7 represents six clustering results using d=100, 200, 300, 400, 500, 700 µm. As evident from the figure, the d=100 µm detected only a very few high-density clusters and left the majority of neurons unassigned. Overall, d<200 µm failed to capture the organization of the cell population. In contrast, d=200–500 µm recognized the highest density regions and captured the main structural components of the system. Again, note the diversity of cluster topology, which would fail any non-cell centered and non-density based clustering algorithm on this data. By further increasing d we reached the bubble diameter (d=700 µm) that forced to fuse bubbles, which made the originally segregated population of bubbles to collapse into a single cluster. Thus although 700 µm bubbles are certainly inadequate to capture the structural organization of the basal forebrain cholinergic system, they may work well in other structures. The optimal range (200–500 µm) is consistent with the initial parameter scan on both monkey databases (Fig. 3E,F).

Figure 7.

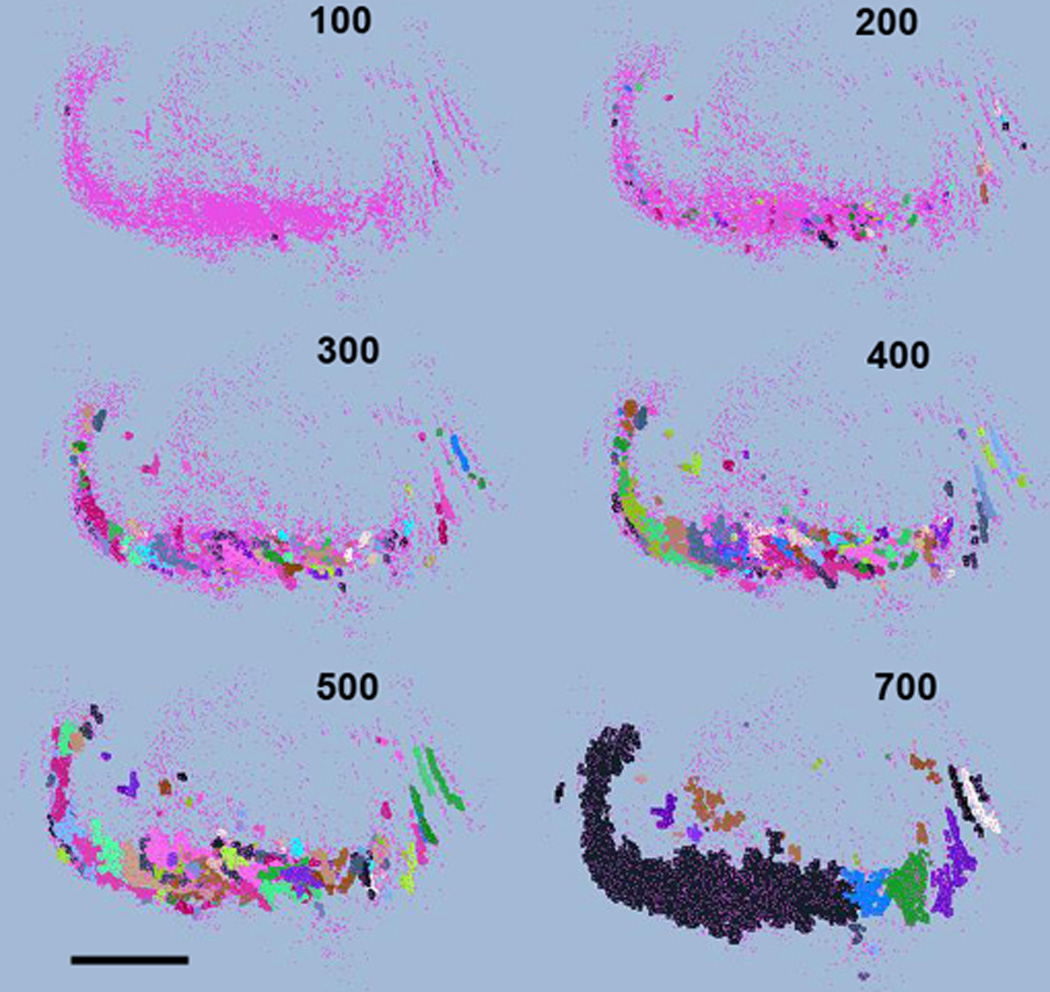
Distribution of clusters from monkey #1 using increasing cluster diameter (from 100 µm to 700 µm) while keeping n=8. Medial is septum, lateral is globus pallidus. Scale: 3.0 mm

When the relevant bubble diameters (d) and cell density (n) had been determined for six individual brains (4 rats and 2 monkeys), we performed a final clustering on them with those parameters. The main results, including the dependent variables number of clusters (c), and mean seeds per cluster (s/c), are summarized in Table 1. Despite the large difference in total cell counts (mean total cell count=6,706; SD=5,1667; N=8), diverse section orientation, and different section gaps the resulting seeds-per-cluster values, i.e., the average number of seeds within a cluster, are surprisingly consistent across preparations and species (grand mean s/c = 53.50; SD=13.89; N=8). Another interesting pattern is that while the average seed density within clusters, the optimal bubble diameter and the seed density thresholds are hardly different across specimens, the number of clusters substantially vary (mean c=14; SD=7.78; N=8). This difference in cluster numbers may be caused by the difference in section gaps, where a larger number of clusters can be lost between sections separated by larger distances (see Discussion 4.1).

3.5 Implementation of the BC algorithm in the VRB program

The VRB program (http://www.virtualratbrain.org/) was developed to support 3D visualization of large neuron populations and to provide data transformation capabilities such as warping. The visualization function includes navigation tools, such as rotation along three axes and zoom-in zoom-out functions. The VRB program uses a special XML format (MorphML) for data modeling developed by Crooke et al. (2007) and can export data from Neurolucida® and Accustage files, thus serving a conversion function as well. Since the VRB program was written in Java, it is platform independent. In addition to the high level data mining tools that are already built in the VRB program (such as overlap analysis: http://www.virtualratbrain.org/modules/Tools/) we implemented the BC clustering. For the BC to generate meaningful results we need to supply the cluster parameters we obtain from the initial parameter scan. Since VRB runs in a batch mode and exports the data in Excel files or simple text files, the user can write a simple script (for example, in Matlab) that plots the result of the parameter scan in a format we used in Figure 3 and read the optimal clustering parameters from the figure. In the future, the pre-scan feature could be completely implemented within the VRB program. Figure 5 illustrates a screenshot of the clustering result. The main menus on the toolbar from left to right are file management, clustering, data saving, export and redraw functions. The left panel of the GUI displays the object hierarchy within the file that is open. The objects are the neurons, neuronal sub-structures and various outlines as they appear in the MorphML description language (Crooke et al., 2007). The clustering function initiates BC. At the end of clustering a new object “Cluster” is created, which describes all the clusters with the total number of seeds included in descending order. The cluster description is color-coded according to the corresponding cluster colors in the data display. Clicking on a given cluster description at the object panel highlights the corresponding cluster in the graphical display, allowing the user quickly explore the resulting clusters in 3D. The clustering parameters can be quickly changed in the lower left corner (not shown in this figure) and the user can assign a different color to a selected cluster. The whole clustering takes only a few seconds and the graphical display automatically updates. The effect of manually changing d and n can be quickly explored and this is how we created Figure 7. Because most data are digitized from individual brain sections of the same brain and assembled together by using special software, the artificial gap between sections cause a spurious clustering artifact. Specifically, clusters tend to segregate along section gaps. In order to avoid this artifact, the user can define the bubbles by diameter and bubble height, where a bubble height larger than section gap enables merging bubbles across sections. This feature allows estimation of the real clustering structure independent of the section separation.

4. Discussion

We introduced a novel clustering procedure that is based on a broader class of “bubble clustering” (BC) methods. We demonstrated that BC is efficient for discovering clusters from large 3D neuronal databases and provides an objective method of quantifying them. We assumed that cells in the 3D database are represented by the Cartesian coordinates of their cell bodies. The VRB software provides additional warping tools and a reference brain (see http://www.virtualratbrain.org) to make an individual database and clustering compatible with other databases (Nadasdy et al., 2006). The procedure we described here is a three-stage process. It relies on pre-scanning the data by BC algorithm, then defining the optimal clustering parameters, followed by the actual clustering. We demonstrated that the stepwise bubble inflation method is capable of capturing the optimal clustering parameters and provides a consistent result within species and meaningful information when comparing the results across different species. Moreover, when the same algorithm was applied to render high-density volumes in a complex architecture of the basal forebrain cholinergic system, it was able to detect a diverse topology of clusters that incorporated the majority of neurons, thus providing a relatively unbiased method to parse the functional sub-structures of the cholinergic system. Nevertheless, the BC algorithm is by no means limited to clustering cell body databases. It can be applied to any spatially well-defined neuronal structures, sub-structures or molecular markers.

4.1. Technical considerations

Although bubble clustering methods are by far not the fastest clustering algorithms, they are sufficiently fast to run on a PC and complete the clustering of data consisting of less than 10,000 cells within a few seconds. The cause of sluggishness is in the core of the algorithm; i.e., rendering bubbles for each neuron and counting the nearest neighbors within them. During this process, a large number of cells are being counted multiple times. Shortcuts, such as subsampling the data to optimize the algorithm for speed, are possible to implement, but it was unnecessary for our given data sizes. On the other hand, the largest fraction of time is spent during the pre-scanning process. We remark that the definition of n and d in the current software implementation of BC is not completely unsupervised; the user needs to determine the optimal clustering parameters. However, extracting the optimal parameters from the pre-scan process could be done automatically by determining the range in the n-d plots within which the global maximum is located. If pre-scanning will be implemented as a completely unsupervised clustering process, then a processing-time optimization has to be considered.

A number of factors concerning the tissue preparation influence the reliability of the quantitative assessment. For example, the clustering algorithm is very sensitive to the spatial gaps between adjacent sections. Even if neurons were traced in 3D from a series of sections, the gaps between sections introduce artificial cluster boundaries. As can be seen in Table 1, large differences in cluster numbers were found between individuals of the same rat strain. Part of these discrepancies derive from the difference in section distances, for example between 96002R rat and VRB rat, where at 200 µm section distance we found 21 clusters while at 300 µm only 8. The smaller section distance partitioned the basal forebrain cholinergic space into more sections, consequently yielding to more artificial clusters. In order to compensate for this bias we introduced the vertical scalability of bubbles, which if it is set to be larger than the section distance, allows capturing clusters across adjacent sections. Although this does not completely eliminate the bias deriving from the gaps, it alleviates it. Section orientation may also influence bubble clustering. The orientation of clusters relative to the sectioning plane could be critical, especially when taken into consideration together with section distances. Elongated cell clusters can be split in half by section gaps. If they are split, the two split parts are not necessarily aligned when projected to the plane of sections, unless they are exactly perpendicular to the section plane. Thus, for any BC method the likelihood of false cluster division is high.

The last factor that the BC method is sensitive to is the average cell density. Different histology and cell mapping procedures label different proportions of neurons. In addition to the large inter-individual differences in cell density (discussed in section 4.3), the differences deriving from histology may significantly modify the clustering result. Neurons in sparsely sampled data may not display the same clusters as neurons from a higher density sample. Obviously, the more neurons are labeled, the more reliable the clustering algorithm. To handle the sparseness of sampling the user can control n (the minimum number of neighbor neurons) to define a bubble. However, sparsely sampled real neuronal clusters can easily dissolve in the background of unassigned neurons and remain undetected. The 50 µm Vibratome sections (cases 96001; 96002; 04012) during the histological processing shrank to 16–16.5 µm; the thickness of plastic sections (case 95124) was 91.5 µm. However, because shrinkage effect was uniform within the brain and we defined the optimal cluster diameter from the given brain, hence tissue shrinkage did not affect the cluster computation for individual brains. On the other hand, cell detection for comparison should be performed in rats of the same age and in approximately the same area, with respect to reference structures. In fact, the medial, lateral, dorsal and ventral extremes of the cholinergic cell distribution were taken as a 3D framework to incorporate the entire rostro-caudal cholinergic space (e.g. the space occupied by cholinergic cell bodies) in order to avoid problems comparing dissimilar spaces. Due to differences in processing, we did not compare cluster locations between individual brains because that would require warping the brains to a common reference.

We need to point out that all of these potential biasing factors are not the caveats of the algorithm, but rather they derive from the limitations imposed by the tissue preparation. By improving the histological, tissue sectioning and digitization process, these problems could be completely eliminated.

4.2. Functional considerations: clusters as integrative units in the basal forebrain?

In the neocortex, since Lorente de No (1938), it is assumed that a defined group of vertically placed neurons could form elementary functional units (cylindrical units, columns), for which Mountcastle (1957) and Hubel and Wiesel (1959) found experimental evidence, although there is ample discrepancy as to how functional columns should be defined anatomically (e.g. Szentagothai, 1978, Mountcastle, 1998; Shepherd et al., 2005; Helmstaedter et al., 2007; Douglas and Martin, 2007; Markram, 2008; Stepanyants et al., 2008).

In subcortical structures, including the striatum (Gerfen 2004), the superior colliculus (Chevalier and Mana, 2000), the pontine nuclei (Leergard and Bjaalie, 2007) and the brain stem auditory nuclei (Malmierca et al. 1998) neuronal clusters can be visualized, which have been suggested to represent specific processing streams in otherwise homogeneously distributed large cell populations. 3D reconstructions with relatively rudimental computational power suggested that cholinergic neurons and the three classes of non-cholinergic, calcium-binding protein-containing neurons (parvalbumin, calretinin and calbindin) show large-scale association in the entire basal forebrain (Zaborszky et al., 1999). By applying density and relational constraints on cell populations combined in a common 3D coordinate system, we were able to show that cholinergic and non-cholinergic neurons show small-scale associations in the form of regionally specific cell clusters in the entire cholinergic basal forebrain space (Zaborszky et al., 2005). Although the existence of cell aggregates in the cholinergic forebrain has been known for more than 20 years, only by adopting and developing new visualization and analytical tools has it become possible for the first time that these cell clusters can be quantitatively treated and specific questions can be raised relating to the organizational principles of the basal forebrain cholinergic system. A preliminary analysis of the spatial relationship between cholinergic cell clusters and various neuronal populations whose cortical targets have been defined (Zaborszky et al., 2008a), suggest that cell clusters in the basal forebrain may serve an associational function that involves transmitting information from specific locations in the basal forebrain to a small subset of cortical areas that most likely are interconnected. Such a network may play a role in attention (see a thorough discussion of attention and how current concepts of basal forebrain organization may support attention in Parikh and Sarter, 2008; Sarter et al., 2009).

4.3. Interindividual differences

Although our preliminary data suggest that the various cholinergic cluster parameters (Table 1) are similar among individuals of the same strain, a thorough quantitative investigation is necessary to estimate the preciosity by which the location and projection target of the clusters can be identified; a prerequisite for interpreting basal forebrain cluster function. The interindividual variance may be due to the histological processing (exact plane of section, section distance, tissue shrinkage, etc), genetic, developmental, environmental factors and age.

Anatomical and imaging studies have revealed significant interindividual variability in the cell number of particular brain structures in rodents and primates, including humans. For example, the number of neurons in the primary visual cortex of rhesus monkeys varies by more than 50% (Pakkenberg and Gundersen, 1997) and interindividual variability in the volume of the human nucleus basalis has been described recently by us (Zaborszky et al., 2008b). We have also shown differences in the cell numbers of midbrain TH cells among genetically different mouse strains (Zaborszky and Vadasz, 2001) and it has been recently described that orientation and ocular dominance columns in cats show interindividual differences that depends on genetic background (Kaschube et al., 2002, 2003). While interindividual variability in the past has often been regarded as ‘noise’ that has to be minimized, more recent studies in humans suggest that interindividual differences point to fundamental mechanism of brain development, and structure-function relationship (Fox and Raichle, 2007). To minimize differences between subjects that may relate to genetic differences, in the future we need to choose the genomically characterized rat brown Norway strain (Twigger et al., 2008) or the genomically characterized mouse strains (http://phenome.jax.org/pub-cgi/phenome/mpdcgi?rtn=docs/pristrains_tree) in order to find out if interindividual variability in basal forebrain cholinergic clusters may relate to inter-trial variability in specific attention tasks.