Combination of Compressed Sensing and Parallel Imaging for Highly Accelerated First-Pass Cardiac Perfusion MRI

Abstract

First-pass cardiac perfusion MRI is a natural candidate for compressed sensing acceleration since its representation in the combined temporal Fourier and spatial domain is sparse and the required incoherence can be effectively accomplished by k-t random undersampling. However, the required number of samples in practice (three to five times the number of sparse coefficients) limits the acceleration for compressed sensing alone. Parallel imaging may also be used to accelerate cardiac perfusion MRI, with acceleration factors ultimately limited by noise amplification. In this work, compressed sensing and parallel imaging are combined by merging the k-t SPARSE technique with SENSE reconstruction to substantially increase the acceleration rate for perfusion imaging. We also present a new theoretical framework for understanding the combination of k-t SPARSE with SENSE based on distributed compressed sensing theory. This framework, which identifies parallel imaging as a distributed multisensor implementation of compressed sensing, enables an estimate of feasible acceleration for the combined approach. We demonstrate feasibility of 8-fold acceleration in vivo with whole-heart coverage and high spatial and temporal resolution using standard coil arrays. The method is relatively insensitive to respiratory motion artifacts and presents similar temporal fidelity and image quality when compared to GRAPPA with 2-fold acceleration.

Introduction

First-pass cardiac perfusion MRI is a promising and much-studied modality for non-invasive assessment of coronary artery disease [1-2]. However, robust implementation for routine clinical use can be technically challenging. In particular, the pulse sequence must be carefully designed to balance conflicting requirements, such as spatial resolution, temporal resolution, contrast-to-noise ratio (CNR), and spatial coverage. Currently, parallel imaging techniques for dynamic MRI, such as TSENSE [3] and TGRAPPA [4], can be used to acquire 3-4 slices per heart beat with adequate spatial and temporal resolution for clinical interpretation, using commercially available radiofrequency (RF) coil arrays.

To extend the slice coverage and/or increase spatial and temporal resolution, more advanced techniques are needed to obtain higher acceleration factors. Such techniques include k-t BLAST and k-t SENSE [5], k-t GRAPPA [6], and SPatiotemporal domain-based unaliasing employing sensitivity Encoding and Adaptive Regularization (SPEAR) [7], which exploit spatiotemporal correlations in the dynamic MRI data either alone or in combination with coil sensitivity information. In these methods, the k_y-t space signal is sampled on a sheared grid, which results in reduced signal overlap in the sparse temporal Fourier domain (y-f), and as a result higher undersampling rates are feasible. However, dynamic training data are required to establish an aliasing pattern in the y-f domain, which reduces the effective acceleration rate. For perfusion imaging, training data must be interleaved with undersampled imaging data to reflect similar contrast enhancement and avoid misregistration due to respiratory motion. Previously described perfusion studies using k-t techniques have reported acceleration factors greater than 6 [8-10]. However, respiratory motion represents a source of reconstruction error for these techniques, since signal overlap increases in the y-f domain due to the presence of higher temporal frequencies and results in residual aliasing artifacts.

An alternative method for reconstruction of undersampled data is compressed sensing, which is based upon the principle that an image with a sparse representation in a known transform domain can be recovered from randomly undersampled k-space data using a non-linear reconstruction [11]. Unlike k-t BLAST and k-t SENSE, compressed sensing does not require training data, and, as a result, it may be less sensitive to inconsistencies between training and imaging data. Application of compressed sensing to dynamic MR imaging has been presented in methods such as k-t SPARSE [12], compressed sensing dynamic imaging [13] and k-t FOCUSS [14], using the temporal FFT as the sparsifying transform (y-f space as the sparse domain) and k_y-t random undersampling. However, the maximum acceleration rate reported by a previous first-pass cardiac perfusion study employing the method described in [13] was only four [15].

Maximum acceleration rate in compressed sensing is determined by image sparsity. In practice, the number of required samples is approximately three to five times the number of nonzero coefficients in the image or in some appropriate transform domain [11,16]. When multiple receiver coils are employed, compressed sensing can be combined with parallel imaging techniques [17-19] to obtain higher accelerations. Previous combinations for non-dynamic MRI have framed compressed sensing as a regularization method for parallel imaging reconstructions such as SENSE, and have demonstrated increased acceleration capability over each of the techniques applied separately [20-23]. Another method applied coil-by-coil compressed sensing to reconstruct regularly aliased images and then used standard SENSE reconstruction to remove the aliasing [24]. This two-step approach, however, runs the risk of inefficiency, since correlations between coils are only used at the second step. The recently introduced theory of distributed compressed sensing [25] extends compressed sensing to include multiple sensors, in order to reduce the number of required samples by exploiting the idea of joint sparsity in the multi-signal ensemble rather than simply exploiting separate sparsity.

In this work, a combination of the k-t SPARSE and SENSE techniques is employed for highly-accelerated first-pass cardiac perfusion imaging using a temporal Fourier transform as the sparsifying transform. It is demonstrated that this approach represents a form of distributed compressed sensing, exploiting joint sparsity in multicoil images rather than coil-by-coil sparsity [26,27]. Using the theoretical framework of distributed compressed sensing, estimates of maximum feasible accelerations for the combination of k-t SPARSE and SENSE are derived. For experimental validation of the maximum practical acceleration rate, fully-sampled, first-pass cardiac perfusion MRI data were acquired in vivo and then undersampled to various degrees. Highly-accelerated in vivo perfusion data were then acquired and reconstructed to demonstrate the feasibility of the method. Sensitivity to respiratory motion was evaluated in terms of residual aliasing artifacts. A comparison of the proposed method at 8-fold acceleration with commercially available GRAPPA at 2-fold acceleration was performed to evaluate their relative performance. Finally, 8-fold accelerated k-t SPARSE-SENSE images were obtained in a patient with acute myocardial infarction.

Theory

Compressed Sensing for First-Pass Cardiac Perfusion MRI

The requirements for a successful application of compressed sensing are: (a) image sparsity in a known transform domain, i.e., few large coefficients and many small coefficients that can be omitted without loss of image quality; (b) incoherent undersampling artifacts in the sparse domain, i.e., the undersampling artifacts look like additive noise; and (c) non-linear reconstruction to recover the sparse coefficients. The cardiac perfusion signal is sparse in the combined temporal Fourier and spatial domain (y-f space) since only portions of the field of view require the full temporal bandwidth and the other regions have only static information or at low temporal frequencies (Fig. 1). The required incoherence can be obtained by randomly omitting phase-encoding lines (k_y) with a different pattern for each time point (t), generating a random undersampling pattern in k_y-t space. Compared with k_y-only random undersampling, k_y-t random undersampling increases the incoherence, since the undersampling artifacts are incoherently distributed along two dimensions rather than one.

Fig. 1.

Conceptual illustration of the compressed sensing technique for cardiac perfusion MRI. (a) Sparsity: the fully-sampled k_y-t data is sparse in y-f space. (b) Incoherence: k_y-t pseudo-random undersampling preserves the original sparse representation in y-f space and presents artifacts that look like additive noise (pseudo-noise). (c) Non-linear reconstruction: the sparse coefficients in y-f space can be recovered with a non-linear reconstruction that minimizes the number of non-zero coefficients (minimum L₁-norm).

Combination of Compressed Sensing and Parallel Imaging

The perfusion data (in k_x-k_y-t space) acquired in each coil can be represented as:

$${\mathbf{m}}_l={\mathbf{F}}^s{\mathbf{S}}_l\mathbf{d},$$ (1)

where d is the perfusion image series to be reconstructed in x-y-t space, F^s is the spatial Fourier transform and S_l represents the coil sensitivities (in x-y space). Note that k_x is fully-sampled. Instead of applying compressed sensing to each coil separately, the multicoil SENSE model given by the concatenation of the individual models is solved:

$$\mathbf{m}=\mathbf{Ed},$$ (2)

where $\mathbf{m}=\left[\begin{array}{c}\hfill {\mathbf{m}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{m}}_{N_c}\hfill \end{array}\right]$, $\mathbf{E}={\mathbf{F}}^s\left[\begin{array}{c}\hfill {\mathbf{S}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{S}}_{N_c}\hfill \end{array}\right]$ and N_c is the number of coils. The compressed sensing reconstruction of the SENSE model is given by:

$$\widehat{\mathbf{d}}=\arg \underset{\mathbf{d}}{\min }\{{\Vert \mathbf{Ed}-\mathbf{m}\Vert }_2^2+\lambda {\Vert {\mathbf{F}}^t\mathbf{d}\Vert }_1\},$$ (3)

where F^t is the temporal Fourier transform, ${\Vert .\Vert }_1$ is the l₁-norm or sum of absolute values given by ${\Vert \mathbf{x}\Vert }_1={\sum }_i\mid x_i\mid$, and ${\Vert .\Vert }_2$ is the l₂-norm given by ${\Vert \mathbf{x}\Vert }_2={\left({\sum }_i{\mid x_i\mid }^2\right)}^{\frac{1}{2}}$. The l₁-norm term enforces sparsity in the temporal Fourier domain, and the l₂-norm term enforces data consistency with a model error threshold given by ε (ε is usually set to the noise level). λ is a weighting parameter that controls the balance between sparsity in the temporal Fourier domain (right-hand term) and parallel imaging data consistency (left-hand term). The reconstruction problem associated with Eq. (3) represents a combination of k-t SPARSE and SENSE using a temporal FFT as sparsifying transform.

Distributed Compressed Sensing Framework

Previous combinations of compressed sensing and parallel imaging have presented compressed sensing as a non-linear regularizer for SENSE reconstruction [20-23]. Even though the k-t-domain reconstruction problem in Eq. (3) may be solved in practice with regularized techniques such as a nonlinear conjugate gradient algorithm (see Methods), it is difficult from this perspective to estimate theoretical bounds for the expected feasible acceleration. In this work, we present a new framework for combinations of compressed sensing and parallel imaging based on distributed compressed theory [25], in order to assess theoretical bounds on the maximal acceleration.

The combination of k-t SPARSE and SENSE does indeed represent a form of distributed compressed sensing, since joint sparsity is exploited instead of individual coil-by-coil sparsity to reconstruct one image series (d in Eq.'s (1)-(3) above) that represents the combination from all coils. In a general sense, one might expect that enforcing joint sparsity would reduce the number of required samples per coil and add incoherence to the problem. First of all, the signal sampled by each coil is given by the convolution in k-space of the object function and the k-space representation of the spatial coil sensitivity. Therefore, multicoil samples with different spatial information content are simultaneously obtained to reduce the required number of samples per coil needed to reconstruct an unaliased image, just as in parallel imaging [17-19]. Second of all, even though the same k_y-t random undersampling pattern is shared for all coils, the convolution in k-space with the coil sensitivities will generate different incoherent artifacts for each coil.

The theory of distributed compressed sensing enables one to place concrete bounds on this intuitive expectation. In practice, the number of required samples to perform accurate reconstructions in compressed sensing alone using l₁-norm minimization is three to five times the number of sparse coefficients K (3-5K) [11,16]. It has been shown, however, that for a distributed compressed sensing model with a large number of sensors [25], the number of required samples approaches K when different random undersampling patterns are used for each sensor. At first glance, it is not obvious that the case of multicoil acquisition in MR meets this condition, since signals from all coils share the same gradient-based undersampling pattern, albeit convolved with distinct coil sensitivity patterns. One might therefore expect a reduction in incoherence and a departure from the theoretical bounds on signal recovery outlined in [25]. Fortunately, however, parallel imaging itself provides the tools needed to match in practice the theoretical condition of distinct random undersampling. At the core of parallel imaging is a principle of physical regridding, in which signals acquired in multiple coils are recombined to generate signals shifted by some amount in k-space. Using techniques like the Grappa Operating Gridding (GROG) method [28], sets of distinct combinations may in fact be chosen to synthesize signals for new virtual “coils” each with a different random undersampling profile. The price to pay for such physical regridding using parallel imaging would be some loss in SNR, which would be modest in this case, since no large shifts in k-space are required to synthesize a k-space pattern which is effectively uncorrelated with the starting pattern, particularly when large numbers of coils are used. In any case, we are not proposing recombination to virtual uncorrelated coils as a practical reconstruction technique, but rather as a means of demonstrating that the combination of compressed sensing and parallel imaging meets the conditions of distinct random undersampling [25]. We may therefore have some confidence (pending formal mathematical proof of the statistical robustness of reconstruction with virtual uncorrelated coils) that the corresponding limits on accurate recovery of signal in the noise-free case may apply.

Our own work [26] has also demonstrated in practice that increasing the number of coils reduces the required number of samples for accurate combined compressed sensing and parallel imaging reconstruction to a minimum of K. The maximum increase in acceleration which may reasonably be expected by combining parallel imaging with compressed sensing as compared with using compressed sensing alone is then about 3- to 5-fold for large numbers of coils. Of course, the baseline degree of acceleration possible with compressed sensing alone depends upon the level of sparsity of the underlying images in each coil. The maximum additional factor of 3-to-5 with parallel imaging represents an upper bound to what parallel imaging can add to the information which is already present inherently in a coil-by-coil compressed sensing reconstruction.

Methods

Data Acquisition

First-pass cardiac perfusion MRI was performed on two healthy volunteers (2 males; ages 32 and 23) and one patient (male, age 38), with 0.1 mmol/kg of gadopentetate-dimeglumine (Gd-DTPA) (Magnevist, Bayer Healthcare). The patient presented with chest pain, electrocardiogram changes, and elevated troponin (peak 52), 6 days prior to MRI. Diagnostic catheterization showed total occlusion of the left posterior descending artery, but revascularization was not performed because the occluded vessel was small in caliber, very distal, and had collateral flow from other vessels. Human imaging was performed in accordance with protocols approved by the Institutional Review Board at the New York University School of Medicine, and all subjects provided written informed consent.

Data were acquired with a modified TurboFLASH pulse sequence on a whole-body 3T scanner (Tim Trio, Siemens Healthcare, Erlangen, Germany). The radio-frequency excitation was performed using the transmit body coil, and 6 anterior elements and 6 posterior elements of the Siemens body matrix array were used for signal reception.

In one volunteer, a fully-sampled perfusion image acquisition was performed in a midventricular short-axis location at mid diastole (trigger-delay 400 ms) with an image matrix of 128×128. This data set was used as a template to simulate acceleration rates R = 4, 6, 8, 10 and 12 (Fig. 2). The relevant imaging parameters include: FOV = 320×320mm², slice-thickness = 8mm, flip angle = 10°, TE/TR = 1.2/2.4ms, BW = 1000Hz/pixel, RF pulse train saturation pulse [29], TD = 10 ms, repetitions = 40, spatial resolution = 3.2×3.2mm², and temporal resolution = 307ms.

Fig. 2.

Fourier reconstruction of the fully-sampled data (R = 1), coil-by-coil compressed sensing (Coil-by-coil k-t SPARSE) and k-t SPARSE-SENSE reconstruction with simulated acceleration factors of R = 4, 6, 8 and 10 for (a) peak blood enhancement and (b) peak myocardial wall enhancement.

In a separate experiment, an 8-fold accelerated multi-slice acquisition with user-defined phase-encoding and temporal (k_y-t) sampling patterns was performed using the same set of imaging parameters with the following exceptions: image matrix = 192×192, spatial resolution = 1.67×1.67mm², TE/TR = 1.3/2.5ms, and temporal resolution = 60ms. R=8 was chosen based on the simulated acceleration results, which are presented below. Low spatial resolution coil sensitivity data were acquired during the first heartbeat, using an image acquisition matrix of 64×24. Acceleration was accomplished using k_y-t random undersampling with variable k-space trajectory, where the undersampling pattern along k_y was varied as a function of time, in order to produce the required incoherence of artifacts in the sparse y-f domain (Fig. 1). Sampling more densely at the center of k_y–space increases incoherence and provides a better starting point for reconstruction than uniform random sampling [11]. The k_y sampling was performed using a reverse-centric k-space reordering, in order to increase the contrast-to-noise ratio (CNR), at the expense of slight blurring in the k_y direction [30]. During the first injection of Gd-DTPA (0.1 mmol/kg at 6 ml/sec with a 20ml saline flush), ten short-axis slices were acquired within a breathhold. After 20 minutes, during the second injection of Gd-DTPA (the same parameters as for first injection), a repeat scan was performed under heavy breathing, in order to evaluate the sensitivity to respiratory motion.

In another volunteer, comparison between k-t SPARSE-SENSE with R=8 and commercially available GRAPPA [19] with R=2 was performed by interleaving SPARSE-SENSE and GRAPPA acquisitions within the same heartbeat. This acquisition scheme enabled to compare image quality with identical contrast agent concentration, slice position, and image scale factors. The TD of both acquisitions was varied to keep the same effective recovery time of magnetization between the saturation pulse and the center of k-space acquisition. The relevant imaging parameters included: image acquisition matrix = 128×128, spatial resolution = 3.2×3.2mm², and temporal resolution = 38.4/173ms for k-t SPARSE-SENSE/GRAPPA, respectively.

In the patient with myocardial infarction, the 8-fold accelerated k-t SPARSE-SENSE acquisition was performed using the same parameters as in the breath-held volunteer study. Delayed-enhancement images were obtained using a phase-sensitive inversion recovery (PSIR) [31] pulse sequence, 15 minutes after the administration of the contrast agent.

Acceleration Analysis

Estimates of expected feasible accelerations were computed using the fully-sampled data set. The maximum compression ratio (CR) provided by the temporal FFT was assessed by truncating the representation of the fully-sampled data in x-y-f space and computing the difference with the full representation in the x-y-t domain. A threshold of 5% root mean square error was used to establish the maximum CR. The maximum feasible acceleration for compressed sensing alone was then estimated to lie between CR^max/3 and CR^max/5. The increase in acceleration provided by the combination with parallel imaging was assessed by reconstructing the fully-sampled data set with simulated accelerations and comparing with the original data.

Image Reconstruction

Combination of k-t SPARSE and SENSE was implemented in Matlab (The MathWorks, Natick, MA) by extending the SparseMRI method [11] to include the time dimension and the coil sensitivities in the acquisition model and to enforce joint sparsity in the reconstruction. A non-linear conjugate gradient algorithm [11] was employed to solve the minimization problem given in Eq. (3), where the l₁-term was computed using the sensitivity-weighted multicoil image combination [32]. The matrix E was not computed explicitly and was replaced by FFT and matrix-vector multiplications, just as in the conjugate-gradient SENSE method [33]. The starting point of the non-linear conjugate gradient algorithm was given by the sensitivity-weighted multicoil image combination of the zero-filled Fourier reconstruction.

The weighting parameter (λ) in Eq. (3) was selected based on simulation results from a sample data set. Specifically, a fully-sampled data set was used to simulated different acceleration rates and was also used as a reference for image quality comparisons. The parameter λ was determined by solving the reconstruction problem with different values and choosing the one that minimizes the error with respect to the fully-sampled data. To apply the selected λ to a different data set, we normalized the intensity of the data set to have the same intensity of the training data. Note that λ was determined only once and that value was used for all subsequent experiments.

For the experiment with simulated acceleration, coil-by-coil compressed sensing was performed for comparison purposes using the k-t SPARSE method [11] followed by sensitivity-weighted multicoil image combination [32].

Image Analysis

Signal intensity time courses were evaluated for the reconstructed perfusion images, using two different manually defined regions of interest (ROIs): one for the entire left ventricle (LV) blood pool and one for the entire myocardial wall. The ROIs were drawn manually, with care to avoid partial volume effects. The myocardial wall curves were characterized by the baseline (pre-contrast) mean and standard deviation, peak and upslope. The upslope was computed using a linear fit of the curve points between 10% and 90% of the relative peak enhancement.

Signal intensity profiles along the x dimension were computed using the central line of the images in Fig. 2 at peak blood enhancement. The spatial profiles were characterized by the myocardial wall signal intensity to assess the effect of spatial blurring on the myocardial wall signal before contrast agent arrival, and by the signal intensity gradient between myocardial wall and left ventricle to assess the sharpness of the image. The intensity gradient was computed using a linear fit of the points between 20% and 80% of the signal increase from myocardial wall to left ventricle.

For the in vivo study with simulated acceleration, the root mean square error (RMSE) with respect to the fully-sampled Fourier reconstruction was evaluated in a subregion surrounding the heart (indicated by the cropped field of view of the images in Fig. 2) and averaged over all time points. The RMSE values were expressed as the percentage of the mean value of the fully-sampled Fourier reconstruction (x_full):

$$RMSE=100\times \sqrt{\frac{\sum _{i=1}^n{\mid x_{acc}\left(i\right)-x_{full}\left(i\right)\mid }^2}{\sum _{i=1}^n{\mid x_{full}\left(i\right)\mid }^2}},$$ (4)

where x_acc is the compressed sensing accelerated reconstruction and n is equal to the number of pixels in the ROI times the number of time points.

Results

Breath-held single-slice experiment with simulated acceleration

k-t SPARSE-SENSE presented superior reconstruction performance when compared to coil-by-coil compressed sensing (Fig. 2). Coil-by-coil compressed sensing RMSE values were 5.3%, 7.9%, 10.5% and 14.4%, whereas k-t SPARSE-SENSE RMSE values were 4.6%, 5.7%, 6.5% and 7.8% for R= 4, 6, 8, and 10, respectively. The myocardial wall signal intensity at peak blood (expressed in arbitrary units) was 177.9 for the fully-sampled Fourier reconstruction; coil-by-coil compressed sensing values were 206.6, 223.9, 288.2 and 348.8, whereas k-t SPARSE-SENSE values were 175.9, 188.2, 188.1 and 244.9 for R= 4, 6, 8, and 10, respectively. The intensity gradient between myocardial wall and left ventricle expressed in arbitrary units per pixel was 262.1 for the fully-sampled Fourier reconstruction; coil-by-coil compressed sensing values were 239.3, 183.8, 174.1 and 109.2, whereas k-t SPARSE-SENSE values were 260.4, 258.9, 242.1 and 190.2 for R= 4, 6, 8, and 10, respectively. The increase in the myocardial wall intensity before contrast agent arrival and the decrease in the intensity gradient were produced by spatial and temporal blurring, which were more significant for coil-by-coil compressed sensing.

The maximum compression ratio provided by the temporal FFT was found to be approximately 18, resulting in predicted maximum acceleration factors between 3.6 and 6 using compressed sensing alone. Coil-by-coil compressed sensing resulted in an adequate reconstruction for R=4 in agreement with previous results [15] and theoretical estimates; however, reconstruction artifacts such as spatiotemporal blurring and residual pseudo-noise were more noticeable for R=6 and increased in prominence with increasing acceleration. Note that low spatiotemporal frequency components result in sparse coefficients with high values, which can be recovered even at high accelerations. On the other hand, high spatiotemporal frequency components present much lower values in the sparse domain, which fall below the pseudo-noise level, and therefore they are more difficult to recover. k-t SPARSE-SENSE presented adequate image quality up to R = 8, which represents a 2-fold increase over compressed sensing alone.

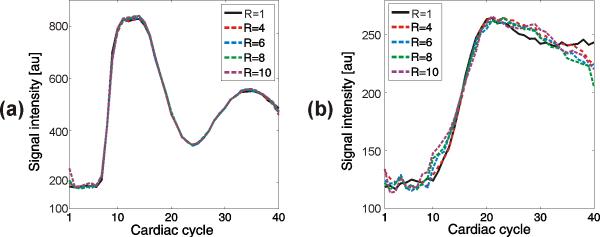
Fig. 3 shows the signal intensity time courses for the blood and myocardial wall for k-t SPARSE-SENSE at different acceleration factors, and Table 1 lists the baseline mean and standard deviation, peak and upslope estimated from the myocardial signal time course. The blood enhancement presented similar temporal fidelity for all accelerations, except for a small amplification of the baseline variation and peak value for higher accelerations. For the myocardial signal-time curve, the mean baseline and peak values were very similar for all accelerations. On the other hand, the baseline variation increased with acceleration, due to the higher pseudo-noise level, and the upslope decreased with acceleration, due to a small loss of high temporal frequencies in the reconstructed images. The upslope decrease with respect to the fully-sampled reconstruction was 2.0%, 8.2%, 10.3% and 17.8% for R = 4, 6, 8 and 10, respectively.

Fig. 3.

Signal intensity curves for Fourier reconstruction of the fully-sampled data (R = 1) and k-t SPARSE-SENSE reconstruction with simulated acceleration factors of R = 4, 6, 8 and 10: (a) blood (left ventricular ROI) and (b) myocardial wall.

Table 1.

Baseline mean value ± standard deviation, peak value, and upslope from the myocardial wall signal intensity time courses for Fourier reconstruction of the fully-sampled data (R=1) and k-t SPARSE-SENSE reconstruction with different simulated acceleration factors (R).

R	Baseline [au]	Peak [au]	Upslope [au/s]
1	120.6 ± 2.8	264.6	14.6
4	120.2 ± 4.6	261.9	14.3
6	122.5 ± 5.9	262.3	13.4
8	123.6 ± 7.9	264.6	13.1
10	125.6 ± 10.7	266.3	12.0

Breath-held multi-slice experiment with true 8-fold acceleration

Fig. 4 shows the reconstructed images (10 slices) for the peak blood and peak myocardial wall enhancement phases from the k-t SPARSE-SENSE reconstruction of the in vivo breath-held experiment with true 8-fold acceleration. The reconstructed images covered most of the heart with adequate blood and myocardial wall enhancement and good image quality. The reconstruction time per slice was approximately 15 min, which represented a total reconstruction time of approximately 2.5 hours for the 10 slices using Matlab (The MathWorks, Natick, MA) on a 64-bit quad core workstation.

Fig. 4.

Breath-held, 8-fold accelerated images in 10 short-axis views at peak blood and peak myocardial wall enhancement. These k-t SPARSE-SENSE reconstructed images exhibited good image quality.

Free-breathing multi-slice experiment with true 8-fold acceleration

Fig. 5 shows the reconstructed images (10 slices) for the peak blood and peak myocardial wall enhancement time points from the k-t SPARSE-SENSE reconstruction of the in vivo experiment with heavy breathing. The reconstruction did not show significant residual incoherent artifacts but did show blurring due to a small loss of sparsity in the temporal Fourier domain. The presence of respiratory motion at higher temporal frequencies than the passage of the contrast agent produces extra low energy components in the temporal Fourier domain, which are more difficult to recover since they are submerged beneath the pseudo-noise created by the incoherent artifacts.

Fig. 5.

Free-breathing, 8-fold accelerated images in 10 short-axis views at peak blood and myocardial wall enhancement. These k-t SPARSE-SENSE reconstructed images are free of residual aliasing artifacts, but at the expense of a moderate loss in spatiotemporal resolution.

Comparison of k-t SPARSE-SENSE with R = 8 and GRAPPA with R =2

Fig. 6 shows corresponding images for GRAPPA with R =2 and k-t SPARSE-SENSE with R = 8. Spatial resolution and blood and myocardial wall enhancement were similar for both methods, but k-t SPARSE-SENSE data acquisition was 4-fold higher in temporal resolution and visually presented lower noise amplification in the reconstructed images. Note that true noise also accumulates incoherently in the sparse domain with low value coefficients. The combination of k-t SPARSE and SENSE presents a regularized solution to the inverse problem, where only the high value sparse coefficients are recovered and the low value combined true noise and pseudo-noise coefficients are neglected. This effectively reduces the noise in the reconstructed images.

Fig. 6.

In vivo comparison of k-t SPARSE-SENSE with R = 8 and commercially available GRAPPA with R = 2 at different points in the contrast update time course.

Patient study

Fig. 7 shows 8-fold accelerated perfusion images at peak myocardial wall enhancement in three short-axis locations (mid to apical) with perfusion defects. The corresponding PSIR delayed-enhancement images show myocardial infarction regions that correlate well with the perfusion defect regions.

Fig. 7.

(a) 8-fold accelerated perfusion images at peak myocardial wall enhancement using the combination of k-t SPARSE and SENSE. These three selective planes show perfusion defects. (b) Corresponding PSIR delayed-enhancement images showing myocardial scarring regions that correlate well with the perfusion defect regions.

Discussion

The high degree of spatiotemporal correlation in the cardiac perfusion data allows for the application of compressed sensing to accelerate data acquisition. When multiple receiver coils are available, the extra correlation between coils can be exploited to obtain higher accelerations. In this work, a combination of compressed sensing and parallel imaging using the SENSE model and the k-t SPARSE method was employed to substantially increase the spatiotemporal resolution and spatial coverage of first-pass cardiac perfusion MRI studies.

Understanding the combined reconstruction from the perspective of distributed compressed sensing theory offers a means to assess theoretical bounds for expected increases in acceleration for combined techniques over each technique applied separately. For example, in this work a 2-fold increase in acceleration over compressed sensing alone was accomplished by using the combined reconstruction with a 12-element coil array, which represents 40-67% of the maximum feasible increase in acceleration for a very large number of coils.

The combination of k-t SPARSE and SENSE presented here shares with previously developed k-t acceleration methods the use of sparsity in the combined spatial (x-y) and temporal frequency (f) domain to reconstruct undersampled data. However, these techniques exploit sparsity differently. Methods such as k-t SENSE and SPEAR exploit regularities in the sparse domain to reduce signal overlap due to regularly undersampled data, whereas k-t SPARSE-SENSE exploits irregularities in the sparse domain to produce undersampling artifacts as pseudo-noise that adds incoherently to the sparse representation. k-t SENSE and SPEAR perform a linear reconstruction, where the aliased image is unfolded using the signal distribution in y-f domain and coil sensitivity information. SPEAR solves the same reconstruction problem as k-t SENSE, except for the baseline signal, where a model-based reconstruction using the RIGR algorithm is used instead of the temporal average, in order to increase the temporal resolution of k-t SENSE. On the other hand, k-t SPARSE-SENSE performs a non-linear reconstruction, where the sparse coefficients are recovered from the interference created by the incoherent undersampling artifacts. Note that k-t SPARSE-SENSE does not require training data, as explicit knowledge of the particular sparse representation in y-f space is not required. Reconstruction artifacts in k-t SENSE and SPEAR appear as unfolding errors, whereas artifacts in k-t SPARSE-SENSE appear as residual pseudo-noise. As a result, k-t SPARSE-SENSE may reduce image artifacts due to respiratory motion.

The method used in this work is more closely related to other compressed sensing techniques proposed for dynamic MRI, such as k-t SPARSE and k-t FOCUSS. However, k-t SPARSE-SENSE exploits joint sparsity whereas the other methods exploit single coil sparsity. As a result, the method used in this work provides increased acceleration capability. Moreover, the reconstruction algorithm used here differs from that of k-t FOCUSS. k-t FOCUSS first produces an initial signal estimate with high temporal resolution using a model-based reconstruction (RIGR algorithm, as in the SPEAR method) and then enforces sparsity on the remaining part of the signal. As a result, k-t FOCUSS may become particularly sensitive to errors in the initial estimate. Another difference is that l₁-norm minimization in k-t FOCUSS is approximated by a series of l₂-norm minimization problems with different weights (reweighted l₂-norm), which might require more samples than using a non-linear algorithm.

Image reconstruction artifacts for higher accelerations include spatiotemporal blurring, attenuation of low-contrast features, and increase of combined noise and pseudo-noise. Ideally, if the signal is truly sparse, with only a few large coefficients, compressed sensing will recover only the sparse signal coefficients and suppress the combined noise and pseudo-noise. However, in practice the signal is only compressible, i.e., it contains a few large coefficients and many small coefficients. k-t SPARSE-SENSE tends to suppress low-valued coefficients in the temporal Fourier domain, such as high spatiotemporal frequencies and low-contrast image features, which are below the combined noise and pseudo-noise level. Both noise and pseudo-noise in the sparse domain increase with acceleration, which also increases the false detection of sparse signal coefficients, and so more noise and pseudo-noise coefficients appear in the solution. However, the filtering of noise coefficients in the sparse domain effectively reduces the noise level in the reconstructed images, at the expense of changing the noise distribution when compared to standard parallel imaging techniques.

The maximum acceleration in k-t SPARSE-SENSE is determined by the number of sparse coefficients in the temporal Fourier domain and the number of receiver coils. Tailored sparsifying transforms, which jointly weight spatial and temporal dimensions, may offer a higher compression ratio than the temporal Fourier transform, and the use of coil arrays with larger numbers of elements may substantially reduce the number of required samples [26], resulting in improved performance for cardiac perfusion MRI.

The current implementation of k-t SPARSE-SENSE performs a sequential slice-by-slice reconstruction. The reconstruction time per slice is about 15 min using Matlab (The MathWorks, Natick, MA) on a 64-bit quad core workstation for the imaging parameters used in this work. For whole-heart coverage, 8-10 slices are required, which represents a total reconstruction time of 2-2.5 hours. Parallel computing can be used to reduce the reconstruction time by reconstructing each slice in parallel. We also expect a further reduction with programming optimization, using a standard programming language such as C++.

Compressed sensing reconstruction can also be performed by minimizing the l₀-norm (number of non-zero coefficients), which in theory would require fewer samples than l₁-norm minimization. However, l₀-norm minimization is a combinatorial optimization problem and therefore computationally intensive. Nevertheless, recently developed methods that approximate the l₀-norm minimization problem have demonstrated fast and stable reconstruction for highly sparse data sets [26,34], and they may be applicable to the combination of compressed sensing and parallel imaging for first-pass cardiac perfusion MRI.

One limitation of the proposed method is the selection of the weighting parameter (λ). In the current implementation, we did not apply any rigorous mathematical criteria to select lambda systematically. Instead, the parameter λ was selected based on simulation results from a single fully-sampled data set. Mathematical tools, such as the L-curve, can be used to select λ in a systematic way for an adequate balance between signal-to-noise ratio (SNR) and spatial-temporal smoothing.

Conclusions

We have presented a technique combining compressed sensing and parallel imaging for highly-accelerated cardiac perfusion MRI. This approach exploits joint sparsity of the multicoil images in x-y-f space. A new theoretical framework for combined reconstruction based on distributed compressed sensing theory was presented to provide estimates of theoretical bounds for feasible accelerations. An in vivo acceleration factor of 8 was feasible with the combined approach using a 12-element coil array, while preserving image quality and temporal fidelity. The combined reconstruction does not require dynamic training data and is relatively insensitive to respiratory motion artifacts. Even higher acceleration rates may be feasible with tailored space-time sparsifying transforms, use of cardiac coil arrays with larger numbers of elements, and four-dimensional acquisitions.