Identification of optimal drug combinations targeting cellular networks: integrating phospho-proteomics and computational network analysis

Abstract

Targeted therapeutics hold tremendous promise in inhibiting cancer cell proliferation. However, targeting proteins individually can be compensated for by bypass mechanisms and activation of regulatory loops. Designing optimal therapeutic combinations must therefore take into consideration the complex dynamic networks in the cell. In this study, we analyzed the insulin-like growth factor (IGF-1) signaling network in the MDA-MB231 breast cancer cell line. We used reverse phase protein array to measure the transient changes in the phosphorylation of proteins after IGF-1 stimulation. We developed a computational procedure that integrated mass-action modeling with particle swarm optimization to train the model against the experimental data and infer the unknown model parameters. The trained model was used to predict how targeting individual signaling proteins altered the rest of the network and identify drug combinations that minimally increased phosphorylation of other proteins elsewhere in the network. Experimental testing of the modeling predictions showed that optimal drug combinations inhibited cell signaling and proliferation, while non-optimal combination of inhibitors increased phosphorylation of non-targeted proteins and rescued cells from cell death. The integrative approach described here is useful for generating experimental intervention strategies that could optimize drug combinations and discover novel pharmacologic targets for cancer therapy.

Introduction

Cell signaling networks are complex systems that integrate information from the cellular environment (1-5). Maps of complex networks were derived by interconnecting the individual pathways obtained from experimental data (6, 7). These studies revealed that signaling networks contain numerous features, such as feedback and feedforward loops (8, 9), which render virtually impossible for the human mind to decipher how signals are integrated within the pathways. Thus, computational approaches are needed to elucidate the regulatory properties of signaling networks (10-12).

Several groups have used ordinary differential equations (ODEs) to analyze the dynamics of signaling networks and generate experimentally testable predictions (6, 13-17). The use of mass-action ODE modeling, however, is impaired because of incomplete knowledge about the concentrations and kinetics of signaling intermediates.

Inferring the parameters for mass-action modeling in signaling networks is challenging. The most common approach is to obtain parameters from the literature and fit the models to the experimental data to infer those that remain unknown (6, 13, 18-24). Unfortunately, the kinetic parameters reported in the literature may differ by orders of magnitude, depending on experimental conditions. Thus, it is difficult to determine whether discrepancies between computational and experimental data are due to inaccurate measures or incomplete modeling. Parameter estimation can be effectively accomplished using optimization methods, which enable quantitative model fitting to experimental data (25-31). However, the experimental techniques used to measure the activity of signaling proteins mainly provide qualitative or semi-quantitative data. Optimization strategies are thus needed to identify sets of model parameters that equally fit the qualitative experimental data.

Another challenge in the analysis of signaling networks is the identification of optimal target combinations. The most common methods of computational target identification are based on formulating mathematical models and designing intervention strategies through environmental, genetic, and signaling perturbations (32-34). This approach can predict the effect of available drugs on signaling network dynamics, but it does not facilitate the search for drug combinations that would optimally inhibit aberrant signaling. Another strategy is to integrate mass-action modeling with simulated annealing into a multiple-target optimal intervention (35). Since this approach is computationally expensive, alternative procedures are needed to enable the rapid search for targets in disease-related networks.

In this study, we used reverse phase protein array (RPPA) to measure the transient response of the MDA-MB231 breast cancer cell line after stimulation by insulin-like growth factor (IGF-1). The reason for choosing the IGF receptor (IGFR) network is two-fold: there is a large amount of experimental data and biological resources allowing us to build a consensus network and experimentally test it; components of this network are being targeted in several clinical trials for cancer therapy, thus having clinical applicability. We developed a computational procedure that integrated mass-action modeling with particle swarm optimization (PSO) to train the model against normalized time courses of phosphorylated proteins in MDA-MB231 cells and infer sets of unknown model parameters that equally fit the measured data. The trained mass-action model was used to predict the effect of a targeted perturbation and tested using experimental data. The trained and tested mass-action model was then used to identify the most influential molecules responsible for aberrant cell signaling and determine the optimal combinations of inhibitors and small-interfering RNAs (siRNAs) for inhibiting abnormal signaling in MDA-MB231 cells. Immunoblotting and cell viability assay were then used to test and validate the effect of drug combinations predicted by the mass-action model. Our integrative approach is useful for generating experimental intervention strategies that could optimize drug combinations and discovering novel pharmacologic targets for cancer therapy.

Quick guide to equations and assumptions

Mass-action modeling

The dynamics of IGFR network in MDA-MB231 cells were described using a mass-action model of ordinary differential equations (ODEs) formulated as follows:

Step 1: The pathways comprising the IGFR network were reconstructed into a set of chemical reactions that described the simplified mechanisms of activation and inhibition of relevant proteins. For example, mitogen-activated protein kinase (MAPK) phosphorylation was assumed to be catalyzed by MAPK kinase (MEK/MAPKK) and occurred through an enzymatic reaction:

$$\mathit{MAPK}+{\mathit{MEK}}^{\ast }\underset{k_1^r}{\overset{k_1^f}{\rightleftarrows }}C\underrightarrow{K_2}{\mathit{MAPK}}^{\ast }+{\mathit{MEK}}^{\ast }$$ (1)

In equation 1, $k_1^f$, $k_1^r$, and K₂ are the forward, reverse, and dissociation kinetic rate constants, respectively.

Step 2: The set of chemical reactions was transformed into a system of coupled ODEs by assuming that the dynamics of IGFR network obeyed the law of mass-action. Specifically, the accumulation rate of the concentration of the ith signaling intermediate was expressed as the difference between its net rates of production (r_p,i) and consumption (r_c,i). Thus, the accumulation rate of the concentration of MEK* was expressed as follows:

$$\frac{{\mathit{dMEK}}^{\ast }}{\mathit{dt}}=\sum _{p,{\mathit{MEK}}^{\ast }}r-\sum _{c,{\mathit{MEK}}^{\ast }}r=-k_1^f\left[\mathit{MAPK}\right]\left[{\mathit{MEK}}^{\ast }\right]+(k_1^r+K_2)\left[C\right]$$ (2)

In equation 2, [MAPK], [MEK*], and [C] denote the concentration of MAPK, MEK* and C, respectively.

The list of chemical reactions that described the consensus activation and inhibition mechanisms of proteins involved in the IGFR network and the corresponding system of ODEs are listed in Supplemental Material S1. To implement mass-action modeling, it was necessary to infer the unknown model parameters, which are the kinetic rate constants and the initial concentrations of the proteins. In this regard, we trained the mass-action model against transient data measured by RPPA using particle swarm optimization (PSO). We selected PSO because of its superior ability to converge to more optimal solutions compared to other optimization algorithms (see discussion).

PSO

PSO is a stochastic algorithm that mimicks the behavior of swarms of animals that search for food (36). Particles in the swarm have a position x_ij, a velocity v_ij, and a fitness f_i, where i and j represent the number of particles and the dimension of the space solution, respectively. Each particle remembers its best position x_ij^L locally and the best position x_j^G globally reached by the entire swarm. During the iterative search for food, particles update their position and velocities to improve their fitness according to the following rules:

$$\begin{array}{c}{\nu }_{ij}(t+1)=\omega {\nu }_{ij}\left(t\right)+c_1{r}_1[x_{ij}^L\left(t\right)-x_{ij}\left(t\right)]+c_2{r}_2[x_j^G\left(t\right)-x_{ij}\left(t\right)]\hfill \\ x_{ij}(t+1)=x_{ij}\left(t\right)+{\nu }_{ij}\left(t\right)\hfill \end{array}$$ (3)

In equations 3, ω is the inertia factor, r₁ and r₂ are two random numbers uniformly distributed in the interval [0,1], and c₁ and c₂ are the coefficients of self-recognition and social component (see (37) and Supplemental Material S2 for details on parameters in Equations 3).

In our settings, the particle positions represented the unknown parameter values used in the mass-action model to generate computationally the time courses of proteins that are measured by RPPA, the particle velocities denoted the extent to which the parameter values were iteratively changed, and the particle fitness was defined as the distance between the time courses of proteins experimentally and computationally measured. Model parameters were randomly initialized and iteratively changed according to equations 3 until the distance between the time courses of the measured and predicted proteins was minimal (i.e. optimal fitness). The distance between computed and measured time courses was evaluated using the standard deviation (SD)-weighted square error:

$$SqE=\sum _{j=1}^r\sum _{i=1}^s\frac{{[{\tilde{y}}_{ij}^m-y_{ij}^c]}^2}{\sigma \left(y_{ij}^m\right)}$$ (4)

In equation 4, ${\tilde{y}}_{ij}^m$ and $\sigma \left(y_{ij}^m\right)$ represent the mean and SD, respectively, of the proteins measured by RPPA, whereas y^c_ij denotes the protein levels computed using the mass-action model. Moreover, s represents the total number of data points comprising a single time course, and r is the total number of time courses. PSO was implemented to minimize the SD-weighted square error and train the mass-action model against RPPA data to estimate the unknown model parameters.

Materials and Methods

Cell culture and stimulation

The human MDA-MB231 breast cancer cell line (K-Ras and B-Raf mutants) was purchased from America Type Culture Collection (ATCC, Manassas, VA). The cell line was validated by STR DNA fingerprinting using the AmpFℓSTR Identifiler kit (Applied Biosystems cat 4322288). The STR profiles were compared to known ATCC fingerprints (ATCC.org) and to the Cell Line Integrated Molecular Authentication database (CLIMA) version 0.1.200808 (38). Cells were cultured in RPMI medium supplemented with 5% fetal bovine serum (FBS). Cells were serum-starved overnight and then subjected to treatment with 75 ng/mL IGF-1 (Cell Signaling Technology, Beverly, MA). For RPPA, cells were pretreated with 10 μM U0126 (Promega, Madison, WI) for 4 hours, followed by IGF-1 stimulation for 5, 15, 30, 60, 90, or 120 minutes. For immunoblotting, cells were pretreated with 10 μM U0126, 50 μM LY294002 (Calbiochem-Nova-biochem Corp., San Diego, CA), and 50 nM rapamycin (Calbiochem-Nova-biochem Corp., San Diego, CA), individually or combined, for 1 hour, followed by IGF-1 stimulation for 5 or 60 minutes. For RPPA and immunoblotting, controls were incubated for the corresponding times with dimethyl sulfoxide (DMSO).

Antibodies

The following antibodies were used for RPPA and immunoblotting: anti-phospho-MAPK (T202/Y204), anti-phospho-GSK3 (S21/S9), anti-phospho-AKT (ser473), anti-phospho-TSC2 (T1462), anti-phospho-mTOR (S2448), anti-phospho-P70S6K (T389), anti-MAPK (p44/42), anti-AKT, anti-TSC2 (28A7), anti-mTOR, anti-P70S6K, and anti-actin (Cell Signaling Technology, Boston, MA); anti-GSK3 (Santa Cruz Biotechnology, Inc., Santa Cruz, CA).

Immunoblotting

Immunoblotting was performed using standard procedures.

RPPA

Serial diluted lysates were arrayed on nitrocellulose-coated FAST slides (Whatman, Kent, UK) using the Aushon 2470 Arrayer (Aushon Biosystems, Billerica, MA). Each slide was probed with a primary antibody plus a biotin-conjugated secondary antibody. The signal was amplified using the DakoCytomation-catalyzed system (Dako, Carpinteria, CA) and visualized using a 3,3′-diaminobenzidine colorimetric reaction. The slides were scanned, analyzed, and quantified using customized Microvigene software (VigeneTech, Inc., Carlisle, MA) to measure spot intensity. Each dilution curve was fitted with the logistic model “Supercurve Fitting” (39). The mean values of the protein levels in the nonstimulated cells were used to normalize the time courses of the phosphorylated proteins measured in IGF-1–stimulated cells.

Crystal violet cell viability assay

Viability assay was performed using standard procedures. Cells were treated for 3 days with: U0126 (concentration of 0.1 to 100 μM), LY294002 (concentration of 0.1 to 100 μM), or rapamycin (concentration of 0.1 to 100 nM); combination of U0126 (concentration of 0.5 to 50 μM) and LY294002 (fixed at its quarter maximal effective concentration (EC₂₅) value of 3.8 μM) or rapamycin (fixed at its EC₂₅ value of 0.1 nM); combination of U0126 (fixed at its EC₂₅ value of 3.5 μM) and rapamycin (concentration of 0.5 to 50 nM). Corresponding controls were incubated with DMSO. The EC₂₅ of each inhibitor was estimated (Supplemental Material S3) using Microsoft GraphPad Prism (Redmont, WA).

Computational procedures

Computational procedures are described in Supplemental Material S2.

Results

IGFR-1 signaling detection by RPPA

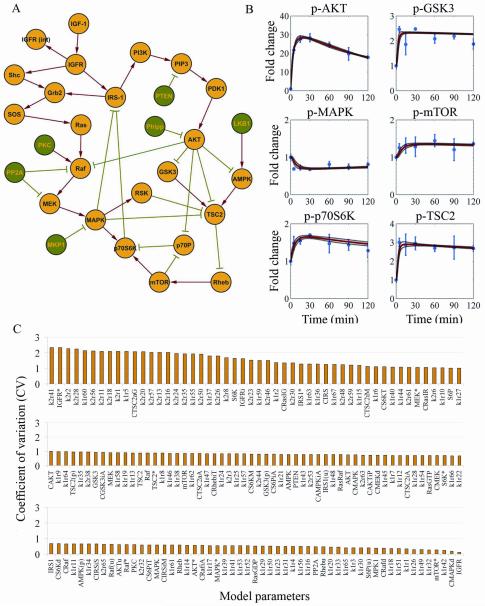
Figure 1A shows the IGFR signaling network in the MDA-MB231 cell line. Signal transduction is originated when IGF-1 complexes with IGFR and triggeres IGFR autophosphorylation (40). Phosphorylated IGFR propagates the signal downstream through the MAPK and phosphoinositide-3-kinase (PI3K) pathways and leads to MAPK and protein kinase B (PKB/AKT) phosphorylation (4, 5). The signals from the MAPK and PI3K cascades are routed to the mammalian target of rapamycin (mTOR) pathway via tuberous sclerosis (TSC2) inactivation (1). Phosphorylated mTOR activates protein S6 kinase of 70 kDa (p70S6K), which inactivates the insulin receptor substrate (IRS-1) through a negative feedback loop (41). A detailed description of the network topology is provided in Supplemental Material S1. We used RPPA (42-46) to determine the changes in the phosphorylation of proteins in the IGFR network after IGF-1 stimulation. To account for the intrinsic variability of these assays, all experiments were performed in three independent repeats. Figure 1B shows the time courses of the measured phosphorylated proteins; the curves show the protein fold change over the corresponding controls (Materials and Methods). After IGF-1 stimulation, the level of phospho-AKT peaked at 30 minutes (28-fold increase) and then settled toward a lower level at 120 minutes (18-fold increase). In contrast, signal transduction across the MAPK cascade remained essentially unchanged likely as a result of MAPK constitutive activation driven by K-Ras and B-Raf mutations in MDA-MB231 cells. AKT activation triggered glycogen synthase kinase (GSK3) and TSC2 downregulation via phosphorylation, and TSC2 inactivation facilitated phospho-mTOR and phospho-p70S6K upregulation. Thus, the levels of p-GSK3, p-TSC2, p-mTOR, and p-p70S6K initially increased and then adjusted to stationary levels.

Figure 1.

(A) IGFR signaling network topology in the MDA-MB231 cell line. Nodes represent proteins, edges represent protein interactions, red arrows describe protein activation, and green plungers describe protein inactivation. (B) Protein profiles were measured on RPPA in triplicate. The mean protein profiles of non-IGF-1–stimulated cells were used as controls for normalization. Circles and error bars represent the mean and SD of the normalized protein profiles. Normalized time courses were computationally evaluated using the trained mass-action model. Solid red lines represent the mean time courses of the trajectories that equally fit the experimental data, and dashed black lines represent the fitting variability. (C) Histogram of model parameter regimens clustered according to the coefficient of variation (CV=SD/mean).

Complementing mass-action modeling with PSO

Mass-action modeling and model reduction

To predict the dynamics of the IGFR network after IGF-1 stimulation in MDA-MB231 cells, we developed a mass-action ODE model. Our formulation was based on a set of 77 chemical reactions that described the consensus activation and inhibition mechanisms of proteins involved in the IGFR network. The resulting mass-action model was structured into 127 ODEs and 313 unknown parameters. To decrease the complexity of the model, we developed a reduced version of the original model. The 77 chemical reactions were reduced to a subset of 41 reactions to describe the simplified interaction mechanisms of the most relevant species in the IGFR network, and the original model was reduced to 65 ODEs and 161 model unknowns (Supplemental Material S4). We tested and validated the ability of the reduced model to adequately describe IGFR dynamics by showing that the protein profiles predicted by the reduced model matched those generated by the original model for randomly selected sets of parameters (Supplemental Material S5). Therefore, throughout the manuscript we exclusively used the reduced model to predict the dynamics of IGFR signaling network.

Model training

The measured time course data of proteins in MDA-MB231 cells contains relevant information about the regulatory loops comprising the IGFR network. To exploit this information to optimally inhibit aberrant pathways, we used PSO to fit the model to the time courses of p-AKT, p-MAPK, p-GSK3, p-mTOR, p-p70S6K, and p-TSC2 proteins and infer the 161 unknown parameters. Studies published in the literature typically use only two or three “readout” molecules to fit ODE models to experimental data and infer unknown parameters (14,15,26). In our study, we trained our model using six “readout” proteins and 126 experimental data points combined into a scalar fitness.

Because of the substantial degree of uncertainty in parameter estimation, fitting mass-action models to the qualitative data measured on RPPA required the identification of multiple trajectories that equally resembled the measured protein profiles. Using the integrative mass-action modeling–PSO procedure, we identified 10 sets of model parameters that equally fit the measured data (Supplemental File S1). We characterized the parameter regimens by ranking the parameters according to their coefficient of variation (CV) and found that 69% of them had a CV smaller than 1 (Figure 1C). We calculated the means and SD of the identified trajectories to represent the entire set and the fitting variability. Figure 1B shows the mean trajectories and the fitting variability identified by the mass-action model, which had been trained using PSO against normalized protein profiles measured on RPPA after IGF-1 stimulation of MDA-MB231 cells. The simulation results indicated that the integrative procedure adequately fit the time courses of all measured proteins.

Model testing

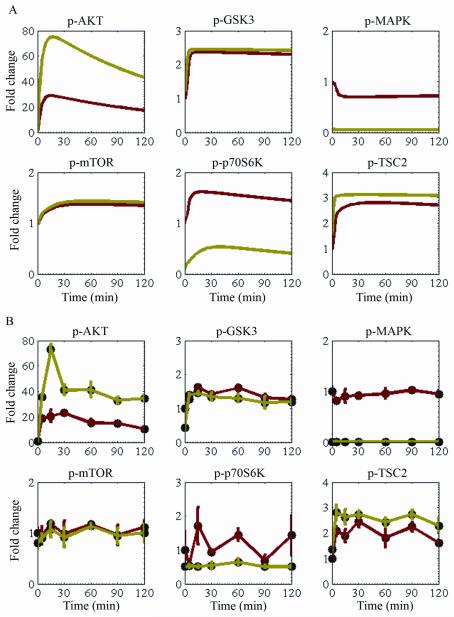
To determine the ability of the trained model to correctly generate responses to perturbations that have not been explicitly included in the training data set, we used it to predict the dynamics of the IGFR network after inhibition of MEK. Figure 2A shows the transient IGFR signaling response to targeted MEK inhibition, as predicted by the trained mass-action model. MEK inhibition led to significant downregulation of its immediate downstream effector, p-MAPK. Inhibition of p-MAPK attenuated inhibition of IRS-1 through direct interaction and through the p70S6K feedback loop. Consequently, p-AKT was upregulated. Activation of p-AKT increased the level of p-TSC2 but did not affect the level of p-mTOR or GSK3. Signals from the MAPK and mTOR cascades were integrated into the p70S6K pathway and led to p-p70S6K downregulation.

Figure 2.

The effect of MEK inhibition on IGFR network dynamics. (A) Protein profiles of IGF-1-stimulated MDA-MB231 cells predicted by the trained mass-action model. Solid red lines represent the protein time courses of the noninhibited cells, and solid green lines represent the protein profiles of MEK-inhibited cells. (B) Protein phosphorylation in MDA-MB231 cell lysates after stimulation with 75 ng/mL IGF-1 detected in triplicate by RPPA. Solid circles and red lines represent the protein time courses of noninhibited cells, and solid circles and green lines represent the protein profiles of cells inhibited with MEK inhibitor for 4 hours.

The computational results were experimentally tested using an independent set of 252 data points measured by RPPA. Figure 2B shows the levels of p-AKT, p-MAPK, p-GSK3, p-mTOR, p-p70S6K, and p-TSC2 detected in triplicate in IGF-1-stimulated MDA-MB231 cells in the absence of the MEK inhibitor and after 4 hours of incubation with the MEK inhibitor. The experimental data indicated that MEK inhibition increased p-AKT and p-TSC2 levels, decreased p-MAPK and p-p70S6K levels, and slightly decreased p-GSK3 levels but had no significant effect on p-mTOR levels. Despite the limited discrepancy between the computed and measured profiles of p-GSK3, the experimental results adequately matched those predicted by the model. Therefore, the trained mass-action model correctly predicted the effect of MEK inhibition on IGFR dynamics.

Predicting inhibition of targeted molecules

Individual inhibition of targeted molecules

To determine how to select drugs with the ability to inhibit the pathways measured in MDA-MB231 cells, we used the trained and tested mass-action model to predict the response of IGFR network after molecules in the network had been individually inhibited (Supplemental Material S6). Figure 3 and Supplemental Material S6 show the differential levels of proteins in inhibited versus noninhibited MDA-MB231 cells after IGF-1 stimulation, as predicted by the mass-action model for 3 out of the 10 sets of parameters inferred using PSO (Supplemental File S2). These 3 sets were randomly selected to repeat the computational analysis in triplicate. The modeling results suggested that targeting one molecule at a time may activate non-targeted molecules, likely as a result of feedback loop compensation. Thus, targeting single-molecule may not be sufficient to adequately inhibit aberrant signaling. While inhibition of molecules in the MAPK pathway was predicted to activate the PI3K/AKT pathway, inhibition of intermediates comprising the PI3K/AKT pathway was predicted to activate the MAPK pathway. Because these pathways are often upregulated in many tumors (47), the combined inhibition of the MAPK and PI3K/AKT cascades emerged as a candidate strategy to inhibit aberrant signaling in MDA-MB231 cells.

Figure 3.

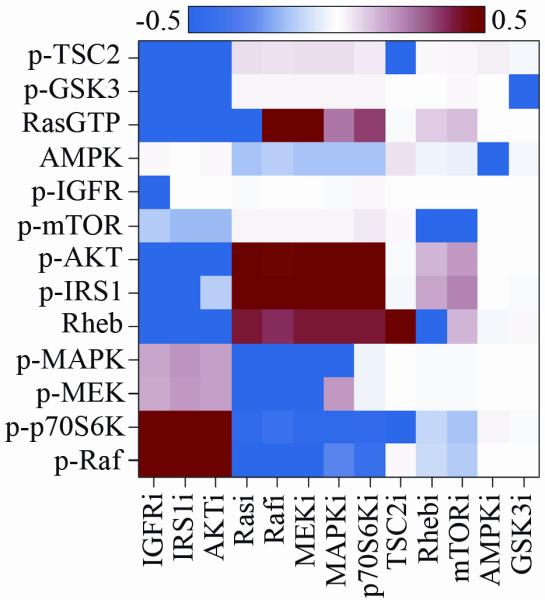
The effect of single-molecule inhibition on IGFR signaling in MDA-MB231 cells. Differential levels of proteins in single-molecule–inhibited versus noninhibited MDA-MB231 cells after 2 hours of stimulation with 75 ng/mL IGF-1 were predicted using the trained mass-action model. Numerical values were converted to log₁₀. Blue represents inhibition, white denotes no variation, and red indicates activation.

Combined inhibition of targeted molecules

Predicting the response of IGFR networks to the inhibition of individual molecules may not necessarily identify optimal drug combinations for pharmacologic intervention. In contrast, perturbing all molecules in the network simultaneously would identify optimal combinations needed to inhibit aberrant signaling. From a computational point of view, the effect of siRNAs can be mimicked by varying the initial concentration of signaling proteins. The effect of the drug inhibitor can be approximately simulated by varying the values of rescaled kinetic rate constants, such as in the classic example of competitive inhibition (48). Integrating mass-action modeling with a random sampling of kinetic constants (inhibitors) and initial protein concentrations (siRNAs) within pre-defined intervals of values would thus provide an unbiased, unsupervised means of computationally predicting the effect of simultaneously perturbing all molecules in the IGFR network (Computational procedures).

Combinations of signaling targets were identified by comparing the model parameters inferred using PSO from data measured in MDA-MB231 cells with randomly sampled model parameters that could restore user-defined signaling output. We defined the signaling network characterized by the measured time courses of p-AKT, p-MAPK, and p-p70S6K as aberrant, as these proteins are often upregulated in many tumors (47). We defined the state at which p-AKT, p-MAPK, and p-p70S6K levels were inhibited by at least five-fold as user-defined signaling output. To obtain reliable results, we identified 200 collections of combined perturbations (Supplemental File S3) that restored the user-defined signaling changes in MDA-MB231 cells for the sets of parameters listed in Supplemental File S2.

The most influential targets were scored according to the absolute value of the median deviation (MD) to the SD ratio (Supplemental Table I). The computational analysis was repeated in triplicate using the same 3 randomly selected sets of parameters used to predict individual inhibition of targeted molecules. Despite being ranked in a different order, the top five targets were the same for the 3 sets. All targets that scored as influential were characterized by a positive MD, which indicated activation of the reactions leading to inhibition of phosphorylated protein. Since p-IGFR, p-IRS-1, p-MEK, p-MAPK, and p-AKT were scored as the most influential targets, combined inhibition of the PI3K/AKT and MAPK pathways was predicted to optimally facilitate disruption of the loops responsible for aberrant signaling in MDA-MB231 cells.

Experimental validation of modeling predictions

The effect of drug combinations on IGFR network in the MDA-MB231 cell line

We used immunoblotting to determine whether the combined inhibition of the MAPK and PI3K/AKT pathways would decrease the levels of p-AKT, p-MAPK, and p-p70S6K and minimize changes in phosphorylation of other signaling proteins in the network. We also tested the combination of MEK and mTOR inhibitors to determine whether targeting pathways that differ from the predicted optimal combination would restore user-defined signaling changes in the MDA-MB231 cells.

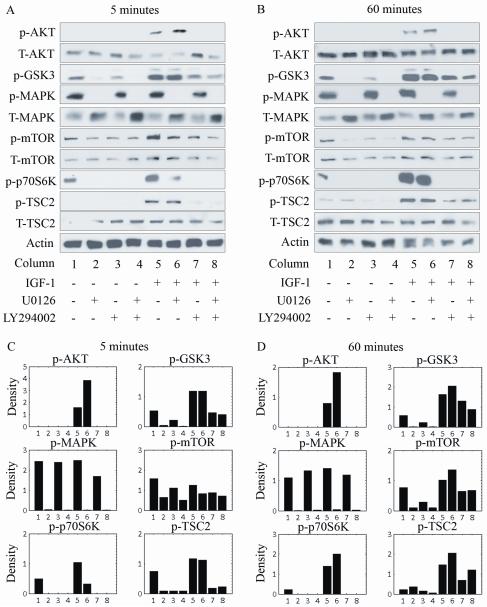
Figures 4A and B show the levels of p-AKT, p-MAPK, p-GSK3, p-mTOR, p-p70S6K, and p-TSC2 detected in the absence of inhibition and after 1 hour of incubation with the MEK or/and PI3K inhibitors in unstimulated cells and IGF-stimulated cells. The experimental data indicated that, in IGF–stimulated cells inhibited with MEK and PI3K inhibitors (column 8), the levels of all phosphorylated proteins were significantly decreased compared with those of the corresponding proteins detected in noninhibited, IGF-stimulated cells (column 5).

Figure 4.

Combined inhibition of MEK and PI3K in MDA-MB231 cells. (A and B) Protein levels were detected in unstimulated cells in the absence of inhibition (columns 1) and after 1 hour of incubation with the MEK or/and PI3K inhibitors (columns 2-4) and in cells stimulated with IGF-1 in the absence of inhibition (column 5) and after 1 hour of incubation with the MEK or/and PI3K inhibitors (columns 6-8). Cells were stimulated with 75 ng/mL IGF-1 for 5 minutes (A) or 60 minutes (B). (C and D) Density of the bands after normalization with respect to actin.

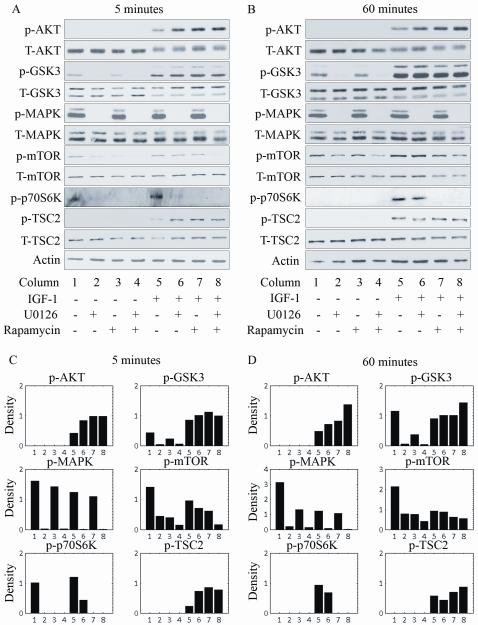
Figures 5A and B show the levels of p-AKT, p-MAPK, p-GSK3, p-mTOR, p-p70S6K, and p-TSC2 measured in the absence of inhibition and after 1 hour of incubation with the MEK or/and mTOR inhibitors in unstimulated cells and IGF–stimulated cells. The experimental data indicated that p-MAPK, p-mTOR, and p-p70S6K levels in IGF–stimulated cells inhibited with MEK and mTOR inhibitors (column 8) were decreased compared with those of the corresponding proteins in noninhibited, IGF-1-stimulated cells (column 5). However, the p-AKT, p-GSK3 and p-TSC2 levels were increased.

Figure 5.

Combined inhibition of MEK and mTOR in MDA-MB231 cells. (A and B) Protein levels were detected in unstimulated cells in the absence of inhibition (column 1) and after 1 hour of incubation with the MEK or/and mTOR inhibitors (columns 2-4) and in cells stimulated with IGF-1 in the absence of inhibition (column 5) and after 1 hour of incubation with the MEK or/and mTOR inhibitors (columns 6-8). Cells were stimulated with 75 ng/mL IGF-1 for 5 minutes (A) or 60 minutes (B). (C and D) Density of the bands after normalization with respect to actin.

Supplemental Table II shows the qualitative comparison between the measured and predicted differential levels of phosphorylated proteins in IGF-stimulated cells in the absence of inhibition and after 1 hour of incubation with MEK and PI3K inhibitors or MEK and mTOR inhibitors. Note that the experimental results are in agreement with the modeling predictions for both drug combinations. Therefore, as predicted by the mass-action model, combined inhibition of the MAPK and PI3K/AKT pathways optimally inhibited aberrant networks, but combinations of MEK and mTOR inhibitors did not decrease the levels of p-AKT, p-MAPK, and p-p70S6K and increased phosphorylation of non-targeted protein.

Cell sensitivity to drug combinations

Optimal inhibition of abnormal signaling networks must inhibit regulatory loops and redundant bypass to ultimately overcome the mechanism of feedback compensation that ensures cancer cell viability. To quantify the sensitivity of the MDA-MB231 cell line to MEK and PI3K or MEK and mTOR inhibition, we used cell viability assays.

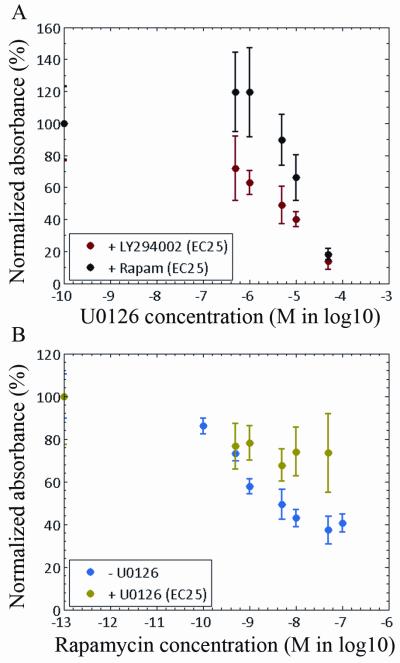
Figure 6A shows the effect of drug combinations on the viability of MDA-MB231 cells, which was measured as the normalized absorbance of viable cells as a function of increasing MEK inhibition (U0126) in combination with PI3K inhibitor (LY294002) or mTOR inhibitor (rapamycin). The experimental results indicated that inhibiting cells with a combination of LY294002 and increasing concentrations of U0126 resulted in a dose-dependent decrease in cell viability. In contrast cells treated with a combination of rapamycin and increasing concentrations of U0126 showed no change in cell proliferation up to 1 μM of U0126 followed by partial rescue of cells with rapamycin. Combined MEK-PI3K inhibition monotonically decreased cell viability, likely as a result of the optimal inhibition of the signaling pathways that led to inactivation of phosphorylated proteins (Figure 4). In contrast, combined MEK-mTOR inhibition increased cell viability at low concentrations of the U0126 inhibitor, likely as a result of the non-optimal inhibition of the signaling network that led to activation of p-AKT (Figure 5). At high concentrations of the U0126 inhibitor, cell viability was significantly decreased for both drug combinations, likely as a result of U0126 inhibitor toxicity (Supplemental Material S3).

Figure 6.

Response curve of MDA-MB231 cells to dose concentration of drug inhibitors. (A) Cells were left untreated as a control and incubated with LY294002 at its EC₂₅ (3.8 μM) or rapamycin at its EC₂₅ (0.1 nM) in combination with U0126 at a concentration of 0.5 to 50 μM. (B) Cells were left untreated as a control and incubated only with rapamycin at concentrations of 0.1 to 100 nM or with a combination of U0126 at its EC₂₅ (3.5 μM) and rapamycin at a concentration of 0.5 to 50 μM. Absorbance was normalized with respect to the value detected for the controls and was expressed as a percentage. Solid circles and error bars represent the means and standard deviations of normalized absorbance.

To test whether the combination of MEK and mTOR inhibitors rescued cell proliferation by activation of p-AKT, we performed cell viability assays with rapamycin alone or with rapamycin in combination with U2016. The experimental results show in Figure 6B indicated that addition of a MEK inhibitor to cells treated with rapamycin increased cell viability from 40% to 73% and rescued cells from cell death. Therefore, the experimental results suggested that optimal inhibition of aberrant signaling through combined inhibition of the MAPK and PI3K pathways was correlated with decreased cell viability. In contrast, non-optimal combined targeted inhibition led to inadequate inhibition of the signaling networks and increased cell viability.

Discussion

Integrating mass-action modeling with optimization schemes is a quantitative approach to train ODE models using experimental data and identify optimal drug combinations that can inhibit signaling networks. PSO converged to more optimal solutions than did other optimization algorithms, including simulated annealing and genetic algorithms. Supplemental Table III summarizes the performance of the three algorithms in training the reduced mass-action model against time courses of proteins (Supplemental File S4). Each simulation was repeated three times with different random seeds of the reduced model unknown parameters.

The most simple and intuitive strategy to inhibit aberrant networks consists of inhibiting the input sources that trigger signal transduction. Thus, individual inhibition of IGFR could restore user-defined pathways in MDA-231 cells. However, constitutive p-MAPK activation driven by K-Ras and B-Raf mutations impairs this approach. The experimental results shown in Figures 4 and 5 and the computational results shown in Figure 3 also suggest that individual inhibition of targeted molecules frequently do not optimally inhibit cell signaling. A more effective inhibition of aberrant signaling is accomplished through multiple combined inhibitions of targeted molecules. The experimental results shown in Figures 4-6 indicate that combined inhibition of the MAPK and PI3K/AKT pathways optimally inhibited the signaling networks and decreased cell viability. In contrast, combined inhibition of the MAPK and mTOR cascades led to significant activation of p-AKT and increased cell viability. Although several other kinases and pathways may potentially regulate viability of the MDA-231 cells, the experimental results indicated that simultaneous inhibition of the MAPK and PI3K/AKT pathways was sufficient to significantly reduce cell proliferation.

In conclusion, we propose a computational procedure that can be used to rapidly generate experimentally testable intervention strategies that may lead to an optimal use of available drugs and the discovery of novel signaling targets. The procedure is currently being used to identify and validate drug combinations that can inhibit aberrant networks in a panel of human cancer cell lines.

Major Findings.

Simple and reliable strategies are needed to identify optimal combinations of molecular targeted drugs to treat individual cancer patients, to realize the fullest potential of a targeted therapeutic approach.