Classic and contemporary approaches to modeling biochemical reactions

Abstract

Recent interest in modeling biochemical networks raises questions about the relationship between often complex mathematical models and familiar arithmetic concepts from classical enzymology, and also about connections between modeling and experimental data. This review addresses both topics by familiarizing readers with key concepts (and terminology) in the construction, validation, and application of deterministic biochemical models, with particular emphasis on a simple enzyme-catalyzed reaction. Networks of coupled ordinary differential equations (ODEs) are the natural language for describing enzyme kinetics in a mass action approximation. We illustrate this point by showing how the familiar Briggs-Haldane formulation of Michaelis-Menten kinetics derives from the outer (or quasi-steady-state) solution of a dynamical system of ODEs describing a simple reaction under special conditions. We discuss how parameters in the Michaelis-Menten approximation and in the underlying ODE network can be estimated from experimental data, with a special emphasis on the origins of uncertainty. Finally, we extrapolate from a simple reaction to complex models of multiprotein biochemical networks. The concepts described in this review, hitherto of interest primarily to practitioners, are likely to become important for a much broader community of cellular and molecular biologists attempting to understand the promise and challenges of “systems biology” as applied to biochemical mechanisms.

Many of us understand enzyme kinetics from the perspective of models developed nearly a century ago by Michaelis and Menten (1913), (who were themsleves building on earlier insights by Henri [1902] ), clarified by Briggs and Haldane (1925) a decade later, and then extended in subsequent decades by many others (Monod et al. 1965; Koshland et al. 1966; Goldbeter and Koshland 1981). These models focus on enzymatic reactions studied in vitro under controlled, well-mixed conditions. More recently, “systems biologists” have revisited mathematical modeling of biochemistry, but with a focus on networks of proteins and reactions occurring in vivo. Many biologsts are unclear as to the relationship between contemporary modeling efforts and the widely understood equations of Michaelis-Menten kinetics. Remarkably, many ascribe greater rigor to the Michaelis-Menten approximation than to more fundamental networks of ordinary differential equations (ODEs) from which the approximation is derived. In this review, we explore the connections between ODE-based models and classical “arithmetic” descriptions of enzymology, as presented in texbooks such as Lehninger (Nelson and Cox 2004) and Stryer (Berg et al. 2006). Specifically, we ask the following questions: (1) How is a simple “canonical” enzymatic process represented as a dynamical system using coupled ODEs? (2) How are familiar quantities such as the Michaelis constant (K_M) and the maximal enzyme velocity (V_max) derived from this dynamical system? (3) How can unknown values (primarily rate constants) required for modeling biochemical process be estimated from data? (4) Can valid conclusions be drawn from models if parameters remain unknown? (5) How appropriate is classical enzymology as a framework for analyzing reactions in living cells? (6) How can models involving complex sets of equations be made intelligible to experts and nonexperts alike?

In presenting these topics, we face the challenge that dynamical systems analysis is largely unfamiliar to experimental biologists, even though it is a well-developed disipline in applied mathematics that ecompasses multiple subfields with differing vocabularies. As applied to biochemical systems, key ideas are not inherently difficult to grasp, and can be approached without detailed prior knowledge of mathematical methods. In the text of this review, we rely on analogies, simple equations, and concrete examples, at the risk of some loss of generality and rigor. We provide more throrough mathematical analysis in the Supplemental Material, along with MatLab files useful for self-study and teaching. Specialized vocabulary is defined in Table 1.

Table 1.

Glossary^a

^aThese informal definitions pertain to usage in this review; more complete definitions can be found at Mathworld (http://mathworld.wolfram.com).

Our discussion of enzyme kinetics is restricted to a mass action approximation. This simply states that the rate of a reaction is equal to a constant multiplied by the product of the concentration of the reactants. The very concept of “concentration” assumes that the distributions of reactants can reasonably be assumed to be continuous (as opposed to discrete), and that reaction dynamics are deterministic. This holds for a well-mixed reaction compartment when the number of molecules is great enough that the properties of single reactants cannot be resolved from the ensemble behavior (to some degree of precision). Mass action kinetics are an approximation to a more fundamental, discrete, and stochastic description based on the chemical master equation (CME). Single-molecule enzymology (Ishijima et al. 1991; Finer et al. 1994; Cai et al. 2006; Kim et al. 2007) and live-cell analysis of stochastic processes in living cells, such as gene transcription (Golding and Cox 2004; Elf et al. 2007; Zenklusen et al. 2008) and protein translation (Munro et al. 2007; Agirrezabala et al. 2008; Choi et al. 2008; Julian et al. 2008), have brought stochastic modeling to the attention of molecular biologists, but it is nonetheless true that many physiological processes can be described quite well using deterministic, continuum models (Grima and Schnell 2006). The magnitude of stochastic fluctuations for a single reaction scales with 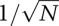, where N is the number of molecules in the compartment. Thus, deterministic models are a good description of reactions having >10²–10³ molecules per reactant (although, to be more precise, it is not the total number of molecules that is relevant, but rather the minimum number in one or more reaction compartments). In eukaryotic metabolism and signal transduction, these numbers justify the use of deterministic kinetic models. Such models can also be analyzed using efficient numerical methods, whereas analysis of complex stochastic models remains a relatively challenging problem in applied mathematics (Gillespie 2007). Deterministic models are also easier to analyze for relationships among rate constants or initial protein concentrations and product dynamics (e.g., sensitivity analysis). We refer readers interested in stochastic models to an elegant experimental demonstration of the link between stochastic and deterministic kinetics (English et al. 2006), and to several excellent reviews on stochastic simulation (Sun et al. 2008; Wilkinson 2009). We also note that our discussion of dynamical systems and of connections between models and expeirments is as relevant to stochastic as to deterministic models, but with added complexity in the former case.

We omitted from this review a specific discussion of spatial gradients. Protein localization is, of course, a critical determinant of biological activity. Transport and diffusion are modeled (in a continuum framework) using partial differential equations (PDEs). Concepts that are discussed in this review with respect to temporal variables such as nondimensionalization and scaling also apply to spatial dimensions. Thus, our discussion of ODE models is relevant to PDE models, but PDE models are more complex. Changes in protein localization are usually represented in ODE models by postulating a reversible reaction corresponding to movement of a species from one well-mixed compartment to another (such models are frequently referred to as compartmental ODE models).

We do not mean to imply that stochastic methods and PDEs are not important in representing actual biochemistry in cells, but instead that fundamental concepts in modeling cellular biochemistry can be explored more simply by considering deterministic models that rely on a simplified representation of space. Such ODE models are, in many cases, entirely adequate as a modeling formalism, and their relative simplicity facilitates detailed model analysis, representation of elaborate mechanisms and multiprotein networks, and rigorous comparison of model-based prediction of experimental data. The latter issue is particularly challenging, and arises with all modeling methods.

The models of Michaelis-Menten and Briggs-Haldane

Even complex biochemical processes are usually described as a succession of simple and reversible binding steps and largely irreveriblse catalytic steps, each of which constitutes an elementary reaction (as mentioned above, protein relocalization in a compartmental ODE model is represented as a reversible first-order reaction). By combining binding and catalysis, we arrive at the classical treatment of a simple enzyme-mediated biochemical transformation (Fig. 1, Eq. 1). The majority of this review involves this fundamental reaction. Enzymes and substrates first bind to each other to form a complex (E + S ↔ ES, where ES is henceforth called C to simplify formulae). The enzyme faciliates passage over an activation barrier, thereby accelerating chemical transformation of the substrate into product. Enzymes and products then dissociate to form E and P. Formation of C is characterized by a forward rate constant (k_f) that is second order in our example (in units of M⁻¹sec⁻¹), a first-order reverse rate constant (k_r; in sec⁻¹), and a first-order catalytic rate constant (k_cat; in sec⁻¹). The reverse catalytic rate constant is set to 0, representing a situation in which the catalytic step is effectively irrversible because ΔG ≪ 0.

Figure 1.

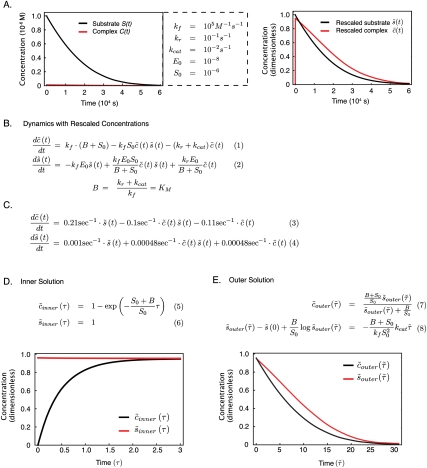
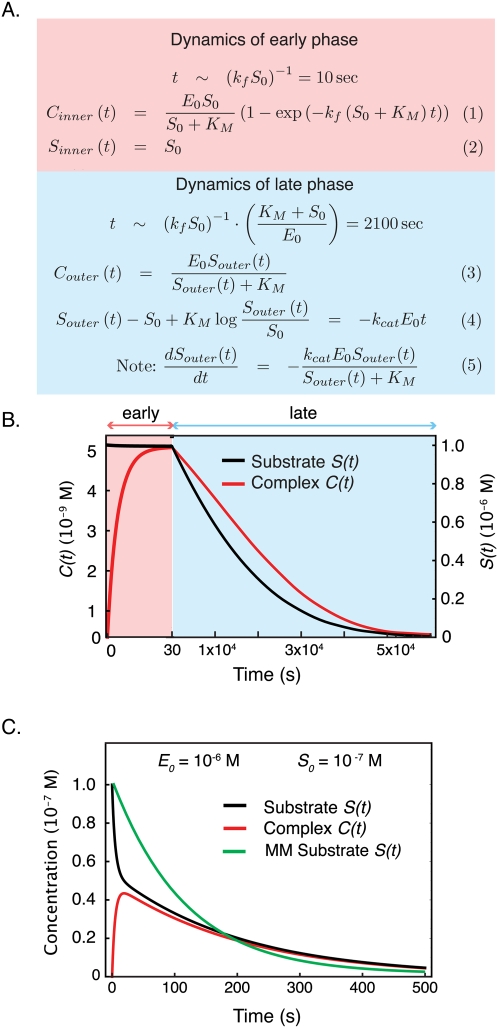
The canonical enzymatic reaction (Eq. 1) analyzed by Michaelis-Menten, and the resulting equations defining K_M (Michaelis constant) and V(t) (velocity) (Eqs. 2,3). (Eqs. 4–7) The same enzymatic reaction described using a coupled set of four ODEs, defining changes in the concentration of enzyme, substrate, complex, and product over time. Using conservation conditions (Eqs. 8,9), the set of four ODEs can be reduced to two equations, describing the change over time of complex and substrate (Eqs. 10,11).

In their 1913 paper on invertase, Michaelis and Menten (1913) first applied to biochemical reactions in solution the concept of mass action kinetics developed for gas-phase reactions. Michaelis and Menten (1913) also recognized the value of distinguishing between rapid steps, leading to formation of C, and subsequent slower catalytic steps, leading to product formation. By assuming C to be in equilibrium with E and S, Michaelis and Menten (1913) derived an analytic approximation for the dynamics of the slower phase in which a direct link could be made between experimental data and reaction rate constants (as outlined below). The related treatment of Van Slyke and Cullen (1914) a year later assumed E and S to bind irreversibly to each other, but Briggs and Haldane (1925) realized that a more general formulation could be achieved by assuming that C rapidly achieves a steady state that need not represent a true equilibrium. The nomenclature of the Briggs-Haldane treatment is easily understood today, and leads directly to the contemporary form of the Michaelis constant (K_M) and to equations for reaction velocity (Fig. 1, Eqs. 2,3). The steady-state approximation of Briggs-Haldane plays a central role in many subsequent treatments of coupled multienzyme systems (Goldbeter and Koshland 1981), allosteric regulation in the concerted MWC (Monod, Wyman, and Changeux) (Monod et al. 1965), or induced-fit KNF models (Koshland, Nemethy, and Filmer) (Koshland et al. 1966). The work of Michaelis and Menten (1913) has been extended to describe enzymes having more than one substrate, ultimately giving rise to a rich ecology of models with names such as bi-bi, random, and sequential (Segel 1975; Rudolph 1979). What we have to say about the Michaelis-Menten model applies to these models as well.

Representing a canonical enzymatic reaction as a dynamical system

Michaelis-Menten and Briggs-Haldane models are an approximation, under a very specific set of conditions, to a more fundamental description of an elementary enzymatic reaction as a dynamical system involving ODEs. Mass action kinetics finds a precise mathematical description in differential equations, but the frequent use of reaction velocity (V) in introductory textbooks obscures the simple fact that V ≡ dS/dt. For our two-step model of an enzymatic reaction, the dynamical system consists of four coupled ODEs in which C, E, S, and P are dynamic variables, E_o and S_o are enzyme and substrate concentrations at the start of the reaction (the initial conditions), and k_f, k_r, and k_cat are free parameters (rate constants) (Fig. 1, Eqs. 4–7). Two additional pieces of information are available for the system in the form of conservation or mass balance conditions: (1) The total concentration of free enzyme and complex equals the initial enzyme concentration (E + C = E₀), and (2) the total concentration of free substrate, complex, and product equals the initial concentration of substrate (S + C + P = S₀) (Fig. 1, Eqs. 8,9). It follows that P = S₀ − C − S and E = E_o − C, making it possible to reduce our original system of four differential equations to two (Fig. 1, Eqs. 10,11). Solving this dynamical system yields the concentration of S and C with respect to time [S(t) and C(t)], but no known method provides an analytical solution to the system (i.e., a set of equations true for all parameter values). We can, however, calculate numerical solutions for any specific values of the initial conditions and kinetic parameters by evaluating the equations in a computer (using an ODE solver that steps through the equations in a succession of small time steps).

Even in the absence of specific experimental data, it is possible to study our dynamical system by choosing reasonable parameter values. A robust theory exists to calculate diffusion-limited rate constants for small molecules from first principles (k_f ∼ 10⁸–10⁹ M⁻¹ sec⁻¹), but in the case of enzymes and their substrates, the active site can be accessed only over a limited range of collision geometries, which effectively restricts diffusion-limited reaction rates for binding of small substrates to enzymes to k_f ∼ 10⁵–10⁶ M⁻¹ sec⁻¹(Northrup and Erickson 1992). On-rates can be much lower if conformational changes in the enzyme are involved; for example, during binding of imatinib (Gleevec) to the active site of the oncogenic Bcr-ABL kinase (Schindler et al. 2000). Reverse rate constants are determined by dissociation enthalpies and entropies: for K_d ∼ 1 μM and diffusion limited binding, k_r is ∼10⁻¹ sec⁻¹. We will assume a catalytic rate constant of 10⁻² sec⁻¹, a value that is atypically slow for many metabolic enzymes, but reasonable for phosphorylation of peptide substrates by receptor kinases (Li et al. 2003; Yun et al. 2007, 2008). Because we can choose the amount of substrate and enzyme in an in vitro reaction, we set the initial values at convenient values: S₀ = 1 μM and E₀ = 10 nM (1 μg/mL for a 100-kDa enzyme). Examining trajectories from a numerical solution to the dynamical system, we see that S(t) falls steadily from its initial value, but the abundance of C(t) is so low we need to rescale the axes to discern any detail. In a numerical simulation, this can be accomplished simply by finding the high and low values in the trajectory, but we can also use the analytical approach known as nondimensionalization to place all variables on a unitless scale of 0–1. We will accomplish this in two steps: by nondimensionalizing first for concentration, and then for time (nondimensional variables have no units, and can therefore be compared directly). In so doing, we will uncover the connection between our dynamical system and the Michaelis-Menten equations.

Nondimensionalization and separation of time scales

To eliminate concentration units from our dynamical system, we replace the original variables with rescaled values: 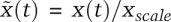, where x(t) is the original variable, and x_scale is the rescaling constant. is then a nondimensional variable lying between 0 and 1. In the case of S(t), an obvious rescaling constant is the initial substrate concentration, S_scale = S₀, and the nondimensional dynamical variable 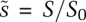now starts at 1 and falls to 0 as t → ∞. Rescaling C(t) is more subtle: At the beginning and end of the reaction, it has a value of C(t) = 0, and the trajectory must therefore have a maximum somewhere in between; this is the C_scale value we seek. The maximum naturally occurs when the slope is 0 (dC/dt = 0), which we show in the Supplemental Material (Supplemental Eqs. 3–6) to be C_scale ≈ E₀S₀/(S₀ + B), where B is a composite of several elementary rate constants. As we will see, the composite parameter B is identical to K_M, but we temporarily ignore this fact to make clear that, from the perspective of nondimensionalization, B simply arises as a scaling constant. Knowing C_scale, we make the simple substitution 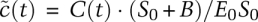, and, by plugging in actual values for the parameters, we can plot S(t) and C(t) [or any derived value, such as P(t)] on an axis of 0–1 (Fig. 2A–B, Eqs. 1, 2). Nondimensionalization with respect to concentration also recasts rate constants in a rather helpful way: We see that 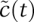is determined by rate constants on the order of ∼0.1 sec⁻¹ but 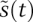is determined by rate constants ∼0.001 sec⁻¹ (Fig. 2C, Eqs. 3, 4). Thus, the dynamics of 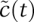are 100-fold faster than those of 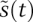. Such a comparison is simply not possible in the original dimensional equations, because forward rate constants have different units than the reverse and catalytic rate constants (M⁻¹ sec⁻¹ for k_f, and sec⁻¹ for k_cat and k_r).

Figure 2.

Nondimensionalization and singular perturbation analysis of a simple enzymatic reaction, fulfilling the Michaelis-Menten conditions. (A, left) The trajectories for concentrations of substrate (black) and complex (red) over time. (Right) The rescaled graph using nondimensionalized parameters illustrates the behavior of both species on a common axis, and suggests the existence of two separable time scales. (B) The dynamic ODEs after rescaling for concentration. (C) The same equations as in B, with a specific set of parameters drawn from A. The difference of approximately two orders of magnitude in the nondimensionalized reaction rate constants indicates two distinct and therefore separable time scales. (D) The inner solution of the nondimensionalized dynamical system showing the early, fast phase, during which complex formation rises exponentially (red), while the substrate concentration remains constant (black). (E) The outer solution of the nondimensionalized dynamical system showing the coupled decay of complex (red) and substrate (black), with complex in rapid pseudoequilibration with falling substrate.

Because 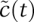and 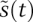are controlled on different time scales (typically differences of 100-fold imply fundamentally different dynamics), it is possible to separate fast and slow processes in such a way that the fast events are stretched out relative to slower events. A dynamical system that operates on two or more time scales can be decomposed using singular perturbation analysis. The basic idea is that fast processes evolve on time scales over which slow processes can be assumed to be constant (that is, to be at quasistatic state; QSSA). Conversely, when slower processes dominate, the fast processes are assumed to be continuously in quasiequilibrium. Singular perturbation analysis can be accomplished from several points of view, and we refer readers to a wonderfully clear and thorough discussion of this topic by Segel and Slemrod (1989). As a starting point for our relatively simple treatment, notice that, by choosing a rescaling constant of t_scale = 1/k_fS₀ and a scaled dimensionless time of τ = t/t_scale, the rate constants for 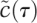are now ∼1, and those for 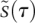are ∼10⁻². Thus, during the interval, 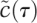is changing rapidly, 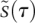is essentially stationary, and we can effectively ignore its dynamics. We therefore approximate the dynamical system in the early phase by a single ODE for 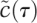and a constant value for 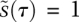(Fig. 2D, Eqs. 5,6). This is known as the inner solution, and has a particularly simple and satisfying shape, with 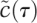asymptotically approaching 1. The dynamics of a 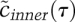do not change much after τ ∼ 3, which defines the limit of utility of the inner solution (the unit of t_scale is k_f S₀⁻¹ ∼10 sec), so the inner solution holds for ∼30 sec.

Turning to the slow phase, we rescale time yet again, but now we want rate constants for 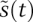to be on the order of 1. Again, several rescaling possibilities exist, but we chose the dimensionless coefficient 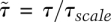and τ_scale = E₀/(S₀ + B). Now, the nondimensional rates for 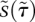are on the order of 1, and those for 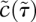are 100, so we can assume that 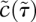is always quasiequilibrated with 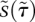. This assumption yields the dynamics at late times, known as the outer solution (Fig. 2E, Eqs. 7,8). Recall from the inner solution that 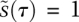, and the complex ends up at its steady-state value ∼1 (nondimensionalized units). The dynamics of the outer solution involve a fall from these initial values, at first linearly and then logarithmically as the reaction proceeds [we arrive at dimensionless time in the outer solution by successively scaling time by two constants, so that 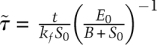or 2100 sec]. If we join the inner and outer solutions together, we arrive at a complete description of our dynamical system (Fig. 3A, Eqs. 1–5). These dynamics can be expressed in either nondimensional or dimensionalized units. Moreover, we remind ourselves that the compound rate constant B has a value of 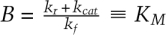, the Michaelis constant. Inspection of the dimensionalized outer solution for substrate S_outer(t) (Fig. 3A, Eq. 4) reveals that it is identical to the analytical solution of the enzyme velocity equation derived by Michaelis and Menten (1913), a point that becomes more obvious if we take the derivative dS(t)/dt (Fig. 3A, Eq. 5). Note that we did not force K_M onto the outer solution; it arose naturally from a consideration of the dynamics of substrate at later times.

Figure 3.

Singular perturbation analysis of the classical enzyme reaction. (A) The equation set describing the dynamics of the early (fast; pink) and late (slow; blue) phase of the reaction. The time scale of each of the phases is indicated. (B) Nondimensionalized changes in complex (red) and substrate (black) smoothly joined following singular perturbation analysis for the early (pink) and late (blue) phase of the reaction. (C) Example of a reaction system that can be analyzed by singular perturbation methods but that does not fulfill requirements of the classical Michaelis-Menten approximation. Complex (red) and substrate (black) exhibit a fast and slow phase. The Michaelis-Menten approximation of substrate (green) shows substantial deviation from the true dynamics.

We now arrive at a key insight: The Michaelis-Menten equation is the outer solution to the complete dynamical system, and is valid over precisely the range of parameter values for which a separation into fast and slow dynamics is valid. This statement is identical to saying it is the quasistatic state approximation for later times. Conversely, the inner solution is the enzyme velocity equation for the initial “burst phase” of the reaction. It is by no means necessary that our dynamical system be separable into fast and slow processes: This is true only over a relatively narrow range of parameter values. Moreover, not all systems that can be separated into multiple time scales by singular perturbation analysis obey Michaelis-Menten kinetics (Borghans et al. 1996; Tzafriri and Edelman 2004; Ciliberto et al. 2007). For example, consider a reaction in which C forms rapidly relative to P, but E is not in excess of S (Fig. 3C). Parameters for this solution derive from published models of receptor-mediated phosphorylation of the Shc adaptor protein by epidermal growth factor receptor (Birtwistle et al. 2007; Chen et al. 2009). In this case, separable early/fast and late/slow phase solutions can be defined (Supplemental Eqs. 63–66), but K_M does not appear in the singularly perturbed solution, and no correspondence between the Michaelis-Menten model and actual enzyme dynamics can be discerned. Thus, we see that the Michaelis-Menten approximation is a very special case of a more general representation of a simple enzymatic reaction as a network of ODEs, and that the conditions under which the approximation holds are a small subset of the conditions under which enzymes function in real biological systems.

The Michaelis-Menten equations are generally held to be valid when either S₀ ≫ E₀ or k_r ≫ k_cat, but a more general and powerful description of these limits is as follows: The Michaelis-Menten model (the outer solution) is acceptable when the QSSA dynamics exhibit an acceptable deviation from the full dynamical description. This condition can be formulated as 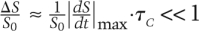(Segel and Slemrod 1989), where ΔS is the change in substrate from its initial concentration and τ_C is the time it takes for the complex to reach its steady-state value. The physical interpretation of the condition is that the relative change in substrate must be small (much less than 1) in the early phase of the reaction (t < τ_C), during which the complex accumulates,. Under the conditions shown in Figure 3C, the change in concentration of substrate over time (black) has a value of 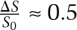, and therefore exhibits substantial deviation from the dynamics given by the Michaelis-Menten approximation (green).

With these considerations in mind, we might ask what subset of elementary biochemical reactions in cells are reasonably approximated by Michaelis-Menten kinetics. In the case of the signal transduction networks currently being studied using kinetic modeling, the conclusion appears to be that few if any reactions can be so approximated, even though many can be described quite well by a mass action dynamical system (Chen et al. 2000, 2009; Birtwistle et al. 2007; Albeck et al. 2008). The observed mismatch does not involve an absence of well-mixed compartments or the stochastic nature of cellular biochemistry (although both are true), but the very limited range of parameter values over which the Michaelis-Menten approximation holds. In the case of metabolic reactions, however, it appears that Michaelis-Menten kinetics do have wider applicability (Costa et al. 2010). In many cases, in vitro biochemical analysis of cell signaling proteins is performed under conditions that yield valid Michaelis-Menten kinetics, but that cannot be extrapolated to conditions in vivo in which substrate and product concentrations are radically different. In constructing models of complex cellular biochemistry, we often find ourselves struggling to use K_M measurements when estimates of elementary rate constants would be much more useful.

Determining parameter values from experimental data

Thus far, we have assumed that values for free parameters (rate constants) are known, but this is not usually true. Instead, we must infer these values from experimental data. The procedure involved is variously known as parameter estimation, model calibration, or model training (we will use the first term). As we will see, the truly elegant feature of Michaelis-Menten kinetics is a close connection between model parameters and features of the system that can be measured empirically (experimental observables). With a simple enzymatic reaction in vitro, observables such as the rate of formation of product over time might correspond directly to a dynamical variable, but, in more complex models, the connection between data and dynamical variables is more subtle. In cells, most observables are composites of multiple dynamic variables, or they derive from some biosensor whose own biochemistry must be considered (this is analogous to the use of coupled enzymatic reactions as a means to monitor product formation in classical enzymology) (Hansen and Schreyer 1981; Bartelt and Kattermann 1985).

To calibrate a model, data are collected for a set of observables, and the data are then compared with model-based predictions using an objective function:

where obj(parameters) refers to the value of the objective function for a particular set of parameters, and the squared term prevents positive and negative deviations from canceling trivially. If we evaluate this at one point for the dynamic variable S(t), we obtain

where σ² is the variance in the data. Equation 2 is also known as a least-squares difference function or the χ² function. Usually, we evaluate the objective function at multiple time points such that

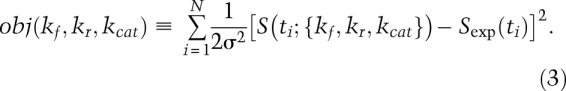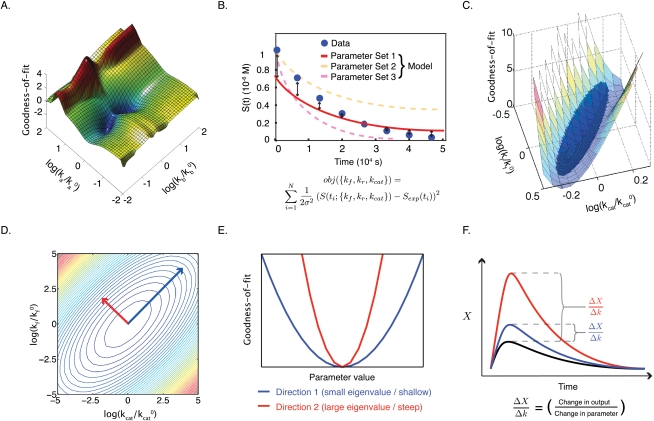
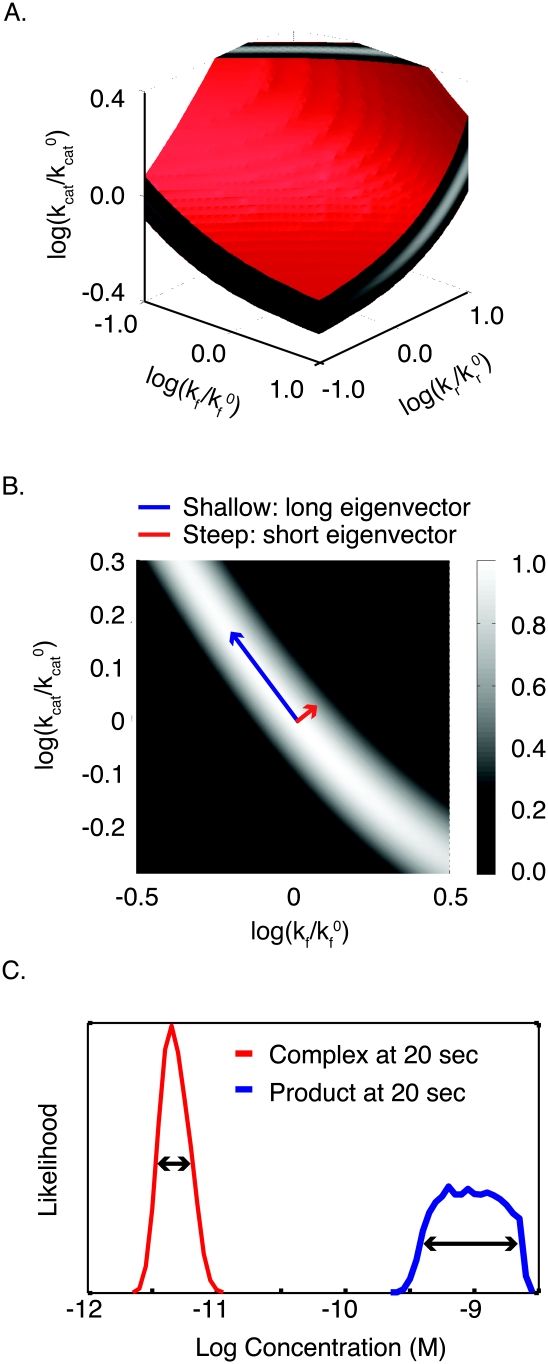
Estimation is performed by systematically varying parameters over a biophysically plausible range (e.g., within the range of diffusion limited rates), and then computing the value of the objective function [obj({k₁…k_Np}), where N_p is the number of parameters] for the data. This generates a “landscape” of the objective function, with as many dimensions as parameters being estimated, and with a value encoded in the “altitude.” A landscape of the objective function is directly analogous to an energy landscape, and the aim of parameter estimation is to find the global minimum in the landscape: With a χ² objective function, the global minimum corresponds to the most probable value of the parameters. Figure 4A shows an example of such a landscape, in which the axes are scaled with respect to decadal “fold changes” over nominal values for two parameters (k_a⁰ and k_b⁰). These “nominal values” typically define a point in parameter space at which the objective function has a reasonable value, or a position from which further exploration is undertaken. Much as fold change is a useful way to think about data, it is a natural way to think of moves in parameter space.

Figure 4.

Parameter values for dynamical systems described by ODEs can be estimated from data using an objective function. (A) In the objective function, each unknown parameter of the ODE system corresponds to a dimension. The surface of the objective function resembles an energy landscape, with the altitude at each point denoting the goodness of fit of a specific set of parameters to data. Here, a three-dimensional slice through a complex objective function (corresponding to two parameters) shows numerous steep inclines/declines, local maxima/minima, and large areas where the objective function is independent of the two parameters displayed. (B) The deviation between points of synthetic data and model trajectories can be measured and used to evaluate the parameters. The effect of assuming perfect data means that there is a well-defined minimum that is the “true” parameter set, while the assumption of a variance means that the χ² landscape has realistic values for its peaks and valleys. (C) The approximated surface of a particular valley in the complex landscape is shown in blue. (D) The curvature of the approximated surface area can be calculated as the second term of the Taylor expansion of the objective function, the Hessian. The eigenvectors of the Hessian represent the short and long axes of the paraboloid, and generally do not point in the direction of any single parameter. (E) Short eigenvectors indicate the direction of a steep parabola (large eigenvalue; red), and long eigenvectors indicate the direction of a shallow parabola (small eigenvalue; blue). (F) Moving in the direction of either eigenvector in parameter space has different consequences for model trajectories. Moving along a steep eigenvector of a Hessian leads to significant changes in the trajectory (red), while moving along the shallow eigenvector leads to only minor changes (blue), corresponding respectively to large and small changes in the values of the objective function.

We cannot distinguish values of obj({k₁…k_Np}) that differ by less than experimental error. This places an absolute limit on the identifiability of model parameters; that is, on the precision with which parameters can be estimated from data. As we will see, identifiability is also limited by the mathematical relationship of model parameters to dynamic variables, a subset of which correspond to experimental observables. Oddly, model calibration—or, more commonly, “model fitting”—is often presented in a pejorative light. The reasoning appears to be that if a model matches data without any fitting, then it is somehow more valid. This is simply nonsense: All plausible models of biochemical processes have free parameters that must be estimated in some way. Moreover, a model with constant topology can exhibit radically different input–output behavior, as parameters vary across a biophysically plausible range. It is true that a reasonable match to data can be achieved using parameters that are estimated from first principles, in which case calibration is “inductive” rather than formal. However, formal calibration is always the more rigorous approach.

Consider an attempt to estimate parameter values for our simple enzymatic reaction, again assuming the rate constants (k_f = 10⁵ M⁻¹ sec⁻¹, k_r = 10⁻¹ sec⁻¹, and k_cat = 10⁻² sec⁻¹) that yielded a valid Michaelis-Menten approximation. Since we are performing analysis in silico, we use synthetic data obtained from simulation of the model (Fig. 2B, Eqs. 1,2). The concept of synthetic data is initially rather odd, since it would seem to assume precisely what we want to test, but this is not, in fact, the case. Synthetic data play an important role in developing and validating most numerical algorithms, and reveal the fact that information is lost when we move from parameter values to simulated synthetic data, and then back to parameters via estimation (naturally, we keep the parameters used to create synthetic data “secret”). Synthetic data are computed by running model simulations with particular parameter sets, and then adding an appropriate level of experimental noise (based on an error model, which often but not necessarily realistically assumes noise to be normally distributed).

For our simple reaction, we attempt to estimate parameters from synthetic data corresponding to measures of S at 12 points in time. We assume an error model with a root mean square (RMS) deviation of 10% at each data point. This provides real numbers for the variance term in Equations 2 and 3, and gives meaning to the χ² interpretation of the objective function. We assume that the equations in our model are the same as those used to create the synthetic data. The efficacy of model calibration can then be judged by seeing how close estimated parameters are to the “true” parameters used to create the synthetic data (Fig. 4B). Of course, the question also arises as to how we can model biochemical processes for which we do not known a priori the nature of order of the reactions.. This is a distinct and interesting problem known as network inference or network reverse engineering (Werhli et al. 2006; Marbach et al. 2010).

The landscape of obj({k₁…k_Np}) can be determined using numerical methods for any set of synthetic data, but we can gain a good intuitive understanding of its key features using analytical approximations. At any point near a local or global minimum, the landscape resembles an ellipsoidal valley (a paraboloid) whose curvature differs in various dimensions (Fig. 4C shows a parabolic approximation for a two-parameter landscape). The curvature of this parabola is simply the second term in a Taylor expansion 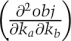of the objective function (recall that many functions can be approximated as a Taylor series, a power series in which the coefficients of each term are simply the derivatives of the function). The first two coefficients are the slope and the curvature of the objective function, and it makes sense that we would use these first in attempting to approximate a landscape with an arbitrary shape. For functions with two or more dimensions, we require curvatures in multiple dimensions, and the second term in the Taylor expansion corresponds to a matrix known as the Hessian (Fig. 4D). The useful feature of this analytical approximation is that axes of our parabolic valley in the landscape of the objective function have directions given by the eigenvectors of the Hessian and lengths given by the eigenvalues (Fig. 4D, red and blue arrows). Engineers will also recognize this to be nearly identical to the Fisher Information Matrix (Kremling and Saez-Rodriguez 2007). With respect to the current discussion, the important thing is that we transformed a poorly defined analysis of an arbitrary and unknown landscape into an intuitively simpler analysis of parabolic valleys whose shapes are described by eigenvectors and eigenvalues.

With biochemical models, we usually observe that, at any point in parameter space, eigenvalues differ dramatically, meaning that valleys are long and shallow in some directions, and narrow and steep in others (Fig. 4E). To find a minimum in the landscape, we need to move through these valleys to a low point using as a guide only “altitude” (that is, of obj({k₁…k_Np}), whose measurement is degraded by experimental error. It is apparent we can reasonably evaluate the consequences of moving up steep walls of the parabola, which correspond to short eigenvalues (these are bad moves), or down steep walls (these are good moves) (Fig. 4F), but it is much harder to determine in which direction we should move along the shallow valley floor. The inability of the objective function to pinpoint the low point of flat valleys is often referred to as structural nonidentifiability, and arises, as the name implies, directly from the structure of the equations in the dynamical system. Structural nonidentifiability imposes a severe limit on parameter estimation. Moreover, because long eigenvectors usually point at an angle to the axes (Fig. 4D), nonidentifiability often involves combinations of parameters (Gutenkunst et al. 2007). In our model, nonidentifiability arises because C(t) is controlled by a ratio of elementary rate constants, and this also explains why the long axis of the valley in the landscape of the objective function lies at an angle relative to the k_cat and k_f axes.

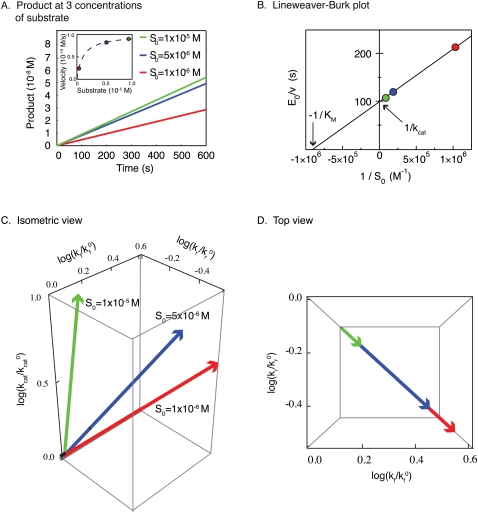
What is the relationship between estimation using the landscape of the objective function and the classical approach to determining parameter values in Michaelis-Menten kinetics? To explore this, we use a full dynamical system describing the enzymatic reaction (Fig. 1, Eqs. 9,10) to create synthetic data for S(t) at each of three values of S₀. In classical enzymology, parameter values are determined by measuring the rate of product formation for each value of S₀ after the burst phase, but early enough that product formation is still linear in time (Fig. 5A). This generates a curve of enzyme velocity as a function of initial substrate concentration (Fig. 5A, inset) that can be transformed into a Lineweaver-Burke plot to extract the constants K_M and k_cat (Fig. 5B). This works (Fig. 5A, green dot) because, at saturating levels of substrate, V_max is given by k_catE₀, allowing k_cat to be estimated, but when S₀ is smaller, enzyme velocity (V) is a function of both k_cat and K_M, allowing K_M to be determined (in modern practice, numerical estimation procedures are used in place of actual Lineweaver-Burke plots) (Atkins and Nimmo 1975; Woosley and Muldoon 1976).

Figure 5.

The Michaelis-Menten approximation of a classical enzymatic reaction and the connection to parameter identifiability. (A) In typical experiments, V_max (enzyme velocity) can be determined for various concentrations of substrate. (B) The reciprocal plots of the measured values can be plotted to determine the Michaelis constant (K_M) and the catalytic constant (k_cat). (C) Measuring enzyme velocity for three substrate concentrations projects individual vectors in the three-dimensional parameter space. (D) While altering the substrate concentration allows for the determination of k_cat, the ratio of the reverse rate constant to the forward rate constant (k_r/k_f) remains unchanged. Thus, only K_M can be determined, leaving the k_f and k_r reaction rate constants undetermined.

A satisfying correspondence exists between approaches to rate constants in classical enzymology and parameter estimation based on an objective function. To illustrate this, we analyze the landscape of obj(k_f,k_r,k_cat) directly using our knowledge of the analytical solution to S_outer(t) (i.e., using the QSSA approximation) (Fig. 3, Eq. 4). The landscape of obj(k_f,k_r,k_cat) has three parameter dimensions and a single parabolic minimum. While it is difficult to plot such a four-dimensional object, the eigenvectors of the Hessian approximation lie in a three-dimensional space that can easily be visualized. The shorter and more identifiable eigenvector projects onto all three parameter axes (Fig. 5C). As S₀ increases (to 10 × 10⁻⁶ M in Fig. 5D), the eigenvector swings upward, decreasing the projection along the k_f and k_r so that it becomes nearly parallel to the k_cat axis. Estimation under these conditions is akin to obtaining k_cat from measuring V_max at saturating concentrations of substrate. At lower concentrations of substrate, the identifiable eigenvector points at an angle to k_f and k_r, meaning that we can estimate a ratio for these parameters. Importantly, when, we vary S₀ in this lower range, the projection of the eigenvectors onto the k_f and k_r axes does not change (something that is readily apparent when viewed top down) (Fig. 5D), and we do not gain additional information on the individual parameter values. This corresponds in classical enzymology to measuring enzyme velocity at subsaturating substrate concentrations when 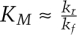. Overall, then, the full dynamical system for the canonical enzymatic reaction is structurally nonidentifiable, given data on S(t), but the outer solution is most identifiable with respect to the parameters k_cat and K_M. Thus, the truly elegant aspect of the Michaelis-Menten equation is that it transforms a nonidentifiable system into an approximation that is highly identifiable.

Thus far, we implied that some parameters are identifiable, and some are not (given the data), but this binary classification is too restrictive. In reality, our ability to estimate even the most identifiable parameters is limited by error in the data, and it is therefore more accurate to think of parameters as spanning a range of identifiability. The exponent of obj(k_f,k_r,k_cat) is a χ² error function that returns maximum likelihood estimates, and thus parameter estimation will return likelihood distributions for the rate constants. The concept of “degree of identifiability” is expressed by the width of this distribution. A likelihood function computed for obj(k_f,k_r,k_cat) for the complete dynamical system describing our canonical enzyme substrate system is shown by the isosurface plot in Figure 6A (in this plot, each color maps out a surface of constant probability). The most likely parameter values are white (Fig. 6A), and the least likely are black (Fig. 6A), with a red surface showing the cutoff P = 0.01 (Fig. 6A). For simplicity, consider a two-dimensional slice of this plot (Fig. 6B) corresponding to k_f versus k_cat, with k_r = k⁰_r (10⁻¹ sec⁻¹). As before, we immediately observe different degrees of parameter identifiability: Decreasing k_f and increasing k_cat (Fig. 6B, blue arrow) has little effect on obj(k_f,k_r,k_cat), whereas increasing k_f and k_cat in the perpendicular direction has a significant effect (Fig. 6B, red arrow). These directions correspond precisely to the long and short eigenvectors in the Hessian for the appropriate slice of the objective function.

Figure 6.

The likelihood function ascribes the likelihood of correctness to parameter sets based on how well they explain the observed data. (A) The surface plot of the χ² error function of the classical enzyme reaction in parameter space. The likelihood of a given parameter set is given by the brightness (white being most likely), while red denotes a cutoff boundary. (B) A two-dimensional slice through the χ² function shows that the likelihood of one parameter (e.g., k_f) is dependent on another parameter (e.g., k_cat). The region of high likelihood (white) corresponds directly to the shallow direction of a Hessian (i.e., all yielding similarly low values of the objective function). (C) Sampling of parameter sets using the likelihood function can be used to make probabilistic predictions of product (blue) and complex (red) formation at 20 sec after the start of the reaction. While individual parameters of the reaction rate constants remain nonidentifiable, specific and unique predictions can be made.

In summary, parameter estimation returns an infinite family of possible parameter values, the probability of which is given by the exponential of the objective function. In this scheme, the contributions of experimental error and structural nonidentifiability are both accounted for, and all parameters become distributions of varying width (and greater or lesser correlation). We can use these distributions and their correlations to generate predictions that are also distributions, reflecting parametric uncertainty. For example, when we compute the values of P(t = 20 sec) and C(t = 20 sec), we return likelihood distributions with different mean values and width: The estimate for P spans a fivefold range, but C is better determined, and its estimate spans a twofold range (Fig. 6C). Note that uncertainty in these predictions is significantly larger than the 10% RMS error we assumed in the synthetic data. This arises because we used data collected at later times to make predictions about the values of dynamical variables at earlier times. In making such model-based predictions, both identifiability and experimental error are important .

We learned several things from this exercise. First, parameter estimation for our simple enzymatic systems using observations traditionally available in classical enzymology returns an infinite number of parameter values having different probabilities. Nonetheless, it is possible to make useful model-based predictions about the levels of species of interest (product and complex in our case). Second, the likelihood plot for parameter values has a remarkably complex shape, implying varying degrees of model identifiability across multiple independent parameters, and illustrating the fact that it is difficult to intuit precisely how data and model parameters are linked. This is a sobering thought, given the prevalence of informal thinking in molecular biology and the common assumption that moving from data to an understanding of the underlying biochemistry is straightforward. Third, under special circumstances in which the QSSA is valid, control parameters for the Michaelis-Menten model are maximally identifiable, and uncertainty in parameter values arises only from experimental error. In the case of complex models of cellular biochemistry, all of these considerations hold, but the landscape of the objective function is much more rugged, and we typically observe multiple maxima and minima (Fig. 4A; Chen et al. 2009). Finding the minimum in such a landscape is not trivial, and multiple points may have values of obj({k₁…k_Np}), close to that of the global minimum.

Discussion

In this review, we compared classical Michaelis-Menten approaches to analyzing a simple biochemical reaction with a modeling approach based on systems of ODEs. ODEs are the natural language for representing mass action kinetics in a deterministic, continuum framework. By comparing the classical and ODE-based approaches, we arrive at four important conclusions, all of which have been known for many years, but generally not by experimental molecular biologists.

Conclusion 1: Michaelis-Menten kinetics represent a singularly perturbed form of a complete model based on a network of ODEs

The Michaelis-Menten equations (in the Briggs-Haldane formulation) can be derived from a dynamical system of ODEs over the limited range of parameter values in which the system exhibits quasi-steady-state behavior. When this holds, singular perturbation analysis returns an outer solution that is identical to the Michaelis-Menten model, and has familiar control parameters (K_M and k_cat). The validity of the Michaelis-Menten approximation for any set of parameters is captured by the deviation between the outer solution and the full dynamical system. The range of parameter values and initial conditions over which the Michaelis-Menten approximation is valid is commonly encountered with enzymatic reactions in vitro, but is probably rare in cells. For example, signal transduction networks appear to exhibit significant deviation between the Michaelis-Menten approximation and either the full dynamical system or separation of time scale approximations arising from singular perturbation analysis. Thus, it is entirely appropriate that deterministic models of intracellular biochemistry are based on coupled ODEs in which K_M rarely appears. Moreover, even when single steps in an enzymatic cascade are well approximated by Michaelis-Menten kinetics, the overall cascade cannot simply be modeled as a succession of Michaelis-Menten reactions; the coupling between successive reactions is too great. Instead, the full dynamical system must be subjected to singular perturbation analysis. An important corollary is that many biochemical parameters measured by biochemists in vitro—e.g., K_M and V_max—are less useful to cell-based modeling than estimates of k_f and k_r (see also Ciliberto et al. 2007 for further discussion of this point).

We discussed the value of nondimensionalizing concentration and time when analyzing systems of ODEs, but this remains rare in modeling biochemical systems. The use of raw parameter values is acceptable for simulation models, but is a potential source of error with methods such as stability analysis. The process of separating dynamical systems into difference time scales by singular perturbation analysis is also difficult, but we note that “rough and ready” nondimensionalization can be achieved more simply. In our enzymatic system, rescaling concentrations with C_scale ≈ E₀ rather than C_scale ≈ E₀S₀/(S₀ + B) is already highly informative, albeit without regenerating the classical Michaelis-Menten model.

Conclusion 2: on the identifiability of model parameters

The precision with which unknown parameters can be identified in a model is determined by two factors: (1) experimental error, and (2) the relationship between experimental observables and model parameters (structural identifiability). Structural nonidentifiability arises in large part because changes in k_f can be balanced by compensatory changes in k_r and vice versa. In these cases, estimation shows the rate parameters to be poorly identifiable, but k_f and k_r are strongly correlated, so that, even in the face of uncertainty, we can make well-substantiated predictions about the overall velocity of the reaction. In the case of reactions obeying Michaelis-Menten kinetics, this fact is elegantly encapsulated in the equation for K_M. Nonidentifiability arising from experimental errors and model structures interact in real experiments to determine the overall precision of estimation: The lower the experimental error, the greater our ability to distinguish small differences in the value of the objective function (Bandara et al. 2009). Thus, an approach to parameter estimation based on probability is more effective than one that assumes some parameters to be identifiable and others to be nonidentifiable. In such an approach, all hypotheses are probabilistic, and their likelihood of being true is a function of model structure, data availability, and experimental error (see Conclusion 4, below).

Conclusion 3: maximizing identifiability through experimental design

An important point to which we alluded, but did not specifically discuss, is that the precision with which parameters can be estimated (and useful predictions made) depends on experimental design. A relatively robust theory of optimal experimental design exists to specify how a fixed number of assays should be distributed over time and concentration in the experimental domain (S₀ or E₀, for example) (Atkinson and Donev 1992; Pukelsheim 1993). The theory is widely used in pharmacokinetics, but it is not well known to molecular biologists. Rigorous analysis nonetheless supports the intuitive notion that increasing the amount of data on a specific dynamic variable is subject to the law of diminishing returns. In the case of complex biochemical models probed with synthetic data, it has been demonstrated that even perfect data encompassing all dynamic variables are insufficient to constrain more than a subset of the underlying parameters (in terms of a Hessian approximation to the objective function, this manifests itself as spectrum of eigenvalues that vary over many orders of magnitude). Sethna and colleagues (Gutenkunst et al. 2007) describe such models as “sloppy,” insofar as most parameter values are very poorly determined. The situation with real data is worse, of course, because only a subset of the variables (protein phospho states for example) can usually be measured. Thus, the relative paucity of measurements contributes directly to parametric uncertainty.

Although valuable, these insights into model identifiability do not take into account the impact of fundamentally new types of experiments that can reveal otherwise poorly observable features of a dynamical system. In the case of our canonical enzyme reaction, this is illustrated by stopped-flow experiments that make the dynamics of the initial transient observable and allow estimation of k_f (Lobb and Auld 1979). In this case of cell-based studies, a general theory to evaluate the impact of parameter estimability has not yet been developed, but it seems likely we need to combine perturbation (using RNAi and small molecule drugs) with pulse-chase and dose–response studies. As illustrated by stopped-flow enzymology, when systems have large separations in time scales, it is also important to assay processes operating at each of the relevant time scales. The ready availability of methods for perturbing biological systems (at least in cell lines) stands in contrast to the primacy of observation in models of climate, astrophysical events, and most other natural phenomena. Formal analysis of cellular biochemistry should therefore yield interesting general advances in the interplay between modeling and experiments.

Unfortunately, the current era of high-throughput science de-emphasizes experimental design in favor of systematic gene-by-gene perturbation coupled with a few simple, predetermined readouts. We are hopeful that rigorous analysis of experimental design will change this situation by demonstrating the central role that design and hypothesis testing should play in all experiments (even systematic “annotation” experiments), and by identifying precisely which types of perturbations and measurements are most valuable.

Conclusion 4: toward a probabilistic framework for reasoning about biochemical networks

Both critics and proponents of biochemical modeling continue to run into two misconceptions about parameterization. The first is an optimist's view: It is both feasible and desirable to pin down all rate constants with experiments before a model becomes useful. The second misconception is a pessimist's view: Not only is it impossible to measure all parameters, but such models have so many parameters that they can fit any sort of data, and thus cannot give meaningful predictions. Neither is true. High-confidence predictions can be made using nonidentifiable models, but it is also true that some predictions have little experimental support. We therefore require a probabilistic or Bayesian framework, in which both parameters and model-based predictions are assigned varying degrees of belief.

When parameter estimation is performed for a dynamical model using real (and therefore noisy) experimental data, we recover a range of values for each parameter. The shapes of the distributions and the extents of their correlation will depend on both the structure of the equations in the dynamical system and the type and accuracy of the experimental data. In some cases, the estimated distributions will be narrow, meaning that we can infer quite a bit about specific rate constants, and in other cases the parameter distribution will be nearly flat, meaning that we have virtually no knowledge of actual values. However, we are rarely interested in parameter values per se: Instead, we want to predict some model output or distinguish between different model topologies (corresponding to different arrangements of the reactions). Thus, consideration of model identifiability and parametric uncertainty should occur in hypothesis space, not in parameter space: We want to design experiments and structure models to optimally distinguish between specific hypotheses, not to hone parameter estimates. Here we encounter an interesting paradox: Models with realistically detailed depictions of biochemistry are significantly less identifiable than simple models in which biochemistry is represented in a less realistic manner. We therefore require new analytic approaches for judiciously weighing the merits of model detail and estimability.

When we discuss biochemical systems in terms of a degree of belief in a prediction, given a specific set of experimental data and a particular model structure, we are reasoning in a Bayesian framework. Bayesian parameter estimation (which is distinct from constructing Bayesian networks) is commonly used in the physical sciences and engineering (Calvetti et al. 2006; Coleman and Block 2006; Eriksen et al. 2006), but the first applications to biochemical networks have just started to appear (Flaherty et al. 2008; Klinke 2009). One challenge to their widespread use is developing algorithms able to sample rugged objective functions. However, once in place, Bayesian frameworks for analyzing cellular networks will be very powerful. They will provide an effective means to apply rate constants collected in vitro or in vivo to networks in cells: The in vitro data will simply constitute a prior (to which we assign a greater or lesser degree of belief) for estimation of parameters from cell-based data. Moreover, they will allow rigorous comparison of competing proposals about biochemical mechanisms, pinpoint which data are required to resolve disagreements at specific P-values, and allow us to re-evaluate historical data with the aim of creating new hypotheses.

Modeling complex biological processes in cells

The concepts described here can be extended directly to deterministic modeling of complex biochemical networks in cells (Kholodenko et al. 1999; Chen et al. 2000; Albeck et al. 2008). Each step in the network is represented as an elementary reaction involving either reversible binding–unbinding, movement between reaction compartments, or enzyme-mediated catalysis. The initial concentrations of proteins are assessed using quantitative Western blotting or mass spectrometry, dynamical trajectories are measured experimentally, and rate parameters are estimated using obj(k₁..k_i), with any available knowledge on rate constants (obtained in vitro or from previous modeling) included as priors in the estimation scheme. The vast majority of these biochemical models are likely to remain nonidentifiable, given available data, but we learned that this does not preclude our making high-likelihood predictions. Currently, it is common to see simulation models published in which a single good fit is discussed. Many models are also calibrated using population average data, even though both deterministic and stochastic models are actually single-cell representations. Neither of these should be regarded as lethal weaknesses in today's studies, but, over time, we are likely to demand more rigorous approaches. As we learned, making rigorous probabilistic statements about cellular biochemistry will involve (1) model calibration tools that enable effective sampling of the objective functions to obtain parameter distributions and parameter correlations, and (2) experimental design tools that aid in selecting experiments that have the greatest impact on the reliability of model-based predictions.

Future perspectives

It is now time for molecular biologists to think about biochemical processes in the language of dynamical systems and move beyond largely inappropriate QSSA (Michaelis-Menten) approximations. However, we must acknowledge that, even to practitioners, detailed biochemical models are difficult to understand. A major problem is that, when many proteins are involved, or when combinatorial assembly must be modeled (for example, when considering binding of multiple adaptor proteins to multiple phosphotyrosine sites on receptor tails) (Blinov et al. 2004; Faeder et al. 2009), equations become extremely complex and opaque. It is virtually impossible to understand such equations, and many models contain errors that are hard to identify. The fundamental problem is excessive detail in the model description (although not necessarily in the models themselves). In modeling biochemical reactions, we require abstraction layers akin to those distinguishing machine code from programming languages or graphical user interfaces from command lines. Fortunately, a new set of “rules-based” modeling tools have been developed recently with precisely this goal in mind (Blinov et al. 2004; Faeder et al. 2009; Feret et al. 2009; Mallavarapu et al. 2009). As these tools become more mature, they will make models much easier to understand.

While cellular biochemistry is likely to remain strongly hypothesis-driven and mechanism-oriented, it needs to become more integrative, probabilistic, and model-driven. Powerful mass spectrometry, flow cytometry, and single-cell measurement technologies are continuously being developed, thereby supplying the necessary experimental methods. However, the computational tools required for effectively modeling cellular biochemistry are still in their infancy and are grievously underappreciated. It is nonetheless our opinion that the development of appropriate conceptual frameworks for discussing biochemical models, data, and hypotheses will revolutionize cellular biochemistry in much the same way that machine learning and new measurement methods revolutionized genomics.