Microliter-bioreactor array with buoyancy-driven stirring for human hematopoietic stem cell culture

Abstract

This work presents the development of an array of bioreactors where finely controlled stirring is provided at the microliter scale (100–300 μl). The microliter-bioreactor array is useful for performing protocol optimization in up to 96 parallel experiments of hematopoietic stem cell (HSC) cultures. Exploring a wide range of experimental conditions at the microliter scale minimizes cost and labor. Once the cell culture protocol is optimized, it can be applied to large-scale bioreactors for stem cell production at the clinical level. The controlled stirring inside the wells of a standard 96-well plate is provided by buoyancy-driven thermoconvection. The temperature and velocity fields within the culture volume are determined with numerical simulations. The numerical results are verified with experimental velocity measurements using microparticle image velocimetry (μPIV) and are used to define feasible experimental conditions for stem cell cultures. To test the bioreactor array’s functionality, human umbilical cord blood-derived CD34⁺ cells were cultured for 7 days at five different stirring conditions (0.24–0.58 μm∕s) in six repeated experiments. Cells were characterized in terms of proliferation, and flow cytometry measurements of viability and CD34 expression. The microliter-bioreactor array demonstrates its ability to support HSC cultures under stirred conditions without adversely affecting the cell behavior. Because of the highly controlled operative conditions, it can be used to explore culture conditions where the mass transport of endogenous and exogenous growth factors is selectively enhanced, and cell suspension provided. While the bioreactor array was developed for culturing HSCs, its application can be extended to other cell types.

INTRODUCTION

Hematopoietic stem cell (HSC) therapeutics is important because of HSC’s ability to differentiate into the different types of blood cells.¹ HSCs reside in bone marrow of adults and are also recognized in human umbilical cord blood (UCB).² The use of HSCs from UCB offers several advantages with respect to bone marrow, such as minor immunological response after transplantation.³ However, the current therapeutic use of HSCs from UCB is limited to pediatric patients because of the low cell count from a single unit and the increased immunological response if two units are used in the same transplantation.⁴ The expansion in vitro of UCB HSCs has been proposed as a feasible solution, but is still under development.⁵

Currently, stem cell cultures are mainly performed within static systems, such as single or multiwell plates and T-flasks. The stagnant state of the medium in these conditions produces spatial gradients of gas, metabolite, and growth factor concentrations, which are strongly dependent from cell density and distribution.⁶ Research is being conducted to improve the culture environment using stirred bioreactors, considering that HSCs do not require surface attachment to grow.^{7, 8, 9, 10} These types of bioreactors are closed vessels where stirring is usually mechanically provided. They can have different levels of complexity, in terms of number of ports for inlets, sampling accesses, and probes for online culture monitoring and control. This system of utilities associated to the bioreactor is essential for cell production process for safe clinical use. The main advantage of a stirred bioreactor, such as the one presented in the current work, over more traditional static systems is the reduction in spatial gradients, which facilitates a more homogeneous culture environment. This ensures more defined and repeatable culture conditions and reduces the heterogeneity in the cell population.¹¹ Cell population heterogeneity is a critical parameter because some cell subsets can contribute negatively to the clinical success of stem cell transplantation.¹² Additionally, depending on the stirring velocity, HSCs can be suspended to produce a three-dimensional culture, advantageous considering that an equivalent number of cells in a two-dimensional culture system would require a much larger surface.¹³

The cell culture protocols need to be optimized in order to use stirred bioreactors for HSC therapeutic production. It is necessary to reproduce in vitro the stem cell niche signals¹⁴ that allow a reliable and effective expansion of HSCs, e.g., type, timing, and dose of growth factors.¹⁵ This is the current bottleneck for a wider clinical use of HSCs from UCB.¹⁶ For HSC protocol optimization, the use of large-scale (∼100–1000 ml) bioreactors is not feasible due to prohibitive costs. An affordable process optimization demands a high-throughput, small-scale technology that is suitable for testing a wide range of culture conditions. This allows for efficient transfer of protocol information to larger production scale systems.¹³ A desirable testing volume is on the order of hundreds of microliters, allowing for many parallel experiments using cells from the same unit of UCB and yielding a sufficient amount of cells for postculture cell characterization. This facilitates a low-cost process, as cost approximately scales with the culture volume. Perfused bioreactors of this scale are currently being developed for cells that require surface attachment.¹⁷ Instead, a precisely controlled small-scale stirring technology still needs to be developed. The stirring method should not adversely affect cell viability and phenotype, nor be invasive. In this small-scale context, mechanical stirring is essentially impractical, especially when performing many parallel experiments.

In this work, we developed a microliter-bioreactor array with a novel stirring method that fulfills the requirements of small-scale (250 μl culture volume), cost effective, parallel experiments (up to 96), and precise control of medium fluid dynamics. It is suitable for a wide screening of culture conditions during HSC protocol optimization. The developed device provides stirring to an array of wells from a standard 96-well plate. Considering the amount of information on HSC cultures developed in static conditions, this system was developed such that it is in close continuity with the conventional static culture systems. Thus, many available protocols can be a used as a starting point for the optimization of culture conditions in this system. An additional advantage is that the cell culture is in contact only with the internal surface of the polystyrene well, which is a well-tested biocompatible material,¹⁸ and no extraneous objects, such as a mechanical stirrer or magnetic beads, are in contact with cell culture medium.

MATERIALS AND METHODS

Bioreactor device

Complete bioreactor system

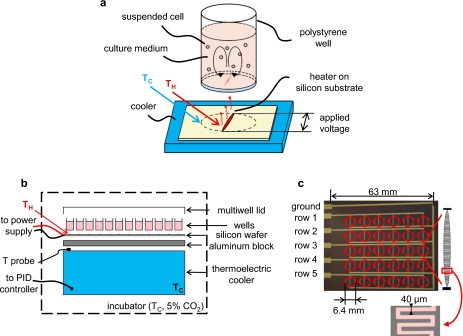
The stirring within each culture volume is provided by buoyancy-driven thermoconvection [Fig. 1a]. At the base of each well, an external microheater produces a localized temperature increase, ΔT=T_H−T_C, where T_H is the microheater temperature and T_C=36 °C is the surrounding incubator temperature. This temperature difference generates a convective flow within the well, which increases with increasing ΔT, and thereby homogenizes the culture medium. Figure 1b illustrates the main components of the microliter-bioreactor array. A conventional 96-well plate (CLS3614; Sigma-Aldrich, Milano, Italy), covered with a lid (CLS3099; Sigma-Aldrich, Milano, Italy), is made of polystyrene and has a flat bottom of 0.127 mm thickness. The bottom surface of the polystyrene is in direct contact with a silicon wafer with a microelectrical circuit, including microfabricated heaters for each well, patterned on its surface (see details below). Electrical wires were epoxied to the contact pads of the miniaturized circuit first with a conductive epoxy (Chemtronics, Kennesaw, GA), applied overnight, and then, to guarantee a stronger mechanical adhesion, with a 2 ton Clear Epoxy (Devcon, Danvers, MA) applied for 2 h. The wires are connected to a dc power supply (6220B, Hewlett-Packard, Milano, Italy), which provides a stable voltage. A thermoelectric cooler (CP-031; TE Technology, Traverse City, MI), paired with an aluminum block (8 mm thick), is in contact with the backside of the silicon substrate and set to T_C. The temperature T_C is regulated with a temperature probe (PT100, 10 mm, class A; RS Components, Milano, Italy) on the upper surface of the thermoelectric cooler and a Proportional-Integral-Devide (PID) controller (model 998, Watlow Electric Manufacturing Co., St Louis, MO). The 96-well plate, the silicon wafer, the aluminum block, the temperature sensor, and the thermoelectric cooler are the components inside the biological incubator, whereas the electrical wires provide the connections with components outside.

Figure 1.

(a) Schematic of an individual microliter-bioreactor stirred by buoyancy-driven thermoconvection. A microfabricated heater on a silicon substrate is in direct contact with the external bottom of the well (∼32 mm²) and produces a local temperature hot spot, T_H. The thermoelectric cooler, which is beneath the silicon wafer, maintains the overall bioreactor temperature near the incubator temperature, T_C. (b) Schematic of the microliter-bioreactor array. A conventional 96-well plate is in contact with an electrical circuit microfabricated on a silicon wafer. An aluminum block between the silicon wafer and the thermoelectric cooler enhances temperature homogeneity. A PT100 temperature probe and PID controller maintain the thermoelectric cooler’s temperature at T_C. (c) Top view of the microfabricated electrical circuit. It is composed of five rows with six parallel heaters, which correspond to the position of the wells (dashed red line) of the 96-well plate. Each microheater is serpentine shaped (see enlargement) to maximize the resistance. A different voltage (1.01–1.60 V) is applied to each row to perform cell cultures at five different stirring conditions.

Miniaturized electrical circuit fabrication

A miniaturized electrical circuit was microfabricated (University of California at Santa Barbara Nanofabrication Facility) on a silicon substrate (70×50×0.5 mm³). A 2 μm layer of insulating silicon dioxide (SiO₂) was thermally grown using an oxidation furnace. Photolithography techniques were employed to transfer the microcircuit design from a transparency mask to the SiO₂ layer. The microcircuit was made of thin films: 200 Å of titanium and 1800 Å of platinum, deposited via electron-beam evaporation. Titanium is used as an adhesive layer, and platinum provides the robustness and linear resistance-temperature relationship needed for the microheater characterization. As shown in Fig. 1c, the microcircuit includes five parallel rows, where each row contains six identical parallel microheaters. A different voltage, ranging from 1.01 to 1.60 V, was applied to each row to produce five different localized temperature increases, and thereby five different stirring conditions.

Heater characterization

The microfabricated heaters function through resistive heating. Each heater is in direct contact with the bottom surface of the polystyrene well and aligned in the center of the well. According to Ohm’s law, a constant voltage, V, applied to each microheater produces a current I=V∕R and dissipates a sourced power, P,

$$P=R{I}^2,$$ (1)

where R is the resistance of each microheater. In order to maximize the heat produced while minimizing the necessary current, the microheaters were designed to maximize their resistance. The resistance of an individual heater is given by

$$R=\frac{\rho L}{wt},$$ (2)

where ρ is the resistivity, L is the length of the resistor, w is the width, and t is the thickness. The length was maximized with a serpentine structure (L=28.11 mm) and the width was minimized enough to create the winds in the serpentine within the resolution limits of a transparency mask (w=40±5 μm). The theoretical resistance of the heater, calculated by Eq. 2, is R=420±20 Ω at 22 °C, in accordance with that experimentally measured. As shown in Fig. 1c, the serpentine heater is rod shaped, such that the ratio between the rod width and the parallel chord of the circular well remains at the value of 0.1.

An additional consideration in the microheater characterization is the temperature dependence of platinum’s resistivity, which is linear for the narrow operating temperature ranges. The change in the resistance of each heater with temperature was calculated by the simplified Callendar–Van Dusen equation,¹⁹

$$\Delta R=R_{o}a\Delta T,$$ (3)

where ΔT=T−T₀ is the temperature difference between operative temperature, T, and reference temperature, T₀; ΔR=R−R₀ is the difference between the resistance R at T, and the resistance R₀ at T₀; a is the temperature coefficient of resistance, which was determined experimentally to be 0.0033 °C⁻¹.

Fluid dynamics characterization

Numerical model

A three-dimensional numerical model was developed to investigate the buoyancy-driven thermoconvective flow in the well using the software COMSOL MULTIPHYSICS V3.5A (COMSOL, Inc., Stockholm, Sweden). The numerical simulation includes three subdomains: the fluid inside the well, the polystyrene well bottom, and the silicon wafer with a microheater embedded on its surface. Because of the system’s symmetrical geometry, one-quarter of an individual well was simulated.

The temperature field was solved with an energy balance at steady state applied to all three subdomains,

$$k{\nabla }^{2}T=\rho C_p\vec{u}\cdot \nabla T,$$ (4)

where T is the temperature, $\vec{u}$ is the velocity, k is the thermal conductivity, ρ is the mass density, and C_p is the heat capacity at constant pressure of the fluid medium, approximated with water in this case, polystyrene, and silicon, respectively. The bottom of the silicon base was maintained at T_C=36 °C to match the thermoelectric cooler and aluminum block. All other external boundary conditions were insulation. The serpentine heater was specified as the local temperature hot spot, T_H [Fig. 1a].

In the fluid subdomain, the local temperature gradient creates inhomogeneities in the mass density, which results in a buoyancy force on the fluid. This body force was added to the momentum equation, assuming the Boussinesq approximation for small density variations. The fluid velocity is governed by the continuity equation for an incompressible fluid,

$$\nabla \cdot \vec{u}=0,$$ (5)

and the Stokes equation,

$$0=\rho \vec{g}\beta \left(T-T_c\right)+\mu {\nabla }^2\vec{u},$$ (6)

where $\vec{g}$ is the gravitational acceleration, β is the volumetric thermal expansion coefficient, and μ is the medium dynamic viscosity. The boundary conditions were set as symmetry on the two symmetry planes sectioning the well, no slip on the walls, and open boundary on the fluid top surface. The coupled system of Eqs. 4, 5, 6 was solved to determine the temperature and the velocity fields within a well of the bioreactor array, using parameter values summarized in Table 1. A relative tolerance of 10⁻⁶ was used for the solution. Coarsening and refining of the mesh space grid ensured that the results were independent of the spatial discretization. The microheater’s heat flux, derived by the numerical simulation, was used to determine the necessary required experimental voltage.

Table 1.

Parameter values.

	Medium	Polystyrene	Silicon
Thermal conductivity (W∕m K)	0.632a	0.13b	1.05a
Heat capacity (J∕kg K)	4190a	1200b	840a
Density (kg∕m3)	994a	1050b	2600a
Dynamic viscosity (Pa s)	0.711×10−3a
Volume expansivity (1∕K)	3.53×10−4a
Cell density (kg∕m3)	1065c
Cell radius (m)	4.03×10−6d

^aFrom COMSOL material library.

^bFrom Ref. 28. Medium properties are approximated with water properties at 36 °C.

^cFrom Ref. 27.

^dFrom cell volume in Ref. 23 under the assumption of cell spherical shape.

Microparticle image velocimetry

The fluid velocity in a thermoconvectively stirred well was experimentally measured with flow-tracing particles by microparticle image velocimetry (μPIV), as described in detail in Refs. ^{20, 21}. A single well, from a 96-well plate (Sigma-Aldrich), was filled with 76 μl of de-ionized water and seeded with 1 μm diameter fluorescent polystyrene beads (Duke Scientific, Fremont, CA). A frequency-doubled Nd:YAG (yttrium aluminum garnet) laser (532 nm) (New Wave Research Inc., Fremont, CA) illuminated the flow-tracing particles, which were imaged with an epifluorescent microscope (Nikon E600FN, Japan) through a 10× lens (numerical aperture of 0.25). The particle images were recorded with a cooled charge coupled device camera (PIVcam 13-8; 1024×1024; TSI Inc., Shoreview, MN) with a time delay of either 0.5 or 1 s between exposures. The captured images pairs were interrogated and ensemble averaged using a μPIV algorithm software to determine the in-plane velocity field, $\vec{u}\left(x,y\right)$. The velocity was measured as a function of fluid depth, z, as well of applied voltage, V. Measurements were taken at a room temperature of 22 °C.

Cell culture

Cell isolation and culture conditions

UCB units were obtained from Bone Marrow Stem Cell Transplant Laboratory (Department of Pediatric Oncohematology, Padova, Italy) after informed consent. Cord blood was eluted with 20 ml Phosphate buffer saline (PBS) 1X (Gibco, Invitrogen, Milano, Italy) and mononuclear cells were isolated using Ficoll (GE Healthcare, Milano, Italy) density centrifugation (2000 rpm, 30 min). Mononuclear cells were counted with a hematocytometer and analyzed by flow cytometry as a negative control. CD34⁺ cells were isolated by superparamagnetic microbeads (CD34 antibody, QBEND-10, Abcam, Cambridge, U.K.) selection using high-gradient magnetic field and mini-MACS^® columns (Miltenyi Biotech, Bergisch Glodbach, Germany). More than 70% of cells were CD34⁺, as verified by flow cytometry (FACSCalibur, Becton Dickinson, Milano, Italy) after counterstaining with CD34-PE antibody (AC136 clone, Miltenyi Biotec). The selected cells were suspended in Iscove’s modified Dulbecco’s medium (Gibco), 10% complemented (56 °C, 30 min), with 10% fetal bovine serum (FBS) (Gibco), 1% penicillin∕streptomycin (Gibco), and supplemented with the following human cytokines (PeproTech Inc., Rocky Hill, NJ): hSCF (50 ng∕ml), hTPO (10 ng∕ml), hIL-6 (10 ng∕ml), and hFL (50 ng∕ml) according to the protocol in Ref. 22. CD34⁺ cells were seeded into the 96-well plate of the microliter-bioreactor array, in correspondence to the heaters on the silicon wafer below. Each well was filled with 250 μl of medium. The microliter-bioreactor system was placed inside the biological incubator at a temperature T_C of 36 °C. Additional control wells were seeded for static culture both at 36 and 37 °C. Cell seeding density was 10⁴ cell∕ml in all wells. The experimental conditions are summarized in Table 2.

Table 2.

Biological results. V is the voltage applied to an individual microheater. ΔT=T_H−T_C, as shown in Fig. 1. u_max,fluid is the maximum fluid velocity. Fold expansion, cell density after 4 and 7 days in culture divided by initial cell density. Viability results after 7 days in culture, derived from flow cytometry analyses after 7-AAD staining. CD34 expression results after 7 days in culture, drawn by flow cytometry analyses after CD34 staining. D-statistic results are derived by a Kolmogorov–Smirnov analysis of the data of each row, compared to data from control sample. Data for each row are based on six parallel experiments.

	V (V)	ΔT (°C)	vmax (μm∕s)	Fold expansion		Viability		CD34 expression
				4 days	7 days	% dead	D-statistic	% CD34+	D-statistic
Control	0.00	0.00	0.00	1.9±0.7	16.2±6.0	3.2		97.4
Row 1	1.01	0.006	0.24	1.8±0.7	17.1±2.6	2.9	0.03	99.5	0.15a
Row 2	1.10	0.007	0.28	1.8±0.9	14.2±2.4	2.7	0.15a	99.5	0.16a
Row 3	1.18	0.008	0.32	2.1±0.7	14.1±2.5	2.5	0.10a	99.8	0.17a
Row 4	1.35	0.010	0.41	1.7±0.6	14.9±2.2	2.3	0.06a	99.8	0.21a
Row 5	1.60	0.015	0.58	1.6±0.7	15.2±3.6	2.6	0.02	99.8	0.22a

^ap<0.001.

Cell viability, cell count, and flow cytometry analyses

On days 4 and 7, live cells were counted with a hematocytometer. On day 7, cells were suspended with 40 μl PBS 1X and incubated at 4 °C for 15 min with 8 μl anti-CD34-PE antibody (Gibco, Invitrogen), and 5 μl of 7-amino-actinomicyn D (7-AAD). Labeled cells were suspended in 1 ml PBS 1X, centrifuged (1200 rpm, 5 min), and suspended in 200 μl PBS 1X. Cells were then analyzed by flow cytometry acquiring 10⁴ events.

RESULTS

Numerical simulation and μPIV results

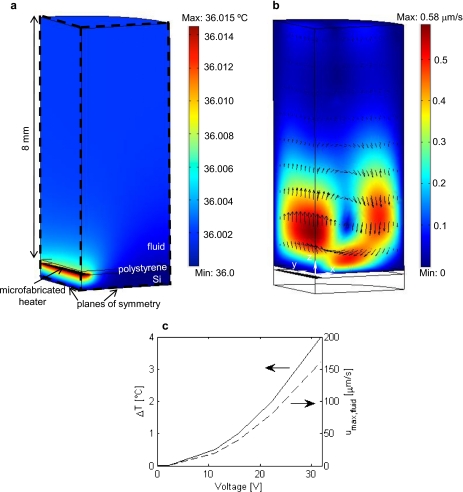
The numerical model demonstrates the temperature field and the buoyancy-driven velocity field within a bioreactor well, as shown in Figs. 2a, 2b, respectively. The case shown in Fig. 2 is the model prediction for the biological experiment, i.e., for 250 μl of medium volume in the well, with the fastest experimental velocity, with a specified temperature of the serpentine microheater, T_H, of 36.015 °C. The simulation results show the maximum temperature in the fluid of approximately 36 °C, directly above the microheater [Fig. 2a]. The local temperature gradient produces natural convective flow and results in the velocity field with a maximum velocity of 0.58 μm∕s in the positive z-direction, directly above the heater [Fig. 2b]. A temperature rise of 0.015 °C in the numerical model corresponds to an applied voltage of 1.60 V to an individual resistive heater.

Figure 2.

Numerical simulation results of (a) the temperature field and (b) the velocity field within one-fourth of an individual bioreactor for a total liquid volume of 250 μl (8 mm in height) and for the highest stirring conditions used in the biological experiments. The microheater is set to T_H=36.015 °C, which generates the convective flow with a maximum fluid velocity of 0.58 μm∕s. (c) Numerical results of the temperature increase, ΔT (solid line, left axis), and the fluid maximum velocity in the positive z-direction, u_max,fluid (dashed line, right axis), as functions of the applied voltage, V, to the microheater.

Additionally, the model was solved for a range of temperature increases, ΔT, up to 4 °C, including the remaining biological experimental culture conditions presented in this paper. For each ΔT, the corresponding range of applied voltages was calculated and results are displayed in Fig. 2c. This relationship was extended to correlate the applied voltage with the maximum stirring velocity [Fig. 2c] and directly used in determining the desired experimental operative conditions.

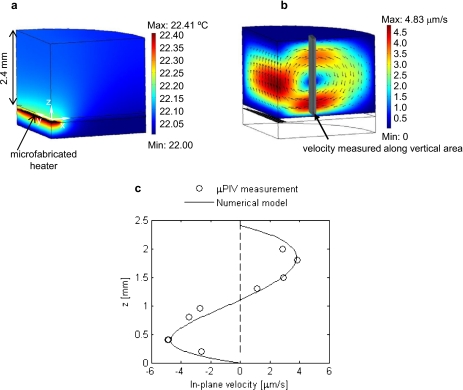
The accuracy of the numerical model was validated using experimental μPIV analysis. The bioreactor HSC cultures have a working volume of 250 μl (8 mm fluid height), whereas for μPIV experiments the working volume was reduced to 76 μl (2.4 mm in height). The reduced volume was chosen to improve the quality of the μPIV data because a larger working volume would create significant background glow and impair imaging of discrete particles in the measurement plane. The numerical model was adapted to account for the reduced working volume, as well as for the laboratory environmental temperature of 22 °C (i.e., β∼2.1×10⁻⁴ K⁻¹), where μPIV experiments were performed. Comparing the μPIV measurements to the 76 μl numerical model yields insight to the accuracy and predictability of the 250 μl model to the conditions of the biological experiments. The temperature and velocity fields calculated by the 76 μl numerical model for a ΔT of 0.41 °C are shown in Figs. 3a, 3b, respectively. The temperature rise of 0.41 °C corresponds to an applied voltage of 10 V to the resistive heater.

Figure 3.

Numerical simulation results and experimental μPIV measurements as a function of fluid depth, z. Numerical simulation results of (a) the temperature field and (b) the velocity field in a quarter of a well as used for the μPIV conditions: 76 μl (2.4 mm in height) of de-ionized water, T_C=22 °C, and ΔT=0.410 °C. In (b), the region of interest for the μPIV measurements is indicated. (c) μPIV in-plane fluid velocity measurements and numerical simulation in-plane velocity results as a function of z.

The μPIV experiments were first used to provide measurements of the velocity field as a function of height, z, in the fluid at the fixed voltage of 10 V applied to the microheater. Velocity measurements were taken in the region of highest in-plane velocity to improve data accuracy and averaged in the portion of (x,y)-plane considered. The region of interest is shaded in Fig. 3b. The velocity measurements as a function of the distance from the well bottom are plotted along with the numerically simulated in-plane velocity in Fig. 3c. The experimentally measured in-plane velocity and the numerical results match well.

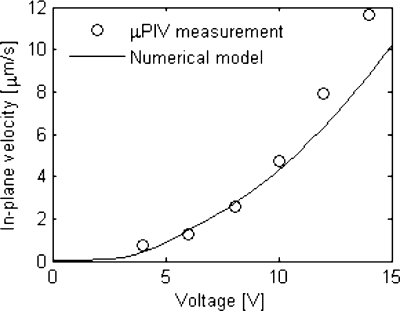
The μPIV experiments were also used to determine the in-plane fluid velocity dependence on the applied voltage to the resistive heater, and thereby the velocity’s dependence on temperature increase, ΔT. These velocity measurements were taken at a distance z=400 μm from the well bottom, in the same (x,y) region of interest shaded in Fig. 3b, with increasing voltages applied to the microheater. Figure 4 shows the μPIV experimental data as well as the numerical model results for this case. The measured in-plane fluid velocities are in close agreement with the numerical model. As expected, there is a square dependence of fluid velocity on the voltage applied. The two sets of μPIV results validate the numerical model and confirm its reliability in predicting the fluid dynamics in the bioreactor well. In particular, they provide confidence to the velocity dependence on ΔT, shown in Fig. 2c, and, thus, on the voltage applied to the microheater.

Figure 4.

Comparison between μPIV fluid velocity measurements and numerical simulation results as a function of voltage, V. The working volume is 76 μl of de-ionized water and velocity is measured in the region of interest shown in Fig. 3b at z=400 μm from the well bottom.

Transport scaling of the bioreactor

The validated numerical model results were then used to analyze different flow regimes and to define the operating conditions for a cell culture. In particular, this section analyzes the effects of the local temperature increase, ΔT, and of the fluid volume, ∀, on conditions for different growth factor mass transport regimes and cell suspension.

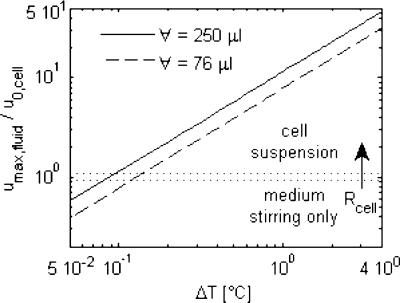
As illustrated in Fig. 5, the numerical model predicts that increasing ΔT increases the convective flow, represented by the normalized maximum upward velocity of the medium, u_max,fluid. In addition, for a given ΔT, increasing the medium volume of the wells increases u_max,fluid. However, this difference is relatively small in the range of volumes of ∼100–300 μl (Fig. 5). Therefore, small variations in the well volume have a negligible effect on the convective flow.

Figure 5.

Numerical simulation results of the normalized maximum fluid velocity, u_max,fluid, as a function of the temperature increase, ΔT. The terminal falling velocity, u_0,cell=3.53 μm∕s, is calculated by Eq. 7. Numerical results are shown for working volumes of 76 μl (used in μPIV measurements) and 250 μl (used in biological experiments). The horizontal dotted lines show the transition region between cell suspension and that of medium stirring only, without cell suspension, for a range of cell radii, R_cell.

In the region of no cell suspension, below the dotted area in Fig. 5, the transport of molecules of gases, growth factors, and metabolites can be either diffusion driven or convection driven, depending on the magnitude of medium convective flow and the diffusivity of the molecules. To determine the dominant transport mechanism, the Péclet number, Pe, the ratio of convection rate to diffusion rate, is analyzed. Pe is expressed as Pe=ul∕D, where u is a characteristic velocity of the fluid, in this analysis u_max,fluid, l is a characteristic length of the system and D is the diffusivity of the molecule of interest in the medium. When Pe<1 diffusion prevails, conversely, when Pe>1 convective transport is dominant. For a specified ΔT, and, thereby, fixed u_max,fluid, the transport regime of different growth factors is governed by their individual diffusivity, D, and, therefore, for some can be regulated by diffusion and for others by convection, even in the same fluid dynamic conditions. Depending if the molecule under consideration is externally provided (exogenous factor) or produced by the cells (endogenous), l is defined differently. For exogenous factors, l is the medium height in the well; for endogenous, l is the average cell-cell distance, which is cell concentration dependent, and thus time dependent. Thus, on average, endogenous factors require a higher stirring velocity to be convectively homogenized in the culture medium.

As already mentioned, cell suspension depends on the intensity of medium stirring. Cells in culture have a relative velocity with respect to the medium because they settle with a terminal velocity given by Stokes’ equation,

$$u_{0,\text{cell}}=\frac{2\left({\rho }_{\text{cell}}-\rho \right)R_{\text{cell}}^{2}g}{9\mu },$$ (7)

where ρ and μ are the medium density and viscosity, respectively, g is the acceleration due to gravity, ρ_cell is the cell density, and R_cell is the average cell radius (Table 1). The calculated average cell terminal settling velocity is u_0,cell=3.53 μm∕s. The condition for cell suspension in the medium is represented by u_max,fluid∕u_0,cell>1. Due to variations in cell radii of a given cell population,²³ the transition between cells that are suspended and not suspended is not sharp. In Fig. 5, a region is highlighted for the range of cell radii in a HSC population; when u_max,fluid equals the respective cell terminal velocity, cells begin to be suspended. The analysis above, based on Pe, is valid also in the region where cells are suspended, once modified the characteristic length of the system, l.

Experiments of HSC culture

The culture of human cord blood-derived CD34⁺ cells in the microliter-bioreactor array was examined at five different stirring conditions of medium and compared to cell cultures in a 96-well plate under static conditions at 36 °C. Within each of the five rows, six parallel bioreactor wells were used for repeated experiments. Cells were seeded at an initial cell concentration of 10⁴ cell∕ml and allowed to expand for 7 days. Stirring was produced by applying a voltage, V, to the heaters. Experimental conditions and results are summarized in Table 2.

Cell viability analysis by flow cytometry at day 7 shows a comparable percentage of dead cells after 7 days in culture at different stirring conditions, confirmed by a Kolmogorov–Smirnov test (Table 2). No statistically significant effect on cell proliferation rate is observed for any of the stirring rates tested, as compared to the static control, both at days 4 and 7 (Table 2).

The expression level of marker CD34 is analyzed by flow cytometry after a 7-day culture. In all the different stirring conditions, the cell population results substantially CD34⁺ (Table 2). A Kolmogorov–Smirnov test was applied for quantification, by D-statistic, of the difference in CD34 expression between cells cultured under static conditions, and in the stirred bioreactors. Results show a comparable CD34 expression with respect to static culture (Table 2).

DISCUSSION

This work demonstrates finely tuned medium stirring within the cell cultures of a standard 96-well plate. The volume in each well is on the order of a few hundreds of microliters, satisfying the need of a small cost-effective volume and a sufficient number of cells required for biological characterization. Mechanical stirring is not practical at these small length scales, especially when many experiments need to be performed in parallel. Furthermore, inserting mechanical parts into the culture volume introduces additional variables, such as cell interaction with the materials used for the stirrer, and increases the risk of culture contamination. Other stirring mechanisms, such as electrokinetics, whereby an electric field drives the fluid motion, are only applicable at smaller scales, ≤100 μm.²⁴ In this work, stirring was generated by buoyancy-driven thermoconvection via an external microfabricated heater placed at the bottom of the culture well. This is a suitable noninvasive technique for generating finely controlled fluid motion, in a culture volume range that is adequate for protocol optimization.

Using a standard 96-well plate in the microliter-bioreactor array has several advantages. It facilitates the use of protocol knowledge from typical static cultures as a starting point for optimizing dynamic culture conditions. Also, the 96-well plate is composed of polystyrene, a well-tested biocompatible culture environment.¹⁸ Lastly, 96 parallel experiments can be run using only a small volume each (100–300 μl). This allows for a wide screening of different experimental conditions. Because of the variability between different UCB units and of the low number of cells per unit, it is important to have such a device in order to investigate many different HSC culture conditions, such as medium composition or stirring velocity, using cells from the same UCB unit.²⁵

The bioreactor array was designed with the assistance of a numerical model, which also aided in establishing the operative conditions for biological experiments. In particular, it was used to define the parameters needed to obtain medium stirring without overheating the culture medium. Numerical simulations were performed for ΔT up to 4 °C, thus a lowest temperature in culture of 33 °C. In Ref. 26 pioneering work, hematopoiesis in vitro was maintained for several months at 33 °C, demonstrating that this temperature does not impair HSC expansion. In this work, cells were cultured at a temperature between 36 and 37 °C, which has a negligible effect on HSC cultures. We verified in six repeated control experiments under static conditions that the proliferation rate is comparable at 36 and 37 °C, with a doubling time of 46±6 and 40±2 h, respectively. In addition to temperature, other parameters are important for a successful stem cell culture, such as pH and the biocompatibility of the materials used. pH was maintained at 7.4 by the biological incubator atmosphere at 5% CO₂, and the cell culture was only in contact with the polystyrene multiwell, as in standard static culture conditions.

In vivo HSC behavior is critically affected by the local microenvironment surrounding the cell, namely, the stem cell niche, containing both endogenous and exogenous factors.¹⁴In vitro serum and cytokines are added to the medium mimicking the in vivo situation. These molecular signals are transported either by diffusion or by convection within the culture medium, depending on Pe number. Thus, once decided the flow regime, evaluating Pe for two different growth factors gives insight on the different availabilities of the two species at the cell surface. For example, let us consider an endogenous and an exogenous growth factors, both with diffusivity D=10⁻¹⁰ m²∕s, a cell concentration of 10⁵ cell∕ml, and a fluid velocity u_max,fluid=0.5 μm∕s. For the endogenous factor, l is the average cell-cell distance, about 35 μm in conditions of no cell suspension. Instead, for the exogenous factor, l is medium height, i.e., ∼8 mm. Calculating the Péclet number, Pe≈0.18⪡1 for the endogenous factor and Pe≈40⪢1 for the exogenous one. This simple example illustrates the great difference in flow conditions for the two molecules considered.

In the biological experiments, human UCB CD34⁺ cells were cultured in conditions of no cell suspension, i.e., u_max,fluid∕u_0,cell<1 (Fig. 5), at low cell concentration [∼(10⁴–15)×10⁴ cell∕ml], for a short-term culture (7 days), and at a growth factor concentration well above the physiological level. These conditions guaranteed that growth factor transport is not a concern in these experiments and were used to verify that the system does not adversely affect cell behavior. Biological results confirmed that cells cultured in presence of stirring are comparable to the static culture. Because of the small culture volume (250 μl) the entity of medium evaporation could have been critical but less than 5% evaporation was detected after 7 days.

Although the bioreactor array was developed for HSC culture, its range of applicability includes other cell types. In case of cells that do not require surface attachment to grow, it is also possible to suspend the cells producing a three-dimensional culture, using Fig. 5 to choose appropriate operating conditions.

CONCLUSIONS

Experiments and numerical simulations demonstrate the ability and practicality of the microliter 96-array bioreactor to provide finely controlled stirring within parallel HSC cultures. The external microfabricated heaters that generate the buoyancy-driven thermoconvection are fully characterized with resistance-temperature dependence measurements. Additionally, velocity measurements and numerical simulations characterize the consequent fluid dynamics in the well. Five different stirring conditions were induced within the microliter bioreactor, and experiments of UCB-derived CD34⁺ cell culture verified the biocompatibility of the system. Therefore, the microliter-bioreactor array can be reliably used for future protocol optimization experiments in order to homogenize the medium in the bulk volume, selectively enhancing mass transport of endogenous and exogenous factors, or to suspend cells.