Ultrasonic backscatter coefficients for weakly scattering, agar spheres in agar phantoms

Abstract

Applicability of ultrasound phantoms to biological tissue has been limited because most phantoms have generally used strong scatterers. The objective was to develop very weakly scattering phantoms, whose acoustic scattering properties are likely closer to those of tissues and then compare theoretical simulations and experimental backscatter coefficient (BSC) results. The phantoms consisted of agar spheres of various diameters (nominally between 90 and 212 μm), containing ultrafiltered milk, suspended in an agar background. BSC estimates were performed at two institutions over the frequency range 1–13 MHz, and compared to three models. Excellent agreement was shown between the two laboratory results as well as with the three models.

INTRODUCTION

This work investigates ultrasonic scattering from homogenous media containing very weak scatterers. Such weak ultrasonic scatterers are typical of biological materials (Wear et al., 1995), but with biological materials, there is always sample-to-sample variation. This sample-to-sample variation does not allow for a fundamental comparison of measurements with theory. Physical phantoms are stable spatially and temporally and if well characterized allow for a fundamental comparison of measurements with theory. Such comparisons with weakly scattering physical phantoms that are well characterized thus are needed to assure the scientific and clinical communities that quantitative ultrasonic backscattered estimates have validity.

Previous work has demonstrated that estimates of backscatter coefficients (BSCs) from media containing a suspension of glass spheres (Madsen et al., 1984; Hall et al., 1989; Insana et al., 1990) show good agreement with the theoretical scattering from spheres predicted by the theory of Faran (1951). These early studies establish a firm relationship between backscatter measurement results and underlying physical properties of the medium. However, the glass or nylon bead scatterers used in early studies do not verify our ability to characterize submillimeter sized, weak ultrasonic scatterers, such as those that are believed to contribute to scattering from tissues. Various “biological” phantoms have been explored by researchers, including Sephadex spheres (Campbell and Waag, 1984; Chen and Zagzebski, 1996) and fish eggs (Lizzi and Elbaum, 1979). A drawback of these phantoms is the limited acoustic impedance distributions and size ranges that are available.

This work focuses on estimates of BSC from phantoms containing weakly scattering spheres of known and controlled size distributions. The target spheres are manufactured from concentrated milk and agar, sieved, and then distributed randomly in an agar background. The measured BSCs were compared to a simple scattering model based on the fluid sphere form factor (Insana et al., 1990) and to an exact solution to scattering from fluid spheres (Anderson, 1950). BSCs were measured for the same three weakly scattering phantoms at both the University of Illinois at Urbana-Champaign (UIUC) and the University of Wisconsin-Madison (UW). Different methods were used at each institution to demonstrate that the measurements are not equipment or technique dependent. The measurements from each laboratory were compared to each other and to the model BSCs.

METHODS AND MATERIALS

Phantom description and construction

Spheres composed of anechoic material were produced from a mixture of agarose solution plus whole milk, the latter having been concentrated from whole bovine milk by ultrafiltration through a 10,000 Dalton system. The agarose solution consisted of agarose (Cat. no 820723, MP Biomedicals, Solon, Ohio, USA), deionized water and Liquid Germall^® Plus, a preservative (ISP Technologies, Inc., Wayne, New Jersey, USA). The milk was concentrated by a factor of 3 in an ultrafiltration unit (Model UFP-10-C-55, A∕G Technology Corporation, Needham, Massachusetts, USA), and then passed through a nylon mesh filter with 12 μm×12 μm openings. The agarose solution and concentrated milk were mixed when each was at 60 °C and Liquid Germall^® Plus was added at 50 °C. The net mixture was cooled to 50 °C and sprayed from a needle-bearing hypodermic syringe with vigorous agitation into a column of vegetable oil where the upper part was at 50 °C and the lower part was at room temperature or lower; this procedure was a variation of a method for mass-producing spheres described previously (Chin et al., 1990). The spheres were subsequently transferred from the oil into an aqueous solution containing 1.4% by weight Liquid Germall^® Plus, and the spheres were sieved using the same solution and WS Tyler sieves (Mentor, Ohio, USA).

Each total tissue-mimicking material is a macroscopically uniform (i.e., randomly distributed) suspension of a diameter fraction of the spheres described above in a background material. The background material is composed of deionized water, agarose and Liquid Germall^® Plus. Each diameter fraction is obtained by sieving with sieves with the desired mesh. The compositions of the sphere material and suspending material are given in Table 1.

Table 1.

Compositions of spheres and background material.

Phantom material	Weight percent of component material
	Spheres	Background
Deionized water	63.6	96.7
Agarose (dry weight)	1.9	1.9
3× concentrated milk	33.1	0
Liquid Germall® Plus	1.4	1.4

Test cylinders of the pure background and pure sphere media were made to measure the density, sound speed, attenuation and backscatter from the component media. The results were then used to estimate the acoustic impedances of these media for estimating the magnitude of scattering based on the model form factor function, as described below. In the case of the exact scattering solution from fluid spheres (Anderson, 1950), the densities and sound speeds of the media were used to calculate the BSC.

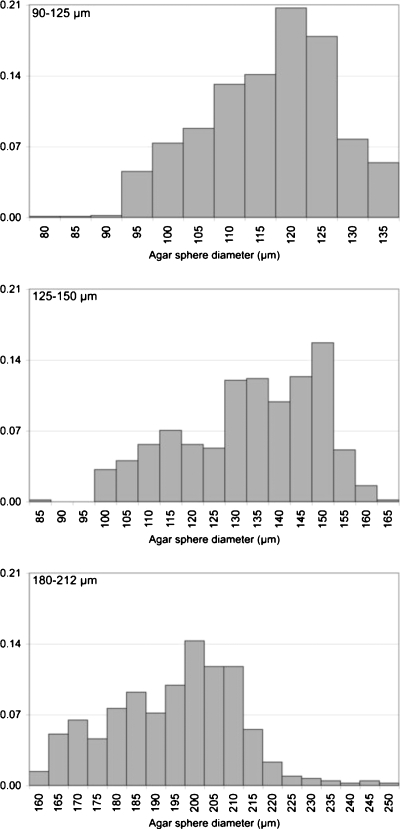
Three phantoms were constructed, each with a different scatterer size distribution. The three diameter distributions were nominally 90–125 μm, 125–150 μm and 180–212 μm with estimated sphere volume fractions of 0.0033, 0.0040 and 0.0080, respectively. When each phantom was made, syringes filled with each phantom’s materials were also created. These were used to make measurements of the sphere diameter distribution within each phantom. At UW, several 1 mm slices were taken from each syringe and examined under a light microscope (Olympus BH-2). About 100 spheres were manually measured for each phantom using a calibrated video caliper system (Cue Micro-100 Video Caliper, Mercer Scientific International). At UIUC, an automated procedure was developed to measure the diameter of several hundred agar spheres from each sample. Small slices from the phantom materials in the syringes were removed using a razor blade and images of the phantom spheres were acquired under a fluorescent microscope (Zeiss Axiovert 200M Microscope, Oberkochen, Germany). These sample images were magnified and exposed to a bright field. Images were acquired with a camera (512×512 pixel array), converted to a JPEG file, and transferred to a computer for processing with the circle detection program. A 2D mask (circular) was convolved over the entire image space, peaking in value wherever there was a circular structure surrounded by a black ring in the image. By setting a threshold based on the method of Otsu (1979) on the convolved image and equating all pixels within the convolved image with values above the threshold to one and the remaining pixels to zero, the convolved image essentially becomes a binary image that marks the position of all the circular structures in the image file. The area of all of the circular structures in the threshold image was then tabulated, the diameter estimated based on the size of each pixel, and a histogram of diameters constructed. The entire procedure was calibrated against latex spheres of known diameter. The results of the measured size distributions are listed in Table 2, and the combined normalized histograms are shown in Fig. 1.

Table 2.

Means and standard deviations of agar spheres that were measured at UW and UIUC, as well as the combined results. Note that the sizing method was different for each group.

Nominal diameter (μm)		Mean diameter (μm)	Standard deviation (μm)	Count
90–125	UW	111	12.1	108
	UIUC	117	10.1	927
	Combined	116	10.5	1035
125–150	UW	139	11.2	109
	UIUC	132	16.2	458
	Combined	133	15.6	567
180–212	UW	207	15.8	91
	UIUC	191	15.2	343
	Combined	195	16.6	434

Figure 1.

Normalized histograms of combined sphere size measurements for the nominally sized 90–125 μm (top), 125–150 μm (middle), and 180–212 μm (bottom) phantoms as a function of sphere diameter.

UIUC phantom scanning and BSC estimation

The phantoms were ultrasonically scanned using six single-element transducers (Table 3). The transducers were driven using a Panametrics 5800 pulser∕receiver (Panametrics, Waltham, MA) and scans were conducted in a tank filled with degassed water at room temperature. The amplified radio-frequency echo signals were digitized (10-bit at 200 MHz) with an Agilent U1065A compact-PCI digitizer (Agilent Technologies, Englewood, CO).

Table 3.

Transducer information for UIUC and UW BSC measurements.

Institution	Nominal center frequency (MHz)	Analysis bandwidth (MHz)	f-number	Focal length (mm)
UIUC	1	0.9–1.3	3	57
UIUC	2.25	1.5–3.2	2.67	51
UIUC	3.5	1.2–5.0	3	57
UIUC	5	3.5–6.4	3	57
UIUC	7.5	4.1–10	4	76
UIUC	10	6.5–14	4	51
UW	3.5	2.4–4.9	4.8	95
UW	5	3.0–8.0	2.9	54
UW	7.5	4.5–9.0	5.0	94
UW	10	4.9–13	2.7	51

The scanning procedure for each transducer and phantom began by acquiring a reference scan from a planar Plexiglas^® plate to calibrate the system. This reference scan was taken by recording the reflection off the water-Plexiglas^® interface at the set of positions over the axial range for which the reflection magnitude was greater than half the reflected magnitude at the focus; within this range, the reflected signal was recorded at half-wavelength intervals. Next, the transducer focus was positioned below the surface of the phantom at a distance of half the axial length of the region of interest (ROI) to be used for processing plus 1 mm. A raster scan was then performed, with lines of RF data recorded at intervals equal to approximately half of the beamwidth (beamwidth at focus is approximately the f-number multiplied by the wavelength). Averaging power spectra from lines that are a half beamwidth apart further reduces electronic noise in the power spectra and coherent signal in the power spectra because the spectra are partially uncorrelated at a half a beamwidth. Generally, the scan covered a sufficient length so that several ROIs could be extracted and processed from each slice, where five slices were recorded from each phantom. The number of lines varied for each scan depending on the transducer frequency in use because the length of the scan was limited by the physical size of the phantom. For the 1 MHz and 2.25 MHz scans, 2 ROIs were processed per slice, while 3 ROIs were processed per slice for all other scans.

BSC processing was performed by using range-gated data from within the ROIs. The analysis ROI size was chosen to be 20 wavelengths in both the lateral and axial directions, where the wavelength was computed using the nominal transducer frequency (Table 3) and a sound speed of 1500 m∕s. A Hanning window was used to gate the scan lines.

The BSCs were computed from the RF scan data using the method described in (Chen et al., 1997). This method accounts for equipment dependent effects by dividing the power spectrum calculated for an ROI by a reference power spectrum from the Plexiglas^® echo signal. The reference power spectrum was created by averaging the spectra of each planar interface signal taken over the axial length of the ROI. A correction was also made for the layer of Saran covering the phantom (Wear et al., 2005), and a linear correction was made for the attenuation within each phantom, measured using standard through-transmission techniques.

UW phantom scanning and BSC estimation

The phantoms were ultrasonically scanned using four single-element transducers (Table 3). The transducers were driven using a Panametrics 5800 pulser∕receiver and scans were conducted in a tank filled with degassed water. The amplified RF echo signals were digitized to 8-bit precision in a LeCroy (Chestnut Ridge, NY) LT342 digital oscilloscope. The scope’s “autoscale” feature was enabled, which optimized the A∕D precision for the echo signal amplitudes.

The phantoms were placed at the focal distance for the transducers and moved vertically and horizontally to ensure that the phantoms’ interface was normal to the acoustic beam. For the 90–125 μm and 125–150 μm phantoms, a 20 mm×20 mm area was scanned using a 1 mm step size in both directions; for the 180–212 μm phantom, a 40 mm×40 mm area was scanned using a 2 mm step size in both directions. A gate length of 10 μs and a delay of 7 μs relative to the phantom’s surface were used to acquire waveforms from each of the phantoms. A reference echo signal from a quartz optical flat placed at the focus of the transducer was also recorded after adding an additional 40 dB of electronic attenuation at the input to the pulser-receiver so that the signal stayed within the dynamic range of the Panametrics 5800. A Hamming window was applied to the data and BSCs were computed using the method described by Madsen et al. (1984) and Chen et al. (1998). A correction was also made for the layer of Saran covering the phantom (Wear et al., 2005), and a polynomial fit correction was made for the attenuation within each phantom, measured using standard through-transmission techniques.

Scattering models

Three models were used to study the scattering from the agar-in-agar phantoms, namely, the Anderson (1950) model, the Faran (1951) model and the form factor model for fluid-filled spheres is given by (Insana et al., 1990)

$$F\left(k,a\right)={\left[\frac{3}{2}\frac{j_1\left(2ka\right)}{ka}\right]}^2,$$ (1)

where k is the wave number, a is the radius of the scatterer, and j₁ is the spherical Bessel function of the first kind. The fluid filled sphere form factor is a simple scattering model which is applied under the assumptions of plane wave incidence, no multiple scattering, and the validity of the Born approximation. Over the 1–13 MHz frequency range of interest, the results of this simple model were observed to agree very well with results computed using the theory of Anderson (1950) for sound scattering by a fluid sphere.

For a collection of randomly positioned spherical scatterers with a known size distribution, the theoretical BSC ${\overline{\sigma }}_{\mathrm{b}}$ can be computed by combining Eqs. 4 and (11) of Insana and Hall (1990), so that

$${\overline{\sigma }}_{\text{b}}={\text{Cf}}^4{\gamma }_0^2\frac{1}{{\overline{\text{n}}}_{\text{T}}}{\int }_0^{\infty }\overline{\text{n}}\left(\text{D}\right){\text{D}}^6\text{F}\left(\text{f},\text{D}\right)\text{dD},$$ (2)

where $\overline{\mathrm{n}}\left(\mathrm{D}\right)$ is the distribution of the number density of scatterers versus size. C is equal to (1∕36)(π∕c)⁴, c is the speed of sound in the background medium, f is frequency, γ₀ is the relative scattering strength, F(f,D) is the form factor, and ${\overline{\mathrm{n}}}_{\mathrm{T}}$ is the total number of scatterers; that is,

$${\overline{\text{n}}}_{\text{T}}={\int }_0^{\infty }\overline{\text{n}}\left(\text{D}\right)\text{dD}.$$ (3)

However, because there are a finite number of spheres and the distribution of sphere sizes was determined (Fig. 1), a discrete distribution of spheres was used to estimate the backscatter coefficient,

$${\overline{\sigma }}_{\text{b}}={\text{Cf}}^4{\gamma }_0^2\frac{1}{{\overline{\text{n}}}_{\text{T}}}\sum _{\text{i}=1}^{\infty }{\overline{\text{n}}}_{\text{i}}^2{\text{D}}_{\text{i}}^6\text{F}\left(\text{f},{\text{D}}_{\text{i}}\right),$$ (4)

where ${\overline{\mathrm{n}}}_{\mathrm{i}}$ is the number of scatterers with a diameter between D_i and D_i+ΔD.

The Faran (1951) model was developed to predict scattering from solids spheres and therefore includes the effects of shear waves in the boundary conditions. To model the agar sphere, a Poisson ratio of 0.499 was assumed (thus including shear waves). The differential scattering cross section at 180° was computed for each sphere size using the Faran code and then scaled by the number density corresponding to sphere sizes. The first twenty-five terms of the Faran model were calculated.

The Anderson model assumes fluid scatterers in a fluid background (thus not including shear waves) and was calculated based on the equations provided in Anderson’s paper (1950). The distribution of sphere sizes was accounted for in the same manner as the other models. The first twenty-five terms of the Anderson model were calculated. It should be noted that the Faran model converges to the Anderson model as the Poisson ratio approaches 0.5, making these models very similar in this work.

RESULTS

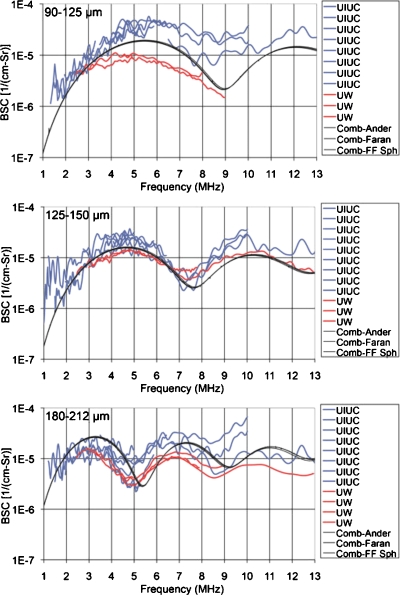
The attenuation-compensated (Fig. 2) results of the BSC estimates from both UIUC and UW measurements are shown in Fig. 3 for each of the three phantoms. Also shown in Fig. 3 are the three theoretical model BSCs, namely, Anderson, Faran and FF sphere. The model curves were generated from the combined UIUC and UW sphere size distribution measurements using Eq. 2.

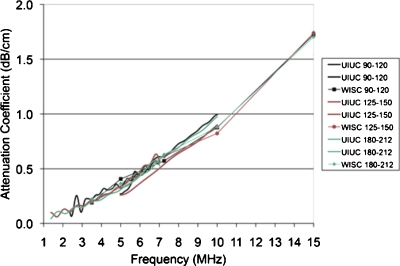
Figure 2.

Attenuation coefficient results for the 90–125, 125–150, and 180–212 μm phantoms. The attenuation coefficients measurements were conducted at each laboratory using standard insertion loss techniques (Anderson et al., 2010) wherein at UIUC a broadband technique was used and at UW a narrow band technique was used.

Figure 3.

BSC results for the 90–125 μm (top), 125–150 μm (middle), and 180–212 μm (bottom) phantoms. The BSC theory curves used the measured combined sphere diameter distributions with the three BSC theories.

Number density values of 3.6 scatterers∕mm³, 2.3 scatterers∕mm³, and 1.8 scatterers∕mm³ were used to compute the model curves for the 90–125 μm, 125–150 μm, and 180–212 μm phantoms, respectively. The scattering strength was computed from the density and speed of sound of the sphere material and the background material as 4(Δz∕z)² (Insana and Hall, 1990), where z is the acoustic impedance of the background material and Δz is the difference in acoustic impedance between the sphere material and the background material. Acoustic impedance was computed as the product of the material’s density and sound speed. The density of the sphere material was measured as 1.03 g∕mL and the density of the background material was measured as 1.005 g∕mL. Likewise, the speed of sound of the sphere material was measured as 1492 m∕s and the speed of sound of the background material was measured as 1491 m∕s. These density and speed values yield the acoustic impedance of the sphere material to be 1.537 Mrayl and the acoustic impedance of the background material to be 1.498 Mrayl. Deviation in these sound speed values primarily affects the magnitude, not the frequency dependence, of the results.

Figure 3 presents three different charts, one for each sphere size distribution. The theoretical calculations for each distribution exhibit BSC maxima and minima over the frequency range tested. The number and positions of the BSC minima and maxima depend on the agar sphere sizes, with fewer inflection points over the 1–13 MHz range for smaller spheres. The curves using all three models are barely distinguishable from one another, with the largest rms difference of 8.5×10⁻⁷ (cm-Sr)⁻¹ between the fluid-filled sphere and the Anderson models for the 180–212 μm sphere diameters.

Experimental results agree qualitatively and show reasonable agreement quantitatively with the predicted BSC vs frequency behavior independently calculated using measured physical properties of the phantoms. Each separate UIUC and UW curve (Fig. 3) is a result of applying a different ultrasonic transducer, each only applicable to a part of the frequency over which measurements are made. For the 90–125 μm sphere diameters, the rms difference between measured and theoretical backscatter results over the range of frequencies tested is 6.6×10⁻⁶ (cm-Sr)⁻¹ for the UW results and 15×10⁻⁶ (cm-Sr)⁻¹ for the UIUC results. For the 125–150 μm spheres these results are 1.9×10⁻⁶ (cm-Sr)⁻¹ for the UW and 8.5×10⁻⁶ (cm-Sr)⁻¹ for the UIUC, while for the 180–212 μm spheres the mean deviations are 7.5×10⁻⁶ (cm-Sr)⁻¹ for the UW and 8.8×10⁻⁶ (cm-Sr)⁻¹ for the UIUC.

Agreement between the theoretical and experimentally calculated backscatter coefficients decreased as the size of the scatterers increased. Specifically, the frequency dependent behavior was consistent between experiment and theory, i.e., the peaks and dips appeared to correlate well. Several sources of error may have contributed to the differences between theory and experiment. Inaccuracies in the sphere size distributions would affect the theoretical curves, and the method of sampling the agar sphere in agar media may have missed some representative sphere targets. Also, errors in estimating the number density of scatterers would affect the overall magnitude of the theoretical curves.

DISCUSSION

The BSC estimates from measurements made from the same three very weakly scattering phantoms presented here show reasonable agreement between two laboratories. Additionally, BSC estimates show reasonable agreement with the theoretical model BSCs, namely, Anderson, Faran and fluid-filled sphere, for small density and sound speed variations. Previous measurement comparisons were performed when the BSC was 2 to 3 orders of magnitude higher (better electronic SNR) (Wear et al., 2005), namely, 10⁻² to 10⁻³ (cm-Sr)⁻¹ vs. 10⁻⁵ to 10⁻⁶ (cm-Sr)⁻¹. Also, the previous BSC estimates were typically over the 2–8 MHz frequency range whereas those reported herein are over the 1–13 MHz frequency range.

Given the nature of these acoustical measurements and the slight although noteworthy uncertainties in specifying the properties of the materials for insertion into the theoretical calculations, from the figures it can be observed that the measurement results of the BSC from each laboratory (Fig. 3) are in reasonable agreement with one another. In addition, the measurement results are in excellent agreement with theory. Therefore, such novelty of the very weakly scattering BSC estimates over an extended frequency range reported herein suggest the ability to obtain good agreement in biological media that might also be weakly scattering.

CONCLUSION

These results demonstrate the ability of two separate laboratories to make BSC estimates from very weakly scattering phantoms, using different estimation techniques, which show reasonable agreement among each other and with theoretical BSC curves. This provides a valuable foundation in the investigation of scattering from weakly scattering biological media for the purpose of tissue characterization. Future studies should carefully examine the methods for characterizing phantoms for theoretical calculations of backscatter coefficients. In addition, the use of weakly scattering phantoms as reference materials for backscatter coefficient estimation could also be explored. The advantage of using the weakly scattering phantoms as reference phantoms is that the scattering is on the order of scattering expected from soft tissues. Therefore, signal strength from tissues can be maximized without concern for saturating signals from the reference.