Privacy-Maintaining Propensity Score-Based Pooling of Multiple Databases Applied to a Study of Biologics

Abstract

Introduction

A large study on the safety of biologics required pooling of data from multiple data sources, but while extensive confounder adjustment was necessary, private, individual-level covariate information could not be shared.

Objectives

To describe the methods of pooling data that investigators considered, and to detail the strengths and limitations of the chosen method: a propensity score (PS)-based approach that allowed for full multivariate adjustment without compromising patient privacy.

Research Design

The project had a central data coordinating center responsible for collection and analysis of data. Private data could not be transmitted to the data coordinating center. Investigators assessed 4 methods for pooled analyses: full covariate sharing, cell-aggregated sharing, meta-analysis, and the PS-based method. We evaluated each method for protection of private information, analytic integrity and flexibility, and ability to meet the study’s operational and statistical needs.

Results

Analysis of 4 example datasets yielded substantially similar estimates if data were pooled with a PS versus individual covariates (0%–3% difference in point estimates). Several practical challenges arose. (1) PSs are best suited for dichotomous exposures but 6 or more exposure categories were desired; we chose a series of exposure contrasts with a common referent group. (2) Subgroup analyses had to be specified a priori. (3) Time-varying exposures and confounders required appropriate analytic handling including re-estimation of PSs. (4) Detection of heterogeneity among centers was necessary.

Conclusions

The PS-based pooling method offered strong protection of patient privacy and a reasonable balance between analytic integrity and flexibility of study execution. We would recommend its use in other studies that require pooling of databases, multivariate adjustment, and privacy protection.

Studies in small subgroups call for very large populations to provide sufficiently precise effect estimates, especially when outcomes are rare. In cases where the required number of patients cannot be drawn from a single database, pooling data from multiple databases can yield the necessary sample size. A multicenter study of the safety of biologic medicines for the treatment of autoimmune diseases necessitated pooling data from multiple administrative data sources to attain sufficient statistical power to study certain rare safety outcomes.

Regulations or data use agreements often preclude sharing individual-level data outside of the source database. Most pooling methods currently described make a trade-off: they either use no individual-level data and adjust only for a limited set of covariates¹ or use extensive individual-level data and offer full multivariate adjustment.² In the study we discuss, the sharing of private information—such as patients’ comorbidities, prescription drug usage, and prior medical procedures—was restricted by data use agreements, Centers for Medicare and Medicaid Services rules and federal regulations, but full multivariate adjustment was required because of substantial confounding, including strong confounding by indication.³ Consequently, the study team considered a series of methodological alternatives, each with a set of operational and statistical benefits and limitations.

In this article, we address the multiple methods considered in the design and planning of the project, and detail our chosen method. We examine both the practical challenges and epidemiological concerns and describe how we overcame limitations. We conclude with an example application comparing the usual approach to secure data pooling. Because the desired comparison required full visibility into patient-level data, we carried out the example in different study setting.

METHODS

Study Background and Collaboration Framework

The Safety Assessment of Biologic Therapy (SABER) study is a broad-ranging inquiry into the safety of biologics for the treatment of auto-immune diseases. The study is based at the University of Alabama at Birmingham with working groups at other research centers around the United States. The Kaiser Permanente Division of Research in Oakland, CA serves as the study’s single data coordination center (DCC). The DCC creates standardized data definitions, facilitates transmission of data among parties, compiles study datasets, and provides standardized programming code and other analytic support.

For each specific safety question within the SABER study, the investigators sought to pool clinical and administrative data from a number of participating research organizations (“centers”). The centers maintained data from Kaiser Permanente, Medicare, Medicaid, state tumor registries, vital statistics providers, and state pharmaceutical assistance programs for low-income elderly. At the beginning of the project, programmers at each center standardized their data files based on HMO Research Network protocols and data dictionaries.⁴ Each center was subject to strict data use agreements and/or federal rules and regulations concerning patient privacy.

We anticipated that pooling basic, non-identifying data from the multiple centers would yield the number of patients and outcome events needed to precisely estimate treatment effects,⁵ but validity of the estimates remained a concern. For the outcomes under consideration, we saw strong potential for confounding by indication.³ For example, patients with more severe autoimmune disease received more potent immunosuppressant therapy, but the severity of their disease put them at risk for adverse events such as infection. Consequently, simple age/sex adjustment was not sufficient; the study required full multivariate adjustment for all outcomes.

Pooling Alternatives Considered

We considered 4 main pooling methods. Table 1 and the following text detail the privacy, statistical, and operational trade-offs involved in selecting among the techniques.

TABLE 1.

Summary Comparison of Pooling Methods Considered

Feature	Covariate Sharing	Aggregated Data	Meta-Analysis	Propensity Score-Based Pooling
Privacy issues
Ability to distribute study data to working groups without compromising patient privacy or proprietary data	↓	↓	↑	↑
Ease of complying with HIPAA law and Centers for Medicare and Medicaid Services rules	↓	⇆	↑	↑
Analytic and statistical issues
Ability to cross-tabulate individual covariates and explore data	↑	↑	↓	↓
Ability to match patients across rather than within centers	↑	↓	↓	↑
Ability to use propensity score trimming to find the most representative patient population	⇆	⇆	↓	↑
Ability to evaluate dose-response relationships	↑	⇆	↑	⇆
Ability to detect effect modification by patient-level factors	↑	↓	↓	⇆
Ability to detect effect modification among center populations	↑	⇆	↑	↑
Ability to evaluate performance of confounder adjustment techniques	↑	⇆	⇆	↑
Operational issues
Ease of transferring and compiling centers’ datasets into a single analytic database	⇆	↑	N/A	⇆
Ability to have limited expertise in statistical analysis within each center	↑	↑	↓	⇆
Flexibility in modifying outcome models to include or exclude certain covariates	↑	⇆	↓	↓
Flexibility to perform subgroup analysis on subgroups that were not specified a priori	↑	↓	↓	↓
Flexibility to match cohorts on factors that were not specified a priori	↑	↓	↓	⇆
Flexibility to add or modify exclusion criteria that were not specified a priori	↑	↓	↓	↓
Ease of reuse of data for parallel research questions or other outcomes	↑	↑	↓	⇆
Computing time required	↑	↑	⇆	⇆
Speed of study execution	⇆	⇆	⇆	⇆
Investigators’ overall ability to understand and sense transparency in the analyses and results	↑	↑	⇆	⇆

↑ indicates method is well-suited for noted issue;

⇆, method is moderately well-suited for noted issue;

↓, method is poorly-suited for noted issue.

The first method we considered was the most straightforward: sharing individual patients’ full covariate information (“covariate sharing method”). This method requires each center to create an analytic dataset and then to transmit that dataset—with full covariate information—to the DCC. Despite its advantages with respect to study speed and flexibility, we quickly ruled out this approach due to privacy concerns.

The project team next considered aggregating like patients into cells and then adjusting for confounders based on counts of patients in each cell (“aggregated data method”). For example, there might be 140 exposed men with a history of heart disease versus 220 exposed women with that history; for these patients, the centers could transmit just the 2 summary counts. While this method would likely work with few covariates, we determined that it would not scale to the 50 or more confounders required for this complex study. In particular, the method requires creating a cell for each observed combination of exposure, outcome, and covariates; with rare outcomes and the numerous covariates, we anticipated that cells with only one patient would be common. With frequent occurrence of single-person cells, the aggregated data method would provide little more privacy than covariate sharing.

To that end, Centers for Medicare and Medicaid Services regulations require cell counts of at least 11 patients. For cells with fewer than 11 patients, one option would be to drop the cells entirely. However, in the case of the rare safety outcomes we were considering, dropping the cells would have led to the loss of most of the study’s statistical power. Alternatively, a series of smaller cells could be combined until they reached a size of 11, but this approach would have required mixing dissimilar patients into a single stratum, and thus a substantial loss of confounder information.

The third alternative we explored was fixed or random effects meta-analysis of results (“meta-analysis”). This is the same statistical technique commonly applied to the compilation of data from multiple trials,⁶ here applied among our study centers. For each study exposure and outcome, each center would generate a point estimate and variance. The centers would then transmit the point estimates and variances to the DCC, which would in turn combine the results with standard meta-analytic techniques.

Statistically speaking, meta-analysis should yield very similar point estimates and confidence intervals (CIs) as compared to covariate sharing. For our study’s purposes, however, we noted several limitations: (1) the burden of the analysis would move from the DCC to the center such that each center would be required to have full analytic capabilities, including SAS software and statistically-trained staff; (2) all aspects of the outcome models would need to be specified a priori at the centers, which would limit any later-stage analytic flexibility; and (3) subgroup analyses, sensitivity analyses, and data exploration would become operationally difficult. The related method of creating matched cohorts within the centers and transmitting either unadjusted point estimates or 2 × 2 tables to the DCC would be impeded by the same issues.

Pooling Methodology Used

Because of the limitations of the 3 approaches described above, we chose a pooling method developed by 2 of the coauthors (J.A.R., S.S.).⁷ This method allows for pooling based on a propensity score (PS, “PS-based pooling”). A PS is the predicted probability of being exposed given the patient’s set of measured covariates (Fig. 1). A PS captures all patient covariate information into a single, opaque number. A man from the aggregated data example described above—the 140 exposed men and 220 exposed women, each with a history of heart disease—might have a PS of 0.37 (37% probability of exposure, based on his covariates), while a woman could have a PS of 0.52 (52% probability of exposure). The differences might be due to gender (women could be more likely to be exposed than men) as well as the individuals’ unique medical histories. Adjusting the outcome model by the PS generally functions as well as adjusting by individual covariates.^8,9 Consequently, by pooling with PSs, we could adjust for confounders in patients’ medical histories while keeping those histories concealed.

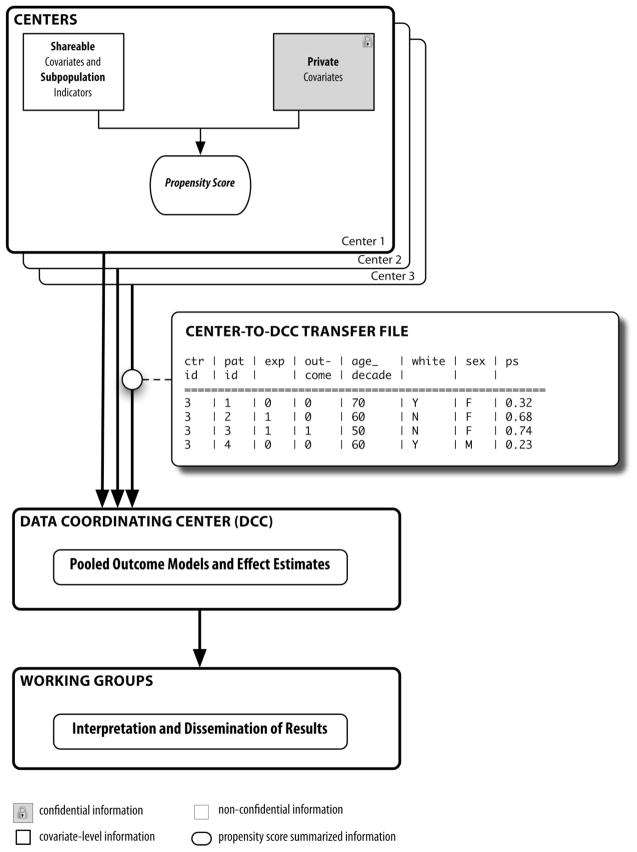
FIGURE 1.

Schematic of data flow in the Safety Assessment of Biologic Therapy project using the propensity score-based pooling method. Adapted from Pharmacoepidemiol Drug Saf. 2010 Feb 16; Epub ahead of print.

In our study, we estimated a set of PSs within each center (Fig. 1).¹⁰ Only non-identifying information (age in decades, gender) and the PSs were transmitted to the DCC, which in turn used this information to produce fully adjusted outcome models. While we chose to use only deciles of PS in our outcome models, the PS-based pooling method does not imply any specific analytic technique: the PSs can be used as continuous values, in quintiles or deciles, or as variables on which to match, and outcome models can be adjusted for the PS alone, or for both the PS and the non-identifying information.

Analytic Challenges Arising from PS-Based Pooling

Despite the advantages of the PS-based pooling method, several key analytic challenges arose. In this section, we note those challenges and describe our responses to them.

Multiple Exposure Categories

The SABER study examined a series of treatment groups—4 tumor necrosis factor (TNF) antagonists, other biologic disease-modifying antirheumatic drugs (DMARDs; eg, abatacept, rituximab, efalizumab), and several nonbiologic DMARDs (nb-DMARDs; eg, methotrexate)—and then compared those groups with respect to safety outcomes. However, PS matching usually predicts the probability of receiving a single study treatment versus a single referent. The PS is almost always estimated using logistic regression, which is built on the 2-category binomial distribution.¹¹ A polytomous logistic regression can predict the probability of one option among a set of multiple choices¹²: it might predict that, based on his patient characteristics, the man from the example above has a 37% chance of being treated with methotrexate, a 22% chance of a DMARD, a 23% chance of a nb-DMARD, and an 18% chance of a TNF antagonist. However, there is minimal literature on using polytomous regression for estimation of PSs.^13–15 We therefore compared each study treatment individually to a single prespecified referent group. For example, we compared each of the TNF antagonists to methotrexate and, separately, compared nb-DMARDS to methotrexate. This pairwise approach allowed us to be fully confident of the underlying statistical and epidemiologic theory without losing much or any statistical power.¹² One limitation of this method is its increased complexity and a large number of propensity scores. To minimize logistical complexity and computing time, we only estimated those pairwise PSs that were of scientific interest, as specified by study investigators.

Time-Varying Exposures

Patients treated with biologics can follow a treatment pattern in which they are “stepped up” from an initial therapy to more effective medications or combinations of medications. Moreover, although there is guidance on which therapies one might select as first line agents,¹⁶ there is only limited evidence to guide the decision to add or switch medications. Patients in our study switched frequently among the study exposures, and certain investigators therefore wished to conduct time-varying exposure assessment. The usual procedure with PSs is to estimate the probability of treatment at baseline (PS_Baseline) and to use that baseline score for confounding adjustment. Because a change in drug treatment during follow-up can be informed by the patient’s condition and prognosis,³ the most conservative study choice would be either to censor the patient in an as-treated analysis or to knowingly misclassify the exposure in an intention-to-treat-style analysis. Alternatively, if second-line agents were of higher interest, investigators could modify the study design to start follow-up at the time of initial use of the second-line exposure,¹⁷ rather than at the time of initiation of the first-line therapy.

In the instances where the investigators wished to assess both the original and the second-line exposure within the same analysis, several options were possible: (1) re-estimate the PS at the time of the change of exposure (COE) and use resulting PS_COE alone for confounding adjustment; (2) use the PS_Baseline and PS_COE side-by-side for confounding adjustment; (3) use PS_Baseline plus additional individual co-variates measured at the time of exposure change; or (4) use only PS_Baseline and do no further adjustment at the time of exposure change. Statistically, none of these options is ideal for reasons entirely separate from the pooling method: to varying degrees, options 1, 2, and 3 each run the risk of adjusting for an intermediate on the causal pathway and thereby obscuring any safety issues with the study medication, while option 4 runs the risk of underadjustment. Given the complexity of the analytic trade-offs, the SABER investigators determined the most appropriate approach individually for each of the study’s exposures and outcomes.

Time-Varying Confounding

Certain working groups desired to adjust for confounders that varied over the course of treatment, such as concomitant oral glucocorticoid use, even if exposure did not change. While the epidemiologic issues are distinct from those of time-varying exposures, the available options for updating the confounders using the PS-based pooling method are similar to those described in the section above. In our study, the investigators chose to measure key commonly occurring time-varying confounders (eg, mean daily prednisone dose) at prespecified times during follow-up. The DCC transmitted those key confounders alongside the baseline PS.

Multiple Subgroup Analyses

Study investigators wished to assess the drugs within certain subgroups of the patient population. For this to be possible, subgroup indicators needed to be based on nonprivate information and then transmitted with the PSs. We questioned whether the PSs required re-estimation in the subgroup, or whether the PS estimated in the entire population would remain valid within a subgroup analysis. Both theory⁸ and preliminary research by 2 of the coauthors (J.A.R., S.S.) indicate that in large subgroups, and under certain assumptions, no re-estimation of the PSs is required. Due to the ambiguity of the “correct” way to handle this issue, the study investigators chose to handle subgroup analyses on a case-by-case basis.

Heterogeneous Center Effects

In this multicenter study, detection and handling of heterogeneity among the centers’ populations was a key issue. We divided heterogeneity into 2 categories: (1) heterogeneity due to the information content available at each center and (2) heterogeneity due to distinct patient populations at each center.

Heterogeneity due to information content is most obvious when some centers are able to provide measured covariates—such as laboratory results—that other centers cannot provide. In such a case, each center can provide both a universally defined PS (PS_Univ)—one that includes just the covariates available at all centers—as well as one that includes both the universal covariates plus all local information available at the specific center (PS_Local).⁷

Note that even if each center ostensibly provides the same covariates, it is possible that certain centers can measure the covariates better than others. Consider the example of a “history of high blood pressure” variable: if one center relies on ICD-9 codes while another has access to blood pressure measurements from an electronic medical record, the center with the electronic medical record data may able to supply superior information.

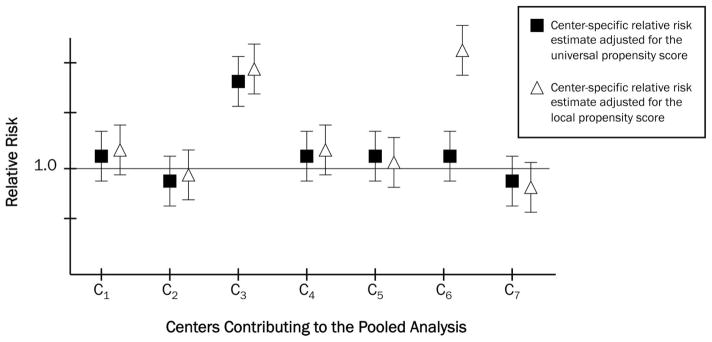
In the hypothetical example illustrated in Figure 2, each center-specific relative risk (RR) estimate is adjusted for each of the 2 PSs described above: a PS_Univ that is estimated with the “lowest common denominator” of covariates or covariate measurement available at the centers, and a PS_Local that includes each center’s best available information. A visual inspection of Figure 2 demonstrates the 2 differing types of heterogeneity. Overall, most centers show a RR of approximately 1.0, but Centers 3 and 6 are anomalous. Center 3 exhibits an RR that is elevated regardless of the PS used. It is likely that Center 3’s population is distinct from those of the other centers and is truly heterogeneous. A comparison of absolute event rates within Center 3 versus the other centers could shed additional light on how Center 3’s population might differ. Conversely, Center 6 shows a distinct RR, but only after adjustment with PS_Local. The use of PS_Local—estimated using a superset of the variables contributing to PS_Univ—moved the point estimate away from that observed with adjustment just for PS_Univ. It is likely that the additional information contained in PS_Local included important confounders that were not measured in the other centers. This observation is a strong indicator that additional confounder control would be necessary.

FIGURE 2.

Hypothetical Illustration of 2 types of observed treatment effect heterogeneity: heterogeneity due to differing information content, and heterogeneity due to true differences in treatment effect in study populations. See the text for a description of the universal and local propensity scores. Note that only a universal propensity score was used in the SABER study.

EXAMPLE OF THE POOLING METHOD

Because to demonstrate the PS-based pooling method we required several datasets into which we had full visibility into all patient-level information, we conducted an example study that was separate from the biologics project. In this example, we assessed a reported interaction between clopidogrel and proton pump inhibitors (PPIs). The results have been published previously,^7,18 but here we discuss the results further and present the data differently.

Recent literature suggests a potentially negative interaction between PPIs and clopidogrel (Plavix), an antiplatelet agent.^19–21 The reports indicate that PPIs may block the antiplatelet effects of clopidogrel, resulting in more thrombotic events in clopidogrel users who concurrently take PPIs than in clopidogrel users who are not PPI users. We assembled 4 cohorts of patients who had recently undergone inpatient percutaneous coronary intervention or who had been hospitalized for myocardial infarction (MI) or unstable angina, and who subsequently filled an initial prescription for clopidogrel within 7 days of hospital discharge. We counted as exposed those patients who, within those same 7 days, had recorded use of a PPI. Clopidogrel users with no recorded PPI use were counted as unexposed.

At the end of the 7-day run-in period, we sought outcomes of hospitalization for MI or revascularization. To demonstrate and test the method, we combined individual data from 4 data sources for which we had direct access to covariate-level information. We also mimicked a situation in which we were not permitted to pool individual raw data (as with the SABER study) to demonstrate the results from the aforementioned pooling methods.

Each of our 4 datasets (equivalent to centers) originated from health insurance programs: government programs from Pennsylvania, New Jersey, and British Columbia, and a private program from commercial insurer Horizon. The Institutional Review Board of the Brigham and Women’s Hospital approved this study and data use agreements were in place.

We estimated the PS_Univ using a logistic regression model. We considered age and sex to be non-identifying, shareable information. We selected a number of important clinical factors occurring in the 180 days before the index date as universal covariates. These factors included past use of nonselective nonsteroidal anti-inflammatory drugs, coxibs, or statins; history of MI or gastrointestinal bleed; prior diagnosis of diabetes or hypertension; and number of generic medications used by the patient. A PS_Local was computed with the high-dimensional PS (hd-PS) algorithm.²² The hd-PS contained the maximum information available at each center, including drug usage, in- and outpatient diagnoses, in-and outpatient procedures, and nursing home diagnoses and procedures.

We analyzed the data using logistic regression adjusted for decile of PS, and estimated the cumulative risk ratio over a fixed 120-day follow-up period. For validation, we also performed these analyses with full covariate information using the aggregated, individual-level data. We hypothesized that the universal PS-adjusted and covariate-adjusted point estimates and their CIs would be nearly equal. All pooled models were stratified by center.

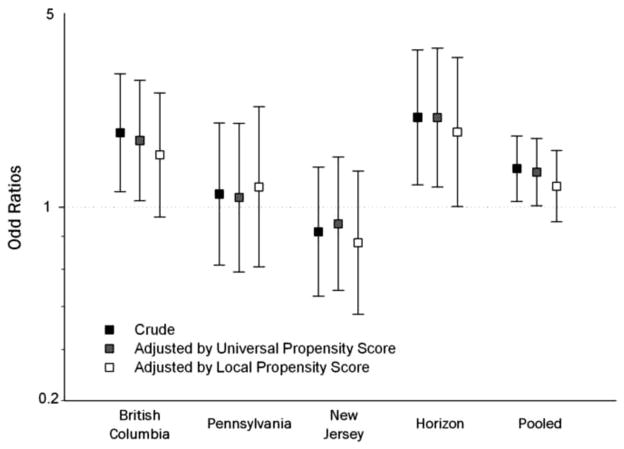
Table 2 displays the results of this analysis. For the MI outcome, the covariate-adjusted estimate is odds ratio (OR) = 1.20, 95% CI: 1.03–1.41, while the universal PS-adjusted estimate is 1.16, 95% CI: 1.00–1.36. For revascularization, the results are also similar: covariate-adjusted OR = 1.15, 95% CI: 1.02–1.30 versus the universal PS-adjusted OR = 1.13, 95% CI: 1.00–1.28. Adjusting by the local PS brought the point estimates toward the null for both outcomes. An assessment of heterogeneity (Fig. 3) indicates that there is heterogeneity among the centers, but while the local PS probably adds to the covariate adjustment, its effect is not as striking as that of the hypothetical example in Figure 2.

TABLE 2.

Estimates for Risk of 2 Outcomes in the Example Study

Outcome	Within-Center Analyses				Combined Analysis
	British Columbia (n = 19,979)	Pennsylvania (n = 4176)	New Jersey (n = 3998)	Horizon (n = 3451)	Pooled* (n = 31,604)
Myocardial infarction hospitalization
Unadjusted	1.68 (1.39, 2.03)	1.19 (0.83, 1.70)	1.35 (0.91, 2.02)	~1.47 (0.87, 2.48)	1.52 (1.30, 1.76)
Adjusted by individual covariates	1.23 (1.00, 1.52)	1.18 (0.80, 1.72)	~1.21 (0.79, 1.86)	~1.05 (0.60, 1.86)	1.20 (1.03, 1.41)
Adjusted by universal propensity score	1.23 (1.01, 1.50)	1.19 (0.82, 1.74)	1.14 (0.75, 1.71)	~1.11 (0.65, 1.91)	1.16 (1.00, 1.36)
Adjusted by local propensity score	1.15 (0.94, 1.41)	1.03 (0.69, 1.56)	1.27 (0.82, 1.98)	~0.99 (0.55, 1.78)	1.11 (0.95, 1.31)
Second hospitalization for revascularization
Unadjusted	1.30 (1.06, 1.61)	1.05 (0.81, 1.35)	0.92 (0.73, 1.15)	~1.38 (1.08, 1.75)	1.15 (1.02, 1.29)
Adjusted by individual covariates	1.23 (0.99, 1.53)	1.02 (0.78, 1.34)	0.96 (0.75, 1.22)	~1.39 (1.09, 1.79)	1.15 (1.02, 1.30)
Adjusted by universal propensity score	1.27 (1.02, 1.57)	1.03 (0.79, 1.35)	0.94 (0.74, 1.20)	~1.38 (1.07, 1.77)	1.13 (1.00, 1.28)
Adjusted by local propensity score	1.21 (0.97, 1.50)	1.07 (0.81, 1.43)	0.88 (0.68, 1.14)	~1.31 (1.00, 1.71)	1.07 (0.94, 1.21)

Figures indicated are odds ratios and their 95% confidence intervals, estimated with logistic regression models adjusted as indicated. The models adjusted by individual covariates and universal propensity score include the same variables and should therefore be substantially similar. Adapted from Pharmacoepidemiol Drug Saf. 2010 Feb 16, Epub ahead of print.

Universal PS included all measured covariates. Local PS included all measured covariates plus the best information available at the center.

PS-adjusted models are adjusted by decile of PS. Deciles are computed within each center.

^~indicates model failed to converge and value is approximate.

^*Pooled odds ratios are estimated with conditional logistic regression.

FIGURE 3.

Plot of observed heterogeneity for the revascularization outcome in the example study. For this outcome—one that involves a large amount of physician discretion—we observed heterogeneity among the centers. The additional information in the local propensity score moved the point estimates in each case. The difference was detectable but arguably in substantial.

CONCLUSION

This study presented a series of methodological challenges. This article details how the study investigators arrived at the choice of data pooling methodology. The chosen method, PS-based pooling, offered strong protection of patient privacy, and a reasonable balance between analytic integrity and flexibility of study execution. We would recommend its use in other studies that require both pooling of databases and multivariate adjustment, each in a manner that protects the privacy of the patients involved.