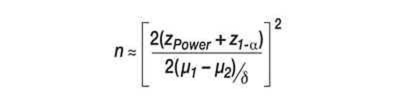Abstract
Background
In this article, we discuss the purpose of sample size calculation in clinical trials, the need for it, and the methods by which it is accomplished. Study samples that are either too small or too large are unacceptable, for clinical, methodological, and ethical reasons. The physicians participating in clinical trials should be directly involved in sample size planning, because their expertise and knowledge of the literature are indispensable.
Methods
We explain the process of sample size calculation on the basis of articles retrieved by a selective search of the international literature, as well as our own experience.
Results
We present a fictitious clinical trial in which two antihypertensive agents are to be compared to each other with a t-test and then show how the appropriate size of the study sample should be calculated. Next, we describe the general principles of sample size calculation that apply when any kind of statistical test is to be used. We give further illustrative examples and explain what types of expert medical knowledge and assumptions are needed to calculate the appropriate sample size for each. These generally depend on the particular statistical test that is to be performed.
Conclusion
In any clinical trial, the sample size has to be planned on a justifiable, rational basis. The purpose of sample size calculation is to determine the optimal number of participants (patients) to be included in the trial. Sample size calculation requires the collaboration of experienced biostatisticians and physician-researchers: expert medical knowledge is an essential part of it.
Design is essential for the quality of every clinical and epidemiological study and sample size calculation is an essential component of study design (1). For methodological reasons, the sample size must be determined and specified in the study protocol before recruitment starts. Departures from this procedure are only acceptable in the context of the general guidelines for clinical studies. If the investigator neglects to give the sample size, it is impossible for an independent monitor to decide retrospectively whether the investigator has selected data or statistical methods in such a way that the desired result could be “demonstrated.” It is also necessary to control the probability with which a real effect can be identified as statistically significant. For example, if a pharmaceutical company plans to introduce a new drug, it will not take the risk of failing to demonstrate efficacy or non-inferiority relative to other drugs by using an excessively small sample size; this is both for economic and for ethical reasons. It is just as true that it is unacceptable for a drug to be tested on too many patients. Thus, studies with either too few or too many patients are both economically and ethically unjustified (2– 4). Even for descriptive and retrospective studies, the sources of data and the scope of the data to be collected must be planned in advance. Sample size planning is inevitable in medical research. If it is not performed, this indicates that the quality of the study is poor and the results will be regarded sceptically.
The present article concentrates on sample size calculation when it is intended to use a single statistical test, i.e., we do not take into account the problem of multiple tests. The objective of sample size calculation is to calculate and fix a sample size which is adequate for it to be highly probable that the study will detect a real effect as statistically significant. Conversely, there must be adequate confidence that this effect is genuinely absent if it is not detected in the study (4).
Determination of sample size
Consider a study to compare two antihypertensive drugs, A and B. The study participants are randomly assigned (“randomized”) into two homogenous treatment groups. The patients in the first treatment group are given drug A and those in the second group drug B. The primary endpoint is taken as the mean reduction in blood pressure after four weeks.
It is known from published studies that the reduction in the blood pressure of hypertensive patients can be regarded as being normally distributed during treatment with both drugs. It is also known that drug A reduces the blood pressure of hypertensive patients by a mean value of about 10 mm Hg. Previous studies indicate that drug B is more potent and will reduce mean blood pressure by about 15 mm Hg. This is regarded as a clinically relevant improvement. Moreover, clinical knowledge suggests that the standard deviation of the reduction in blood pressure with both drugs can be taken as 5 mm Hg.
To clarify whether drug B causes a statistically significantly greater decrease in blood pressure than drug A, a one-tailed Student t-test for unpaired samples can be performed (5, 6). To ensure that neither too few nor too many patients are included in the study, the sample size is planned in advance. This requires the prespecification of statistical power and the level of significance of the statistical test (7). The level of significance is the probability of obtaining a statistically significant test result, even when there is no real difference. This is conventionally taken as 2.5% for one-tailed tests (cf. [8], section 5.5). Nevertheless, other values would be conceivable, depending on the question to be answered. The statistical power is the probability of identifying a real difference with the statistical test and is often taken as 80% or 90%.
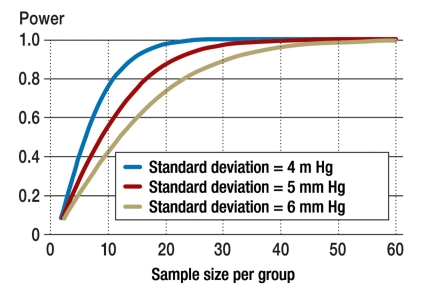
The Figure illustrates the relationship for standard deviations of 4, 5, and 6 mm Hg. With a standard deviation of 5 mm Hg, a power of 80%, and the other parameters specified above, it can be calculated that a sample size of 17 is needed for each group. If the standard deviation is 4 mm Hg, only 12 patients are needed in each group; if the standard deviation is 6 mm Hg, 24 patients per group are needed (figure). The Box includes a short calculation as example.
Figure.
Statistical power of a one-tailed t-test at the level of 2.5%, depending on sample size. For example, comparison of drugs A and B. (t-test with the same standard deviation in both study groups A and B, to compare means).
Box. Typical calculation.
Two populations are to be tested for a statistically significant difference between the means, using the one-tailed unpaired t-test. For the sake of simplicity, we will assume that the groups are of the same size (n1 = n2) and that the standard deviations are the same (σ1 = σ2= σ). The mean difference between the two populations is taken as µ1– µ2The power is normally given as 0.8 or 80% and the level of significance is α. Let n = n1 + n2. The objective is to determine the desired total sample size, n. The following simplified and approximate formula can be used for sample size calculation (even though the simplification leads to a loss of precision):
where z1-α signifies the 1-α quantile of the standard normal distribution, of which the value can be taken from statistical tables. To determine the sample size for the unpaired t-test, α in this equation is simply replaced by α/2; otherwise the procedure is unchanged. This equation can be found in Chapter 2 of (16).
Example:
The above equation will be used to determine the sample size for a study with the two antihypertensives A and B, with an expected mean difference of 5 mm Hg and an expected standard deviation of 6 mm Hg. The single tailed unpaired t-test is to be used, with the level of significance of 2.5% and the power of 80%. According to statistical tables, z0.8 = 0.8416 and z0.975 = 1.96 (see, for example, [17]). If these values are inserted into the above equation, they give the total sample size as follows:
It has been assumed for the calculation that the samples are equal in size. The individual samples should then be about 45.2/2 or 22.6 in size. This means that 23 patients are needed in each group. However, a more exact calculation gives 24 patients per group.
Requirement for expert medical knowledge
In the above example, expert medical knowledge is needed to estimate the expected difference and the scatter of the antihypertensive activity of the two drugs. Literature searches or pilot studies are often used for this purpose. The biometrician can support the physician in determining this information. Nevertheless, only the physician can assess these values. For example, it is the responsibility of the physician, not of the biometrician, to decide whether the expected difference in mean reduction in blood pressure with the two drugs is of clinical importance. Thus, if the difference between the two drugs is only 1 mm Hg, it would probably not be permissible to infer that the patients with the more active antihypertensive would benefit from this treatment—perhaps in the reduction of the risk of cardiovascular events.
This procedure to determine the sample size can also be applied in principle to other tests, such as the Mann-Whitney test for differences in location or Fisher’s exact test for the comparison of two rates. Depending on the statistical procedure, different information is required from the physician. Table 1 lists the information required for sample size calculation with different statistical procedures.
Table 1. Necessary assumptions for sample size calculation or power analysis with various tests to compare two populations.
| Test procedure | Medical assumption |
| Unpaired t-test with different standard deviations | Standard deviations σ1, σ2 Means μ1, μ2 |
| Unpaired Wilcoxon-Mann-Whitney rank sum test | Probability p (X1 < x2) |
| Fisher’s exact test to compare two rates | Relative proportions π1, π2 |
For the t-test, the physician requires assumptions about the means (µ1 and µ2) in two populations, together with the standard deviations (σ1 and σ2) in these populations.
For Fisher’s test, it suffices to have estimates of the relative proportions or rates of events (π1 and π2) in the two populations. This means that the literature must be studied to determine about how often an event (such as an adverse reaction) occurs in 100 patients during treatment 1 and how often during treatment 2 (relative frequencies).
The Mann-Whitney test requires an expert estimation of the probability that the target variable from a randomly drawn individual in population 1 is smaller than from a randomly drawn individual in population 2. It is essential that this should be estimated in collaboration with a biometrician.
Careful estimation of the necessary parameters is worthwhile and can greatly help to prevent faulty power calculations and sample size calculations (9).
Sample size calculation
This example of the unpaired t-test illustrates a scheme to determine sample size which is often used. Firstly, the necessary parameters are estimated, such as means and standard deviations, and the level of significance has to be specified. The sample size is then calculated, using different assumptions about the power of the relevant test. In general, the greater the power—the confidence that an important result will be detected—, the greater is the necessary sample size for the study. The minimum sample size is selected to attain the prescribed power.
On the other hand, it may be the case that the sample size is limited by external factors—such as the duration of recruitment, the rarity of a disease or the limited duration of financial support—, but it is nevertheless planned to evaluate the results with a statistical test. In such a case, the attainable power should be calculated during planning. The lower the power is, the lower are the chances of demonstrating the relevant hypothesis (2, 3). If the power is too low, the study may be modified during planning, or not performed at all. Breckenkamp et al. (10) reported a planned cohort study, in which the correlation between occupational exposure to electromagnetic fields and cancer was to be investigated. The authors reported that insufficient numbers of individuals had been exposed in any of the possible professional cohorts. As a consequence, no study was performed, even though the issue was of interest for environmental politics.
If the primary aim of a study is not to prove a hypothesis, but to estimate a parameter, sample size planning may be based on the expected width of the confidence intervals (7). For example, the prevalence of individuals with increased blood pressure may have to be estimated, including a 95% confidence interval. The smaller the range is, the more precise is the estimation of the population parameter (prevalence in this case). If the expected width of the confidence interval is specified, the number of cases can be calculated. For this procedure, it is necessary to have a rough idea of the prevalence and to specify the desired precision.
Even with expert knowledge, the estimates of the parameters used in calculating sample sizes are often only rough and highly unreliable. For this reason, several different scenarios are often examined. Consider the example of the antihypertensive study and the Figure. If the standard deviation of 5 mm Hg is assumed, 17 patients would be needed per group for a power of 80%. If, contrary to expectation, the standard deviation is 6 mm Hg, the power is then only 65% and only reaches about 80% if the number of patients per group is increased to 24. It is clear that an increase in scatter leads to an increase in required sample size. A reduction in the level of significance also leads to an increase in required sample size, as this reduces the probability of mistakenly demonstrating the effect. Nevertheless, the level of significance may not be varied for the sake of sample size planning. Other relationships of this type are demonstrated in Table 2 for the unpaired t-test.
Table 2. Consequences for the sample size of changes in different parameters: one-tailed unpaired Student t-test. assuming the same standard deviation in the two groups.
| Change | Effect*1 | Standard deviation | Effect strength*2 | Level of significance | Power | Sample size (per group) |
| Effect | 5 | 5 | 1 | 0.025 | 0.8 | 17 |
| 3 | 5 | 0.6 | 0.025 | 0.8 | 46 | |
| 1 | 5 | 0.2 | 0.025 | 0.8 | 401 | |
| 0.5 | 5 | 0.1 | 0.025 | 0.8 | 1600 | |
| Standard deviation | 5 | 25 | 0.2 | 0.025 | 0.8 | 401 |
| 5 | 10 | 0.5 | 0.025 | 0.8 | 65 | |
| 5 | 8 | 0.625 | 0.025 | 0.8 | 42 | |
| 5 | 3 | 1.666 | 0.025 | 0.8 | 7 | |
| Level of significance | 5 | 5 | 1 | 0.05 | 0.8 | 14 |
| 5 | 5 | 1 | 0.01 | 0.8 | 22 | |
| 5 | 5 | 1 | 0.001 | 0.8 | 34 | |
| Power | 5 | 5 | 1 | 0.025 | 0.95 | 27 |
| 5 | 5 | 1 | 0.025 | 0.9 | 23 | |
| 5 | 5 | 1 | 0.025 | 0.7 | 14 |
*1Effect: difference between the two means; *2Effect strength: effect divided by the standard deviation
In addition, it is important to bear in mind that the difference to be detected should also be clinically relevant. The clinical investigator regards the 5 mm Hg greater reduction in blood pressure with drug B as being clinically relevant. However, if the effect expected in the study is too low, then the benefit of the study may be doubted. In such a case, even statistically significant results may be irrelevant (7).
One important point in sample size planning is to consider losses to follow-up or drop-outs (11). If, for example, it must be assumed that adequate data cannot be collected for a proportion of the volunteers in a study—for whatever reason—, the sample size must be proportionately increased. The necessary increase in the sample size depends on the estimated rate of participation and the study conditions. It must, nevertheless, be pointed out that these adjustments may influence the representative character of the data and generally lead to biased results. This must also be considered when planning the study.
Explicit formulae are available for calculating sample sizes for the most common tests (12– 14). Machin et al. (12) present extensive tables for reading off sample size, given typical values for the parameters used in calculating sample size.
Common software programs for calculating sample size include Nquery, SPSS with SamplePower, and SAS with the procedures PROC POWER and PROC GLMPOWER. The program G*Power 3 from the Department of Experimental Psychology at Heinrich Heine University Düsseldorf can be used free of charge (www.psycho.uni-duesseldorf.de/abteilungen/aap/gpower3/). It is advisable to use a validated program—such as one of the above.
Discussion
Planning the sample size of a clinical study requires prior information. The type of prior information depends on the statistical methods which are to be used. If the desired parameters cannot be estimated, it may be desirable to perform a pilot study in advance, in order to estimate the appropriate population parameters. In any case, the expected effect should be at least as large as the minimal clinically relevant effect.
The size of the study group(s) have to be determined even for exploratory or descriptive studies (1), so that the precision of the parameter estimates will not be excessive. If there is no sample size planned, this indicates that the quality of the study is poor.
Sample size planning for a clinical study is based on an estimate from prior information, which may be of different precision in different studies. This should be considered when interpreting the results. If the treatment effect is overestimated during the planning phase, this usually leads to an excessively small sample size. The observed treatment effect may then not be significant—but only because the sample size is too small.
Sample size planning must also include the procedures for dealing with missing values and with patients who leave the study.
We have only been able to consider a few aspects of sample size planning. There are additional aspects, which may be important with specific study designs. For example, the method of sample size planning may be different if a clinical study is to include a test for superiority, non-inferiority, or equivalence (13). Non-inferiority studies may require really large sample sizes, as the mean difference to be detected is often specified as the smallest relevant clinical difference, which then acts as the non-inferiority limit. This is usually much smaller than the actual mean difference.
It often happens that a data set is used to test several hypotheses. The problems of multiple testing must be considered during sample size planning. For this reason, only a single main question to be answered is often specified.
Moreover, the sample size is not always totally specified in modern studies. For example, an adaptive design can be used. The sample size may then be influenced or controlled during the study, in accordance with a scheme which is strictly specified in the planning phase. However, this procedure necessitates careful and statistically demanding planning and should never be performed without the support of an experienced biometrician.
As sample size calculation is so complex and has such important consequences, collaboration is desirable between experienced biometricians and physicians. The quality and validity of studies can be greatly improved if all important details are planned together (2, 3, 15).
Key Messages.
Sample size planning is an essential step in the performance of clinical studies.
Sample size planning requires the expert knowledge of clinicians or physicians, who provide an estimate of the relevant effect.
Sample size planning depends on the planned method of statistical evaluation and thus on the medical question to be answered.
The chances of success in a clinical study and the quality of the research results are highly dependent on sample size planning.
Sample size planning should always be carried out in collaboration with an expert statistician or biometrician.
Acknowledgments
Translated from the original German by Rodney A. Yeates, M.A., Ph.D.
Footnotes
Conflict of interest statement
The authors declare that there is no conflict of interest in the sense of the guidelines of the International Committee of Medical Journal Editors.
References
- 1.Röhrig B, du Prel JB, Blettner M. Study design in medical research - Part 2 of a series on evaluation of scientific publications [Studiendesign in der medizinischen Forschung. Teil 2 der Serie zur Bewertung wissenschaftlicher Publikationen] Dtsch Arztebl Int. 2009;106(11):184–189. doi: 10.3238/arztebl.2009.0184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Eng J. Sample size estimation: how many individuals should be studied? Radiology. 2003;227:309–313. doi: 10.1148/radiol.2272012051. [DOI] [PubMed] [Google Scholar]
- 3.Halpern SD, Karlawish JHT, Berlin JA. The continuing unethical conduct of underpowered clinical trails. JAMA. 2002;288:358–362. doi: 10.1001/jama.288.3.358. [DOI] [PubMed] [Google Scholar]
- 4.Altman DG. Practical Statistics for medical research. London: Chapman and Hall. 1991 [Google Scholar]
- 5.du Prel JB, Röhrig B, Hommel G, Blettner M. Choosing Statistical Tests. Part 12 of a series on evaluation of scientific publications [Auswahl statistischer Testverfahren: Teil 12 der Serie zur Bewertung wissenschaftlicher Publikationen] Dtsch Arztebl Int. 2010;107(19):343–348. doi: 10.3238/arztebl.2010.0343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sachs L. Angewandte Statistik: Anwendung statistischer Methoden. 11th edition. Springer. 2004:352–361. [Google Scholar]
- 7.du Prel JB, Hommel G, Röhrig B, Blettner M. Confidence interval or p-value? Part 4 of a series on evaluation of scientific publications [Konfidenzintervall oder p-Wert? Teil 4 der Serie zur Bewertung wissenschaftlicher Publikationen] Dtsch Arztebl Int. 2009;106(19):335–339. doi: 10.3238/arztebl.2009.0335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.ICH E9. Statistical Principles for Clinical Trials. London UK: International Conference on Harmonization. 1998 adopted by CPMP July 1998 (CPMP/ICH/363/96). [Google Scholar]
- 9.Blettner M, Ashby D. Power calculation for cohort studies with improved estimation of expected numbers of death. Soz Präventivmed. 1992;37:13–21. doi: 10.1007/BF01369097. [DOI] [PubMed] [Google Scholar]
- 10.Breckenkamp J, Berg-Beckhoff G, Münster E, Schüz J, Schlehofer B, Wahrendorf J, Blettner M. Feasibility of a cohort study on health risks caused by occupational exposure to radiofrequency electromagnetic fields. Environ Health. 2009;8 doi: 10.1186/1476-069X-8-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schumacher M, Schulgen G. 3rd edition. Berlin, Heidelberg, New York: Springer Verlag; 2008. Methodik klinischer Studien: Methodische Grundlagen der Planung, Durchführung und Auswertung (Statistik und Ihre Anwendungen) pp. 1–436. [Google Scholar]
- 12.Machin D, Campbell MJ, Fayers PM, Pinol APY. 2nd edition. Oxford, London, Berlin: Blackwell Science Ltd.; 1987. Sample size tables for clinical studies; pp. 1–315. [Google Scholar]
- 13.Chow SC, Shao J, Wang H. Sample size calculations in clinical research. Boca Raton: Taylor & Francis. 2003:1–358. [Google Scholar]
- 14.Bock J. München: Oldenbourg Verlag; 1998. Bestimmung des Stichprobenumfangs für biologische Experimente und kontrollierte klinische Studien; pp. 1–246. [Google Scholar]
- 15.Altman DG. Statistics and ethics in medical research, misuse of statistics is unethical. BMJ. 1980;281:1182–1184. doi: 10.1136/bmj.281.6249.1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Altman DG, Machin D, Bryant TN, Gardner MJ. 2nd edition. BMJ Books; 2000. Statistics with confidence. [Google Scholar]
- 17.Fahrmeir L, Künstler R, Pigeot I, Tutz G. 4th edition. Berlin, Heidelberg, New York: Springer Verlag; 2003. Statistik: Der Weg zur Datenanalyse; pp. 1–608. [Google Scholar]