Automatic Determination of Optimal Linear Drilling Trajectories for Cochlear Access Accounting for Drill Positioning Error

Abstract

Background

Cochlear implantation is a surgical procedure in which an electrode array is permanently implanted in the cochlea to stimulate the auditory nerve and allow deaf people to hear. Percutaneous cochlear access, a new minimally invasive implantation approach, requires drilling a single linear channel from skull surface to the cochlea. The focus of this paper addresses a major challenge with this approach, which is the ability to determine, in a pre-operative CT, a safe and effective drilling trajectory.

Methods

A measure of the safety and effectiveness of a given trajectory relative to sensitive structures is derived using a Monte Carlo approach. The drilling trajectory that maximizes this measure is found using an optimization algorithm.

Results

In tests on thirteen ears, the technique is shown to find approximately twice as many acceptable trajectories as those found manually by an experienced surgeon.

Conclusions

Using this method, safe trajectories can be automatically determined quickly and consistently.

Introduction

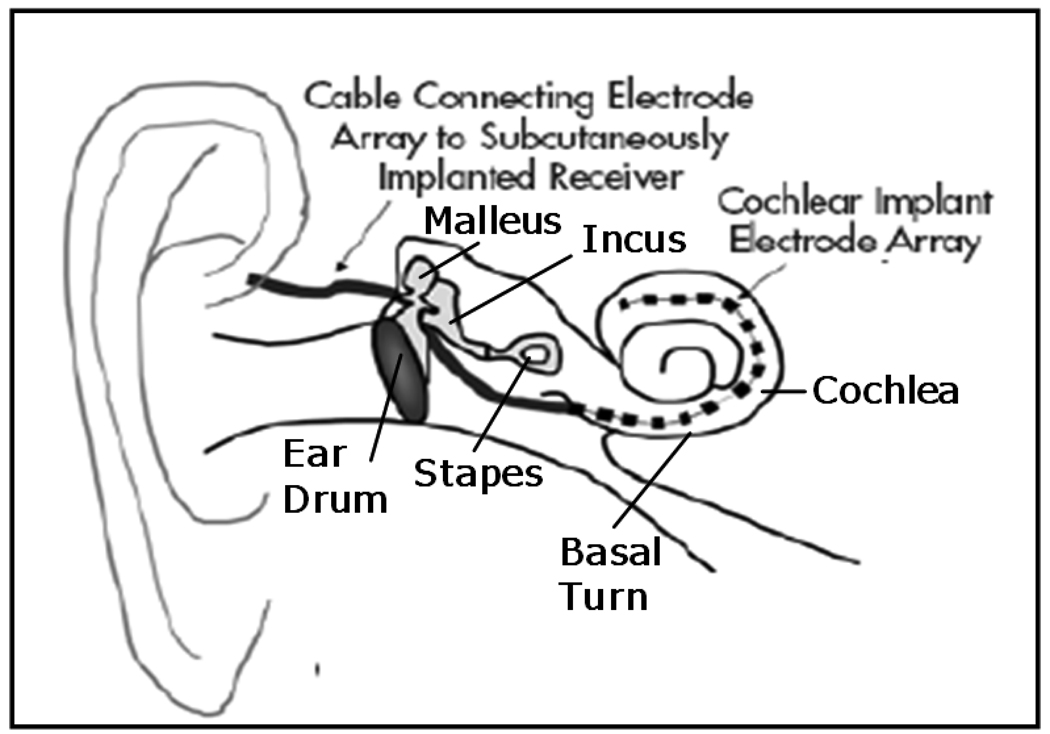
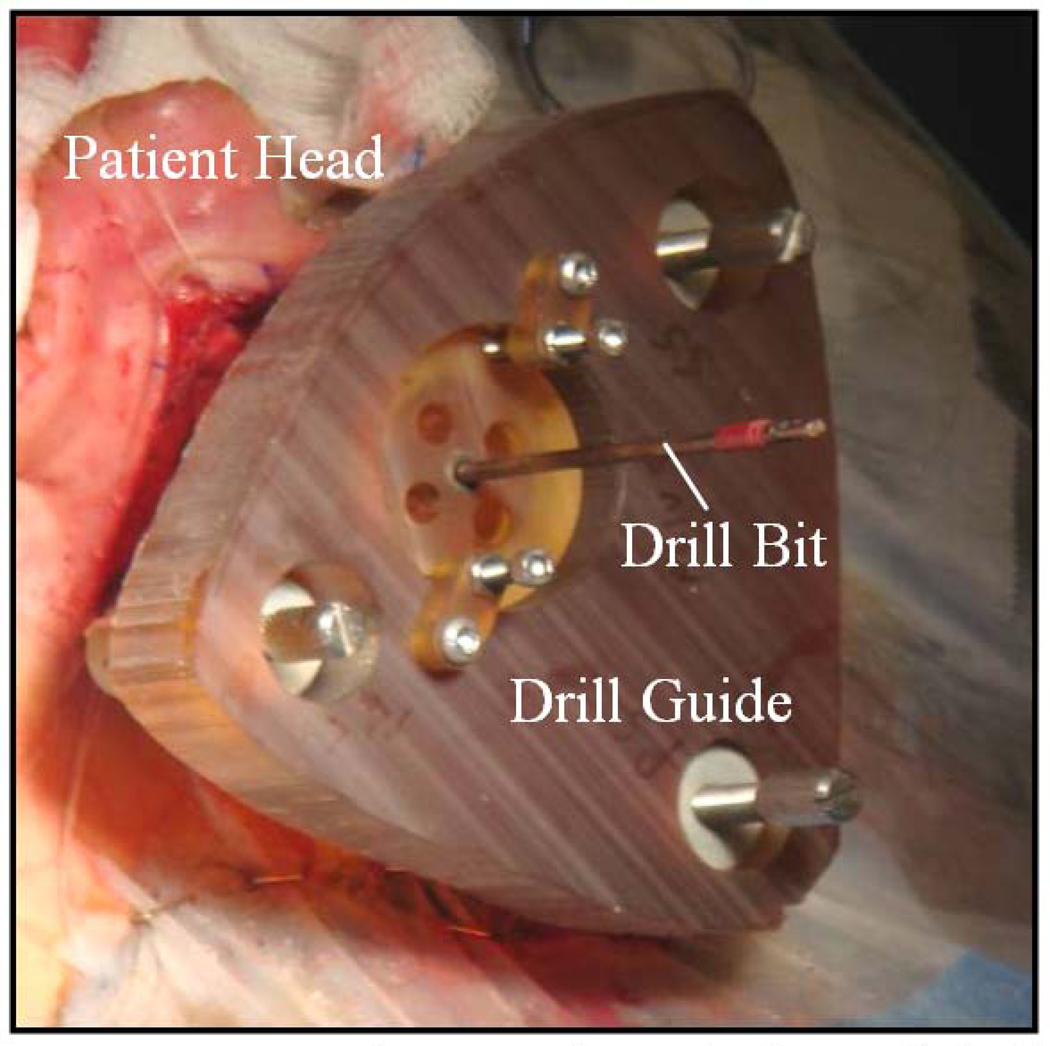
Cochlear Implantation (CI) is a surgical procedure performed on individuals who experience profound to severe sensorineural hearing loss, i.e., individuals who are deaf. In surgery, an electrode array is permanently implanted into the cochlea by threading the array through its basal turn (Figure 1). The array is connected to a receiver mounted securely under the skin behind the patient’s ear. When activated, the external processor senses sound, decomposes it (usually involving Fourier analysis), and digitally reconstructs it before sending the signal through the skin to the internal receiver which then activates the appropriate intracochlear electrodes causing stimulation of the auditory nerve and hearing. Current methods of performing the surgery require wide excavation of the mastoid region of the temporal bone by means of a hand-held surgical drill. The precautionary measures necessary to safely avoid sensitive structures can prolong surgery time from one to three hours. Recently, an alternative approach has been proposed—percutaneous cochlear implantation (PCI) (1–4). In this approach, the surgical trajectory is planned in a pre-operative CT. In surgery, three screws, or “anchors,” are affixed to the patient’s skull, and an intra-operative CT is acquired. By aligning the preoperative CT and the intra-operative CT, the positions of the anchors and the surgical trajectory are known in the same coordinate space. This information is sufficient to permit the construction a patient-customized drill guide that, when attached to those three anchors, constrains the path of a mounted drill to lie along the planned linear channel from the skull surface to the cochlea with high accuracy (see Figure 2).

Figure 1.

Anatomy of the ear. An electrode array is threaded through the basal turn into the cochlea.

Figure 2.

Picture taken during clinical testing of percutaneous CI method. The image shows a drill guide fixed to anchors implanted in a human skull.

Percutaneous access can become a preferred solution only if the surgical method proves to be at least as safe and effective as traditional methods. An effective CI drilling procedure can be simply defined as a procedure in which “effective” access to the cochlea is achieved. In optimal procedures, the CI electrode array is implanted entirely into the scala tympani, an internal cavity of the cochlea. Recent studies have shown that in approximately 27% of all implantations, the arrays either miss the scala tympani entirely, being inserted instead into a second internal cavity of the cochlea, the scala vestibuli, or are initially inserted into scala tympani but then breach the membrane between these two cavities and cross into scala vestibuli (5). In order to maximize the likelihood of implantation into the scala tympani with minimal likelihood of crossover, a proper scala-tympani cochleostomy must be performed, and the array must enter the scala tympani tangentially to the basal turn, thereby introducing as little stress as possible on the membrane separating the scalae and reducing the likelihood of a breach. Thus, we term an “effective” drilling trajectory to be one that reaches the round window at a position and orientation that are conducive to insertion into the scala tympani. A safe CI drilling procedure can be defined as a procedure in which sensitive anatomical structures encountered along the path to the cochlea are avoided. Thus, we term a “safe” drilling trajectory to be a trajectory that is placed such that a surgical drill following the trajectory would not contact a sensitive structure before entering the cochlea. These structures include the facial nerve, the external auditory canal (for lack of a more concise anatomic definition, in this manuscript we refer to the canal and tympanic membrane together as the “external auditory canal”), the chorda tympani (or simply, “chorda”), and the ossicles. The facial nerve is a highly sensitive structure that controls all movement of the ipsilateral face. If this nerve is damaged, the patient may experience temporary or permanent facial paralysis. Violation of the external auditory canal can lead to a breach in sterility and open a potential avenue for future infection with possible implant extrusion. Injury to the chorda tympani can result in temporary or permanent loss in the ability to taste on the ipsilateral tongue. Chorda injury is undesirable, but may occur in as many as 20% of all CI surgeries and therefore is typically not considered catastrophic. Injury to the ossicles can result in damage to residual hearing, and therefore is also not considered catastrophic in current procedures, since implanted patients are already deaf. However, in the future, implants will most likely involve individuals with residual hearing where violation of the ossicles would be discouraged. Thus we include the ossicles as vital, adjacent structures.

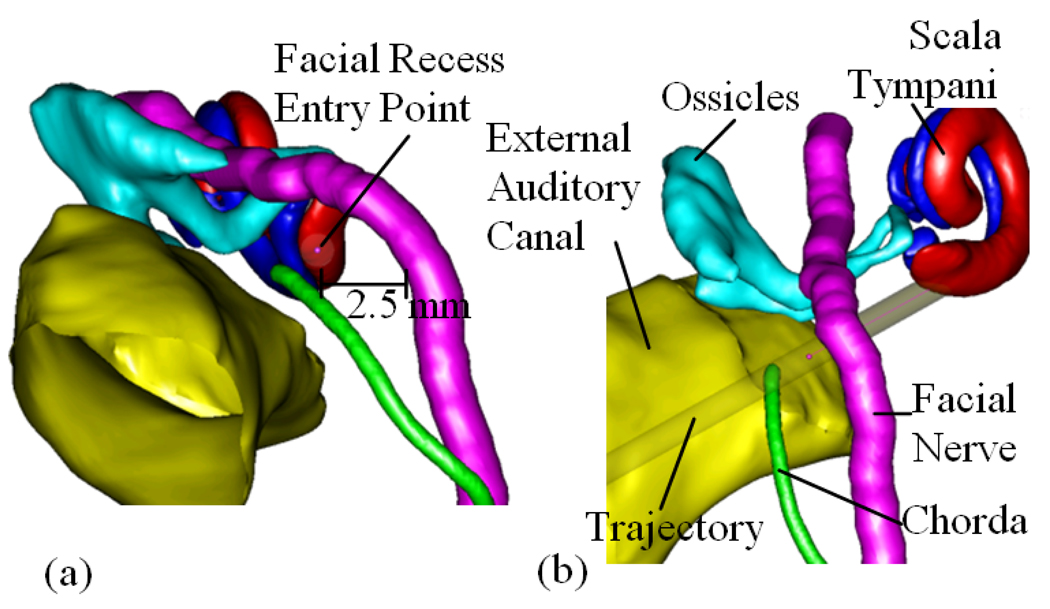
Clearly, the safety and effectiveness of a PCI procedure will depend largely on the choice of the pre-operatively planned drilling trajectory as well as any errors in drill placement. In this paper, we will show that it is possible to automatically identify trajectories that would allow CI placement in individual subjects, and to find an optimally safe and effective trajectory with respect to the distribution of drill placement error, but this requires that the exact locations of the scala tympani, facial nerve, chorda, external auditory canal, and ossicles are identified. These features are often difficult to discern in a CT image, but recent advances have made it possible nevertheless to identify them reliably via specialized image-processing algorithms. These algorithms employ anatomical knowledge and take advantage of subtle morphological similarities from one person to another. The structures are first painstakingly identified in a limited set of carefully acquired CT images, which are referred to as the “atlas”. Then, this atlas is employed to transfer this knowledge to each new patient’s CT, followed by post-processing that takes advantage of the known shapes of the structures. The result is that the facial nerve, the external auditory canal, the chorda tympani, the ossicles, and the scala tympani can all be localized automatically (6–10). Figure 3 shows an example of the result of this processing. Each of the identified structures is rendered in a distinct color.

Figure 3.

3D rendering of the structures of the left ear. (a). Left-right, Posterior-Anterior view along the preferred drilling trajectory. The round window target point is located at the scaly tympani surface. (b). Posterior-Anterior view. Included are the facial nerve, scala tympani, chorda, ossicles, and external auditory canal.

A CI drilling trajectory can be completely defined by a target point (at the scala tympani via the round window) and an entry point (at the surface of the skull). While the target point is constrained explicitly by the scala tympani, the skull entry point is constrained implicitly by the need to avoid sensitive anatomical structures that lie between the entry and target regions. Specifically, the entry point is constrained as follows: (1) The trajectory must pass through the “facial recess,” which is the region bounded posteriorly by the facial nerve and anteriorly by the chorda. (2) Medially from the facial recess, the trajectory is bounded superiorly by the ossicles, specifically, the short process of the incus and the stapes. (3) The trajectory is bounded anteriorly by the external auditory canal. In many cases, the chorda tympani provides a more limiting anterior constraint on the drilling trajectory than the external auditory canal, but the canal can become important in the following two plausible situations: (a) In cases where the auditory canal curves posteriorly at a position lateral to the facial recess, it is possible that the auditory canal can become a more limiting anterior constraint on the drilling trajectory than the chorda. (b) In cases where the chorda must be sacrificed to ensure the safety of the facial nerve, the external auditory canal becomes the only immediate anterior constraint on the drilling trajectory.

When looking through the facial recess to the cochlea along the preferred drilling trajectory, it can be seen that these structures create a window approximately 1.0 mm to 3.5 mm in diameter through which a safe path to the cochlea can be planned (see Figure 3).

The proposed method of percutaneous cochlear access has undergone cadaveric studies (2), and has now moved to clinical validation (3). Currently, the major challenges of the proposed method of percutaneous cochlear access are the management of various sources of error. Recent studies suggest that there is a root-mean-square (RMS) positioning error in the drill guide system of only 0.44 mm at the specified target point (11). A value of 0.44 mm RMS would be a safe estimation of the total error if there were no arbitrariness in the physician’s choice of the appropriate path in the preoperative CT. Choosing a path to avoid three-dimensional structures within a CT volume by examining a sequence of two-dimensional images has proven to be difficult, even for experienced physicians. While finding a line segment through the facial recess to the cochlea that avoids sensitive structures is not so difficult, manually choosing a safe line segment that accounts for the 1.0 mm diameter of the surgical drill bit as well as the 0.44 mm RMS error in the drill guide system is highly difficult, if not impossible, to do manually. These tasks can, however, be accomplished using automated algorithms.

Recently, an atlas-based approach to automatically determine CI drilling trajectories has been proposed (12). This method uses image registration techniques to map a specified target and entry point chosen manually in an atlas image onto any patient image, thus defining a drilling trajectory for the patient. We will show that this technique produces results that are reasonable but do not adequately guarantee safe and effective trajectories.

In this work, we have developed an approach to automatically find a safe and effective drilling trajectory by optimizing a reasonably placed trajectory, such as one extracted using the atlas-based technique, while accounting for error in the positioning of the surgical drill. To facilitate our approach, we have developed methods to (1) detect whether a drill bit following an arbitrary drilling trajectory subject to zero error is safe, (2) detect whether a trajectory subject to zero error is effective, (3) compute the probability that a trajectory subject to non-zero error is safe and effective, and (4) automatically find a probabilistically safe and effective drilling trajectory for access to the cochlea.

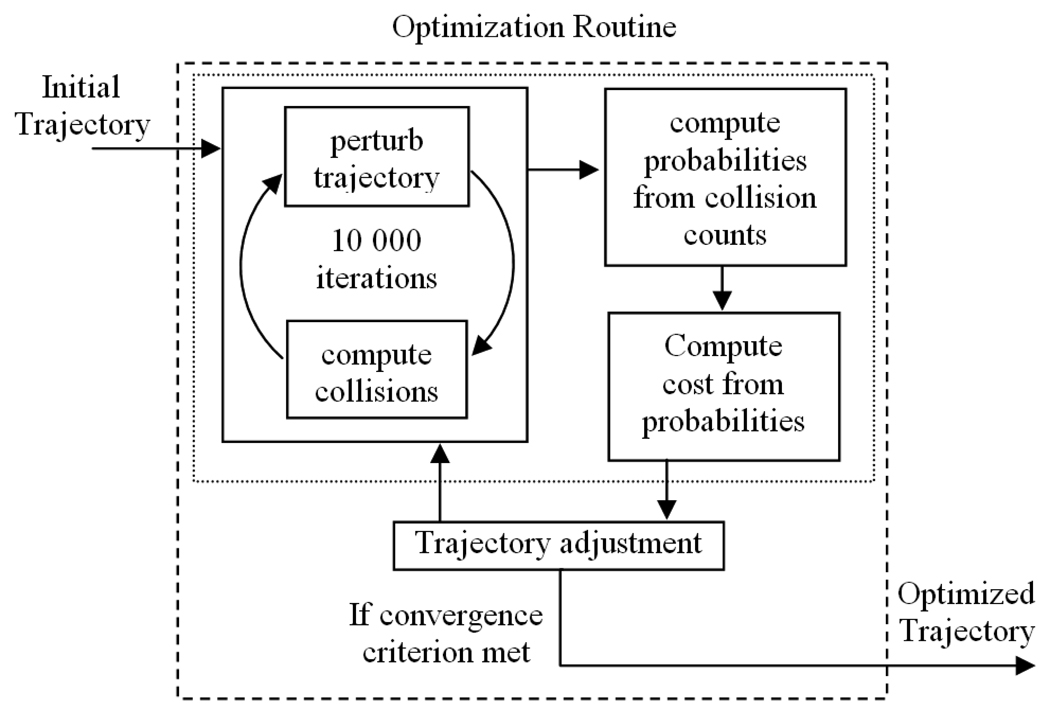
The general approach is illustrated in Figure 4. For any particular trajectory, probabilities that the trajectory is effective and that it will not damage each individual structure are estimated using Monte Carlo simulations, i.e., by iteratively perturbing the trajectory with error of the expected distribution and calculating the fraction of iterations for which the displaced trajectories are effective and safe with respect to each sensitive structure. Using a cost function, these probabilities are combined into a single number representing the “cost” for the trajectory. A probabilistically safe and effective drilling trajectory can then be found by using a minimization technique to optimize a roughly placed trajectory with respect to the cost function. The rest of this paper details our methods.

Figure 4.

Approach for computing an optimally safe and effective surgical drilling trajectory.

Materials and Methods

The proposed method to automatically plan a probabilistically safe and effective drilling trajectory requires some prior information. It is necessary to know the distribution of error along the trajectory, to know the radius of the surgical drill bit, and to have all sensitive structures localized and represented as signed distance maps aligned with the patient CT. A distance map can be extracted from a binary mask or a point set using, for instance, fast marching methods (13).

Detecting surface contact

In order to determine whether a given trajectory will cause the drill bit to contact a structure, we first need to be able to calculate the closest distance between the planned trajectory and the surface of the structure. The value of a distance map at any given grid location is the distance to the closest point on the zero-level set surface. Suppose there is a drill path line L which passes through entry point p_e and target point p_t. Any arbitrary point m on the line L can be represented as

$$m=p_e+\mathit{\text{av}},v=\frac{p_t-p_e}{\Vert p_t-p_e\Vert }$$ (1)

where a is some scalar. Suppose now that we have a surface S represented by distance map D_S. The distance d between L and S can be calculated by

$$d=\text{dist}(S,L)={\text{min}}_a{D}_s(m(a))$$ (2)

where evaluation of D_S is performed using trilinear interpolation of the grid values.

It is possible to estimate d by evaluating D_S along L at discrete intervals, e.g., by evaluating D_S at every one tenth of a voxel along L and choosing the minimum of all such evaluations. However, a much more precise and efficient method for computing d is to minimize the trilinear interpolant of D_S along L over each 8-voxel neighborhood through which L passes. A 2D version of the method is illustrated schematically in Figure 5. In 2D, we again wish to find the minimum distance between a line L and a contour represented by a 2D distance map D_S. This can be computed by determining the minimum distance map value along the continuous line L. Portions of L will no doubt pass between the distance map discrete grid values, i.e., it will pass through a set of four-pixel neighborhoods in the distance map. The distance value within a four-pixel neighborhood of the discrete distance map is defined only at the centers of the four pixels at the corners of the neighborhood, but distances at other points can be estimated by bilinear interpolation. Let us first examine computation of the minimum distance, d_N in a single neighborhood along L. The bilinear function used for interpolation within the neighborhood can be parameterized as an explicit function of x and y using four neighboring pixel distance values. The pixels representing the corners of a neighborhood can be represented with the coordinates (x_i,y_j), (x_i,y_j+1), (x_i+1,y_j), (x_i+1,y_j+1). Let the distance map values at each point be labeled g_1–4, and assume, for the sake of simplicity, that the coordinate system has been translated as a preprocessing step such that x_i = y_j = 0. Then, the bilinear function q(x,y) which defines distance values within the neighborhood can be written as

$$\begin{array}{c}q(x,y)=Q_1+Q_{2}x+Q_{3}y+Q_4\mathit{\text{xy}}\hfill \\ Q_1=g_1\hfill \\ Q_2=-g_1+g_3\hfill \\ Q_3=-g_1+g_2\hfill \\ Q_4=g_1-g_2-g_3+g_4\hfill \end{array}$$ (3)

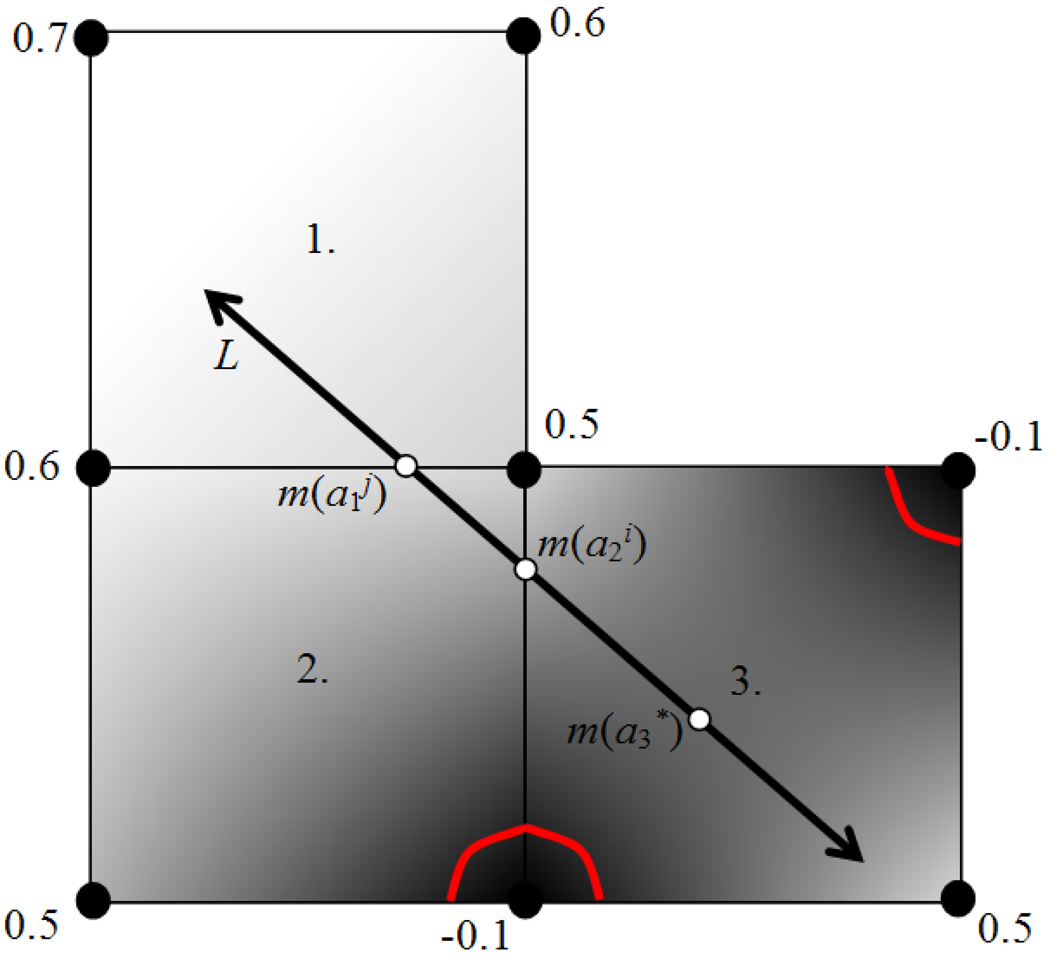
Figure 5.

2D example of the minimizer of a linear interpolant function along a line. The nodes denote pixel positions in the distance map, each with an assigned distance value. The gray level intensities illustrate the relative interpolated distance values between the known pixel values. The red contours indicate the position of the surface implied by the distance values. The minimizers along L of the interpolation function for three 4-pixel neighborhoods through which L passes (labeled 1, 2, and 3) are displayed, labeled as a₁, a₂, and a₃.

Assume any point along L is represented as in Eq. (1), and the x and y components of p_e and v are represented by x_e, y_e, x_v, and y_v. Then the function q(x,y) evaluated at any point along L is a 1D quadratic function w(a) and can be written as

$$\begin{array}{c}w(a)=A_1+A_{2}a+A_3{a}^2\hfill \\ A_1=Q_1+x_e{Q}_2+y_e{Q}_3+x_e{y}_e{Q}_4\hfill \\ A_2=x_v{Q}_2+y_v{Q}_3+(x_v{y}_e+y_v{x}_e)Q_4\hfill \\ A_3=x_v{y}_v{Q}_4\hfill \end{array}$$ (4)

If A₃ is nonzero, the minimum (or maximum) value w_c of q(x,y) along L is found by computing the zero of the derivative of w and is given by

$$w_c=w(a^{*}),a^{*}=\frac{-A_2}{2A_3},$$ (5)

and if w_c falls within the neighborhood, d_N is the minimum of {w(aⁱ), w(a^j), w_c}, where m(aⁱ) and m(a^j) are the two points on L which fall on the boundary of the neighborhood. If w_c does not fall within the neighborhood, or if A₃ equals zero, then d_N is the minimum of {w(aⁱ), w(a^j)}. Figure 5 shows a 2D example of the different types of minima. Now, let {d_N} be the set of minimum distances associated with the set of all four-pixel neighborhoods through which L passes. Then, the minimum distance d along L is determined as the minimum of the set {d_N}. This process is extendable to the 3D case, where d is determined by minimizing the trilinear interpolant function over each 8 voxel neighborhood through which the line passes.

Determining whether the drill bit along line L will hit surface S can now easily be defined by the following criterion. For any given path L, if d is greater than the radius r of the drill bit, then a bit following line L will miss surface S. If d is less than r, then a drill bit following L will hit S.

Evaluating smoothness of electrode insertion

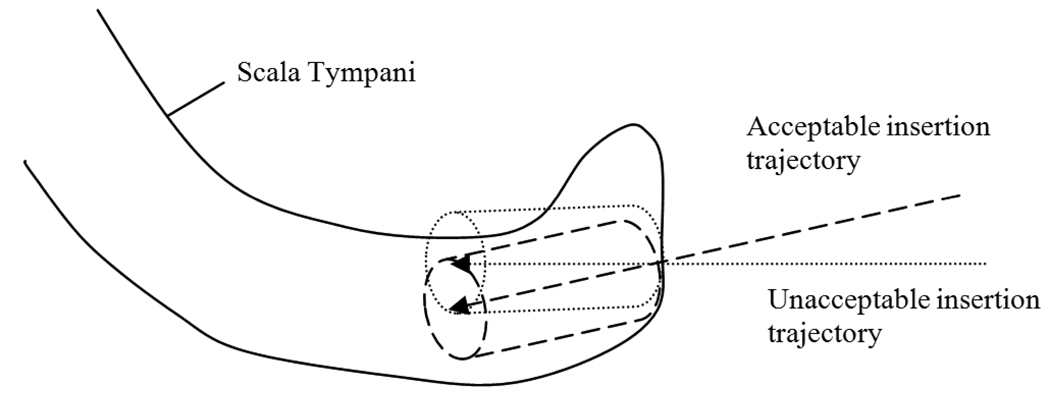
There are two properties that a trajectory must satisfy to allow easy insertion of the electrode array into the scala tympani: (1) the well created by a drill bit following that trajectory must create an entrance into the scala tympani of diameter greater than the that of the electrode array so that insertion is possible, and (2) since the array has a certain degree of rigidity and damage to the soft tissue of the scala tympani is undesirable, the well should be oriented at a similar angle to the axis of the scala tympani such that the entire process of insertion of the array into the scala tympani via the well is smooth. Both of these properties can be captured through a fairly simple criterion: the properties are said to be satisfied if a cylinder of radius ρ = 0.26 mm (the radius of the tip of the electrode array) and length γ centered around the drilling trajectory can fit within the segmented scala tympani surface, where γ was chosen by an experienced physician to be 2.0 mm (see Figure 6). To measure whether this criterion is met, a cylinder along the trajectory is approximated by a discrete set of points. The points were chosen to be distributed around the trajectory at every π/4 radians and along the trajectory every 0.3 mm. A point along the cylinder lies outside (inside) the scala tympani if the distance map representing the scala tympani is greater than or equal to 0 (less than 0) at that point. With this information it is possible to determine the longest length along the drilling trajectory for which this cylinder lies entirely within the structure. If that length is larger than γ, then the trajectory is said to be acceptable with respect to the target structure.

Figure 6.

Examples of trajectories which are acceptable and unacceptable for insertion. As illustrated in the figure, detecting whether the cylinder surrounding the trajectory exits the structure can be used to decide whether electrode insertion will be feasible and smooth.

Calculating probability of success

With a method of determining whether any given drill trajectory contacts a sensitive structure and whether it appropriately reaches the target structure, a safety probability model can be constructed using a Monte Carlo simulation-based approach. With the drill guide system we are using in this application, we expect the drill at the target point to experience isotropic normally distributed error, while error at the skull entry point is negligible because it is so close to the center of the fiducial system. Therefore, using a normally distributed pseudorandom number generator, we create a vector q of dimensions 3 × 1 such that each component of q is drawn from the zero-mean normal distribution with standard deviation σ. Given that σ_RMS is the expected RMS error at the target point, σ is computed using the equation

$$\sigma =\frac{{\sigma }_{\text{RMS}}}{\sqrt{N}}.$$ (6)

Then q is used to displace the trajectory at the site of the selected target position to p_t’ = p_t + q. To determine whether the displaced path would damage a particular structure, d is computed for the displaced path using Eqns. (1) and (2), and a ‘hit’ or ‘miss’ for the structure is determined. If a ‘hit’ or ‘miss’ is recorded iteratively, each iteration using a new random displacement q, a large set of hits or misses can be collected. Given a large enough number of iterations, the probability that the original drilling trajectory can successfully avoid damage to a particular surface, P_s, can be approximated by

$$P_s\cong \frac{n^{\text{misses}}}{n^{\text{misses}}+n^{\text{hits}}},$$ (7)

where n^misses denotes the number of misses over all iterations and n^hits is defined similarly. In our experiments we found that the 10 000 iterations was sufficient. Beyond this number the probabilities remained the same to three significant digits. P_s is the quantified measure of safety that a drill bit following path L will not damage structure S.

The same process is applied to estimate P_T, the probability that any given drill path will be effective with respect to its target surface. P_T can be approximated by

$$P_T\cong \frac{n^{\text{effective}}}{n^{\text{not effective}}+n^{\text{effective}}},$$ (8)

where n^effective is the number of displaced trajectories which are effective and n^{not effective} is defined similarly.

Drilling trajectory optimization

The drilling trajectory is defined as the line that includes the skull entry point p_e and scala tympani target point p_t. Different possible trajectories are generated by varying p_e and p_t. The undesirability, or cost, of any given trajectory is determined from the probability values generated in Section 2.4 using the simple function

$$c=-(b_1\text{log}{P}_{S_1}+b_2\text{log}{P}_{S_2}+b_3\text{log}{P}_{S_3}+b_4\text{log}{P}_{S_4}+b_5\text{log}{P}_T),$$ (9)

where S₁, S₂, S₃, and S₄ denote the facial nerve, external ear canal, ossicles and chorda surfaces, and b₁, b₂, b₃, b₄, and b₅ denote constant coefficients. Note that the formula in Eq. (9) does not represent a probability, but is simply a way to combine five probabilities into one scalar value that can be optimized by some searching method. The logarithm functions weigh the effect of lower probability values greater relative to higher ones, while the coefficients are used to weight each logarithm term with a relative importance. Values for coefficients b_1–5 may be derived using any appropriate method. In this application we derive these coefficients based on goals for safety and effectiveness established by an experienced surgeon. Those goals are probabilities of 0.999, 0.950, 0.800, and 0.800 for avoiding damage to the facial nerve, external ear canal wall, ossicles, and chorda, respectively, and 0.800 for effectively targeting the scala tympani. These probabilities were chosen to make the percutaneous approach at least as safe and effective as traditional methods. The relative weighting of the goals can be understood by recognizing that damage to the facial nerve is the most catastrophic, followed by violation of the external auditory canal, while damage to the ossicles and chorda, although serious, is more acceptable. Due to the relatively low current success rate for proper implant insertion by traditional methods, effective targeting is considered to be of approximately the same level of importance as the safety of the ossicles and chorda. A planned trajectory is deemed acceptable only if the trajectory’s probability levels meet this set of goals. To account for these goals in the cost function, b_1–5 are chosen such that, if the probabilities on the right side of Eq. (9) equal their specified levels, then all of the probability terms in the cost function are equal. Equality is achieved by choosing values of the exponents such that

$$b_n=\frac{b_m\text{log}(G_m)}{\text{log}(G_n)},$$ (10)

where n denotes the nth term in the cost function, m denotes the mth term, and G_n and G_m are the respective goals. Coefficient b₅ was arbitrarily set to 1, and coefficients b_1–4 were calculated using Eq. (10) to be 223.03, 4.35, 1.0, and 1.0.

To minimize Eq. (9), we use Powell’s direction-set method with Brent’s line-minimization algorithm (14). A pair of search directions 1 v⃗ and 2 v⃗ are chosen orthogonal to the initially specified trajectory and orthogonal to each other. In the search process, p_t and p_e are each varied in these two directions, constituting 4 degrees of freedom. Constraining the search space to these four dimensions, rather than varying both points in 3D space, simplifies the optimization process while still allowing any trajectory to be represented.

Results

All programs were written in C++. The initial trajectory was specified using the methods presented in (12). All sensitive structures were localized automatically using an atlas-based strategy as presented in (6,7) combined with other techniques (8–10). The drill bit used for the proposed surgery has a radius of 0.5 mm. A complete optimization requires about 1 minute on a 2.4 GHz Intel Xeon Processor machine.

Experimental Results

Experiments were conducted using patient CT scans of four left and nine right normal ears. Experiments followed Institutional Review Board approved protocols. For each ear in the dataset, drilling trajectories were generated with our fully automatic approach at both target positioning error levels of 0.44 mm RMS and a more conservative level of 0.52 mm (~20% larger); for comparison to human optimization, a third trajectory was chosen manually by an experienced physician on the basis of visual inspection of the CT images. The results are shown in Table 1 for each of 13 ears from CT volumes of 10 patients (one ear per column). That table gives the probabilities of safety for each of the four anatomic structures (Facial Nerve through Chorda) and the probabilities of effectiveness (Smooth Insertion). For each case, probabilities are given for six trajectories. These trajectories are the initial trajectory, the final, optimized trajectory, and the manually selected trajectory as determined for each of the two error levels of target positioning (0.44 mm and 0.52 mm). In addition, at the bottom of the table, the value of the cost function corresponding to each trajectory is given. As mentioned above, the probabilities of success for the planned trajectories with respect to the structures were calculated via 10,000 trials of randomly displaced paths. Several probabilities of 1.000 are listed in the table. While in reality perfection is clearly impossible, those trajectories endured all 10,000 trials without hitting the relevant structure. Given our methodology, those probabilities of success are approximately 1.000.

Table 1.

Drilling trajectory safety results across test subjects. Shown are probabilities of safety that the automatic initialization, automatically optimized, and manually chosen trajectories do not damage the sensitive structures and probabilities of effectiveness that they reach the target point in a manner conducive to smooth electrode array insertion. Numbers shown in bold are below the goals for safety for the manual and optimized trajectories.

Volume			1		2		3	4	5	6	7	8	9	10
Ear			L	R	L	R	L	R	R	R	R	R	R	L	R
	Error Level	Trajectory	Probabilities of Safety or Effectivness													Goals
Facial Nerve	0.44 mm	Initial	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.980	0.759	0.999
		Refined	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.991	0.994
		Manual	1.000	1.000	0.993	0.997	1.000	1.000	1.000	1.000	1.000	1.000	0.993	0.636	0.854
	0.52 mm	Initial	1.000	1.000	1.000	1.000	1.000	1.000	0.997	1.000	1.000	1.000	1.000	0.960	0.714
		Refined	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.999	0.996	0.996
		Manual	1.000	0.999	0.983	0.990	0.997	1.000	1.000	0.998	1.000	1.000	0.977	0.622	0.810
External Auditory Canal	0.44 mm	Initial	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.950
		Refined	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
		Manual	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	0.52 mm	Initial	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.999	1.000	1.000
		Refined	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.998	0.999
		Manual	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
Ossicles	0.44 mm	Initial	1.000	1.000	1.000	1.000	1.000	0.999	1.000	1.000	1.000	1.000	1.000	1.000	0.997	0.800
		Refined	0.999	1.000	0.998	0.999	0.995	0.999	1.000	1.000	1.000	1.000	1.000	1.000	1.000
		Manual	1.000	1.000	1.000	1.000	1.000	0.980	0.946	0.912	1.000	1.000	0.902	0.970	0.999
	0.52 mm	Initial	1.000	0.999	0.998	0.999	0.998	0.994	0.999	1.000	1.000	1.000	1.000	0.998	0.990
		Refined	0.999	0.992	1.000	0.994	0.982	0.983	0.999	1.000	0.999	1.000	0.999	1.000	1.000
		Manual	1.000	0.999	1.000	1.000	1.000	0.955	0.987	0.862	0.996	1.000	0.856	0.937	0.998
Chorda	0.44 mm	Initial	0.407	1.000	0.685	0.954	0.949	0.799	1.000	0.987	1.000	0.998	0.074	0.346	0.964	0.800
		Refined	1.000	1.000	1.000	0.997	1.000	1.000	0.983	0.999	1.000	1.000	0.960	0.256	0.477
		Manual	0.946	1.000	1.000	1.000	1.000	1.000	0.985	1.000	1.000	1.000	0.811	0.948	0.940
	0.52 mm	Initial	0.411	1.000	0.650	0.913	0.907	0.754	0.998	0.967	0.998	0.991	0.111	0.361	0.939
		Refined	0.999	1.000	0.999	0.982	0.994	0.998	0.899	0.992	1.000	0.997	0.867	0.104	0.323
		Manual	0.906	1.000	0.999	1.000	1.000	1.000	0.982	0.998	1.000	0.997	0.777	0.916	0.909
Smooth Insertion	0.44 mm	Initial	0.875	0.788	0.858	0.820	0.887	0.813	0.791	0.873	0.882	0.717	0.868	0.815	0.728	0.800
		Refined	0.975	0.945	0.954	0.926	0.983	0.978	0.928	0.956	0.982	0.949	0.917	0.495	0.836
		Manual	0.927	0.809	0.924	0.952	0.966	0.706	0.937	0.872	0.971	0.007	0.477	0.061	0.010
	0.52 mm	Initial	0.799	0.710	0.777	0.723	0.814	0.745	0.711	0.789	0.830	0.644	0.805	0.728	0.664
		Refined	0.926	0.847	0.932	0.828	0.925	0.942	0.851	0.864	0.936	0.898	0.748	0.297	0.484
		Manual	0.862	0.748	0.877	0.905	0.915	0.619	0.863	0.800	0.926	0.013	0.460	0.075	0.021
			Cost Function Value
	0.44 mm	Initial	0.448	0.103	0.231	0.154	0.075	0.188	0.102	0.065	0.055	0.145	1.192	2.480	26.502
		Refined	0.011	0.025	0.021	0.064	0.010	0.010	0.040	0.020	0.008	0.023	0.055	1.761	0.974
		Manual	0.057	0.092	0.705	0.308	0.015	0.160	0.078	0.099	0.013	2.155	1.128	44.491	17.107
	0.52 mm	Initial	0.484	0.149	0.298	0.181	0.133	0.253	0.437	0.117	0.082	0.195	1.051	4.531	32.396
		Refined	0.034	0.076	0.031	0.092	0.044	0.034	0.117	0.067	0.029	0.048	0.284	1.897	1.191
		Manual	0.107	0.222	1.696	1.004	0.326	0.228	0.125	0.354	0.035	1.887	2.738	46.557	21.853

Very positive results can be seen for most of the experimental trials. The numbers shown in bold indicate probability levels that fall below the goals. At a level of 0.44 mm RMS in drill positioning error, the automated planning algorithm meets the goals for safety for all but the two ears of volume 10. Both the left and right facial recess regions for this individual have a width of approximately 1.0–1.5 mm. Thus, fitting a 1.0 mm diameter trajectory through this region which meets all goals for safety given the estimation of error is not possible. For this individual, percutaneous implantation might not be recommended. Manually chosen trajectories at this error level fail to meet the safety goals on seven ears. In the ears of volume 10, the manually chosen trajectories significantly jeopardize the integrity of the facial nerve. The disparity between automatic and manual success rates are even higher at the higher error level, where the goals are not met in 3 of 13 ears for the automatic trajectory and 10 of 13 for the manual trajectories. In total, for the range of errors we considered, the automatic method found approximately twice as many safe and effective trajectories as the manual method.

It can be seen that even for initial positions whose probabilities are well below those of the manually selected trajectories, the automatic method consistently manages to find trajectories that achieve its goals. In all cases, the optimization algorithm converges to a solution exhibiting a lower cost than manually chosen trajectories. These results suggest that the employed optimization method (i.e., Powell/Brent) is indeed effective and robust in this application. Several examples of automatically generated trajectories are shown in Figure 7. Although precise safety estimations are difficult to determine with the human eye, all generated trajectories appear visually to be reasonable and safe.

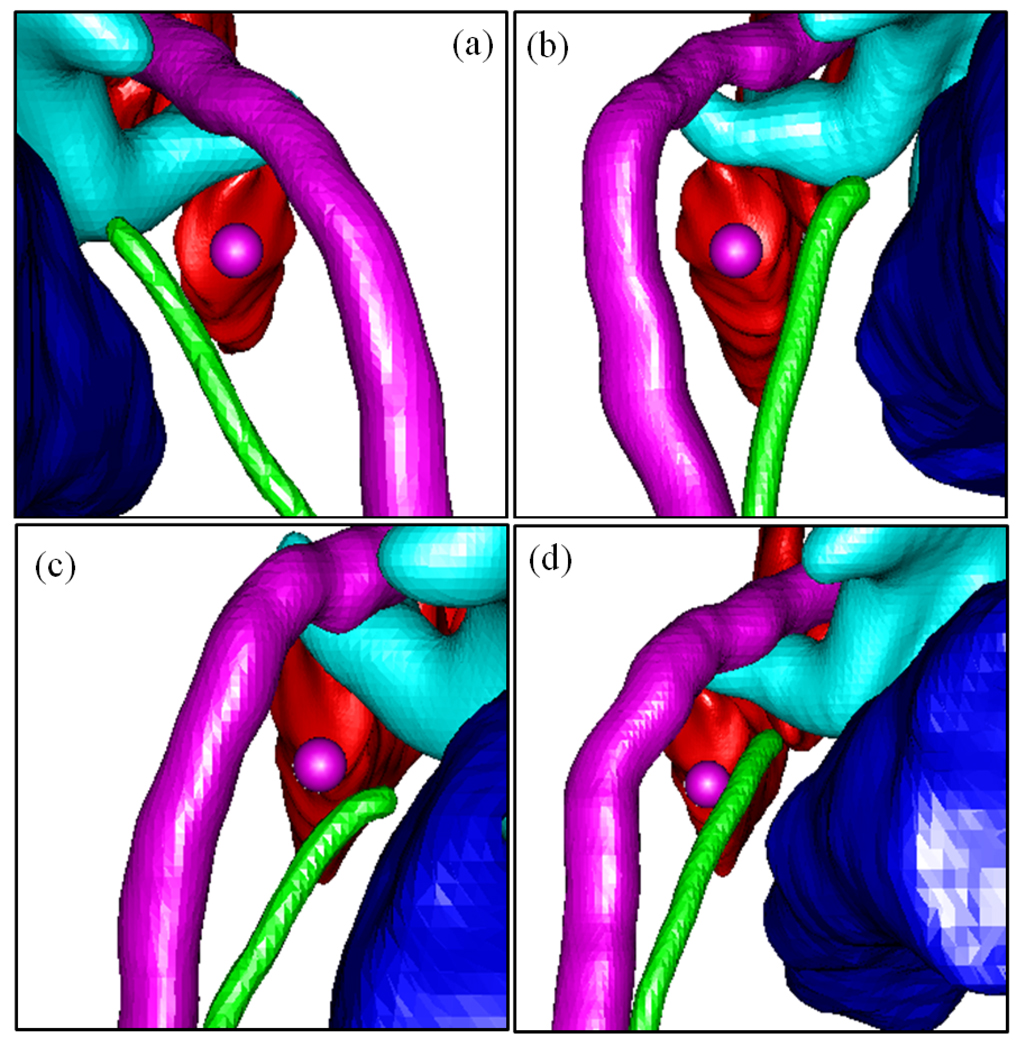
Figure 7.

View along automatically planned trajectories (purple sphere, 1.0mm diameter). Shown are facial nerve (purple), chorda (green), scala tympani (red), ossicles (blue-green), EAC (blue). (a–d) Volume 3, left ear; volume 4, left ear; volume 9, right ear; volume 10, right ear. The facial recess is noticeably thinner in volume 10.

Discussion

We have presented a method to compute the safety of a given drilling trajectory, as well as a method for automatically finding a safe linear drilling trajectory for percutaneous cochlear implant surgery. Our results suggest that percutaneous cochlear access may be a viable alternative to traditional surgical methods for placing cochlear implants. With the current estimation of drill positioning error at the entrance to the cochlea, manual determination of drilling trajectories is prone to high variability in safety. Using the method presented in this article, however, safe trajectories can be automatically determined quickly and consistently. Unlike manual path selection, the automatic method accounts for error in the drill platform system, estimates the relative safety of any path in statistical terms, and indicates whether percutaneous access may be preferable to traditional methods for a specific patient.

All of the trajectories in the table result in a relatively high probability of safety for the ossicles and external auditory canal, as compared to the facial nerve and chorda. This difference is to be expected, since the ossicles and external auditory canal usually impose much more forgiving constraints over the range of feasible trajectories than the facial nerve and chorda. Thus, it is typically much easier, both manually and automatically, to find an effective trajectory that is safe with respect to both the ossicles and external auditory canal. Given these high probabilities, it may appear that the ossicles and the external ear canal are irrelevant to the optimization. However, there are important reasons for including them. First, the anatomy of the external auditory canal is such that it is not a straight cylinder from the lateral surface to the ear drum. Rather it curves posteriorly at the midpoint at the temporo-mandibular joint. Thus, even though a trajectory that courses posterior to the chorda would avoid the external auditory canal medially, it may still violate the EAC laterally. Second, for a number of patients, the facial recess is too narrow to protect both the facial nerve and chorda using traditional or percutaneous excavation techniques. When unavoidable, our optimization technique, mimicking a typical surgeon, chooses to sacrifice the chorda. When this sacrifice occurs, we need to define a new anterior bound on the range of feasible drilling trajectories to guide the optimization algorithm. The next immediate sensitive structure anterior to the facial recess is the external auditory canal. For these two reasons, the external auditory canal is accounted for in our algorithm. Third, regarding the ossicles, the stapes (the third ossicle) sits approximately 1.5 to 2 mm superior to the round window. The ossicles are rarely endangered by traditional approaches, but the automatic approach must account for the position of the ossicles to ensure that there is an appropriate superior bound on the range of feasible trajectories (please see Figure 3a for a visual reference). The sigmoid sinus is another sensitive structure that can obstruct the natural path to the cochlea in a small percentage of individuals. Although it was visually confirmed that no trajectories in this study would have damaged this structure, in order to make our approach as safe as possible, in future studies the sigmoid sinus will be a sensitive structure included in the trajectory optimization.

This work suggests that, with the automatic determination of a safe and effective trajectory, percutaneous cochlear access may be a viable alternative to traditional wide mastoidectomies, but it also provides a means to identify, for a given level of error in drill positioning, those patients whose anatomy does not accommodate any safe linear channel. Thus this study highlights the benefits of error estimation to safely perform percutaneous cochlear implant surgery.

Based on the results from this study, automatic trajectory determination does appear to be feasible. This conjecture is further supported by initial in vitro and in vivo studies. The method in this paper was successfully used in drilling six cadaveric temporal bones in (4). In each case, effective access to the cochlea was achieved and the facial nerve was preserved. In two of the six cases, sacrifice of the chorda was expected and did indeed occur. The method has also been used in an in vivo validation study (3). In this study, a traditional mastoidectomy is performed, the patient-customized drill guide is attached, and a dummy drill bit is passed through the guide to determine the path that a drill would have followed, had it been used. This study was conducted on 18 ears, and it was determined that the drill would have achieved effective access to the cochlea and safely avoided all sensitive structures in every case.

In future work, we will continue clinical and cadaveric testing, and will also explore the feasibility of our approach for use with different kinds of electrodes. The results of our method become more attractive with a smaller electrode array diameter because it allows for a smaller drilling radius. Therefore, it would also be beneficial to this technology to explore the use of thinner arrays.