Abstract
We introduce an algorithm for learning patient-specific models from clinical data to predict outcomes. Patient-specific models are influenced by the particular history, symptoms, laboratory results, and other features of the patient case at hand, in contrast to the commonly used population-wide models that are constructed to perform well on average on all future cases. The patient-specific algorithm uses Markov blanket (MB) models, carries out Bayesian model averaging over a set of models to predict the outcome for the patient case at hand, and employs a patient-specific heuristic to locate a set of suitable models to average over. We evaluate the utility of using a local structure representation for the conditional probability distributions in the MB models that captures additional independence relations among the variables compared to the typically used representation that captures only the global structure among the variables. In addition, we compare the performance of Bayesian model averaging to that of model selection. The patient-specific algorithm and its variants were evaluated on two clinical datasets for two outcomes. Our results provide support that the performance of an algorithm for learning patient-specific models can be improved by using a local structure representation for MB models and by performing Bayesian model averaging.
Keywords: patient-specific, population-wide, Bayesian networks, Markov blanket, Bayesian model averaging, prediction, algorithm
I. INTRODUCTION
Critical activities in clinical care like risk assessment, diagnosis, and prognosis, entail making predictions in individuals under uncertainty [1, 2]. The better these predictions can be performed, the better the decisions and the ensuing outcomes are likely to be both for the individual and for society at large. Even modest improvements in predictive performance can have significant impact on healthcare in terms of patient care, outcomes and costs. For example, in [3] the authors examine conditions in which the improved prediction of pneumonia outcomes would be expected to reduce hospital admissions of pneumonia patients by one percent, without any expected decrease in the clinical quality of care. Just such a one-percent reduction is estimated to save approximately 90 million dollars (in 1994 dollars) in healthcare costs per year in the United States. Thus, finding ways to improve predictive performance of current modeling techniques is an important problem.
Many of the commonly used predictive algorithms, such as logistic regression, neural networks, and Bayesian networks, learn a single model from databases of patient cases, which is then applied to predict outcomes for any future patient case. We call such a model a population-wide model because it is intended to be applied to an entire population of future cases. Recent research has shown, however, that learning models that are specific to the particular features of a given patient case can improve predictive performance [4]. We call such a model a patient-specific model since it is specialized to the particular features of the patient case at hand, and is optimized to predict especially well for that case. Thus, a population-wide model is optimized to have good predictive performance on average on all future cases, while a patient-specific model is optimized to perform well on a specific patient case.
In this paper, we introduce and evaluate a patient-specific algorithm that learns patient-specific models to predict outcomes of interest in clinical datasets. Specifically, the algorithm learns Bayesian network models represented using local structures, carries out Bayesian model averaging over a set of models to predict the outcome of interest for the patient case at hand, and employs a patient-specific heuristic to locate a set of suitable models to average over. Bayesian network algorithms typically use a global representation to represent the model structure. The patient-specific algorithm uses a local representation (specifically, decision graphs) that provides a richer Bayesian network model space than the global representation. For a set of variables, there are many more Bayesian networks that can be constructed from them when represented using local structures than when represented using global structures; thus the space of local structures is richer than the space of global structures. As we discuss in detail, the richer model space of local structures represent relationships among variables that are sensitive to the values of those variables. Thus, the modeled relationships can be specific to the values of the variables for the current patient case at hand.
Many algorithms that learn predictive models from data, including those that learn Bayesian network models, perform model selection wherein a single good model is identified which is then applied to predict outcomes for any future patient case. However, given finite data, there is uncertainty in choosing one model to the exclusion of all others, and this can be especially problematic when the selected model is one of several distinct models that all summarize the data more or less equally well. One approach to dealing with the uncertainty in model selection is to perform model averaging wherein the prediction is obtained from a weighted average of the predictions of a set of models. The patient-specific algorithm performs Bayesian model averaging over a selected set of Bayesian network models to predict the variable of interest (target variable). In addition, the algorithm selects a set of suitable models to average over that are individualized to the patient case at hand by employing a patient-specific heuristic to direct the search. Specifically, the algorithm uses the features of the patient case at hand to inform the Bayesian network learning algorithm to selectively average over models that differ considerably in their predictions for the target variable of the case at hand. The differing predictions of the selected models are then combined to predict the target variable.
Our hypothesis is that the patient-specific algorithm benefits from learning Bayesian networks with local structure in addition to performing Bayesian model averaging over such structures when compared to learning only the global structure or performing only model selection. We have extensively studied and shown that Bayesian model averaging over standard Bayesian network models with global structure that are chosen using the patient-specific heuristic improves predictive performance [5]. Here, we show that using Bayesian network models using local structure has the ability to improve performance over using models with global structure when the number of available cases for learning is small. We evaluate the performance of the patient-specific algorithm on two clinical datasets to predict two outcomes of interest. In the next section, we describe these concepts in greater detail, and provide additional background for understanding the methods and evaluation sections that follow.
II. BACKGROUND
In this section, we introduce Bayesian networks and Markov blankets and describe a global structure representation and a local structure representation for them.
Bayesian Networks (BNs)
A Bayesian network (BN) model is a probabilistic model that combines a graphical representation (the BN structure) with quantitative information (the probability parameters of the BN) to represent the joint probability distribution over a set of random variables [6]. Specifically, a BN M representing the set of variables X consists of a pair (G, ΘG). G is a directed acyclic graph (DAG) that contains a node for every variable1 in X and an arc between every pair of nodes if the corresponding variables are directly probabilistically dependent. Conversely, the absence of an arc between a pair of nodes denotes probabilistic independence (often conditional) between the corresponding variables. ΘG represents the parameters of the model, which are probability distributions. A BN structure refers only to the graphical structure G, while a BN model refers to both the structure G and a corresponding set of parameters ΘG.
In a BN M, the immediate predecessors of a node Xi in X are called the parents of Xi, and the successors, both immediate and remote, of Xi in X are called its descendants. The immediate successors of Xi are called the children of Xi. For each node Xi, there is a probability distribution (that may be discrete or continuous) on that node given the state of its parents. The complete joint probability distribution over X, represented by the parameterization ΘG, can be factored into a product of probability distributions defined on each node in the network. This factorization is determined by the independences captured by the structure of the BN and is formalized by the BN Markov condition: A node (representing a variable) is independent of its non-descendants given just its parents. According to the Markov condition, the joint probability distribution on model variables X = (X1, X2, …, Xn) can be factored as follows:
| (1) |
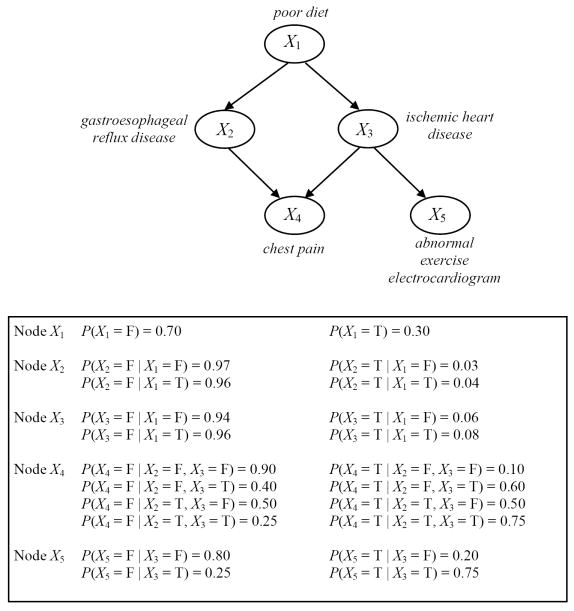
where Pai denotes the set of nodes that are the parents of Xi. If Xi has no parents, then the set Pai is empty and P(Xi ∣ Pai) is just P(Xi). An illustrative example of a BN is shown in Figure 1, where the top panel shows the graphical structure G and the bottom panel gives an example set of parameters ΘG for G.
Figure 1.
A simple hypothetical BN for a medical domain. All the nodes represent binary variables, taking values in the domain {T, F} where T stands for True and F for False. The graph at the top represents the BN structure. Associated with each variable (node) is a conditional probability table representing the probability of each variable’s value conditioned on its parent set. (Note that these probabilities are for illustration only; they are not intended to reflect the frequency of events in any actual patient population.)
Markov Blanket
The Markov blanket (MB) of a variable Xi, denoted by MB(Xi), defines a set of variables such that conditioned on MB(Xi), Xi is conditionally independent of all variables outside of MB(Xi) [6]. The minimal Markov blanket of a node Xi, which is sometimes called its Markov boundary, consists of the parents, the children, and the parents of the children (spouses) of Xi, as illustrated in Figure 2. As can be seen from the figure, the parents and children of Xi are directly connected to it and are hence in its MB. In addition, the spouses are included in the MB, because of the phenomenon of explaining away which refers to the observation that when a child node is instantiated its parents in general are statistically dependent. The MB of a node Xi is noteworthy because it identifies nodes that make Xi independent of all other nodes in the network. In particular, when interest centers on the distribution of a specific target node, as is the case in classification, the structure and parameters of only the MB of the target node need be learned. For this reason, the patient-specific methods, which are described below, search in the space of MBs of the target variable rather than in the space of BNs. An excellent overview of MB methods of classification and the discovery of MBs from data is provided in [7, 8].
Figure 2.
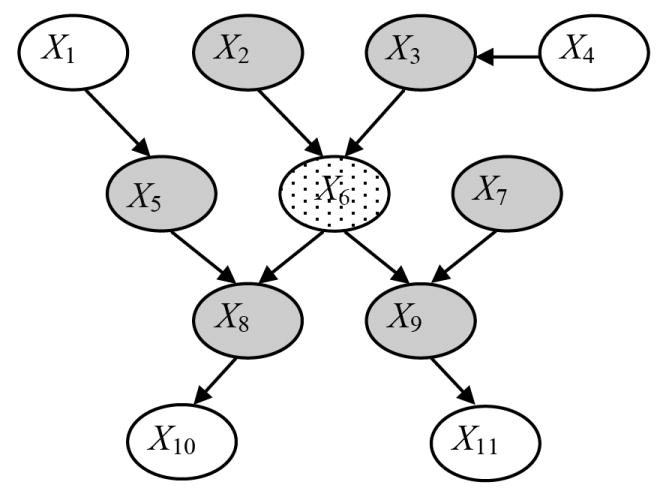
Example of a Markov blanket within a BN. The minimal Markov blanket of the node X6 (shown stippled) consists of the set of parents (X2 and X3), children (X8 and X9), and parents of the children (X5 and X7) of that node, as indicated by the shaded nodes. Nodes X1, X4, X10 and X11 are not in the minimal Markov blanket of X6.
Global and Local Structures
The DAG of a BN encodes statements of variable independence. Consider the following example. According to standard usage, a variable X is independent of Y given variable Z if P(x ∣ y, z) = P(x ∣ z) for all values x, y and z that the variables X, Y, Z can assume. In the standard BN, the graphical structure makes explicit independence relations of the form X ⊥ Y ∣ Z, which implies that P(X ∣ Y, Z) = P(X ∣ Z) for all values of the variables X, Y and Z. However, these are not the only independencies that may be present in a domain. For instance, consider value-specific independence relationships that hold for only particular assignments of values to certain nodes; these relationships cannot be entirely represented by a BN graphical structure. Value-specific independence relationships are of the form X ⊥ Y ∣ Z = z1, which implies that P(X ∣ Y, Z = z1) = P(X ∣ Z = z1) for all values of the variables X and Y when Z takes the particular value z1. For other values of Z, such as z2, it may be that X and Y are not conditionally independent, that is, P(X ∣ Y, Z = z2) ≠ P(X ∣ Z = z2). This type of independence relation is also known as context-specific independence [9]. The preceding example can be interpreted as X is independent of Y in the context of Z taking the value z1, but not the value z2. In general, these independent statements imply that in some contexts, defined by an assignment of specific values to the variables in the BN, specific independences hold [10].
We refer to BNs that do not explicitly represent context-specific structure as BNs with global structure, in contrast to BNs that explicitly capture context-specific structure, which we refer to as BNs with local structure. We first describe conditional probability tables, a typical representation used in BNs with global structure. We then describe one representation used for BNs with local structure, namely, decision graphs.
Associated with a node in a BN is a set of conditional probability distributions (CPDs) that in domains with discrete random variables are typically represented by a table. In this representation, P(Xi ∣ Pai) is a table that contains an entry for each joint instantiation of Xi and Pai. Each column (or row) in the table represents a single conditional probability distribution, P(Xi ∣ Pai = pai), corresponding to a particular instantiation of the variables in Pai to a set of values given by pai. Tabular CPDs are aptly called conditional probability tables (CPTs) and are commonly the representation used in discrete BNs. For example, the CPD for node X4 in the top panel in Figure 1 is represented by the CPT shown in the bottom panel in Figure 1 that contains eight parameters. CPTs provide a general representation for discrete nodes in that every possible discrete conditional probability distribution can be represented by a conditional probability table. The CPT representation has the disadvantage that in general the number of parameters of a node grows exponentially in the number of parents of the node. When parameters are estimated from data, this expansion of the CPT leads to poor estimates of the parameters since fewer data points contribute to the estimate of each parameter. Representations that capture structure and regularities within the CPDs provide additional domain knowledge about the interactions among the parents of a node and reduce the number of parameters needed to specify the CPDs. We now briefly describe representations used in BNs with local structure.
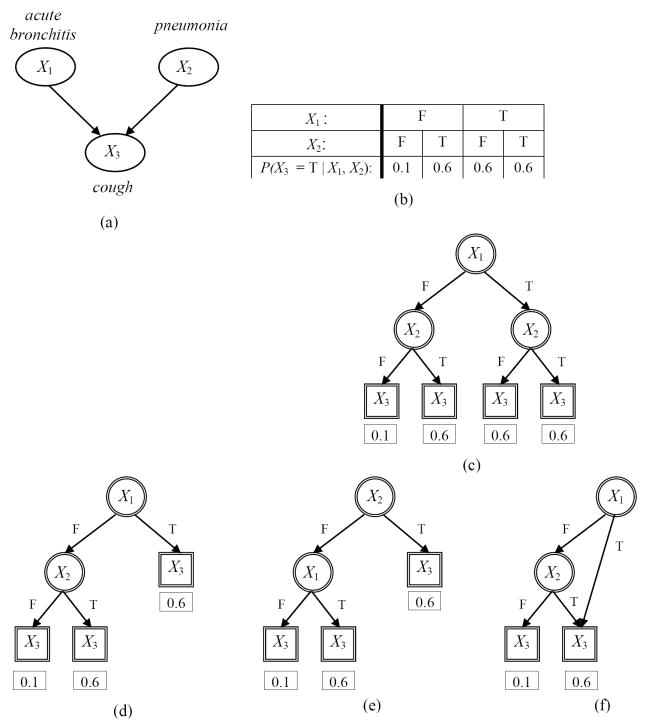
Several representations for local structure have been described for capturing context-specific independencies. Friedman and Goldszmidt describe a default table representation which is similar to a CPT except that it provides a default CPD for a subset of the parent states, and a decision tree representation, where a decision tree is used to represent the local structure for a BN node Xi [11]. A decision tree is a graph (not a BN graph) where the root node has no parents, and all other nodes have one parent. Nodes that have children and appear in the interior of the tree are called interior nodes, and terminal nodes are called leaf nodes. Figure 3 gives several examples of local structures represented by decision trees. A small BN with three nodes is shown in Figure 3 (a) and an example CPT for node X3 is given in Figure 3 (b). The CPT can be equivalently represented by a complete decision tree as shown in Figure 3 (c). Figure 3 (d) and (e) show alternate decision trees where each one captures one of the two context specific independence relations that is present but not both.
Figure 3.
Examples of CPD representations for a small hypothetical BN where all nodes represent binary variables taking values in the domain {T, F} where T stands for True and F for False. Several CPD representations for the BN node X3 (cough) in panel (a) are shown in subsequent panels. Panel (b) shows a CPT in a standard BN for the node X3 with four parameters (only the values for P(X3 = T ∣ X1, X2) are shown). The CPT can be equivalently represented by a complete decision tree as shown in panel (c). Panels (d) and (e) show alternate decision trees where each one captures one of the two context specific independence relations that is present but not both (see text for details). Panel (f) shows a decision graph that captures both the context specific independence relations (see text for details). Nodes of a BN are shown as ellipses with single lines while nodes of decision trees and decision graphs are shown as either circles with double lines (interior nodes) or as rectangles with double lines (leaf nodes). The values for P(X3 = T ∣ X1, X2) are shown under each leaf node.
Chickering and colleagues generalized the decision tree representation to decision graphs, which can capture a richer set of context-specific independence relations [12]. A decision graph differs from a decision tree in that a node may have multiple parents, rather than just one parent. A decision graph, thus, allows two or more distinct paths from the root node to terminate in the same leaf node. As an example, Figure 3 (f) shows a decision graph CPD representing the local structure of the node X3 in Figure 3 (a). In this example, the decision graph CPD is more compact than either the CPT or the several decision tree representations; it requires one fewer set of parameters than the decision tree CPDs (Figure 3 (d) and (e)) and two fewer sets of parameters than the CPT or the complete decision tree CPD (Figure 3 (c)). The decision graph is able to capture both context-specific independence relations given in the example, demonstrating that it is a more general representation than the decision tree
For a BN node Xi that is represented by a decision graph, all paths that lead to the same leaf node represent distinct parent states for which Xi has the same conditional distribution. The decision graph representation is more general than the decision tree representation, in that, any local structure that can be represented compactly as a tree can be represented as a graph, but the converse is not true. The patient-specific methods described later use the CPT representation for learning MBs with global structure and the decision graph representation for learning MBs with local structure.
III. PATIENT-SPECIFIC PREDICTION ALGORITHMS
We now describe the patient-specific Markov blanket algorithm that is intended to predict well a discrete target variable of interest, such as a patient outcome. The algorithm (1) uses Markov blanket models, (2) carries out Bayesian model averaging over a selected set of models to predict the outcome of interest for the patient case at hand, and (3) employs a patient-specific heuristic to locate a set of suitable models to average over.
Bayesian model averaging over all models has been shown to provide better predictive performance compared to that of any single model over a range of applications involving different model classes and types of data [4]. However, in almost all practical situations, averaging over all models to obtain the Bayes optimal estimate is computationally intractable. One approach, termed selective model averaging, approximates the Bayes optimal prediction by averaging over a subset of the possible models, and has been shown to improve predictive performance [4, 13, 14]. The patient-specific algorithm performs selective model averaging and uses a novel heuristic search to select the models over which averaging is done. The patient-specific characteristic of the algorithm arises from the observation that the search heuristic is sensitive to the features of the particular case at hand.
The model space employed by the algorithm is the space of Markov blankets of the target node, since this is sufficient for predicting the target variable. Two versions of the patient-specific algorithm are considered that differ in the representation employed for the conditional probability distributions. Both use model averaging (MA). The patient-specific Markov blanket global structure (PSMBg-MA) algorithm learns MBs with CPTs, while the patient-specific Markov blanket local structure (PSMBl-MA) algorithm learns MBs with decision graph CPDs. This implies that the PSMBl-MA algorithm employs a richer space of models than the PSMBg-MA algorithm.
Bayesian Model Averaging and Selection
We first give a detailed description of PSMBg-MA and PSMBl-MA that are two versions of the patient-specific algorithms that use Bayesian model averaging. Later, we briefly describe two additional versions of the patient-specific algorithms that use Bayesian model selection.
The objective of the patient-specific algorithms is to derive the posterior distribution P(Zt ∣ xt, D) for the target variable Zt given the values of the other variables Xt = xt for the case at hand and the training data D. For example, the patient-specific algorithms might derive for a patient t who is admitted to a hospital with potential sepsis, the posterior distribution of the target variable Zt of mortality within 90 days, from information xt known about the patient at the time of admission and from a database D of previous patients who were admitted for sepsis. The ideal computation of the posterior distribution P(Zt ∣ xt, D) by Bayesian model averaging is as follows:
| (2) |
where the sum is taken over all MB structures G in the model space M. The first term on the right hand side, P(Zt ∣ xt, G, D), is the probability P(Zt ∣ xt) computed with a MB that has structure G with parameters that are estimated from training data D using Equation 3 below. The second term, P(G ∣ D), is the posterior probability of the MB structure G given D, which is also known as the Bayesian score for structure G. In essence, Equation 2 states that a conditional probability of interest P(Zt ∣ xt) is derived by taking a weighted average of that probability over all MB structures, where the weight associated with a MB structure is the probability of that MB structure given the data. In general, P(Z t ∣ xt) will have different values for the different sets of MB structures over which the averaging is carried out.
Inference in MB structure
Computing P(Zt ∣ xt, G, D) in Equation 2 involves performing inference in the MB with a specified structure G. First, the parameters associated with MB structure G are estimated using Bayesian parameters as given by the following expression [15, 16]:
| (3) |
where (1) Nijk is the number of cases in dataset D in which Xi = k and the parents of Xi have the state denoted by j, (2) Nij = Σk Nijk, (3) αijk is a parameter prior that can be interpreted as belief equivalent to having previously (prior to obtaining D) seen αijk cases in which Xi = k and the parents of Xi have the state denoted by j, and (4) αij = Σk αijk. For the patient-specific algorithms in this paper, we assume that αijk is set to 1 for all i, j, and k, which represents a simple non-informative parameter prior [15]. Next, the parameterized MB model is used to compute the distribution over the target variable Zt of the case at hand given the values xt of the remaining variables in the MB by applying standard BN inference [17].
Posterior of MB structure
The second term P(G ∣ D) in Equation 2 is derived by the application of Bayes rule:
| (4) |
Since the denominator P(D) does not vary with the structure G, it simply acts as a normalizing factor that does not distinguish between different structures. Dropping the denominator gives the following Bayesian score:
| (5) |
The second term on the right in Equation 5 is the prior over structures, while the first term is the marginal likelihood which measures the goodness of fit of the given structure to the data. The marginal likelihood is computed as follows:
| (6) |
where P(D ∣ θG,G) is the likelihood of the data given the MB (G, θG) and P(θG ∣ G) is the specified prior distribution over the possible parameter values for the network structure G. Intuitively, the marginal likelihood measures the goodness of fit of the structure, as averaged over all possible values of its parameters. We note that the marginal likelihood is distinct from the maximum likelihood, although both represent a likelihood function of the data given a model structure. The maximum likelihood is the maximum value of this function over all parameters while the marginal likelihood is the integrated (or the average) value of this function, with the integration being carried out with respect to the prior P(θG ∣ G).
Marginal Likelihood of MB structure
We now provide closed-form solutions for computing the marginal likelihood as given by Equation 6 for MBs with global structure represented by CPTs and for MBs with local structure represented by decision graphs. For a MB with CPTs, the marginal likelihood P(D ∣ G), can be evaluated analytically given the following assumptions: (1) the variables are discrete and the data D are a multinomial random sample with no missing values; (2) global parameter independence holds, that is, the parameters associated with each variable given its parents are independent of the parameters of each other variable given its parents; (3) local parameter independence holds, that is, the parameters representing the distribution of variable Xi given a state of its parents (e.g., all such parents having the state “True”) are independent of the parameters of Xi for each other state of its parents (e.g., all parents having the state “False”); and (4) the parameters’ prior distributions are represented using a Dirichlet distribution [18]. Given these assumptions, the closed form solution for P(D ∣ G) is given as follows [15, 16]:
| (7) |
where Γ denotes the Gamma function,2 n is the number of variables in G, qi is the number of joint states of the parents of variable Xi that occur in D, and ri is the number of states of Xi that occur in D. Also, as described above, Nijk is the number of instances in the data where node i has value k and the parents of i have the state denoted by j, and Nij = Σk Nijk. In addition, as previously mentioned, αij = Σk αijk.
For a MB with local structure represented by decision graphs, the graphical structure consists of the global structure G and a set of local structures, where DGi is the local decision graph structure for node Xi in G, and the complete structure specification is given by {G, DG1, …, DGi, …, DGn}. The marginal likelihood for a MB with local structure is derived in an analogous fashion to Equation 7 for the MB with global structure:
| (8) |
where ∣Li∣ is the cardinality of the set of leaves in the decision graph DGi of Xi in dataset D, Nilk is the number of cases in D that have Xi = k and have parent states of Xi that correspond to one of the paths in the decision graph leading to the leaf node l, and Nil = Σk Nilk. The key difference between Equation 7 and Equation 8 is in the middle product, which in Equation 7 runs over all the columns in the CPT, while in Equation 8 it runs over all the leaf nodes of the decision graph of Xi.
Prior of MB structure
The term P(G) in Equation 5 is the structure prior, which represents a prior belief that the data was generated by a distribution that is consistent with MB structure G in predicting node Z. For the PSMBg-MA algorithm, we assume a uniform prior belief over all G. Let KG denote the number of possible MBs of Z. Thus, for any given MB, P(G) = 1 / KG. Therefore, for the PSMBg-MA algorithm, Equation 5 becomes:
| (9) |
For the PSMBl-MA algorithm, a two-level hierarchical structure prior is used, corresponding to the global and the local structure being considered. As mentioned previously, the complete structure specification of a MB with local structure is given by {G, DG1, …, DGi, …, DGn}, where G is the global MB structure and DGi is the local decision graph structure for node Xi in G. As with PSMBg-MA, in PSMBl-MA we assume a uniform prior belief over all MBs of Z. For each such MB G, we consider all possible decision graph structures consistent with G. Thus, the global component of the PSMBl-MA structure prior is 1 / KG. The local component is derived as follows. The number of possible decision graph structures is the same as the number of ways in which the values of the nodes in G can be partitioned into nonempty sets. The number of ways in which k elements can be partitioned into nonempty subsets is called a Bell number and is denoted by B(k) [19]; B(k) is efficiently computable. The prior for a local structure for node Xi in G is therefore given as 1 / B(∣Pai∣), where ∣Pai∣ is the number of joint parent states of Xi regardless of whether these joint parent states are realized in D. For example, if Xi has three binary variables, then ∣Pai∣ = 8. Overall, the prior for structure {G, DG1, …, DGi, …, DGn} is then taken to be the following:
| (10) |
This structure prior strongly biases the PSMBl-MA algorithm to prefer simpler local structures over more complex ones; such a prior tends to prevent local structures from overfitting the data. Combining the above results, the Bayesian score for the PSMBl-MA algorithm is as follows:
| (11) |
In summary, given a MB structure, the two terms on the right hand side in Equation 2 can now be computed.3 If it is tractable to enumerate all structures in the model space, then the target distribution P(Zt ∣ xt, D) can be computed exactly using Equation 2. However, this is usually not possible; an alternative is to perform selective model averaging, which we describe next.
Selective Bayesian Model Averaging
Summing over the very large number of MBs in Equation 2 is usually intractable; hence Equation 2 is approximated with selective model averaging, and heuristic search (described in the next section) is used to sample the model space. For a set R of MB structures (that are global MB structures for the PSMBg-MA algorithm and local MB structures for the PSMBl-MA algorithm) that have been chosen from the model space by heuristic search, selective model averaging estimates P(Zt ∣ xt, D) as:
| (12) |
From Equations 4 and 5, it can be seen that:
| (13) |
Substituting Equation 13 into Equation 12, we obtain:
| (14) |
where, score(G, D) is given by Equations 9 and 10 for PSMBg-MA and PSMBl-MA respectively. The PSMB algorithms perform selective model averaging and seek to locate a good set of models R over which the averaging is carried out by performing patient-specific search, as described next.
Patient-Specific Search
Both the PSMBg-MA and the PSMBl-MA employ a two-phase search. We first describe the two-phase search performed by the PSMBg-MA algorithm to sample the space of MB structures, and then indicate how the PSMBl-MA differs from it. The first phase ignores the evidence xt from the case at hand, while searching for MB structures that best fit the training data. The second phase continues to add to the set of MB structures obtained from the first phase, but now searches for MB structures that have the greatest impact on the prediction of Zt for the case at hand. We now describe in greater detail the two phases of the search.
The first phase uses greedy hill-climbing search and adds to a set R the best model discovered at each iteration of the search. At each iteration of the search, successor models are generated from the current best model in R; the best of those successor models is added to R only if this model is better than current best model in R; the remaining successor models are discarded. Successor models are generated from a given MB model by the application of the following operators: (1) add an arc between two nodes if one does not exist, (2) delete an existing arc, and (3) reverse an existing arc, with the constraint that an operation is allowed only if it generates a legal MB structure. No backtracking is performed and the first phase search terminates in a local maximum. Since the MB structures identified during the first phase are determined only by the training data and not by the patient case at hand, this phase is not patient-specific.
The second phase uses best-first search and adds the best model discovered at each iteration of the search to the set R. Unlike greedy hill-climbing search, best-first search contains models that have not been expanded (i.e., whose successors have not be generated) in a priority queue. Since, the number of successor models that are generated can be quite large, the priority queue Q is limited to a capacity of at most w models. The queue allows the algorithm to keep in memory a limited number of best scoring models found so far, and facilitates limited backtracking to escape local maxima.
The second phase searches for MB models that change the current model-averaged estimate of P(Zt ∣ xt, D) the most. The goal is to find viable competing MB models for making this posterior probability prediction. When no competitive MB models can be found, the prediction is assumed to be stable. Each candidate MB model G* in Q is evaluated based on how much it changes the current estimate of P(Zt ∣ xt, D) that is obtained by model averaging over the MB models in R. More change is better. Specifically, we use the Kullback-Leibler (KL) divergence between the two estimates of P(Zt ∣ xt, D), one estimate computed with G* and the other computed without G*, in the set of models over which the model averaging is carried out. The KL divergence, or relative entropy, is a quantity that measures the distance between two probability distributions [20]. Thus, the score for a candidate model G* is given by:
| (15) |
where
By Equation 13 the term P(G ∣ D) that appears in p(x) and q(x) can be substituted with the term score(G, D). Using this substitution, the score for a candidate model G* for PSMBg-MA is:
| (16) |
where
where scorePSMBg-MA is given by Equation 9. In an analogous fashion, the score for a candidate model G* for PSMBl-MA is:
| (17) |
where
where scorePSMBl-MA is given by Equation 11.
At the beginning of the second phase, R contains MB structures that were selected in the first phase. Successors to these models are generated, scored using Equation 15 and added to the priority queue Q. In each iteration, the MB structure in Q with the highest score is removed and added to R and, in addition, its successors are scored and added to Q. The second phase terminates when no MB structure in Q has a score higher than some small value ε or when a period of time t has elapsed, where ε and t are specified by the user. In the second phase the patient case at hand determines the selection of MB structures in conjunction with the training data, and thus this phase is patient-specific. The pseudocode for the PSMBg-MA algorithm is given in Figure 4 (a).
Figure 4.
(a) High level pseudocode for the two-phase search procedure used by the PSMBg-MA algorithm. (b) High level pseudocode for the two-phase outer search procedure and the inner search procedure used by the PSMBl-MA algorithm. The PSMBl-MA algorithm differs from the PSMBg-MA algorithm in that invokes ProcedureDGSearch for the inner search to identify a local decision graph for each node modified in the MB structure by the outer search procedure. Note that MBNode is a node in the MB structure while DGNode is a node in a decision graph.
The PSMBl-MA algorithm differs from the PSMBg-MA algorithm in that it supplements each phase in the two-phase search procedure used by the former with an outer search procedure and an inner search procedure. The outer search procedure generates MB structures as in the PSMBg-MA algorithm, and for each such MB structure, the inner search procedure identifies a local decision graph for each node in the MB structure. For a given node, the selected local decision graph is the one with the best PSMBl-MA score (computed using Equation 11) as found by greedy hill-climbing search. Given a decision graph, the operators used for generating successor decision graphs are: (1) the complete split operator that replaces a leaf node with an internal node and a set of leaf nodes corresponding to the states of the parent variable which is used for the split, (2) the binary split operator that is similar to the complete split operator, except that only two leaf nodes are introduced, and (3) the merge operator that merges two leaf nodes into a single leaf node. Further details of the operators are given in [12] which first described the use of decision graphs for representing local structure. The pseudocode for the PSMBl-MA algorithm is given in Figure 4 (b).
We now briefly describe two additional versions of the patient-specific algorithms that use Bayesian model selection. Model selection is the process of using data to select one model from a set of models under consideration and can be done using either non-Bayesian or Bayesian approaches. Non-Bayesian methods of model selection include choosing among competing models by maximizing the likelihood, by maximizing a penalized version of the likelihood or by maximizing some measure of interest (e.g., accuracy) using cross-validation. In Bayesian model selection, the posterior probability of each model under consideration is computed and the model with the highest posterior probability is chosen. The patient-specific Markov blanket global structure algorithm that performs model selection (PSMBg-MS) conducts the same search as PSMBg-MA but predicts the outcome of the patient case at hand using the model with the highest score (where the score is given by Equation 9). In an analogous fashion, the patient-specific Markov blanket local structure algorithm that performs model selection (PSMBl-MS) conducts the same search as PSMBl-MA but predicts the outcome of the patient case at hand using the model with the highest score (where the score is given by Equation 11).
IV. EXPERIMENTAL METHODOLOGY
In this section we describe the two clinical datasets on which the patient-specific algorithms were evaluated, the preprocessing of the datasets, the performance measures used in the evaluation, and the experimental settings used for the algorithms. The two clinical datasets included one on sepsis and another on heart failure.
A. Sepsis Dataset
Sepsis is a syndrome of systemic inflammation in response to infection that leads to complex physiologic and metabolic changes and can result in multi-system organ dysfunction and failure [21]. Sepsis is a major cause of death with a mortality rate of 30 percent in the United States [22]. However, the risk factors, causes and prognosis of sepsis are not fully understood.
The data in the sepsis dataset were collected in the GenIMS (Genetic and Inflammatory Markers of Sepsis) project coordinated by the Department of Critical Care Medicine in the University of Pittsburgh School of Medicine. GenIMS was a large, multicenter, observational cohort study of subjects with community acquired pneumonia (but not necessarily with sepsis) presenting to the emergency departments of 28 hospitals in western Pennsylvania, Connecticut, Michigan, and Tennessee in the United States. The data used in our experiments consisted of 1,673 patients who were eventually admitted to a hospital and 21 variables as predictors that included three demographic variables, six clinical variables, two inflammatory markers and 10 genetic variables (see Table 1). These variables were selected by the GenIMS project investigators to investigate the role of the macrophage migration inhibitory factor (MIF) gene in the susceptibility, severity, and outcome of community acquired pneumonia. The clinical variables are summary variables obtained from data collected at the time of admission and during the first three days of hospital stay. Two binary outcome variables, which were the focus of investigation in the original study, were selected for prediction: (1) death within 90 days of inclusion in the study (sepsis-d in Table 2), and (2) the development of severe sepsis during the hospitalization (sepsis-s in Table 2). Of the 1,673 patients 187 (11.2%) patients died within 90 days and 466 (27.8%) patients developed severe sepsis during the hospitalization.
Table 1.
List of the 21 predictor variables in the sepsis dataset. PSI is the Pneumonia Severity Index which is a prediction rule that classifies patients who have pneumonia into five strata of increased risk for short-term mortality on the basis of 20 clinical variables that are routinely available at the time of admission. The Charlson score assesses comorbidity by accounting for the presence or absence of nineteen different medical conditions at the time of admission. APACHE III is the Acute Physiologic and Chronic Health Evaluation score (introduced in 1991) that assesses disease severity from 27 physiological and clinical parameters.
| Category | Predictors |
|---|---|
| Demographic | Age, gender, and race |
| Clinical | PSI at the time of admission, PSI at the end of first day of stay, Charlson score, APACHE III score on first day of stay, APACHE III score on second day of stay, and APACHE III score on third day of stay, |
| Inflammatory markers | Interleukin 6 and Interleukin 10 |
| Genetic markers | Ten genetic polymorphisms for the macrophage migration inhibitory factor, the tumor necrosis factor A, the interleukin-6, the interleukin-10, and the heme oxygenase genes. |
Table 2.
Brief descriptions of the clinical datasets. The # Predictors column states the number of continuous (cnt) and discrete (dsc) predictors, as well as the total number of predictor variables (excluding the outcome variable). The outcome variables are all binary. The training set and the test set give the number of cases in each set respectively and the percentage of the cases with the positive outcome variable are given in parentheses. The total set gives the sum of the cases in the training and the test sets.
| Dataset | # Predictors (cnt + dsc = total) | Outcome variable | Training set | Test set | Total set |
|---|---|---|---|---|---|
| sepsis-d | 7 + 14 = 21 | death | 1,115 (11.1%) | 558 (11.4%) | 1,673 |
| sepsis-s | 7 + 14 = 21 | severe sepsis | 1,115 (27.4%) | 558 (28.8%) | 1,673 |
| heart failure-d | 11 + 10 = 21 | death | 7,453 (4.3%) | 3,725 (4.4%) | 11,178 |
| heart failure-c | 11 + 10 = 21 | complications incld. death | 7,453 (7.1%) | 3,725 (7.2%) | 11,178 |
B. Heart Failure Dataset
Heart failure is an acute and chronic condition that affects 5 million people in the U.S. leading to about one million hospital admissions each year with a primary discharge diagnosis of heart failure and another approximately two million with a secondary discharge diagnosis of this condition [23, 24]. Accurate evaluation of heart failure patients in the Emergency Department followed by appropriate treatment (including the decision whether to admit a patient to the hospital or not) is an important clinical problem.
All hospitals in Pennsylvania are required by law to record more than 300 key clinical findings for each hospitalized patient, including demographic, historical, physical examination, laboratory, electrocardiographic, and imaging data that are collected during the course of care. These data are recorded using standardized data collection instruments and documentation. The heart failure data was obtained from the data collected by 192 general acute care hospitals in Pennsylvania for the year 1999 and consist of heart-failure patients who were hospitalized from the Emergency Departments. The data used in our experiments consisted of 11,178 cases and 21 variables as predictors that included demographic, clinical, laboratory, electrocardiographic and radiographic findings (see Table 3). These variables were identified as prognostic factors in a study that developed a prediction rule to detect low-risk patients with heart failure [25]. Two binary outcome variables were selected for prediction: (1) the occurrence of death from any cause during the hospitalization (heart failure-d in Table 2), and (2) the development of one or more serious medical complications (including death) during the hospitalization (heart failure-c in Table 2). Of the 11,178 patients 484 (6.5%) patients died during the hospitalization and 797 (10.7%) patients developed one or more serious medical complications during the hospitalization.
Table 3.
List of the 21 predictor variables in the heart failure dataset.
| Category | Predictors |
|---|---|
| Demographic | Gender |
| Historical | Coronary artery disease, angina, percutaneous transluminal coronary angiography, diabetes, and lung disease |
| Vital signs | Systolic blood pressure, pulse, respiratory rate, and temperature |
| Laboratory | Blood urea nitrogen, sodium, potassium, creatinine, glucose, white blood cell count, and arterial pH |
| Electrocardiographic | Acute myocardial infarction and acute myocardial ischemia |
| Radiographic | Pulmonary congestion and pleural effusion |
C. Preprocessing
All continuous variables were discretized using the method described by Fayyad and Irani [26]. This is an entropy-based method that analyzes the values of a continuous variable and creates thresholds such that the resulting intervals have high information gain in predicting the outcome variable. The discretization thresholds were determined only from the training sets and then applied to both the training and test sets. Missing values were imputed using an iterative non-parametric imputation algorithm described by Caruana [27]. This method has previously been applied to fill in missing predictor values for a clinical dataset with good results [28].
D. Algorithms
For both the PSMBg-MA and PSMBl-MA algorithms, the MB structures were selected through a two-phase search. The first phase terminated after 20 MB models had accumulated and the second phase terminated after 20 more had been accumulated. The prediction for the outcome variable of the test case was obtained by averaging the predictions of the 40 models. The PSMBg-MS and PSMBl-MS algorithms accumulated the same 40 models in the two search phases as the respective model averaged algorithms and identified the model with the highest model score as given by Equations 9 and 11 respectively. The prediction for the outcome variable of the test case was obtained from the single highest scoring model. Salient features of the four algorithms are given in Table 4. All four algorithms were implemented in Java.
Table 4.
Four versions of the patient-specific algorithm with a synopsis of each. All four use a first phase of search that is non-patient-specific and a second phase that is patient-specific.
| Acronym | Algorithm | Global vs Local Model | Model Averaging | Prediction |
|---|---|---|---|---|
| PSMBg-MA | Patient-Specific Markov Blanket (global) – Model Averaged | global | yes | Based on model averaging over models selected in both phases |
| PSMBg-MS | Patient-Specific Markov Blanket (global) – Model Selection | global | no | Based on the highest scoring model from models selected by PSMBg-MA |
| PSMBl-MA | Patient-Specific Markov Blanket (local) – Model Averaged | local | yes | Based on model averaging over models selected in both phases |
| PSMBl-MS | Patient-Specific Markov Blanket (local) – Model Selection | local | no | Based on the highest scoring model from models selected by PSMBl-MA |
In addition to the patient-specific algorithms, we applied logistic regression as an example of a population-wide algorithm. In the experiments we used the implementation of logistic regression in the WEKA software package (version 3.4.3) with its default settings [29].
E. Experiments
We performed several experiments to evaluate the performance of the patient-specific algorithms. As a measure of learning efficiency, we are particularly interested in evaluating how different amounts of training data affect the algorithms’ predictive performance. We first describe the experiments performed with the sepsis dataset which has a total of 1,673 cases. The original sepsis dataset was first randomly split into a training set approximately consisting of two-thirds of the data and a test set consisting of the remaining one-third, such that the proportions of the states of both outcome variables were approximately the same in the two sets (see Table 2). Thus, the sepsis dataset was split into a training dataset of 1115 cases (with 11.1% 90-day mortality and 27.4% rate of development of severe sepsis during hospitalization respectively) and a test dataset of 558 cases (with 11.4% 90-day mortality and 28.8% rate of development of severe sepsis during hospitalization respectively). Then, the complete training set was used to construct training subsets of sizes of 64, 128, 256, 512, and 1024. Each larger training dataset contained all the cases included in the preceding smaller training datasets. The cases in the test dataset were used only for evaluation and were not used for learning the models. We applied the five algorithms described in the previous section (PSMBl-MA, PSMBl-MS, PSMBg-MA PSMBg-MS and logistic regression) to each of the training sets to learn models and evaluated the models on the test dataset. The five evaluation measures that we used are described in the next section.
We performed similar experiments on the heart failure dataset which has a total of 11,178 cases and is about 8 times larger than the sepsis dataset. The heart failure dataset was randomly split into a training dataset of 7453 cases (wherein 90-day mortality was 4.3% and the rate of serious medical complications during hospitalization was 7.1% respectively) and a test dataset of 3725 cases (wherein 90-day mortality was 4.4% and the rate of serious medical complications during hospitalization was 7.2% respectively). The complete training set was used to construct training subsets of sizes of 64, 128, 256, 512, and 1024. The five algorithms were applied to each of the training sets to learn models that were evaluated on the test dataset using the five evaluation measures described next.
F. Performance Measures
The performance of the algorithms was evaluated on two discrimination measures and three probability measures. For discrimination measures we used the misclassification error and the area under the ROC curve (AUC). These discrimination measures evaluate how well an algorithm differentiates among the various classes, by which we mean the values of the outcome variable. For probability measures we used the mean squared error, logarithmic loss, and calibration. For calibration, we used a score called CAL that was developed by Caraua and is based on reliability diagrams [30]. The probability measures are uniquely minimized (in expectation) when the predicted value for the target of each instance coincides with the actual fraction of that case taking that target value in the test set. A brief summary of the performance measures is given in Table 5.
Table 5.
Brief description of the performance measures used in evaluation of the performance of the algorithms. For each measure a score closer to 0 indicates better performance.
| Performance measure | Range | Best score |
|---|---|---|
| Misclassification error | [0, 1] | 0 |
| 1 - area under the ROC curve (1 - AUC) | [0, 1] | 0 |
| Squared error | [0, 1] | 0 |
| Logarithmic loss | [0, ∞) | 0 |
| Calibration score (CAL) | [0, 1] | 0 |
We used the Wilcoxon paired-samples signed-rank test for comparing the performance of the algorithms. This test is a non-parametric procedure used to test whether there is sufficient evidence that the median of two probability distributions differ in location [31]. In evaluating algorithms, it can be used to test whether two algorithms differ significantly in performance on a specified measure.
V. RESULTS
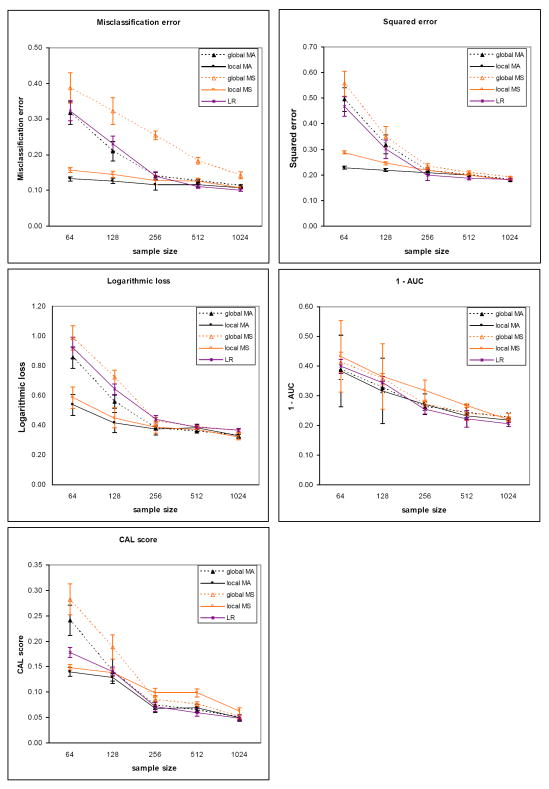
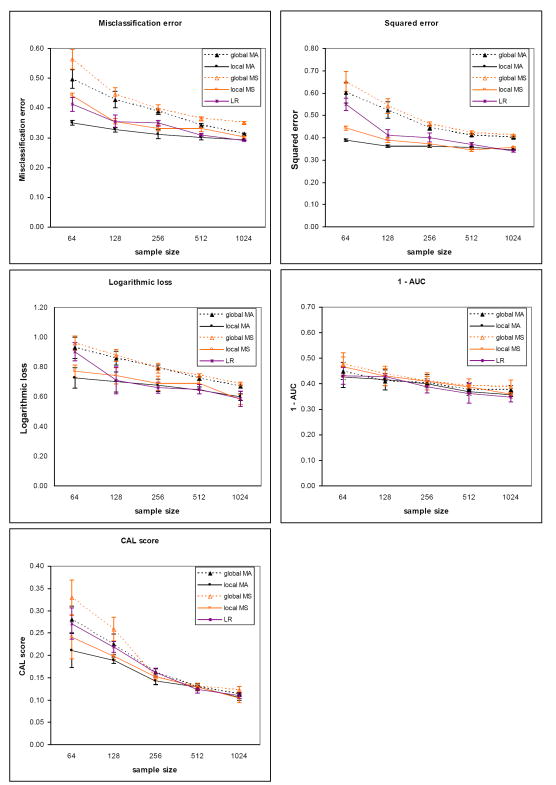
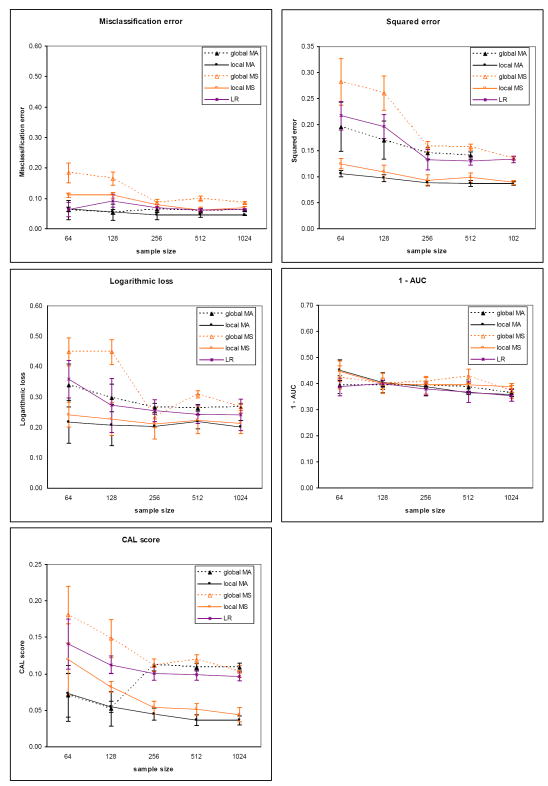
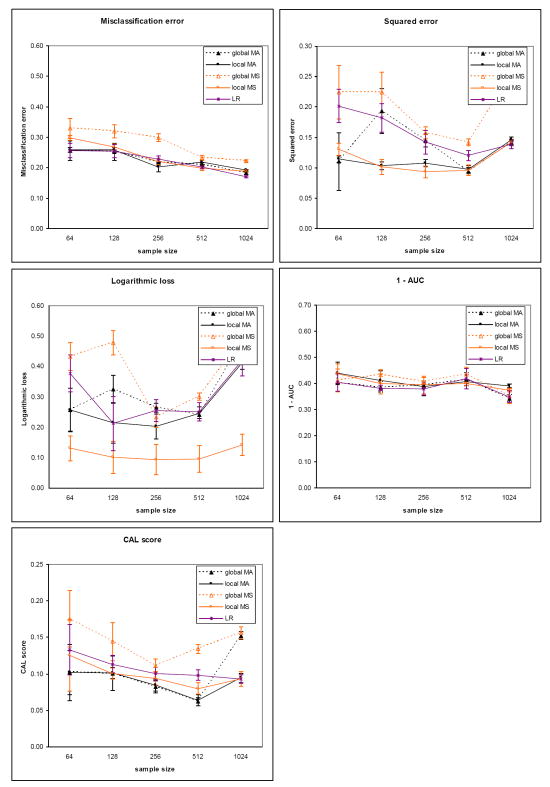
The results for the five evaluation measures on the sepsis dataset for the two outcomes are plotted in Figure 5 (death) and Figure 6 (severe sepsis). The corresponding results on the heart failure dataset for the two outcomes are plotted in Figure 7 (death) and Figure 8 (complications). Each plot contains results comparing model averaging with global structure (global MA) obtained from PSMBg-MA, model averaging with local structure (local MA) obtained from PSMBl-MA, the single best MB model with global structure (global MS) obtained from PSMBg-MS, the single best MB model with local structure (local MS) obtained from PSMBl-MS, and logistic regression (LR). Five separate plots are given for each dataset; one plot each for the misclassification error, the 1 - AUC, the squared error, the logarithmic loss, and the CAL score respectively. In all plots, smaller scores indicate better performance. The tables in the appendix (Tables A1 to A4) give the mean evaluation measures of the different algorithms for the training dataset sizes of 64, 128, 512, and 1024.
Figure 5.
Sepsis dataset results for the outcome death. Plots show the mean classification error, mean squared error, mean logarithmic loss, mean 1-AUC and mean CAL score of the patient-specific model averaging algorithms vs. model selection versions of these algorithms. For all performance measures lower is better. The sizes of the training dataset vary from 64 to 1024 patient cases. The plots in the solid lines are for the PSMBl-MA (local MA) and the PSMBl-MS (local MS) algorithms; plots in the broken lines are for the PSMBg-MA (global MA) and the PSMBg-MA (global MS) algorithms; and plots in the dotted lines are for logistic regression (LR). The error bars represent one standard deviation.
Figure 6.
Sepsis dataset results for the outcome severe sepsis. See the legend of Figure 5 for details.
Figure 7.
Heart failure dataset results for the outcome death. The sizes of the training dataset vary from 64 to 4096 patient cases. See the legend caption of Figure 5 for details.
Figure 8.
Heart failure dataset results for the outcome complications, which includes death. The sizes of the training dataset vary from 64 to 4096 patient cases. See the legend caption of Figure 5 for details.
Tables 6 and 7 report results from pair-wise comparisons of the performance of the PSMBl-MA algorithm versus the PSMBg-MA, PSMBl-MS, and LR algorithms. We did not compare PSMBl-MA with PSMBg-MS since in previous work we observed that PSMBg-MA outperformed PSMBg-MS on a large number of datasets [5]. For each pair-wise comparison, the Wilcoxon paired-samples signed-rank test was applied to results obtained from a set of 8 training datasets: the sepsis dataset with two outcomes at two sample sizes and the heart failure dataset with two outcomes at two sample sizes. Table 6 gives the results at the smaller sample sizes of 64 and 128 cases, while Table 7 gives the results at larger sample sizes of 512 and 1024. Table 6 shows that at the smaller training datasets of 64 and 128, PSMBl-MA performs better than all the other methods listed there on all measures, although statistically significant so for only a subset of them, as described next. PSMBl-MA when compared to PSMBl-MS performed statistically significantly better at the 0.05 significance level on four of the five measures, namely, misclassification error, logarithmic loss, squared error and the CAL score. When compared to PSMBg-MA, PSMBl-MA performed statistically significantly better on two of the measures, namely, logarithmic loss and squared error. When compared to LR, PSMBl-MA performed statistically significantly better on three of the measures, namely, logarithmic loss, squared error, and the CAL score. Table 7 shows that at larger training datasets of 512 and 1024 there is no statistically significant difference in the performance of the algorithms on any of the measures.
Table 6.
Wilcoxon paired-samples signed-rank test comparing the performance of PSMBl-MA with other algorithms at small training sample sizes of 64 and 128. PSMBl-MS denotes the single best MB model with local structure and LR is the logistic regression model. For each performance measure the number on top is the Z statistic and the number at the bottom is the corresponding p-value. The Z statistic is negative when PSMBl-MA has a lower (i.e., better) score on a performance measure than the competing algorithm. Thus, a negative Z statistic indicates better performance by PSMBl-MA. Underlined results indicate the two-tailed p-values of 0.05 or smaller, indicating that PSMBl-MA performed statistically significantly better at that level.
| Performance measure | PSMBl-MS | PSMBg-MA | LR |
|---|---|---|---|
| Misclassification error | -2.521 | -1.120 | -1.680 |
| 0.012 | 0.263 | 0.093 | |
| 1 - AUC | -1.120 | -1.120 | -0.420 |
| 0.263 | 0.263 | 0.674 | |
| Logarithmic loss | -2.521 | -2.380 | -2.380 |
| 0.012 | 0.017 | 0.017 | |
| Squared error | -2.380 | -2.380 | -2.380 |
| 0.017 | 0.017 | 0.017 | |
| CAL score | -2.380 | -1.120 | -2.521 |
| 0.017 | 0.263 | 0.012 | |
Table 7.
Wilcoxon paired-samples signed-rank test comparing the performance of PSMBl-MA with other algorithms at larger training sample sizes of 512 and 1024. See the caption of Table 6 for details.
| Performance measure | PSMBl-MS | PSMBg-MA | LR |
|---|---|---|---|
| Misclassification error | -1.400 | -1.680 | -0.140 |
| 0.161 | 0.093 | 0.889 | |
| 1 – AUC | -1.540 | -1.400 | -1.260 |
| 0.123 | 0.161 | 0.208 | |
| Logarithmic loss | -0.560 | -1.680 | -1.820 |
| 0.575 | 0.093 | 0.069 | |
| Squared error | -0.421 | -0.840 | -1.260 |
| 0.674 | 0.401 | 0.208 | |
| CAL score | -1.820 | -1.402 | -0.840 |
| 0.069 | 0.161 | 0.401 | |
Model Averaging versus Model Selection
Overall, there is a general trend of better performance on all the measures except the AUC by the PSMBl-MA algorithm that employs model averaging when compared to the PSMBl-MS algorithm that employs model selection. This difference in performance is statistically significant at the 0.05 level at the smaller training set sizes on all measures except the AUC (see Table 6) and becomes less marked and not statistically significant at the larger training set sizes (see Table 7). The results indicate that model averaging is particularly helpful when the number of training cases is smaller.
Global Structure versus Local Structure
On comparing models with global structure with those with local structure, there is a trend of better performance on logarithmic loss and squared error by the PSMBl-MA over the PSMBg-MA. At the smaller training set sizes this difference in performance is statistically significant at the 0.05 level on these two measures (see Table 6), and at larger training set sizes the difference in performance in less marked (see Table 7) and not statistically significant. This trend in performance indicates that searching the richer space of local structures is able to improve on two of the measures when the number of training cases is smaller.
Patient-Specific versus Population-Wide
The PSMBl-MA performs significantly better at the 0.05 significance level at the smaller sample sizes than the population-wide LR on the three of the performance measures (see Table 6), while on larger training set sizes the difference in performance in less marked and is not statistically significant (see Table 7). This trend in performance indicates that the patient-specific search for models to average over improves some measures of performance compared to a population-wide model when the training set size is smaller.
Running Times
For one patient case, the PSMBg-MA algorithm runs in O(b d m n) time, where m is the number of cases in the training dataset, n is the number of domain variables, d is the total number of iterations of the search in the two phases, and b (the branching factor) is the number of successors generated from a MB structure in either phase of the search. For a patient case, the PSMBl-MA algorithm runs in O(b d m n 2n) time; thus it has exponential time complexity in the number of domain variables. The PSMBl-MA algorithm, which uses model averaging and searches over local structure, performs relatively well, but it has a high computational time complexity. Further details of the time complexity analysis are given in [5].
On a PC with a 3.0 GHz CPU and 2 GB of RAM running Windows XP, the average running time of the PSMBg-MA algorithm for a single test case was approximately 1 hour and 30 minutes, while the corresponding average running time of the PSMBl-MA algorithm was 5 hours and 30 minutes.
VI. DISCUSSION
One way to assist healthcare providers in making decisions under uncertainty is to support their clinical decision making with predictions from mathematical models. Improving the predictive performance of such models has the potential to improve outcomes in patient care. We have developed novel patient-specific algorithms that perform Bayesian model averaging over a set of models that is located using the features of the patient case at hand. Combining the predictions of a set of models has been shown previously to improve predictive performance over that of a single model [4], and our results show that selective Bayesian model averaging over MB structures is superior to selecting a single MB structure.
Our results indicate that the performance of the patient-specific algorithm that learns MBs with a standard global structure can be improved by searching in the richer model space of MBs represented using decision-graph local structures. In our experiments, the PSMBl-MA algorithm that performs model averaging over local structure models never did worse than any of the following alternative methods: the PSMBl-MS that performs model selection over local structure models, the PSMBg-MA that performs model averaging over global structure models, or the logistic regression (LR) algorithm that performs population-wide model selection. At smaller training set sizes (64 and 128 samples) the PSMBl-MA performed statistically significantly better than PSMBl-MS on four of the five performance measures we used. At larger training set sizes (512 and 1024 samples) the PSMBl-MA algorithm performed better than the other algorithms, though not statistically significantly so. These results suggest that in datasets for which the number of training cases is small relative to the number of variables, prediction performance will be best when (1) learning local structure models, and (2) performing model averaging.
In the PSMBg-MA and the PSMBl-MA algorithms, the computation of the score associated with a candidate MB structure in the second phase uses a similarity metric, namely KL divergence, to measure the change in the model-averaged predictive distribution of the target variable due to the candidate MB structure. The experimental results indicate that KL divergence optimizes the probability measures the most (logarithmic loss and squared error). Alternative similarity measures may optimize other performance measures, such as the discriminative measures, namely, AUC and misclassification error; developing and investigating such measures is an open research problem.
Several situations are possible where the patient-specific algorithms may not have an advantage over population-wide algorithms. As one example, in a domain where complete Bayesian model averaging is tractable and carried out over all models in the model space, a search heuristic that selects a subset of models, such as the one used by the patient-specific algorithms, is superfluous. Typically, in real life domains complete model averaging over all models is not tractable due to the enormous number of models in the model space. Thus, the patient-specific method is useful for selective model averaging where it identifies a potentially relevant set of models that is predictive of the patient case at hand. Another situation where patient-specific algorithms may not have better performance is when a relatively large number of patient cases are available with respect to the number of variables. However, increasingly translational datasets include genomic data such as single nucleotide polymorphisms (SNPs) that consist of many thousands of variables and relatively limited numbers of patient cases. In such high-dimensional datasets, the “effective” training sample is quite small, and for such datasets, the PSMBl-MA may prove to be a competitive predictive method.
The patient-specific methods that we evaluated have several limitations. First, in our experiments the number of models chosen to average over was constrained to 40 to limit the running times. Averaging over more models might improve the performance of the patient-specific algorithms further. Second, the patient-specific algorithms are computationally expensive and learning MBs with local structure is several times more expensive than learning MBs with global structure. The running times of the patient-specific algorithms for a patient case increase dramatically as the number of variables increases. However, our focus in this paper was predictive performance and not computation time. Concentrating on computational issues is worthwhile only if the predictive performance of the more computationally demanding methods yield improved performance, as happened in the results reported here. We now plan to turn our attention to pursuing a number of approaches for optimizing the patient-specific algorithms. Third, while model averaging improves predictive performance, explaining to the user how those predictions were derived is less straightforward than for a single model. For example, interest may center on which variables are the most predictive of an outcome in a given patient. In a single MB structure, the variables comprising that structure are the important predictors for the outcome of interest. In model averaging, one way to judge the importance of a variable is to rank a variable by the sum of the posterior probabilities of the MB structures in which it appears. Despite these limitations, the results reported here provide support that patient-specific models can improve predictive performance over population-wide models.
In summary, we introduced a patient-specific model averaging approach for learning predictive models that are influenced by the particular history, symptoms, laboratory results, and other features of the patient case at hand, implemented this approach for learning patient-specific Markov blanket models, and found that overall these models exhibited superior predictive performance on two clinical datasets. These positive results provide an impetus for additional research on patient-specific model averaging methods for predicting clinical outcomes.
Supplementary Material
Acknowledgments
This work was supported by grants NLM R01-LM008374 and NIGMS R01-GM061992, and by training grant T15-LM/DE07059 from the National Library of Medicine to the University of Pittsburgh’s Biomedical Informatics Training Program.
Footnotes
Nodes in the BN graph represent variables. Because of their direct correspondence, we use the terms node and variable interchangeably in this paper.
When n is a positive integer, Γ(n) = (n-1)!, and thus, the gamma function is a generalization of the factorial function.
In the case of scoring a local structure, the term G in Equation 2 is replaced by the term {G, DG1, …, DGi, …, DGn}, and elsewhere in this paper. We only show G to keep the notation simple.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.van Bemmel JH, Musen MA. Handbook of Medical Informatics. 1. New York: Springer-Verlag; 1997. [Google Scholar]
- 2.Abu-Hanna A, Lucas PJ. Prognostic models in medicine. AI and statistical approaches. Methods of Information in Medicine. 2001 Mar;40(1):1–5. [PubMed] [Google Scholar]
- 3.Cooper GF, Aliferis CF, Ambrosino R, Aronis J, Buchanan BG, Caruana R, et al. An evaluation of machine-learning methods for predicting pneumonia mortality. Artificial Intelligence. 1997 Feb;9(2):107–38. doi: 10.1016/s0933-3657(96)00367-3. [DOI] [PubMed] [Google Scholar]
- 4.Hoeting JA, Madigan D, Raftery AE, Volinsky CT. Bayesian model averaging: A tutorial. Statistical Science. 1999 Nov;14(4):382–401. [Google Scholar]
- 5.Visweswaran S. PhD dissertation. Pittsburgh: University of Pittsburgh; 2007. Learning patient-specific models from clinical data. [updated 2007; cited]; Available from: http://etd.library.pitt.edu/ETD/available/etd-11292007-232406/unrestricted/visweswaran_etd__7_Dec_2007.pdf. [Google Scholar]
- 6.Pearl J. Probabilistic Reasoning in Intelligent Systems. San Mateo, California: Morgan Kaufmann; 1988. [Google Scholar]
- 7.Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local Causal and Markov Blanket Induction for Causal Discovery and Feature Selection for Classification Part I: Algorithms and Empirical Evaluation. Journal of Machine Learning Research. 2010;11:171–234. [Google Scholar]
- 8.Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD. Local Causal and Markov Blanket Induction for Causal Discovery and Feature Selection for Classification Part II: Analysis and Extensions. Journal of Machine Learning Research. 2010:235–84. [Google Scholar]
- 9.Boutilier C, Friedman N, Goldszmidt M, Koller D, editors. Context-specific independence in Bayesian networks. Proceedings of the Twelfth Annual Conference on Uncertainty in Artificial Intelligence; 1996 August 1-4; Reed College, Portland, Oregon. Morgan Kaufmann; [Google Scholar]
- 10.Friedman N, Goldszmidt M. Learning in graphical models. MIT Press; 1999. Learning Bayesian networks with local structure; pp. 421–59. [Google Scholar]
- 11.Friedman N, Goldszmidt M, editors. Learning Bayesian networks with local structure. Proceedings of the Twelfth Annual Conference on Uncertainty in Artificial Intelligence; 1996 August 1-4; Reed College, Portland, Oregon. Morgan Kaufmann; [Google Scholar]
- 12.Chickering DM, Heckerman D, Meek C, editors. A Bayesian approach to learning Bayesian networks with local structure. Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence; 1997 August 1-3; Brown University, Providence, Rhode Island. Morgan Kaufmann; [Google Scholar]
- 13.Madigan D, Raftery AE. Model selection and accounting for model uncertainty in graphical models using Occam’s window. Journal of the American Statistical Association. 1994;89:1335–46. [Google Scholar]
- 14.Raftery AE, Madigan D, Hoeting JA. Model selection and accounting for model uncertainty in linear regression models. Journal of the American Statistical Association. 1997;92:179–91. [Google Scholar]
- 15.Cooper GF, Herskovits E. A Bayesian method for the induction of probabilistic networks from data. Machine Learning. 1992 Oct;9(4):309–47. [Google Scholar]
- 16.Heckerman D. A tutorial on learning with Bayesian networks. In: Jordan M, editor. Learning in Graphical Models. Cambridge, MA: MIT Press; 1999. [Google Scholar]
- 17.Neapolitan RE. Learning Bayesian Networks. 1. Upper Saddle River, New Jersey: Prentice Hall; 2003. [Google Scholar]
- 18.Wilks SS. Mathematical Statistics. New York: Wiley; 1962. [Google Scholar]
- 19.Bell ET. Exponential numbers. American Mathematical Monthly. 1934;41:411–9. [Google Scholar]
- 20.Cover TM, Joy AT. Elements of Information Theory. 2. Wiley-Interscience; 2006. [Google Scholar]
- 21.Wheeler AP, Bernard GR. Treating patients with severe sepsis. The New England Journal of Medicine. 1999 Jan 21;340(3):207–14. doi: 10.1056/NEJM199901213400307. [DOI] [PubMed] [Google Scholar]
- 22.From the Centers for Disease Control. Increase in National Hospital Discharge Survey rates for septicemia--United States, 1979-1987. Journal of the American Medical Association. 1990 Feb 16;263(7):937–8. [PubMed] [Google Scholar]
- 23.NHLBI. Morbidity and Mortality: 2002 Chartbook on Cardiovascular, Lung, and Blood Diseases: National Institutes of Health. 2002 Contract No.: Document Number∣. [Google Scholar]
- 24.Popovich JR, Hall MJ. 1999 National Hospital Discharge Survey, Advance Data, No. 319: Centers for Disease Control and Prevention, National Center for Health Statistics. 2001 Contract No.: Document Number∣. [Google Scholar]
- 25.Auble TE, Hsieh M, Gardner W, Cooper GF, Stone RA, McCausland JB, et al. A prediction rule to identify low-risk patients with heart failure. Academic Emergency Medicine. 2005 Jun;12(6):514–21. doi: 10.1197/j.aem.2004.11.026. [DOI] [PubMed] [Google Scholar]
- 26.Fayyad UM, Irani KB, editors. Proceedings of the International Joint Conference on Artificial Intelligence. Chambry, France: Morgan Kaufmann; 1993. Multi-interval discretization of continuous-valued attributes for classification. [Google Scholar]
- 27.Caruana R, editor. Proceedings of Artificial Intelligence and Statistics. 2001. A non-parametric EM-style algorithm for imputing missing values. [Google Scholar]
- 28.Cooper GF, Abraham V, Aliferis CF, Aronis J, Buchanan BG, Caruana R, et al. Predicting dire outcomes of patients with community acquired pneumonia. Journal of Biomedical Informatics. 2005;38(5):347–66. doi: 10.1016/j.jbi.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 29.Witten IH, Frank E. Data Mining: Practical Machine Learning Tools and Techniques. 2. Morgan Kaufmann; 2005. [Google Scholar]
- 30.Caruana R, Alexandru N-M, editors. Data mining in metric space: An empirical analysis of supervised learning performance criteria. Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Seattle, WA. ACM Press; 2004. [Google Scholar]
- 31.Daniel W. Applied Nonparametric Statistics. 2. PWS-KENT Publishing Company; 1990. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.