Abstract
Dimeric ligands can be potent inhibitors of protein-protein or enzyme-substrate interactions. They have increased affinity and specificity toward their targets due to their ability to bind two binding sites simultaneously and are therefore attractive in drug design. However, few studies have addressed the kinetic mechanism of interaction of such bivalent ligands. We have investigated the binding interaction of a recently identified potent plasma-stable dimeric pentapeptide and PDZ1–2 of postsynaptic density protein-95 (PSD-95) using protein engineering in combination with fluorescence polarization, isothermal titration calorimetry, and stopped-flow fluorimetry. We demonstrate that binding occurs via a two-step process, where an initial binding to either one of the two PDZ domains is followed by an intramolecular step, which produces the bidentate complex. We have determined all rate constants involved in the binding reaction and found evidence for a conformational transition of the complex. Our data demonstrate the importance of a slow dissociation for a successful dimeric ligand but also highlight the possibility of optimizing the intramolecular association rate. The results may therefore aid the design of dimeric inhibitors in general.
Keywords: Glutamate Receptors Ionotropic (AMPA, NMDA); Kinetics; Ligand Binding Protein; Pre-steady-state Kinetics; Synapses; PDZ Domain; Bivalent Interaction; Dimeric Inhibitor
Introduction
Biological molecules that comprise two or more binding units enable di- or multivalent binding to their protein partners. This concept is well known in nature as a way to increase affinity and selectivity, such as in virus-cell and antibody-antigen recognition (1). Consequently, linking two ligands together can be a strategy to enhance binding of drug candidates to therapeutically relevant proteins by exploiting a bivalent binding site (2–5). It is proposed that such dimeric inhibitors will foster a more potent response by increasing the affinity toward their targets by some hundred-fold (6, 7). Indeed, in vitro binding studies have shown improved affinities of dimeric inhibitors toward their targets as compared with their monomeric counterparts (5, 8–11). It is complex to predict the overall affinity enhancement by linking two ligands because the observed binding energy is not a direct summation of the binding energies of individual components, and the entropy and enthalpy compensation are difficult to estimate (6, 7, 12). Therefore, experimental determination of the binding mechanism of dimeric ligands is useful for future design of dimeric ligands. However, there are only a few cases where in solution methods have been used to determine the mechanism of interaction of such ligands (5, 7, 10). One class of proteins where dimeric ligands have been exploited in an attempt to develop potential inhibitors for therapeutically relevant interactions in the cell is the PDZ (PSD-95/Dlg/Zonula occludens-1) domain family of proteins (5, 8). PDZ domains constitute a class of protein-protein interacting modules that functions as scaffolds and adapters in signaling cascades, and they are found in a few hundred proteins in the human genome (13). PDZ domains generally bind to the C termini of their target proteins (14, 15), although neuronal nitric oxide synthase binds to postsynaptic density protein-95 (PSD-95)3 via an internally located sequence (14). PDZ domains often occur as concatenates of two or more domains. For example, there are three PDZ domains in PSD-95, numbered PDZ1, PDZ2, and PDZ3. PDZ1 and PDZ2 are closely related in terms of sequence identity as well as ligand binding preference and are separated by only five amino acids (16).
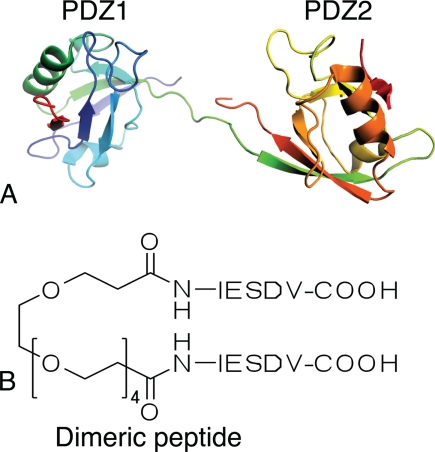
The interaction between PSD-95 and the N-methyl-d-aspartate (NMDA) receptor leads to increased production of nitric oxide (NO) by neuronal nitric oxide synthase in the cell. During brain ischemia an overstimulation of the NMDA receptor leads to toxic levels of NO and hence cell death (17). Therapeutic uncoupling of the PSD-95/NMDA receptor interaction is therefore a potential approach to reduce ischemic cell death (18). We have recently designed and prepared a dimeric pentapeptide that interacts with the tandem PDZ1–2 of PSD-95 with nanomolar affinity. This inhibitor is therefore a promising candidate for further drug development (see Fig. 1) (8). In this report, we clarify the kinetic mechanism of interaction of this dimeric pentapeptide, explain the improved affinity toward the tandem PDZ1–2, and discuss possible strategies for further optimizations.
FIGURE 1.
Structures of dimeric ligand and PDZ1–2 tandem. A, model of the PSD-95 PDZ1–2 tandem structure in complex with cypin peptide (Protein Data Bank code 2KA9) from Wang et al. (11). B, structure of the dimeric ligand, made by dimerization of two pentapeptides with a polyethylene glycol (PEG) linker (8).
MATERIALS AND METHODS
PDZ wild type and Trp variants were cloned as described previously (8). Mutants (PDZ1 R70A/K98A, PDZ2 K165D/K193D, PDZ1-2 R70A/K98A, and PDZ1–2 K165D/K193D) were made using a QuikChangeTM site-directed mutagenesis kit (Stratagene) according to the manufacturer's instructions. All mutants were sequenced throughout the entire coding region. The expression and purification of PDZ domains were carried out as described (8, 19). Protein concentrations were determined either by amino acid analysis or by absorbance measurements using extinction coefficients calculated from amino acid analysis. In addition to wild type proteins, PSD-95 PDZ domains containing Trp (denoted as *) at position 100 (PDZ1*, PDZ1*–2 and PDZ1*–2 K165A/K193A) or position 195 (PDZ2*, PDZ1–2* and PDZ1–2* R70A/K98A), respectively, were used for the time-resolved binding experiments. The Trp residues served as fluorescence probes for stopped-flow ligand binding experiments. Synthesis and characterization of peptides (monomer pentapeptide (IESDV), dimeric ligand (PEG4-(IESDV)2, and fluorescently labeled peptide, Cy5-CSGYEKLSSIESDV (Cy5-NR2B)) were prepared as described (8).
Fluorescence Polarization (FP)
For FP experiments, binding was performed with PDZ WT and four mutant constructs (PDZ1 R70A/K98A, PDZ2 K165D/K193D, PDZ1–2 R70A/K98A, and PDZ1–2 K165D/K193D) and fluorescent monomeric peptide (Cy5-NR2B). Binding and displacement experiments were done as described previously (8). Briefly, in the displacement reaction, unlabeled peptide (increasing concentrations from 0–512 μm) was added to 50 nm of Cy5-NR2B in complex with PDZ (3–25 μm depending on the PDZ construct) and incubated for 20–30 min at room temperature (see Ref. 8). FP measurements were recorded at excitation/emission wavelengths of 635/670 nm on a Safire2 plate reader (Tecan, Männedorf, Switzerland). Readings were then fitted to the standard equation for an equilibrium displacement, and the KD and Ki values were determined as described previously (8).
Isothermal Titration Calorimetry (ITC) Experiments
Calorimetric experiments were performed using a microcalorimeter (ITC200, Microcal, MA, USA) at 10 °C in 50 mm potassium phosphate, pH 7.5, by titration of the ligand (20 × 2 μl injections at 180-s intervals; stirring speed of 1000 rpm) into the PDZ solution. Experiments were designed so that c-values were generally within 1–1000 (c-value = Ka × [protein] × N; Ka is the equilibrium association constant, [protein] is the protein concentration, and N is the stoichiometry of the binding event). Heats of dilution were initially determined by titrating buffer into protein, which were subtracted from the observed “heat values” of ligand into protein. Titration of ligand into buffer yielded negligible heats. ORIGIN (version 7.0; Microcal, MA, USA) was used to determine the thermodynamic properties of ligand binding using nonlinear least squares fitting assuming a single-site model because the difference in affinity toward the respective PDZ domain was too small to fit a more complex model. All values presented here are the average of two to five individual experiments.
Stopped-flow Fluorescence Binding Experiments
Stopped-flow binding experiments were done in 50 mm potassium phosphate, pH 7.5, at 10 °C on an SX-20MV stopped-flow spectrometer (Applied Photophysics, Leatherhead, UK). Excitation was at 290 nm, and emission was recorded at 330 ± 30 nm using an interference filter. Binding rate constants, kon and koff, for PDZ and peptide ligands were estimated using different approaches. In both cases, experimental traces were fit to either a single exponential (Equation 1) or a double exponential (Equation 2).
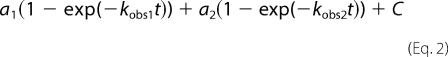 |
a is the amplitude, and kobs is the observed rate constant associated with the kinetic phase. The choice between a single or a double exponential for a particular kinetic trace was based on analysis of the residuals from the curve fitting. Most importantly, any significant trend in the residuals when fitting a single exponential justified the use of a double exponential (i.e. systematic deviations from an even distribution around the fitted line).
First, the dissociation rate constants were estimated as follows: PDZ wild type variant (3 μm) in complex with peptide ligand (5 μm) was mixed rapidly with a Trp mutant PDZ* resulting in a single exponential trace as the respective PDZ wild type was competed out. At high concentrations of PDZ*, the observed rate constant approached the overall off-rate constant for the binding reaction (koffapp) between wild type PDZ and peptide ligand. The apparent overall off-rate constant for the wild type PDZs, koffapp, was estimated as the average of the kobs values at high concentration of the “chase ligand” (≥30 μm).
Second, the PDZ* mutant or peptide (in the concentration range 0–20 μm) was mixed rapidly with a constant amount of peptide (1.5–5 μm for different data sets) or PDZ* (1.5–5 μm), respectively, and the change in fluorescence was recorded over time. The kinetic traces of such experiments were fitted either to a single or double exponential function to obtain one or two observed rate constants. Observed rate constants were plotted against the concentration of the varied species and microscopic rate constants estimated from fitting data to Equation 3, which is valid at all concentrations of [A]0 and n (i.e. under second order as well as pseudo first order conditions).
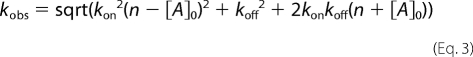 |
kon is the association or on-rate constant, koff is the dissociation or off-rate constant, and [A]0 and n are the initial concentrations of the varied and constant species, respectively (20, 21).
The slow phase observed upon mixing PDZ1–2* with dimeric peptide, which increased up to a constant value with peptide concentration, was analyzed with a model-free polynomial equation (Equation 4), to calculate kobs at 15 μm dimeric peptide by intrapolation.
The kobsmax value for this phase reflects the rate constant(s) for the intramolecular binding event(s) and simulations showed that kobs at 15 μm dimeric peptide is a good estimate of the largest intramolecular rate constant. Under pseudo first order conditions, a hyperbolic function may be used to analyze these data, but at the concentrations used here for the nonvaried species, such an equation gives a poor fit.
To validate our mechanism against experimental data, we simulated various scenarios using the software Copasi (version 4.1). Briefly, each step in the kinetic scheme is listed in the program, along with rate constants determined in real experiments (cf. Table 2 and see Fig. 6). The software solves the differential equations by numerical integration to give time courses for each species. These time courses were then fitted to double or triple exponential equations to obtain putative observed rate constants for the scheme. Because a fluorescent label (Trp) was used either in PDZ1 or PDZ2, only complexes with an expected signal change were considered in the analyses. It should, however, be noted that the real fluorescence yields may differ from those in the simulations. Such differences would modulate the observed amplitudes of the phases and thus which rate constants that will be observed.
TABLE 2.
Rate constants for the reaction between different PDZ constructs and monomeric and dimeric peptide, respectively
These rate constants were obtained by varying the peptide at constant PDZ* concentration.
| PDZ construct | kon for monomeric peptide | koff for monomeric peptide | kon for dimeric peptide | koff for dimeric peptide | kintramolecular |
|---|---|---|---|---|---|
| μm−1s−1 | s−1 | μm−1s−1 | s−1 | s−1 | |
| PDZ1* | 5.1 ± 1.1a | 27 ± 0.4b | NDc | NDc | |
| PDZ2* | 11.5 ± 0.2a | 15 ± 0.3b | NDc | NDc | |
| PDZ1*–2 | 5.4 ± 1.1a | 15 ± 1b,d | 35 ± 8.0a | 0.9 ± 0.03b,d | phase not visible |
| PDZ1–2* | 11.8 ± 0.2a | 15 ± 1b,d | 41.0 ± 0.6a | 0.9 ± 0.03b,d | 62 ± 6a |
| PDZ1*–2 K163A/K193A | 5.1 ± 0.2a | 24 ± 0.1e | 5.8 ± 0.1a | 31 ± 1e | phase not visible |
| PDZ1–2* R70A/K98A | 10.8 ± 0.2a,f | 14 ± 0.7b | 14 ± 1a,f | 15 ± 0.5b | phase not visible |
a Shown are kon (and kintramolecular) values from PDZ with the Trp probe as indicated by the asterisk.
b Shown is the koff value from wild type PDZ without the Trp probe, measured in a displacement reaction.
c Off-rate constants between single PDZ domains and dimeric peptides were very high, probably due to unfavorable interactions with the linker, and rate constants were therefore difficult to determine.
d In the displacement reaction from wild type tandem PDZ1–2 only the lowest of the two microscopic intramolecular rate constants can be determined.
e koff values from PDZ1–2 K163D/K193D are shown. For the purpose of determining on-rate constants, we used PDZ1*–2 K163A/K193A, to avoid a change of charge by −four.
f A slow phase corresponding to the one in Fig. 4E was present in addition to the linear phase.
FIGURE 6.
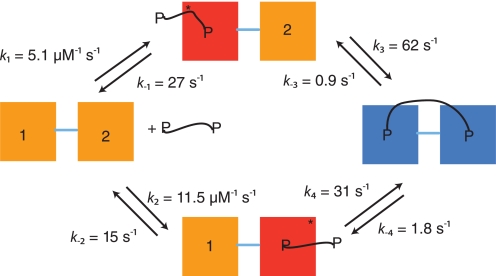
Kinetic reaction scheme for the interaction between PSD-95 PDZ1–2 and a dimeric peptide. The initial association and dissociation rate constants (k1, k2, k−1, k−2) in the scheme were obtained from experiments with monomeric peptide, but are fully consistent with the dimeric peptide binding data. The reverse rate constants (k−3, k−4) were measured from displacement kinetics of the PDZ tandem constructs and dimeric peptide. In the displacement reaction from wild type PDZ1–2 tandem, only the slowest intramolecular koff can be determined (0.9 s−1); the rate constant of 1.8 s−1 is inferred from, first, the intermolecular koff values between monomeric peptide and single PDZ domains and, second, from the ratio of intramolecular koff values from dimeric peptide and Trp mutant tandems PDZ1*–2 and PDZ1–2* (not shown). In both cases the off-rate constant from PDZ1 is roughly two times that of PDZ2. The intramolecular forward rate constant k3 was determined from the dependence of the slow step for PDZ1–2* and dimeric peptide (Fig. 5F, kobsmax ≈ k3 = 62 s−1), as described in the Results section. Finally, k4 was calculated as 31 s−1, given that the product of rate constants on one half of the scheme must equal that of the other half.
RESULTS
We want to determine the components contributing to the binding energy and elucidate the kinetic path of interaction of a dimeric ligand binding to a two-binding site protein. To this end, we have performed kinetic and equilibrium binding experiments with the bivalent peptide PEG4-(IESDV)2 and PDZ1–2, a tandem of the first two PDZ domains of PSD-95 (Fig. 1). Theoretically, one can imagine the dimeric ligand interacting with the tandem PDZ1–2 protein in several ways and forming a variety of ternary and even higher order complexes. The simplest scenario is a square scheme (see Fig. 6). Formation of plausible “off pathway intermediates” is discussed toward the end of “Results.”
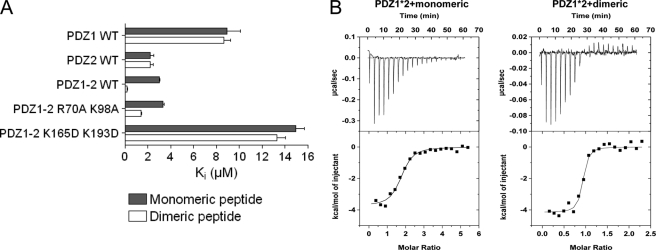
First, we performed FP binding experiments to confirm that both PDZ1 and PDZ2 bind the dimeric peptide in the tandem PDZ1–2. For this purpose, we mutated key residues within the binding pockets of PDZ1 and PDZ2 in the tandem construct to obliterate the binding ability of either domain, respectively. Specifically, we introduced the double mutants PDZ1 R70A/K98A, PDZ2 K165D/K193D, PDZ1–2 R70A/K98A, and PDZ1–2 K165D/K193D. In a sequence alignment with PSD-95 PDZ3, Arg70 and Lys165 of PDZ1 and -2, respectively, correspond to Arg318 of PDZ3, which has been shown to contribute to the binding of the peptide (19, 22). Ala or Asp mutations were introduced to reduce the affinity to the respective PDZ domain. We determined the Ki and IC50 values from binding and displacement experiments of these PDZ wild type and mutant proteins (Fig. 2A). As shown in Fig. 2 and as suggested previously (8), both PDZ1 and PDZ2 bind to the dimeric peptide in the PDZ1–2 tandem, and PDZ2 makes the strongest contribution to the binding. The PDZ1–2 R70A/K98A mutant, in which the ligand binding in the PDZ1 domain is disrupted, binds the monomeric and dimeric peptides with affinities comparable to PDZ2 WT, as expected. In the PDZ1–2 K165D/K193D mutant, in which the ligand binding in the PDZ2 domain is disrupted, the affinity for the dimeric ligand is considerably lower than for PDZ1–2 WT and in the range of PDZ1 WT, and there is no longer a preference for the dimeric ligand over the monomeric ligand. Thus, these data demonstrate that both PDZ domains in PDZ1–2 are responsible for the increased affinity observed for dimeric ligands and thereby substantiate that the dimeric ligand binds concomitantly to both domains (8).
FIGURE 2.
Equilibrium binding experiments. A, Ki values for PDZ-peptide interactions measured from fluorescence polarization displacement experiments. Error bars were calculated from the average of three independent measurements. B, ITC data for PDZ1–2* with monomeric peptide inhibitor and dimeric inhibitor at 10 °C. Top, raw data. Bottom, integrated titration curves. Fitting of a single site model (solid line) yielded the parameters reported in Table 1.
ITC has previously been used to determine the stoichiometric ratio of peptide ligand to protein in the complex and to calculate the enthalpic and entropic contributions of the different species. The monomeric and dimeric peptide interact with PDZ1–2 in a 2:1 ratio and 1:1 ratio, respectively, at 25 °C (KD = 32 nm for dimeric peptide) (8). To confirm these results at 10 °C, which is the temperature of our kinetic experiments, we repeated the ITC experiments (Fig. 2B, Table 1). Whereas binding was primarily enthalpy-driven at 25 °C (8), both entropy and enthalpy favored binding of the dimeric peptide at 10 °C.
TABLE 1.
Isothermal titration calorimetric data for the interaction between PDZ1–2*, PDZ1*–2 and monomeric and dimeric peptide, respectively
| Peptide | ΔH | −TΔS | KD | ΔG |
|---|---|---|---|---|
| kcal mol−1 | kcal mol−1 | nm | kcal mol−1 | |
| PDZ1–2*-monomeric peptide | −3.2 ± 0.2 | −3.8 ± 0.1 | (4.7 ± 1.0) × 103 | −6.9 ± 0.2 |
| PDZ1–2*-dimeric peptide | −2.9 ± 0.3 | −6.6 ± 0.3 | 45 ± 1.0 | −9.5 ± 0.1 |
| PDZ1*–2-monomeric peptide | −4.1 ± 0.3 | −3.4 ± 0.3 | (1.7 ± 0.4) × 103 | −7.5 ± 0.1 |
| PDZ1*–2-dimeric peptide | −3.4 ± 0.6 | −6.1 ± 1.3 | 96 ± 8.0 | −9.5 ± 0.8 |
We then performed stopped-flow binding experiments to understand the sequence of events, and probe the free energy landscape “en route” to the final complex by determining the rate constants and thus the relative amounts of the intermediates along the reaction path(s). Our working hypothesis for the binding reaction was a square mechanism containing four steps (see Fig. 6). Theoretically, three exponential phases are expected for such a scheme. In our experiments, we observed single (Equation 1) or double (Equation 2) exponential binding kinetics. However, if the phases are of similar magnitude, only one or two phases may be visible. Furthermore, the fluorescence yields of the respective species will affect the amplitudes of the phases and thus the observed kinetics. Because of the complexity of any kinetic scheme involving more than two steps and because the reaction is second order at low peptide concentration, it is not possible to find analytical solutions to the dependence of kobs on dimeric peptide concentration. We therefore resorted to solve the rate equations numerically using the software Copasi (23) for each PDZ-protein concentration and compare these theoretical results with experimental data.
We used a stepwise strategy to map all rate constants for the binding mechanism of the PDZ-peptide interactions leading to the binary complex. Because the PSD-95 PDZ1–2 wild type does not contain Trp residues, there is no suitable natural probe for time-resolved fluorescence studies. The Trp mutants described under “Materials and Methods” were therefore used in the stopped-flow experiments. However, the off-rate constants from wild type PDZ1, PDZ2, and PDZ1–2, respectively, could be determined by displacement (chase) experiments (Fig. 3 and Table 2). Here, an excess of the Trp-labeled PDZ domain was used to make the dissociation reaction of wild type PDZ and peptide irreversible. As the peptide dissociated from the wild type PDZ, it was bound to the mutant, which resulted in an increase in Trp fluorescence.
FIGURE 3.
Displacement experiments for wild type PDZs and peptides. Observed rate constants for single PDZ2 WT/monomeric peptide displacement (A), tandem PDZ1–2 WT/monomeric and dimeric peptide displacement (B), by a Trp-containing PDZ. In B, data for the PDZ1–2 R70A/K98A mutant also is shown. Observed rate constants were obtained by fitting of Equation 1 to experimental traces (not shown).
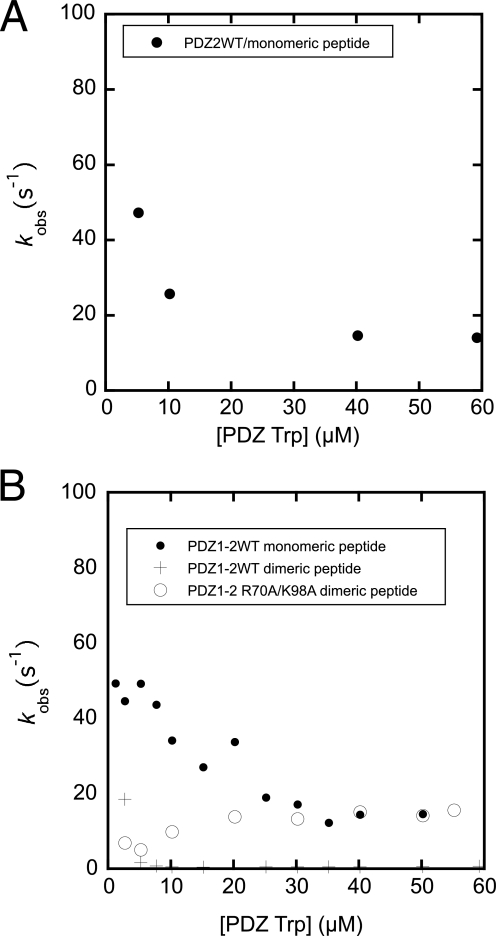
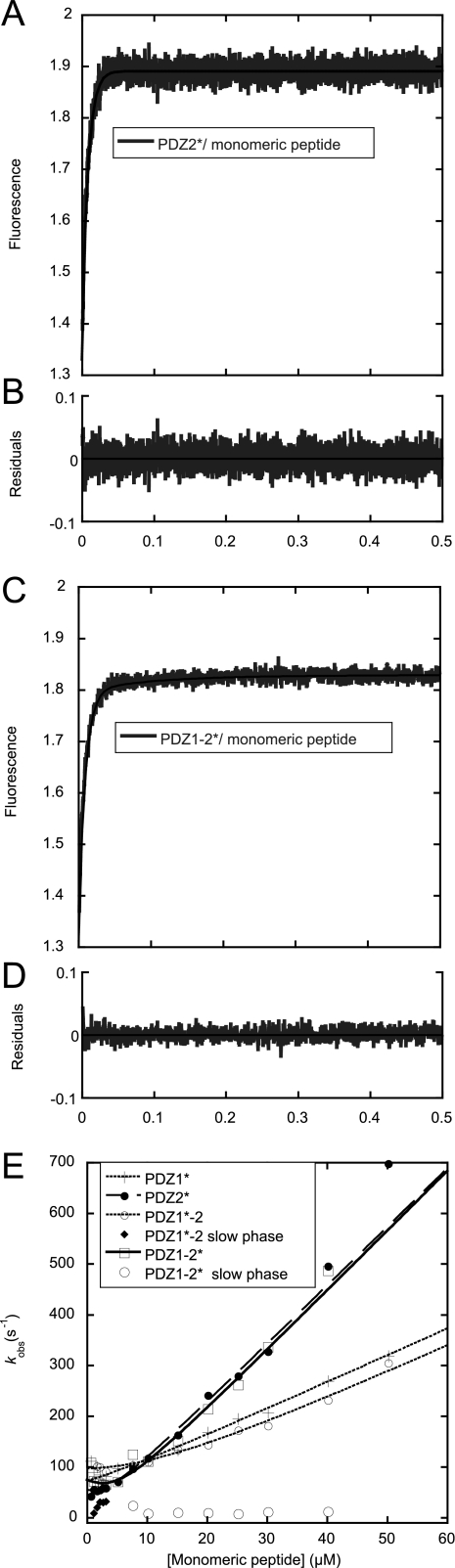
To be able to measure on-rate constants of the interaction directly, the Trp mutants were used in direct binding experiments. Previous experiments with SAP97 PDZ2 showed that a Trp in the corresponding position did not significantly affect the kon (24). First, transient binding experiments between monomeric peptide and the single PDZ domains PDZ1* and PDZ2*, respectively, were performed. All binding traces for these interactions appeared perfectly monophasic and were fitted to a single exponential function (Equation 1) to obtain the observed rate constants and these were in turn fitted to Equation 3 to obtain association rate constants (Fig. 4 and Table 2). The association rate constant of PDZ2* was twice that of PDZ1*. The reason for this may be slightly different binding pockets or the different charges of the two domains at the experimental pH (PDZ1 and peptides were negatively charged, whereas PDZ2 was slightly positively charged). The association rate constants measured for the interaction between the tandems PDZ1*–2 and PDZ1–2*, and monomeric peptide were similar to those of the single PDZ domains (Fig. 4 and Table 2). For example, association rate constants were 11.5 μm−1 s−1 and 11.8 μm−1 s−1 for PDZ2*-monomeric peptide and PDZ1–2*-monomeric peptide interaction, respectively. A faster phase corresponding to the sum of the two kon values of PDZ1 and PDZ2 could be present theoretically but may not be visible due to low amplitude of this phase. Importantly, the binding interaction between the monomeric peptide and PDZ1*–2 as well as PDZ1–2* were biphasic (Equation 2 and Fig. 4, C and D). The second phase for PDZ1*–2 (Fig. 4E) was manifested by a negative amplitude, which approached zero with increasing peptide concentration and probably corresponded to the faster observed phase of PDZ1–2* (11.8 μm−1 s−1). The slow phase of PDZ1–2* (Fig. 4E), on the other hand, saturated around 10 s−1 and displayed a positive amplitude, which increased with increasing peptide concentration. The observed rate constants for PDZ1*–2 and the fast kobs for PDZ1–2* are consistent with an initial event where the binding is partitioned between the two routes according to the on-rate constants (see Fig. 6), followed by progression to equilibrium involving all microscopic rate constants. However, the slow rate constant observed for PDZ1–2* (10 s−1) suggests the presence of an additional step, for example, a conformational change of one of the molecules. This slow phase also was observed with the PDZ1–2* R70A/K98A mutant, further suggesting it to represent a conformational transition and not partitioning between PDZ domains in the tandem.
FIGURE 4.
Binding kinetics of Trp PDZs, PDZ1*, PDZ2*, PDZ1*–2, and PDZ1–2* to monomeric peptide. A, binding trace for the interaction between PDZ2* (3 μm) and monomeric peptide (10 μm) along with a fit to a single exponential (solid line, Equation 1). B, residuals from the single exponential fit in A. C, binding trace for the interaction between PDZ1–2* (3 μm) and monomeric peptide (10 μm) along with a fit to a double exponential (solid line, Equation 2). D, residuals from the double exponential fit in C. E, observed rate constants for PDZ/monomeric peptide interactions plotted against increasing concentration of monomeric peptide and fitted to Equation 3 to obtain on-rate constants (Table 2).
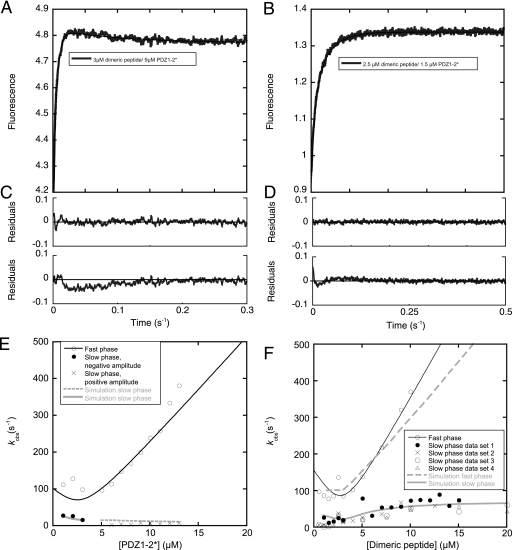
Finally, stopped-flow experiments were carried out with the tandem PDZ1–2 and the dimeric ligand. Binding traces for PDZ1–2* clearly were not single exponentials and were fitted to a double exponential time course (Equation 2) to obtain two observed rate constants (Fig. 5, A–D). We varied both the tandem PDZ1–2* and dimeric peptide at a constant amount of the nonvaried species. A fast phase with a linear concentration dependence and of similar rate constant (kon ∼ 41 μm−1 s−1) was obtained when either PDZ1–2* or dimeric peptide was varied. For PDZ1*–2, the traces appeared monophasic and fitting of Equation 1 to data yielded kobs values that increased linearly with increasing dimeric peptide concentration (kon ∼ 35 μm−1 s−1, Table 2). Theoretically, the highest observed kon is the sum of all microscopic on-rate constants involved in the reaction, multiplied by two because the dimeric peptide can bind in two ways, with equal probability. In fact, the observed kon values (35 and 41 μm−1 s−1 for PDZ1*–2 and PDZ1–2*, respectively) agree well with the expected one, calculated from the microscopic kon values in Table 2 (2 × 11.5 + 2 × 5.1 = 33 μm−1 s−1). This shows that the initial binding event appears noncooperative with regard to the two PDZ domains in the tandem.
FIGURE 5.
Binding reaction of Trp PDZs, PDZ1*, PDZ2*, PDZ1*–2, and PDZ1–2* to dimeric peptide. A, binding trace for PDZ1–2*/dimeric peptide interaction with [PDZ1–2*]>[peptide], fitted to a double exponential (solid line, Equation 2). B, binding trace for PDZ1–2*/dimeric peptide interaction with [peptide]>[PDZ1–2*], fitted to a double exponential (solid line, Equation 2). C, residuals from the double exponential fit in A (upper panel). For comparison, the residuals of a single exponential fit (Equation 1) is shown in the lower panel. D, residuals from double (upper panel) and single (lower panel) exponential fits for the experiment in B. E and F show plots of observed rate constants for the PDZ1–2/dimeric peptide interaction. Observed rate constants were plotted against increasing concentrations of PDZ1–2* E or dimeric peptide F (four data sets reported for the slow phase; in data set 1 the concentration of PDZ1–2* was 1.5 μm and in the other three 3.0 μm). The fast phases in E and F were fitted to Equation 3 (thin solid line), whereas the slow phases in F were fitted to Equation 4 to estimate kobsmax for each set (at 15 μm dimeric peptide, fit not shown), the rate constant of the intramolecular association, which corresponds to k3 in Fig. 6 (62 ± 6 s−1). Simulated data using the rate constants shown in Fig. 6 and a concentration of the non-varied species of 3 μm are in gray. In E, the slow phase is divided into two, since the amplitudes of the phase changed sign around 4 μm dimeric peptide, in agreement with experimental data. Furthermore, in E, a scheme with accumulation of the ternary complexes between two PDZ1–2 and one dimeric peptide was used in the simulation, whereas, in F, a square according to Fig. 6 was simulated.
The slow phase observed upon mixing of PDZ1–2* and dimeric peptide differed depending on the species varied. When the concentration of PDZ1–2* was increased, the phase was apparently constant with a negative amplitude and a value of ∼7 s−1 (Fig. 5, A, C, and E). Based on numerical solutions of a scheme where ternary complexes containing two PDZ tandems and one dimeric peptide accumulate, this observed rate constant appears to be a composite of several microscopic rate constants and reflects a slow equilibration of the system. With increasing concentrations of dimeric peptide, the lower kobs increased hyperbolically (with a positive amplitude) to a constant value of ∼62 s−1 (average of four measurements, Fig. 5, B, D, and F), which we assigned to the intramolecular association of peptide and PDZ domain based on the following arguments. In kinetic analyses, the golden rule is to find the simplest possible scheme, which adequately fits the data. The simplest reaction scheme for the association of a bivalent ligand with a tandem protein is a square (Fig. 6). In such a scheme, the kobsmax of the slow phase will be close to the largest of the two intramolecular forward rate constants (k3 and k4 in Fig. 6, see simulation in Fig. 5F). Indeed, when performing kinetic binding experiments with a mutant where binding to PDZ1 in the tandem was abolished, PDZ1–2* R70A/K98A, this phase disappeared (and also was not present in the PDZ1*–2 K165A/K193A mutant). Furthermore, we assigned the phase to the intramolecular rate constant for association of PDZ2 and the second peptide in the bivalent ligand k3 because (i) we only observe it for PDZ1–2*, and (ii) the intermolecular association rate constant is higher for PDZ2. The second intramolecular forward rate constant k4 can thus be calculated as 31 s−1 (see legend to Fig. 6). Finally, the slow dissociation of dimeric peptide from PDZ1–2 (0.9 s−1) was not present in the double mutants used to abolish binding to the respective PDZ domain in the tandem (Fig. 3B), demonstrating that this phase from the dissociation experiment also can be assigned to the intramolecular step.
This mechanism and the assumptions are further validated by the apparent average Kd calculated from the rate constants of the proposed scheme, ∼68 nm (at 10 μm PDZ1–2 and 10 μm dimeric peptide; calculated as the product of free PDZ1–2 and peptide divided by the sum of all bound species), which agrees well with those determined by ITC (32 nm for PDZ1–2 at 25 °C and 45 nm for PDZ1–2* and 96 nm for PDZ1*–2 at 10 °C; the Kd values of the Trp labeled PDZ tandems are slightly higher than for wild type PDZ1–2, due to a 2–3-fold increase in off-rate constant. The ITC experiments also demonstrate that the binary complex is the major product, further corroborating the proposed scheme.
It should, however, be noted that the ternary complex formed between two dimeric peptides and one PDZ1–2 tandem will indeed accumulate as the concentration of peptide is increased in the experiment. The kobsmax may then be a more complex function of several rate constants. However, at low concentrations of PDZ1–2 and dimeric peptide, the binary bidentate complex is the dominating product species, and formation of any ternary complex is unfavorable energetically and thus a rare event. For example, simulations where accumulation of ternary complexes were considered (both PDZ1–2 with two peptides and one peptide with two PDZ1–2 molecules), at 3 μm PDZ1–2 and 3 μm dimeric peptide, demonstrated that the tandem PDZ1–2 will be present at roughly 72% in binary bidentate complex and at ∼2% as various ternary complexes. In fact, the slow phase in Fig. 5E is the result of accumulation of a ternary complex between two PDZ1–2 tandems and one dimeric peptide. Nevertheless, under our experimental conditions and when peptide concentration is varied, these off-pathway intermediates will not accumulate to such an extent that they could give rise to a phase with a rate constant as high as 62 s−1. Because these side reactions can be neglected, the estimation of k3 to 62 s−1 is valid.
DISCUSSION
By linking monodentate ligands, one can develop inhibitors with increased potency and selectivity. In particular, PDZ domain binding peptides linked together with a non-peptide spacer hold potential for development of ligands with increased binding affinity and selectivity. We set out to evaluate the contribution of the binding rate constants to the binding free energy of such a dimeric ligand interacting with the tandem PDZ1–2 domain of PSD-95 (Fig. 1), which was designed to inhibit the interaction between PSD-95 and the NMDA receptor (8). Based on our results, we summarize the kinetic binding mechanism in Fig. 6.
Based on the kinetic, ITC, and FP data, we propose here a minimal scheme for the interaction of a dimeric peptide to a tandem PDZ1–2 domain (Fig. 6). The scheme in its simplest form is a square where there is an initial binding to one of the PDZ moieties by one end of the peptide moiety. This is followed by an intramolecular rearrangement where the second binding epitope of the peptide binds the other PDZ domain in the tandem and thereby increasing the affinity of the interaction by almost two orders of magnitude.
In our previous study on the design and synthesis of this dimeric ligand, the avidity effect of linking two peptides together was investigated by linking peptides of increasing affinity, with regard to the monopeptide-PDZ interaction (8). Indeed, assuming that the decrease in intermolecular off-rate constants k−1 and k−2 of a certain factor results in a similar reduction in the intramolecular reverse rate constants k−3 and k−4 (Fig. 6), would account fully for the observed effect of linking the two peptides together (see Ref. 8). In addition, we find here that the intramolecular off-rate constant is 10-fold lower than the corresponding intermolecular constant, which contributes significantly to the increased affinity toward the dimeric ligand. Although it is clear that the effect of entropy and enthalpy is complex for bidentate ligands, it was predicted that the affinity enhancement of linking a second ligand was manifested in the dissociation rate constant (7). In general, emphasis should therefore be on optimizing the monomeric inhibitor for a low off-rate constant (7), because the resulting affinity will increase according to a power law, upon linking the inhibitors. In addition, as observed here, linking may lead to an even lower reverse rate constant for the intramolecular step as compared with the intermolecular dissociation, further increasing the affinity.
Optimizing the affinity by modulating the forward intramolecular rate constant would be achieved by avoiding unfavorable interactions and is less straightforward. In addition, the linker also should not make unfavorable interactions nor constrain the linked ligands in unfavorable conformations. Often, linkers are composed of peptides (25, 26), which do not offer any pharmacokinetic advantages to the compound. Polyethylene glycol (PEG), on the other hand, is a nontoxic chemical, which can be linked to proteins to lower renal clearance, protect against enzyme cleavage, reduce immunogenicity, increase solubility, and even increase membrane permeability (27). The dimeric peptide studied here was optimized with regard to linker length (8)), yet the PEG linker appears to make unfavorable interactions with the PDZ tandem as reflected in the roughly 5-fold higher off-rate constant for the interaction between single domains and dimeric peptide as well as a higher Kd between monomeric peptide with PEG linker and PDZ1–2 tandem as determined by ITC (8).
The contribution of the binding constants to the total binding free energy of a dimeric ligand binding to two sites has been evaluated theoretically (6, 7, 12). In general, the effect is attributed to the high effective concentration of the ligand due to the linker between them (KdAKdB/KdA–B; see Refs. 6, 7, 12). In the case of the dimeric inhibitor studied here, the effective concentration would be ∼0.1 mm. Much higher values have been found in biological systems (12), and further improvement of this ligand thus appears possible with regard to the two intramolecular forward binding steps.
This work was supported by grants from the Swedish Research Council, the Carl Trygger Foundation and the O. E. and Edla Johansson Foundation (to P. J.), the Lundbeck Foundation (to K. S.), and the Danish Council for Independent Research, Technology and Production Sciences (to A. B.).
- PSD-95
- postsynaptic density protein-95
- FP
- fluorescence polarization
- WT
- wild type.
REFERENCES
- 1.Mammen M., Choi S. K., Whitesides G. M. (1998) Angew. Chem. Int. Ed. 37, 2754–2794 [DOI] [PubMed] [Google Scholar]
- 2.Clemons P. A. (1999) Curr. Opin. Chem. Biol. 3, 112–115 [DOI] [PubMed] [Google Scholar]
- 3.Corson T. W., Aberle N., Crews C. M. (2008) ACS Chem. Biol. 3, 677–692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li L., Thomas R. M., Suzuki H., De Brabander J. K., Wang X., Harran P. G. (2004) Science 305, 1471–1474 [DOI] [PubMed] [Google Scholar]
- 5.Long J. F., Tochio H., Wang P., Fan J. S., Sala C., Niethammer M., Sheng M., Zhang M. (2003) J. Mol. Biol. 327, 203–214 [DOI] [PubMed] [Google Scholar]
- 6.Zhou H. X. (2001) Biochemistry 40, 15069–15073 [DOI] [PubMed] [Google Scholar]
- 7.Zhou H. X. (2003) J. Mol. Biol. 329, 1–8 [DOI] [PubMed] [Google Scholar]
- 8.Bach A., Chi C. N., Pang G. F., Olsen L., Kristensen A. S., Jemth P., Strømgaard K. (2009) Angew. Chem. Int. Ed. 48, 9685–9689 [DOI] [PubMed] [Google Scholar]
- 9.Paduch M., Biernat M., Stefanowicz P., Derewenda Z. S., Szewczuk Z., Otlewski J. (2007) Chembiochem. 8, 443–452 [DOI] [PubMed] [Google Scholar]
- 10.Tian L., Heyduk T. (2009) Biochemistry 48, 264–275 [DOI] [PubMed] [Google Scholar]
- 11.Wang W., Weng J., Zhang X., Liu M., Zhang M. (2009) J. Am. Chem. Soc. 131, 787–796 [DOI] [PubMed] [Google Scholar]
- 12.Jencks W. P. (1981) Proc. Natl. Acad. Sci. U.S.A. 78, 4046–4050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Harris B. Z., Lim W. A. (2001) J. Cell Sci. 114, 3219–3231 [DOI] [PubMed] [Google Scholar]
- 14.Hillier B. J., Christopherson K. S., Prehoda K. E., Bredt D. S., Lim W. A. (1999) Science 284, 812–815 [PubMed] [Google Scholar]
- 15.Jemth P., Gianni S. (2007) Biochemistry 46, 8701–8708 [DOI] [PubMed] [Google Scholar]
- 16.Lim I. A., Hall D. D., Hell J. W. (2002) J. Biol. Chem. 277, 21697–21711 [DOI] [PubMed] [Google Scholar]
- 17.Dingledine R., Borges K., Bowie D., Traynelis S. F. (1999) Pharmacol. Rev. 51, 7–61 [PubMed] [Google Scholar]
- 18.Aarts M., Liu Y., Liu L., Besshoh S., Arundine M., Gurd J. W., Wang Y. T., Salter M. W., Tymianski M. (2002) Science 298, 846–850 [DOI] [PubMed] [Google Scholar]
- 19.Chi C. N., Engström Å., Gianni S., Larsson M., Jemth P. (2006) J. Biol. Chem. 281, 36811–36818 [DOI] [PubMed] [Google Scholar]
- 20.Gianni S., Engström Å., Larsson M., Calosci N., Malatesta F., Eklund L., Ngang C. C., Travaglini-Allocatelli C., Jemth P. (2005) J. Biol. Chem. 280, 34805–34812 [DOI] [PubMed] [Google Scholar]
- 21.Malatesta F. (2005) Biophys. Chem. 116, 251–256 [DOI] [PubMed] [Google Scholar]
- 22.Doyle D. A., Lee A., Lewis J., Kim E., Sheng M., MacKinnon R. (1996) Cell 85, 1067–1076 [DOI] [PubMed] [Google Scholar]
- 23.Hoops S., Sahle S., Gauges R., Lee C., Pahle J., Simus N., Singhal M., Xu L., Mendes P., Kummer U. (2006) Bioinformatics 22, 3067–3074 [DOI] [PubMed] [Google Scholar]
- 24.Chi C. N., Bach A., Engström Å., Wang H., Strømgaard K., Gianni S., Jemth P. (2009) Biochemistry 48, 7089–7097 [DOI] [PubMed] [Google Scholar]
- 25.Hopfner K. P., Ayala Y., Szewczuk Z., Konishi Y., Di Cera E. (1993) Biochemistry 32, 2947–2953 [DOI] [PubMed] [Google Scholar]
- 26.Szewczuk Z., Gibbs B. F., Yue S. Y., Purisima E., Zdanov A., Cygler M., Konishi Y. (1993) Biochemistry 32, 3396–3404 [DOI] [PubMed] [Google Scholar]
- 27.Harris J. M., Martin N. E., Modi M. (2001) Clin. Pharmacokinet. 40, 539–551 [DOI] [PubMed] [Google Scholar]