Summary
Background
Cellular activities such as endocytosis and secretion require that cargos actively switch between the microtubule (MT) and actin filament (AF) networks. Cellular studies suggest that switching may involve a tug-of-war or coordinate regulation of MT- and AF-based motor function.
Results
To test the hypothesis that motor number can be used to direct the outcome of a tug-of-war process, we reconstituted cargo switching at MT-AF intersections in a minimal system with purified myosin V and dynein-dynactin motors bound to beads. Beads containing both motors often paused at the intersections and rotated about an axis perpendicular to both filaments, suggesting that competing motors apply a torque on their cargo. Force measurements showed that motor forces scale with the number of engaged myosin V and dynein-dynactin motors. Whether beads remained on a MT or AF or switched to the alternate track was determined by which set of motors collectively produced greater force. Passing and switching probabilities were similar whether the bead approached an intersection on either a MT or AF. Beads with a force ratio near unity had approximately equal probabilities of exiting on the MT, exiting on the AF, or remaining stalled at the intersection. A simple statistical model quantitatively describes the relationship between switching probability and motor number.
Conclusions
Cargo switching can be tuned via combinations of 1-4 myosin V and 1-4 dynein-dynactin engaged motors through a simple force-mediated mechanism.
Introduction
Cells rely on molecular motors for transport of cargos to various intracellular destinations, a process crucial to a multitude of cellular activities [1-2]. Two of the known motor families, kinesin and cytoplasmic dynein, drive cargos along microtubules (MTs) [3], whereas a third motor family, myosin, carries cargos along actin filaments (AFs) [4]. Numerous cargos have been observed to utilize both MT and AF tracks, including squid axoplasmic organelles [5], mitochondria [6], synaptic vesicles [7], contractile vacuoles [8], and melanosomes [9-10]. According to the classic dual filament model of transport, MTs serve as long-distance highways, and AFs serve as the local roads of the cell [11]. Another model similarly asserts that MTs function as the primary track for transport but proposes that AFs function as sites for dynamic tethering interactions [12-13].
These models, which are not necessarily mutually exclusive, raise the question of how cargos switch from the MT system to the AF network and vice versa. Can such switches arise from a simple tug-of-war between cargo-bound MT motors and AF motors at intersections between their respective tracks? Studies showing evidence for the simultaneous presence of myosin V and kinesin on ER vesicles [14] and increases in MT-based organelle movement in Xenopus melanophores, mouse melanocytes, neurons, and macrophages upon impairment of myosin Va lend support to a tug-of-war mechanism [7, 12, 15-16]. However, this mechanism has not been tested directly.
The development of in vitro motility assays with increasing complexity has provided new insights into how molecular motors drive cargos through the complex environment of the cell [17-19]. Using purified proteins in reconstituted systems, the mechanical properties of transport have been studied by altering the number of actively engaged motors, adding obstacles along the cytoskeletal track, subjecting motors of a single type to track intersections, or combining multiple motor types on artificial cargos for transit along a single track [20-27].
In this study, we reconstituted filament track switching in vitro using intersections between MTs and AFs and both types of motors bound to the same cargo. Myosin V and dynein-dynactin interact with their respective tracks simultaneously at these intersections. We find that MT-AF switching can be regulated solely via the number of actively engaged motors. With combinations of 1-4 myosin V motors and 1-4 dynein-dynactin motors, a graded transition can be achieved from retention on the cognate track through switching onto the intersecting one, through a simple force-mediated mechanism.
Results
Cargo Switching at Different Motor Densities
In order to probe the effect of motor number on cargo switching at MT-AF intersections, we coincubated polystyrene beads with varying concentrations of both myosin V and dynein-dynactin. Cytoplasmic dynein requires the large multiprotein complex dynactin, for the majority, if not all, of its cellular functions [28-29]; dynactin has been shown to increase dynein's processivity in vitro and to properly localize dynein to cargos in vivo [29-31]. Henceforth we refer to dynein-dynactin as dynein. Orthogonal arrays of microtubules and actin filaments were constructed on the surface of flow cells by sequential flow at right angles (Figure 1A); microtubules were attached to the surface first and then actin filaments adhered second, resulting in actin filament “overpasses” crossing over microtubule “underpasses” (Figure 1B). An optical trap was used to place motor-bound beads on either MTs or AFs near MT-AF intersections and the beads were observed as they approached, encountered, and departed the MT-AF intersections (Figures 1C-E). Beads could “pass” the intersection by exiting along the same track from which they entered (Figure 1D; Movie S1) or “switch” by exiting along the perpendicular track (Figure 1E; Movie S2). A “stop,” the third possibility, occurred if the bead failed to leave the intersection within an observation time of ∼10 minutes.
Figure 1.
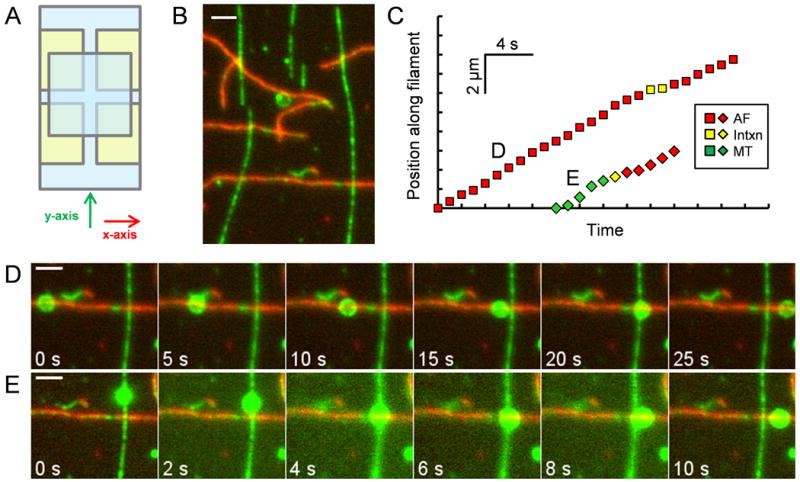
Crossed-flow-path sample chamber and representative time series of beads traversing intersections. (A) Four pieces of double-sided adhesive tape (yellow) hold two cover slips (blue) together to make two perpendicular (x and y) 3 mm wide flow paths. (B) Image of rhodamine-biotin-labeled microtubules and Alexa 647-rhodamine-biotin-labeled actin filaments bound to the cover slip of a crossed-path flow chamber. The microtubules (green) serve as “underpasses,” and actin filaments (red) serve as “overpasses.” The opposite geometry was also tested in some experiments. (C) Distance vs. time plot for the two beads shown in (D) and (E). Yellow symbols indicate pausing at the intersection. (D) Time series of a rhodamine-labeled bead that starts on an AF, encounters a MT, “passes,” and exits on the AF. (E) Time series of a bead that starts on a MT, “switches” at the intersection, and exits on an AF. Scale bars represent 2 μm. See also Movies S1 and S2.
Increasing the ratio of myosin V to dynein motors incubated per bead markedly increased the frequency with which the beads exited the intersections along the AF and correspondingly decreased the frequency of exiting on the MTs (Figure 2i; Figure S1). Notably, these results were independent of whether the beads entered the intersection along an AF or MT; i.e. there was no statistically significant difference in the percentage of beads that left on either a MT or AF at any given [myosin V]/[dynein] ratio when comparing beads that started on MTs to those that started on AFs (Figure 2i). Moreover, in experiments using the opposite geometry, in which AFs were closer to the glass than MTs, we did not see an alteration in the probability of switches (Figure 2i, thin dotted bars).
Figure 2.
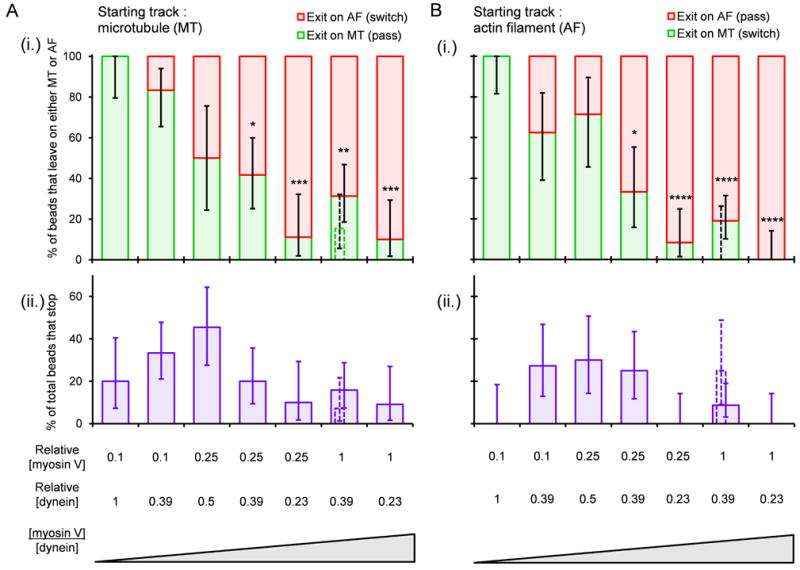
Outcome following bead encounters with MT-AF intersections at different ratios of myosin V to dynein. (A) Outcome when bead enters the intersection along a MT. (B) Outcome when bead enters the intersection along an AF. In (A) and (B), panels (i) show the distributions of exits on AFs (red) and MTs (green) for those beads that did not stop at the intersections. Panels (ii) show the percentage of all beads that “stopped” (failed to leave intersection within ∼10 min). Loading concentrations of the motors, relative to a 7 nM myosin V stock and a 62 nM dynein stock, are shown below the bar plots. Wide solid bars represent the MT underpass, AF overpass geometry. Thin dotted bars represent the opposite geometry (MT overpass, AF underpass). Vertical error bars represent 68% confidence intervals calculated from binomial distributions. Numbers of total beads observed at each concentration ratio were between 8 and 23. Statistical significance was evaluated using Fisher's exact test with comparison to the lowest myosin V/dynein ratio: p<*0.05, **0.01, ***0.001, ****0.0001. See also Figure S1.
While beads often paused briefly at intersections, they usually continued on with either a pass or switch. The median pause time was 9 s (n=161). The percentage of beads that actually stopped at the intersection ranged from 0-45% with a trend toward higher values in the middle range of [myosin V]/[dynein] ratios where myosin V and dynein had similar probabilities of pulling the cargo onto their respective tracks (Figure 2ii).
Force Measurements on Myosin V and Dynein
The probability of a switch shows a clear dependence on the ratio of myosin V to dynein motors incubated per bead, but this ratio does not take into account the proportion of the motors that successfully attach to the cargo in the correct orientation and can simultaneously engage with the track. We used force measurements on the beads to estimate the number of motors that could actively engage the track at the various loading concentrations. It has been previously shown for cytoplasmic dynein and kinesin-1 that stall force scales with the number of actively engaged motors [20, 22].
Using a static optical trap, we measured the unitary stall force of myosin V to be 1.8 ± 0.5 pN (mean ± SD) (Figures 3A-B), which agrees with published values [32-33]. When beads were incubated with a higher myosin V concentration, an additional peak appeared in the stall force histogram centered at 3.1 pN which we attribute to the activity of 2 motors simultaneously generating force (Figures 3A-B). Detection of the second peak was confirmed using two automated methods of analysis, which relied on either the identification of force plateaus preceding sudden force drops or force maxima over a period of time (Figure S2A). The slightly subadditive nature of stall forces for myosin V mirrors findings on kinesin-1 [34]. Our dynein force measurements at the lowest dynein concentration producing detectable force events are consistent with a unitary stall force of ∼1 pN as measured earlier for cytoplasmic mammalian and Dictystelium dynein (Figure S2B) [20, 24, 35-36]. While a higher force has been reported in one study of mammalian dynein using Protein A-coated beads [37], we could not replicate this result (Figure S2C).
Figure 3.
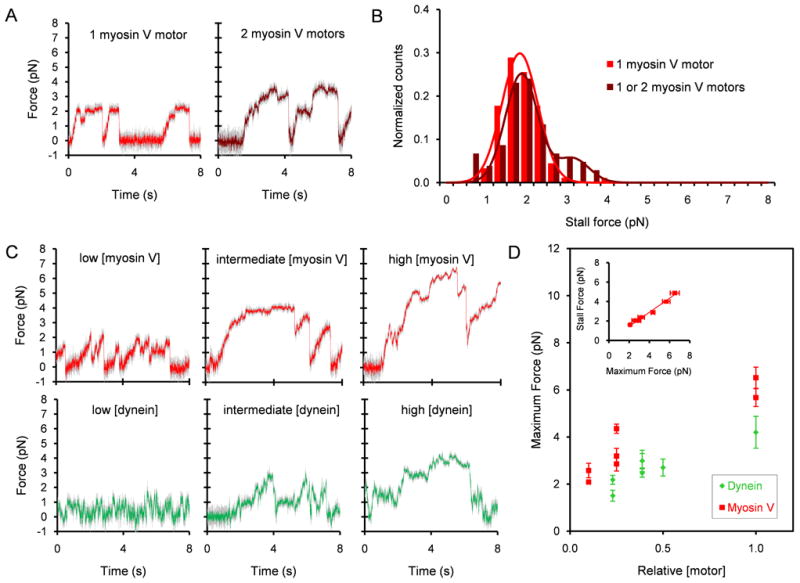
Force recordings. (A) Typical force traces, unfiltered (gray) and median filtered (red or brown, window size = 11 time points, i.e. 0.0055 s) for myosin V at two concentration ranges (0.0049 – 0.0070 nM, left panel) and 0.039 – 0.070 nM, right panel) in the absence of dynein. The trap stiffness was 0.022 pN/nm (left) and 0.040 pN/nm (right). (B) Histogram of myosin V stall force events in the absence of dynein for the same two loading concentration ranges. Only stall events that were followed by a snapback of the force trace to baseline were included. Left, n = 90 events, 11 beads; right n = 104 events, 16 beads. (C) Typical force traces, unfiltered (gray) and median filtered (red or green, window = 11), are shown for myosin V and dynein at the three loading concentrations for each motor (myosin V: low, intermediate, and high, 0.1, 0.25, and 1, respectively relative to 7 nM; dynein: 0.23, 0.39 or 0.5, and 1, respectively relative to 62 nM). The trap stiffness was 0.024 – 0.029 pN/nm. (D) Maximum force exhibited by beads coated with both myosin V and dynein versus relative loading concentrations. Each data point represents the average maximum force produced per bead in a median filtered (window = 201) force trace lasting typically 50 s. 4 – 10 beads were used for the myosin V data points and 8 - 13 beads for the dynein data points. (inset plot) Myosin V stall force exhibited by the same group of beads coated with both myosin V and dynein versus the myosin V maximum force. Only stall events that were preceded by a >36 nm displacement in the force trace away from the baseline due to motor stepping and followed by a snapback of the force trace >36 nm were used. Stall force events were pooled from multiple force traces and then averaged to obtain the population mean. Maximum and stall force measurements are plotted as mean ± SEM for 37 – 112 stall events for 4 – 9 beads. See also Figure S2.
We performed force measurements on beads coincubated with both myosin V and dynein. We define the maximum force for a bead as the largest force produced in a median filtered force trace lasting typically 50 s. Each force trace can contain multiple stalls at forces equivalent to or significantly less than the maximum force. As expected, increasing the loading myosin V concentration increased the maximum force displayed by the beads on actin filaments (Figures 3C-D; Figure S2D). Higher dynein concentrations produced higher maximum forces on microtubules (Figures 3C-D; Figure S2E). The maximum number of motors that simultaneously drove the beads at each density can be calculated by dividing the maximum force by the motor's unitary stall force (1.8 pN for myosin V and 1 pN for dynein). The observations of stall forces that are either additive or slightly subadditive for low numbers of engaged dynein [20, 24], kinesin [22], and, in this work, myosin V motors suggest that this calculation provides a reasonable approximation, which may be a slight underestimate. Thus, the beads were driven by about 1, 1-2, and 3-4 myosin V motors and 2, 2-3, and 4 dynein motors at times of maximum force production at low, intermediate, and high loading concentrations, respectively. The histogram of myosin V stall forces for beads coincubated with both myosin V and dynein shows two peaks at 1.7 and 3.1 pN at low [myosin V], again suggesting that 1 and 2 motors actively generate force. At intermediate and high [myosin V], the distributions are multimodal with peaks at higher forces (Figure S2D).
As the myosin V concentration is varied, the myosin V stall force is approximately proportional to the maximum force (R2=0.98). The slope (0.72, Figure 3D inset), of a line fitted to this relationship provides an estimate of a quantity we term the “engagement ratio,” which is the average number of engaged motors Navg relative to maximum number of engaged motors N.
Cargo Switching as a Function of the Force Ratio
From force measurements we obtain the ratio of maximum myosin V force to maximum dynein force exerted by the motor-bound beads at each set of loading concentrations. The percentage of beads exiting intersections along the AF increases with the myosin V:dynein maximum force ratio (Figure 4A). Concomitantly, the percentage of beads exiting on the MT decreases. We define the mean force for a bead as the average force produced in a median filtered force trace lasting typically 50 s including periods of detachment following the initial force event. Using the ratio of mean myosin V force to mean dynein force gives the same results (Figure S3A). These results were independent of whether the bead entered the intersection along an AF or MT (Figure S3B). As mentioned previously, employing the opposite geometry (AFs underpasses, MTs overpasses, open symbols) also did not affect the results. Importantly, the likelihood of exiting on an AF and exiting on a MT is equivalent at a myosin V:dynein maximum force ratio near unity. This result suggests that the force constitutes a major determinant of the outcome of an encounter. The percentage of beads that stop at the intersections also reaches a peak when myosin V and dynein maximum forces are approximately equal (Figure 4A).
Figure 4.
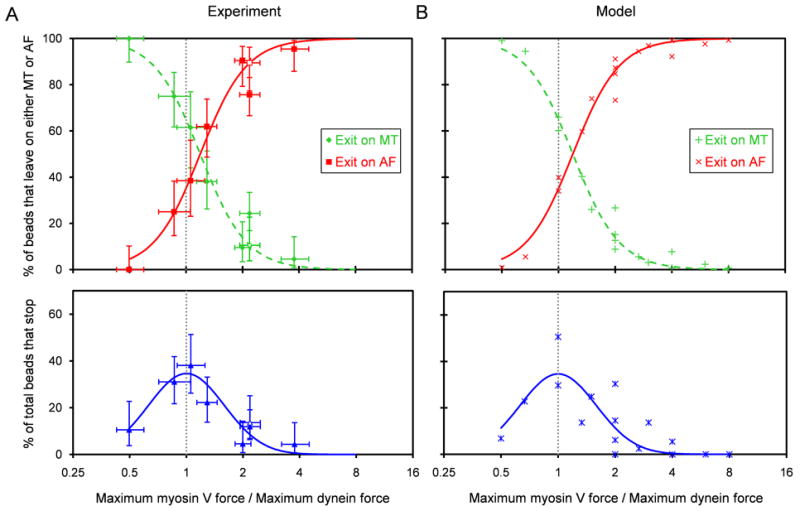
Outcomes following encounters with intersections as a function of the myosin V:dynein maximum force ratio. (A top) For beads that exited the intersections, the percentages exiting on the MT (green), and on the AF (red) are plotted versus the ratio of myosin V and dynein maximum forces from Figure 3D. (A bottom) Percentages of total beads that stopped (blue). From Figure 2, data from MT and AF starting tracks are combined here. Closed symbols represent the MT underpass, AF overpass geometry; open symbols represent the opposite geometry. Vertical error bars represent 68% confidence intervals calculated from binomial distributions. Horizontal error bars represent 68% confidence intervals of the force ratios. Note that the MT and AF exit curves cross and the “Stop” curve reaches a peak at a myosinV:dynein maximum force ratio near 1. (B) Intersection statistics versus the myosin V:dynein maximum force ratio based on the statistical model described in the text (adjustable parameters: pmyosin V=0.7 and pdynein=0.85). S-shaped and Gaussian curves fitted to the model points (see text) are plotted in both (A) and (B). Vertical gray dotted lines denote a maximum force ratio of 1. See also Figures S3 and S4.
Statistical Model
A model that takes into account the known stochastic nature of motor attachment and detachment replicates the probabilistic nature of track switching that we observed (Figure 4B). This model, used to produce the curves in Figure 4A, follows from two main premises: 1) the number of actively engaged motors, n, out of a maximum number of motors available for engagement, N, from each motor group follows a binomial distribution,
where p is the “engagement ratio,” the probability that an individual motor is engaged, and 2) the motor group producing greater force at the moment of selection, which we term the instantaneous force, pulls the bead onto its respective track. As an example, consider the case in which the motor density on the bead's surface, assuming a random distribution, allows a maximum of 2 myosin V motors and 2 dynein motors to actively engage their tracks. The myosin V:dynein maximum force ratio (x-coordinate in Fig 4B) is calculated as the product of Fs myosin V/Fs dynein (which for simplicity we approximate as 2) and Nmyosin V/Ndynein. The myosin V:dynein instantaneous force ratio is the product of Fs myosin V/Fs dynein and nmyosin V/ndynein. A binomial distribution, with pmyosin V (myosin V's engagement ratio), gives the probability that nmyosin V motors over the range 0 through Nmyosin V are actually engaged. A second binomial distribution gives the probability that ndynein motors are engaged. For the case in which maximally 2 motors of each type are available, the probability for each of the 9 possible combinations of engaged motors (nmyosin V=0, 1, or 2 vs. ndynein=0, 1, or 2) is a product of the probabilities given by the two binomial distributions. Each combination has one of four possible outcomes: (1) dissociation from both tracks (nmyosin V=ndynein=0), (2) exit along the AF (myosin V:dynein instantaneous force ratio > 1), (3) exit along the MT (myosin V:dynein instantaneous force ratio < 1), and (4) stop (myosin V:dynein instantaneous force ratio=1). Thus, the total probability of an exit along the AF, an exit along the MT, and a stop (y coordinate in Figure 4B) can be calculated for each case of a maximum of Nmyosin V motors and Ndynein motors. This process was followed for the 16 possible cases in which a maximum of 1-4 myosin V and 1-4 dynein engaged motors were combined on a cargo, and the corresponding percentages are plotted in Figure 4B. The resulting percentages for exiting along AFs and MTs were fit using the S-shaped curve of the form, y=100/(1+e-(x-b)/c), and the percentages of cargos stopping (equal instantaneous force of the two motor groups) using a Gaussian curve. For both curves, the independent variable is the logarithm of the myosin V:dynein maximum force ratio. The same fitted curves were overlaid on the experimental data in Figure 4A. The only adjustable parameters in fitting this simple statistical model to the data are the two engagement ratios, pmyosin V and pdynein. Good agreement with experimental data was obtained using p values of 0.7 and 0.85 for myosin V and dynein, respectively (Figure 4). Sensitivity of the model predictions to changes in these two parameters is shown in Figure S4. The predicted curves would shift leftward if Pmyosin V were increased and rightward if Pdynein were increased. If both engagement ratios were raised, the model curves would steepen, and in the limit of Pmyosin V=Pdynein=1 (no stochastic detachment), the model curves would become abrupt step functions that cross at the position of equal force. The data on passing and switching probabilities explained by the statistical likelihood of motor engagement show that motor number alone can be effective for controlling the probability that a cargo will switch tracks apparently through a simple force-mediated mechanism.
Pauses and Rotation at Filament Intersections
Beads coincubated with myosin V and dynein motors usually paused at MT-AF intersections and occasionally deflected one filament with respect to the other or shifted off axis before passing. These results indicate that both motor groups simultaneously engage their tracks at the intersections. Only 15% of beads exhibited a pause time at the intersection of <2 s (n=30 out of 205 beads), and, of those beads that passed or switched, the median pause time was 9 s (n=161). The shortest pause times occurred at the largest myosin V:dynein maximum force ratio tested (∼4); the duration of pausing at this force ratio was significantly shorter than pause times at lower force ratios (<2) (Figure 5A).
Figure 5.
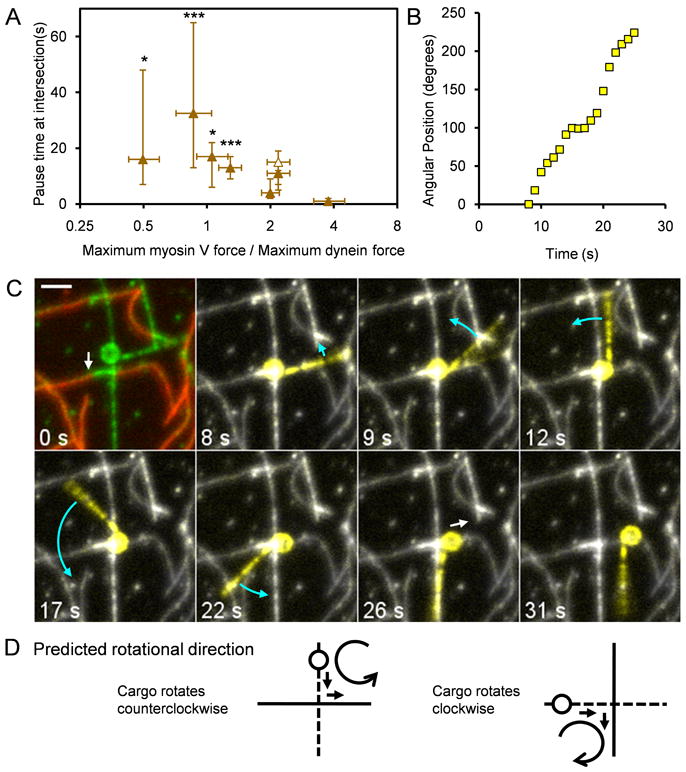
Beads pause and rotate at MT-AF intersections. (A) Plot of the pause time at intersections versus the ratio of the myosin V and dynein forces from Figure 3D. The shortest pause times occurred at the largest myosin V:dynein maximum force ratio of 3.8. Pause times at force ratios below 2 were statistically different from the shortest group (Fisher's exact test, p<*0.05, ***0.001). Closed symbols represent the MT underpass, AF overpass geometry; open symbols, the opposite geometry. Measurements are plotted as median ± 68% confidence intervals calculated from binomial distributions. 13 – 37 beads were included in each point. (B) Angular position vs. time for a myosin V and dynein coated bead while paused at a MT-AF intersection. (C) Sequence of images of the same bead used for panel (B) undergoing rotation. The bead approached the intersection on a MT underpass, rotated at least 224° at the intersection as indicated by the rigidly attached MT fragment, and exited on an AF overpass. White and blue arrows denote predominantly translational and rotational movement, respectively. In the first image, green and red represent rhodamine (AF and MTs) and Alexa 647 fluorescence (AFs), respectively. In the subsequent images, the motile bead and attached MT were highlighted in yellow by displaying the difference between the median z-projection for the entire 100 s rhodamine fluorescence movie and the data of each frame. The scale bar represents 2 μm. (D) Schematic showing the predicted direction of rotation of a bead that approaches an intersection from an underpass (dotted line) and switches onto an overpass (solid line) based on the force vectors operating on the bead (arrows). See also Movies S3 and S4.
While beads were paused at intersections, they often rotated about an axis approximately normal to the slide surface. In Figures 5B and 5C, a bead is shown with a fortuitously attached microtubule that serves as a fiduciary marker. The bead, approaching along an underpass MT, rotated counterclockwise at least 224° at the filament intersection (mean angular velocity of 13°/s) before exiting on the overpass AF (Movie S3). Speckles of fluorescence from rhodamine BSA sparsely bound to the beads enabled us to monitor rotation of many beads (Movie S4). At least 23% of beads were observed to rotate at the intersections (n=47 out of 205 beads). This percentage likely represents an underestimate since rotation was occasionally difficult to score if the BSA fluorescence was not sufficiently speckled. The median angular displacement per rotating bead was 69° with a range of 15° to 849°. Rotations often occurred at intersections but were rare during translocation along a single MT or AF. We found no clear dependence of the extent of rotation per encounter on the myosinV:dynein maximum force ratio.
Rotation of beads at intersections indicated that competing motors apply a torque on the bead at the intersection until one class of motors eventually “wins”. If this explanation is correct, the direction of rotation should be predictable from the position of the bead relative to the intersection and the directions of the two force vectors. The latter directions are known based on directions of bead transport before and after the pause. Most of the current data were collected with MT underpasses and AF overpasses. With this geometry, a cargo entering from the MT and exiting on the AF enables the clearest prediction for rotational direction because the AF constitutes an obstacle encountered while the bead is on the near side of the intersection, i.e. the interaction with the AF occurs at the leading edge of the bead assuming the average motor density is uniform over the bead surface. Indeed, 10 out of 11 beads with this geometry and with detectable rotation turned in the expected direction (Figure 5D). Encounters resulting in a “pass” or “stop,” as well as encounters from an overpass, are more difficult to predict because the interaction with the crossing filament might take place before and/or after the center of the intersection. In these cases, the direction of rotation appeared to be random (n=11).
Discussion
We used an in vitro system to test whether switching of polymer bead cargos at microtubule-actin filament intersections can be regulated solely via the number of engaged myosin V and dynein motors through a tug-of-war mechanism. We measured the forces produced by the motors along their respective tracks with an optical trap and found for both myosin V and dynein that these forces scaled with motor number (Figure 3). When the density of myosin V on the bead was high relative to dynein so that the ratio of maximum myosin V force along actin was greater than the maximum force of dynein along the MT, the beads most often continued along the AF or switched onto it after encountering a MT-AF intersection. Similarly, when the maximum dynein force was greater than the myosin V force, the beads primarily continued along the MT or switched onto it at an intersection. When the forces of the two motors were approximately equal, the beads stopped at the MT-AF intersection, left the intersection on their starting filament, or switched onto the other filament with about equal probability (Figures 4 and 6). These results are consistent with a straightforward model of track switching by beads in vitro in which the maximum force exerted by the motors determines the outcome at the intersection, a “tug of war” between the two types of motors (Figure 4).
Figure 6.
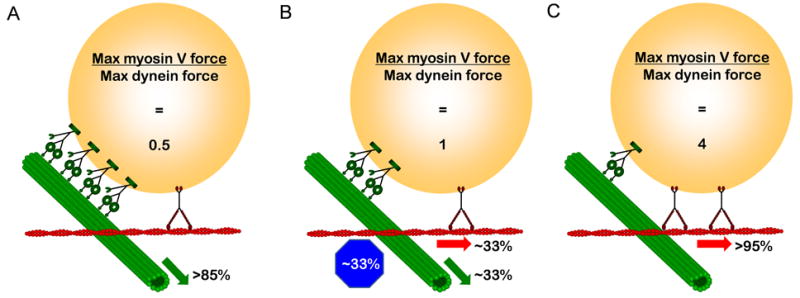
Cartoon of tug-of-war scenarios in which number of motors control cargo switching at MT-AF intersections. (A) At myosin V:dynein maximum force ratio of 0.5 (1 myosin V per 4 dyneins), the cargo mostly exits on the MT. (B) At a force ratio of 1 (1 myosin V per 2 dyneins), the cargo has an approximately equal chance of stopping at the intersection, exiting on the AF, or exiting on the MT. (C) At a myosin V:dynein force ratio of 4 (2 myosin Vs per dynein), the cargo mostly exits on the AF.
Pausing of beads at the intersections, rotation of beads about an axis normal to the glass surface, and bending of the filaments or deflection of the bead trajectory from a straight path indicate that beads containing dynein-dynactin and myosin V interact with both filaments simultaneously at the intersections. The likelihood of pausing, passing through the intersections, or switching to the crossing track is fairly independent of whether an AF or MT is the starting filament or which filament type is closer to the glass. This independence of the geometry at the intersection seemed surprising at first but is most easily explained by the simultaneous interaction with both filaments. When a bead enters the intersection from an underpass (the filament closer to the glass), the overlying crossing filament is an obstacle, so simultaneous interaction is obligatory. When the bead enters from the overpass (the filament farther from the glass), though, the dual interaction suggests that the bead wobbles enough as it translocates that it comes into contact with the crossing filament below. We speculate that once both motor types on a bead are engaged with both filaments, the initial conditions become irrelevant.
The optical trap force measurements led to estimates of the number of myosin V and dynein motors actively engaged with their respective filaments at the various loading concentrations. It had been shown previously that stall force scales with the number of actively engaged kinesin-1 and dynein motors [20, 22, 24]. We found that this behavior is true for myosin V, as well (Figures 3A-B). Based on maximum force measurements (Figure 3D), we estimate that beads incubated with the lowest ratio of myosin V to dynein motors used had ∼1 myosin V motor and ∼4 dynein motors engaged at the time of maximum force production at the intersection. These beads always exited on the MT (Figure 2). Beads incubated with the highest ratio of myosin V to dynein motors used had ∼3-4 myosin V motors and ∼2 dynein motors engaged at the intersections and exited on the AFs 90-100% of the time (Figure 2). Thus, the probability of switching filaments can be tuned by pairing 1-4 myosin V motors and 1-4 dynein motors on a cargo.
These low motor numbers agree with estimates for the number of actively engaged motors driving cargos in vivo. In vivo optical trapping of motile lipid droplets in Drosophila embryos and evidence from cryo-electron microscopy (cryo-EM) indicate that the number of engaged MT motors may typically range between 1 and 5 [17, 38]. Endosomes purified from Dictyostelium cells display forces consistent with the engagement of 1 kinesin and 4-8 dyneins [36]. Photobleaching and quantitative western blotting of vesicles containing GFP-dynamitin purified from mouse brain combined with mathematical modeling of the in vitro motility of these purified vesicles provide an estimate for the number of engaged motors in a similar range [A.G. Hendricks, J.L. Ross, E. Perlson, H.W. Schroeder III, M. Tokito, and E.L.F. Holzbaur, unpublished data]. Less information is available on the number of myosin V motors driving cargos, but indirect statistical estimates suggest that 1 – 2 myosin V's may be engaged in transporting Xenopus melanosomes [39].
The simple statistical model fitted to the data (Figure 4 and S8) is similar to that of Müller, et al. [40]. In their work, they applied statistical distributions of engaged motors to simulate dynein and kinesin pulling a cargo in opposite directions along the MT axis. Due to stochastic changes in the number of engaged motors and the force dependence of the unbinding rate, the formerly predominant motors are forcibly detached and the direction of transport is reversed.
The situation in our experiments differs from the scenario modeled by Müller et al. because the two motor types, myosin V and dynein, simultaneously engage only near a filament intersection at which point they can exert sideways forces on one another that are perpendicular to their direction of travel. In vitro studies show that myosin V and kinesin-1 are relatively resistant to sideways deflection. Forces that would stall the motor(s) from moving forward often failed to detach the motor(s) when applied in the sideways direction [22, 41-42]. We also observed that beads were more likely to detach from both MTs and AFs if we applied alternating forward and backward loads near the stall force than alternating left and right sideways loads. Nevertheless, the probabilities of switching onto the crossing filaments were closely related to the relative axial stall forces, indicating that sideways detachment forces scale with motor number as do the maximum axial forces.
Once the maximum numbers of motors available for engagement with the filaments (1-4 myosin Vs or dyneins) and the unitary stall force ratio (Fs myosin V/Fs dynein = 2) are set, the only parameters that are adjustable in fitting the model to the data are the engagement ratios, pmyosin V and pdynein, for the two motors. The engagement ratio is similar to the duty ratio of a single motor head, but here it is the proportion of time the double-headed molecule stays attached under load. For myosin V, the optical trap data allowed an estimate of pmyosin V of ∼0.7 from the ratio of average stall force during bead-actin interactions and the maximum force (Figure 3D inset). For dynein, setting pdynein to 0.85, provided the best fit to the data. Interestingly, the value of 0.85 for pdynein is very close to the value of 0.86 calculated by dividing the dynein on rate constant by the sum of the on (1.6 s-1) and off (0.27 s-1) rate constants found by Müller et al. [40] to fit the bidirectional switching of lipid droplets in Drosophila embryos.
What are the physical processes that lead to a bead pausing at the intersection and then suddenly exiting along one of the filaments? Beads pause at intersections, especially when the forces applied by the dynein and myosin V motors are nearly equal. During these pauses, the occasional rotation of the bead around an axis perpendicular to the plane of the slide suggests that a torque is applied by the concurrent action of the two motor types. As the bead rotates, the bound motors will be affected differentially by forward, backward, and sideways forces, based on their attachment points on the bead relative to the axis of rotation. These forces may affect the kinetics of motor attachment/detachment, in a tug-of-war that is expected to continue until there is a clear difference in the relative forces generated by engaged motors of each type. Pausing time at intersections correlates with balance of forces, and observed rotations > 360° indicate that this tug-of-war is sometimes prolonged. However, once the moment of selection is reached, the bead exits the intersection along the filament track of the dominant class of motor.
In the cell, the transfer of cargos from the microtubule to the actin network and back may occur via a coordinated mechanism in which the MT motors disengage from their track(s), and subsequently, the AF motors engage their track(s) and vice versa. However, evidence from studies on mouse melanocytes, neurons, macrophages, and Xenopus melanophores points toward a tug-of-war mechanism in which both motor classes, the MT motors and the AF motors, simultaneously engage and compete for their respective tracks [7, 12, 15-16]. In both cases, regulation of cargo switching could occur via control of motor-cargo attachment, motor activity, and/or modification of the tracks [17]. Our experimental data shows that alteration of the maximum number of engaged motors, Nmyosin V and Ndynein, alone permits control of cargo switching at MT-AF intersections in vitro. The data fit a straightforward model that provides a framework for understanding one possible mechanism for transfer of cargos between the MT and AF cytoskeletal networks, a crucial step in many cellular functions such as endocytosis and secretion.
Experimental Procedures
Protein Preparation
Rabbit muscle G-actin was purified as described [43]. F-actin was prepared from G-actin, Alexa 647-actin (Invitrogen, Inc.), and biotin-actin (Cytoskeleton, Inc.) at 1 μM total actin monomer concentration with a ratio of 21:15:1 of G-actin:Alexa 647:biotin and stabilized with 1.1 μM rhodamine phalloidin (Invitrogen, Inc.). Microtubules were prepared from unlabelled tubulin, rhodamine-tubulin, and biotin-tubulin at 45 μM tubulin dimer with a ratio of 50:2:1.5 of tubulin dimer:rhodamine:biotin and stabilized with 40 μM Taxol (all four reagents from Cytoskeleton, Inc.). Wild-type chicken calmodulin (CaM) was expressed in bacteria and purified [44]. Chick brain myosin V was purified as described [45] and stored at -80°C at a concentration of 422 nM myosin dimer as determined by Bradford protein assay (Bio-Rad). Bovine brain cytoplasmic dynein-dynactin was isolated by microtubule-affinity ATP extraction and sucrose density gradient fractionation as described [46], supplemented with 25% (w/v) sucrose, rapidly frozen, and stored at -196°C. Purity and integrity of the dynein-dynactin complex was assessed by Coomassie blue staining of SDS-PAGE gels and Western blotting for dynein and dynactin subunits. The concentration of dynein dimer for typical protein preps was determined to be 125-150 nM by Sypro Red (Sigma, Inc.) staining calibrated by a dilution series of purified recombinant dynein intermediate chain (DIC) run on the same gels.
In Vitro Motility Assay with Cytoskeletal Intersections
Flow chambers (∼10 uL volume) were assembled from two cover slips bound at the corners by double-sided adhesive tape to make two perpendicular crossed flow paths, denoted as the x- and y-directions (Figure 1A). Microtubules and actin filaments were bound to the cover slips via biotin-streptavidin linkers. First, 10 μL of 1 mg/mL biotinylated-BSA (Sigma) in actin buffer (AB: 25 mM imidazole, 25 mM KCl, 4 mM MgCl2, 1 mM EGTA, 10 mM DTT, pH 7.4) was flowed in to coat the cover slips, incubated for 2 min, and washed out in both the x- and y-directions with two chamber volumes of wash buffer (WB, AB supplemented with 1 mg/mL BSA and 20 μM Taxol, used for all washes below). Second, 10 μL of AB with 2 mg/mL streptavidin was flowed in both directions, incubated for 2 min, and washed out in both directions. Third, 10 μL of rhodamine-labeled, biotinylated microtubules (0.45 μM tubulin dimer) in 10 mM Na-PIPES, 50 mM potassium acetate, 5 mM MgSO4, 1 mM EGTA, pH 7.0, with 20 μM Taxol, were flowed into the chamber in the y-direction and incubated for 30 s; this step was repeated two times and then followed by a wash in the y-direction with two chamber volumes. Fourth, 10 μL of rhodamine phalloidin-labeled, biotinylated, Alexa-647-labeled actin filaments (50 nM actin monomer) in AB with 20 μM Taxol were flowed into the chamber in the x-direction and incubated for 1 min; this step was repeated a second time and then followed by a wash in the x-direction with two chamber volumes. Note that we term the MTs flowed along the y-axis as “underpasses” and the AFs subsequently flowed along the x-axis as “overpasses” because the MTs are closer to the glass at MT-AF intersections. Fifth, 10 μL of AB with 5 mg/mL casein and 20 μM Taxol was flowed in the y-direction, incubated for 1 min, and washed out in both directions with one chamber volume of motility wash buffer (MWB, WB supplemented with 60 μg/mL CaM, 2 mM ATP, 10 mM phosphocreatine, 0.45 mg/mL creatine phosphokinase, 3 mg/mL glucose, 100 μg/mL glucose oxidase, and 40 μg/mL catalase). In order to create the opposite geometry, the order of adding microtubules and actin (steps 3 and 4) was reversed.
Bead motility solution was made in the following order: (i) polystyrene beads (1 μm diameter, 2.5% solids, Polysciences) were pre-blocked by diluting 1:100 in AB with 5 μg/mL rhodmaine BSA (3-15% tetramethylrhodamine isothiocyanate BSA, Sigma, Inc.), 2 min incubation, (ii) pre-blocked beads were mixed 1:1 with a mixed motor solution containing myosin V (0.72, 1.8, or 7.2 nM dimer concentration) and dynein-dynactin (at 14, 24, 31, or 62 nM dimer concentration), 2 min incubation, (iii) motor-coated pre-blocked beads were blocked from binding additional motors by adding 1 mg/mL casein in AB, (iv) the beads were added to MWB described above. 10 μL of this bead mixture was flowed in the y-direction, and the flow cell was sealed with vacuum grease. For experiments on myosin V alone, flow cells were constructed with a single channel, addition of MTs and Taxol was omitted, and pre-blocked beads were mixed 1:1 with a motor solution containing only myosin V (0.0049, 0.0070, 0.039, or 0.070 nM dimer concentration). At 0.0049 and 0.0070 nM loading concentrations, ≤0.5 of the beads bound to actin filaments. Thus, by Poisson statistics, the probability that a bead has two or more bound motors is <0.14 [47]. For experiments on dynein-dynactin alone, flow cells were constructed with a single channel, addition of AFs was omitted, and pre-blocked beads were mixed 1:1 with a motor solution containing only dynein-dynactin (0.041, 0.12, 0.41, 4.1 nM dimer concentration).
Instrumentation and Analysis
Filaments and beads were viewed by epifluorescence microscopy on an inverted microscope (Olympus, Inc. IX71). The beads were captured with an optical trap and positioned onto MTs or AFs near MT-AF intersections. Image sequences were collected at 1 frame/s using a CCD camera (Hamamatsu, Inc., ORCA-ER C4742-95-12ER) or an electron multiplying CCD camera (Andor, Inc., IXON DV887DCS-BV). Image analysis was performed using ImageJ (NIH). The same optical trap setup described by Takagi et al. [48] was applied to the Olympus microscope with water immersion lenses (objective: UPlanApo/IR 60×, condenser: PlanApoUV 60x) with the modification that only one trap was used. Trap stiffness was measured by fitting a Lorentzian to the power spectrum of thermal oscillations of a trapped bead [49]. Trap stiffness values were between 0.02 and 0.04 pN/nm. For force measurements, quandrant photo-diode (QPD) data were anti-alias filtered at 1 KHz and digitized at 2 KHz for 50 - 200 second intervals. All track switching measurements and force measurements were performed on the same microscope. In a given experiment, force measurements were typically performed on different beads from those used for the track switching measurements to avoid motor damage due to prolonged exposure to the infrared laser light. Data acquisition and analysis were performed using custom software written in LabVIEW (National Instruments) and MATLAB (The Mathworks).
Highlights.
MT-AF cargo switching depends on the myosin V:dynein-dynactin force ratio
Force scales with the number of myosin V and dynein-dynactin motors
A statistical model relates switching probability to motor number
Pairing of 1-4 motors of each type is sufficient to modulate cargo switching
Supplementary Material
Acknowledgments
We thank J.F. Beausang, X. Cui, A.G. Hendricks, R. Kuduravalli, M. Pring, J.L. Ross, and M. Tokito for technical assistance and helpful suggestions and J.A. Hammer III for the kind gift of the anti-myosin V antibody. This work was supported by NIH grants P01 GM087253 (to E.L.F.H. and Y.E.G.) and GM-071339 (to H.W.S.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Caviston JP, Holzbaur EL. Microtubule motors at the intersection of trafficking and transport. Trends Cell Biol. 2006;16:530–537. doi: 10.1016/j.tcb.2006.08.002. [DOI] [PubMed] [Google Scholar]
- 2.Guzik BW, Goldstein LS. Microtubule-dependent transport in neurons: steps towards an understanding of regulation, function and dysfunction. Curr Opin Cell Biol. 2004;16:443–450. doi: 10.1016/j.ceb.2004.06.002. [DOI] [PubMed] [Google Scholar]
- 3.Vale RD. The molecular motor toolbox for intracellular transport. Cell. 2003;112:467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
- 4.Krendel M, Mooseker MS. Myosins: tails (and heads) of functional diversity. Physiology (Bethesda) 2005;20:239–251. doi: 10.1152/physiol.00014.2005. [DOI] [PubMed] [Google Scholar]
- 5.Kuznetsov SA, Langford GM, Weiss DG. Actin-dependent organelle movement in squid axoplasm. Nature. 1992;356:722–725. doi: 10.1038/356722a0. [DOI] [PubMed] [Google Scholar]
- 6.Morris RL, Hollenbeck PJ. Axonal transport of mitochondria along microtubules and F-actin in living vertebrate neurons. J Cell Biol. 1995;131:1315–1326. doi: 10.1083/jcb.131.5.1315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bridgman PC. Myosin Va movements in normal and dilute-lethal axons provide support for a dual filament motor complex. J Cell Biol. 1999;146:1045–1060. doi: 10.1083/jcb.146.5.1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jung G, Titus MA, Hammer JA., 3rd The Dictyostelium type V myosin MyoJ is responsible for the cortical association and motility of contractile vacuole membranes. J Cell Biol. 2009;186:555–570. doi: 10.1083/jcb.200810147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rodionov VI, Hope AJ, Svitkina TM, Borisy GG. Functional coordination of microtubule-based and actin-based motility in melanophores. Curr Biol. 1998;8:165–168. doi: 10.1016/s0960-9822(98)70064-8. [DOI] [PubMed] [Google Scholar]
- 10.Rogers SL, Gelfand VI. Myosin cooperates with microtubule motors during organelle transport in melanophores. Curr Biol. 1998;8:161–164. doi: 10.1016/s0960-9822(98)70063-6. [DOI] [PubMed] [Google Scholar]
- 11.Langford GM. Actin- and microtubule-dependent organelle motors: interrelationships between the two motility systems. Curr Opin Cell Biol. 1995;7:82–88. doi: 10.1016/0955-0674(95)80048-4. [DOI] [PubMed] [Google Scholar]
- 12.Wu X, Bowers B, Rao K, Wei Q, Hammer JA., 3rd Visualization of melanosome dynamics within wild-type and dilute melanocytes suggests a paradigm for myosin V function In vivo. J Cell Biol. 1998;143:1899–1918. doi: 10.1083/jcb.143.7.1899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Woolner S, Bement WM. Unconventional myosins acting unconventionally. Trends Cell Biol. 2009;19:245–252. doi: 10.1016/j.tcb.2009.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tabb JS, Molyneaux BJ, Cohen DL, Kuznetsov SA, Langford GM. Transport of ER vesicles on actin filaments in neurons by myosin V. J Cell Sci. 1998;111(Pt 21):3221–3234. doi: 10.1242/jcs.111.21.3221. [DOI] [PubMed] [Google Scholar]
- 15.Al-Haddad A, Shonn MA, Redlich B, Blocker A, Burkhardt JK, Yu H, Hammer JA, 3rd, Weiss DG, Steffen W, Griffiths G, et al. Myosin Va bound to phagosomes binds to F-actin and delays microtubule-dependent motility. Mol Biol Cell. 2001;12:2742–2755. doi: 10.1091/mbc.12.9.2742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gross SP, Tuma MC, Deacon SW, Serpinskaya AS, Reilein AR, Gelfand VI. Interactions and regulation of molecular motors in Xenopus melanophores. J Cell Biol. 2002;156:855–865. doi: 10.1083/jcb.200105055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gross SP, Vershinin M, Shubeita GT. Cargo transport: two motors are sometimes better than one. Curr Biol. 2007;17:R478–486. doi: 10.1016/j.cub.2007.04.025. [DOI] [PubMed] [Google Scholar]
- 18.Ross JL, Ali MY, Warshaw DM. Cargo transport: molecular motors navigate a complex cytoskeleton. Curr Opin Cell Biol. 2008;20:41–47. doi: 10.1016/j.ceb.2007.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Holzbaur EL, Goldman YE. Coordination of Molecular Motors: From in Vitro Assays to Intracellular Dynamics. Curr Opin Cell Biol. doi: 10.1016/j.ceb.2009.12.014. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mallik R, Petrov D, Lex SA, King SJ, Gross SP. Building complexity: an in vitro study of cytoplasmic dynein with in vivo implications. Curr Biol. 2005;15:2075–2085. doi: 10.1016/j.cub.2005.10.039. [DOI] [PubMed] [Google Scholar]
- 21.Leduc C, Ruhnow F, Howard J, Diez S. Detection of fractional steps in cargo movement by the collective operation of kinesin-1 motors. Proc Natl Acad Sci U S A. 2007;104:10847–10852. doi: 10.1073/pnas.0701864104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vershinin M, Carter BC, Razafsky DS, King SJ, Gross SP. Multiple-motor based transport and its regulation by Tau. Proc Natl Acad Sci U S A. 2007;104:87–92. doi: 10.1073/pnas.0607919104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dixit R, Ross JL, Goldman YE, Holzbaur EL. Differential regulation of dynein and kinesin motor proteins by tau. Science. 2008;319:1086–1089. doi: 10.1126/science.1152993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vershinin M, Xu J, Razafsky DS, King SJ, Gross SP. Tuning microtubule-based transport through filamentous MAPs: the problem of dynein. Traffic. 2008;9:882–892. doi: 10.1111/j.1600-0854.2008.00741.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ali MY, Lu H, Bookwalter CS, Warshaw DM, Trybus KM. Myosin V and Kinesin act as tethers to enhance each others' processivity. Proc Natl Acad Sci U S A. 2008;105:4691–4696. doi: 10.1073/pnas.0711531105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ross JL, Shuman H, Holzbaur EL, Goldman YE. Kinesin and dynein-dynactin at intersecting microtubules: motor density affects dynein function. Biophys J. 2008;94:3115–3125. doi: 10.1529/biophysj.107.120014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ali MY, Krementsova EB, Kennedy GG, Mahaffy R, Pollard TD, Trybus KM, Warshaw DM. Myosin Va maneuvers through actin intersections and diffuses along microtubules. Proc Natl Acad Sci U S A. 2007;104:4332–4336. doi: 10.1073/pnas.0611471104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Karki S, Holzbaur EL. Cytoplasmic dynein and dynactin in cell division and intracellular transport. Curr Opin Cell Biol. 1999;11:45–53. doi: 10.1016/s0955-0674(99)80006-4. [DOI] [PubMed] [Google Scholar]
- 29.Schroer TA. Dynactin. Annu Rev Cell Dev Biol. 2004;20:759–779. doi: 10.1146/annurev.cellbio.20.012103.094623. [DOI] [PubMed] [Google Scholar]
- 30.King SJ, Schroer TA. Dynactin increases the processivity of the cytoplasmic dynein motor. Nat Cell Biol. 2000;2:20–24. doi: 10.1038/71338. [DOI] [PubMed] [Google Scholar]
- 31.Kardon JR, Reck-Peterson SL, Vale RD. Regulation of the processivity and intracellular localization of Saccharomyces cerevisiae dynein by dynactin. Proc Natl Acad Sci U S A. 2009;106:5669–5674. doi: 10.1073/pnas.0900976106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Clemen AE, Vilfan M, Jaud J, Zhang J, Barmann M, Rief M. Force-dependent stepping kinetics of myosin-V. Biophys J. 2005;88:4402–4410. doi: 10.1529/biophysj.104.053504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kad NM, Trybus KM, Warshaw DM. Load and Pi control flux through the branched kinetic cycle of myosin V. J Biol Chem. 2008;283:17477–17484. doi: 10.1074/jbc.M800539200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kunwar A, Vershinin M, Xu J, Gross SP. Stepping, strain gating, and an unexpected force-velocity curve for multiple-motor-based transport. Curr Biol. 2008;18:1173–1183. doi: 10.1016/j.cub.2008.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mallik R, Carter BC, Lex SA, King SJ, Gross SP. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- 36.Soppina V, Rai AK, Ramaiya AJ, Barak P, Mallik R. Tug-of-war between dissimilar teams of microtubule motors regulates transport and fission of endosomes. Proc Natl Acad Sci U S A. 2009 doi: 10.1073/pnas.0906524106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Toba S, Watanabe TM, Yamaguchi-Okimoto L, Toyoshima YY, Higuchi H. Overlapping hand-over-hand mechanism of single molecular motility of cytoplasmic dynein. Proc Natl Acad Sci U S A. 2006;103:5741–5745. doi: 10.1073/pnas.0508511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shubeita GT, Tran SL, Xu J, Vershinin M, Cermelli S, Cotton SL, Welte MA, Gross SP. Consequences of motor copy number on the intracellular transport of kinesin-1-driven lipid droplets. Cell. 2008;135:1098–1107. doi: 10.1016/j.cell.2008.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Snider J, Lin F, Zahedi N, Rodionov V, Yu CC, Gross SP. Intracellular actin-based transport: how far you go depends on how often you switch. Proc Natl Acad Sci U S A. 2004;101:13204–13209. doi: 10.1073/pnas.0403092101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Muller MJ, Klumpp S, Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc Natl Acad Sci U S A. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Block SM, Asbury CL, Shaevitz JW, Lang MJ. Probing the kinesin reaction cycle with a 2D optical force clamp. Proc Natl Acad Sci U S A. 2003;100:2351–2356. doi: 10.1073/pnas.0436709100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gebhardt JC, Clemen AE, Jaud J, Rief M. Myosin-V is a mechanical ratchet. Proc Natl Acad Sci U S A. 2006;103:8680–8685. doi: 10.1073/pnas.0510191103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pardee JD, Spudich JA. Purification of muscle actin. Methods Cell Biol. 1982;24:271–289. doi: 10.1016/s0091-679x(08)60661-5. [DOI] [PubMed] [Google Scholar]
- 44.Putkey JA, Slaughter GR, Means AR. Bacterial expression and characterization of proteins derived from the chicken calmodulin cDNA and a calmodulin processed gene. J Biol Chem. 1985;260:4704–4712. [PubMed] [Google Scholar]
- 45.Cheney RE. Purification and assay of myosin V. Methods Enzymol. 1998;298:3–18. doi: 10.1016/s0076-6879(98)98003-x. [DOI] [PubMed] [Google Scholar]
- 46.Steffen W, Hodgkinson JL, Wiche G. Immunogold localisation of the intermediate chain within the protein complex of cytoplasmic dynein. J Struct Biol. 1996;117:227–235. doi: 10.1006/jsbi.1996.0087. [DOI] [PubMed] [Google Scholar]
- 47.Svoboda K, Block SM. Force and velocity measured for single kinesin molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 48.Takagi Y, Homsher EE, Goldman YE, Shuman H. Force generation in single conventional actomyosin complexes under high dynamic load. Biophys J. 2006;90:1295–1307. doi: 10.1529/biophysj.105.068429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Svoboda K, Block SM. Biological applications of optical forces. Annu Rev Biophys Biomol Struct. 1994;23:247–285. doi: 10.1146/annurev.bb.23.060194.001335. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


