Chronic Disease Modeling and Simulation Software

Abstract

Computers allow describing the progress of a disease using computerized models. These models allow aggregating expert and clinical information to allow researchers and decision makers to forecast disease progression. To make this forecast reliable, good models and therefore good modeling tools are required. This paper will describe a new computer tool designed for chronic disease modeling. The modeling capabilities of this tool were used to model the Michigan model for diabetes. The modeling approach and its advantages such as simplicity, availability, and transparency are discussed.

1. Introduction

Chronic diseases have a significant impact on national health. A chronic disease such as diabetes may develop over a long time period and may involve many complications. Conducting longitudinal clinical trials to cover such long periods of time is a difficult task from practical reasons. This is one reason why computer models are gaining popularity.

Perhaps the best sign for this increase in popularity is the diversity of disease models that can be found in the literature [1]. Another sign for the popularity is the need for proper modeling guidelines for general disease modeling [2], and specifically for diabetes [3].

Diabetes models are evaluated during the Mount Hood conference [4]. This is a main stage for models to be compared and contrasted. Yet, even in such environments, comparing models is difficult since models are not necessarily accessible. Accessibility to researchers varies between proprietary models, where little is known about internals, to full transparency where the model structure and software tools are available for researchers. This varied access is shown on notable models from the Mount Hood conference.

For example, the Archimedes model [5,6,7] is commercial and proprietary, which makes it less accessible to researchers. In contrast, the software for the Centers for Disease Control and Prevention / Research Triangle Institute (CDC/RTI) model [8] is not published, yet the model is described in details in their Technical report [9]. The Eagle simulation model [10] is also available upon request as a technical report [11]. The global diabetes model also reveals modeling equations in [12]. The United Kingdom Prospective Diabetes Study (UKPDS) Outcomes Model [13] is even more accessible: not only it is described in details in their publications, it is also provided as software that can be requested through their web site http://www.dtu.ox.ac.uk/outcomesmodel/index.php. The most accessible diabetes model to date, however, is the Michigan model for diabetes. It is the most transparent one since it is fully documented, and upon accepting the license terms it is freely available for download from the web site http://www.med.umich.edu/mdrtc/cores/DiseaseModel/model.htm

Even with accessible models, often a user would like the ability to modify it at some point. Thus, a basic and necessary requirement from the software is to allow manipulation of model parameters. However, the ability to easily modify the structure (topology) of the disease model, or the ability to create new disease processes using the same software tool are more advanced, and therefore typically overlooked. For example, the models mentioned above such as the UKPDS model or the CDC/RTI model do not describe how a new disease process can be added or removed. Even these publicly assessable disease model software tools do not focus on providing a modeling environment that allows manipulating the structure of the disease model.

In this paper, we will present disease modeling software that provides a platform where users can define the structure and the parameters to implement their disease models. This general modeling environment includes a Graphical User Interface (GUI), model parameter estimation software, and a simulation compiler, and it is published freely with open source under General Public License (GPL). This set of modeling tools allows users to run, modify, estimate, and create new models using the same set of tools.

Beyond handy modeling tools, we use a combination of a simplified modeling approach based on state transitions and a free modeling environment to facilitate increased human capabilities with regards to creating disease models. These capabilities, which are based on state transitions, are intuitive for humans to work with [14].

In this paper we will describe the modeling software environment and demonstrate important features in it. We will provide several examples regarding the usefulness of this modeling environment with regards to the Michigan model for diabetes.

2. Supported Disease Model

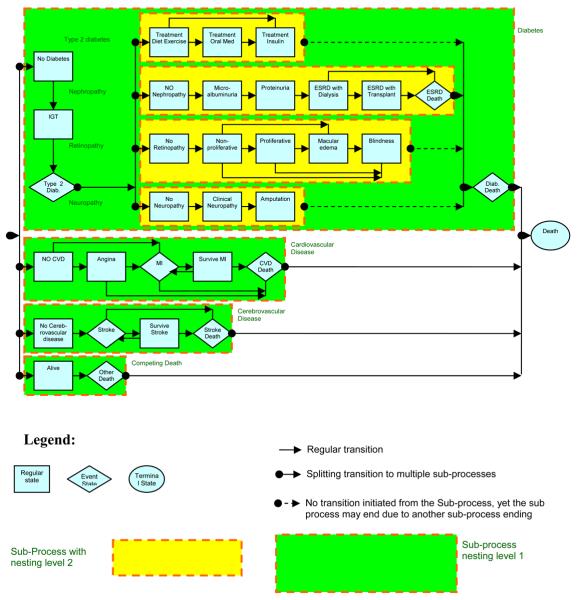
The Michigan model has been previously published and validated against Wisconsin Epidemiological Study of Diabetic Retinopathy (WESDR) data in [15]. At that time, the Model did not use the advanced modeling environment described in this paper. Recently the model has been updated and validated against UKPDS published results [16]. During its update the model has been generalized and our modeling software was developed to support this generalization. This generalization not only allows users to modify the Michigan model for diabetes, but also allows modeling of other disease models with similar structures. These modeling capabilities are therefore described with specific examples from the Michigan model that is shown in Figure 1.

FIGURE 1.

The Michigan model for diabetes. IGT means Impaired Glucose Tolerance, ESRD means End Stage Renal Disease, and MI means Myocardial Infarction.

The Michigan model is a state transition model that generalizes the Markov model. Each state in the model (marked as boxes in Figure 1) is associated with a stage of disease progression. Progression of the disease is modeled as transitions between states (marked as arrows in Figure 1) and each transition can be assigned with specific transition probabilities. The Michigan model is a discrete time model using a preset constant time step (usually one year) to time transitions between states. The modeling environment, however, allows implementing non-Markov models. These traits are useful for disease modelers, and are part of our simplified approach and are discussed hereafter.

2.1. Instantaneous event states

The Michigan model allows defining states that take no time to pass through. The need of such instantaneous states has been recognized by other models such as the CDC/RTI model. In Figure 1 these states are represented as rhombuses and include the states of Stroke or Myocardial Infraction (MI). Such states represent an event that occurs and immediately passes, rather than a state that an individual can occupy at the end of a simulation time step. Therefore transition probabilities leading out of an event state sum to 1. The existence of these states does not change the Markov property since an equivalent Markov model can be constructed without using event states. However, the existence of these states makes it easy for the modeler to indicate an event and model event recurrence and therefore the introduction of such states is useful for interactive human modeling.

2.2. Nested sub-processes

Modeling of diseases requires focusing in more than one disease process. This is demonstrated with regards to the diabetes model. Looking at Figure 1, one can recognize processes such as cardiovascular disease, nephropathy, cerebrovascular disease, retinopathy, and neuropathy. These are all related to diabetes, yet each sub process has distinct states not shared with other processes. Furthermore, disease progression may be independent in each sub-process. For example an individual can progress from angina to an MI (Mayocardial Infarction) to survive MI, and at the same simulation step progress from clinical neuropathy to amputation while staying in a state of No-retinopathy. This example demonstrates the process in terms that are relatively easy for a human to comprehend.

An alternative way to model such progression is using an equivalent Markov model that is composed of aggregate states such as No Cardivascular Disease + No Nephropathy + No Cerebrovascular disease + Blindness + No Neuropathy. However, this is not intuitive to the user since the number of different states will be too large, and their description too long to effectively manage. Moreover, defining transition probabilities would be nonintuitive and cumbersome.

For these reasons, we are defining sub-processes that can each progress independently during simulation. These sub-processes are marked with dashed outline boxes. Each sub-process can be a Markov model containing states and transitions of its own. A set of parallel sub-processes is initiated by progressing to a splitter state marked as a dot in Figure 1. When an individual reaches a splitter state in the model, multiple sub-processes are initiated and the subject is placed in the first state in each of these sub-processes. To maintain fairness each of these sub-processes are processed in random order during simulation and the combination of states in the sub-processes defines the condition of the individual. The individual progresses in parallel through each of these sub-processes as long as none of these sub-processes are exited. Exiting a sub-process means collapsing all parallel sub-processes and proceeding to a joiner state that is also marked as a dot in Figure 1. Collapsing sub-processes is usually associated with death and therefore the need to stop and collapse all parallel sub-processes. Note that a joiner state is always associated with a splitter state. It is enough to reach the joiner state by exiting one sub-process to collapse all parallel sub-processes starting from the same splitter state. This includes sub-processes that usually will not lead to the joiner state that are marked as a dashed arrow in Figure 1, e.g. reaching ESRD death will result in ending the retinopathy sub-process, and collapsing all sub-processes to diabetes death through a joiner state.

Joiner and splitter states are artificial states treated as instantaneous states. Their definition allows encapsulating a set of sub-processes as if they were a single state. Therefore it is possible to nest sub-processes within one another. In Figure 1, for example, the neuropathy sub-process is encapsulated within the diabetes sub-process, meaning that this is diabetic neuropathy as opposed to general neuropathy that may or may not be associated with diabetes. This treatment of sub-processes allows breaking processes within a disease to a finer level of detail dealing with more specific disease complications while maintaining a hierarchical structure that is more intuitive for modeling purposes.

This use of sub-process capabilities can lead to concurrent modeling of multiple diseases in the future. In a sense our diabetes model already does this to some degree, since it includes several disease processes already. Yet the focus of the model is still diabetes and parallel processes were modeled using information from diabetics.

Yet even within diabetes, we are already modeling dependencies between sub-processes. This is accomplished using the methods described in the next section.

2.3. Transition Probabilities Dependant on Parameters

Our diabetes model addresses individual characteristics such as Age and Gender. This is made possible by allowing the user to define transition probabilities as functions of various parameters. These functions can be general mathematical expressions using mathematical, Boolean, and equality operators, and a set of mathematical functions such as exp, log, min, max etc. As will be shown later, these functions can also include conditional statements (similar to an “if” statement in a programming language).

Each such expression may involve one or more parameters that can represent various individual and system characteristics. Below is a list of relevant parameter types the system supports:

• Covariates: these are parameters representing general individual characteristics such as Age and Gender

• State Indicators: indicating if the individual is in a certain state/sub-processes. There are several types of state indicators for each state: the entered state indicator indicates if a state was first entered in this simulation step; the diagnosed state indicator indicates if the state was diagnosed which may be different than the actual state the individual is in; the treated state indicator representing that the individual is treated for this state; and the complied state indicator specifies if the individual complied with the treatment. Note that the computer automatically assigns values to the actual and entered state indicators whereas the user controls the values of the diagnosed, treated, and complied state indicators.

• Intervention parameters: additional parameters beyond diagnosed, treated, and complied state indicators associated with interventions. For example, compliance rate to treatment.

• Cost and Quality of Life parameters: parameters such as yearly costs or health utility score that reflect costs of treatment and the quality of life of individuals.

• User defined Functions: these are expressions composed of other parameters saved under a parameter name. These user defined functions can later be used in other expressions to simplify and shorten the text. The system is responsible for expanding the functions within the expression similar to a substitution of a mathematical expression.

The use of such parameters in transition probabilities can govern the progression of an individual in the model. For example in our model the transition from no-cerebrovascular disease to a stroke is heavily based on to the UKPDS 60 risk engine [17]. The UKPDS part of the expression is:

1.0 − Exp( − 0.00186 * 1.092**(AgeAtDiagnosisOfDiabetes−55) * 0.700**IsFemale * 1.547**Smoke * 8.554**AF* 1.122**((SBP − 135.5)/10) * 1.138**(LipidRatio − 5.11) *1.145**(DurationOfDiabetes) ) )

Where AgeAtDiagnosisOfDiabetes, Male, Smoke, AF (Atrial fibrillation), and SBP (Systolic Blood Pressure) are covariates associated with the individual; IsFemale is a user defined function defined as 1-Male that converts our definition of the Male covariate to the UKPDS usage of gender in the formula. DurationOfDiabetes is defined as Age-AgeAtDiagnosisOfDiabetes. And LipidRatio is defined as TotalCholesterol/ HDLCholesterol.

The formula above is an example of a continuous function depending on parameters that govern the transition probability. However, our modeling system also supports conditional transition probabilities. These can be accomplished by using the Table and Iif functions.

The Iif function that stands for “immediate if” and is similar in structure to other languages. This function gets three arguments 1) The conditional expression, usually a Boolean expression where 0 means a false conditional; 2) A value/Expression to be returned in case of a true conditional; 3) A value/Expression to returned in case of a false conditional. For example, the transition probability between Survive Stroke and Death is governed by the formula:

Iif(Diabetes_with_treatment_by_Insulin, 0.0148, 0.0166)

Where Diabetes_with_treatment_by_Insulin is a state indicator defining the desired treatment level. If the person is in a diabetes state that requires taking insulin, the transition probability will be 0.0148, otherwise it will be 0.0166. Note that the system would have accepted more elaborate expressions for the true and false values. This includes additional Iif statements to other functions allowing the creation of a complicated decision tree to calculate transition probabilities.

To further aid in creating complicated conditional statements, the system can use the Table function. This function allows defining a multi-dimensional table that can be accessed by one or more parameters to retrieve the value associated with the value in the parameter domain. For example, the probability of a diabetic to die after surviving a MI is governed by the following table:

Table(3, 2,2,5, 0.0156,0.0156,0.0156,0.0156,0.0156,0.0013,0.006,0.0116,0.01 93,0.0193,0.0034,0.0034,0.0089,0.0133,0.0133,0.0034,0.0034, 0.009,0.0131,0.0131, Type_2_Diabetes,NaN,0,1, Male, NaN, 0, 1, Age, 0,24.999,54.999,64.999,74.999, 100)

Where the initial 3, colored in red, indicates the number of dimensions, then the three next numbers 2,2,5, indicated in green, are the sizes of the dimensions that define the array. The next 2*2*5=20 numbers, indicated in blue, are the data to populate the table. Finally, the dimension names and their ranges are defined – these represent the table headers. Table 1 shows how this table would look using a more intuitive depiction. Note that this table handles both continuous parameters and discrete parameters using the same representation.

TABLE 1.

Example of a multidimensional table as defined by the system

		Male<=0	0<Male<=1
Type_2_Diabetes<=0	0<Age<=24.999	0.0156	0.0013
	24.999<Age<=54.999	0.0156	0.006
	54.999<Age<=64.999	0.0156	0.0116
	64.999<Age<=74.999	0.0156	0.0193
	74.999<Age<=100	0.0156	0.0193
0<Type_2_Diabetes<=1	0<Age<=24.999	0.0034	0.0034
	24.999<Age<=54.999	0.0034	0.0034
	54.999<Age<=64.999	0.0089	0.009
	64.999<Age<=74.999	0.0133	0.0131
	74.999<Age<=100	0.0133	0.0131

Using such table definitions, it is possible to relatively easily specify transition probabilities that depend on multiple continuous or discrete parameters and includes ranges. This is a common way information appears in the literature, which is where our information comes from, and therefore a relatively intuitive way to define transition probabilities avoiding complicated and a long set of Iif statements.

Note that parameters which control the transition probabilities may hold historical information derived from state indicators or previously generated random numbers. In general this invalidates the Markov property of being memory-less and the model may no longer be a Markov model. Yet, since dependency on historical events is important when describing disease progression, and since the Markov model is intuitive, our model is a compromise between the two. We tried to maintain the intuitive part of a state transition model while allowing the user to create dependencies on memory. This compromise methodology no longer allows us to calculate disease progression using matrix representation and multiplication as it is traditional with a Markov model. Instead we have to use Monte-Carlo simulation as explained in the next section.

2.4. Monte-Carlo Simulation with Rules

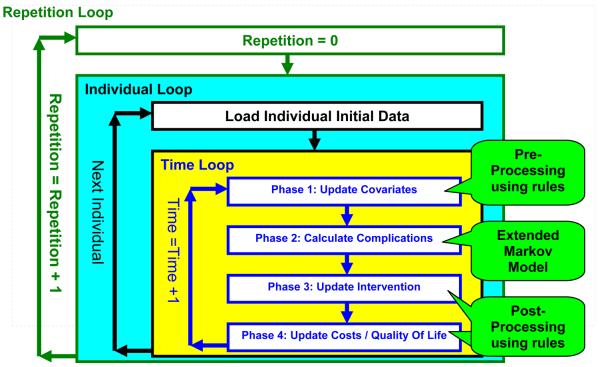
Choosing Monte-Carlo for simulation allows extending the model even further by adding additional rules before and after each time step in the Markov Model. Figure 2 represents the flow diagram of the simulation and the new rules. The simulation is composed of three nested loops:

FIGURE 2.

Flow diagram of the Monte-Carlo simulation

The outermost loop is the repetition loop that repeats the same simulation many times. Each repetition generates potentially different results due to the random nature of a Monte-Carlo simulation. After collecting these different results, mean values and the distribution characteristics of the results can be determined. A large number of repetitions will statistically decrease the uncertainty created by the randomness of the Monte-Carlo simulation at the price of longer execution times. This tradeoff of calculation time and uncertainty has to be balanced by the modeler.

The second nested loop is the individual loop that iterates through individuals in the simulation population. This baseline population defines initial parameter values to be used for each individual. For example the Age, Gender, and Smoking status of an individual are loaded as the initial value of these parameters before starting the time loop.

The innermost nested loop is the time loop that handles the changes in the parameters and states. In this loop the disease progression occurs for each individual. Note that only the box titled “Phase 2: calculate complications” corresponds directly to the extended Markov model seen in Figure 1, the rest of the boxes represent sets of rules to be applied as pre-processing or post-processing terms. Simulation rules can be considered as general programming statements and are of the following form:

If Individual is in [Rule State] then:

• If random number < [Occurrence Probability Threshold] then:

  $$\left[\text{Affected parameter}\right]=\left[\text{Given formula}\right]$$

where the modeler can define the rule arguments marked with brackets. This allows the user easy control of parameters before and after the Markov Model is processed. The [Rule State] argument represents a state indicator and defaults to “all states”. The [Occurrence Probability Threshold] argument defines a threshold to control the random execution of the rule and defaults to 1. The [Affected Parameter] argument holds the name of the parameter that its value will change. The [Given Formula] argument holds an expression that defines the value that the [Affected Parameter] argument will receive if the conditional parts of the rule are valid.

A rule, for example, can indicate the increase in age every year as in: Age = Age +1

A rule can also be more complicated. For example, in diabetes modeling, Glycated hemoglobin (HbA1c or A1c for short) is an underlying physiologic measurement used in many cases to diagnose diabetes and classify its severity. Our model simulates A1c progression in people without diabetes using a probabilistic bounded increase in a variable named A1c using the following rule:

If Individual is in No_Diabetes:

• If random < 0.03 then:

  $$\mathrm{A}1\mathrm{c}=\mathrm{Min}((\mathrm{A}1\mathrm{c}+0.68),15)$$

Note that the expression is general and may contain mathematical operations and functions, other parameters, and even conditional Table and Iif functions. This allows the user to change the model in a general way.

Although the rules are general, the system structures the modeling tasks by defining different phases of rule application. These phases limit the type of parameters that can be used as the [Affected parameter]. Phase 1 allows the update of covariates such as age or A1c. Phase 2 executes a single simulation step in the previously described Extended Markov model. Phase 3 limits the update to diagnosed, treated, and complied state indicators and to intervention parameters. Phase 4 is limited to updating cost and quality of life parameters.

These limitations follow the following reasoning: At the beginning of the year the individual characteristics are updated. Then the disease progresses according to these new characteristics using the extended Markov model. Then the individual is diagnosed and treated for new conditions. Finally the cost of treatment and the individual's quality of life is determined. Then the same cycle can be repeated for the next year within the time loop. This simulation is repeated for each individual in the individual loop. Finally, the entire population undergoes the simulation in the repetition loop. Results can then be analyzed using additional tools described in the next section.

3. System Capabilities

A software tool was developed allowing chronic disease modeling similar to the Michigan model for diabetes. The system supports the following features:

• Parameter storage: The system allows storage of multiple parameters that are used within the system, including multi-dimensional tables that can be accessed using another parameter defined in the system. The user can define the parameter name, its type, and validation rules to be observed during simulation. Validation rules may restrict parameter values to be integer, general numbers, matrix/vector, tables, or general expressions. Validation rules may also include maximal and minimal bounds on the parameter value. Validation rules are important in increasing the programmatic integrity of the model and can be used as a simple model debugging tool, especially with larger models where the chance for human error increases. This validation feature proved to be essential during the development of the Michigan model for diabetes.

• Storage of multiple disease models: The system can hold multiple disease models defined by states, sub-processes and transition probabilities. Different models can share states and therefore allows building a model using common terminology. This also allows maintaining several versions of the same model in the system at the same time. This has proved to be a useful option during earlier development stages where there is a lot of uncertainty and therefore several model versions.

• Storage and Manipulation of multiple population sets: The system allows storing population cohort information as a snapshot of the individual characteristics. The system can support storage of multiple such population sets, each can be later used to initialize simulation parameters. Note that population sets are stored separately from the models to allow simulating a model with different population sets or the same population set with different models. The system allows importing these population sets from comma separated values text files. The system also supports definition of population sets as distributions and expressions. Such distribution-based populations allow describing a population set in a similar way populations are described in the literature. It can then be used by the system to create a new data-based population set by random generation. This capability allows imitation of study populations from publicly available data, without the need to access propriety data gathered by this study. This allows independent modeling as experienced in our diabetes model. For example, we did not need access to the UKPDS dataset during validation, the UKPDS publication [16] that can be found in the literature was sufficient. Note that similar population generation mechanism is provided by the Global Diabetes Model [12]. However, that generator is limited to a certain set of studies and complications and does not allow correlation between complications. In contrast, our population generation method is general and a population can be defined by a set of expressions that can depend on other population parameters, e.g. the age distribution can depend on gender in our method and the same is true for disease states.

• Storage of simulation projects: A simulation project is defined by a combination of a model, a population set, simulation rules, and some other simulation parameters. Combining these together with clerical information allows defining different simulation projects that can explore different situations of interest. This option was useful when a single parameter, such as compliance level to treatment, was changed between different simulations and we needed to compare results between these projects.

• Simulation execution and storage of its results: The system can compile the project into a Python program that is run to generate simulation results. These results are then loaded back to the system to be stored with association to the simulation project. The use of python as a programming language allowed debugging simulation programs with external python tools, while still maintaining readable text pertaining to the disease model.

• Model parameter estimation: Beyond simulation, the system is capable of model parameter estimation for a single Markov process using a maximum likelihood technique. This technique allows gathering summary data from the publicly available literature and using it to estimate model parameters of a single sub-process. The model parameter estimation method is described in further details in [18,19] . The implementation of the estimation method was accomplished using the Python with the Scipy optimization library that allows constrained optimization routine [20,21]. The Estimation Technique is also freely available online as a Matlab Prototype as the project web site: http://www.med.umich.edu/mdrtc/cores/DiseaseModel/software.htm

• Storage of the data as files: The system is currently a standalone system and allows maintaining all the above entities in a file. The system allows minimal version control of its saved files. This has been sufficient so far, however, future development is geared towards shared environment by multiple users.

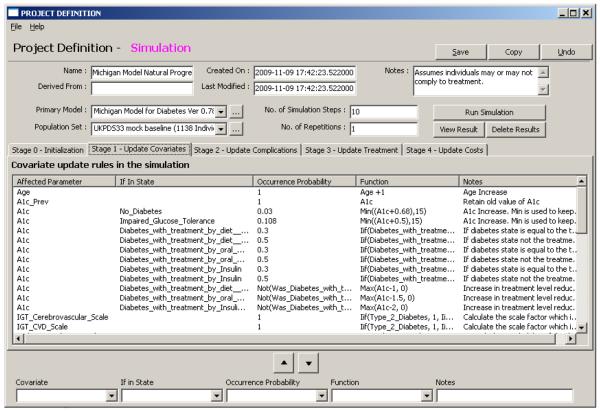
• Graphic User Interface (GUI): The system can be controlled using forms and reports based on WxPython that enable management of the above entities. The form system allows drilling down the information hierarchy to locate and edit details of interest. For example double clicking the model in the project page will pop up the model form and then clicking on the main process of the model will bring the states form with the appropriate process definition and so forth. The GUI also supports the use of a cost wizard that aids with calculating cost and quality of life in phase 4 of the simulation. Figure 3 shows the project form to demonstrate how the system handles easy definition of rules. This GUI proved extremely useful when developing our diabetes model. The ability to visually access the model allowed quicker and easier modeling by the human. Just to give an idea of the importance of the GUI, consider that our diabetes model when described as a document is about 40 pages long. Whereas using the GUI we reach each parameter with several guided clicks and perform controlled changes that accompanied with feedback. For example, when a user types in a bad expression, the GUI will raise an error correcting the user, this syntax check was useful to filter out human errors in our diabetes model. Even during development, once our GUI was operational, many testing tasks were modeled using the GUI and exported back as code since the human user found it easier than coding.

FIGURE 3.

An example of the project form. This form allows defining the model and population set to be used as well as simulation parameters such as the number of simulation steps and the number of repetitions. The form allows manipulating rules according to their phase in the simulation. Each phase is displayed in a different tab for the convenience of the user.

The described system was tested using several case scenarios that test its expression, simulation and other capabilities. The test suite for the software, the source code, the user documentation, and the developer documentation, are all published freely. The system is published under GPL license and can be obtained using the following URL: http://www.med.umich.edu/mdrtc/cores/DiseaseModel/software.htm

4. Results

The utility of a system such as described in this paper depends heavily on the feasibility and validity of the models used. To demonstrate the system feasibility, we have created many simulation tests that are published with the software. This first level of validation demonstrates correctness and serves for quality assurance.

To demonstrate applicability to disease modeling, we have developed the Michigan model for diabetes using our software framework. This model includes 7 disease subprocesses with about 30 states and about 50 transitions as seen in Figure 1. More than 100 variables and more than 100 simulation rules are used by this model. The model went through more than 30 versions during its development process. The development process included the following stages: 1) literature review; 2) model formulation; 3) validation of our model against clinical study results. These development stages were repeated until convergence to the published model version was achieved. The model file titled “Michigan model for diabetes 11-May-2009” can be downloaded from the model section of web site using the following link: http://www.med.umich.edu/mdrtc/cores/DiseaseModel/model.htm

This model file is a compressed archive that contains a documentation file that details the above development stages: 1) The literature used to create the model is provided in the bibliography; 2) The manual calculations used to extract the transition probabilities from the literature are described in great detail so these can be replicated by others; and 3) The model validation against the UKPDS 33 results are summarized in more detail than will be presented below.

To allow model validation, a population of 1138 individuals was artificially generated from distributions provided by the UKPDS33 population as described in section 3. This population was used as a baseline population for the model simulation the results of which were validated.

Model validation was conducted by repeating the model simulation for 100 times. The simulation process took about 18 hours on 4 processor cores (about 3 days on a single processor core). At the end of the simulation process, a large array of records was generated. Each record contained the values of all model parameters for each person in each living year for each repetition. An example of such output is presented in the appendix. These simulation results were analyzed and compared against UKPDS 33 results appearing in [16].

Table 2 shows selected simulation results compared to UKPDS 33 aggregate results. This validation shows a good fit in most categories. The micro-vascular category, as defined by UKPDS 33 [16], includes elements from the retinopathy process, which we recognize needs improved modeling. This is an area of active research.

Table 2.

Validation of Michigan model for diabetes simulation results after 10 years against results reported in UKPDS 33. The Michigan model results show the mean, Standard Deviation (SD), Min, Median, and Max values from 100 repetitions. The relative error column compares the highlighted columns using the following formula (Mean - UKPDS)/UKPDS.

UKPDS 33 definition	UKPDS 33 reported	Michigan model simulation results					Relative Error
		Mean	SD	Min	Median	Max
Diabetes related deaths	129	135.35	9.77	111	135	164	0.049
All cause mortality	213	213.89	12.16	181	213	255	0.004
Myocardial Infarction	186	189.93	11.11	159	189	219	0.021
Stroke	55	48.17	6.21	32	48	63	−0.12
Micro-vascular	121	101.72	8.98	80	101	132	−0.16

Our diabetes model used parameters based on the UKPDS. For example we calculated death rates from MI based on published rates in the UKPDS 33. Simulation results were tabulated to comparable summary measures as reported in figure 4 in [16].

Our report engine allowed proper counting of incidences and of persons affected by incidences for each category for specified periods. More specifically, using our software, it is possible to count the number of persons who had a stroke in the first 10 years, or the total number of strokes in the population in the same time period. Our framework also calculates statistics of repetitions. The results in table 2 were calculated using these mechanisms.

To allow further and more detailed scrutiny of our work, these validation results along with a fully documented diabetes model are available online at our web site.

5. Discussion

Recent interest in disease forecast has resulted in a multitude of disease models with competing strengths and weaknesses. For example, most disease models are dedicated software tools in a variety of languages that are developed for the sole purpose of simulating a specific disease model. The UKPDS outcomes model [13] is embodied within an XL workbook, the global diabetes model [12] is implemented in Visual Basic, and the eagle diabetes model [10,11] is coded in C++.

These models use Monte-Carlo simulation, which is the simulation engine that is generalized and implemented by our software. The CDC/RTI model was designed using a Markov model, which our tool also allows. All of these tools are limited to diabetes, this is reasonable considering the huge cost involved in developing the model.

In contrast, the Archimedes model [5,6,7] is different from the above models in that it uses an object oriented approach to model progression of continuous variables. Archimedes has been published extensively, yet being proprietary and of a different mathematical framework, it is conceptually different than our open framework.

Similar to our framework, some diabetes models have an associated GUI. The Global diabetes model [12] has an interface that allows defining population parameters before simulation. Another notable user interface is the Diabetes Ph.D. web site [22] that uses the Archimedes simulation engine. However, these interfaces are limited to managing values of model specific parameters and model structure can not be changed. It is also not possible to define a new model using these user interfaces.

In contrast, our framework can accommodate and manipulate multiple distinct models and it is not dedicated to a single model. This is a major difference between our software framework and other modeling tools. For example, our software can be used to develop disease models other than diabetes. Furthermore, by modifying our model structure, diabetes researchers can use our existing diabetes model to project outcomes based on the results of their own innovative research. We consider this to be an important benefit of our general simulation engine and GUI.

However, disease models are not limited to diabetes. During the work on our project we encountered disease models and related tools for various other diseases, including Influenza [23], Coronary Heart Disease [24], and Cancer [25]. This is just a partial list that demonstrates the variety of dedicated tools available. To our knowledge to date there is no other software framework that is flexible enough to accommodate multiple chronic disease models that has the following capabilities: 1) The ability to define the model structure, 2) the ability to define parameters and formulas, 3) the ability to set simulation rules and perform simulation, 4) the ability to analyze the output data.

These simulation capabilities, offered by our framework are general enough to model chronic diseases. Yet our framework is not suitable for modeling infectious diseases since these require interaction between individuals, which our framework does not currently support. Also, our support does not extend to general continuous time modeling as we are confined by a constant length simulation step. Since our simulation engine includes event states, it already handles event queues, which can be extended further in future research. Another gap in our framework is that our simulation capabilities are more advanced than the estimation capabilities. Estimation of model parameters is currently confined to a Markov model in a single process. Expanding estimation capabilities is currently a research topic of much interest. Possible research directions include multiple subprocesses, and model expression support. To allow others to participate in this research effort, we are publishing our methodology [18,19], and we have published our estimation source code both in Matlab and Python environments.

Publishing the disease modeling software for free along with its open source is compatible with the design of the modeling approach that uses simpler more intuitive techniques to model diseases. These intuitive approaches reduce the learning curve for researchers who are entering the field. It also enables collaboration between researchers specializing in different facets of a single disease. Finally, it enables researchers to develop new disease models without recreating a GUI or a computation engine. The tool exists, and clinical collaborators can focus their efforts on clinical matters rather than technical matters.

Another advantage of our software framework is that with our relatively simple modeling techniques, we support a wider human comprehension of disease processes. Using standardized “base” models of the natural history of disease, researchers can incorporate the effect of proposed interventions into the base model and simulate expected long-term outcomes of early intervention. This not only gives feedback to researchers about the utility of their preventive actions; but it provides a motivation to target transitions in a model where an intervention will have the most significant effect. Then, as studies are conducted, that data may be used to calibrate and correct the base model as the state of the science advances. Together, these and other practical uses of the software will help researchers comprehend complex disease processes. Making this tool available freely and openly, facilitates disease modeling activities and therefore contributes to better understanding of disease progression.

Not only can researchers benefit from a disease modeling software, we hope that in the future physicians can eventually use the software as an educational tool. Working with a patient, a physician can simulate patient outcomes based on the demographic characteristics of a specific patient, for a variety of proposed treatment plans. In this manner, a patient can become a more active participant in his or her own health care decisions.

Our web site also contains additional information on the project, beyond the published software and diabetes model. The web site can be accessed online at: http://www.med.umich.edu/mdrtc/cores/DiseaseModel/

APPENDIX

This appendix shows the Michigan Model for diabetes raw simulation output. It is representative of output results typically generated by our software framework. Table 3 demonstrates a sample of this raw output for a single simulation repetition. Due to the size of the table, only part of the information is shown. This raw information was analyzed by tools provided with our software framework to create the results in table 2.

Table 3.

Sample output from simulation results. This table shows selected result columns (out of 111) for a few individuals. Time 0 means the initial baseline population as generated by the system before simulation. State indicator values are set to 1 if the individual is in that state during a certain time step. Note that entering a state raises the _Entered state indicator.

IndividualID	Repetition	Time	Age	Male	A1c	Death_Entered	Stroke_Entered	No_CVD	Angina_Entered	Angina	No_Retinopathy	Non_Proliferative_Entered	Non_Proliferative	… (a total of 111 parameters)
1	0	0	45.2	1	7.3842	0	0	1	0	0	1	0	0	…
1	0	1	46.2	1	8.1342	0	0	1	0	0	1	0	0	…
1	0	2	47.2	1	6.6342	0	0	1	0	0	1	0	0	…
1	0	3	48.2	1	6.6342	0	0	1	0	0	0	1	1	…
1	0	4	49.2	1	6.6342	0	0	1	0	0	0	0	1	…
1	0	5	50.2	1	6.6342	0	0	1	0	0	0	0	1	…
1	0	6	51.2	1	6.6342	0	0	1	0	0	0	0	1	…
1	0	7	52.2	1	6.6342	0	0	1	0	0	0	0	0	…
1	0	8	53.2	1	6.6342	0	0	1	0	0	0	0	0	…
1	0	9	54.2	1	6.6342	0	0	1	0	0	0	0	0	…
1	0	10	55.2	1	6.6342	0	0	1	0	0	0	0	0	…
2	0	0	37.8	1	7.2903	0	0	1	0	0	1	0	0	…
2	0	1	38.8	1	7.2903	0	0	1	0	0	0	1	1	…
2	0	2	39.8	1	8.0403	0	0	1	0	0	0	0	1	…
2	0	3	40.8	1	6.5403	0	0	1	0	0	0	0	1	…
2	0	4	41.8	1	6.5403	0	0	1	0	0	0	0	0	…
2	0	5	42.8	1	6.5403	0	0	0	1	1	0	0	0	…
2	0	6	43.8	1	7.0403	0	0	0	0	1	0	0	0	…
2	0	7	44.8	1	7.0403	0	0	0	0	1	0	0	0	…
2	0	8	45.8	1	7.5403	0	0	0	0	1	0	0	0	…
2	0	9	46.8	1	8.0403	0	0	0	0	1	0	0	0	…
2	0	10	47.8	1	8.0403	0	0	0	0	1	0	0	0	…
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
1138	0	6	61.6	1	6.2802	1	1	1	0	0	1	0	0	…