Relationship Between Firing Rate and Recruitment Threshold of Motoneurons in Voluntary Isometric Contractions

Abstract

We used surface EMG signal decomposition technology to study the control properties of numerous simultaneously active motor units. Six healthy human subjects of comparable age (21 ± 0.63 yr) and physical fitness were recruited to perform isometric contractions of the vastus lateralis (VL), first dorsal interosseous (FDI), and tibialis anterior (TA) muscles at the 20, 50, 80, and 100% maximum voluntary contraction force levels. EMG signals were collected with a five-pin surface array sensor that provided four channels of data. They were decomposed into the constituent action potentials with a new decomposition algorithm. The firings of a total of 1,273 motor unit action potential trains, 20–30 per contraction, were obtained. The recruitment thresholds and mean firing rates of the motor units were calculated, and mathematical equations were derived. The results describe a hierarchical inverse relationship between the recruitment thresholds and the firing rates, including the first and second derivatives, i.e., the velocity and the acceleration of the firing rates. This relationship describes an “operating point” for the motoneuron pool that remains consistent at all force levels and is modulated by the excitation. This relationship differs only slightly between subjects and more distinctly across muscles. These results support the “onion skin” property that suggests a basic control scheme encoded in the physical properties of motoneurons that responds consistently to a “common drive” to the motoneuron pool.

INTRODUCTION

The manner in which motor units are controlled to generate force has been of interest ever since we have had the technology to observe the firing characteristics of motor units. The early works of Adrian and Bronk (1929) and Seyffarth (1940) have shown that, as the level of the contraction increases, additional motor units are recruited, and the firing rates of motor units increase. Later Henneman (1957) showed that, in response to increasing excitation, motoneurons are recruited in order of increasing size. Our own work (De Luca and Erim 1994; De Luca et al. 1982a,b) has shown that there exists an inverse relationship between the firing rate and recruitment threshold of motor units at any specified force level. Thus at any time and force, the firing rates of earlier recruited motor units are greater than those of later recruited motor units, and as the excitation to the motoneuron pool varies, the firing rates of all the motor units respond proportionally. A similar behavior had been previously shown by Seyffarth (1940), Person and Kudina (1972), and Tanji and Kato (1973), as well as several more recent researchers. We termed this phenomenon “the onion skin” because when the firing rates of the motor units are plotted as functions of time, they assume the layering pattern of an onion.

In this study, we revisited the task of characterizing the firing behavior of motor units during constant force contractions and attempted to formulize the behavior in a structured manner. We used a new technique that decomposes surface electromyographic (EMG) signals collected during isometric contractions ranging up to the maximal level. This technology has been described by De Luca et al. (2006), Chang et al. (2008), and Nawab et al. (2009, 2010). We have been able to decompose the firings of motor unit action potential trains of ≤40 motor units from isometric constant force contractions. The accuracy of the technology has been proven to be 92.5% on average and reaches values of ≤97% in some contractions. The high accuracy and the large number of motor units observable in individual contractions increase the resolution and the sample size of the data. This increase in turn better characterizes the behavior of motor units at different force levels and in different muscles.

METHODS

Subjects

Six subjects, three male and three female (21 ± 0.63 yr), volunteered to participate in this study. All engaged in regular, moderate physical activity; none reported any neurological defects. Each read, understood, and signed an informed consent form approved by the Institutional Review Board of Boston University before participating.

Muscles

Three muscles were chosen because they represented a range of size and motor unit control parameters found in limb muscles. They were the vastus lateralis (VL), the tibialis anterior (TA), and the first dorsal interosseous (FDI). The VL exhibits relatively low firing rates, with a maximal value reported in the range of 37–50 pulses per second (pps) and a maximal recruitment threshold of 85% of the maximum voluntary contraction (MVC) force level (Jakobi and Cafarelli 1998; Woods et al. 1987). The TA, a smaller lower limb muscle, contains ∼445 motor units (Feinstein et al. 1955) whose firing rates exhibit larger values, reportedly in the range of 40–58 pps (Connelly et al. 1999; Rubinstein and Kamen 2005), and a maximum recruitment threshold of ∼70% MVC (De Luca and Erim 1994). The FDI, a small muscle in the hand, contains ∼119 motor units (Feinstein et al. 1955). Its firing rates are reported in the range of 47–92 pps (Duchateau and Hainaut 1990; Kamen et al. 1995; Seki et al. 2007), with a maximum recruitment threshold of ∼55% MVC (De Luca et al. 1982a; Duchateau and Hainaut 1990).

Force measurements

Subjects were seated in a chair that performed several functions: restraint of hip movement and immobilization of the dominant leg at a knee angle of 60° of flexion; restraint of the toes of the dominant leg with the ankle resting at a 90° angle; and immobilization of the dominant forearm and restraint of the wrist and fingers. Isometric force during leg extension (VL), index finger abduction (FDI), and dorsiflexion of the foot (TA) were measured via load cells attached to the lever arms of each restraint. Visual feedback of the contraction force was displayed on a computer screen.

EMG recording

Surface EMG signals were recorded from each muscle using a surface sensor array that contained five cylindrical probes (0.5 mm diam) with blunted ends that protrude from the housing. The probes are located at the corners and in the middle of a 5 × 5-mm square. The sensors are sized to ensure proper electrical contact without piercing the skin when pressed forcefully. For additional details, refer to De Luca et al. (2006). The output of the sensors was connected to an EMG amplifier (a modified Bagnoli 16-channel system developed by Delsys). The subject's skin was prepared by removing the superficial dead skin with adhesive tape and sterilized with an alcohol swab. The surface sensor was placed on a location near the center of the belly of the muscle. The signals from four pairs of the sensor electrodes were differentially amplified and filtered with a bandwidth of 20 Hz to 9.5 kHz. The signals were sampled at 20 kHz and stored on a computer for off-line analysis.

Protocol

Subjects were asked to first participate in a training session to become familiar with the experiment. They practiced performing maximum voluntary contractions. Because all the force target levels were measured as percentages of the MVC value, it was crucial that the recorded MVC level reflected a value as close to the subject's strongest effort as possible. Both physiological and psychological familiarities with the performance of the MVC are necessary to understand how a maximal effort feels. Accordingly, subjects showed improvement in the maximum level reached with several repetitions. They also practiced several contractions using visual feedback of their force output to match a target force trajectory. Smooth performance of the contractions reduces erratic behavior of motor units and renders the analysis of the EMG signals less difficult. See the Caution Note in appendix 2 for additional details on this issue.

After the initial training session, the subjects returned the next day for a data collection session, lasting ∼2 h. They were first asked to contract each muscle at the highest level they could sustain for ∼3 s in duration. After they rested for 3 min, the procedure was repeated two more times. The greatest value of the trials was recorded as the MVC level. This process was repeated for each muscle. The subjects were asked to follow a series of force trajectories displayed on a computer screen. The trajectories followed a trapezoidal paradigm: they increased at a rate of 10% MVC/s; were sustained at 20, 50, 80, and 100% MVC for 10, 8, 8, and 4 s, respectively; and decreased at a rate of 10% MVC/s. The procedure was repeated for each muscle.

Data analysis

Sixty contractions were processed. Three of the contractions from the VL yielded poor signal quality. Two of the 100% MVC VL contractions exhibited force trajectories of very poor compliance. In these cases, subjects either did not reach the target force level or were unable to match their force output to the trajectory shape. The remaining 55 contractions were analyzed. Table 1 lists the distribution of these motor units for all the analyzed contractions.

Table 1.

Distribution of analyzed motor units by muscle and force level

	Total Number of Motor Units per Contraction Level (Average Accuracy of Decomposition)			Average Number Motor Units per Contraction
Force Level	VL	FDI	TA	VL	FDI	TA
20%	39 (91%)	77 (90%)	62 (91%)	13.0	19.3	12.4
50%	139 (92%)	85 (92%)	111 (93%)	23.2	21.3	22.2
80%	210 (91%)	99 (92%)	151 (93%)	35.0	24.8	30.2
100%	106 (92%)	86 (93%)	108 (94%)	26.5	21.5	21.6

VL, vastus lateralis; FDI, first dorsal interosseous muscle; TA, tibialis anterior. The number in brackets represents the average accuracy of the decomposed firing instances of the set of motor units per contraction level.

The four channels of raw EMG data collected by the sensor were decomposed into their constituent motor unit action potential trains using the surface EMG signal decomposition algorithms first described by De Luca et al. (2006), with subsequent improvements reported by Chang et al. (2008) and Nawab et al. (2010). The algorithms use artificial intelligence techniques to separate superimposed action potentials in the EMG signal, identifying the presence of an action potential and allocating it to an individual train belonging to a specific motor unit. The technique generally identifies all the firings of 20–30 motor unit action potential trains per contraction.

The procedure for measuring the accuracy of the decomposed firing instances is discussed in Nawab et al. (2010). A summary description of the procedure is described in appendix 1. Nawab et al. (2010) found that the average accuracy of the firing instances tested on a set of 22 contractions was 92.5%, at times reaching 97%. A similar level of accuracy was found for the data used in this study. The values for the individual contraction levels and muscles are presented in Table 1.

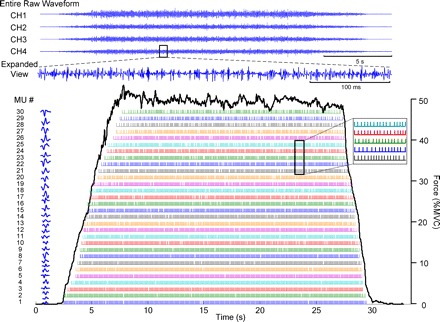
The algorithm produces a file containing the number of motor units observed and the instances of their firings. An example is shown in Fig. 1A, which shows the individual firings of the 21 active motor units detected during a 50% MVC of the FDI. The force trajectory traced by the subject is shown as a dark continuous line. Firing instances (the locations of the action potentials) are plotted as bars (impulses) at the time of occurrence. Figure 1B shows a plot of the firing rates of these motor units over time. The firing rate curve of each motor unit was computed by low-pass filtering the impulse train with a unit area Hanning window of 2-s duration. For additional details on the filtering procedure, refer to De Luca et al. (1982a).

Fig. 1.

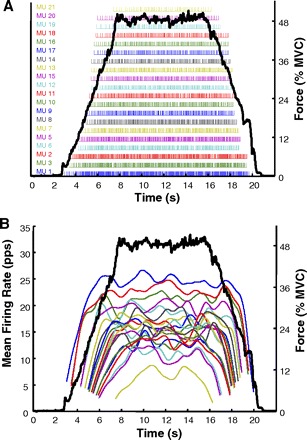
A: example of the incidences of firing of 21 motor units decomposed from the surface EMG signal obtained from the first dorsal interosseous muscle (FDI). Each bar represents the firing time of an action potential. The dark solid line represents the force output of the FDI muscle. The force in percentage of maximal voluntary contraction (MVC) level is scaled on the right and the motor unit number in order of recruitment order is listed on the left. B: these are the averaged time-varying firing rates for each of the 21 motor units calculated from the timing data above. Note the hierarchical relationship of the firing rates of each motor unit. The earlier recruited motor units (lower-threshold) have greater firing rates. Note that the firing rate values at recruitment and de-recruitment are influenced by the filter used to smoothen the firing rate values.

RESULTS

Recruitment threshold versus firing rate

We analyzed the relationship between the firing rates and the recruitment thresholds of motor units observed during the contractions. The recruitment threshold of each motor unit was recorded as the force level achieved, measured in percent MVC, at the instance at which the first firing of the motor unit occurred. The mean firing rate was calculated using the firing rate curve of the motor unit during the period of constant force. The average value of the curve during this period was recorded as the mean firing rate of the motor unit at the sustained force level.

INDIVIDUAL SUBJECTS.

Figure 2 depicts the firing behavior of motor units active during contractions of the VL, FDI, and TA in three individual subjects. The plots show linear relationships between the recruitment thresholds and the mean firing rates. Separate regressions, indexed by color, represent the data from each contraction target level. For each of the three muscles, the intrasubject variability of the mean firing rates was low compared with the data of the grouped subjects, shown in the following section. The R² values are presented in Table 2.

Fig. 2.

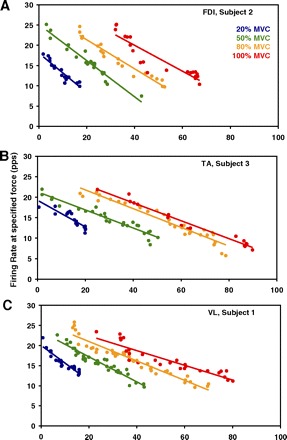
Average value of the motor unit firing rates plotted as functions of recruitment threshold—separately for contractions sustained at 20, 50, 80, and 100% MVC. The data are representative of different subjects and different muscles (the vastus lateralis, the FDI, and the tibialis anterior). The regression lines are drawn through the data from individual contractions, with each data point representing an individual motor unit. The average R² values are provided in Table 2.

Table 2.

Comparison of average R² values of individual subjects to R² values of common regressions

	R2 (Subjects, Averaged)			R2 (Common Regressions)
Force Level	VL	FDI	TA	VL	FDI	TA
20%	0.843	0.886	0.814	0.810	0.733	0.721
50%	0.902	0.927	0.888	0.748	0.812	0.749
80%	0.917	0.890	0.909	0.788	0.798	0.843
100%	0.913	0.866	0.870	0.798	0.750	0.603

See Table 1 for abbreviations. Values are universally lower for the common regressions.

In all subjects, muscles, and force levels, the slopes of these regressions were negative, indicating that motor units recruited at higher thresholds tended to sustain lower average firing rates in a contraction, regardless of target force level. As the force level increased, more motor units were recruited, indicated by the detection of motor units at higher recruitment thresholds in subsequent contractions. The firing rates of motor units recruited near the same threshold were greater in contractions of higher target force level, which is reflected by the increasing intercept of the firing rate regressions.

The firing rates achieved at maximum force in the FDI were, on average, greater than those in the VL and TA. Because the earlier-recruited motor units achieve higher firing rates than later-recruited motor units and firing rates increase with further excitation, the extrapolated intercept of the 100% MVC regression shows a maximal firing rate sustainable by the lowest threshold motor units in the muscle. The extrapolated maximal firing rate values are as follows: in the VL (subject 1), 26.0 pps; in the TA (subject 3), 27.4 pps; and in the FDI (subject 2), 32.7 pps. In fact, the regressions suggest that during the 100% MVC contraction, the firing rates of all motor units recruited before 50% MVC in the FDI were higher than those of the same recruitment threshold in both the VL and TA.

In these examples, the slopes of the regressions, averaged across the four force contractions for the VL (–0.30 ± 0.11) and for the TA (–0.25 ± 0.05), were comparable in value, whereas the average slope for the FDI contractions (–0.40 ± 0.08) was much steeper. Note also that the standard deviation SD of the slope values was greater for the VL than for the FDI and the TA: that is, there was greater variance in the slopes of the four VL regressions than in those of the FDI and those of the TA, although the analysis was performed for the same force levels in each muscle. Thus the slope of the firing rate–recruitment threshold relationship changed less relative to the change in excitation force for the FDI and the TA than for the VL.

GROUPED SUBJECTS.

The variability increased as data from multiple subjects were aggregated. Figure 3 shows the same linear relationships in the VL, FDI, and TA using the combined data of all subjects. As in the individual cases, both the recruitment range and the sustained mean firing rate were greater for contractions of higher target force levels. In the full data set, the maximum recruitment thresholds of the VL and TA were 95 and 90% MVC, respectively. The last motor unit of the FDI was recruited at 67% MVC. The firing rates of the FDI across all subjects were still greater overall than those of the VL and TA. The value for the FDI is greater than that earlier reported by De Luca et al. (1982a) and Duchateau and Hainaut (1990): however, higher values such as 60 and 78% MVC have been reported by others such as Kamen et al. (1995) and Thomas et al. (1987). The values for the TA are greater than those previously reported (De Luca et al. 1996). The generally greater values for the maximal recruitment threshold are likely because of the fact that the new EMG signal decomposition technology allows for the observation of a greater number of concurrently active motor units. Therefore there is a greater likelihood of observing the rare, very high-threshold motor units.

Fig. 3.

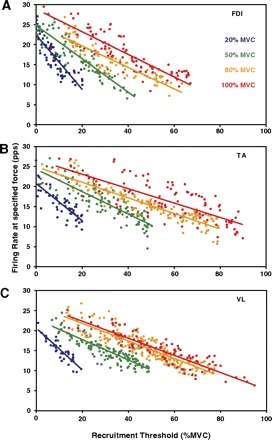
Average value of the motor unit firing rates plotted as functions of recruitment threshold. Data are from all analyzed contractions from the vastus lateralis (VL), FDI, and tibialis anterior (TA) for contractions sustained at 20, 50, 80, and 100% MVC. The regression lines are drawn through the data from all the contractions at each force level, with each data point representing an individual motor unit. As expected, the regression lines for the greater contractions have higher values. Note that the data scatter is greater in these grouped data than in the data for the individual subjects. The R² values are provided in Table 2.

The universal increase in variability of the firing rate data are reflected by lower R² values for the intersubject analysis given in Table 2. In this table, the R² value averaged across the individual subjects' regressions is given alongside the R² value for the regression of the common data. The former measures the average strength, in terms of correlation, of the firing rate versus recruitment threshold relationship at the individual subject level, whereas the latter indicates the strength of the same relationship when the data of all subjects are combined together. For each corresponding contraction, this value decreases as the subjects' data are combined, suggesting that the parameters of the regression are more precise for individuals, although for the group, the relationship structure remains the same, as shown in Fig. 3.

The mean firing regression slopes of the FDI were more negative at each force level than those of the VL and TA. The slopes of the firing rate regressions were increasingly positive with stronger contractions for all muscles in the intersubject case; the amount by which the slope changed between subsequent contractions was less at higher force levels. There was also greater separation between regressions at lower force levels in each muscle, indicating a greater increase in overall firing rates between subsequent contractions at lower force levels. Between 80 and 100% MVC in the VL, there was little separation and thus a slight increase in firing rates; in the TA, the separation between these two contractions was greater; and it was greatest in the FDI, with an increase of 3.8 pps between the intercepts of the two regressions.

To verify that the protocol structure was not generating the behavioral phenomenon seen in the average firing rates, we recruited an additional subject to perform the protocol in reverse order—from 100 to 20% MVC. Figure 4 shows the FDI contractions performed by subject 7. Whereas the 80% MVC contraction was not decomposed because of the large number of clipped samples in the signal, the 20, 50, and 100% MVC contractions still show the slope decrease in the mean firing rate regression. This indicates that the protocol structure does not influence the behavior of the slopes of the operating point.

Fig. 4.

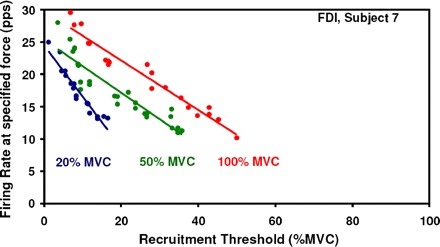
Motor unit firing rates and recruitment threshold from the FDI muscle from an additional subject under the reverse protocol. Contractions performed at 100, 50, and 20% MVC are shown.

De-recruitment

The relationship between the recruitment threshold and the de-recruitment threshold of a motor unit varied among muscles. Although the relationship for each subject was linear, differences in the magnitude of the slope and both the sign and magnitude of the intercept described different behavior. Figure 5 shows this relationship for the separate subjects in all three muscles.

Fig. 5.

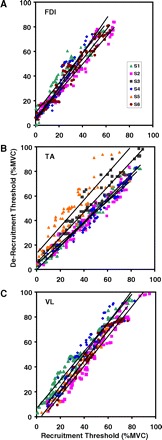
Relationship between recruitment threshold and de-recruitment threshold is shown. The data from the VL, FDI, and TA are shown. The data from all force levels were grouped together. The lines represent the regression analysis for the data from each subject. Note that the relationship varies slightly in slope for all the subjects in each muscle. In the FDI muscle, all the data points lie above the unity line, indicating that the de-recruitment threshold is always greater than the recruitment threshold. In the VL, a few motor units from 2 subjects lie below the unity line in the range below 50% MVC. In the TA, the shift from the unity line is less well organized.

In the VL muscle (Fig. 5C), four of the five subjects from which these data could be obtained exhibited a slope >1 (1.23 ± 0.03) and a negative intercept. That is, low-threshold motor units were de-recruited at a lower force level than the level at which they were recruited; for high-threshold motor units, the converse was true. The crossover point at which the relationship shifts varied between these four subjects, with an average of 19.66 ± 11.43% MVC. The gap between recruitment and de-recruitment thresholds was thus greater for motor units nearer to either end of the spectrum. One subject differed with a positive intercept.

In the FDI muscle (Fig. 5A), each subject exhibited a slope >1 (1.20 ± 0.09) and a positive intercept (5.70 ± 1.67% MVC). In contrast to the VL, motor units were thus de-recruited at higher force levels than those of recruitment, regardless of threshold value. The gap between recruitment and de-recruitment thresholds was increasingly larger for motor units recruited later in the contraction, which was also true of high-threshold motor units in the VL.

In the TA muscle (Fig. 5B), the relationship varied among subjects. Two of the five subjects analyzed exhibited a slope >1 (0.99 ± 0.08), and four showed a positive intercept (5.50 ± 4.95% MVC).

In all three muscles, and the majority of the subjects, motor units were de-recruited at higher force levels than at recruitment. This effect was most apparent in the FDI. It implies that the same level of force was produced with fewer motor units at de-recruitment than at recruitment. A reasonable explanation for this effect is that the force twitches of the motor units increase in amplitude after the contraction begins, a phenomenon known as potentiation. Potentiation in the human VL has been observed during the first minute of activity during a sustained contraction by Adam and De Luca (2005). In that report, the potentiation was subsequently followed by a diminution of the force twitch. Similar findings have been reported in the VL by Eom et al. (2002) during electrical stimulation and have been observed by us in the FDI during voluntary isometric contractions.

When a motor unit is activated it produces a unit of force proportional to the magnitude of its force twitch and firing rate. Over the course of the short-term contractions performed in this study, the increased mechanical output of the potentiating motor unit allows it to progressively produce more force for the same firing rate. As the contraction force decreases, the excitation to the motoneuron pool decreases. When the excitation decreases to the level at which a motor unit was recruited, because of the force-twitch potentiation, the motor unit produces more force, hence the observed increase of the de-recruitment force threshold. In Fig. 5, there seem to be slight differences in the degree of influence of the potentiation among subjects, as would be expected because of physical and physiological variability as well as differing intersubject rates and degrees of force twitch potentiation. The FDI muscle stands out among the other two with a greater degree of recruitment/de-recruitment shift that seems to be more consistent among subjects.

Model for the firing rate and recruitment relationship

It is apparent that the behavior of the regression lines in the group data in Fig. 3 change with force level. Therefore the firing rate is a function of both the recruitment threshold and the force level. It can be modeled according to the following equation

$$\lambda (\phi ,\tau )=m(\phi )\tau +b(\phi )$$ (1)

where λ is the firing rate in pps; τ is the normalized recruitment threshold 0 < τ <1; with τ_max ranging from 0.65 to 1.0, depending on the muscle; and φ is the normalized force 0 < φ <1.

The slope, m(φ) changes as φ changes and may be modeled by an exponential function

$$m(\phi )=C-A{e}^{-\phi /\mathrm{B}}$$ (2)

The values of the slopes m(φ) from Eq. 2 for each muscle are plotted in Fig. 6A, where it may be seen that the VL and the TA muscles behave similarly, whereas the FDI differs. The MATLAB toolkit Curve-Fitting Tool (cftool.m) was used to obtain the values of parameters A, B, and C through an iterative process. The values of the parameters that provided the best fit are presented in Table 3. The R² values for the FDI, TA, and VL are 0.989, 0.998, and 0.999, respectively.

Fig. 6.

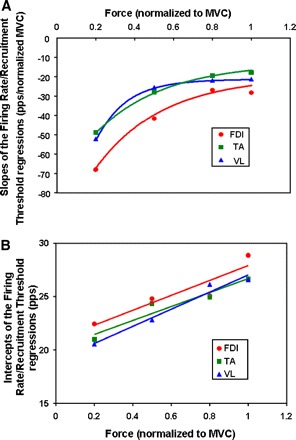
A: regression slopes for grouped data, as functions of excitation. Data points consist of the 4 slopes of the mean firing rate vs. recruitment threshold regressions for each of the 3 muscles. Data points are taken from slopes of Fig. 3. An exponential equation was used to fit the data. B: The y-intercept values for the grouped data are plotted as a function of excitation. Data points consist of the 4 values of the mean firing rate for each of the 3 muscles. Data points are taken from slopes of Fig. 3. A linear equation was used to fit the data.

Table 3.

Equation 4 parameters for group data

	A	B	C	D	E
VL	1.16	0.15	−0.21	8.03	19.0
FDI	0.85	0.32	−0.23	6.93	20.9
TA	0.65	0.30	−0.30	6.54	20.2

See Table 1 for abbreviations.

The intercepts of the regression lines in Fig. 3 increase in a linear fashion as a function of contraction force and can be described as

$$b(\phi )=D\phi +E$$ (3)

The values of the intercepts from Eq. 3 for each muscle are plotted in Fig. 6B, where it again may be seen that the parameter values for the FDI are distinct from those of the VL and the TA. The R² values for the FDI, TA, and VL are 0.851, 0.927, and 0.969, respectively.

By substituting Eqs. 2 and 3 into Eq. 1, we obtain the following equation that describes the relationship for the firing rates as a function of recruitment threshold and normalized force

$$\lambda (\phi ,\tau )=D\phi +(C-A{e}^{-\phi /\mathrm{B}})\tau +E$$ (4)

The values of the parameters (A, B, C, D, and E) for each muscle are listed in Table 3. The characteristics of this equation for the VL muscle may be seen in Fig. 7A. This equation predicts the firing rate values of motor units as functions of the excitation or force level, given their recruitment thresholds between 10 and 90% MVC. It is apparent that the rate of increase of the firing rates is greater for the earlier recruited motor units than for the later recruited motor units. This phenomenon may be seen more clearly by calculating the velocity of the firing rate by differentiating Eq. 4. The velocity equation can then be expressed as

$$V(\phi ,\tau )={}^d{/}_{d\phi }\lambda (\phi ,\tau )=\tau ({}^A{/}_B{e}^{-\phi /\mathrm{B}})+D$$ (5)

The projected firing rate velocities from this equation are plotted in Fig. 7B. A cursory comparison of the velocities calculated from Eq. 5 with the tangents of the firing rate values showed a close agreement.

Fig. 7.

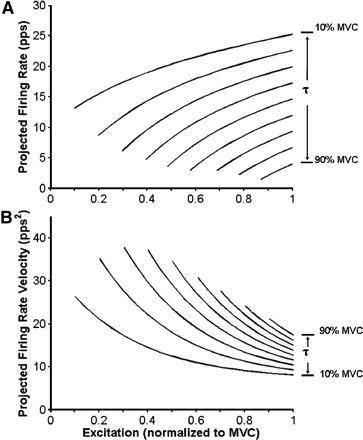
A: projected firing rates of motor units in the VL muscle calculated from Eq. 4. The firing rates of motor units recruited between 10 and 90% MVC at intervals of 10% MVC are shown. The curves are limited to this range because the empirical data were so limited. B: projected velocity of the firing rates of motor units in the VL muscle calculated from Eq. 5. The firing rates of motor units recruited between 10 and 90% MVC at intervals of 10% MVC are shown. The curves are limited to this range because the empirical data were so limited.

DISCUSSION

In past studies such as those of De Luca et al. (1982a,b), De Luca and Erim (1994), and De Luca et al. (1996), patterns in motor unit firings have indicated a control scheme that maintains a consistent structure among muscles, wherein the values of the scheme's parameters account for the differences among muscles. In this study, we expanded on the results of previous work with the benefit of a new technology that allows the observation of a larger set of motor units during individual isometric contractions up to the maximal force level.

Primarily, we observed that the regressive relationship between firing rate and recruitment threshold was consistent across force levels but varied among muscles and to a lesser extent across subjects. This was particularly clear in individual subjects (Fig. 2). At each target force level, the mean firing rate regression shifts vertically with slight change in slope, indicating that the firing rates increased consistently relative to the excitatory input. The firing rate versus recruitment threshold line describes an “operating point” of the motoneuron pool that shifts in response to excitation, whereas the control characteristics of the motor units remain invariant; that is, the relationship between the recruitment threshold and the average firing rate achieved at a particular force maintains a fixed relationship defined by the slope of the regression equations. The magnitude of the slope or operating point decreases monotonically relative to excitation. This gradual slope change may be seen in the VL of the individual subject presented in Fig. 2A and more emphatically in each muscle when considering data from multiple subjects (Fig. 3). However, even at the 100% MVC level, there remains a discernible hierarchical separation among the firing rates of the motor units. This observation is consistent with that of our previous work (De Luca and Erim 1994). Although the results of the previous work suggested that the mean firing rates of motor units converge at the MVC level, the previous study included observation of only a few motor units at MVC that could be tracked with our earlier and less sophisticated technology described in LeFever and De Luca (1982) and LeFever et al. (1982). The present technology, which enables numerous motor units to be monitored at high force levels, including MVC, provides more convincing evidence that the firing rates tend to group closer together as the force increases but do not fully converge.

Figures 2 and 3 also show that the three muscles have different maximal recruitment thresholds, with the FDI having the lowest at 67% MVC, the TA at 90% MVC, and the VL at 95% MVC. Correspondingly, the shift in the operating point between 80 and 100% MVC in the three muscles is greatest for the FDI, which has the lowest maximal recruitment threshold, and least for the VL, which has the greatest maximal recruitment threshold. This complement indicates that muscles such as the FDI, which stop recruiting motor units at lower force levels, activate the firing rates to a greater degree after recruitment ceases, whereas muscles such as the VL and the TA recruit motor units at greater force levels and accordingly implement less dramatic modulation of the firing rates.

The gradual decrease in the slope of the operating point with increasing force level indicates that the excitability decreases as the force of the contraction increases, as evidenced by the firing rates of the lower threshold motor units. Eq. 2 describes this behavior. As may be seen in Fig. 4, the protocol structure does not influence the behavior of the slopes of the operating point.

We found that the maximal firing rates we observed were lower than some reported in the literature, although the reported values have a considerable range. For example, Roos et al. (1999) reported a maximal firing rate in the quadriceps muscles of 47 pps, but a mean firing rate of 26.4 ± 7.6 pps during MVC. Seki et al. (2007) reported that motor units in the FDI achieved firing rates ≤65 pps. However, they also report a Gaussian distribution of the mean firing rates observed at 100% MVC, centered at ∼35 pps. The recruitment thresholds of these motor units were not reported. Connelly et al. (1999) observed a maximum firing rate of 58 pps, but a mean firing rate of 41.9 ± 8.2 pps during MVC in the TA. However, <6% of the nearly 2,000 action potential trains they observed achieved firing rates >45 pps. Bigland-Ritchie et al. (1992) similarly reported lower mean firing rate values (32.1 ± 10.7 pps) in the TA.

The variation among the reports is caused, in large part, by two factors. First, reliable observation of the firing rates of motor units during MVC presents significant technical challenges. Second, there is an issue as to how the maximal firing rate values are calculated. If the value is obtained during a brief epoch of a few milliseconds during a force inflection, it is likely to be a greater value. If it is calculated from firing intervals during a short force burst, it would also be a greater value. The values we report are calculated via the regression of all motor units observed at 100% MVC, and each of the data points in the regression was calculated from the firings over an epoch of 4 s. This approach yields lower average firing rates, but the values are more indicative of the average sustained maximal value of the firing rate.

When considering data from the group of subjects as a whole, variability in each individual mean firing rate regression increased. However, the differences between muscles in this view were clear, and the hierarchical relationship that we saw in individual subjects was preserved. The intersubject data provided a more comprehensive indication of the fundamental structure of the control scheme; the intrasubject data showed strong statistical correlation and thus a more accurate measurement of an individual subject's parameters. Note that the values of the parameters vary among muscles (Table 3). The distinction is particularly notable between the FDI and the other two larger muscles: the VL and the TA. This difference is caused either by how the muscles respond to excitation or to how they receive excitation. In the first case, different intrinsic electrical properties of the muscle fibers, particularly those that influence parameters A and B in Table 3, between the VL and the other two muscles could account for the different slopes. Alternatively, it may be caused by different excitatory/inhibitory feedback from the proprioceptive sensors in the different muscles.

The relationship between the firing rates, the recruitment threshold, and the level of excitation expressed by Eq. 4 clearly shows the onion skin property described by De Luca and Erim (1994). The projected values in Fig. 7A show that earlier recruited motor units have greater firing rates at recruitment and continuously have greater firing rates than later recruited motor units. The velocity of the firing rates expressed by Eq. 5 and whose projected values may be seen in Fig. 7B show that earlier-recruited motor units decrease their firing rate velocity slower as the excitation increases. This arrangement enables the early active motor units to meet the rising force output demand until new motor units are recruited. As excitation increases, their velocities decrease and cluster closer together, while new motor units are recruited. This deceleration of active motor units continues as a maximal velocity is approached at 100% MVC or φ = 1. High-threshold motor units have an initial velocity that is close in value to the terminal velocity and exhibit the least deceleration. These characteristics of the firing rates, the velocities of the firing rates, and the acceleration of the firing rates are clearly evident in the empirical data in Figs. 1 and 3, where the firing rates of earlier recruited motor units have a faster rise and those of the later motor units have a much slower rise.

Our findings of a hierarchical inverse relationship between the recruitment threshold and the mean firing rates of motor units are in agreement with those of all our previous studies on this topic dating back to 1982. They are also consistent with those of Seyffarth (1940), Tanji and Kato (1973), Monster and Chan (1977), and Kanosue et al. (1979), who used needle electrodes to collect the EMG signals in human muscles and analyzed their data by direct visual measurements. Our results also agree with those from studies that used various sophisticated signal decomposition techniques for identifying motor unit firings from EMG signals collected with indwelling needle sensors inserted in human muscles or surface sensors (Masakado 1991, 1994; Masakado et al. 1995; McGill et al. 2005; Rose and McGill 2001; Stashuk and de Bruin 1988). The algorithms used by different laboratories are unique unto themselves. Therefore it is highly improbable that they would all report a similar finding accidentally.

However, our findings contrast with those of Gydikov and Kosarov (1974), Kosarov and Gydikov (1976), Moritz et al. (2005), Tracy et al. (2005), and Barry et al. (2007), all of whom also worked with voluntarily controlled human muscles and who reported greater firing rates for higher threshold motor units.

All the studies whose results agreed with ours had in common the fact that the observations of the firing rate behavior were made on individual contractions from individual subjects. Those that found a firing rate recruitment relationship contrary to ours had in common the fact that the data analysis was performed on grouped data from multiple contractions and/or multiple subjects. This is an important distinction because, in this work, we found the intersubject variance to be considerably greater than that within a single contraction of an individual subject (Figs. 2 and 3; Table 2). Also, in our earlier work (De Luca and Erim 1994), we showed that, when firing rate curves from different subjects are plotted together, the onion skin characteristic is disturbed by overlapping curves. In the same study, the onion skin was preserved when the data from individual subjects alone were considered. A similar observation can be made in the data of Monster and Chan (1977), which show the onion skin property for individual subjects (their Fig. 9) and disturbed onion skin characteristics when data from several subjects are plotted together on a logarithmic scale (their Fig. 2). Grouping data across subjects introduces various confounding factors. Also, grouping data that are collected on different days and are normalized to the likely different MVC values of each day can produce relationships that are more a factor of the differing force levels than the characteristics of the underlying control scheme. More details are presented in the Caution Note in appendix 2.

There are reports on animal experiments that also counter our results. Eccles (1936, 1953) reported that motoneurons innervating fast contracting motor units have a much shorter afterhyperpolarization and a faster firing rate compared with motoneurons innervating slow contracting motor units. Kernell (1965) also observed that the upper and lower limits of the motoneuron firing rate were significantly correlated with the time course of their afterhyperpolarization and reinforced the motoneuron-motor unit firing rate and force twitch match. Their observations were made on anesthetized, decerebrated cats by electrically stimulating severed ventral roots.

Burke (1968) also worked with anesthetized, decerebrated cats, severing the ventral roots except L₇ and S₁. He observed that, during homonymous muscle stretch, the type F* motor units with short time to peak, low-amplitude force twitches tended to fire at faster rates than type S motor units with long time to peak. This result implies that F* units have a greater threshold. However, over the past three decades, studies by Young and Meyer (1981), Elek et al. (1992), and Gossen et al. (2003) have questioned whether the time to peak is linearly related to the recruitment threshold of a motor unit. They posit that the relationship is better described by a unimodal distribution skewed toward fast contraction times.

It is therefore not surprising that Hoffer et al. (1987), working with awake cats with an intact nervous system, found a firing rate behavior consistent with the onion skin property. They made their measurements while the cats walked and generated voluntary contractions. The work of Hoffer et al. (1987) raises questions about what relevance the firing rate data obtained with electrical stimulation of severed nerves in anesthetized, decerebrated cats may have in describing motor control schemes used in voluntary contractions. Henneman et al. (1965) were confronted with the same quandary and concluded that “there is no reason therefore to regard electrical excitability as an index of physiological excitability.”

Based on their observations Eccles et al. (1958) proposed a hypothesis that later recruited motor units, with shorter-duration force twitches, would possess greater firing rates than the lower threshold motor units with longer-duration force twitches, which require lower firing rates to obtain “optimal tetanic fusion.” According to Eccles et al. (1958), a greater firing rate for slow motor units would merely serve to fatigue them, and lower firing rates for the fast motor units would be inefficient in fusing them. The hypothesis was supported by Burke (1981) and Kernell and colleagues (Bakel and Kernell 1993; Kernell 1992, 2003). This is an appealing concept under which the control scheme would enhance the force production of a muscle and enable the body to require smaller muscles to perform necessary activities of daily living, which in turn would require less energy. During the evolution of the neuromuscular system, the need of less caloric input would have been advantageous for survival.

Thus the question remains as to why the control scheme should be organized according to the onion skin property. The teleological argument above misses one important point. High-threshold motor units are generally fast-fatiguing. If they fire at relatively higher rates, they will fatigue more quickly, and the force will not be maintained. According to our data, the scheme for motor unit control did not evolve to enhance force; instead, it seems to have optimized some combination of force magnitude and time duration. The onion skin control scheme would seem to better serve the flight-and-fight response by providing the capacity to generate force and the capacity to sustain it.

In conclusion, the results of this study support the proposition that in isometric contractions the control of the motoneurons in the motoneuron pool maintains its structure among different muscles but varies among individuals. The firing rate and its first and second derivative, the velocity and the acceleration, are inversely related to the recruitment threshold. Thus the recruitment threshold of a motoneuron determines the firing rate characteristics of that motoneuron. These parameters of the control scheme seem to be constants embedded in the motoneuron pool. The relationship establishes an “operating point” that is modulated by the level of excitation.

GRANTS

This work was supported in part by National Institutes of Health Grants NS-058250 to Delsys for the development of the decomposition system and HD-050111.

DISCLOSURES

C. J. De Luca is the CEO of Delsys, the company that developed the technology used in the collection and analysis of the data in the manuscript.

APPENDIX 1

Surface electromyographic signal decomposition algorithm

The surface electromyographic (sEMG) signal decomposition problem is complex. The task is threefold. First, one must decompose a signal that consists of a superposition of multiple unknown pseudorandom time series (motor unit action potential trains), each having a unique action potential pulse shape that can change to some degree throughout the signal. (The condition that action potentials from different motor units have unique shapes is imposed by the uniqueness of the spatial relationship between the sensor and the fibers belonging to each motor unit in the vicinity of the sensor.) Second, one must perform this task so that a maximal number of motor unit action potential trains is identified with the greatest possible accuracy. Third, one must design a test that provides a measure for the accuracy.

In our procedure for decomposing the sEMG signal, we collect the sEMG signal with a five-pin sensor and obtain four differential channels of sEMG signals. The decomposition algorithm operates on all four channels simultaneously. Each channel presents, more-or-less, signals from the same motor units, seen differently by each channel. The same action potential thus has a different electrical signature in each of the four channels; this property assists the decomposition algorithms in identifying the contributory action potentials by providing four independent representations of the same event. This enables the algorithm to parse complex superpositions more accurately than it could using fewer channels. An example of the four-channel sEMG signals along with an expanded epoch to show the complexity of the signals and the firing instances of the identified motor units is presented in Fig. 8.

Fig. 8.

Example of the 4 channels of surface electromyographic (sEMG) signals obtained by the sEMG sensor. A 100-ms epoch is expanded to display the complexity of the signal that is to be decomposed. The firing instances of the identified motor units are located below. The action potential of each train is presented to the left of the motor unit train.

The algorithm is an evolution of that reported by De Luca et al. (2006), with important improvements reported by Nawab et al. (2010). It consists of an artificial intelligence approach which uses the integrated processing and understanding (IPUS) concept described in Lesser et al. (1995). The IPUS framework basically allows artificial intelligence rules to be conveniently encoded (see Winograd and Nawab 1995 for details) in support of the mathematical structure of an algorithm to permit run-time modification of its behavior in response to different conditions throughout the signal to be decomposed. The proof-of-principle algorithms described in De Luca et al. (2006) had limited success in dealing with complex superpositions of motor unit action potential trains (MUAPTs). The decomposition algorithm described in Nawab et al. (2010) introduced new processes that help to resolve complex superpositions for a larger number of the MUAPTs identified by the original IPUS algorithms. The signal decomposition algorithm used in the data analysis of this work has two distinct stages. The first is the IPUS stage, followed by the iterative generate and test (IGAT) stage.

IPUS STAGE.

This stage consists of three segments: motor unit action potential (MUAP) template creation, MUAP template matching, and MUAP template updating. The signal decomposition algorithm begins by identifying as many templates for the various MUAP shapes as possible. This is accomplished by extracting signal shapes in the vicinity of data peaks in the sEMG signal. When a sufficient number of similar shapes is identified, they are averaged and designated a MUAP template (De Luca et al. 2006). The matching of MUAP templates against the remaining sEMG signal takes place through a maximum a posteriori probability classifier (LeFever and De Luca 1982). Updating of MUAP templates takes place through a recursive weighting process whenever the matching procedure detects a new instance of a previously detected MUAP (Nawab et al. 2002).

IGAT STAGE.

This is the “iterative generate and test” stage of the artificial intelligence that identifies any template whose presence is objectively indicated in any of the complex superpositions within the sEMG signal. A template-matching procedure is performed on the sEMG signal to identify locations where the shape of the sEMG signal and the shape of an identified MUAPT template exhibit a correlation of ≥20%. A discrimination analysis is performed at each of those locations to determine which of the multiple matching templates has contributed. The likelihood of a template combination at a particular signal location is determined by the degree to which each of the combination's constituent templates matches the signal shape in the vicinity of that location and the degree to which the location is consistent with a locally estimated firing rate for the corresponding MUAPT (for more details, see Nawab et al. 2004). Once the template combinations have been selected for the entire sEMG signal, the resulting MUAPTs are required to meet the following criteria: 1) the mean interfiring interval of any MUAPT is limited to 350 ms and 2) the mean energy of the residual signal (the difference between the original signal and all the identified MUAPTs) at the firing locations of any MUAPT must be a small fraction of the mean energy in all the MUAPT constituents at those locations. For more complete details, the reader is referred to Nawab et al. (2010).

Procedure for assessing the accuracy of the decomposition algorithms

The accuracy of the decomposition algorithms used in this study was validated with two methods: 1) the two-sensor test and 2) the decompose-synthesize-decompose-compare test. These two tests are the most comprehensive and rigorous devised to date. However, given the complexity of the task, additional methods may strengthen the proof of accuracy.

TWO-SENSOR TEST.

This test was introduced by Mambrito and De Luca (1984). It uses two EMG sensors placed adjacent to each other. Each sensor detects motor unit firings from a common set of motor units, but each sensor also detects firings from motor units that are not in common and are specific to each sensor. Thus each of the two EMG signals presents a different challenge to the decomposition algorithm. The two EMG signals are decomposed. The common motor unit trains are identified. The accuracy of the firings in the in-common trains is measured as follows

$$\text{Accuracy}=(\text{total number of firings}-\text{number of noncoincident firings})/\text{total number of firings}$$

The accuracy of the decomposed motor unit trains is obtained by averaging the individual accuracies for each train. This test was one of the two tests used for measuring the accuracy of decomposed surface EMG signals in De Luca et al. (2006) and Nawab et al. (2010). In the example provided in those works, one sensor produced 31 motor units, and the other produced 32. Eleven of them were common motor units. Their average accuracy was 92% and the recruitment orders of the 11 motor units were identical.

In a precursor study, De Luca et al. (2006) used the two sensor test to compare the accuracy of motor unit firings detected with a needle sensor and a surface sensor. For three common motor units, the accuracy was found to be 97.6%: 996 firings of a total of 1,021 were coincident firings. The accuracy obtained in this case was greater than that for the two surface-sensor test. However, only three motor units were available for comparison.

A limitation of the two-sensor test is that it only tests the accuracy of the common motor units and it cannot determine the accuracy of the remainder of the identified motor units. Another limitation is that, to compare surface and needle EMG signals, different decomposition algorithms need to be used for each signal.

DECOMPOSE-SYNTHESIZE-DECOMPOSE-COMPARE TEST.

This test, introduced by Nawab et al. (2010), was devised to overcome the limitations of the two-sensor test. The sequence of steps in the test is depicted in Fig. 9. Briefly, the EMG signal is decomposed. The firing instances and the MUAP shape of each train are obtained. A synthesized signal is reconstructed with the MUAPTs. Gaussian noise with an RMS value similar to that of the residual of the decomposition is added. The synthesized signal is decomposed with the same algorithm. The firings of each train and the action potential shape of each train are obtained. They are compared by superimposing the results, as shown in Fig. 10.

Fig. 9.

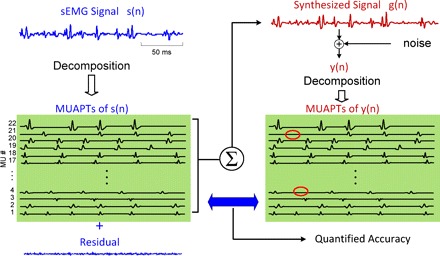
A schematic diagram of the decompose-synthesize-decompose-compare test. The sEMG signal, s(n), is decomposed, and the action potentials are used to reconstruct a synthetic signal, y(n), which in turn is decomposed. The number of motor units is identified, and the shapes and firing times of the action potentials are compared. The comparison provides a metric for the accuracy of the decomposition algorithms. (This figure is modified from one that appears in Nawab et al. 2010.)

Fig. 10.

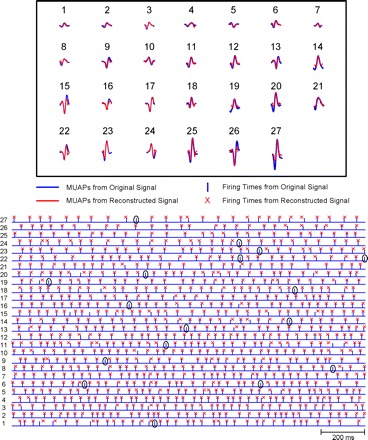
Comparison of the decomposition of the original sEMG signal and that of the synthesized signal. Top: the action potential shapes of the 28 motor unit action potential (MUAPs) that were identified in both the original sEMG signal and the synthesized signal. Note the similarity in the shapes of each individual motor unit recognized in both decompositions. Bottom: a short epoch of the firings of the 28 motor unit action potential trains (MUAPTs). The bar represents the firing instances from the decomposition of the original sEMG signal; the X indicates those from the decomposition of the synthesized signal. Note that in those firings where the two instances are not superimposed, the location of the X remains in the same motor unit. In other words, there may be some misalignment resulting from 1 of the 2 decompositions (unpaired events), but identification errors were rare. Seventeen are identified in the figure.

The top of Fig. 10 presents the shapes of the action potentials of the motor units identified in both decompositions. The blue colored shapes represent those of the first decomposition, and the red represent those of the second decomposition. Note that both decompositions produced the same number of motor units, and the identified shapes of each motor unit were, in large part, similar.

The bottom of Fig. 10 presents an epoch of the firings of the detected motor units. The blue bars represent the firings from the first decomposition, and the red X indicates the location of the firings of the second decomposition. A bar and an X are considered to be coincident if they are within ±4 ms. Given that the action potentials typically have a time duration of 10–15 ms and that the identification of the peak of the action potential, which is used for alignment, may be distorted by the successive removal of superimposed action potentials, this margin is reasonable. Note than even when the firings are further out than ±4 ms, in the majority of cases, the firing from the synthesized signal remains in the right sequence in the time series. That is, it is not misclassified with that of another motor unit and it may well represent a correctly identified motor unit firing that is slightly misaligned.

The accuracy is calculated as described above. In Nawab et al. (2010), this test was performed on a database of 561 motor unit action potential trains from 22 isometric contractions of five muscles. The average accuracy across all the contractions in the data set was 92.6%. Please see Nawab et al. (2010) for more complete details.

APPENDIX 2

Note of caution concerning subject's force compliance during data collection

We found that the subject's ability to closely follow the force trajectory greatly influenced the group analysis. A subject who did not reach and sustain the target force level, when grouped with others who did, shifted the regression downward. The motor units active during such a contraction fired at rates indicative of a lower target excitation level than that performed by the other subjects. Another more challenging issue concerned the proper use of the muscle during a contraction. Although we instructed subjects to perform contractions in a specific manner and used restraints to immobilize the joints, there were still physical shortcuts the subjects could take. Rotating the wrist during an FDI contraction, for example, reduces strain on the FDI itself but still registers the same force output. Such strategies are usually unnecessary and therefore not used at lower force levels, but can be at higher force levels, especially in the FDI and TA muscle. Yet another confounding factor is the degree to which each subject produces what he/she perceives to be the MVC level. Generating an MVC is an abnormal effort. Most individuals may not have ever produced an MVC in such muscles as the FDI and TA during their lives. That is why we took great caution in having each subject trained by the same individual.