Canal–Otolith Interactions and Detection Thresholds of Linear and Angular Components During Curved-Path Self-Motion

Abstract

Gravitational signals arising from the otolith organs and vertical plane rotational signals arising from the semicircular canals interact extensively for accurate estimation of tilt and inertial acceleration. Here we used a classical signal detection paradigm to examine perceptual interactions between otolith and horizontal semicircular canal signals during simultaneous rotation and translation on a curved path. In a rotation detection experiment, blindfolded subjects were asked to detect the presence of angular motion in blocks where half of the trials were pure nasooccipital translation and half were simultaneous translation and yaw rotation (curved-path motion). In separate, translation detection experiments, subjects were also asked to detect either the presence or the absence of nasooccipital linear motion in blocks, in which half of the trials were pure yaw rotation and half were curved path. Rotation thresholds increased slightly, but not significantly, with concurrent linear velocity magnitude. Yaw rotation detection threshold, averaged across all conditions, was 1.45 ± 0.81°/s (3.49 ± 1.95°/s²). Translation thresholds, on the other hand, increased significantly with increasing magnitude of concurrent angular velocity. Absolute nasooccipital translation detection threshold, averaged across all conditions, was 2.93 ± 2.10 cm/s (7.07 ± 5.05 cm/s²). These findings suggest that conscious perception might not have independent access to separate estimates of linear and angular movement parameters during curved-path motion. Estimates of linear (and perhaps angular) components might instead rely on integrated information from canals and otoliths. Such interaction may underlie previously reported perceptual errors during curved-path motion and may originate from mechanisms that are specialized for tilt-translation processing during vertical plane rotation.

INTRODUCTION

Linear and angular movements are detected by separate receptors—the otolith organs and semicircular canals—in the peripheral vestibular system. However, the two sets of signals converge onto single central vestibular neurons as early as the vestibular nuclei (Angelaki and Dickman 2003; Bush et al. 1993; Dickman and Angelaki 2002; Jian et al. 2002; Uchino et al. 2005; Yakushin et al. 2006; Zhang et al. 2001, 2002). The functional significance of this convergence has been of interest for some time. In recent years, the functional role of canal–otolith convergence has focused on vertical planes. These studies have been motivated by extensive theoretical and behavioral evidence showing that semicircular canal cues are important for the segregation of net linear acceleration detected by the otolith organs into estimates of inertial acceleration generated during translation and changes in head orientation relative to gravity (Angelaki et al. 1999; Green and Angelaki 2003, 2004; Green et al. 2007; Merfeld and Young 1995; Merfeld et al. 1993, 1999, 2001; Zupan et al. 2000). The neural basis of such semicircular canal–otolith interactions in vertical planes has been identified in brain stem, cerebellum, thalamus, and cortical areas (Angelaki et al. 2004; Liu and Angelaki 2009; Meng et al. 2007; Yakusheva et al. 2007; see review by Angelaki and Yakusheva 2009). Recent behavioral work has shown that vertical semicircular canal and otolith signals also interact extensively during detection of vertical plane rotation (Merfeld et al. 2009).

Much less is currently known about canal–otolith interactions in the horizontal plane, particularly in situations where the path followed by a subject is curved (e.g., turning a corner). During curved-path motion, linear and angular acceleration components activate both the otoliths and the semicircular canals. Using a series of transient angular and linear motion components in the horizontal plane, Ivanenko et al. (1997) asked whether human subjects are able to reconstruct their exact trajectory during simultaneous rotation and translation. They reported that subjects tended to appropriately perceive their angular body orientation regardless of the concomitant linear stimuli. In contrast, subjects' interpretation of the linear displacement was not always accurate, often yielding illusory trajectories. These illusory trajectories could be due to low-level canal–otolith interactions or could result from path integration errors. Measurements were qualitative, based on subjects' drawings of their perceived paths (Ivanenko et al. 1997).

Here we also address canal–otolith interactions in the earth-horizontal plane, but using more quantitative methods. In particular, we use signal detection theory to measure both rotation and translation detection thresholds during curved-path motions. We reason that, if canal and otolith signals interact such that the presence of angular motion affects perceived linear displacement, translation detection thresholds should vary as a function of angular velocity, and vice versa: if linear acceleration interacts with perceived angular motion, rotation detection thresholds should depend on the concurrent linear velocity.

In addition to directly characterizing canal–otolith interactions in the earth-horizontal plane, these experiments also allowed us to measure translation and rotation detection thresholds in a way that avoids the confound of background vibration and other extraneous cues. This was possible because all trials included actual platform motion; subjects distinguished movements that were either pure rotation (translation signal absent) or pure translation (rotation signal absent) from curved-path motion (signal present) (Figs. 1 and 2). Preliminary results have been presented in abstract form (Turner et al. 2008).

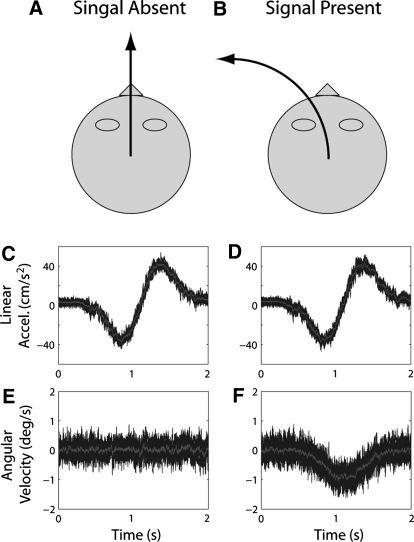
Fig. 1.

Rotation detection. (A, B) Schematic and (C–F) example stimulus traces for signal absent and present trials. C–F show superimposed, multiple examples of linear acceleration and angular velocity recorded by an accelerometer and rate sensor attached to the motion platform. The gray trace in each panel shows the average across examples. On signal absent trials (A), linear motion was forward along the nasooccipital at axis with Gaussian velocity profile (peak velocity/acceleration of 15.79·cm/s⁻¹·38.05·cm/s⁻² in this example) generating a linear acceleration like that shown in C; no angular movement was presented (E). On signal present trials (B), in addition to the identical linear motion profile (D), counterclockwise (leftward) angular motion around the yaw axis was presented with a synchronized Gaussian velocity profile (peak velocity 1°/s), generating traces like those shown in F.

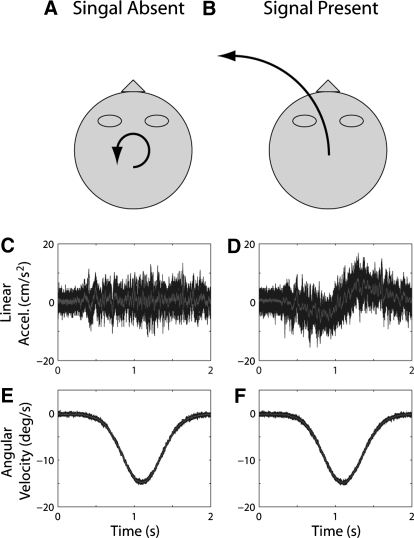
Fig. 2.

Translation detection. (A, B) Schematic and (C–F) example stimulus traces for signal absent and present trials. C–F: same conventions as those in Fig. 1. On signal absent trials (A), angular motion was counterclockwise around the yaw axis with Gaussian velocity profile (peak velocity/acceleration of 15°/s⁻¹·36.15°/s⁻² in this example) like that shown in E; no linear movement was presented (C). On signal present trials (B), in addition to the identical angular motion profile (F), nasooccipital linear motion was presented with a synchronized Gaussian velocity profile (peak velocity/acceleration 3.16°/s⁻¹·7.61/cm/s⁻²), generating traces like those shown in D.

METHODS

Equipment

Experiments were conducted using a 6-degree-of-freedom (df) MOOG motion platform (6DOF2000E; MOOG, Amsterdam, The Netherlands). Subjects were seated in a padded racing seat mounted on the platform. A five-point harness held subjects' bodies securely in place. A custom-fit plastic mask secured the head against a cushioned head mount, thereby holding head position fixed relative to the chair. Sounds from the platform were masked by playing white noise in headphones worn by the subjects. In addition, subjects wore ear plugs inside the headphones. Informed consent was obtained from all participants and all procedures were reviewed and approved by the ethics committee of Washington University.

Experimental procedures

ROTATION DETECTION.

Experiments used a classic signal detection paradigm. Each trial consisted of a single 2-s movement and both angular and linear components (if present) of the motion trajectory followed synchronized Gaussian velocity profiles of varying amplitude (see following text). Movements were presented in complete darkness, but lights were illuminated between trials to extinguish any possible motion aftereffects (e.g., velocity storage). Linear motion was forward along the nasooccipital axis at one of four linear velocities and angular motion was counterclockwise around the dorsoventral (yaw) axis (Fig. 1). Angular velocity was chosen to be 1°/s (2.41°/s² acceleration), near detection thresholds measured in preliminary experiments (see Supplemental material).¹ Four suprathreshold linear velocities were chosen to maximize the chances of observing an interaction: 5.26, 10.52, 15.79, and 21.05 cm/s, yielding peak linear accelerations of 12.67, 25.35, 38.02, and 50.70 cm/s², respectively. We expect that if there is an interaction, stronger linear velocity signals will have a bigger, easier to observe effect on the detection of angular velocity.

Within each 100-trial block, half of the trials were pure translation (Fig. 1A, rotation signal absent) and half were curved path (Fig. 1B, rotation signal present) and subjects indicated whether they perceived a curved path (signal) or pure translation (noise). In all, eight subjects participated (three male, five female; age 27–37 yr) and each subject ran a total of three blocks (300 total trials) at each of the four linear velocities. Responses were used to calculate hit rate (H) and false alarm rate (FA) (Fig. 3A), and the z-transform of these rates was used to calculate detectability (d′) of the rotation signal for that linear velocity according to the following equation (Green and Swets 1966; Wickens 2001)

$$d\mathrm{\prime }=\mathrm{Z}(\mathrm{F}\mathrm{A})-\mathrm{Z}(\mathrm{H})$$ (1)

The experiment was conducted in 1-h sessions of three blocks, each with a different linear velocity, run in pseudorandom order.

Fig. 3.

Signal detection methods. A: response classification table for a classic signal detection experiment. Each trial is either signal present or signal absent (rows of the table) and the subject can respond signal present or absent (columns of the table). Detectability is calculated using the hit and false alarm rates from this table (see Eq. 1). B: signal detection model. The 2 distributions represent the probability associated with different stimulus values given that signal is present (signal distribution) or absent (noise distribution). The model assumes that observers respond signal present when they observe a stimulus value greater than the criterion and signal absent otherwise. Note that the location of the criterion along the x-axis varies from observer to observer and even from condition to condition for the same observer.

TRANSLATION DETECTION.

This protocol was identical to that used for rotation detection, except that each movement was either a pure rotation (Fig. 2A, translation signal absent) or curved path (Fig. 2B, translation signal present) and subjects indicated whether they perceived curved path (signal) or pure rotation (noise). Again, linear movement was forward along the nasooccipital axis and angular movement was counterclockwise around the dorsoventral (yaw) axis. Linear velocity was chosen to be 3.16 cm/s (7.61 cm/s² acceleration), near detection thresholds measured in preliminary experiments (see Supplemental material), whereas the four angular velocities were chosen to be significantly above threshold to maximize the chance of observing an interaction: 5, 10, 15, and 20°/s, yielding angular accelerations of 12.05, 24.10, 36.15, and 48.20°/s², respectively. As before, three blocks were run at each angular velocity for a total of 300 trials. Eight subjects (three male, five female; age 25–35 yr) participated and seven of these were the same as in the rotation detection experiment. Responses at each angular velocity were used to calculate H and FA rates and d′ was computed according to Eq. 1. The experiment was conducted in 1-h sessions of three blocks run in pseudorandom order (different for each subject).

Data analysis

For these experiments the dependent measure is detectability of the rotation signal (Fig. 1F) or translation signal (Fig. 2D). Our detectability measure, d′, assumes the signal detection model depicted in Fig. 2B. Signal and noise distributions are Gaussian and d′ quantifies the separation between these two distributions in units of average SD as follows (Wickens 2001)

$$d\mathrm{\prime }=\frac{{\mu }_{\mathrm{S}}-{\mu }_{\mathrm{N}}}{\sqrt{\frac{{\sigma }_{\mathrm{S}}+{\sigma }_{\mathrm{N}}}{2}}}$$ (2)

Thus d′ depends on both the separation between these distributions (the numerator in Eq. 2) and their variability (the denominator). Note that the benefit of using the d′ metric is that it does not depend on the criterion the observer is using (i.e., their a priori tendency to say signal present or absent). In contrast, because the percentage correct in a one-interval task depends on the criterion, this measure was not used in the present analysis.

If we further assume that the noise distribution is centered at a value of zero (μ_N = 0) and that the signal and noise distributions have equal variance (σ_N = σ_S, the standard equal-variance assumption), we can quantify observer sensitivity (threshold) from Eq. 2 as the SD of the underlying estimator (of linear or angular velocity) as follows

$$\sigma ={\mu }_{\mathrm{S}}/d\mathrm{\prime }$$ (3)

Detection thresholds calculated in this way correspond to stimulus values for d′ = 1 and to 76% correct discrimination thresholds measured in an equivalent two-interval-forced-choice task (Green and Swets 1966; Klein 2001).

Note that we first pooled trials across all three repetitions and then calculated d′. This pooling across blocks assumes that the criterion remains constant across the different blocks for a given observer and a given condition. Indeed, these values were very similar to those obtained by calculating d′ separately for each of the three blocks and then taking the average (see Supplemental Table S3 for a list of the hit rate, false alarm, d′, and other parameters for each subject in each condition). Once d′ was calculated, we then used Eq. 3 to compute angular (rotation detection experiment) and linear (translation detection experiment) motion thresholds. To test the interaction hypothesis (i.e., that translation and rotation thresholds depend on simultaneous angular and linear motion, respectively), we compared these threshold measures for all linear/angular velocity combinations using ANOVA with repeated measures (rmANOVA), with angular and linear velocity as factors, respectively. A similar nonparametric analysis, the Friedman test, was also applied. Finally, linear regression analysis was used to quantify the dependence of thresholds on linear or angular velocity (Table 1).

Table 1.

Linear regression results

	Rotation Detection			Translation Detection
Subject	Slope	CI	P	Slope	CI	P
1	0.00	−0.09, 0.09	0.96	0.33	−0.69, 1.35	0.30
2	0.03	−0.02, 0.07	0.13	0.61	−0.58, 1.80	0.16
3	0.03	−0.04, 0.09	0.20	0.06	−0.62, 0.75	0.73
4	−0.09	−0.31, 0.13	0.23	0.23	−0.11, 0.57	0.10
5	0.01	−0.05, 0.07	0.65	1.97	−6.42, 10.36	0.42
6	0.08	−0.12, 0.30	0.23	0.39	0.05, 0.72	0.04
7	0.03	−0.41, 0.48	0.77	1.35	−5.35, 8.04	0.55
8	0.07	−0.09, 0.24	0.19	N/A	N/A	N/A
9	N/A	N/A	N/A	0.80	0.21, 1.38	0.03
ALL	0.02	−0.03, 0.07	0.41	0.72	−0.40, 1.83	0.20

Each row shows the slope, 95% confidence interval (CI), and P value for linear fits to the data (n = 4) from each subject in both rotation and translation detection experiments. Note that, because of the small number of data points per subject, it was often the case that P > 0.05; nevertheless, slopes were almost always positive. The last row shows results from fits to data from all subjects (n = 32); note that these fits are influenced by variability across subjects.

Measurement and analysis of vibrations

Given the nature of the MOOG hexapod motion platform, it is unlikely that there were ancillary cues specific to, for example, angular movement, because all movements, whether linear or angular, must always be achieved by simultaneous movement of all six actuators, the legs of the hexapod. Furthermore, subjects reported that it was impossible to distinguish signal from noise trials based on platform sounds or vibrations.

To verify these subjective reports, we used a three-dimensional (3D) rate sensor and accelerometer to measure the actual movement of the platform during our various conditions. We measured multiple exemplars of each trajectory (13–19, depending on condition) and calculated the average across exemplars. Example traces of nasooccipital acceleration and yaw angular velocity for one of the rotation detection conditions and one of the translation detection conditions are superimposed in Figs. 1, C–F and 2, C–F, respectively; the average across these traces is illustrated by the gray lines. To isolate noise associated with linear and angular movement, the average trace was subtracted from each exemplar of each condition to obtain linear and angular “noise” traces and the Fourier transform of each trace was computed to obtain the amplitude spectrum of the noise in each exemplar. (See Supplemental Figs. S1 and S2 for examples of mean amplitude spectra associated with the traces illustrated in Figs. 1 and 2.)

Ultimately, the goal of this analysis was to determine whether there is characteristic movement noise (i.e., vibration) such that subjects could have discriminated signal from noise trials based on vibrations rather than linear or angular velocity/acceleration signals. Therefore we performed an ANOVA on the noise amplitude spectra with three factors: frequency (0.5 to 100 Hz in 0.5-Hz increments), condition (the four linear/angular velocities), and signal (present or absent). This ANOVA was run separately for linear and angular movement noise during rotation detection and for linear and angular movement noise during translation detection. If linear or angular vibrations differed depending on whether the signal was present or absent we would observe a significant effect of the signal factor. The effects of the signal factor from the four ANOVA analyses were as follows: rotation detection, angular motion (F = 0.18; df = 1; P = 0.68); rotation detection, linear motion (F = 3.28; df = 1; P = 0.07); translation detection, angular motion (F = 0.32; df = 1; P = 0.57); translation experiment, linear motion (F = 0.34; df = 1; P = 0.56). Thus despite some differences in signal and noise amplitude spectra at certain frequencies (see Supplemental Figs. S1 and S2), we conclude that overall platform vibration was similar enough during signal and noise trials that it would not have influenced the detection measurements reported in the following text. The potential confound of vibrational cues will be present in any vestibular psychophysical experiment. Therefore vibrational analysis should be a necessary component of any such study and the present analysis sets an important precedent for this kind of approach.

RESULTS

Rotation detection

We set out to test whether otolith and canal signals interact by measuring rotation detection thresholds at different linear velocities. In a classical signal detection paradigm, where half of the trials were pure translation (Fig. 1A, rotation signal absent) and half were curved path (Fig. 1B, rotation signal present), blindfolded subjects reported whether they perceived a curved path (signal) or pure translation (noise). Angular velocity was around the psychophysical threshold (such that detectability, d′, could be reliably assessed) and linear velocity was suprathreshold (5–21 cm/s), such that a potential dependence of rotation thresholds on simultaneous linear motion could be observed.

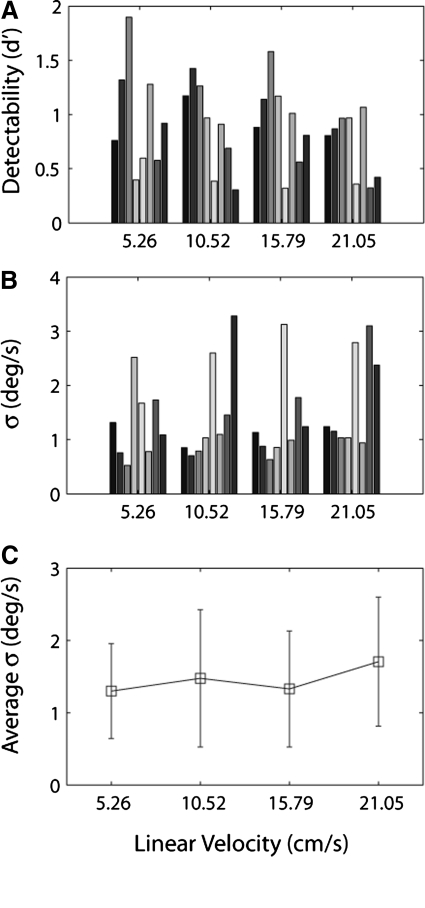
Values of d′, calculated from Eq. 1 for all subjects in all conditions, are plotted in Fig. 4A. These values, along with associated hit rates, false-alarm rates, and criteria, are also presented in Supplemental Table S3. Individual gray bars in Fig. 4A show d′ for each of the eight subjects, whereas each group of bars shows d′ values for the four different linear velocities (abscissa). Using Eq. 3 with μ_S = 1°/s (the signal mean, Fig. 3B), these d′ values were converted into measures of sensitivity or threshold (Fig. 4B), defined as the SD of the underlying estimator (σ) (see methods). Note that because d′ is the denominator of Eq. 3, smaller values of d′ yield larger associated thresholds. The mean (±SD) threshold, averaged across all subjects, has been plotted as a function of linear velocity in Fig. 4C. These values are: 1.30 ± 0.66°/s (3.13 ± 1.59°/s²) for linear velocity 5.26 cm/s; 1.48 ± 0.95°/s (3.57 ± 2.29°/s²) for linear velocity 10.52 cm/s; 1.33 ± 0.80°/s (3.21 ± 1.93°/s²) for linear velocity 15.79 cm/s; and 1.71 ± 0.89°/s (4.12 ± 2.15°/s²) for linear velocity 21.05 cm/s. Statistical analyses do not support the hypothesis that linear velocity influences angular detection thresholds (rmANOVA, F = 0.79; df = 3; P = 0.51) (Friedman test, χ² = 4.2; df = 3; P = 0.24).

Fig. 4.

Rotation detection results. A: values of d′ calculated for all 8 subjects at all 4 linear velocities. Groups of bars show data at different linear velocities and different shades of gray bar indicate different subjects. B: rotation detection thresholds calculated from d′ using Eq. 3. C: mean and SD of threshold across subjects at each linear velocity.

Visual inspection of Fig. 4C, however, suggests a modest increase in mean threshold with increasing linear velocity. This was quantified further using linear regression, fit separately to data from each subject. The corresponding P values, the linear regression slopes, and their 95% confidence intervals (CIs) are illustrated for each subject in Table 1. Note that the slopes tended to be positive and the 95% CIs always included zero. A similar linear regression analysis, now applied to data from all subjects simultaneously, yielded a slope of 0.02 (95% CI: [−0.03 0.07], P = 0.41), which is similar to the average slope across subjects (0.02 ± 0.04, SD). Although the slope was positive for the majority of subjects (Table 1), a sign test to quantify the probability of observing this distribution of positive versus negative slopes showed that this result could reasonably have been obtained by chance (P = 0.07).

Although our analysis focuses primarily on within-subject effects, we also observed variability in thresholds across subjects. This is quite common in vestibular threshold studies. For example, in a sample of 30 subjects Benson et al. (1989) observed angular motion direction thresholds ranging from about 0.5 to 5°/s. In the present experiment, some of this variability may be explained by the fact that four subjects (represented by the first four bars in each group of bars in Fig. 4, A and B) participated in preliminary experiments (see Supplemental material) and thus had more experience with the task.

Translation detection

To further examine canal–otolith interactions, we also measured translation detection thresholds at different angular velocities. Similar to the first experiment, half of the trials were pure rotation (Fig. 2A, translation signal absent) and half were curved path (Fig. 2B, translation signal present) and subjects indicated whether they perceived a curved path (signal) or pure rotation (noise). Linear velocity was near the psychophysical threshold (such that detectability, d′, could be reliably assessed), whereas angular velocity was suprathreshold (5–20°/s), such that a potential dependence of thresholds on simultaneous yaw rotation could be determined. Canal–otolith interaction would be revealed by an effect of angular velocity on the subjects' ability to detect linear self-motion stimuli.

Values of d′ and σ for each of the four angular velocities are displayed for all subjects in Fig. 5, A and B. Each gray bar shows data for one subject and each group of bars shows data for each of four different angular velocities. The mean (±SD) translation detection thresholds, averaged across all subjects, are shown in Fig. 5C. These values are: 2.11 ± 1.33 cm/s (5.09 ± 3.21 cm/s²) for angular velocity 5°/s; 2.49 ± 1.57 cm/s (6.00 ± 3.78 cm/s²) for angular velocity 10°/s; 3.7 ± 3.01 cm/s (8.92 ± 7.25 cm/s²) for angular velocity 15°/s; and 3.39 ± 2.03 cm/s (8.17 ± 4.90 cm/s²) for angular velocity 20°/s. Statistical analyses support the hypothesis that angular velocity influences detection of linear motion (rmANOVA, F = 4.15; df = 3; P = 0.02) (Friedman test, χ² = 15; df = 3; P = 0.002).

Fig. 5.

Translation detection results. A: values of d′ calculated for all 8 subjects at all 4 angular velocities. Groups of bars show data at different angular velocities and different shades of gray bar indicate different subjects. B: rotation detection thresholds calculated from d′ using Eq. 3. C: mean and SD of threshold across subjects at each angular velocity.

Figure 5C shows an increase in mean thresholds with increasing linear velocity. To investigate this trend further, we calculated the slopes of regression lines fit to the data from each subject (Table 1). Using data from all subjects yielded a slope of 0.72 (95% CI: [−0.40 1.83], P = 0.20) and the average slope across subjects was 0.72 ± 0.60 (SD). Slope was positive for all subjects and a sign test shows that this outcome is highly unlikely to have occurred by chance (P = 0.008). The finding that translation detection thresholds increase with the magnitude of concurrent angular velocity (along with the possible trend for rotation detection thresholds to increase with linear velocity) is suggestive of significant canal–otolith interactions in the horizontal plane.

Although our analysis focuses primarily on within-subject effects, we also observed variability in thresholds across subjects. This is quite common in vestibular threshold studies. For example, in a sample of 24 subjects Benson et al. (1989) observed linear motion direction thresholds ranging from about 0.02 to 0.30 m/s². In the present experiment, at least part of this variability may be explained by the fact that five subjects (represented by the first five bars in each group of bars in Fig. 5, A and B) participated in preliminary experiments (see Supplemental material) and thus had more experience with the task.

DISCUSSION

We used a classic signal detection paradigm to examine perceptual interactions between otolith and semicircular canal signals during rotation/translation along a curved path. In the rotation detection experiment, subjects indicated the presence or the absence of angular motion in blocks where half of the trials were pure translation and half were curved path (simultaneous translation and rotation). In separate, translation detection experiments, subjects indicated the presence or the absence of linear motion in blocks where half of the trials were pure rotation and half were curved path. Detection thresholds averaged 1.45 ± 0.81°/s (3.49 ± 1.95°/s²) for yaw rotation and 2.93 ± 2.10 cm/s (7.07 ± 5.05 cm/s²) for translation along the nasooccipital axis. Translation thresholds depended on simultaneous angular motion. The effect of linear motion on rotation thresholds was less clear. We conclude that linear (and perhaps angular) components of curved-path motion might not be sensed independently. In the following text we discuss these findings in the context of previous research on linear and angular detection thresholds and canal–otolith interaction during both vertical plane rotation and earth-horizontal curved-path motion.

Thresholds for detection of angular motion in the earth-horizontal plane

Reported angular motion thresholds vary between 0.035 and 4.0°/s² for rotation about an earth-vertical axis (for reviews see Clark 1967; Guedry 1974). This large range is attributable to a combination of factors, including the type of psychophysical procedure, frequency of stimulation, definition of threshold, subject variability, and differences in the equipment generating the motion (e.g., different levels of vibration and noise of the actual rotator). Importantly, in the present experiments we have measured translation and rotation detection thresholds in a way that is less dependent on background vibration. This was possible because all trials included actual platform motion; subjects distinguished curved path motion (signal—rotation or translation—present) from runs that were either pure rotation (translation signal absent) or pure translation (rotation signal absent). We also used a stimulus with most of the power at frequencies of 0.5–1 Hz and standard definition of threshold (σ, the SD of the underlying estimator, i.e., the stimulus value that yields d′ = 1).

Here we compare our results to more recent attempts to measure vestibular thresholds using signal detection methods, i.e., alternative-forced-choice tasks that aim to quantify parameters of probability-based models like that shown in Fig. 3. These methods yield rigorous quantifications of sensory efficiency. Alternative methods (e.g., magnitude estimation or reaction time) can be useful, but their interpretation is usually more subjective. For reviews of earlier work using a range of methods see Clark (1967) or Guedry (1974).

Grabherr et al. (2008) used an adaptive two-alternative forced-choice procedure, where subjects indicated by button press whether they perceived earth-horizontal yaw rotation to the left or to the right. They reported 80% correct yaw velocity thresholds to range from 2.8°/s at 0.05 Hz to <1°/s at 0.5–5 Hz. These values are comparable with the detection thresholds reported here. Note, however, that Grabherr et al. (2008) measured minimum angular velocity for discriminating direction of movement (left/right), whereas we measured minimum velocity for absolute detection of angular motion. Although these threshold values seem similar for earth-vertical yaw rotation, they are reported to be quite different in other cases, for example for earth-vertical linear acceleration (Melvill Jones and Young 1978), suggesting these behaviors may be mediated by different mechanisms. Measurement of present/absent detection thresholds and left/right discrimination thresholds are complementary approaches and both are necessary for a complete characterization of sensory function. The use of a present/absent task rather than a left/right task is one of the unique contributions of this study.

Although semicircular canals are the dominant source of sensory information for detection of angular motion around an earth-vertical axis, other signals also contribute. For example, previous studies have reported that angular motion thresholds are significantly reduced by a factor of 2.7 during fixation of a head-fixed target (Benson et al. 1989; Guedry 1974); either increased levels of spatial attention and/or the extraretinal signal that is generated to suppress the VOR are thought to contribute to the sensitivity increase in movement sensation. Even in darkness, extravestibular motion cues contribute to the perception of self-rotation. For example, individuals without vestibular function can correctly indicate the direction of rotation during angular accelerations of sufficient magnitude and duration (Mann 1951). However, when constant velocity is attained, the exponential response decay of rotational experience (that is reported by normal subjects) is not present in labyrinthine-deficient subjects. Instead, as soon as constant velocity is attained, labyrinthine-deficient subjects typically report either continuous rotation (if they make use of cognitive cues) or cessation of rotation (Guedry 1974; Mach 1902).

In the absence of linear motion, it is likely that detection in an experiment like ours would be limited only by noise on the signal from the semicircular canals. However, Fig. 4C shows a modest increase in mean threshold as the magnitude of simultaneous linear motion increases. Although this result is not statistically significant, it is consistent with the notion that human observers might not have independent access to separate estimates of linear and angular movement parameters during curved-path motion. Detection may be limited by factors other than noise of the canal signal. For example, detection may rely on a combined linear/angular motion estimate that integrates information from canals and otoliths, such that otolith signals could influence detection of angular motion. Conscious perception may not have direct access to isolated, low-level sensory signals derived only from canal signals. However, this effect, if present, is weak in comparison with the converse effect of angular motion on detection of linear acceleration discussed in the following text.

Thresholds for detection of linear acceleration

Previously reported thresholds of linear motion perception at frequencies <1 Hz also differ by more than an order of magnitude (Benson et al. 1986; Greven et al. 1974; Walsh 1961, 1962; reviewed by Guedry 1974). Specifically, during 0.3 Hz sinusoidal oscillations, thresholds have been described to vary between 1.4 and 18 cm/s² (Guedry 1974) and to increase more than 10-fold in subjects without vestibular function (Walsh 1961). Detection thresholds of linear motion typically decrease with increasing frequency during steady-state sinusoidal oscillations (for review see Guedry 1974) and increase as a monotonic function of stimulus duration during bell-shaped velocity profiles ranging in duration between 1 and 7 s (Benson et al. 1986). Thresholds of detecting linear motion in darkness are not significantly different from those obtained during fixation of a target fixed relative to the head (Benson et al. 1989).

The dynamics of linear motion detection have remained controversial. On one hand, it was proposed that the detection process is dependent on a combination of both linear acceleration and the rate of change of linear acceleration (jerk) (Benson et al. 1986). In contrast, Young and Meiry (1968) suggested that perceptual processes are dominated by a lag term (integrator) at frequencies >0.24 Hz. In fact, Melvill Jones and Young (1978) reported that stimulus detection occurred at a constant linear velocity of about 22 cm/s. Israel and Glasauer (1999) observed similar results when asking subjects to detect linear motion during simultaneous angular motion. However, interpretation of these results is complicated because the dependent measure was reaction time. The sluggish dynamics might be an artifact of decision processes used during a reaction-time task, rather than low-level sensory integration of the linear acceleration stimulus. Indeed, in contrast to phase lags reported during continuous tracking of the velocity of the sensed motion, phase leads were observed during reports of peak velocity with sinusoidal stimuli <1 Hz (Benson et al. 1986; Walsh 1962). Future studies using rigorous signal detection measures are needed to further address the dynamics of linear motion perception.

Perhaps most comparable with the present experiment is the study by Benson et al. (1986); using signal detection theory, a bell-shaped velocity profile, and earth-horizontal translation stimuli, detection of movement direction was characterized by relatively small thresholds of 5–6 cm/s² for lateral and fore–aft movements (Benson et al. 1986). In contrast, our translation detection experiment quantified minimum linear acceleration for absolute detection of linear motion rather than discrimination of motion direction. Despite this difference, we report a similar range of thresholds values.

We also observed that during curved-path motion, translation detection thresholds increase with increasing angular velocity (Fig. 5C). We suggest that this effect could be a manifestation of the same or similar canal–otolith interactions that have been observed in the context of tilt and translation estimation during vertical-plane rotation (Angelaki et al. 1999; Green and Angelaki 2003, 2004; Green et al. 2007; Merfeld and Young 1995; Merfeld et al. 1993, 1999, 2001; Zupan et al. 2000). Translation detection probably relies on integrated information from canals and otoliths, such that conscious perception does not have direct access to isolated, low-level sensory signals from the otoliths. This explanation is consistent with our translation detection data and may also be consistent with path estimation errors observed in previous studies of curved-path motion perception described next.

Curved-path motion: otolith–semicircular canal interactions and path integration

Several studies have used combined angular/linear motion to investigate perception of two-dimensional motion trajectories in the earth-horizontal plane (Guedry et al. 1992; Israel and Glasauer 1999; Ivanenko et al. 1997; Mittelstaedt 1995; Mittelstaedt and Mittelstaedt 1996). Using a series of transient angular and linear motion components in the horizontal plane, Ivanenko et al. (1997) reported that human subjects tended to appropriately perceive their angular body orientation regardless of the concomitant linear stimuli. This result is consistent with our observation that yaw angular detection thresholds are less affected by simultaneous linear movement.

In contrast, Ivanenko et al. (1997) reported that subjects' interpretation of the displacement depended on the angular acceleration stimulus, often yielding illusory trajectories. In particular, qualitatively correct path trajectory was detected during a simple curved-path trajectory. In contrast, during a purely linear trajectory with a superimposed left/right yaw rotation, the path was misperceived as being circular. It was thus concluded that the brain cannot always reconstruct the path of travel based on an arbitrary combination of angular and linear motion signals. However, the underlying reason for such errors remains unclear. These errors could be due to a low-level influence of canal signals on otolith interpretation, something like what we observed in our translation detection experiment. Alternatively, it may be that these errors are due to limitation of higher-level processes that reconstruct the 3D trajectories from linear and angular motion estimates. Our observation that linear motion detection thresholds depend on simultaneous angular motion provides evidence in favor of the first alternative.

However, it must be noted that higher-level processes may also play a role. As Ivanenko et al. (1997) suggest, internal models of self-motion may be specialized for estimating path of travel for observers facing the direction of motion. Also, whereas our study examined detection of linear motion near threshold, their study used linear and angular motions that were clearly suprathreshold and different interactions may be observed in this range. In addition, because these conclusions are based on subjects' drawings of their perceived path, what look like path integration deficits could conceivably be due to deficits in subjects' ability to accurately depict the path of travel.

In other studies, using much lower frequency motions within the frequency range of activation of the velocity storage mechanism, linear acceleration stimuli have been shown to significantly affect perceived yaw rotation (Cohen 1977; Guedry et al. 1992; Mittelstaedt 1995; Mittelstaedt and Mittelstaedt 1996). For example, subjects undergoing prolonged centrifugation experienced a large asymmetry between angular perception in the initial acceleration and final deceleration phases (Guedry et al. 1992). These low-frequency illusions can be explained by recent models of canal–otolith interactions (Merfeld 1995; Zupan et al. 2002).

Conclusions

We used rigorous signal-detection methods to measure absolute detection thresholds for angular and linear movements. An advantage of our approach is that we minimize contamination by extraneous cues (e.g., equipment vibration or noise), which often prove difficult to eliminate in such experiments. This is because the motion platform was similarly engaged and active during both signal and noise trials. We measured absolute detection thresholds similar to previously reported direction discrimination thresholds (Benson et al. 1986; Grabherr et al. 2008). We found a modest, but not statistically significant, dependence of yaw rotation thresholds on the velocity of concurrent linear motion. Translation thresholds exhibited a stronger statistically significant dependence on the velocity of concurrent angular motion, consistent with low-level canal–otolith interactions. This type of interaction could partially explain previously reported illusory trajectories during combined linear/angular motion in the earth-horizontal plane (e.g., Ivanenko et al. 1997). Yet, this result is somewhat surprising. Although extensive, nonlinear canal–otolith interactions during vertical plane rotation are functionally relevant for segregating translational and gravitational accelerations (Green and Angelaki 2003, 2004; Green et al. 2007; Merfeld et al. 1999; Zupan et al. 2000, 2002), such interactions are inappropriate and even maladaptive during rotation in the earth-horizontal plane. Our results suggest that canal–otolith interactions may not be limited to vertical planes; in other words, they may not depend appropriately on the orientation of the rotation axis relative to the estimated gravitational vector. Further rigorous quantitative research is needed to characterize relative influence of low-level canal–otolith interactions and higher-level path integration on navigation processes.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grant R01 DC-007620 to D. E. Angelaki, National Eye Institute Institutional National Research Service Award 5-T32-EY-13360-07, and a National Space Biomedical Research Institute Fellowship PF-01103 to P. R. MacNeilage through National Aeronautics and Space Administration 9–58.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).