Theta Modulation in the Medial and the Lateral Entorhinal Cortices

Abstract

Hippocampal neurons show a strong modulation by theta frequency oscillations. This modulation is thought to be important not only for temporal encoding and decoding of information in the hippocampal system, but also for temporal ordering of neuronal activities on timescales at which physiological mechanisms of synaptic plasticity operate. The medial entorhinal cortex (MEC), one of the two major cortical inputs to the hippocampus, is known to show theta modulation. Here, we show that the local field potentials (LFPs) in the other major cortical input to the hippocampus, the lateral entorhinal cortex (LEC), show weaker theta oscillations than those shown in the MEC. Neurons in LEC also show weaker theta modulation than that of neurons in MEC. These findings suggest that LEC inputs are integrated into hippocampal representations in a qualitatively different manner than the MEC inputs. Furthermore, MEC grid cells increase the scale of their periodic spatial firing patterns along the dorsoventral axis, corresponding to the increasing size of place fields along the septotemporal axis of the hippocampus. We show here a corresponding gradient in the tendency of MEC neural firing to skip alternate theta cycles. We propose a simple model based on interference of delta oscillations with theta oscillations to explain this behavior.

INTRODUCTION

The theta rhythm (6–10 Hz) is the most prominent oscillatory activity in the hippocampus of freely moving rats. Neurons in the hippocampus show entrainment to these oscillations, with the preferred phase of firing advancing as the animal moves through the place field of the neuron. This phase precession is thought to be a temporal code, which organizes the spikes of neurons with overlapping place fields in subtheta timescales (O'Keefe and Recce 1993; Skaggs et al. 1996). These timescales are within the operating time window of spike timing dependent plasticity (Bi and Poo 1998). Entrainment of spiking activity to the ongoing theta rhythm is a prerequisite for this phase precession to operate. Rate and temporal codes have been shown to be dissociable and hypothesized to independently code for different variables in the hippocampus (Huxter et al. 2003; O'Keefe and Burgess 2005). Inputs that show theta-modulated activity are likely to be involved in the generation of this temporal code, whereas inputs that are not theta-modulated might contribute to the rate code in the hippocampus.

Medial entorhinal cortex (MEC) and lateral entorhinal cortex (LEC) are the two major cortical inputs to the hippocampus. Compared with LEC, MEC receives stronger inputs from visuospatial regions (primary, lateral, and medial visual cortical areas, in addition to cingulate, retrosplenial, and posterior parietal cortices) (Burwell and Amaral 1998; Witter and Amaral 2004). Correspondingly, MEC neurons encode spatial information (Fyhn et al. 2004; Hafting et al. 2005; Hargreaves et al. 2005; Quirk et al. 1992), but LEC neurons show little or no spatial specificity (Hargreaves et al. 2005).

Local field potentials (LFPs) in MEC show theta oscillations under a variety of conditions (Alonso and Garcia-Austt 1987a; Mitchell and Ranck Jr 1980). In contrast, the prevalence of theta oscillations in LEC in behaving animals is largely unknown. With respect to theta modulation of unit spiking, rat MEC neurons are known to exhibit such theta modulation (Brun et al. 2008; Hafting et al. 2008; Ranck Jr 1973; Stewart et al. 1992). Alonso and Garcia-Austt (1987b) and Frank et al. (2001) showed theta modulation of neurons in the entorhinal cortex, but they did not distinguish between LEC and MEC. During epochs of low-frequency (∼5 Hz), low-amplitude theta in quiet, awake rabbits, LEC neurons do not show theta modulation, whereas a small fraction of MEC neurons are theta modulated (Stafekhina and Karanov 1984; Vinogradova 1995). Thus it is not known whether there are differences in the degree of movement-related theta modulation between superficial MEC and LEC neurons in freely moving rats. In this study, we recorded both LFPs and single neurons in LEC and MEC in cue-rich environments. In one task, the rats foraged for food in a large box. In the other task, the animals ran clockwise laps on a circular track. In both tasks, LFPs in LEC showed significantly fewer theta oscillations than those in MEC. Similarly, LEC neurons were significantly less modulated by the theta rhythm than MEC neurons.

The spatially periodic firing patterns of MEC grid cells increase in scale along the dorsoventral axis (Brun et al. 2008; Hafting et al. 2005). Similarly, in in vitro studies, the intrinsic oscillation frequency of MEC stellate cells at depolarized membrane potentials decreases along the dorsoventral axis from >8 to about 4 Hz (Giocomo and Hasselmo 2008; Giocomo et al. 2007). Here we show that the MEC cells display a propensity to skip alternate theta cycles; this propensity increases along the dorsoventral axis, in register with the above-mentioned gradients. Interference between theta- and delta- (∼4 Hz) frequency, inputs can give rise to this theta alternation phenomenon.

METHODS

Subjects and surgery

Seven male Long–Evans rats, aged 5–6 mo, were housed individually on a 12:12-h reversed light/dark cycle. Animal care, surgical procedures, and euthanasia were performed in accordance with guidelines promulgated by the National Institutes of Health and the University of Texas Health Science Center at Houston Institutional Animal Care and Use Committee.

A custom-built hyperdrive with 20 independently movable recording probes (18 tetrodes and 2 references) was implanted over the right hemisphere of each rat under surgical anesthesia (4% isoflurane followed by 60 mg/kg ketamine + 8 mg/kg xylazine for induction; 0.5–2% isoflurane for maintenance). For MEC recordings (n = 4 rats; some of the results from these rats were previously reported in Savelli et al. 2008), the most posterior tetrode was positioned approximately 600–800 microns anterior to the transverse sinus and 4.8–5 mm lateral to the midline. The recording probes were implanted to make vertical penetrations through the brain. This allowed us to record from neurons along the dorsal to ventral axis of the MEC. For LEC recordings (n = 3 rats), the central tetrode in the array was positioned at 7.7 mm posterior to bregma and 3.2–4.6 mm lateral to the midline. The electrodes were angled at 25° mediolaterally to allow them to access the lateral to medial extent of the LEC. Rats were given ketoprofen (5 mg/kg) subcutaneously after surgery for analgesia. Antibiotics [tetracycline (30 mg) and enrofloxacin (Baytril, 3.4 mg)] were mixed with the food every day from surgery to the end of the experiment.

Training

Rats were allowed to recover for 5–6 days after surgery, until they regained and stabilized weight. During subsequent training and recordings, the rats were maintained at 80–90% of their free-feeding weights. The rats were trained on two behavioral paradigms using food reward (chocolate sprinkles). The first paradigm consisted of rats running clockwise on a circular track for 30 min looking for food rewards placed at arbitrary locations on the track (one to two rewards per lap); the second consisted of rats foraging for food reward that was scattered at irregular intervals in a large box. The circular track (76 cm OD; 56 cm ID) contained four distinct textures, each occupying one fourth of the track. The circular track was located in the center of a room with a 275-cm-diameter black curtain reaching from ceiling to floor, with six prominent cues (three hanging on the curtain, three on the floor) arranged along the perimeter of the curtain. The ceiling was covered with a black curtain and a 25-W bulb centered on the circular track illuminated the arena. A white noise generator was placed directly beneath the table supporting the circular track to mask external sounds. All rats with MEC implants and two rats with LEC implants also foraged in a large box (135 × 135 × 30 cm) with brown paper at the bottom. Multiple, prominent visual cues, such as the recording system and the doors to the room, were clearly visible from inside the large box. A single lamp placed in the corner of the room provided illumination.

Experimental protocol

Recordings began after the rats were well trained on both tasks, so that they spent most time in motion with a few stops, and after the electrodes were assessed to be in the target area (MEC or LEC) by monitoring for zones with and without spiking activity as the electrodes were advanced and correlating these zones with LFP patterns such as the presence of theta oscillations and theta phase reversal around layer II of MEC (Alonso and Garcia-Austt 1987a; Mitchell and Ranck Jr 1980). The tetrodes were advanced at the end of recording each day to sample different cells on subsequent days. Experiments stopped when all tetrodes were estimated to have reached layer I of MEC or LEC. Every day, the rats ran five sessions on the circular track; the second and fourth sessions involved cue manipulations (Knierim 2002) that are not analyzed in the present study. The rats ran 15 laps in each session, followed by a session in which the rats foraged in the large box (Savelli et al. 2008). Rats took about 4 min to run 15 laps in the circular track sessions and they foraged for 34 min during the large box sessions. For the present study, we analyzed data from the first session of each day in the circular track and the session in the large box.

Recording electronics

Recordings were performed with the Cheetah Data Acquisition system (Neuralynx, Bozeman, MT). For single-unit recordings, neural signals were amplified 2,000- to 10,000-fold, filtered between 600 Hz and 6 kHz, and digitized at 32 kHz. Every time one of the channels on a tetrode crossed a preset threshold, a 1-ms snapshot of activity from all four channels of the tetrode was stored on a PC. One channel from each of the tetrodes and the two references were used as the source of LFPs, for which the signals were amplified 2,000-fold, filtered between 1 and 475 Hz, digitized at 1 kHz, and stored continuously on the PC.

Data analysis

UNIT ISOLATION.

Clusters were cut manually, using custom software, to isolate single units. Waveform characteristics for all four tetrode channels, such as peak amplitude, spike width, and energy, were used for classification. Each cell was assigned an isolation quality on a subjective scale of 1 (very well isolated) to 5 (poorly isolated), based on how well the cluster was isolated from the background and the neighboring clusters. Spatial or temporal firing characteristics of the cells were not considered while assigning the quality. Cells rated 4 or 5 were excluded from the analysis. Cells firing <50 spikes in a session were excluded from this analysis. Further, fast spiking cells with firing rates >10 Hz were assumed to be interneurons and were also excluded from the analysis (Frank et al. 2001; Hargreaves et al. 2005).

THETA OSCILLATIONS IN THE LFPS.

Power spectra of the LFPs recorded from all locations in MEC and LEC were determined using the fast Fourier transform (FFT). Power in the theta band (6–10 Hz) is referred to as absolute theta power in the following text. Relative theta power at each recording location was calculated by dividing power in the theta band (6–10 Hz) by the total power of frequencies in the 1- to 50-Hz range.

THETA MODULATION BASED ON SPIKE TRAIN AUTOCORRELOGRAMS.

Spike-train autocorrelograms were created and normalized by the peak. The relative theta power in the autocorrelogram of each neuron was calculated by dividing the total power in the theta band (6–10 Hz) by the total power of frequencies in the 1- to 50-Hz range.

THETA MODULATION RELATIVE TO LFP.

Because the autocorrelograms might not detect theta modulation in sparsely firing neurons, a theta modulation index was calculated based on the assignment of spikes to phases of theta recorded in the LFP signal. Not all electrodes, especially in LEC (see results), showed a theta oscillation strong enough to be useful for this analysis. Therefore for both MEC and LEC data, a single tetrode with the greatest power in the theta band of the LFP spectrogram was selected as a reference signal. For all MEC data sets, the best signal was from a tetrode located in the MEC. For about one third of the LEC data sets, the best signal was from a tetrode located in the LEC; in the remaining data sets, the best signal was recorded from tetrodes in the perirhinal cortex, near LEC. Theta oscillations in the perirhinal cortex of cats are coherent with theta oscillations in EC (Collins et al. 1999); perirhinal neurons in rats are modulated by the hippocampal cholinergic theta rhythm (Muir and Bilkey 1998); and rat perirhinal cortex receives inputs from the medial septum/diagonal band of Broca (Deacon et al. 1983), which is thought to be the pacemaker for theta oscillations (Buzsáki 2002). These findings suggest that the perirhinal LFP may be used as the theta reference signal for LEC neurons. In confirmation, we detected no differences in the results between neurons that were referred to LEC theta rhythms and neurons that were referred to perirhinal theta rhythms.

The LFP signal from the selected theta reference electrode was band-pass filtered between 6 and 10 Hz. To avoid spurious assignment of spikes during periods of low theta, we assigned a spike to a theta phase only during epochs where theta could be visually detected in the LFP trace (Skaggs et al. 1996). The following criteria were empirically determined to accurately identify such periods in both MEC and LEC: 1) The theta/supratheta ratio [defined as the ratio of power in the theta (6–10 Hz) band to power in the supratheta (11–500 Hz) band] at a given time must be greater than (mean − 0.8SD) of the theta/supratheta ratio of the whole session. The theta/supratheta ratio was calculated in sliding 1-s windows with 0.5-s overlap. 2) The peak amplitude of the filtered LFP at a given time must be higher than (mean + 0.7SD) of the filtered LFP amplitudes of the whole session. These criteria were identified empirically by comparing with epochs that were visually identified as showing theta rhythm. The locations of the peaks of theta in the filtered LFP trace during good theta epochs were determined using the findpeaks function in MATLAB (The MathWorks, Natick, MA), with minimum 100 ms (10 Hz) and maximum 166 ms (6 Hz) between consecutively detected peaks. The peaks were assigned a phase of 0° and the phase between peaks was determined by linear interpolation (Skaggs et al. 1996). Each spike was assigned the phase of theta in which it fired and a histogram of the number of spikes in each of 36 phase bins (10°/bin) was constructed. The histogram was smoothed with a seven-point Gaussian filter (SD = 1) to reduce binning artifact and was normalized by its maximum value. The theta modulation index was then defined as 1 − the minimum value of the histogram (the procedures for assigning theta phase to spikes and calculation of theta modulation index follow those used in Frank et al. 2001).

To determine the probability of obtaining a high theta modulation index value by chance, a randomized distribution of theta modulation indices was generated as follows. A random theta phase ranging from 0 to 360° was assigned to each of the spikes for each neuron, generating a randomized theta phase distribution. To maintain the temporal integrity of the assignment of spikes within a burst to similar phases of theta, consecutive spikes were assigned the same phase if they 1) occurred <50 ms apart and 2) were assigned the same phase in the real data. Smoothed and normalized theta phase histograms were constructed from this random theta phase distribution for each neuron and the theta modulation index was calculated as described earlier. This procedure was carried out 100 times for each neuron, to generate a distribution of randomized theta modulation indices corresponding to LEC and MEC data. The distribution of the real theta modulation indices in LEC and MEC was then compared with the corresponding randomized distributions using the Wilcoxon rank-sum test.

ALTERNATE THETA CYCLE SKIPPING ANALYSIS.

Visual inspection of the autocorrelograms revealed that some neurons in the MEC showed higher activity every other theta cycle (i.e., they tended to skip cycles). To quantify this phenomenon, cells that showed visible theta or delta oscillations in their autocorrelograms were selected (see results). The normalized autocorrelograms were band-pass filtered between 1 and 10 Hz. The amplitudes of the first and second theta peaks were determined by finding a first peak (defined as a point that has a higher value than that of its preceding and following neighbors) between 100 and 200 ms (corresponding to 5- to 10-Hz frequency) and a second peak after 200 ms in the filtered autocorrelograms. The peak-finding algorithm failed to find a peak in the 100- to 200-ms interval for two neurons (which showed visible delta, but not theta, modulation), so the maximum value in the interval was used instead. The proportional difference between the first and second peaks was calculated using the formula (peak1 − peak2)/max (peak1, peak2).

THETA PEAK FREQUENCY.

Power spectra for autocorrelograms and LFPs were generated using FFT. Peaks of the power spectra of autocorrelograms and LFPs in the theta range (6–10 Hz) were determined using the findpeaks function in MATLAB (The MathWorks).

ALTERNATE THETA CYCLE SKIPPING SIMULATION.

Interference patterns were generated by summing delta (4 Hz) and theta (7 or 8 Hz) sine waves with randomized phase lags. Spike trains were generated by passing this summed waveform (3,600 s long) through a simple Poisson firing neuron model. The instantaneous firing probability of the neuron was calculated as p(t) = A(t) · α, where A(t) is the amplitude of the sum waveform at time t and α is a scale factor to produce a mean firing rate appropriate for MEC neurons (∼1.8 Hz in the present data set). A spike train s(t) was generated as s(t) = 1 if p(t) > random (0, 1) and s(t) = 0 if p(t) ≤ random (0, 1). A 5-ms refractory period was implemented. Autocorrelograms were then constructed from these spike trains.

Histology

Marker lesions were made on a subset of the tetrode tips by passing 10 μA current for 10 s at the end of the experiment. On the following day, the rats were perfused transcardially with 4% formalin, after which the brain was extracted and kept in a 30% sucrose/4% formalin solution until the brain sank. Sections (40 μm coronal for LEC rats; or parasagittal for MEC rats) were cut on a freezing microtome, mounted, and stained with 0.1% cresyl violet. Tetrode tracks were reconstructed on the digital photomicrographs of the serial sections using information about the configuration of the tetrode array in conjunction with tetrode tracks on the sections and the marker lesions. Specific layers of MEC and LEC recorded in each session were identified by reconstructing the trajectory of the identified tetrode tracks over days and plotting the recording sites relative to the end of the tetrode track or relative to the location of the layer II–layer I transition. The dorsoventral locations of MEC tetrodes were quantified by measuring the distance along the brain surface in the sagittal plane from the dorsal border of MEC (which, in most sagittal sections, abuts the postrhinal cortex).

RESULTS

Theta oscillations in the LFPs

Local field potentials were recorded from 178 locations in LEC in three rats and 357 locations in MEC in four rats as they ran 15 laps around the circular track. These data were collected over a number of days and electrodes were advanced at the end of a recording day, to collect data from different locations. Figure 1 shows the distribution of relative power in the theta band (the ratio of power in the 6- to 10-Hz frequency range with total power in the 1- to 50-Hz range) across LEC and MEC. Theta oscillations in the LEC were weaker than MEC theta oscillations, across a large range of recording locations. A reduction in theta amplitude, corresponding to theta phase reversal around layer II of MEC (Alonso and Garcia-Austt 1987a; Mitchell and Ranck Jr 1980), is also visible. We did not analyze theta phase reversal in LEC or MEC, since we did not have a stable reference in the hippocampus to which we could refer the theta phase in the entorhinal cortex. However, during the course of recording, we did see the phase reversal around layer II of MEC, compared with the other tetrodes in deeper layers.

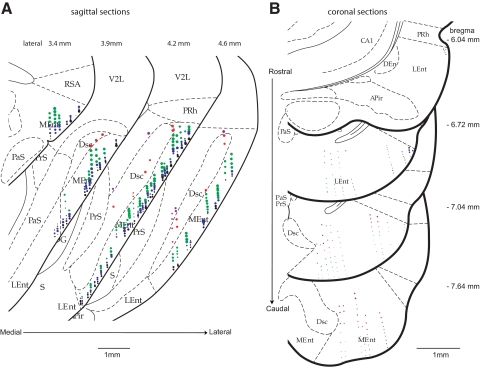
Fig. 1.

Distribution of relative theta power in medial entorhinal cortex (MEC, A) and lateral entorhinal cortex (LEC, B) recorded while the rat ran on a circular track. Locations of the local field potentials (LFPs) are marked by dots on schematics of sections from the rat brain atlas (Paxinos and Watson 1998). (The atlas uses acronyms LEnt and MEnt for LEC and MEC, respectively.) Colors of the dots correspond to the layer: black, layer I; blue, layer II; green, layer III (including ambiguous layer II/III recording sites); red, layer IV; and purple, layers V–VI. The size of the dots is proportional to the relative power in the theta band. LEC dots are smaller than most MEC dots regardless of cortical layer or mediolateral location of the recording electrode in LEC. One of the MEC sections shows 2 penetrations in an area labeled LEnt. We have included these penetrations in our MEC data set because the newest edition of the Paxinos and Watson (2007) atlas includes this area as part of the MEC (subfield ME, following the nomenclature of Insausti et al. 1997), not LEC. The relative theta power did not depend on the location of the reference electrode (median relative theta powers on circular track: LEC with frontal reference = 0.17, with cerebellar reference = 0.16; MEC with frontal reference = 0.50, with cerebellar reference = 0.49, with MEC reference = 0.52; median relative theta powers in large box: LEC with frontal reference = 0.16, with cerebellar reference = 0.12; MEC with frontal reference = 0.52, with cerebellar reference = 0.51, with MEC reference = 0.50). The sagittal sections in A correspond to plates 86 (lateral 3.4 mm), 87 (lateral 3.9 mm), 88 (lateral 4.2 mm), and 89 (lateral 4.6 mm) in the atlas from left to right, whereas the coronal sections in B correspond to plates 44 (bregma: −6.04 mm), 46 (bregma: −6.72 mm), 48 (bregma: −7.04 mm), and 50 (bregma: −7.64 mm) in the atlas from top to bottom. The actual locations of the electrodes are different because of strain and age differences between the atlas and the rats of the current study, although the locations were matched based on similarity of the sections with the standardized atlas for ease of comparison. APir, amygdalopiriform transition area; CA1, area CA1 of the hippocampus; DEn, dorsal endopiriform nucleus; DG, dentate gyrus; Dsc, lamina dissecans of the entorhinal cortex; Ect, ectorhinal cortex; LEnt, lateral entorhinal cortex; MEnt, medial entorhinal cortex; PaS: Parasubiculum; PRh: perirhinal/postrhinal cortex [the atlas classifies both these as perirhinal cortex, but Burwell and Amaral (1998) subdivide it into perirhinal cortex and postrhinal cortex; the sagittal sections in A show postrhinal cortex, whereas the coronal sections in B show perirhinal cortex]; PrS, presubiculum; RSA, retrosplenial agranular cortex; S, subiculum; V2L, secondary visual cortex, lateral area. Atlas sections are reproduced, with permission, from Paxinos and Watson (1998).

Three different reference electrodes were used in different animals for differential recording of LFP signals: 1) a screw implanted on top of the frontal cortex was used as the reference for LFPs in three rats (2 LEC, 1 MEC); 2) a wire on top of the cerebellum was used as the reference for LFPs from three rats (1 LEC, 2 MEC); and 3) a reference tetrode located in layer I of MEC was used as the reference for LFPs from one rat (MEC). Within each entorhinal area, there were no differences in the median relative theta power depending on the reference electrode location (see Fig. 1 caption). Thus for the following analyses, we pooled recordings from animals regardless of the source of the reference signal.

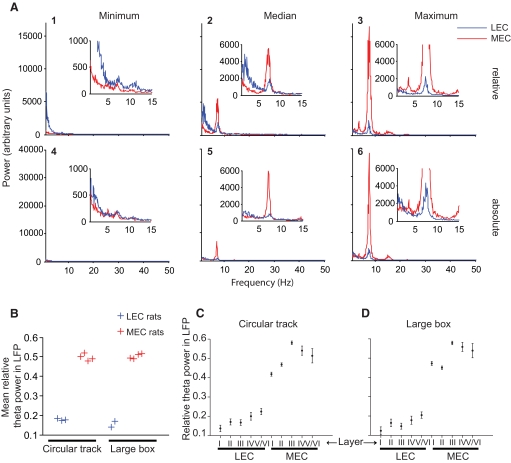
Figure 2A shows examples of power spectra from LEC and MEC. The top row shows the recording sites with the minimum, median, and maximum relative power in the theta band for both LEC (blue) and MEC (red). The bottom row shows the comparable data for absolute theta power. The maximum power sites in MEC had almost all of the power concentrated in the theta band (Fig. 2, A3 and A6), whereas the minimum power sites contained little power in the theta range beyond the 1/fⁿ pink noise (Fig. 2, A1 and A4). LEC power spectra show a range as well, but across the board, the amplitudes of theta power in LEC are much less than those in MEC for both relative and absolute power measures. Even the median relative theta power in MEC is greater than the maximum relative theta power in LEC.

Fig. 2.

Analysis of power spectra from LEC and MEC. A: power spectra for recording sites displaying the minimum (1, 4), median (2, 5), and maximum (3, 6) power in the theta band of LFP data recorded while the rats ran on a circular track (LEC, blue; MEC, red). The top row shows LFPs with minimum, median, and maximum relative theta power (power in 6- to 10-Hz range divided by power in the 1- to 50-Hz range) and the bottom row shows LFPs with minimum, median, and maximum absolute theta power (power in 6- to 10-Hz range). The MEC plots in 1 and 4 are the same because the same recording site had minimum relative as well as absolute theta powers. All other plots are from different electrodes. Main plots in the top row are scaled to the MEC peak in plot 3, whereas main plots in the bottom row are scaled to the MEC peak in plot 6. Note that the median relative theta power in MEC (2) is greater than the maximum relative theta power in LEC (3) and the median absolute theta power in MEC (5) is comparable to the maximum absolute theta power in LEC (6). Insets show details at higher magnifications for plots with low-amplitude data; insets in plots 1 and 4 show theta powers about an order of magnitude lower than the median theta powers for LEC and MEC and thus a bad signal-to-noise ratio. All other plots show clear peaks in the theta range and sustained theta oscillations can be easily discerned in the corresponding LFP traces. These LFP traces were recorded from the following locations: 1, MEC layer I, LEC layer I; 2, MEC layer I, LEC layer I; 3, MEC layer III, LEC layer II; 4, MEC layer I, LEC layer III; 5, MEC layer III, LEC layer V/VI; 6 MEC layer III, LEC layer V/VI. B: ratwise mean relative theta power in LFPs (the rats with electrodes in LEC are in blue and the rats with electrodes in MEC are in red) recorded in circular track and large box sessions. Mean relative theta power was significantly higher in MEC rats than that in LEC rats in both paradigms. C and D: relative theta power is higher in all layers of MEC compared with all layers of LEC. Means of relative theta power are plotted as a function of layer in LEC/MEC. Error bars are SEs. These plots show that layerwise differences cannot account for the observed differences in relative theta powers in LEC and MEC. No statistical tests were run on these data. C: circular track [178 samples in 3 rats in LEC (34 samples in layer I, 39 in layer II, 45 in layer III, 24 in layer IV, and 36 in layers V/VI) and 357 locations in MEC in 4 rats (91 samples in layer I, 127 in layer II, 115 in layer III, 17 in layer IV, and 7 in layers V/VI)]. D: large box [146 locations in LEC in 2 rats (24 samples in layer I, 25 in layer II, 40 in layer III, 22 in layer IV, and 35 in layers V/VI) and 358 locations in MEC in 4 rats (91 samples in layer I, 128 in layer II, 115 in layer III, 17 in layer IV, and 7 in layers V/VI)].

Because each animal contributed multiple recording sites, some of which were separated by <150 μm, the individual data points cannot be considered independent measures. Thus to test the statistical significance of the difference between MEC and LEC, we calculated the mean relative theta power for all of the recording sites in each animal (Fig. 2B) and ran unpaired t-tests on these per-animal mean values. The mean relative theta power of LEC was significantly less than the mean relative theta power of MEC for circular track data (0.18 ± 0.01 vs. 0.50 ± 0.02 SD, respectively; t₅ = −29.30, P < 0.0001) and for large box data (0.15 ± 0.02 vs. 0.50 ± 0.01 SD, respectively; t₄ = −24.28, P < 0.0001). For descriptive purposes, the means and SEs of relative theta power are broken down by cell layer in Fig. 2, C and D. It is clear from this graph and from Fig. 1 that the overall difference in theta power between MEC and LEC is apparent in all cortical layers, although incomplete sampling for each animal and the lack of independent sampling preclude a rigorous statistical analysis of these laminar differences.

Relative theta power provides internal normalization for irregularities such as differences in total power in the spectrum, which could possibly be caused by factors such as local anatomy and minor variance in the amplifier gain. However, this measure makes the estimate of theta power dependent on differences in power in other frequency ranges. Thus we also compared the absolute theta power in LEC and MEC, to complement the relative theta power analysis. The mean absolute theta power in LEC was significantly less than the mean absolute theta power in MEC for circular track data (1.7 × 10⁴ ± 2.4 × 10³ vs. 6.3 × 10⁴ ± 1.8 × 10⁴ SD, respectively; t₅ = −4.23, P = 0.008) and for large box data (1.3 × 10⁴ ± 326 vs. 5.5 × 10⁴ ± 9.8 × 10³ SD, respectively; t₄ = −5.73, P = 0.005), indicating that the differences in relative theta powers were not merely due to increases in the power of nontheta frequency bands. (Note that the units of power are arbitrary, given that the data acquisition units in LFPs were not converted to volts before running the FFT.)

Because the power and frequency of theta oscillations can be modulated by the speed of the rat, we compared the mean running speeds of LEC rats with those of MEC rats in circular track and large box sessions. There was no statistically significant difference in speeds of LEC and MEC rats for circular track data (17.8 ± 1.8 vs. 18 ± 2.6 cm/s SD, respectively; t₅ = −0.15, P = 0.88, n.s.) and for large box data (14.7 ± 0.9 vs. 15.4 ± 2.4 cm/s SD, respectively; t₄ = −0.39, P = 0.72). Thus the differences in theta powers between LEC and MEC cannot be explained by differences in the rats' running speeds.

Theta modulation of single-unit activity

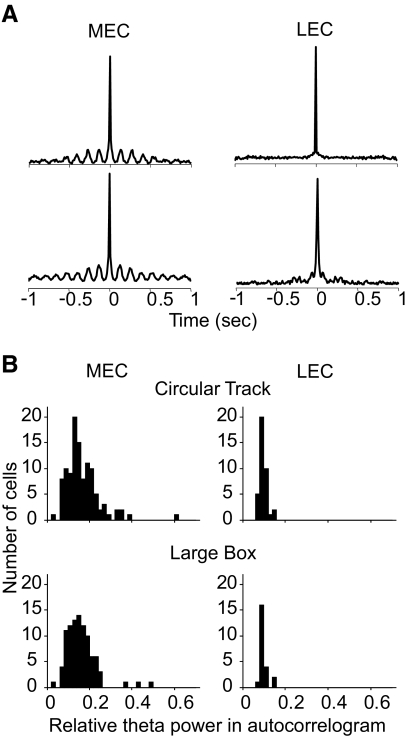
We recorded 109 single units in MEC from four rats and 38 single units in LEC from three rats while they ran on the circular track. We also recorded 95 single units in MEC from four rats and 23 single units in LEC from two rats as they foraged in the large box. Figure 3A shows two representative spike train autocorrelograms each from superficial MEC and from superficial LEC. Visual inspection of the autocorrelograms revealed clear peaks at the theta frequency in many of the MEC autocorrelograms, whereas LEC cells did not show clear peaks at the theta frequency. To quantify this difference, the relative theta power in the autocorrelograms of MEC and LEC neurons was calculated by dividing the total power at the theta frequency (6–10 Hz) by the total power of all frequencies in the 1- to 50-Hz range. MEC neurons had significantly higher relative theta power than that of LEC neurons, in both the circular track and large box sessions (Wilcoxon rank-sum, P < 0.0001; Fig. 3B). The bottom autocorrelogram for LEC in Fig. 3A has the highest relative theta power for LEC neurons.

Fig. 3.

Theta modulation of firing in autocorrelograms of MEC and LEC neurons. A: representative examples of autocorrelograms of superficial MEC (left) and LEC (right) neurons. These example autocorrelograms are from 4 different neurons from 4 different rats recorded during the circular track session. Many of the autocorrelograms of superficial MEC neurons showed modulation of firing at the theta frequency, whereas almost all LEC neurons showed little or no theta modulation in the autocorrelograms (the best example for LEC is shown on the bottom right). B: histograms of the distribution of relative theta power in the autocorrelograms of superficial MEC and LEC neurons. Relative theta power of the superficial MEC neurons was significantly higher than the relative theta power of the superficial LEC neurons in both circular track (MEC median = 0.15, LEC median = 0.1, Wilcoxon rank-sum, P < 0.0001) and large box (MEC median = 0.15, LEC median = 0.09, Wilcoxon rank-sum, P < 0.0001) sessions.

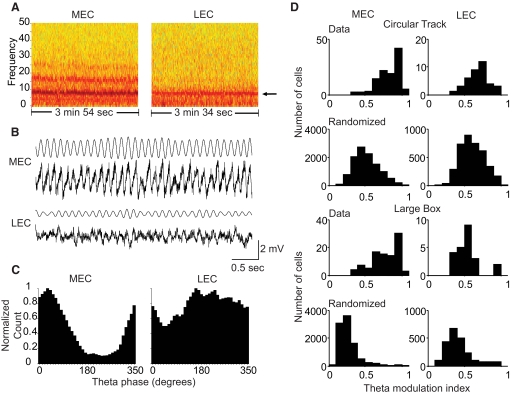
One potential reason for the lack of strong theta modulation in the LEC autocorrelograms is the relatively sparse firing of these cells, compared with that in MEC neurons. That is, if the LEC cells were modulated by the theta rhythm but tended to fire at low rates with most interspike intervals >1 s, then not enough spikes would populate the ±1-s time window of the autocorrelogram to detect the theta signal. Thus theta modulation of MEC and LEC neurons was also addressed by referencing the timing of spikes to the ongoing theta signal recorded in the LFP. Most MEC and many LEC recording sites showed visible theta signals in the LFP, although the signal was more robust in MEC than that in LEC (Fig. 4, A and B). To quantify the modulation of each neuron, a theta phase histogram was plotted by assigning each spike to a phase of theta from the simultaneously recorded LFP with strongest theta oscillations (see methods for details). The histogram was normalized to its peak bin and the depth of theta modulation was quantified by a theta modulation index, calculated as 1 − the minimum value of the histogram (Frank et al. 2001). The theta modulation index is close to 0 when the neuron is not theta modulated and gets closer to 1 with increasing theta modulation. Figure 4C shows representative examples of theta phase histograms from MEC and LEC, with theta modulation indices of 0.89 and 0.50, respectively. Consistent with the autocorrelogram analysis, the superficial MEC neurons had significantly higher theta modulation indices than those of the superficial LEC neurons (Fig. 4D) in both circular track and large box sessions (Wilcoxon rank-sum, P < 0.0001). This led to a question as to whether the distribution of theta modulation indices in LEC could be obtained by random chance. To test this possibility, we generated randomized theta modulation index distributions corresponding to each of these populations, as described in methods. The theta modulation indices of MEC and LEC neurons were significantly higher than the corresponding randomized theta modulation indices, in both circular track and large box sessions. This result demonstrates that both MEC and LEC neurons are modulated by theta, although the theta modulation of LEC neurons is much weaker than that of MEC neurons.

Fig. 4.

Theta modulation of superficial MEC and LEC neurons relative to the LFP. A: power spectrograms (0–50 Hz, power in dB) of LFPs recorded from tetrodes in MEC and LEC in a circular track session, showing higher power in the theta frequency range (indicated by arrow on the right). The MEC example shows theta oscillations typically seen in MEC, whereas the LEC example shows the largest relative theta power in LEC. B: LFP traces [raw (bottom trace) and filtered between 6 and 10 Hz (top trace)] from MEC and LEC (taken from the same data as in A), showing theta signals in both regions, although the signal was stronger in MEC than that in LEC. C: examples of smoothed and normalized theta phase histograms showing strong (theta modulation index = 0.89; MEC cell) and weak (theta modulation index = 0.50; LEC cell) theta modulation. D: histograms showing the distribution of theta modulation indices of MEC and LEC neurons on circular track and large box sessions. Superficial MEC neurons had significantly higher theta modulation indices than those of superficial LEC neurons in both circular track (MEC median = 0.85, LEC median = 0.70, Wilcoxon rank-sum, P < 0.0001) and large box (MEC median = 0.80, LEC median = 0.53, Wilcoxon rank-sum, P < 0.0001) sessions. Further, the theta modulation indices of both MEC and LEC neurons were significantly higher than the randomized theta modulation indices in both circular track (MEC median = 0.85, MEC randomized median = 0.50, Wilcoxon rank-sum, P < 0.0001; LEC median = 0.70, LEC randomized median = 0.60, Wilcoxon rank-sum, P < 0.01) and large box (MEC median = 0.80, MEC randomized median = 0.24, Wilcoxon rank-sum, P < 0.0001; LEC median = 0.53, LEC randomized median = 0.38, Wilcoxon rank-sum, P < 0.001) sessions, revealing a significant theta modulation of even LEC neurons. Note the downward shift in the distributions of the theta modulation indices in the large box compared with those in the circular track. This shift is caused by the difference in duration of the large box and circular track sessions. The rats take about 4 min to run 15 laps in the circular track session, whereas the large box session is 34 min long. This difference leads to an order of magnitude increase in the number of spikes recorded in the large box compared with those in the circular track, for neurons with comparable firing rates. When there are fewer spikes in a session, the normalized theta modulation histogram is noisier and is likely to have bins with lower values by random chance. This leads to a higher theta modulation index by random chance in the circular track, compared with the theta modulation index in the large box. The number of spikes in the randomized data are matched to the number of spikes in the real data, to account for the effect the number of spikes have on theta modulation index. All LEC and MEC data sets show significantly higher median theta modulation indices compared with those in the corresponding randomized data.

Alternate theta cycle skipping in MEC

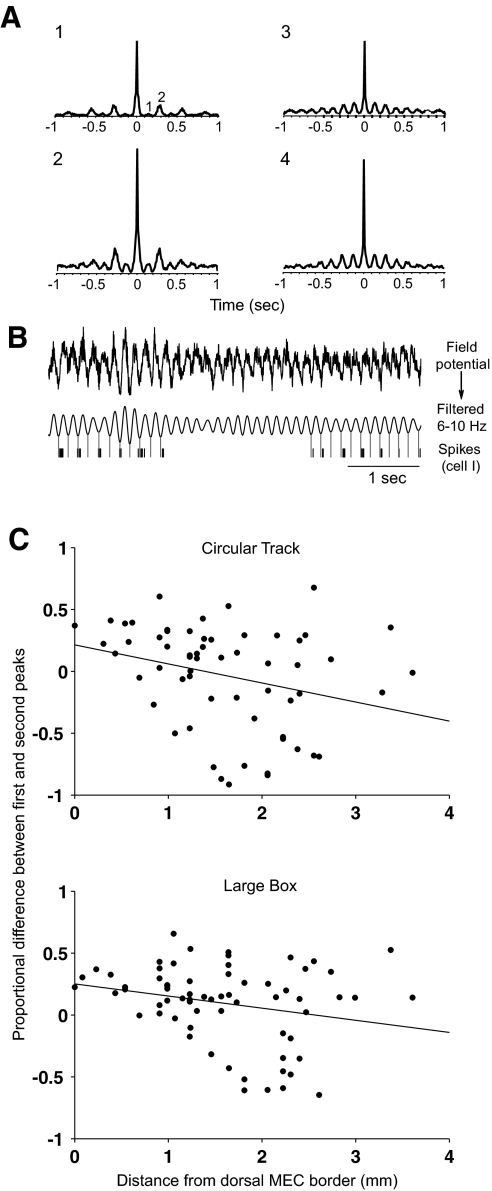
The previous analyses showed that MEC neurons showed much stronger theta modulation than that of LEC neurons, especially in the spike autocorrelograms (Fig. 3). Further inspection of the MEC spike autocorrelograms revealed a heterogeneity of patterns in the relative heights of the theta peaks. Most strikingly, some of the autocorrelograms of MEC neurons displayed a second theta peak that was substantially higher than the first theta peak (Fig. 5A, 1 and 2), suggesting a tendency to skip alternate theta cycles (Fig. 5B). This effect was quantified for the subset of cells that showed clear oscillatory activity in the 2- to 10-Hz range in their autocorrelograms. Of 109 neurons recorded on the circular track, 60 passed the criteria; of the 95 neurons recorded in the large box, 66 passed the criteria. For these cells, the proportional difference between the first and second theta peaks was calculated as (peak1 − peak2)/max (peak1, peak2), such that a negative number indicated that the second peak was higher than the first peak and a positive number indicated that the first peak was higher than the second peak; absolute values close to 0 indicate small differences in peak sizes, whereas absolute values closer to 1 indicate large differences. On the circular track, the second theta peak was higher than the first theta peak in 25 of 60 cells. In the large box, the second theta peak was higher than the first theta peak in 17 of 66 cells. These cells tended to be located in more ventral regions of MEC. Using sagittal histological sections (as in Fig. 1), the distance of each recording site from the dorsal border of MEC was measured and plotted against the proportional difference between the first and the second theta peaks of the autocorrelogram (Fig. 5C). For both the circular track and the large box, there was a significant negative correlation (circular track: r = −0.29, P < 0.05; large box: r = −0.24, P < 0.05). In the most dorsal recording sites (<0.5 mm), none of the cells showed a negative proportional difference between the first and the second peaks; cells recorded in the more ventral recording sites showed either a positive or a negative proportional difference between the first and the second theta peaks. Thus the tendency for grid cells to display increased grid scaling along the dorsocaudal–ventral axis (Brun et al. 2008; Hafting et al. 2005) is mirrored by an increasing tendency to skip alternate theta cycles along the dorsocaudal–ventral axis [see Fig. 4 of Savelli et al. (2008) for examples of grid cells included in this data set]. Consistent with Fig. 5 of the present study, the three high-resolution grid cells recorded in dorsal MEC (310 μm from the dorsal border) did not show alternate theta-cycle skipping, whereas one of the 11 medium-resolution grid cells recorded more ventrally (at 1,150 μm) showed a moderate degree of theta-skipping [cell 5 of Fig. 4 in Savelli et al. (2008)] and another recorded even deeper (1,730 μm) showed clear theta-skipping [cell 4 of Fig. 4 in Savelli et al. (2008)]. Because of the size of the recording box, it was not clear whether cells recorded further ventrally (>2,000 μm)—where theta-skipping is more prominent—were grid cells.

Fig. 5.

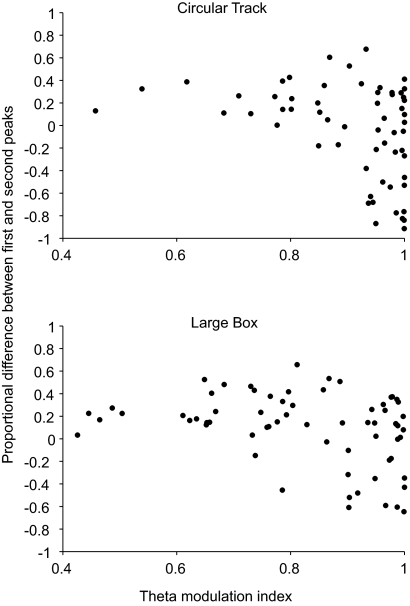
Some MEC neurons skip alternate theta cycles. A: representative autocorrelograms of superficial MEC neurons. The autocorrelograms on the left (1, 2) displayed a second theta peak (peak 2) that was higher than the first peak (peak 1). The autocorrelograms on the right (3, 4) showed the more typical pattern of theta-modulated cells, in which the magnitudes of the peaks decrease with time from the origin. B: representative spikes from cell 1 in A, plotted relative to the LFP from one of the electrodes on the tetrode. The top trace shows the raw LFP (filtered between 1 and 475 Hz during acquisition) and the bottom trace shows the LFP filtered between 6 and 10 Hz. Tick marks indicate spikes. Gray lines mark positions of valleys in the filtered waveform, for ease of comparison with spike timing. The comparison shows that the cell fired at similar phases of theta cycle, but it skipped every other cycle on most occasions. C: scatterplots of the proportional difference between the first and the second theta peaks of the autocorrelograms and the distance from the dorsal border of MEC for circular track (top plot) and large box (bottom plot) showed that the alternate theta cycle skippers were more likely to be located in the ventral regions of the MEC. Trend lines are the least-square fits to the data. Proportional difference between first and second peaks was negatively correlated with distance from the dorsal border of MEC for both circular track (r = −0.29, P < 0.05) and large box (r = −0.24, P < 0.05) sessions.

In vitro recording from MEC stellate cells shows that not only the intrinsic oscillatory frequency of the neurons at depolarized membrane potentials, but also the resonant frequencies of these neurons decrease from about 10 to about 4 Hz along the dorsoventral axis (Giocomo and Hasselmo 2008; Giocomo et al. 2007). We analyzed whether the theta-skipping phenomenon was largely a result of a corresponding reduction of frequency in the autocorrelograms of ventral neurons. Visual inspection of the autocorrelograms showed that most of the alternate theta-cycle skipping cells had small but distinct bumps at the first theta peaks of their autocorrelograms (such as those shown in Fig. 5A, 1 and 2), indicating that there was a significant theta (∼8 Hz) modulation in the alternate theta-cycle skipping cells. We quantified the relationship between the alternate theta-cycle skipping behavior and the cell's relationship to the ongoing theta rhythm in the LFP (the theta modulation index). Figure 6 shows that in both the circular track and large box data, the alternate theta-cycle skippers (neurons with negative values on the y-axis) were among the most highly theta-modulated neurons in the sample (Wilcoxon rank-sum test on theta modulation indices for skippers vs. nonskippers yielded P < 0.01 for the circular track and for the large box). Moreover, these ventrally located cells (Fig. 5C) were colocalized with cells that did not show the theta-skipping phenomenon, showing that the theta skipping was not the result of a simple reduction in the oscillation frequencies at ventral locations and a corresponding reduction in the temporal frequencies of the peaks of the autocorrelograms.

Fig. 6.

Alternate theta cycle skippers are among the strongest theta modulated neurons. Scatterplots of theta modulation index vs. proportional difference between the first and second peaks for the circular track (top) and the large box (bottom) show that the units with negative proportional differences (alternate theta cycle skippers) have theta modulation indices clustered near 1, whereas the units with positive proportional difference had theta modulation indices that were more distributed.

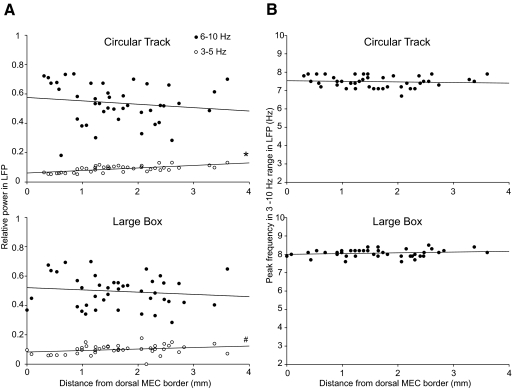
We further analyzed the relative power of theta and delta (3–5 Hz) oscillations in the LFP along the dorsoventral axis of MEC. Figure 7 shows that theta was the dominant oscillation in the MEC along the entire dorsoventral axis from 0–4 mm away from the dorsal border. Relative power in the theta band in LFPs did not change significantly along the dorsoventral axis (Fig. 7A, closed circles). Although relative power in the delta band (3–5 Hz) remained well below that in the theta band, it showed a statistically significant increase along the dorsoventral axis of MEC in the circular track data and a similar trend in the large box data (Fig. 7A, open circles). The LFP peak frequency in the 3- to 10-Hz range (which covers theta as well as delta bands) in MEC was independent of dorsoventral location (Fig. 7B; circular track median = 7.5 HZ, large box median = 8.1 Hz).

Fig. 7.

Contributions of theta and delta frequency oscillations to LFPs along the dorsoventral axis of MEC. A: relative power in theta (6–10 Hz; filled circles) and delta (3–5 Hz; open circles) bands in LFPs from tetrodes with simultaneous single unit recordings against distance from the dorsal border of MEC. The relative theta power in LFP did not show a significant trend in the circular track data (top; r = −0.14, P = 0.37, n.s.) or the large box data (bottom; r = −0.12, P = 0.45, n.s.). The relative delta power in LFP showed a significant increase along the dorsoventral axis in the circular track data (r = 0.65, *P < 0.0001) and a similar trend in the large box data (r = 0.27, ^#P = 0.085). B: scatterplots of peak frequency in the 3- to 10-Hz range against distance from the dorsal border of MEC in the circular track data (top; r = −0.0872, P = 0.59, n.s.) and the large box data (bottom; r = 0.16, P = 0.30, n.s.) show no dependence of peak frequency on dorsoventral location in MEC. Trend lines are least-square fits to the data.

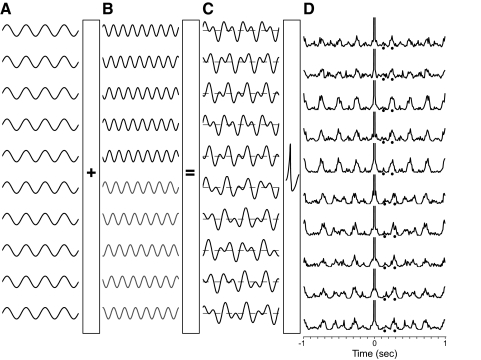
The slight increase along the dorsoventral axis in the weak relative power in the delta band does not necessarily reflect an increase in delta oscillations per se and it might be a consequence of the increasing proportion of theta-skipping cells along this axis (Fig. 5). However, the increase may be related to the gradient along the dorsoventral axis in resonant frequency of MEC neurons recorded in vitro (Giocomo et al. 2007). When depolarized, dorsal MEC neurons show a resonant frequency of around 8 Hz, whereas ventral neurons show a resonant frequency of about 4 Hz. One hypothesis is that a subthreshold delta input, when amplified by the 4-Hz intrinsic frequencies of ventral neurons, might create interference with the stronger theta-oscillatory input to create the theta-skipping phenomenon because the cells fire with a greater probability when the two inputs are aligned in phase. To test the general plausibility of this hypothesis, we simulated a Poisson firing neuron receiving a theta + delta interference pattern as an input and generated autocorrelograms from the spike trains (Fig. 8). All of the autocorrelograms (Fig. 8D) showed the first theta peak smaller than the second, regardless of not only the phase offset between the theta and delta inputs, but also the frequency of theta input (7 or 8 Hz). We did not exhaustively simulate all combinations of phases and frequencies of theta and delta waves. This simulation is merely intended to demonstrate that the autocorrelograms generated by the real MEC neurons (Fig. 5) need not rely on a specific combination of phase and frequency of the theta wave relative to delta, but can occur with many such combinations. A more detailed simulation that incorporates biophysical mechanisms of resonant frequencies and differential inputs at theta and delta frequencies, beyond the scope of the present study, would be required to demonstrate conclusively that the prevalence of alternate theta-cycle skipping in the ventral MEC is related to the in vitro results of Giocomo and colleagues (2007).

Fig. 8.

Interference between theta and delta frequency inputs can give rise to theta skipping. A: delta frequency sine waves (4 Hz). B: theta frequency sine waves. Two frequencies of theta are simulated (top 5 traces, black, 8 Hz; bottom 5 traces, gray, 7 Hz). The phase lags for the theta frequency sine waves have been randomized. C: sum of the theta and delta frequency sine waves. Horizontal lines indicate amplitude of 0. D: autocorrelograms of spike trains generated by passing the sum waveform (3,600 s long; a, b, and c show only first 1 s) through a simple Poisson firing neuron model (see methods for details). The central peaks of the autocorrelograms are clipped to show the details of the theta and delta periodicity. Dots under the autocorrelograms indicate locations of the first and second peaks predicted by the theta waveform alone.

DISCUSSION

In this study, LFPs in the LEC showed much less theta oscillation than that in LFPs in the MEC, irrespective of the layer from which they were recorded. Correspondingly, LEC neurons showed less theta modulation than that of MEC neurons, although they did demonstrate modulation that was significantly higher than chance. These differences reinforce previous findings that LEC and MEC engage in fundamentally different types of information processing (Hargreaves et al. 2005). In addition, we showed that neurons in the ventral MEC have a propensity to skip alternate theta cycles. Although this phenomenon might be explained by a number of mechanisms, computer simulations showed that the result is consistent with a model of interference between a dominant theta-modulated input and a weaker delta-modulated input, possibly amplified by intrinsic cellular resonance at about 4 Hz in the ventral MEC (Giocomo et al. 2007).

Entorhinal theta rhythm was first demonstrated in cats (Adey et al. 1960; Holmes and Adey 1960), but these experiments did not distinguish between MEC and LEC. Using phase and amplitude profiles through MEC layers, Mitchell and Ranck (1980) showed that the theta rhythm is generated in the MEC, not volume-conducted from the hippocampus. Similar analyses of LEC theta are rare. Alonso and Garcia-Austt (1987a) studied physostigmine (a cholinesterase inhibitor) induced theta in anesthetized rats. Their data set included only two LEC penetrations. Although it is apparent from Fig. 2 in that study that the LEC theta amplitude is lower than that of MEC theta amplitudes shown, the study does not discuss this finding. Physostigmine-induced theta frequency is about 4 Hz, which is in the range of a-theta, associated with attention, and not t-theta (∼8 Hz), associated with locomotion (Buzsáki 2002) and the focus of the present study. The present study conclusively demonstrates that under two common behavioral paradigms used for hippocampal place cell recordings (random foraging in an arena and directed running on a closed-loop track), MEC inputs to the hippocampus are much more strongly modulated by theta rhythm than are LEC inputs.

Functional implications of differential theta modulation of MEC and LEC

A prominent theory of hippocampal function states that the hippocampus is the neural locus of a cognitive map, in which nonspatial information such as events and objects are encoded in a spatial framework (O'Keefe and Nadel 1978). The spatial correlate of hippocampal activity has been well established since the discovery of place cells by O'Keefe and Dostrovsky (1971) (e.g., O'Keefe 1976; Wilson and McNaughton 1993). Hippocampal place cells also show phase precession with respect to ongoing theta oscillations (O'Keefe and Recce 1993). Huxter et al. (2003) showed that phase precession within the place field can be dissociated from firing rate within the place field. That is, the rate of phase precession is the same on multiple trials, even when the firing rate differs by as much as tenfold between trials (but see Harris et al. 2002; Mehta et al. 2002). Thus phase might be particularly important for encoding the spatial location of the rat (or the temporal sequences of spatial locations; Schmidt et al. 2009), whereas rate encodes nonspatial variables, such as speed (Huxter et al. 2003; McNaughton et al. 1983; Wiener et al. 1989), odors (Wood et al. 1999), auditory stimuli (Moita et al. 2003), and object identity (Komorowski et al. 2009; Manns and Eichenbaum 2009).

The difference in theta modulation between MEC and LEC neurons and field potentials is consistent with the above-cited observations. MEC, which encodes spatial information (Fyhn et al. 2004; Hafting et al. 2005; Hargreaves et al. 2005; Quirk et al. 1992), shows stronger theta oscillations in the LFP and higher theta modulation of single neurons than those in LEC. Many MEC neurons show theta phase precession (Hafting et al. 2008). Thus MEC input appears to be associated with the theta-modulated, spatial mapping functions of the hippocampus, whereas the LEC inputs, which are weakly theta modulated and spatially nonselective (Hargreaves et al. 2005), could influence the rate code for nonspatial information. A preliminary report of reduction in rate remapping in CA3 and dentate gyrus caused by LEC layer II damage is consistent with this hypothesis (Leutgeb JK et al. 2008; for the details of rate remapping in hippocampus, see Leutgeb S et al. 2005).

It is possible that the low firing rates of LEC neurons in the present study may be a factor in the weak theta modulation of these neurons. Thus LEC cells may show stronger theta modulation under sensory conditions that cause them to fire more robustly than in the present study. It will be important to revisit this question if future studies uncover sensory stimuli that drive LEC cells more strongly during theta-related behaviors. Similarly, a task with stronger attentional or mnemonic demands, with stronger cholinergic activation, might lead to stronger theta modulation of LEC layer III neurons. LEC layer III pyramidal cells show theta-modulated, persistent activity in slices (Tahvildari et al. 2007). These recordings were done in the presence of glutamatergic and GABAergic blockers (to isolate the neuron from the local network) and a muscarinic agonist, carbachol (to simulate cholinergic input, which is thought to be important in mnemonic processing). A prolonged, 2- to 8-s depolarizing stimulus was necessary to switch this activity on and off. These results—with the caveats about the isolated nature of the preparation and the long duration of the stimulus required—suggest that there are conditions under which LEC cells may naturally show stronger theta modulation than that in the present study. Such results would implicate LEC as part of the theta-tuned temporal coding network under strong attention/memory demands, but not under the present conditions of random foraging or trajectory running, which are typical of many hippocampal place-cell studies.

Alternate theta-cycle skipping in ventral MEC

The tendency of some ventral MEC neurons to fire at alternate theta cycles (i.e., skipping every other cycle) is an intriguing result. MEC layer II stellate cells in vitro show subthreshold theta oscillations when they are depolarized, but action potentials are fired only on a subset of the theta peaks (Alonso and Klink 1993; Alonso and Llinás 1989). Contrary to the present study, the spikes seem to skip theta cycles irregularly. Such irregular skipping would reduce the depth of modulation in an autocorrelogram, but is unlikely to produce the higher secondary peak—indicative of a systematic skipping of alternate theta cycles—shown in the present study. The alternate theta-cycle skipping may be related to the scaling of grid-cell firing patterns along the dorsoventral axis of MEC (Brun et al. 2008; Hafting et al. 2005). Grid cells in the dorsocaudal MEC show the most fine-grained grids and the grids become coarser as recordings are made at increasingly ventral locations in the MEC. This scaling is matched by the scaling of place fields along the dorsoventral (septotemporal) axis of the hippocampus (Jung et al. 1994; Kjelstrup et al. 2008), which receives topographically organized inputs from the dorsoventral axis of the MEC. Alternate theta-cycle skipping is also evident (albeit weak) in autocorrelograms from ventral hippocampal neurons (Royer et al. 2010), although future studies may find stronger examples. One class of models of grid-cell formation proposes that the periodic patterns of grid-cell firing vertices result from beat frequencies caused by the interference of two oscillators (Blair et al. 2008; Burgess et al. 2007; Hasselmo et al. 2007). In support of these models, Giocomo et al. (2007) showed that the intrinsic oscillations of entorhinal stellate cells decreased along the dorsoventral axis of MEC. Further, they showed that ventral MEC cells showed subthreshold oscillations at nearly 4 Hz, regardless of the membrane potential of the cell, whereas dorsal MEC cells showed an increase in subthreshold oscillation frequency from about 4 to >8 Hz as the membrane became depolarized (Giocomo and Hasselmo 2008).

The difference between dorsal and ventral MECs in subthreshold oscillation frequency at depolarized potentials may help explain the alternate theta-cycle skipping phenomenon. The dominant oscillation frequency along the entire dorsoventral axis is in the theta range (Fig. 7). A small increase from dorsal to ventral in the relatively weak delta power may indicate an increasing, 4-Hz synaptic drive onto ventral cells. One potential source of this input is the prefrontal cortex, which has 4-Hz oscillations that conditionally phase lock with hippocampal theta oscillations (Fujisawa et al. 2009). Since ventral neurons have a resonant frequency at 4 Hz (Giocomo et al. 2007), they would respond more strongly to a 4-Hz input than would dorsal neurons with a resonant frequency of 8 Hz. Both dorsal and ventral cells would respond at theta frequency to a dominant theta input, but the 4-Hz intrinsic frequency of ventral cells would make them more prone to constructive interference of theta and delta inputs, resulting in the alternate theta-skipping phenomenon. In the absence of a known source of delta oscillations and a biophysical model showing a link between oscillatory interference and resonant/intrinsic oscillatory frequencies, however, the oscillatory interference model is only a hypothesis to explain the theta skipping phenomenon. Alternative mechanisms, such as a prolonged, local feedback inhibition lasting for about 200 ms, could also be invoked to explain the phenomenon.

Summary

The present study shows two significant phenomena related to theta oscillations in the entorhinal cortex. First, the dissociation between MEC and LEC in spatial tuning (Hargreaves et al. 2005) is matched by the difference between the areas in the theta modulation of neural firing, at least under the conditions studied here. This dissociation might differentially affect the ability of these two regions to influence the rate and theta-phase temporal codes in the hippocampus. Second, the gradient along the dorsoventral axis of MEC in the propensity of neurons to skip alternate cycles of theta matches similar gradients in the scaling of MEC grid cells (Brun et al. 2008; Hafting et al. 2005) and in the intrinsic frequencies of MEC stellate cells in vitro (Giocomo et al. 2007). Although the relationship between these latter phenomena and the theta-skipping phenomenon is not clear, a computer simulation showed that the theta-skipping phenomenon is consistent with an interference model of delta- and theta-modulated inputs.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grants R01 NS-039456 and P01 NS-038310.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).