CFD simulations of enhanced condensational growth (ECG) applied to respiratory drug delivery with comparisons to in vitro data

Abstract

Enhanced condensational growth (ECG) is a newly proposed concept for respiratory drug delivery in which a submicrometer aerosol is inhaled in combination with saturated or supersaturated water vapor. The initially small aerosol size provides for very low extrathoracic deposition, whereas condensation onto droplets in vivo results in size increase and improved lung retention. The objective of this study was to develop and evaluate a CFD model of ECG in a simple tubular geometry with direct comparisons to in vitro results. The length (29 cm) and diameter (2 cm) of the tubular geometry were representative of respiratory airways of an adult from the mouth to the first tracheobronchial bifurcation. At the model inlet, separate streams of humidified air (25, 30, and 39 °C) and submicrometer aerosol droplets with mass median aerodynamic diameters (MMADs) of 150, 560, and 900 nm were combined. The effects of condensation and droplet growth on water vapor concentrations and temperatures in the continuous phase (i.e., two-way coupling) were also considered. For an inlet saturated air temperature of 39 °C, the two-way coupled numerical (and in vitro) final aerosol MMADs for initial sizes of 150, 560, and 900 nm were 1.75 μm (vs. 1.23 μm), 2.58 μm (vs. 2.66 μm), and 2.65 μm (vs. 2.63 μm), respectively. By including the effects of two-way coupling in the model, agreements with the in vitro results were significantly improved compared with a one-way coupled assumption. Results indicated that both mass and thermal two-way coupling effects were important in the ECG process. Considering the initial aerosol sizes of 560 and 900 nm, the final sizes were most influenced by inlet saturated air temperature and aerosol number concentration and were not largely influenced by initial size. Considering the growth of submicrometer aerosols to above 2 μm at realistic number concentrations, ECG may be an effective respiratory drug delivery approach for minimizing mouth–throat deposition and maximizing aerosol retention in a safe and simple manner. However, future studies are needed to explore effects of in vivo boundary conditions, more realistic respiratory geometries, and transient breathing.

1. Introduction

It is well known that inhaled pharmaceutical aerosols are often deposited in the lung at very low deposition efficiencies (Borgstrom, Olsson, & Thorsson, 2006; Byron, 2004; Cheng, Fu, Yazzie, & Zhou, 2001; Leach, Davidson, & Bouhuys, 1998; Zhang, Gilbertson, & Finlay, 2007). Perhaps more significant than the quantity of drug deposited is the large inter- and intra-subject variability that is often observed with these medicinal aerosols and the associated dose delivered to the lung. In order to make many next-generation inhaled medications a viable drug delivery alternative, increased lung delivery and decreased inter- and intra-subject variability are of critical importance (Byron, 2004; Smaldone, 2006).

To improve the delivery of inhaled drugs, a number of well known and novel generation techniques are becoming commercially available that can create relatively monodisperse nanoparticle and submicrometer aerosols without significant spray inertia effects (Gupta, Hindle, Byron, Cox, & McRae, 2003; Mazumder et al., 2006; Newth and Clark, 1989; Rabinowitz et al., 2004; Sham, Zhang, Finlay, Roa, & Lobenberg, 2004). Submicrometer aerosols (100–1000 nm) delivered in a low inertia airstream can significantly reduce unwanted deposition in the mouth–throat region (Longest, Hindle, Das Choudhuri, & Xi, 2008). In a recent study, Borgstrom et al. (2006) showed that reduced deposition in the mouth–throat region can significantly decrease inter-subject lung deposition variability. However, a major problem with this delivery approach is that a high percentage of nanoparticle and submicrometer aerosols are not retained in the lung and are exhaled (Heyder, Gebhart, Rudolf, Schiller, & Stahlhofen, 1986; Hofmann, Morawska, & Bergmann, 2001; Jaques & Kim, 2000; Morawska, Barron, & Hitchins, 1999; Morawska, Hofmann, Hitchins-Loveday, Swanson, & Mengersen, 2005; Stahlhofen, Rudolf, & James, 1989). For example, Jaques and Kim (2000) report that the total lung retention of 100 nm aerosols can be as low as 25% without a breath hold.

Enhanced condensational growth (ECG) applied to respiratory drug delivery is a recently proposed concept that seeks to combine the advantages of both submicrometer and micrometer aerosols. In this approach, a submicrometer aerosol is delivered to the respiratory airways in conjunction with an airstream that is saturated or supersaturated with water vapor and above body temperature. The initially submicrometer particles or droplets, in the approximate size range of 100–900 nm, have very low deposition values in the mouth–throat (MT) and upper tracheobronchial regions (Cheng, 2003; Cohen, Sussman, & Lippmann, 1990; Xi & Longest, 2008a, 2008b). As a result, aerosol loss in the MT can be largely eliminated. The inhaled water vapor is used to create supersaturated conditions within the respiratory airways. Submicrometer droplets in this supersaturated environment will increase in size at a controlled rate due to condensation. Size increases to within the range of 2–3 μm can be used to ensure deposition and full lung retention of the aerosol. Furthermore, engineering the rate of size increase can be used to target deposition within specific regions of the lung. Factors influencing the amount and rate of size increase with the ECG approach include the degree of supersaturation, temperature, particle or droplet hygroscopicity, initial size, and aerosol number concentration. However, the effects of these variables on aerosol size growth have been investigated only on a very limited basis.

The relative humidity (RH) of the tracheobronchial airways beyond the first several bronchi is generally expected to be 99.5% (Ferron, 1977). Furthermore, many inhaled environmental and pharmaceutical aerosols are soluble. As a result, hygroscopic effects are known to influence the deposition of these inhaled respiratory aerosols (Ferron, 1977; Ferron, Kreyling, & Haider, 1988; Finlay & Stapleton, 1995; Li & Hopke, 1993; Martonen, Bell, Phalen, Wilson, & Ho, 1982; Zhang, Kleinstreuer, & Kim, 2006b). Hygroscopic particle growth has been investigated experimentally for NaCl particles (Cinkotai, 1971), pharmaceutical aerosols (Peng, Chow, & Chan, 2000), and combustion droplets (Li & Hopke, 1993). A number of mathematical models have also been formulated for hygroscopic growth of respiratory aerosols at RH values below 100% (Broday & Georgopoulous, 2001; Ferron, 1977; Ferron et al., 1988; Ferron, Oberdorster, & Hennenberg, 1989; Finlay & Stapleton, 1995; Robinson & Yu, 1998; Varghese & Gangamma, 2009). These studies typically indicate a maximum size increase of approximately 400% for NaCl particles. Hygroscopic growth of most other salts and pharmaceutical aerosols results in size increases less than 100% at RH values of 99.5% and below (Ferron et al., 1988, 1989). Recently, Zhang, Kleinstreuer, and Kim (2006a) developed a CFD model of hygroscopic growth in the upper respiratory tract. It was found that saline concentrations of 10% and higher were required for hygroscopic growth to have a significant impact on deposition. Finlay and Stapleton (1995) applied a numerical model to show that mass coupling between aerosol droplets and the continuous phase was significant for droplet concentrations above 25,000 particles (part)/cm³. However, all of these previous studies considered RH conditions only up to 100%.

Very little work has been done to evaluate the effects of RH conditions above 100% (i.e., supersaturated conditions) on the condensational growth of respiratory aerosols. However, supersaturated conditions can be achieved in the respiratory tract through the inhalation of warm (T > T_body) saturated air. Ferron, Haider, and Kreyling (1984) have shown that RH above 100% is possible in the upper respiratory tract under some inhalation conditions. Significant growth of NaCl particles was observed for very localized supersaturation in the nasal cavity (Ferron et al., 1984). Longest and Xi (2008) considered the inhalation of warm humidified air during smoking. Computational fluid dynamics simulations indicated that inhalation of warm saturated air approximately 3 °C above body temperature could result in supersaturation conditions (RH > 100%) through approximately the 6th respiratory bifurcation. Moreover, submicrometer aerosols exposed to RH conditions in the range of 101% experienced a large and rapid increase in size.

The concept of ECG applied to improve respiratory drug delivery was originally introduced by Longest, McLeskey, and Hindle (2010). In this previous study, the effects of saturated air inlet temperature and initial aerosol particle size on submicrometer aerosol growth were considered based on in vitro experiments and a numerical model in a simple tubular system. The numerical model considered only condensation (and evaporation) of individual droplets with constant far-field temperature and relative humidity conditions based on droplet heat and mass transport equations. The loss of water vapor in the air phase due to condensation on the droplet surface was neglected, i.e., one-way heat and mass coupling was assumed. Results of this simple numerical model in comparison with in vitro experiments indicated that (i) two-way coupling between the continuous and discrete phases may significantly affect aerosol growth in some cases and (ii) predictions of final size may be improved by considering spatially variable three-dimensional (3-D) temperature and humidity fields in conjunction with droplet trajectories. Furthermore, the single-droplet condensation model cannot account for aerosol deposition. As a result, a validated computational fluid dynamics (CFD) model of ECG is needed that can accurately simulate local temperature and humidity fields, droplet trajectories, condensation and evaporation, and two-way coupling between the continuous and discrete phases. This model can then be applied to optimize the ECG approach for minimum MT deposition and maximum lung retention for engineering targeted deposition within the respiratory airways.

The objective of this study is to develop and evaluate a CFD model for simulating ECG in a simple tubular geometry with direct comparisons to in vitro results. Model results are also used to evaluate the potential of ECG for improving respiratory drug delivery. The length and diameter of the tubular geometry are consistent with the respiratory airways of an adult from the mouth to the first tracheobronchial bifurcation. At the model inlet, separate streams of humidified air and submicrometer droplets are combined. Initial aerosol mass median aerodynamic diameters (MMADs) ranging from 150 to 900 nm are considered in conjunction with saturated air temperatures from 25 to 39 °C. The CFD model is used to simulate mixing of these air streams based on a well tested k–ω turbulence model, as well as heat and mass transfer relations. Individual particle trajectories are simulated using a previously developed Lagrangian tracking algorithm supplemented with a new routine to calculate condensation and evaporation for hygroscopic aerosols. The effect of condensation and droplet growth on water vapor in the continuous phase (i.e., two-way coupling) is also considered. Numerical predictions are compared with previously reported in vitro results of final droplet size at outlet aerosol concentrations ranging from 6.0 × 10⁴ to 2.8 × 10⁵ part/cm³. Comparisons of one-way and two-way coupled model results are used to determine conditions for which the more complicated process of air-phase water loss due to aerosol growth needs to be evaluated. Once developed and tested in comparison with in vitro data, the CFD model of ECG can be applied to more realistic geometries and boundary conditions for optimizing respiratory drug delivery in the lungs.

2. Methods

2.1. Geometry and boundary conditions

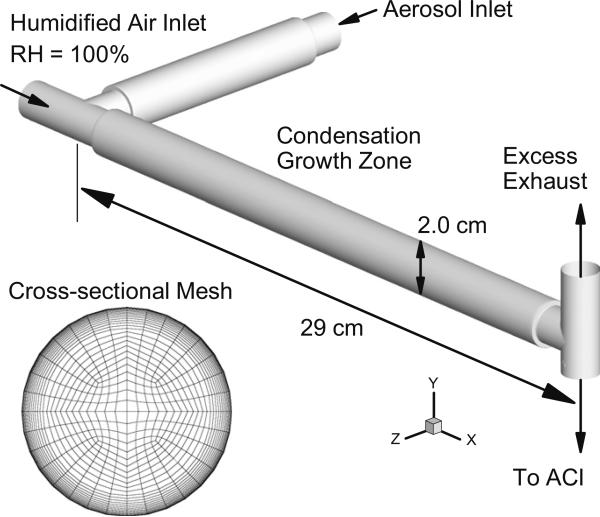
To develop and test a CFD model of ECG, a simple tubular geometry was selected as shown in Fig. 1. At the geometry inlet, separate streams of humidified air and nebulized aerosol droplets are combined. The humidified air stream enters at a relative humidity (RH) of 100% and the amount of entering water vapor is controlled based on inlet temperature. The aerosol enters as submicrometer droplets with a relatively monodisperse distribution. Air temperature of the aerosol stream is below the temperature of the humidified air, resulting in supersaturated conditions when these two streams are mixed. The combined humidified air and submicrometer aerosol then enter a condensational growth zone of length 29 cm and diameter 2 cm. The length of the condensational growth zone is consistent with the distance from the mouth inlet to the first respiratory bifurcation in an adult male. The diameter of the growth zone provides a residence time that is approximately equal to the time required for an inhaled particle to reach the first respiratory bifurcation, i.e., about 0.2 s. At the outlet of the condensational growth zone, a second connection tee is used to route the aerosol for size evaluation. In the experiments, an Andersen cascade impactor (ACI) was used for aerosol sizing. The temperature of the ACI was maintained at the outlet temperature of the condensational growth zone to minimize additional size increase.

Fig. 1.

Model geometry used to evaluate enhanced condensational growth (ECG) of submicrometer aerosols. The length of the condensation growth zone (29 cm) is approximately equal to the distance from the mouth inlet to the main bronchi in an adult. The insert shows a cross-sectional view of the hexahedral computational grid that was implemented in the simulations.

Airflow and droplet boundary conditions employed in the numerical simulations are presented in Table 1. These conditions are identical to those employed in the previous in vitro study of Longest et al. (2010). As shown in the table, three initial aerosol size distributions were generated and considered with MMADs of 150, 560, and 900 nm. These sizes were determined experimentally using a 10-stage MOUDI (150 nm) or 8-stage ACI (560 and 900 nm) and the resulting distributions were implemented for polydisperse aerosol simulations. The aerosol inlet stream was at approximately 21 °C with RH conditions between 82.5% (150 nm) and 97.5% (560 and 900 nm). For each aerosol size, two inlet concentrations were defined in order to provide outlet number concentrations of 1 × 10⁵ and 5 × 10⁵ part/cm³ (Table 1). This range of outlet concentrations was selected to be consistent with the in vitro experiments. The associated numerical inlet number concentrations before dilution with saturated air ranged from 3.2 × 10⁵ to 2.2 × 10⁶ part/cm³ (Table 1). In addition to particle size, the effect of the humidified air inlet temperature was also considered. Temperature conditions of 25, 30, and 39 °C were selected, with each increase in temperature holding more water mass at a RH of 100%. Realistically, the inlet temperature case of 39 °C is most relevant to respiratory drug delivery as this temperature would be required to induce supersaturation in the airways, where wall temperature is assumed to be approximately 37 °C. However, three temperature conditions are considered in this study to better validate the CFD model based on variations in available water mass. Based on the use of thermally insulated plastic in the experiments, no heat flux was assumed to cross the walls. Condensation onto the walls was assumed only if the near-wall relative humidity was greater than 100%. Droplets were assumed to deposit on initial wall contact, and evaporation was not continued after deposition occurred. Finally, outlet aerosol size was assessed in the numerical model at a distance of 5 cm down the vertical outlet tube (Fig. 1). This distance was selected as equal to the first stage of the ACI impactor used for outlet size assessments in the experiments. However, velocities within the impactor as reported by Vinchurkar, Longest, and Peart (2009) were not considered.

Table 1.

Flow conditions used in the CFD model.

MMAD (nm)	Nebulizer inlet	Humidity inlet	ACI inleta
150	Q: 15 L/min (250 cm3/s)b	Q: 25 L/min (416.7 cm3/s)	Q: 32.5 L/min (541.7 cm3/s)
	T: 20 °C	T: 25, 30, and 39 °C
	RH: 82.5%	RH: 100%
	nc: 4.33 × 105 and 2.17 × 106 part/cm3	n: ~0 part/cm3	n: 1 × 105 and 5 × 105 part/cm3
560	Q: 9 L/min (150 cm3/s)	Q: 20 L/min (333.3 cm3/s)	Q: 29.0 L/min (483.3 cm3/s)
	T: 21 °C	T: 25, 30, and 39 °C
	RH: 97.5%	RH: 100%
	nc: 3.22 × 105 and 1.61 × 106 part/cm3	n: ~0 part/cm3	n:1 × 105 and 5 × 105 part/cm3
900	Q: 9 L/min (150 cm3/s)	Q: 20 L/min (333.3 cm3/s)	Q: 29.0 L/min (483.3 cm3/s)
	T: 21 °C	T: 25, 30, and 39 °C
	RH: 97.5%	RH: 100%
	nc: 3.22 × 105 and 1.61 × 106 part/cm3	n: ~0 part/cm3	n: 1 × 105 and 5 × 105 part/cm3

^aAll flow exited through the ACI.

^bThe flow rate of the aerosol inlet was reduced to 7.5 L/min for the 150-nm case prior to entering the condensation growth tube.

^cNebulizer particle number concentrations in the model were adjusted to produce values of 1 × 10⁵ and 5 × 10⁵ part/cm³ at the ACI inlet.

Inlet velocity and particle profiles have previously been shown to significantly influence aerosol deposition (Longest & Oldham, 2006; Longest & Vinchurkar, 2007a, 2007b; Zhang & Kleinstreuer, 2001). In this study, blunt velocity profiles consistent with the study of Longest, Vinchurkar, and Martonen (2006) were implemented. This profile shape represents nearly constant inlet velocity conditions and provides a smooth transition to zero velocity at the wall. The initial particle profile was defined as a function of local inlet mass flow rate (Longest & Vinchurkar, 2007a). Based on experimental measurements and the assumption of zero heat flux at the walls, constant temperature and relative humidity conditions were specified at the inlets. Turbulence intensities of 1% were also specified at the inlets and allowed to evolve downstream. A constant pressure condition was implemented at the downstream ACI outlet and zero excess exhaust was assumed (Fig. 1).

2.2. Continuous phase equations

For the tubular system of interest, the Reynolds number range is 500–2170, based on flow rates of 7.5–32.5 L/min (Table 1) and a 2 cm inner diameter. Considering the presence of 90° bends and the combination of two flow streams, laminar to turbulent flow conditions are expected for this range of Reynolds numbers. To resolve these multiple flow regimes, the low Reynolds number (LRN) k–ω model was selected based on its ability to accurately predict pressure drop, velocity profiles, and shear stress for transitional and turbulent flows (Ghalichi et al., 1998; Wilcox, 1998). This model was also demonstrated to accurately predict particle deposition profiles for transitional and turbulent flows in models of the oral airway (Xi & Longest, 2007, 2008a) and multiple bifurcations (Longest & Vinchurkar, 2007b). The conservation of mass and momentum equations used with the LRN k–ω model are available from Wilcox (1998) and were previously reported by Longest and Xi (2008). Similarly, the equations governing turbulent kinetic energy (k) and specific dissipation rate (ω) were also reported by Longest and Xi (2008).

The mass transport of water vapor is governed by the convective–diffusive equation including turbulent dispersion, as follows (Bird, Steward, & Lightfoot, 1960)

$$\frac{\partial Y_v}{\partial t}+\frac{\partial u_j{Y}_v}{\partial {\chi }_j}=\frac{\partial }{\partial {\chi }_j}\left[\left({\tilde{D}}_v+\frac{{\nu }_T}{S{c}_T}\right)\left(\frac{\partial Y_v}{\partial {\chi }_j}\right)\right]+S_v$$ (1)

In the above expression, Y_v is the mass fraction of water vapor, D̃_v the binary diffusion coefficient of water vapor in air, ν_T the turbulent viscosity (~k/ω), and the turbulent Schmidt number is taken to be Sc_T=0.9 (Bird et al., 1960). The water vapor source term S_v is used to account for the increase (or decrease) in continuous phase water vapor mass fraction from evaporating (or condensing) droplets. In the mass transport relation, transport of thermal energy due to diffusion was excluded based on Lewis numbers close to one for both air and water vapor. For the two species considered, the mass fraction of air was evaluated as Y_a=1.0–Y_v. The binary diffusion coefficient D̃_v was determined on a temperature dependent basis using the correlation of Vargaftik (1975).

To determine the temperature field in the model geometry, the constant property thermal energy equation is expressed as

$$\rho C_p\frac{\partial T}{\partial t}+\rho C_p\frac{\partial u_{j}T}{\partial {\chi }_j}=\frac{\partial }{\partial {\chi }_j}\left[\left({\kappa }_g+\frac{\rho C_p{\nu }_T}{P{r}_T}\right)\left(\frac{\partial T}{\partial {\chi }_j}\right)+\sum _s{h}_s\left(\rho {\tilde{D}}_v+\frac{\partial {\nu }_T}{S{c}_T}\right)\frac{\partial Y_s}{\partial {\chi }_j}\right]+S_e$$ (2)

In this conservation of energy statement, ρ is the mixture density, C_p the constant specific heat, Κ_g the gas conductivity, and Pr_T the turbulent Prandtl number, which is taken to be 0.9 (Bird et al., 1960). The enthalpy of each species is represented as h_s, and the two species are air and water vapor. On the right-hand-side of Eq. (2), the first term represents conductive transport due to molecular and turbulent mechanisms, while the second term accounts for energy transport due to species diffusion. Finally, S_e is the continuous phase energy source (or sink) term due to the presence of the discrete phase.

The relative humidity of the continuous phase is based on both the amount of water vapor present and the air temperature. Relative humidity of the ideal gas mixture can be expressed

$$RH=\frac{P_v}{P_{v,sat}}=\frac{Y_v\rho R_{v}T}{Y_{v,sat}\rho R_{v}T}=\frac{Y_v}{Y_{v,sat}}$$ (3)

where R_v is the gas constant of water vapor and ρ the mixture density. The temperature dependent saturation pressure of water vapor (P_v,sat) was evaluated from the Antoine equation (Green, 1997). The mass flux of water vapor at the wall depends on the local RH conditions. For near-wall RH values less than 100%, zero mass flux at the surface is assumed. If the near-wall RH is greater than 100%, then condensation onto the surface is assumed. The mass flux from the near-wall location to the surface is calculated as

$$n_{v,wall}=\frac{-\rho {\tilde{D}}_v\frac{\partial Y_v}{\partial n}\mid wall}{(1-Y_{v,wall})}$$ (4)

To evaluate droplet condensation and evaporation, cases with one-way or two-way coupling with the continuous phase were considered. In one-way coupling, condensation and evaporation at the droplet surface do not affect the continuous phase. This assumption is valid if the droplet concentration is sufficiently dilute such that water gain or loss from the continuous phase can be neglected. Two-way coupling considers the effect of droplets on the continuous phase. Evaporation or condensation at the droplet surface results in a mass and energy source or sink in the continuous phase. These effects are expressed using the mass (S_v) and energy (S_e) source or sink terms in Eqs. (1) and (2). In this study we are primarily concerned with condensation, so that the mass term will be considered as a continuous phase sink and the energy term will be considered as a continuous phase source. This discussion is equally valid for evaporation, where mass is added to the continuous phase.

To evaluate mass and energy sinks and sources due to two-way coupling, the strength of representative droplet trajectories in units of particles/s is calculated as

$$strength=\frac{nNFQ}{numberofparticlesinbin}$$ (5)

where n is the particle number density in part/cm³, NF the number fraction in each particle size bin, and Q the total inlet flow rate in cm³/s of the nebulizer airstream. The number of size bins was based on the number of impactor stages used for the initial size evaluation, as discussed above. Within each bin, a finite number of droplets is computed to avoid simulating all droplets in the physical system. As shown in Eq. (5), the strength is divided by this number of computational droplets in each bin, resulting in the number of particles per second (part/s) along each computational trajectory. Based on the strength calculation, the mass of water vapor removed from a control volume during condensation is calculated for a single computational trajectory as

$${\stackrel{.}{m}}_p=\Delta mstrength$$ (6)

where Δm is the droplet mass change within the computational cell. The sign of ṁ_p is positive for evaporation and negative for condensation. The vapor sink term for use in Eq. (1) is then calculated as

$$S_v=\frac{{\stackrel{.}{m}}_p}{V_{CV}\rho }$$ (7)

where V_cv is the volume of the current computational cell (control volume) and ρ is the density of the air–vapor mixture. Based on ṁ_p, S_v is negative for condensation (resulting in a vapor sink) and positive for evaporation (resulting in a vapor source).

The energy source term in two-way coupling can be expressed as

$$S_e=-\frac{{\stackrel{.}{m}}_p{L}_v}{V_{CV}}-\frac{{\stackrel{.}{m}}_p{C}_p}{V_{CV}}(T_d-T_{CV})$$ (8)

where L_v is the latent heat of vaporization and C_p the specific heat at constant pressure for water. The droplet and surrounding (control volume) temperatures are expressed as T_d and T_CV, respectively. This source term represents energy transfer to the continuous phase from the aerosol as a result of mass exchange. For condensation, ṁ_p is negative, resulting in a positive latent heat term and energy gain, which increases the surrounding temperature. The second term in Eq. (8) accounts for the energy required to heat the discrete phase. This convective term has the opposite sign of the latent heat term, making it negative during condensation. However, the convective term is typically much smaller than the latent heat term, resulting in continuous phase heat gain during condensation.

2.3. Discrete phase transport equations

Based on experimental evidence, mean droplet sizes from 150 nm to approximately 3 μm are expected in the current ECG system. The associated polydisperse aerosol distributions can range from 25 nm through approximately 6 μm. To address this broad range of aerosol sizes and to accommodate the calculation of aerosol evaporation and condensation, a Lagrangian particle tracking method was employed (Longest, Kleinstreuer, & Buchanan, 2004; Longest & Xi, 2007). The Lagrangian transport equations can be expressed as

$$\frac{d{v}_i}{dt}=\frac{f}{{\tau }_p}(u_i-v_i)+g_i(1-\alpha )+f_{i,Brownian}\text{and}\frac{d{\chi }_i}{dt}=v_i\left(t\right)$$ (9a,b)

Here v_i and u_i are the components of the particle and local fluid velocity, respectively, g_i denotes gravity, and α is the ratio of mixture to droplet density ρ/ρ_d. The characteristic time required for a particle to respond to changes in fluid motion, or the particle relaxation time, is expressed as τ_p=C_cρ_pd_p²/18μ, where C_c is the Cunningham correction factor for submicrometer aerosols based on the expression of Allen and Raabe (1985) and μ the absolute viscosity. The pressure gradient or acceleration term for aerosols was neglected due to small values of the density ratio (Longest et al., 2004). The drag factor f, which represents the ratio of the drag coefficient to Stokes drag, is based on the expression of Morsi and Alexander (1972). The effect of Brownian motion on trajectories of submicrometer particles has been included as a separate force per unit mass term at each time step. This force has been calculated as

$$f_{i,Brownian}=\frac{{\varsigma }_i}{m_d}\sqrt{\frac{1}{{\tilde{D}}_d}\frac{2k^2{T}^2}{\Delta t}}$$ (10)

where Ϛ_i is a zero mean variant from a Gaussian probability density function, k is the Boltzmann constant, Δt the time step for particle integration, and m_d the mass of the droplet. Assuming dilute concentrations of spherical particles, the Stokes–Einstein equation was used to determine the diffusion coefficients D̃_v for various size droplets (Hinds, 1999).

To model the effects of turbulent fluctuations on droplet trajectories, a random walk method was employed (Crowe, Troutt, & Chung, 1996; Gosman & Ioannides, 1981; Matida, Nishino, & Torii, 2000). While deposition is not the focus of this study, a near-wall anisotropic correction to turbulent particle dispersion was also included (Longest, Hindle, Das Choudhuri, & Byron, 2007; Matida, Finlay, & Grgic, 2004).

The droplet evaporation and condensation model employed in this study is similar to previous approximations for salts (Ferron, 1977; Ferron et al., 1988; Hinds, 1999) and multicomponent aerosols (Li & Hopke, 1993; Longest & Kleinstreuer, 2005; Robinson & Yu, 1998). The heat and mass transfer relations for multicomponent hygroscopic droplets used in this study were previously reported by Longest and Xi (2008). This model employs a rapid mixing approach, which assumes conditions inside the droplet are constant and gradients are negligible compared with gradients in the air phase. Implementation of the rapid mixing model for respiratory aerosols was previously validated by Longest and Kleinstreuer (2005). The droplet model accounts for interdependent heat and mass transfer, which results in droplet heating during condensation and cooling during evaporation as a function of surrounding temperature. Mass and heat fluxes at the droplet surface are modified for non-continuum effects using the Knudsen correlation (Finlay, 2001; Fuchs & Sutugin, 1970). Blowing velocity effects were also considered (Longest & Xi, 2008).

The concentration of water vapor on the surface of droplets is expressed as

$$Y_{v,surf}=\frac{C_{w}K{P}_{v,sat}\left(T_d\right)}{\rho R_v{T}_d}$$ (11)

In the above expression, P_v,sat(T_d) is the temperature dependent saturation pressure of water vapor, calculated from the Antoine equation (Green, 1997). The concentration dependent water activity coefficient was calculated using Raoult's law for a two-component droplet expressed as (Hinds, 1999)

$$C_w={\left(1-i\frac{X_s}{X_w}\right)}^{-1}$$ (12)

In the equation above, X_s and X_w represent the solute and water mole fractions in the liquid droplet. The van't Hoff factor for albuterol sulfate was experimentally determined based on mass fractions ranging from 0.005 to 0.3, resulting in a value of i=0.865. The influence of the Kelvin effect on droplet surface concentration of water vapor is expressed as

$$K=\exp \left[\frac{4\sigma \left(T_d\right)}{d_p{\rho }_d{R}_v{T}_d}\right]$$ (13)

where σ(T) is the temperature dependent surface tension of the droplet and ρ_d the multicomponent droplet density. The Kelvin effect increases vapor pressure on the surface of droplets as the size is decreased below approximately 100 nm. As a result, the Kelvin effect enhances evaporation and reduces condensation.

2.4. Numerical methods

To solve the governing mass and momentum conservation equations in each of the cases considered, the CFD package Fluent 6 was employed. User-supplied Fortran and C programs were used for the calculation of initial flow and droplet profiles, hygroscopic droplet evaporation and condensation, near-wall anisotropic turbulence approximations, near-wall particle interpolation (Longest & Xi, 2007), Brownian motion (Longest & Xi, 2007), as well as heat and mass sources and sinks during two-way coupling. All transport equations were discretized to be at least second order accurate in space. For the convective terms, a second order upwind scheme was used to interpolate values from cell centers to nodes. The diffusion terms were discretized using central differences. A segregated implicit solver was employed to evaluate the resulting linear system of equations. This solver uses the Gauss–Seidel method in conjunction with an algebraic multigrid approach. The SIMPLEC algorithm was employed to evaluate pressure–velocity coupling. The outer iteration procedure was stopped when the global mass residual had been reduced from its original value by five orders of magnitude and when the residual-reduction-rates for both mass and momentum were sufficiently small. To ensure that a converged solution had been reached, residual and reduction rate factors were decreased by an order of magnitude and the results were compared. The stricter convergence criteria produced a negligible effect on both velocity and particle deposition fields. To improve accuracy, cgs units were employed, and all calculations were performed in double precision. For improved numerical accuracy, hexahedral grids were employed (Longest & Vinchurkar, 2007a; Vinchurkar & Longest, 2008; Fig. 1). Grid converged results based on negligible changes in velocity and temperature fields (< 1%) as well as negligible differences in outlet droplet size (< 5%) were established for a mesh consisting of 260,000 control volumes. Specifically, grids consisting of 150,000, 260,000, and 500,000 control volumes were considered. As a case study for an initial 560 nm aerosol and a humidity inlet temperature of 39 °C, final droplet sizes for the low, medium, and high resolution grids were 2.52, 2.58, and 2.55 μm, respectively. The 5% criterion for outlet droplet size was satisfied with the medium resolution grid for this case study and all others considered. It is estimated that a similar resolution of the flow field would require approximately one order of magnitude more tetrahedral control volumes (Longest & Vinchurkar, 2007a; Vinchurkar & Longest, 2008).

For the one-way coupled solution, particle trajectories were calculated within the steady flow fields of interest as a post-processing step. The integration scheme employed to solve Eq. (9) was based on the Runge–Kutta or implicit method (depending on particle size) with a minimum of 20 integration steps in each control volume. An error control routine was also employed to actively adapt the particle time step and maintain sufficient accuracy bounds (Longest et al., 2004). Doubling the number of integration steps within each control volume had a negligible (less than 1%) effect on cumulative particle deposition and growth values.

For the two-way coupled solutions, steady state flow fields were again assumed. Inlet droplet concentrations resulting in outlet concentrations (after mixing with the humidified air) of 1 × 10⁵ and 5 × 10⁵ part/cm³ were considered (Table 1). The number continuous phase iterations to discrete phase updates was set at 100. Doubling and halving this value had a negligible impact on the final aerosol size predicted. The coupled simulation was continued through 4000 continuous phase iterations, resulting in a minimum of 40 discrete phase updates. Convergence was determined based on mass, momentum, and energy residuals below 1 × 10^–5. Decreasing this convergence criterion by an order of magnitude and increasing the number of continuous phase iterations by a factor of two had a negligible impact on the results. In each size bin, 1000 computational droplets were simulated, resulting in 12,000 total trajectories for the 150 nm aerosol and 9000 trajectories for the 560 and 900 nm aerosols. Increasing the number of aerosols simulated in each bin by a factor of 10 had a negligible impact on predicted final particle sizes ( < 5%).

2.5. Experimental methods

The experimental determinations of initial and final aerosol sizes for the conditions shown in Table 1 were previously described in Longest et al. (2010). Briefly, nano-sized aqueous albuterol sulfate drug aerosols were generated using a small particle aerosol generator (SPAG- 6000, ICN Pharmaceuticals, Costa Mesa, CA). Droplet particle size was varied by altering the initial albuterol sulfate solution concentration and nebulizer/drying gas flow conditions. Droplet particle size distributions were determined by cascade impaction as the aerosol exited the nebulizer drying tube (initial size) and as the aerosol exited the condensational growth zone (final size). The impactors employed were the 10-stage MOUDI (MSP Corp, Minnesota, MN) and the 8-stage Andersen (Graseby-Andersen Inc., Smyrna, GA) as appropriate for the expected particle size distributions. For the initial particle size determination, humidified co-flow air (99% RH) was supplied to the impactor, which was placed in an environmental chamber (Espec, Environmental Cabinet, Grand Rapids, MI) and held at constant temperature and humidity conditions of 25 °C and 99% RH. For the final particle size determination, the tubular geometry and impactor were maintained at a constant temperature (Espec Environmental Cabinet, Grand Rapids, MI) corresponding to the temperature of the incoming aerosol mixture. The aerosol particle concentration was also determined at the entrance to the cascade impactor using a condensation particle counter (CPC 3022A, TSI Inc, Shoreview, MN) sampling at 25 cm³/s. Chemical analysis of the albuterol sulfate drug deposition on each impactor plate was used to determine the initial and final aerosol aerodynamic particle size distributions. The mass median aerodynamic diameter (MMAD) was defined as the particle size at the 50th percentile on a cumulative percent mass undersize distribution (D50) using linear interpolation. Five replicates of each experiment were performed.

3. Results

3.1. Continuous phase variables

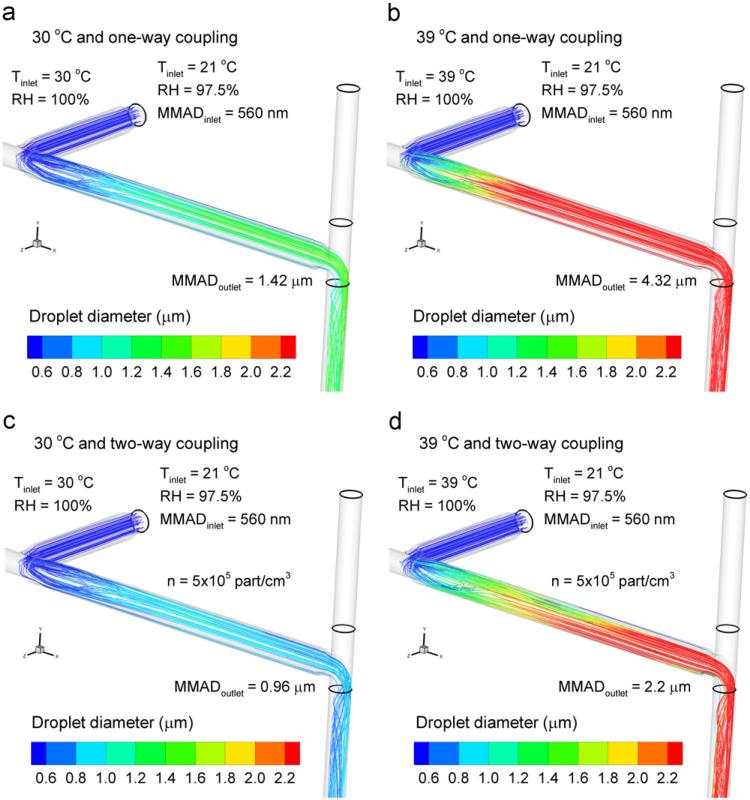
Temperature fields for inlet saturated air conditions of 30 and 39 °C are shown in Fig. 2 based on horizontal and vertical slices through the condensation growth zone. One-way coupled results are shown in Fig. 2a and b, whereas two-way coupled results for a 560 nm aerosol and an outlet concentration of 5 × 10⁵ part/cm³ are displayed in Fig. 2c and d. Considering the one-way coupled results, increasing the inlet humidified air temperature from 30 °C (Fig. 2a) to 39 °C (Fig. 2b), results in a mean outlet temperature increase of approximately 6 °C. Outlet temperatures are based on mass-flow-weighted values taken at the exit of the condensation growth tube. For an inlet temperature of 30 °C, including the effect of two-way coupling increases the outlet temperature by 0.1 °C (Fig. 2a vs. 2c). An increase in continuous phase temperature is expected due to condensational aerosol growth. As shown in Eq. (8), this increase in continuous phase temperature occurs due to droplet heating during condensation and the convective effect of the warmer aerosol on the continuous phase. Considering an inlet temperature of 39 °C, including two-way coupling increases the outlet temperature by approximately 1 °C (Fig. 2b vs. 2d). Furthermore, an increase in the temperature field due to two-way coupling is visually evident for the 39 °C inlet case. This increase in temperature will result in reduced relative humidity (RH) values and reduced condensational growth of the aerosol.

Fig. 2.

Midplane temperature fields for the 560 nm aerosol with humidified air inlet temperatures and coupling conditions as follows: (a) 30 °C and one-way coupling, (b) 39 °C and one-way coupling, (c) 30 °C and two-way coupling, and (d) 39 °C and two-way coupling. The aerosol number concentration for the two-way coupled cases (c, d) was n=5 × 10⁵ part/cm³.

Relative humidity values based on Eq. (3) are reported in Fig. 3 for inlet temperatures of 30 and 39 °C under one-way and two-way coupled conditions. The two-way coupled results are based on a 560 nm aerosol and an outlet concentration of 5 × 10⁵ part/cm³ (Fig. 3c and d). Cooling due to mixing with the aerosol inlet stream of 21 °C results in supersaturated (RH > 100%) conditions throughout the condensation growth zone at both inlet temperatures for one-way coupling (Fig. 3a and b). The higher inlet temperature of 39 °C holds significantly more water vapor at an inlet RH of 100% compared with the 30 °C inlet case. As a result, the RH values in the 39 °C inlet case are higher with a mass-weighted exit value of 104.7% (Fig. 3b). Considering the 30 °C inlet temperature, including the effects of two-way coupling reduces condensation growth zone and outlet RH values by approximately 1%. This reduction is due to (i) an increase in temperature associated with condensation as observed in Fig. 2 and (ii) depletion of the continuous phase water vapor due to aerosol growth. For the case of the 39 °C inlet temperature, two-way coupling has a larger effect on the RH field (Fig. 3b vs. 3d) compared with the lower inlet temperature. Including two-way coupling reduces the outlet RH by approximately 2.6% (Fig. 3d), which is expected to have a significant impact on outlet particle size. Furthermore, the RH field with coupling included and an inlet temperature of 39 °C is observed to have an area of subsaturated conditions. This subsaturated region is likely because of rapid heating of the aerosol due to high humidity exposure (RH ~ 110%) and subsequent reduction in RH values. However, the RH returns to supersaturated conditions through a majority of the condensation growth zone.

Fig. 3.

Midplane relative humidity (RH) fields for the 560 nm aerosol with humidified air inlet temperatures and coupling conditions as follows: (a) 30 °C and one-way coupling, (b) 39 °C and one-way coupling, (c) 30 °C and two-way coupling, and (d) 39 °C and two-way coupling. The aerosol number concentration for the two-way coupled cases (c, d) was n=5 × 10⁵ part/cm³.

Droplet trajectories for the initially 560 nm aerosol are displayed in Fig. 4 for inlet temperatures of 30 and 39 °C. One-way coupled results are shown in Fig. 4a and b, whereas two-way coupled results are shown in Fig. 4c and d based on an outlet aerosol concentration of 5 × 10⁵ part/cm³. Only approximately 200 droplet trajectories are shown in each panel for visualization. For the uncoupled results, the supersaturated RH field in the condensation growth zone results in outlet MMADs of 1.42 and 4.32 μm for inlet temperatures of 30 and 39 °C, respectively. The trajectory paths indicate that a majority of this growth occurs very rapidly near the first connection tee due to the maximum RH values found in this location. Considering the inlet temperature of 30 °C, two-way coupling is observed to significantly reduce the final particle size to 0.96 μm (Fig. 4c). Moreover, some evaporation is observed near the end of the condensation growth zone with an inlet temperature of 30 °C and two-way coupling. For an inlet temperature of 39 °C, two-way coupling is observed to restrict the outlet particle size to 2.2 μm (Fig. 4d). Furthermore, increasing two-way coupling effects slows the rate of droplet size increase such that steady growth is observed over more of the condensation growth zone (Fig. 4d).

Fig. 4.

Sample droplet trajectories for an initially 560 nm monodisperse aerosol with humidified air inlet temperatures and coupling conditions as follows: (a) 30 °C and one-way coupling, (b) 39 °C and one-way coupling, (c) 30 °C and two-way coupling, and (d) 39 °C and two-way coupling. The aerosol number concentration for the two-way coupled cases (c, d) was n=5 × 10⁵ part/cm³.

Numerical predictions of outlet aerosol distributions after condensational growth are presented in Fig. 5 as a function of initial MMAD size for two-way coupling (aerosol concentration of 1 × 10⁵ part/cm³). The distributions are presented in terms of mass fraction per micrometer vs. midpoint values of the ACI size fractionation bins. For all initial sizes, the inlet temperature of 25 °C does not shift the aerosol distribution from the original conditions by a significant amount. Due to coupling, outlet sizes for inlet temperatures of 30 and 39 °C are approximately 1.7 and 2.6 μm, respectively. Moreover, an increase in the first size bin is observed in some cases, as with an initial 560 nm aerosol and an inlet temperature of 30 °C. This somewhat bimodal distribution may be the result of some aerosol evaporation, as observed in Fig. 4. One exception is observed with the 150 nm aerosol at an inlet temperature of 30 °C, which does not appear to grow to a mean size of 2 μm. This reduction in growth may be due to the initially small droplet size and the Kelvin effect. For the case of the 150 nm aerosol and 39 °C, the potential for growth may be sufficient to overcome the Kelvin effect, thereby allowing the aerosol to reach a size near 2 μm, as expected.

Fig. 5.

Polydisperse aerosol size change for a range of humidified air inlet temperatures including two-way coupling effects (n=1 × 10⁵ part/cm³) and initial aerosol mass median aerodynamic diameters (MMAD) of (a) 150, (b) 560, and (c) 900 nm.

A comparison of experimentally determined and numerically predicted final aerosol MMADs is presented in Table 2 based on one-way coupled simulations. Relative percent errors are also presented in Table 2, calculated as |experimental value–numerical value|/experimental value × 100. For inlet temperatures of 25 and 30 °C and one-way coupling, the percent error values range from approximately 15% to 40%. Significantly greater percent errors are observed for an inlet temperature of 39 °C and one-way coupling, ranging from 60% to 230%. To better quantify the potential for two-way coupling, the non-dimensional analysis of Finlay (1998) was also applied. Finlay (1998) defines a non-dimensional parameter γ as the ratio of particle mass to the mass available for condensation until equilibrium is reached. A value of γ greater than 0.1 indicates that two-way coupling is significant. As shown in Table 1, the analysis of Finlay (1998) indicates that two-way coupling is significant for the 560 and 900 nm aerosols at most inlet temperatures based on the experimentally determined aerosol number concentrations.

Table 2.

Comparison of numerical and experimental final MMADs based on a dilute aerosol assumption (one-way coupled growth).

Initial aerosol size (nm)	Humidified air inlet temp. (°C)	Experimental final aerosol size (μm)a	Numerical final aerosol size (μm)	Percent error (%)	Two-way coupling expectedb
150	25	0.43 (0.1)	0.36	16.3	No
	30	0.99 (0.1)	0.57	42.4	No
	39	1.23 (0.1)	4.04	228.5	No
560	25	0.61 (0.0)	0.59	3.3	No
	30	2.26 (0.2)	1.42	37.2	Yes
	39	2.66 (0.1)	4.32	62.4	Yes
900	25	1.16 (0.1)	0.98	15.5	Yes
	30	2.24 (0.1)	1.89	15.6	Yes
	39	2.63 (0.1)	4.40	67.3	Yes

^aExperimental standard deviations (SDs) are shown in parentheses based on n=5.

^bTwo-way coupling predicted based on γ greater than or equal to approximately 0.1 (Finlay, 1998).

The results of two-way coupling on predicted final MMAD sizes are reported in Table 3. The experimental outlet aerosol concentrations for each in vitro case considered are also reported. The predicted results are based on linear interpolations between numerical values for concentrations of 1 × 10⁵ and 5 × 10⁵ part/cm³ to the experimental outlet concentrations. For cases where two-way coupling is expected (Table 2), the coupled simulations either significantly reduced or did not affect the percent error values in comparison with the experimental results. For example, percent errors of 3% and 0.8% are observed for the cases of 560 and 900 nm aerosols at an inlet temperature of 39 °C with two-way coupling. However, the largest percent errors for two-way coupled results ( ~40%) occurred for the 150 nm aerosol. The numerical model consistently underpredicted the growth of this aerosol size compared with the experiments.

Table 3.

Comparison of numerical and experimental final MMADs based on limited aerosol growth due to two-way coupling.

Initial aerosol size (nm)	Humidified air inlet temp. (°C)	Experimental concentration (part/cm3)a	Experimental final aerosol size (μm)b	Numerical final aerosol size (μm)c	Percent error (%)
150	25	5.8 × 104	0.43 (0.1)	0.36d	16.3
	30	5.8 × 104	0.99 (0.1)	0.57d	42.4
	39	6.3 × 104	1.23 (0.1)	1.75	42.3
560	25	1.2 × 105	0.61 (0.0)	0.59d	3.3
	30	1.2 × 105	2.26 (0.2)	1.33	41.1
	39	1.2 × 105	2.66 (0.1)	2.58	3.0
900	25	2.8 × 105	1.16 (0.1)	0.98d	15.5
	30	2.9 × 105	2.24 (0.1)	1.70	24.1
	39	2.8 × 105	2.63 (0.1)	2.65	0.8

^aMeasured at the ACI inlet.

^bExperimental standard deviations (SDs) are shown in parentheses based on n=5.

^cNumerical value interpolated from 1 × 10⁵ and 5 × 10⁵ part/cm³ values to experimental concentrations.

^dUnchanged from one-way coupled solution.

The effect of aerosol concentration on the final growth ratio (d/d_o) is presented in Fig. 6. Based on the results of Table 2, two-way coupling is expected for the 560 nm aerosol and 39 °C inlet temperature. For these conditions, the CFD results predict a gradual decrease in d/d_o over the range of concentrations. Agreement between the in vitro experimental results and CFD predictions is also clearly evident in Fig. 6.

Fig. 6.

Effect of concentration on the growth ratio (d/d_o) of the 560 nm aerosol at a humidified air inlet temperature of 39 °C.

4. Discussion

In this study, a CFD model was developed, tested, and used to explore ECG for potential application in respiratory drug delivery. The ECG concept proposes the inhalation of submicrometer aerosols that avoid deposition in the mouth–throat region and are then retained in the lower airways following enhanced condensational growth. Both numerical and experimental results indicated that each of the three submicrometer aerosols demonstrated significant growth. Specifically, for saturated airstream inlet temperatures of 30 and 39 °C, submicrometer aerosols (> 150 nm) at dilute concentrations increased in size to approximately 2 and 4 μm, respectively. Considering two-way coupling effects for realistic pharmaceutical aerosol concentrations, saturated inlet temperatures of 30 and 39 °C and submicrometer initial sizes above 150 nm resulted in outlet sizes of approximately 1.5 and 2.6 μm, respectively. Final droplet sizes of the initially 150 nm aerosol were smaller than the 560 and 900 nm initial cases, potentially due to the Kelvin effect. It was observed that the final droplet size was largely influenced by initial saturated air temperature and number concentration, and was less dependent on initial aerosol size. By including the effects of two-way coupling in the numerical model, relatively good agreement with the in vitro results was achieved. In particular, two-way coupling improved numerical predictions at an inlet temperature of 39 °C and initial sizes of 560 and 900 nm from percent errors on the order of 100% to approximately 1%. However, the model consistently underpredicted growth of the initial 150 nm aerosol. Details provided by the developed CFD model indicated that enhanced condensational growth may be an effective respiratory drug delivery approach using the tested temperature and RH conditions (39 °C and 100% RH). However, future studies are needed to consider more realistic geometries and wall boundary conditions.

Two-way coupling between the continuous and discrete phases is known to influence condensation and evaporation of aerosols at concentrations consistent with respiratory drug delivery (Finlay, 1998; Finlay & Stapleton, 1995). As indicated in this study, inclusion of two-way coupling effects in the CFD model significantly improved agreement with experimental results. However, modeling heat and mass two-way coupling significantly increases the complexity of the model. It was observed that the non-dimensional analysis of Finlay (1998) effectively predicted when two-way mass coupling should be considered (Table 2). However, one exception occurred for the case of a 150 nm aerosol and an inlet temperature of 39 °C. Under these conditions, the non-dimensional analysis of Finlay (1998) indicates that the γ parameter is two orders of magnitude too small for mass coupling to occur. However, inclusion of both mass and thermal coupling in the CFD model improved agreement with the experimentally determined outlet size of 1.23 μm from predictions of 4.04 μm (one-way coupling) to 1.75 μm (two way coupling).

Results of the current study indicate that two-way coupling may limit aerosol size increase during ECG by two mechanisms. First, two-way coupling may arise as a result of relatively high aerosol concentration compared with available mass of water vapor, as described by Finlay (1998). A second potential mechanism is thermal two-way coupling. As observed in Fig. 2d, condensation onto the aerosol increases the temperature of both the discrete and continuous phases. An increase in gas-phase temperature will raise the amount of water vapor that can be held in air. As a result, the RH surrounding the droplets is reduced (Fig. 3d). A reduction in RH in conjunction with droplet heating and an increase in droplet surface vapor pressure will clearly slow the condensation process. Results of Longest and Xi (2008) showed that changing the RH value by several percent just above saturated conditions had a dramatic effect on the rate of aerosol growth. Therefore, thermal two-way coupling may also limit the size increase of droplets during ECG. It is suggested that thermal two-way coupling, which is considered in the CFD model, is responsible for limiting the size increase of the 150 nm aerosol at an inlet temperature of 39 °C when two-way mass coupling is not expected.

While the effect of two-way coupling significantly improved agreement between experimental results and numerical predictions, some differences remain. In particular, percent errors were largest (15–40%) for the case of the 150 nm aerosol. Furthermore, the two-way coupled numerical model underpredicted the in vitro droplet sizes in almost all cases. As a result, the model provides a conservative estimate of final droplet size growth. Reasons for these differences could include some size change within the impactor, the assumption of a thermally insulated wall, the use of Raoult's law, and limited data on the hygroscopic behavior of albuterol sulfate. As described, numerical estimates of final size were based on conditions near the impactor inlet. However, finite transport times within the impactor may have allowed for continued aerosol growth. This artifact was likely greatest for the smallest aerosol size considered, which remains airborne longer as the droplets travel to lower impactor stages. Droplet trajectories and transport within the multi-nozzle ACI are very complex (Vinchurkar et al., 2009), and were not considered in this study. The outlet aerosol size is also expected to be influenced by wall temperature conditions in the condensational growth zone. In the numerical model, the tube was assumed to be thermally insulated. However, minor heat losses at the wall in the experiments will reduce surface temperature, resulting in larger final aerosol sizes. Finally, an experimentally determined van't Hoff factor was implemented in Raoult's law to predict the activity coefficient of the albuterol sulfate solution. Raoult's law is known to be most accurate for dilute concentrations of drug solute, which is the case as the aerosol increases in size. However, initial droplet sizes were estimated to have high drug concentrations.

In order to advance the ECG approach to clinical applications, future studies are needed to consider the effects of in vivo boundary conditions, more realistic respiratory geometries, and transient breathing. The current model assumed thermally insulated and dry walls. In contrast, temperature of the respiratory airways is often estimated to vary from approximately 34 °C in the mouth to 37 °C in the third bifurcation (Ferron et al., 1984; Kaufman & Farahmand, 2006; McFadden, Pichurko, & Bowman, 1985). Therefore, inhalation temperatures of 25 and 30 °C are not expected to be effective for ECG drug delivery in vivo. However, an inhalation temperature of 39 °C was found to produce significant growth, is above body temperature, and provided the best match between CFD predictions and in vitro results. The current geometry provides a residence time of approximately 0.2 s, which is equivalent to the time it takes a droplet to pass from the mouth to the first bifurcation at an inhalation rate of 30 L/min. However, more realistic MT and tracheobronchial airway geometries are needed to better determine where size increase occurs and how to optimize the parameters of interest for minimal MT deposition. Finally, transient breath profiles may influence saturation and supersaturation conditions in the extrathoracic and tracheobronchial airways. These transient conditions need to be considered to optimize the ECG process for in vivo drug delivery.

The CFD model developed in this study of ECG was found to provide good approximations of final aerosol sizes compared with in vitro data. Results of this study and the previous in vitro study of Longest et al. (2010) indicate that ECG may be an effective respiratory drug delivery approach for minimizing MT deposition and maximizing aerosol retention in a safe and simple manner. The CFD model developed in this study provided valuable transport characteristics related to the ECG approach, which were not available from the experiments. For example, it was found that two-way coupling slowed the rate of condensational growth, which may be beneficial for ensuring droplets remain sufficiently small to pass through the MT region. Furthermore, both mass and thermal two-way coupling can limit the final aerosol size obtained. In future studies, the developed CFD model will be used to explore the effects of in vivo boundary conditions, more realistic respiratory geometries, and transient breathing. Based on these analyses, optimal conditions will be sought for ECG respiratory drug delivery systems that can minimize MT deposition and maximize lung retention, or that can target deposition to specific regions of the respiratory tract.