Pathways and populations: Stereo-electronic insights into the exocyclic torsion of 5-hydroxy-methyl-tetrahydropyran

Abstract

High level ab initio computations in vacuum and with the IEFPCM implicit solvent model are carried out on 5-hydroxy-methyl-tetrahydropyran to investigate the effects of water on the exocyclic torsional surface. Rotamer populations evaluated from the ω (C-C-C-O), θ (C-C-C-O) solvent surface agree almost quantitatively with experimental values for the closely related methyl 4-deoxy-α-D-xylo-hexopyranoside. Potentials of mean force obtained from the two surfaces show substantial solvent stabilization of the TG (ω = 180 ± 60°) rotamer and the barriers at ω = 120 and 240°, but solvent destabilization at the cis barrier (ω = 0°). Natural bond orbital analyses indicate that energetics of these effects are largely explained by overstabilization of the vacuum GT (ω = 60 ± 60°) and GG (ω = 300 ± 60°) rotamers. Solvent stabilization of θ conformations provides entropic stabilization.

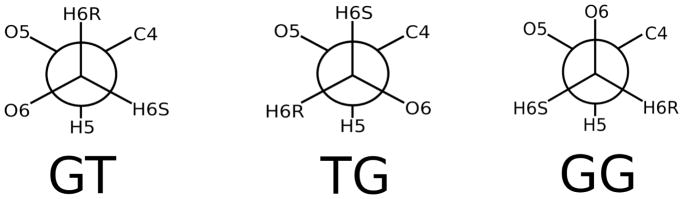
The common form of hexoses such as glucose is a six membered ring (or pyranose) with an exocyclic primary alcohol group (-CH₂OH). While the ring is relatively rigid, the exocyclic torsion angle readily isomerizes and samples the three conformational states denoted GT, TG, and GG (Figure 1).¹ This flexibility allows the primary alcohol in polysaccharides to form an array of intramolecular and intermolecular hydrogen bonds. Examples include the O-antigen of E. coli,² cellulose^3,4 and the antithrombin-heparin complex.⁵ Along with sugar and linkage type, such hydrogen bonds and the overall flexibility of the torsion angles contribute to the ability of polysaccharides, glycopeptides and glycolipids to play their critical structural and functional roles in biology.

Figure 1.

Newman projections of the dominant (GT, TG and GG) rotamers of pyranoses and related compounds.

Ultrasound,⁶ IR,⁷ NMR,^7–11 CD,¹² and neutron diffraction¹³ studies indicate substantial variation in hydroxymethyl conformation and dynamics for exocyclic torsions of different mono- and disaccharides. In addition, numerous computational studies have been carried out, primarily with density functional theory, to address the energetics of hydroxymethyl conformation.^14–20 Nevertheless, a satisfactory understanding of the effects that govern hydroxymethyl structure and dynamics is still not available. As recently described by Naidoo et al.,²¹ present carbohydrate force fields yield dramatically different surfaces for the glucose exocyclic torsion. The importance of internal hydrogen bonding between the hydroxymethyl and the endocyclic oxygen is also under debate.^7,20 Consequently, there is a critical need to apply high level quantum mechanical calculations to provide a through description of the interactions determining the conformational surface in different solvent conditions.

Although for molecules such as alkanes the ab initio surfaces can be used directly to reproduce condensed phase properties,²² biomolecules typically require adjustments for satisfactory agreement with experiment.²³ Unfortunately, it is presently not possible to carry out calculations at a high level of theory and basis set with sufficient water and adequate sampling of the hydroxyl group rotamers to model a carbohydrate/water solution. This limitation motivated the approach recently applied to study the glycosidic linkage of the model carbohydrate 2-ethoxy tetrahydropyran.²⁴ Calculations were performed at the highest level of theory practical, the effects of water were approximated with an implicit solvation model, and primary hydroxyls did not have to be considered. This report addresses the exocyclic torsion of carbohydrates using the same approach: conformations on the ω,θ surface of 5-hydroxy-methyl-tetrahydropyran (Figure 2, I) were optimized at the MP2/cc-pVTZ level of theory, and the IEFPCM model was applied at each point (without further geometry optimization) to account for solvation.²⁵ Calculated rotamer populations of the vacuum and solvated surfaces are compared with experimentally determined populations from the closely related, methyl 4-deoxy-α-D-xylo-hexopyranoside (Figure 2, II).⁴ The substantial differences between the vacuum and solvent surfaces, including the barrier heights, are then simply explained by a natural bond orbital (NBO) analysis.^26,27 The Supporting Information presents results from a higher level of theory for the vacuum surface using the recently developed Layered Composite Method (LCM)²⁴ to rule out significant methodological artifacts. The magnitudes of commonly neglected terms in the IEFPCM model are also provided.

Figure 2.

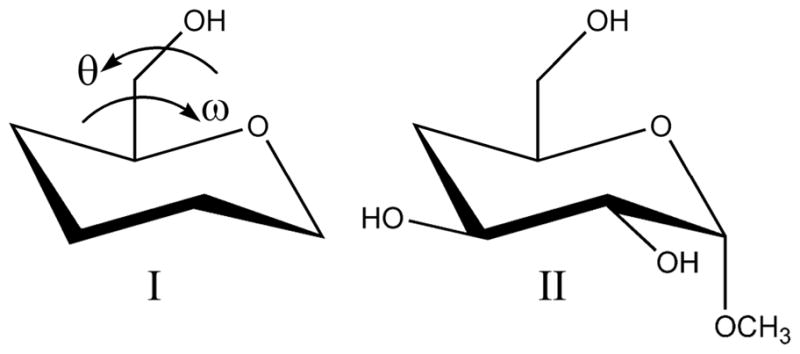
5-hydroxy-methyl-tetrahydropyran (I) and methyl 4-deoxy-α-D-xylo-hexopyranoside (II). Dihedral surface scans (Figure 2) were performed on the ω (O-C-C-O) and θ (C-C-O-H) angles.

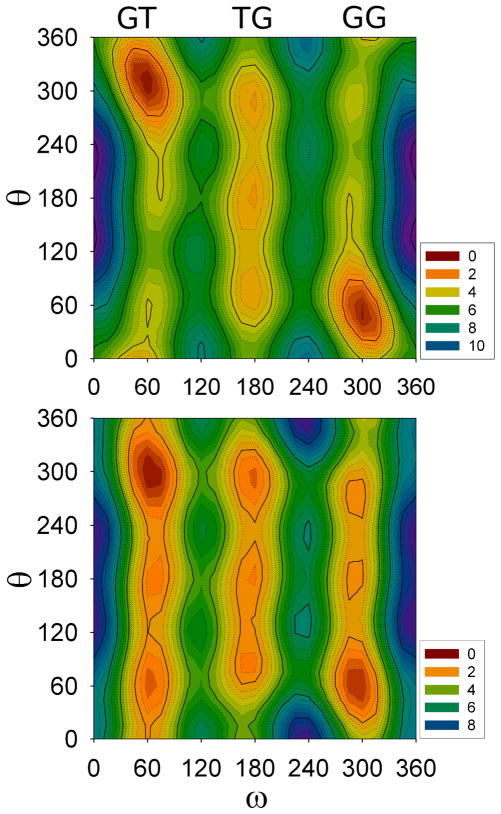
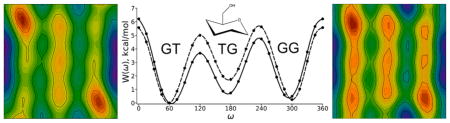
Figure 3 plots E(ω,θ), the potential energy surface for vacuum (top), and W(ω,θ), the potential of mean force (PMF) for implicit solvent; the latter is a PMF because the solvent degrees of freedom are implicitly averaged. Both surfaces exhibit three rotamers along ω (O5–C5-C6-O6). These are denoted GT (ω = 60± 60°), TG (ω = 180 ± 60°) and GG (ω = 300 ± 60°) (see Figure 1 for Newman projections). The θ (C5-C6-O6-H) surface has more stable minima in solvent than in vacuum.

Figure 3.

Dihedral energy surface computed in vacuum at the MP2/cc-pVTZ level of theory (top), and potential of mean force for implicit solvent at MP2/cc-pVTZ/IEFPCM//MP2/cc-pVTZ (bottom). Points were evaluated at 15° intervals of ω and θ; contours in kcal/mol.

To proceed, p(ω), the probability of a particular conformation in ω, was obtained by Boltzmann averaging over θ; i.e., for vacuum

$$p(\omega )=\sum _{\theta }exp(-E(\omega ,\theta )/RT)/\sum _{\omega ,\theta }exp(-E(\omega ,\theta )/RT)$$

and for implicit solvent

$$p(\omega )=\sum _{\theta }exp(-W(\omega ,\theta )/RT)/\sum _{\omega ,\theta }exp(-W(\omega ,\theta )/RT)$$

where R is Boltzmann’s constant, T is temperature; the double sum in the denominator of the preceding equations was obtained from all 576 points on each surface. W(ω) were evaluated directly from each surface as -RT ln p(ω). Table 1 compares the calculated populations for GT, TG and GG in vacuum and solvent. While the populations of GT are comparable, TG is substantially more stable in solvent (and thereby GG is less stable). The agreement of the solvent ab initio populations of Compound I and the experimental populations for Compound II is near quantitative. Although I and II are not identical, this result implies that the underlying interactions modulating their exocyclic torsional surfaces are the same. Populations from the higher level LCM(3,4) treatment are comparable (see Supporting Information for further discussion).

Table 1.

Populations computed at MP2/cc-pVTZ (vac) and MP2/cc-pVTZ/IEFPCM//MP2/cc-pVTZ (sol) for Compound I; experimental values⁴ for Compound II; and stabilization energies associated with the oxygen lone pair orbitals.

Populations (%)a				Orbital Stabilization (kcal/mol)b
	Compound I		Compound II
State	Vac	Sol	Experiment	ω,θ (°)	ΔE
GT	58 (63)	55 (59)	53	60,315 120,285	0.58 0.02
TG	4 (5)	19 (20)	18	180,285 240,75	−0.04 −0.05
GG	38 (32)	26 (21)	29	300,45 0,360	0.50 1.04

^aPopulation values in parenthesis are from vacuum and solvent corrected LCM(3,4).

^bFrom NBO analyses. ΔE is the sum of E(vac)-E(sol) for all interactions more than 0.5 kcal/mol.

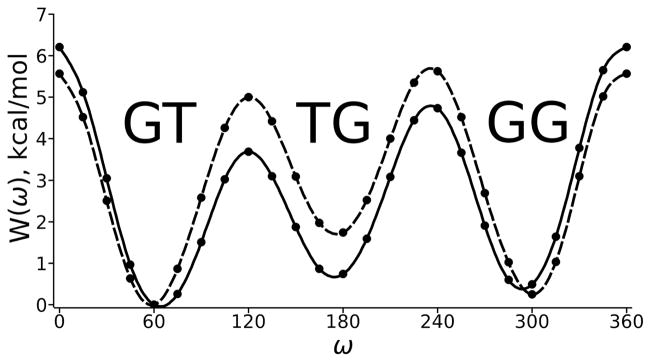
W(ω) are plotted in Figure 4. There is an apparent solvent induced stabilization of TG and the barriers at ω = 120° and 240°. In contrast, the barrier at ω = 0° (cis) is higher in solvent. This implies that transitions over the cis barrier are expected to be rare, and the primary pathway from GT to GG passes though the TG state. In vacuum, roughly 50% of the GG to GT transitions would proceed over the cis barrier. The solvent induced stabilization of TG is important for accurate modeling of carbohydrate structure. For example, although glucose’s dominant conformation in water is the GT state, cellulose (a homopolymer of glucose) fibers are exclusively TG,^3,4 thereby facilitating intra-and inter-chain hydrogen bonding.

Figure 4.

Vacuum (MP2/cc-pVTZ, dashed line) and solvent corrected (MP2/cc-pVTZ/IEFPCM//MP2/cc-pVTZ, solid) 1-dimensional potential of mean force curves for Compound I. The PMF are set to zero at their minima (ω = 60°).

It is clear from the ω,θ surfaces (Figure 3) that the free energy shifts observed in the PMF (Figure 4) can be attributed to both energetic stabilization and favorable entropy changes. In particular, four new θ states in the GT and GG wells, which were not accessible on the vacuum surface, are populated on the solvated surface. Furthermore, the GT/TG and TG/GG barriers on the PMF are entropically stabilized because transitions that are energetically unfavorable on the vacuum surface are accessible. Specifically, the barrier at ω,θ ≈ 120°,300° is the only likely route from GT to TG in vacuum, while there are three possible transition states (120°, 60°; 120°, 180°; 120°, 300°) in solvent.

To examine the solvent induced effects in greater detail NBO analyses were performed on the minima and transition states listed in Table 1. The last column in Table 1 lists the total differences of vacuum and solvent stabilizations (ΔE) for the lone pair of the exocyclic oxygen, O(LP). There is essentially no difference in stabilization at ω = 120°, 180° and 240°; rather, there is overstabilization of the vacuum states at ω = 0°, 60° and 300°. Taken together with the entropic arguments presented earlier, these ΔE largely account for the differences in the vacuum and solvent PMF curves (Figure 4).

A detailed analysis of the NBO results (Supporting Information) indicates that O(LP) stabilization with the C-C anti-bonding orbital is significantly increased when rotating from GT to TG. However, a larger loss of stabilization results from hyperconjugative interactions with adjacent C-H anti-bonding orbitals. Both surfaces show destabilization, though the magnitude in vacuum is larger. This leads to an effective solvent induced stabilization for those states with ΔE ≈ 0. The opposite occurs at the cis barrier (ω = 0°/360°, ΔE ≈ 1), where loss of solvent state O(LP)/C-H anti-bonding interactions relative to GT and GG leads to the net destabilization of approximately 0.5 kcal/mol observed in Figure 4.

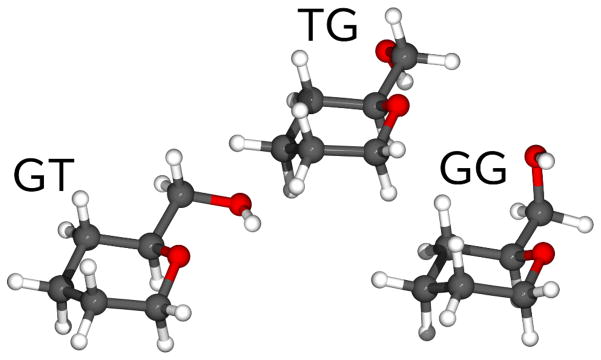
There is active debate regarding the nature of solvent and rotameric stabilization. In particular, it has been postulated that rotamer populations are governed primarily by intra-molecular hydrogen bonding in the GT and GG rotamers.²⁰ Examination of the lowest energy geometries from the present surfaces indicates that intra-molecular hydrogen bonds, if present, are poor (Figure 5). The O···H distances in GT and GG are 2.2 and 2.5 Å, respectively, and the O-H···H angles are 112°. These are weak hydrogen bonds on the Jeffery scale²⁸ (distances of 2.2–3.2 Å and bond angles of 90°–150°). The interactions between the hydroxyl, hydrogen and the endocyclic oxygen may be better described as weak electrostatic attraction. Hence, the current results argue against rotameric stabilization by strong intra-molecular hydrogen bonding. Rather, rotamer populations and pathways are governed by a mixture of structural and stereo-electronic effects.

Figure 5.

Lowest energy GT, TG and GG rotomers of 5-hydroxy-methyl-tetrahydropyran (I). The unfavorable geometry for the purported hydrogen bond in GT (θ =315°) and GG (θ =45°) is evident; there is no hydrogen bond in TG.

In addition to providing insight into solvent induced effects on rotamer populations, the results presented here can aid in the development of carbohydrate force fields. Figures 3 and 4 show that the adjustments to vacuum generated surfaces for Compound I are not obvious: some barriers are lowered by solvent and others are raised. Many force fields have large barriers between GT and TG.^21,29 This limits transitions that occur through TG and favors transitions over cis, in contrast to the results presented here. While the present results are admittedly based on a relatively simple treatment of solvent, as shown by the NBO analysis they are physically reasonable. At a minimum, they could be used to inform the direction of adjustments which could then be tested against experimental target data.⁶ It is possible that an experimental system could be designed to distinguish between these pathways.

In summary, the stereo-electronic and entropic stabilization of the THP-CH₂-OH exocyclic torsion leads to significant differences in the vacuum and solvent ab initio surfaces. Rotamer populations from the solvent surface agree well with experimental results from a similar compound, and transitions over the cis barrier are rare. NBO analyses indicate that both vacuum and solvent surfaces are destabilized with the solvent surface suffering less from this effect and inducing an effective stabilization.