A Model of Redox Kinetics Implicates the Thiol Proteome in Cellular Hydrogen Peroxide Responses

Abstract

Hydrogen peroxide is appreciated as a cellular signaling molecule with second-messenger properties, yet the mechanisms by which the cell protects against intracellular H₂O₂ accumulation are not fully understood. We introduce a network model of H₂O₂ clearance that includes the pseudo-enzymatic oxidative turnover of protein thiols, the enzymatic actions of catalase, glutathione peroxidase, peroxiredoxin, and glutaredoxin, and the redox reactions of thioredoxin and glutathione. Simulations reproduced experimental observations of the rapid and transient oxidation of glutathione and the rapid, sustained oxidation of thioredoxin on exposure to extracellular H₂O₂. The model correctly predicted early oxidation profiles for the glutathione and thioredoxin redox couples across a range of initial extracellular [H₂O₂] and highlights the importance of cytoplasmic membrane permeability to the cellular defense against exogenous sources of H₂O₂. The protein oxidation profile predicted by the model suggests that approximately 10% of intracellular protein thiols react with hydrogen peroxide at substantial rates, with a majority of these proteins forming protein disulfides as opposed to protein S-glutathionylated adducts. A steady-state flux analysis predicted an unequal distribution of the intracellular anti-oxidative burden between thioredoxin-dependent and glutathione-dependent antioxidant pathways, with the former contributing the majority of the cellular antioxidant defense due to peroxiredoxins and protein disulfides. Antioxid. Redox Signal. 13, 731–743.

Introduction

An accumulation of reactive oxygen species within the cell can lead to oxidative stress, resulting in changes in the redox state of many proteins (46). Although cellular processes such as growth, proliferation and apoptosis are controlled by the overall redox state of the cell (41), high levels of ROS can be toxic (24, 42). The oxidant hydrogen peroxide (H₂O₂) is of great interest to researchers because it is continuously produced as a result of cellular metabolism, diffuses across cellular membranes, has a longer half-life than other oxidative species, and reversibly oxidizes protein thiols (3, 9, 24).

The apparent paradox between the role of H₂O₂ as a cellular signaling molecule and its role as a cellular toxin appears to be highly dependent on its intracellular concentration, and the resolution of several key questions regarding how mammalian cells handle peroxide levels will facilitate our understanding of this paradox: Which antioxidant mechanisms exert the most control over the removal of hydrogen peroxide from the cell, and how could this be affected by intervention? How independent are the redox couples from one another during oxidative stress? What role does the global protein thiol pool play in antioxidant defense? To address these questions accurately, quantitative computational modeling that integrates the known mechanisms by which mammalian cells control intracellular H₂O₂ accumulation during periods of oxidative stress is necessary. This form of analysis addresses whether our current knowledge can quantitatively account for observed cellular behavior. Ultimately, modeling can provide additional insight into the discrimination of the physiologic function of H₂O₂ from its pathologic role.

Researchers have a general understanding of the key players involved in a cell's ability to maintain its intracellular redox state, and most models of H₂O₂ depletion can accurately describe one or two aspects of this system (3, 28, 40, 42). A previous mathematical model developed by Antunes and Cadenas (3), for example, offered great insight into the enzymatic contributions of glutathione peroxidase (GPx) and catalase to the development of peroxide gradients across cellular membranes. Antunes' model provided a new quantitative estimate for the H₂O₂ membrane permeability coefficient, one that was an order of magnitude smaller than that cited in the literature (28, 42). Although Antunes' model provided novel findings, the model did not consider the enzymatic contribution of peroxiredoxins and the nonenzymatic contribution of protein thiols. Since the publication of Antunes' model, multiple studies have revealed that the previously accepted reaction rate of peroxiredoxin with H₂O₂ grossly underestimated its true value (29, 37). Increased rates of H₂O₂ consumption, therefore, may suggest an H₂O₂ permeability coefficient that is even smaller than that predicted by Antunes and co-workers. As researchers gain a more thorough understanding of the different components that play a role in intracellular H₂O₂ consumption, the accepted kinetic reactions rates of particular species with H₂O₂ will have to be amended.

Over the past few years, our knowledge of the varied intracellular antioxidant systems has increased, and the need for a comprehensive model that incorporates these new findings is evident. The highly complex nature of the system in question, which results from the interconnectivity between protein thiol oxidation and redox couples during transient oxidative stress, has made development of integrative models difficult. For instance, the antioxidative roles of glutathione peroxidase (GPx) and peroxiredoxins (Prxs) depend directly on the reducing capacities of their respective co-substrate molecules, glutathione (GSH) and thioredoxin (Trx). To maintain their reducing capacities, GSH and Trx depend on the enzymes glutathione reductase (GR) and thioredoxin reductase (TR), respectively, in addition to NADPH. Moreover, the co-dependence of both the GSH and Trx thiol/disulfide redox couples on NADPH regeneration does not readily explain their maintenance at dissimilar nonequilibrium redox potentials (20, 21).

We have generated a network model of major redox reactions and cellular thiol modifications involved in H₂O₂ metabolism to improve our understanding of the processes by which a cell deals with H₂O₂-induced oxidative stress. Before we continue, however, we must clarify the term “buffering” as it applies to the redox systems that are described. Here, the term buffering is not used to describe a system at equilibrium; rather, it is used to describe the process by which the intracellular redox network, as a whole, protects against deviations in the redox states of the individual components that make up the network. This model, therefore, takes into account not only the key components of the network, but also the hierarchic interdependence of each component on the other. It builds in scope on prior modeling studies (3, 28, 40, 42) to explore the collective features of an intact redox system by accounting for all the major enzymes known to consume hydrogen peroxide in the cytosol, as well as the pseudo-enzymatic oxidative turnover of protein thiols. The use of computational modeling to study peroxide buffering allows a detailed investigation of the cellular dynamics of oxidative stress.

Computational Methods

Overview of model structure

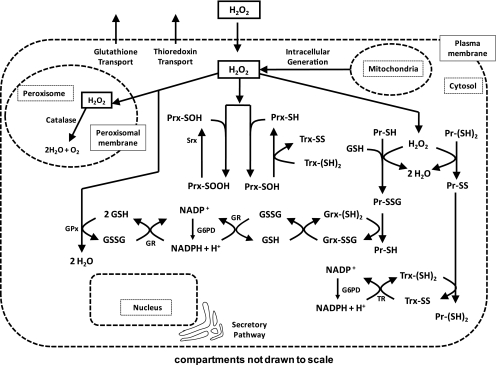
We developed a computational model, based on ordinary differential equations, by using mass action and Michaelis-Menten kinetics to describe the changes in concentration of cellular redox-buffering components on exposure to extracellular H₂O₂. Figure 1 is an illustration of the reactions included in the model. Organellar compartmentation provides additional regulatory control in redox mechanisms by maintenance of nonequilibrium redox potentials (14); this present model was simplified in description to the extracellular medium, intracellular cytosol, and the peroxisomes. Intracellular generation of hydrogen peroxide by the mitochondria was described by a zero-order production term, and the more rapid oxidation rate of Trx2 (14) was excluded from the model.

FIG. 1.

Model of hydrogen peroxide (H₂O₂) elimination by Jurkat T cells. The modeled system was that of an individual cell with three compartments being considered: the extracellular medium, the intracellular cytosol, and the peroxisomes. H₂O₂ freely moved between compartments by permeating through the cytoplasmic and peroxisomal membranes. A constant intracellular H₂O₂ production rate was defined with a mitochondrial source. Within the intracellular cytosol, H₂O₂ was metabolized by a series of reactions (arrows), each with a given reaction-rate constant (Table 1). By four main pathways, H₂O₂ was metabolized by the cell. The first was controlled by catalase, and the second was controlled by glutathione peroxidase (GPx) enzymes working in conjunction with GSH, GR, and NADPH. The third was controlled by the peroxiredoxin enzymes (Prx) working in conjunction with Trx, TR, and NADPH. The fourth and final pathway described the nonenzymatic elimination of H₂O₂ through the oxidation of cysteine residues on intracellular proteins. This can occur at single Cys residues, resulting in sulfenic acids, which react with GSH to form glutathionylated intermediates. Alternatively, this can occur at dithiols resulting in the formation of an internal disulfide.

In this model, the antioxidative capacity of the cell was divided into several branches, with each branch describing a particular mode of H₂O₂ elimination. The first branch described H₂O₂ elimination by the catalase enzyme. An average of two peroxisomes per cell has been measured in Jurkat cells (17), and all the catalase activity within the cell was assumed to occur inside the peroxisomes.

The second branch of H₂O₂ elimination described the glutathione peroxidase enzymes (GPx). Although multiple GPx isozymes are present in cells, and some glutathione S-transferases have GPx activity, a reliable value for the cytosolic concentration of GPx in Jurkat cells is unknown (3). For the purpose of modeling this system, we simplified this description by considering the predominant glutathione peroxidase, GPx1, and implemented the literature-reported estimate of the intracellular concentration of GPx as predicted by a previous generalized mathematical model (33). GPx catalyzes the reaction of hydrogen peroxide with GSH to produce glutathione disulfide (GSSG). Glutathione disulfide is subsequently reduced through the actions of GR and NADPH (3, 28).

The third branch of H₂O₂ elimination accounted for the peroxiredoxin (Prx) enzymes in conjunction with Trx, TR, and NADPH. Mammalian cells have several members of the peroxiredoxin family, but the predominant mammalian cytoplasmic Prxs are peroxiredoxin 1 and 2 (31, 37); the combined contributions of these two isoforms were described in the model. The total concentration of cytosolic Prx in Jurkat cells was estimated from the literature (6, 31). The total concentrations of reduced and oxidized NADPH were estimated from values reported in the literature (30, 41). Cytosolic Trx1, at a concentration of 0.5 μM (48), was distributed between its reduced and oxidized forms, as experimentally determined for this study by redox Western blot.

The fourth branch of H₂O₂ elimination involved the oxidation of cysteine residues of intracellular proteins (Pr-SH/Pr-(SH)₂). Cysteine (Cys) residues of intracellular proteins contain redox-sensitive thiols that are susceptible to oxidation (46). On oxidation, the Cys residues of proteins can be reduced, with different characteristics, depending on the microenvironment, through a system of reactions involving GSH or Trx (9, 36, 46); vicinal dithiols are considered to form protein disulfides (P-SS-P) that are reduced by Trx1. Other thiols are oxidized to protein sulfenic acids (P-SOH), which undergo protein S-glutathionylation (P-SSG). The model reserved protein disulfide reduction exclusively for Trx, whereas protein sulfenic acids were reduced exclusively by GSH-dependent reactions (Fig. 1) (9). Methionine residues are also subject to oxidation, but the rates are not known. Because methionine sulfoxide reductases are thioredoxin dependent, the model, as described, can be considered to have methionine oxidation grouped with Trx-dependent reductions (19).

Parameter and species fitting

For this global model that encompassed 28 kinetic parameters and 24 species, some several values had yet to be appropriately defined in the literature: the H₂O₂ permeability constant, the rate of protein thiol oxidation, and the concentration of protein thiols dependent on GSH and Trx1, respectively, for reduction (Tables 1 and 2). Experimentally determined dynamics, therefore, were used for model fitting to arrive at acceptable estimates for these parameters and species (Fig. 2). The first experimental data set used for parameter fitting was digitized from the results of Antunes and Cadenas (3) describing the consumption of a bolus addition of extracellular H₂O₂ by intact Jurkat cells (Fig. 2B). Four additional data sets were generated under identical experimental conditions and quantified by using HPLC techniques and redox Western blots. These results described the changes in distribution of GSH and GSSG, as well as reduced and oxidized cytosolic Trx1, that occur as a result of H₂O₂ treatment (Fig. 2C and D). Parameters were estimated by minimizing an objective function, comprising the normalized root mean square deviation (RMSD) between experimentally observed time-course data and computed model predictions (8).

Table 1.

Model Parameters

Rxn No.	Expression	Parameter	Reference
R1	k1 ([H2O2]media) (A)a	k1 = 1.0 × 10−5 cm/s	Fitted
R2	H2O2 intracellular generation	k2 = 1.1 × 10−7 M/s	(19)
R3	k3 ([H2O2]cytosol) ([GPxred])	k3 = 2.1 × 107 M−1 s−1	(33)
R4	k4 ([GSH]) ([GPxox])	k4 = 4 × 104 M−1 s−1	(33)
R5	k5 ([GSH]) ([GPx-SSG])	k5 = 1 × 107 M−1 s−1	(33)
R6	k6 ([H2O2]cytosol) ([Catalase])	k6 = 3.4 × 107 M−1 s−1	(1, 37)
R7	k22 ([NADP+] − [NADP+]i)/(k7 + [NADP+])	k7 = 5.7 × 10−5 M	(52)
R8	k8 ([H2O2]cytosol) ([Prx-(SH)2])	k8 = 4 × 107 M−1 s−1	(49)
R9	k9 ([H2O2]cytosol) ([Prx-SOH])	k9 = 7.2 × 104 M−1 s−1	(51)
R10	k10 ([Prx-SO2H])	k10 = 3 × 10−3 per s	(7)
R11	k11 ([Prx-SOH])	k11 = 15 per s	(44)
R12	k12 ([Prx-SS]) ([Trxred])	k12 = 2.1 × 106 M−1 s−1	(26)
R13	k13 ([GSH]) ([GSH])	k13 = 7.4 × 10−5 per s	(40)
R14	k14 ([Pr-(SH)]) ([H2O2]cytosol)	k14 = 1 × 104 M−1 s−1	Fitted
R15	k15 ([GSH]) ([Pr-SOH] − [Pr-SOH]i)	k15 = 1.2 × 105 M−1 s−1	(11, 25)
R16	k16 ([Grx-SH]) ([Pr-SSG] − [Pr-SSG]i)	k16 = 9.1 × 104 M−1 s−1	(36)
R17	k17 ([Grx-SSG] − [Grx-SSG]i) ([GSH])	k17 = 3.7 × 104 M−1 s−1	(43)
R18	k18 ([Pr-(SH)2]) ([H2O2]cytosol)	k18 = 5 × 105 M−1 s−1	Fitted
R19	k19 ([Trxred]) ([Pr-SS] − [Pr-SS]i)	k19 = 1 × 105 M−1 s−1	(16)
R20	k20 ([GSSG] − [GSSG]i) ([NADPH])	k20 = 3.2 × 106 M−1 s−1	(15)
R21	k21 ([Trxox] − [Trxox]i) ([NADPH])	k21 = 2 × 107 M−1 s−1	(4)
R22	k22 ([NADP+] − [NADP+]i)/(k7 + [NADP+])	k22 = 3.75 × 10−4 M/s	(52)
R23	k23([H2O2]cytosol)(B)b	k23 = 3 × 10−3 cm s−1	(38)
R24	GSH synthesis	k24 = 4.1 × 10−7 M/s	(21)
R25	GSSG efflux	k25 = 1.2 × 10−8 M/s	(2)
R26	GSH + GSSG efflux	k26 = 1.2 × 10−7 M/s	(23)
R27	Trx efflux	k27 = 7.5 × 10−10 M/s	(22)
R28	Trx synthesis	k28 = 7.0 × 10−10 M/s	(22)

^aA = 10⁻³ (L cm⁻³) × 6.5 × 10⁻⁵ (cm²) × 1 × 10⁹ (cells/L).

^bB = 10⁻³ (L cm⁻³) × 3.0 × 10⁻⁹ (cm²) × 1.5 × 10¹⁴ (L⁻¹).

Table 2.

Species Initial Concentrations

Species	Initial condition (M)	Reference
[H2O2]media	1 × 10−4	Assigned
[H2O2]cytosol	1 × 10−9	(35)
[GPxred]	5 × 10−5	(33)
[GPxox]	1 × 10−14 a	Assigned
[GPx-SSG]	1 × 10−14 a	Assigned
[GSH]	3.68 × 10−4	Measured
[GSSG]	1.78 × 10−6	Measured
[Catalase]	9 × 10−7	(32, 38)
[H2O2]peroxisome	1 × 10−10 a	Assigned
[Prx-(SH)2]	1.9 × 10−5	(14, 39)
[Prx-(SOH)]	1 × 10−14 a	Assigned
[Prx-(SOOH)]	1 × 10−14 a	Assigned
[Prx-SS]	9.6 × 10−8 b	(19)
[Trxred]	4.3 × 10−7	Measured
[Trxox]	7.5 × 10−8	Measured
[Pr-SH]	1.22 × 10−4	Fitted
[Pr-SOH]	6.1 × 10−7 b	(19)
[Pr-SSG]	6.1 × 10−7 b	(19)
[Grx-SH]	1.2 × 10−6	(27)
[Grx-SSG]	6.0 × 10−9 b	(19)
[Pr-(SH)2]	1.0 × 10−3	Fitted
[Pr-(SS)]	5.5 × 10−6 b	(19)
[NADPH]	3.0 × 10−5	(30)
[NADP+]	3.0 × 10−7	(41)

^aBaseline assignment to highlight the effects of exogenously applied H₂O₂ only.

^bEstimate of 0.5% [protein] in the glutathionylated form (19).

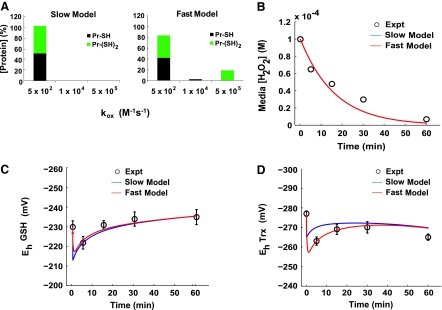
FIG. 2.

A model with rapid protein dithiol oxidation accurately describes hydrogen peroxide consumption. (A) Assignment of the distribution of protein thiol pools and rate constants for the slow and fast protein thiol oxidation models. (B) Experimental data (3) and model fitted results for the slow and fast protein thiol oxidation models showing the consumption of H₂O₂ by intact Jurkat T cells at a density of a 1 × 10⁶ cells/ml after being exposed to a bolus addition of 100 μM extracellular H₂O₂. (C) Redox states of the glutathione redox couple as experimentally determined and model fitted for the slow and fast models. Experimental values represent the mean ± SEM of three separate experiments. (D) Redox states of the thioredoxin redox couple as experimentally determined and model fitted for the slow and fast protein thiol oxidation models. Experimental values represent the mean ± SEM of three separate experiments.

Two models of protein oxidation

Accurate modeling of the contribution of protein thiols to the overall redox network requires both the known values of the protein thiol concentration susceptible to reacting with hydrogen peroxide and the rates at which these reactions occur. We postulated two distinct models of protein thiol oxidation to determine the proper description of protein oxidation, a “slow” model and a “fast” model, and tested the ability of each model to match the experimental data (Fig. 2). The slow model was constructed by assuming the total available protein thiol pool, as estimated by Jones (19), reacted with intracellular hydrogen peroxide with the preestablished rate constant of 5 × 10² M/s, the rate at which GAPDH is estimated to react with hydrogen peroxide (49). In this model, the available protein thiol pool was further divided into two subgroups: the protein monothiol pool (Pr-SH), which contained 50% of the total available protein thiols, and the protein dithiol pool (Pr-(SH)₂), which contained the remaining 50% of the total protein thiol pool (Fig. 2A, left panel). The fast model, conversely, was constructed by assuming that a smaller subset of protein thiols existed, approximately 20% of the total available protein thiol pool, which reacted with hydrogen peroxide at an appreciably faster rate than that estimated for GAPDH oxidation. The remaining 80% of the total protein thiol pool was divided equally between the protein monothiol group and the protein dithiol group and was allowed to react with hydrogen peroxide at the slower rate constant of 5 × 10² M/s. The purpose of the fast model was to determine the percentage of the highly reactive protein thiols that belonged to the protein monothiol group and the protein dithiol group, respectively, and to predict the rates of reactions of these fast-reacting thiols with intracellular hydrogen peroxide (Fig. 2A, right panel).

Parameter estimation

The parameters predicted by the model were (a) the concentration of fast-reacting protein monothiols [Pr-(SH)], (b) the reaction rate constant for the fast-reacting protein monothiols with hydrogen peroxide, (c) the concentration of fast-reacting protein dithiols (Pr-(SH)₂), (d) the reaction rate constant for the fast-reacting protein dithiols with hydrogen peroxide, and (e) the permeability coefficient of the cytoplasmic membrane. The protein oxidation parameters to be fitted were initialized to randomized values that lay within the literature-reported estimates of their upper and lower bounds (9, 49, 50). Because of conflicting estimates of the lower bound of the permeability coefficient (3, 28, 42), it was deemed appropriate to expand the lower bound of the explored parameter space for this parameter by one order of magnitude. Multiple simulations were conducted for each condition (n = 2,000 runs), in which each of the three unknown parameters was simultaneously assigned a random initial value from its allowable parameter space and the objective function calculated. The parameter set that resulted in the minimization of the objective function was selected as the optimal model description.

Membrane H₂O₂ transport

The rate of movement of H₂O₂ across the cytoplasmic membrane was described previously by the following (42):

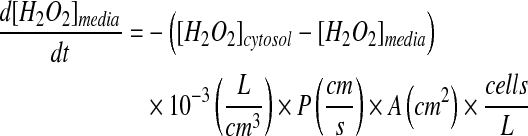(1)

where [H₂O₂]_media and [H₂O₂]_cytosol represent the concentration of peroxide in the extracellular media and the intracellular cytosol, respectively, at time t. H₂O₂ flux across the cytoplasmic membrane was a function of the intra- and extracellular concentration of H₂O₂, the permeability coefficient of H₂O₂ through the cytoplasmic membrane, P, and the surface area of the cell, A, approximately 1.0 × 10⁻⁵ cm², as calculated from the average diameter of the Jurkat cell, 20 μm (ViCell Viability Counter, Beckman Coulter). The volume of the cytoplasmic compartment was calculated by assuming the Jurkat cell to be a perfect sphere. The concentration of H₂O₂ in a cell was described previously as a sum of the influx, production, efflux, and scavenging of H₂O₂ within a particular cellular compartment (5). H₂O₂ flux across the peroxisomal membrane was modeled in a similar fashion by using the concentration of peroxide in the cytosol and the concentration of peroxide in the peroxisome to generate the gradient force for diffusion. The permeability coefficient of H₂O₂ through the peroxisomal membrane, P, was obtained from the literature (38), assuming a uniform concentration of H₂O₂ within a particular compartment.

Parameter values

The majority of the rate constants and initial species concentrations used in this model were derived from published data (Tables 1 and 2, respectively). Where possible, values reported specifically for Jurkat cells were used; reactions and species exist, however, for which Jurkat cell line–specific values were undefined. For these types of reactions, we used published data for other cell lines as an appropriate estimate. The fractional cytosolic volume used for concentration calculations was defined as 30% of total cell volume by estimation from images of Hoescht nuclear-stained Jurkat cells.

Description of reaction kinetics

The series of differential equations was solved by using Matlab R2008a (Mathworks, Natick, MA). The generalized equation for a particular species constituted the sum of all reactions that produced the species minus the sum of all reactions that consumed it. Several components in the model, however, deviated from the generalized equation form, as described later.

Ideally, if the law of mass action were used to describe the reduction of GSSG by GR to produce GSH, the resulting equations would resemble the following:

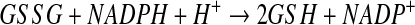(2)

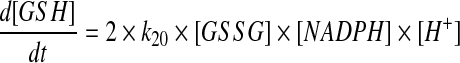(3)

where [GSH], [GSSG], and [NADPH] represented the intracellular concentrations of reduced glutathione, glutathione disulfide, and NADPH, respectively, at time t, and k₂₀ represented the rate constant for the reduction reaction. Instead of Equation 3, the change in concentration of GSH as a result of the reduction of GSSG by GR was described in the model by the following:

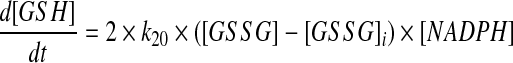(4)

where [GSSG]_i represented the initial concentration of glutathione disulfide in the cell. Because the cell maintains a fixed nonequilibrium ratio of [GSH] to [GSSG] under normal oxidative conditions (21), the spontaneous reduction of GSSG in the absence of oxidants could not be allowed. To prevent this behavior, the reduction of GSSG was modeled as a function of the difference between [GSSG] and [GSSG]_i. Although this model correctly captured any oxidant-induced changes to this reduction rate, the absolute GSSG reduction rate in the model may be somewhat underestimated by the endogenous rate at baseline, because the K_m of GR is high relative to concentrations of GSSG achieved in cells (12). The same basic principles and assumptions also have been applied to the reactions involving the Trx redox couple. The rate expressions governing the change in concentration of each species of the model are listed in Table 1.

Objective function for parameter estimation

Parameters were estimated by minimizing a modified version of a previously described objective function, U, comprising the normalized root mean square deviation (RMSD) between experimentally observed time-course data and computed model predictions (8):

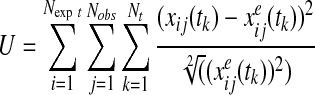(5)

where x was the concentration of some particular species in the model, x^e was the experimentally observed concentration of the same species, N_obs was the number of experimentally observed species, N_expt was the number of experimental conditions, as defined by the relative percentage of proteins assigned to the monothiol and dithiol protein pools, and N_t was the number of time points sampled.

Sensitivity analysis

The finite difference approximation (FDM) method was used to calculate the sensitivity coefficient, s_i,j, which defined the difference between the nominal and perturbed solutions offered by the model, according to the equation (53):

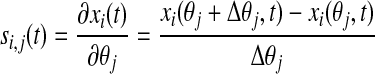(6)

where x_i(θ_j, t) represented a measured model output at time t, when a particular parameter had the value θ_j; subsequently, x_i(θ_j + θ_j, t) represented the value of the same model output when the same parameter had been perturbed by the value θ_j. For the purposes of this model, all parameters were perturbed by 10% of their initial values. As a result of the difference in magnitude between parameters, the absolute sensitivity values obtained from Equation 6 were not accurate measures of relative sensitivity. To calculate the relative sensitivities for a more-direct comparison of model response at different states across different parameters, we used a normalization method previously described (53):

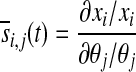(7)

From this equation, the normalized sensitivity of a particular model output to perturbations in a particular parameter at time, t, could be determined. All sensitivity-analysis calculations were done at t = 5 min, and parameter sensitivities were calculated with respect to the concentrations of the experimentally determined model species (extracellular peroxide, intracellular GSH, intracellular GSSG, intracellular reduced Trx1, and intracellular oxidized Trx1).

Experimental Materials and Methods

Materials, cell culture, and stimulation conditions

All reagents were from Sigma-Aldrich, St. Louis, MO, unless specified otherwise. Jurkat cells (clone E6-1) were obtained from American Type Culture Collection (ATCC, Manassas, VA). Cells were cultured in supplemented RPMI-1640 medium (glutamine, nonessential amino acids, 100 U/ml penicillin/streptomycin, 1 mM sodium pyruvate, 10 mM HEPES, 10% FBS). For stimulation, cells were resuspended in fresh media (1 × 10⁶ cells/ml) and treated with H₂O₂ for various times at 37°C before lysing. Pyruvate is known to undergo oxidative decarboxylation in the presence of H₂O₂, so a control experiment was performed to determine the rate of H₂O₂ removal by the culture media alone. An Amplex Red assay (Invitrogen, Carlsbad, CA) showed that the background oxidation of sodium pyruvate in the media by H₂O₂ was not detectable for the duration of the treatment conditions used throughout the study.

Cellular fractionation and derivatization of protein thiols

After treatment, cells were pelleted by centrifugation at 300 g. The cell pellet was immediately resuspended in guanidine-Tris solution (50 mM Tris-HCL, pH 8.3, 3 mM EDTA, 6 M guanidine-HCL, 0.5% Triton X-100) supplemented with 50 mM iodoacetic acid (IAA, pH 8.3), and incubated at 37°C in the dark for 45 min (46). This procedure was carried out to lyse simultaneously the cells and derivatize reduced protein thiols. After incubation, the samples were run through Microspin G-25 columns (GE Healthcare, Buckinghamshire, U.K.) to remove excess IAA.

Redox Western blot analysis

To analyze the redox state of cytosolic Trx1, derivatized proteins were separated by native polyacrylamide gel electrophoresis, as previously described (46). PVDF membranes were probed with antibody to human Trx1 (American Diagnostica, Stamford, CT) and a goat IgG-IRDye 800 CW conjugated antibody (Rockland Immunochemicals, Gilbertsville, PA). Trx1 bands were visualized and quantified by using the LI-COR Odyssey scanner 2.1 (Lincoln, NE) and the LI-COR Odyssey 2.1 gel analysis software, respectively.

Measurement of intracellular GSH and GSSG

GSH and GSSG were measured with high-performance liquid chromatography (HPLC) as S-carboxymethyl N-dansyl derivatives by using γ-glutamylglutamate as an internal standard (18).

Calculation of E_h values

The redox potentials of GSH and Trx1 were calculated by using the Nernst equation. To convert total values for GSH and GSSG into intracellular concentrations, measured intracellular protein concentrations were used, and a constant cellular water volume (5 μl/mg protein) was assumed. The integrated band intensities of reduced and oxidized Trx1, as quantified by the LI-COR Odyssey 2.1 gel analysis software, were assumed to be directly proportional to the normalized intracellular concentrations of these species (47). The intracellular pH was assumed to be 7.4 (34) and to be unaffected by H₂O₂ treatment. E₀ values used for pH 7.4 were as follows: GSH/GSSG redox couple, −264 mV; and for the active site dithiol/disulfide of Trx1, −254 mV (46).

Results

Parameter and species fitting

Table 1 lists the kinetic parameter values obtained from the literature and the fitted values determined for the unknown parameters in the fast model. Whereas the slow model (Fig. 2A, left panel) was able to represent accurately the dynamics of peroxide consumption and the oxidation dynamics of the glutathione redox couple, it was unable to capture accurately the oxidation dynamics of the thioredoxin redox couple, Fig. 2D. The fast model (Fig. 2A, right panel), conversely, was able to capture the entire dynamic dataset. The fitted values in the fast model for the rates of protein oxidation for Pr-SH and Pr-(SH)₂ (k₁₄ and k₁₈, respectively) were 1 × 10⁴ M/s and 5 × 10⁵ M/s. These values were within the order-of-magnitude range of predicted reaction rates for protein thiols with H₂O₂ (10 to 10⁶ M/s) (9). Because the fast model was able to replicate better the experimental data, we used this model to generate all subsequent parameter estimates and model predictions. The permeability constant (Equation 1) that describes the movement of peroxide through the plasma membrane, k₁, was fitted to a value of 1.0 × 10⁻⁵ cm/s. This value was approximately 1 order of magnitude smaller than the value estimated by Antunes and Cadenas (3).

Table 2 lists the initial species concentrations obtained from the literature and the fitted values determined for the concentration of protein thiols dependent on GSH and Trx1, respectively, for reduction. The protein thiol distribution that resulted in the minimization of the objective function was 42% GSH-dependent protein thiols and 58% Trx1-dependent protein thiols.

Consumption of H₂O₂ by intact Jurkat cells

The rate at which Jurkat cells clear the extracellular environment of H₂O₂ is an effective measure of their internal antioxidative response system. We fitted the model to the condition of a bolus addition of 100 μM extracellular H₂O₂ being consumed by 1 × 10⁶ Jurkat cells per milliliter. The model-predicted rate of extracellular H₂O₂ decay was 9.4 × 10⁻⁴ per second per 10⁶ cells. This decay rate was very close to the experimentally determined 1.0 ± 0.1 × 10⁻³ per second per 10⁶ cells reported by Antunes and Cadenas (3).

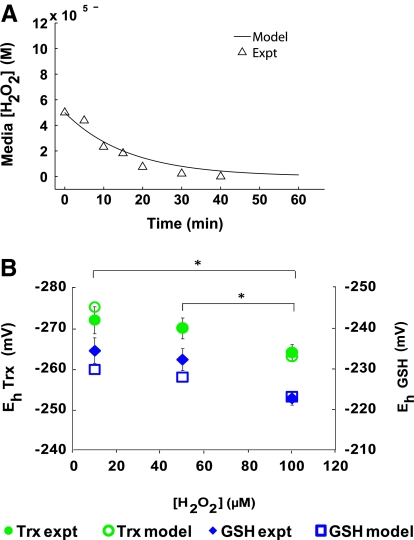
After the model parameters and protein thiol distributions were optimized based on the bolus condition, we investigated the ability of the model to describe hydrogen peroxide consumption by Jurkat cells at varied extracellular peroxide conditions. Without any additional parameter optimization, the fitted model accurately simulated the extracellular decay of 50 μM hydrogen peroxide at a cell density of 1 × 10⁶ cells/ml from another published dataset (13). This new peroxide concentration was 50% less than what was used in the model-fitting exercises (Fig. 3A). We also simulated the peroxide-consumption dynamics of a population of Jurkat cells exposed to low steady-state levels of extracellular H₂O₂. Because the steady-state consumption behavior of Jurkat cells was not used to fit any of the parameters contained in the model, the steady-state consumption experiment, previously carried out by Antunes and Cadenas (3), served as additional validation for the model. In this experiment, cells at a concentration of 1 × 10⁶ cells/ml were incubated simultaneously with a low concentration of H₂O₂ and glucose oxidase to generate a steady-state extracellular H₂O₂ concentration of ∼9 μM (3). The model simulation for this condition accurately predicted that Jurkat cells (1 × 10⁶ cells/ml) would be able to maintain, at a constant level, the low concentration of H₂O₂ in their extracellular environment for ≥1 h after exposure (data not shown).

FIG. 3.

Model validation for varied initial extracellular peroxide concentrations. (A) Model-simulated and experimentally determined (13) consumption of H₂O₂ by intact Jurkat T cells (cell density, 1 × 10⁶ cells/ml) after being exposed to a bolus addition of 50 μM extracellular H₂O₂. (B) Model-simulated and experimentally determined glutathione and thioredoxin redox potentials for varying initial extracellular [H₂O₂] (Jurkat T-cell density, 1 × 10⁶ cells/ml). *Asterisks indicate statistically significant differences (p < 0.05) with respect to the two hydrogen peroxide concentrations being compared.

The intracellular GSH/GSSG pool is transiently oxidized by H₂O₂ treatment

We quantified glutathione disulfide (GSSG) to be ∼0.5% of the total glutathione pool in resting Jurkat cells (E_h value of cytosolic GSH/GSSG = −230 ± 3 mV). At 5 min after H₂O₂ addition, the intracellular GSH/GSSG redox potential had been oxidized by ∼8 mV (Fig. 2C). Within 30 min of treatment, the concentration of GSSG was approaching its baseline level. In contrast, the intracellular GSH concentration increased slightly; therefore, a net change in total glutathione was occurring over the experimental window of observation. At 60 min of exposure, the E_h value of the GSH/GSSG pool was −235 ± 4 mV.

By using the measured baseline values of oxidized and reduced glutathione as initial conditions for GSH and GSSG, the model simulated the changing glutathione redox potential due to H₂O₂ treatment as a function of time (Fig. 2C). A rapid oxidation of the GSH/GSSG pool with H₂O₂ treatment resulted in an E_h value of −224 mV at 5 min after treatment, very close to the 8-mV magnitude oxidation measured. The model curve showed a return to baseline redox potential after 60 min, and, as a result of the incorporation of glutathione transport and synthesis, the model was capable of capturing the slight overshoot seen experimentally.

Cytosolic Trx1 oxidation is sustained after H₂O₂ treatment

We measured cytosolic Trx1 in resting Jurkat cells to be ∼85% reduced, corresponding to an E_h value for cytosolic Trx1 of −277 ± 1.4 mV (Fig. 2D), a value that is in agreement with previous reports of the steady-state redox potential of cytosolic Trx1 (21). The potential of the Trx1 redox couple at 5 min of treatment was approximately −263 mV, reflecting 14 mV oxidation. From 5 to 30 min of treatment, the percentage of oxidized Trx1 began to decline toward its baseline value. At 60 min of treatment, however, the redox potential of the cytosolic Trx1 redox couple was reoxidized. The 60-min Trx E_h value of −265 ± 1.6 mV was very similar to the level of Trx1 oxidation seen at 5 min of treatment (Fig. 2D).

The fitted model was capable of simulating transient E_h values for cytosolic Trx1 after exposure to 100 μM H₂O₂ (Fig. 2D). The baseline distributions of oxidized and reduced Trx1 were used as the initial conditions for the Trx1 species in the simulation. An appropriate degree of Trx1 oxidation on exposure to H₂O₂ was reproduced by the model, and the model was capable of simulating the reoxidation observed at the 60-min time point.

Model sensitivity analysis

We conducted sensitivity analysis to identify the parameters with the greatest influence on model simulation results. The parameter to which a majority of the species investigated was most sensitive was k₁, the permeability constant of the cytoplasmic membrane. Reduced and oxidized Trx1 showed the highest sensitivity to the parameters k₁, k₁₂, and k₂₁, where k₁₂ and k₂₁ represented the rate constant for the reduction of oxidized peroxiredoxin (Prx-SS) by reduced Trx1 and the rate constant for the reduction of oxidized Trx1 by TR and NADPH, respectively. GSH showed the highest sensitivity to k₁ and k₃, where k₃ represented the rate constant for the GPx-catalyzed reaction of GSH with hydrogen peroxide. GSSG showed the highest sensitivity to k₃ and k₂₀, where k₂₀ represented the reduction of GSSG by GR and NADPH. Although both the glutathione and thioredoxin redox couples showed relatively high sensitivity to k₂₂, the rate constant describing the rate of NADPH resupply by the G6PDH enzyme, the Trx redox couple was more sensitive to perturbations in this parameter than was the GSH redox couple. Model components, in general, were “insular” in their sensitivities (i.e., affected by rate constants of reactions in which they played either a direct or very nearly direct role), with very few enzymatic parameters, such as k₂₂ (NADPH supply), affecting both the thioredoxin and glutathione couples.

Model predicts oxidation profiles of glutathione and thioredoxin redox couples for varied initial extracellular [H₂O₂]

The antioxidative properties of our model were capable of replicating in vivo Jurkat dynamics for particular instances of both the transient and steady-state condition of oxidative stress. To interrogate the system further, we explored the model's ability to predict these dynamic responses for a variety of oxidation levels. We simulated a bolus extracellular H₂O₂ addition of 10 μM and 50 μM at a cell density of 1 × 10⁶ cells/ml and compared the results with the redox potential of the glutathione and thioredoxin redox couples experimentally measured 5 min after treatment (Fig. 3B). Significant statistical differences (alpha = 0.05) were found between the experimentally determined redox potentials of the glutathione and thioredoxin redox couples at 5 min of 10 μM peroxide treatment compared with the 100 μM peroxide treatment. Statistically significant differences were also seen between the 50 μM and the 100 μM extracellular peroxide treatments. Model simulations of the redox potential of the glutathione and thioredoxin redox couples for the 10 μM, 50 μM, and 100 μM peroxide treatments deviated slightly from the experimental values but accurately captured the oxidative change between the redox potentials of both redox couples for all peroxide treatment conditions examined (Fig. 3B).

Model predicts intracellular peroxide concentrations and levels of protein thiol oxidation resulting from exogenous hydrogen peroxide

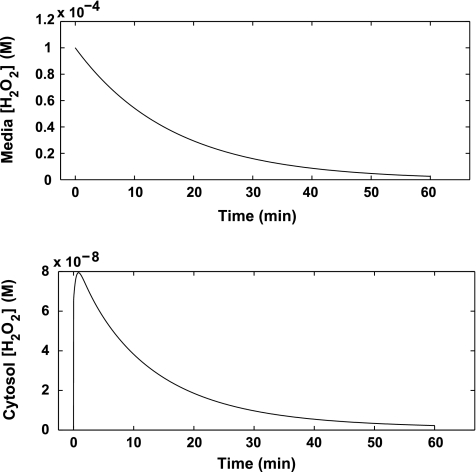
One benefit of the model is the ability to offer quantitative estimates for the intracellular [H₂O₂] resulting from an external source of hydrogen peroxide. The model predicts that a concentration of about 8 × 10⁻⁸ M of hydrogen peroxide develops within the cell when it is exposed to 100 μM extracellular peroxide at a cell density of 1 × 10⁶ cells/ml (Fig. 4), thereby representing a gradient of ∼1,000 that develops between the extracellular environment and the intracellular cytosol.

FIG. 4.

Model-predicted intracellular [H₂O₂]. Dynamic model-simulated extra- (top) and intracellular (bottom) peroxide concentration as a result of 100 μM H₂O₂. (Jurkat T-cell density = 1 × 10⁶ cells/ml).

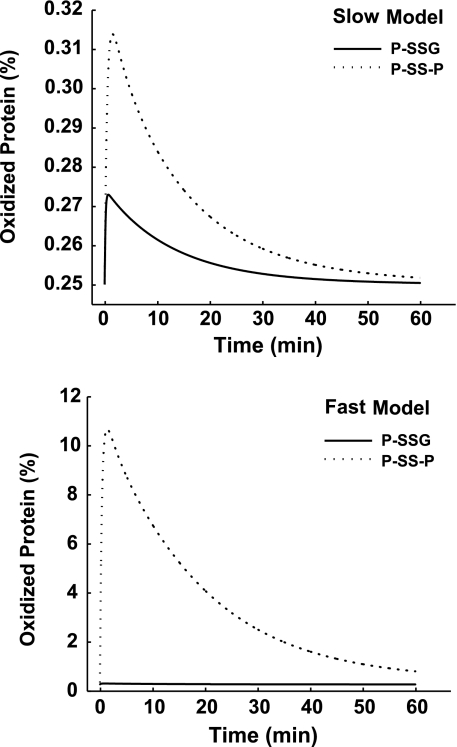
In addition to offering quantitative estimates of the intracellular peroxide concentration, the model is capable of providing predictions of protein thiol oxidation. The protein thiol pool may significantly contribute to the cellular antioxidant defense because of the substantial concentration of protein thiols in the cell (19). To investigate the independent roles of mono- and dithiol proteins during dynamic oxidative conditions, we used the model to predict the level of peroxide-induced protein oxidation as a function of initial extracellular [H₂O₂] (Fig. 5). For this in silico experiment, protein oxidation was quantified by the concentration of protein disulfides ([P-SS-P]) and S-glutathione adducts ([P-SSG]) observed at 5 min of 100 μM H₂O₂ treatment for the slow and the fast model of peroxide consumption. The slow model, which was unable to fit all the experimental data (Fig. 2), showed very little protein oxidation, with the maximum concentration of protein S-glutathione adducts and protein disulfides not exceeding 1% of the total thiol pool (Fig. 5, top). Conversely, the fast model, which was capable of fitting all the experimental data, predicted a significant increase in the concentration of protein disulfides, ∼10% of the total protein thiol pool (Fig. 5, bottom).

FIG. 5.

Model-predicted protein-oxidation profiles. Simulated percentages of S-glutathionylated proteins and protein disulfides that form as a result of oxidative stress (100 μM H₂O₂; Jurkat T-cell density = 1 × 10⁶ cells/ml) for the slow (top) and fast (bottom) models.

Discussion

The development of kinetic computational models of redox enzyme systems presents unique challenges in comparison with other biochemical networks. The nonequilibrium condition of intracellular thiol-based redox couples provides a rapid and highly sensitive switching mechanism in response to changes in intracellular redox state (21). Because many thiol-based redox couples are set at different potentials, the model species tend to equilibrate even in the absence of oxidative stress. The spontaneous change in redox potential that is due to this inherent nonequilibrium condition must be filtered out to focus entirely on those changes that are the result of oxidative stress alone. One modeling approach is to define the driving force for electron transfer to be the function of the difference between the homeostatic potential and the actual potential of the system, as defined by the redox couple of interest (21). With this approach, the defined system can describe the dynamic response to changes in intracellular [H₂O₂] without having explicitly to include the numerous steady-state fluxes that must occur across cellular membranes to maintain the redox couples out of equilibrium.

Importance of membrane permeability in cellular antioxidant defense

The model highlights the sensitivity of the entire redox enzyme network to the membrane permeability constant for hydrogen peroxide and revises estimates for this constant. The first barrier to extracellular hydrogen peroxide consumption is the cytoplasmic membrane. Transmembrane diffusion of H₂O₂ is an important factor in the maintenance of peroxide gradients between the extracellular environment and the intracellular cytosol (5). The model recapitulated this experimental observation by highlighting k₁, the model parameter describing the permeability coefficient of the cytoplasmic membrane, as the parameter to which most model components were the most sensitive. The optimized permeability coefficient was approximately 1 order of magnitude smaller than that previously estimated by Antunes and Cadenas (3). The literature-reported estimate calculated by Antunes and Cadenas was based on the assumption that the GPx and catalase pathways were the only pathways working toward H₂O₂ removal. Realistically, however, the cell has several additional enzymatic and nonenzymatic methods of H₂O₂ clearance, most of which have been integrated into this present model. Without the incorporation of all redox reactions that take place in vivo, an overestimated value for the permeability coefficient is expected. From a systems perspective, therefore, it would be beneficial if the cell could control its cytoplasmic membrane permeability to control the amount of transmembrane H₂O₂ diffusion it experiences. Recent studies have shown that some membranes are poorly permeable to H₂O₂, compared with other membranes, implying that transport of H₂O₂ could be regulated (5). Differences in membrane permeability could be attributed to changes in membrane lipid composition or changes in the number of membrane-bound diffusion-facilitating channel proteins, all of which can be controlled by the cell. The importance of the membrane-permeability coefficient, as dictated by the model-sensitivity analysis, suggested that the cytoplasmic membrane permeability is a parameter capable of being tuned by the cell to control H₂O₂ transport and, ultimately, the concentration of H₂O₂ inside the cell. Whether such transport could be actively controlled by aquaporins is presently unknown.

Precise modeling of the intracellular peroxide consumption dynamics and membrane permeability provides a more-accurate description of intracellular peroxide levels. The model-predicted peak intracellular concentration of hydrogen peroxide that is induced by 100 μM is about 100 nM. The model is the most comprehensive model to date to offer quantitative and dynamic estimates of the intracellular concentration of hydrogen peroxide resulting from external peroxide assault.

Unequal antioxidative burden of intracellular redox enzymes and thiol-containing compounds

The model addresses which redox enzymes and thiol-containing compounds are primarily responsible for the antioxidant capacity of the cell. The Trx1 and GSH redox couples are often used as measures of the overall redox state of the cell (41). We used the model to describe the dynamics of these two redox couples under conditions of oxidative stress. Experimental results showed the E_h value of the Trx1 redox couple to be oxidized by a maximum of 17 mV after treatment with 100 μM H₂O₂. This maximum level of oxidation was about twice as high as that seen for the GSH redox couple. Analysis of the model system under the steady-state peroxide-generation condition (Table 3) suggested that an unequal distribution of the antioxidative burden exists between the Trx1 and GSH redox couples in the intracellular cytosol; this unequal distribution offers one explanation for the unequal oxidation of the Trx1 and GSH redox couples described earlier. These results should be interpreted carefully, as the flux distribution between the Trx1 and GSH redox couples may very well be compartment specific and therefore altered in other subcellular compartments. Furthermore, Trx1 kinetics may change with hyperoxidation of the enzyme (46), and the kinetics of the G6PD enzyme are altered as a result of increasing levels of GSSG in the cell (45). Future modeling efforts may need to account for these complex kinetic regulatory mechanisms to simulate more extreme oxidative conditions appropriately.

Table 3.

Steady State Hydrogen Peroxide Fluxes

Branch	Flux (M/s)	Flux (% of total)	Flux (M/s)	Flux (% of total)
Prx	4.4 × 10−6	32	5.6 × 10−6	42
GPx	6.0 × 10−6	44	7.7 × 10−6	57
Catalase	3.7 × 10−8	<1	4.6 × 10−8	<1
Pr-SH	7.0 × 10−9	<1	1.1 × 10−8	<1
Pr-(SH)2	3.1 × 10−6	23	1.1 × 10−8	<1
	Fast model		Slow model

The steady-state concentration of H₂O₂ that develops within an individual cell as a result of a low (∼9 μM), constant level of extracellular H₂O₂ was ∼1 nM (data not shown). From this steady-state value, and using the respective rate constants of peroxide metabolism for each antioxidative branch [catalase, GPx/GSH, Prx/Trx1, Pr-SH, Pr-(SH)₂], in addition to the relative concentrations of the species in each branch, we were able to calculate the hydrogen peroxide flux (M/s) that passes through each antioxidative branch (Table 3). These calculations revealed that the GPx and Prx enzyme systems were responsible for the majority of the peroxide metabolism at this steady-state condition, with calculated fluxes of 6.0 × 10⁻⁶ M/s and 4.4 × 10⁻⁶ M/s, respectively. In comparison, the flux through the catalase enzyme system was only 3.7 × 10⁻⁸ M/s, approximately 0.6% of the flux through the GPx enzyme system. The contribution of catalase to the consumption of externally generated hydrogen peroxide is low compared with other antioxidant enzymes such as peroxiredoxin and glutathione peroxidase. This result reflects not only the low peroxisomal content of Jurkat cells, but also the inefficiency of intact peroxisomes in degrading externally generated hydrogen peroxide (10). It must be noted that although catalase may be somewhat inefficient at degrading external hydrogen peroxide, it is highly efficient at degrading hydrogen peroxide generated within the peroxisomal matrix.

Another prediction by the model flux analysis was the contribution of the protein dithiol pool to the steady-state peroxide consumption. The flux of hydrogen peroxide through the protein dithiol pool was 3.1 × 10⁻⁶ M/s, ∼23% of the total hydrogen peroxide consumption within the cell. Comparatively, the flux through the protein monothiol pool was <1%. These results are in line with previous predictions of protein thiol oxidation that suggest that a majority of the proteins in the cell react at relatively slow rates with hydrogen peroxide, whereas a few proteins, primarily those that form disulfide bonds, react with hydrogen peroxide at appreciably faster rates (49, 50). This result offers another possible explanation for the thioredoxin redox couple experiencing more pronounced and sustained oxidation during times of oxidative stress as compared with its glutathione counterpart.

The current model advances our understanding of intracellular redox biology

Multiple advances in knowledge have been gained by this modeling study. We asked whether the current knowledge in the redox biology field can explain experimental data, or if additional redox nodes, which have not yet been discovered, may significantly contribute to peroxide clearance from the intracellular environment. We have shown that the model topology, as it currently stands and with current parameter measurements available in the literature, is capable of describing the behavior of a particular cell line on exposure to an external source of hydrogen peroxide if supplemented with the optimized estimates of unknown parameters. Although customized for Jurkat cells, the reactions that are described by the model can easily be adapted to other cell lines by inserting enzyme concentrations and reaction rate constants for the particular cell line of interest. The second contribution given by this model is its ability to provide predictions of the oxidation profiles of specific intracellular components that we cannot yet quantify experimentally. The current model offers what we believe is the first fully quantitative estimate for the concentration of intracellular hydrogen peroxide that results from an extracellular source, in addition to the percentage of protein thiols that undergo both protein S-glutathionylation and protein disulfide formation. By including the contribution of the protein thiols to hydrogen peroxide clearance, the model explains why the glutathione and thioredoxin redox potentials are purported to be independent of one another; the larger flux through the dithiol pool causes a capacitance in the thioredoxin branch that leads to a sustained oxidation of thioredoxin.

Finally, the model is capable of simultaneously determining relative fluxes through each antioxidant branch, which would be extremely difficult to measure by using traditional experimentation.

This framework used carefully controlled induction of oxidative stress to construct a kinetic model that is capable of describing the observed oxidation of redox couples as a function of time. As a tool for interrogation of a particular biochemical network, a bolus condition is extremely useful to “reverse-engineer” features. Although the current model was fitted and validated with data based on the extracellular administration of hydrogen peroxide, this does not negate the ability of the model to simulate and predict the behavior of intracellular components as a result of endogenous generation of hydrogen peroxide. To validate these dynamics, however, advancements in the ability to measure quantitatively the intracellular peroxide must be developed. Furthermore, although compartmentation was included, spatial gradients within the cell were not described by this model. With the network structure and kinetic description intact, future challenges to modeling efforts will involve the added complexity of intracellular H₂O₂ spatial gradients generated by NADPH oxidases, peroxisomes, and mitochondria.

Abbreviations Used

Cys

cysteine

GPx

glutathione peroxidase

GR

glutathione reductase

GSH

glutathione

GSSG

glutathione disulfide

H₂O₂

hydrogen peroxide

Pr-SH

reduced protein thiol

Pr-(SH)₂

reduced protein dithiol

Pr-SOH

protein sulfenic acid

Prx

peroxiredoxin

P-SSG

S-glutathionylated protein

P-SS-P

protein disulfide

ROS

reactive oxygen species

TR

thioredoxin reductase

Trx

thioredoxin

Acknowledgments

We thank Young-Mi Go and Bill Liang for their generous assistance with the redox Western blotting and HPLC techniques. Funding is provided through NSF and Ford Foundation graduate fellowships to NJA. DPJ is supported in part by NIH grants ES011195 and ES009047. MLK is partially supported by an award from the Georgia Cancer Coalition and by the NIH Director's New Innovator Award DP2OD006483.

Author Disclosure Statement

No competing financial interests exist.