A novel approach for determining environment-specific protein costs: the case of Arabidopsis thaliana

Abstract

Motivation: Comprehensive understanding of cellular processes requires development of approaches which consider the energetic balances in the cell. The existing approaches that address this problem are based on defining energy-equivalent costs which do not include the effects of a changing environment. By incorporating these effects, one could provide a framework for integrating ‘omics’ data from various levels of the system in order to provide interpretations with respect to the energy state and to elicit conclusions about putative global energy-related response mechanisms in the cell.

Results: Here we define a cost measure for amino acid synthesis based on flux balance analysis of a genome-scale metabolic network, and develop methods for its integration with proteomics and metabolomics data. This is a first measure which accounts for the effect of different environmental conditions. We applied this approach to a genome-scale network of Arabidopsis thaliana and calculated the costs for all amino acids and proteins present in the network under light and dark conditions. Integration of function and process ontology terms in the analysis of protein abundances and their costs indicates that, during the night, the cell favors cheaper proteins compared with the light environment. However, this does not imply that there is squandering of resources during the day. The results from the association analysis between the costs, levels and well-defined expenses of amino acid synthesis, indicate that our approach not only captures the adjustment made at the switch of conditions, but also could explain the anticipation of resource usage via a global energy-related regulatory mechanism of amino acid and protein synthesis.

Contact: nikoloski@mpimp-golm.mpg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The complexity of a cell is reflected in the necessity to balance the conflicting demands for resources to maintain cell vitality and function with those to support growth (Warner, 1999). The study of cell metabolism has traditionally focused on determining the factors that influence metabolic rate, at levels of both metabolic pathway and the whole organism (Heinrich and Schuster, 1996). Recently assembled condition- and tissue-specific metabolic network models (Shlomi et al., 2008) offer means for determining another compelling feature of metabolic pathways—their metabolic efficiency. In addition, the advances in omics technologies have yielded datasets from various levels of cell organization, which could be employed to make more refined biological interpretations by coupling metabolic rates, efficiencies and levels of the key system constituents (e.g. gene, proteins and metabolites).

Metabolic efficiency can be regarded as the energy-equivalent production of a pathway relative to the energy-equivalent costs for maintaining the pathway (Koehn, 1991). It is related to the energy balance of the cell given by the difference of energy supply and demand. The supply is a direct consequence of the environment, while the demand is influenced by the processes which ensure cell functions and the mechanisms for adaptation. Therefore, it is necessary that any quantification of the cellular energy state incorporates the environmental effects.

Plant growth depends on the photosynthetic assimilation of carbon dioxide and the uptake and assimilation of inorganic nutrients (Stitt and Krapp, 1999), of which nitrogen is quantitatively most important (Marschner, 1995). There is a close interplay between carbon and nitrogen metabolism in higher plants (Stitt et al., 2002). Photosynthesis provides carbon skeletons, reducing equivalents and ATP, required for assimilating inorganic nitrogen and synthesizing nucleotides, amino acids and proteins (Foyer et al., 2003; Stitt and Krapp, 1999). On the other hand, nitrogen-containing metabolites allow for utilization of carbon in growth.

Amino acids, bridging the carbon- and nitrogen-utilization pathways and necessary for protein synthesis, thus, play a pivotal role in coordinating the interactions between these two parts of metabolism. The concentrations of amino acids are likely determined by the interplay of several other processes, such as: export, storage and synthesis of metabolites other than proteins (Noctor et al., 2002). They are also closely linked with protein turnover in different nitrogen- and carbon-starved conditions (Scheible et al., 2004; Thum et al., 2004). Moreover, amino acid daily balances in conjunction with those of carbohydrates, may serve as good indicator of environmental stress, e.g. water deficit (Santos and Pimentel, 2009).

Plants typically grow in a diurnal light/dark cycle, providing an amenable system to analyze the temporal dynamics of changes in amino acid contents and their effects on metabolism (Gibon et al., 2006). For instance, it has been demonstrated that Nicotiana tabacum plants grown in short days have relatively high levels of glutamate and aspartate, and extremely low levels of most of the minor amino acids (i.e. amino acids synthesized by longer and dedicated pathways, usually present at lower levels compared with major amino acids) in their source leaves at the end of the night; moreover, illumination yields to decrease in glutamate and an increase in the minor amino acids. Due to the proximal regulation, the overall amino acid level often changes in parallel to those of sugars. This observation has led to the suggestion that sugars may exert a global control on amino acid metabolism (Matt et al., 1998). On the other hand, recent studies point out that, in Arabidopsis thaliana, fumarate and malate levels show diurnal changes similar to those of starch and sucrose: they increase during the day and decrease during the night, suggesting that they function as transient carbon storage molecules (Fahnenstich et al., 2007; Zell et al., 2010). Fumarate is synthesized from malate, which is an intermediate of the TCA cycle. As both fumarate and malate play an important role as precursors of amino acid synthesis, this raises the question of possible energy considerations in keeping certain levels of amino acids.

One of the challenges in amino acid metabolism research is the development of approaches for testing the hypothesis that the observed amino acid contents are related, and possibly explained, by mechanisms for maintaining the energy balances. Such an approach may then shed light on the long-standing problems of whether or not there is a general control of amino acid synthesis in plants and how it relates to protein synthesis (Noctor et al., 2002). Here, we develop such an approach by proposing a cost measure with respect to a given genome-scale metabolic network of A.thaliana and a specified set of environmental conditions. The results from applying the cost measure are then used to interpret publically available datasets of amino acid concentrations and protein abundances for A.thaliana under light and dark conditions.

2 APPROACH

The existing approaches for determining the cost of amino acid synthesis can be classified into three groups: the first includes the approaches which use the physical properties and atomic composition of amino acids as proxies for their cost. The second group of approaches employs a simplified set of pathways to derive the cost of amino acid synthesis from the simplified stoichiometries, while the third group comprises the approaches which rely on genome-scale metabolic networks.

2.1 Cost from physicochemical properties

Approaches in this group are based on the premise that the physicochemical properties of an amino acid, such as: its weight, atomic content and structural properties, reflect biosynthetic costs, resource investment and perhaps cytoplasmic toxicity (Dufon, 1997). Seligmann (2003) used the molecular weight of an amino acid as a proxy for energetic costs, as it is constant across species. Thus, it can be employed for testing various hypothesis even if the amino acid synthetic pathways are unknown. The approach was used to demonstrate that molecular weight is minimized across a range of bacterial and eukaryotic genomes (Seligmann, 2003). However, such a cost cannot account for the effect of varying environmental conditions.

With respect to the potential costs of the atomic content in biomolecules, Mazel and Marliere (1989) showed that, in the cyanobacterium Calothrix, abundant proteins expressed under sulfur-limiting conditions are depleted for sulfur-containing cysteine and methionine residues. Baudouin-Cornu et al. (2001) found significant correlations between atomic composition and metabolic function in sulfur- and carbon-assimilatory enzymes, which appear depleted in sulfur and carbon, respectively, in both Escherichia coli and Sacchromyces cerevisiae. In addition, by considering 141 genomes, Bragg et al. (2006) showed that the sulfur content of the encoded proteins exhibits large variance and strongly reflects the environmental conditions of an investigated species. While these findings indeed indicate that atomic composition plays an important role in biosynthetic costs, the existing measures based on physicochemical properties do not account for these factors.

2.2 Cost from simplified pathways

In the second group of approaches, the cost of an amino acid is calculated based on: (i) the Embden–Meyerhof pathway, which converts glucose 6-phosphate to pyruvate; (ii) TCA cycle, which oxidizes acetyl CoA to carbon dioxide (CO₂); and (iii) the pentose phosphate pathway, which oxidizes glucose 6-phosphate to CO₂. These pathways are not only the energy generators, but they also contain the molecules from which all amino acids are produced. Energy in the form of ATP is lost whenever a metabolite is diverted from the oxidation of glucose to the synthesis of an amino acid. Therefore, ATP is the common currency through which the bioenergetic costs of amino acids (as well as proteins, nucleotides and related molecules) and, hence, the costs of molecular variation can be compared.

Starting from the ATP equivalents required for synthesis of each of the amino acids (Neidhardt et al., 1990), Craig and Weber (1998) define the synthetic cost of an amino acid as the sum of the number of ATPs sacrificed when the amino acid's precursor metabolite is diverted from one of the three metabolic pathways and the number of ATP equivalents directly invested in its synthesis, starting from the respective precursor. By assuming that all additional costs are constant for different amino acids, the authors investigated the effects on the synthesis and evolution of a small number of E.coli proteins.

Akashi and Gojobori (2002) used a modified version of this approach to show that, in E.coli and Bacillus subtilis, predicted gene expression levels based on codon usage bias show a negative correlation with average protein cost. Recently, Heizer et al. (2006) extended these findings to four additional prokaryotic species, including also photoautotrophs, which demonstrates that this cost optimization occurs regardless of whether the energy source is organic or inorganic. Moreover, Swire (2007) used the cost measure of Craig and Weber (1998) to generate a modified measure, and showed that cost selection affects multiple prokaryotic, archaeal and eukaryotic genomes. Based on Craig and Weber (1998) and accounting for the confounding energy factors related to mRNA and protein synthesis, Wagner (2007) demonstrated that both mRNA and protein expression can change by only small amounts in yeast without additional expenditures that could have altered natural selection.

The approaches in this group have the twofold disadvantage of neglecting the effects of the existing differences in the energy and amino acid production pathways from various organisms and disregarding the influence of environmental conditions.

2.3 Cost from genome-scale models

The existing approaches for determining the cost of amino acid synthesis by means of genome-scale models are based on the principle of supply and demand, i.e. the scarcity of an atom increases the cost of synthesizing molecules including the atom.

Carlson (2007) used the concept of elementary flux modes in the genome-scale network of E.coli to show that this organism favors the expression of pathways using inexpensive proteins in stress-inducing environments (defining different supplies and demands). For the same organism, Varma et al. (1993) used flux balance analysis (FBA; see Section 3) to show that the cost of using molecules involved in energy production changes according to the availability of oxygen. Barton et al. (2008) extended this approach to estimate and compare cost of synthesizing amino acids in S.cerevisiae for four nutrient-limiting conditions (i.e. glucose, nitrogen, sulfur and phosphorus) by: (i) examining the sensitivity of growth rate to the required quantity of the amino acid per gram of biomass, and (ii) multiplying the obtained relative cost by the biomass requirement of the amino acid in the FBA model. Although this approach of fixing biomass and minimizing influx has the advantage of scaling each cost to the same growth rate and account for environmental effects, it may not be robust due to the applied method for perturbing the required amount of amino acid per gram of biomass production. Moreover, the application of this approach to plants strongly depends on the quality of the biomass reaction and the assumption of biomass optimization which is debatable even for unicellular organisms (Schuetz et al., 2007).

2.4 Our approach

Here, we develop an FBA-based approach for estimating the cost of amino acid synthesis based on a recently published genome-scale metabolic network of A.thaliana. The approach overcomes the drawbacks of biomass optimization used in plants, by considering the minimization of nutrient uptake. To investigate the effect of diurnal changes on the amino acid content, we consider the two environmental conditions—light and dark—by modifying the metabolic model according to existing biological knowledge. The calculated costs for the two conditions are then used to interpret publically available proteomics and metabolomics measurements for A.thaliana.

2.5 Datasets

For the dataset from Gibon et al. (2006), A. Col0 WT plants were at least 3 weeks before the measurements transferred to a small growth cabinet with a 12 h light period of 160 μE and 20^○C throughout day and night. Harvests of 15 plant rosettes at a time point were carried out sequentially every 2 h within a day/night cycle. Each sample typically contained three rosettes and was powdered under liquid nitrogen and stored at −80^○C. Each experiment was repeated two times. The extraction and assay of metabolites was done by GC-MS and LC-MS. The amino acid levels used in this study are expressed as ratios between samples and the median calculated for control samples.

The proteomics dataset was obtained from plants grown in a 8 h light period of 145 μE with color fluorescent lights and 20^○C throughout the day/night cycle for 3 weeks before harvesting. Five independent samples of five whole rosettes per sample were gathered and immediately frozen in liquid nitrogen. Sampling was performed in the last hour of the day or of the night, respectively, and completed within 1 h. The relative protein abundance was estimated by emPAI as described in Ishihama et al. (2005).

3 METHODS

3.1 Genome-scale metabolic model of A.thaliana

We use a recently published model of A.thaliana (Poolman et al., 2009), which is the first genome-scale metabolic model of a plant species. The original model consists of 1253 metabolites related via 1406 reactions. The model is capable of producing biomass components, i.e. all amino acids, nucleotide bases, palmitate as a ‘generic lipid’, starch and cellulose, solely from the metabolic precursors: glucose, nitrate NO₃, ammonia NH₃, sulfate SO₄ and phosphate P_i. The precursor metabolites and the biomass components have external counterparts. Together with H⁺ and H₂O, which are external due to inconsistencies in H⁺ and O balances in the included reactions, there are, in total, 44 external metabolites.

The given network was altered in order to provide a biologically meaningful cost measure. The transporter reactions for the influx of precursor metabolites were switched from reversible to irreversible in the direction of influx since the reverse reactions do not take place. The biomass component transporter reactions were constrained to efflux in order to prevent energy production from the degradation of biomass components, which should not enter the system once they have been produced and exported out. The reversibility of few reactions were also altered based on existing knowledge about the physiology of these reactions (cf. Supplementary table). Moreover, in the degradation pathway of threonine and lysine, the reversibility of some reactions had to be altered to avoid production by the reverse degradation pathway (Supplementary Material).

The transporter reactions for bringing amino acids and nucleotides out of the system were corrected to include the energetic costs. Amino acid transporter reactions have been altered in the following way:

(1)

where a denotes an arbitrary amino acid, x_a the corresponding external metabolite and PPi denotes pyrophosphate. Nucleotide transporter reactions have been corrected such:

(2)

where u denotes an arbitrary nucleotide and x_u its external counterpart.

For plant metabolism, we consider two different scenarios: dark (night environment) and light (day environment). The transporter influx reaction of glucose is used in both environments. In the day environment, the phosphofructokinase is set to zero. In the night environment, the fructose 1,6-biphosphatase and phosphoribulokinase reactions are constrained to zero flux since they are mostly inactive; the same argument holds for the RuBisCo reaction, incorporating CO₂, and for sedoheptulose-biphosphatase, which is the most important factor for the RuBP regeneration in the Calvin Cycle.

3.2 FBA

FBA is a modeling framework developed to characterize the synthesizing capabilities of metabolic networks. For every metabolite X_i, a mass balance is derived as dX_i/dt = ∑s_ijv_j − b_i, where s_ij is the stoichiometric coefficient associated with each flux v_j, through reaction j, and b_i, the net transport flux of X_i. The mass conservation relation under the steady-state conditions (dX_i/dt = 0) reduces to the expression:

(3)

where S is the stoichiometric matrix (m rows and n columns), v is the vector of n metabolic fluxes and b is the vector representing m transport fluxes. The transport fluxes for internal metabolites are set to zero. As the system described in Equation (3) is underdetermined (n > m), there exist multiple solutions corresponding to feasible flux distributions, each representing a particular metabolic state satisfying these stoichiometric constraints. The transport fluxes represent environmental conditions that, along with the genotype, define the metabolic state. The question addressed by FBA is then, which of these feasible metabolic states is manifested in the studied metabolic network model.

FBA relies on the assumption that the metabolic system exhibits a metabolic state that is optimal under some criteria. Usually, this objective is expressed as linear combination of fluxes contained in v, which leads to a linear programming (LP) problem:

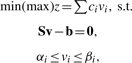with z representing the phenotypic property, and c is a vector of coefficients which are either costs or benefits derived from fluxes. The bounds α_i and β_i, represent known constraints, i.e. the minimum and maximum values of fluxes and, thus, determine reaction reversibility.

Proposition 1. —

Linear scaling of the constraints for the elements of v leads to a linear scaling of the outcome of optimizing z.

Proof. —

Given a stoichiometric matrix S, let v be a vector such that Sv = 0, v_k = d_k with k ⊂ {1,…, n} and min c^Tv = r. To show that when v_k′ = g · d_k, min c^T v′ = g · r with v′ = g · v, we assume that with such that and . A scaled vector then fulfills the conditions Sv′′ = 0 and v_k′′ = d_k and we arrive at contradiction that c^T v′′ < r = min c^Tv.

The most common choice for the objective function is the maximization of yield, which allows a wide range of predictions consistent with experimental observations for simple model organisms (Edwards and Palsson, 2002; Schuster et al., 2008). This function could be employed for environments with nutrient excess. Other optimization functions include: minimization of ATP production, to determine the conditions for energy efficiency and minimization of nutrient uptake, modeling the case of nutrient scarcity (Schuetz et al., 2007).

3.3 Novel FBA-based cost measure

We define the cost of an amino acid a, denoted by C_a as the sum of the energy equivalents of the precursor metabolites necessary for its synthesis. Let the number of molecules of a precursor metabolite p involved in the synthesis of the amino acid a be denoted by N_a^p. The value of N_a^p is defined by the ratio of the influx v_p of the metabolite p and the efflux of the amino acid a, i.e.

(4)

yielding the number of precursor molecules used in the production of one molecule of the amino acid a.

Note that the value of N_a^p is positive, since the influx of a precursor metabolite, like the efflux of an amino acid, is defined as positive. The set of precursor metabolites is given by M = {glucose, NH₃, NO₃, SO₄, P_i}. In the FBA formulation, we minimize the glucose uptake for both day and night environments. According to Proposition 1, the fluxes v_p and v_a scale equally, so we can set efflux v_a to an arbitrary (positive) value. Moreover, the influx of all precursor metabolites is unconstrained from above, while the effluxes of all amino acids, other than a, are constrained to zero. In other words, the solution of the defined linear program yields a distribution of influxes for the precursor metabolites which scale linearly with the efflux of the only amino acid that can be produced under the objective of minimizing the energy equivalents reflected in the uptake of glucose.

Let e_p denote the number of ATP molecules equivalent to one molecule of metabolite p. The cost of the amino acid a can then be formulated as:

(5)

The values of e_p for different precursor metabolites were set, according to (Zerihun et al., 1998), as: e_glucose = 36, e_NO3 = 12 and e_NH3 = 1.33. Our results indicate that the remaining precursor, SO₄, plays a negligible role and is not included in the cost; moreover, P_i is not utilized in the production of any amino acid. Note that the cost of redox equivalents is fully accounted by the utilization of glucose. The FBA analysis was performed by using the CellNetAnalyzer package for MATLAB (Klamt et al., 2007).

4 RESULTS AND DISCUSSION

By applying our approach, the cost of amino acid synthesis for two different scenarios—day and night—were calculated and presented in Table 1. We then investigated the effect of considering two environmental conditions by employing the Kendall rank correlation coefficient. Our cost measure for the day condition is significantly correlated (P < 0.01) with the cost from Craig and Weber, τ = 0.51; Akashi and Gojobori, τ = 0.73; and Seligmann, τ = 0.69, also presented in Table 1; however, for the night environment, significant correlation is not present between our cost and that of Craig and Weber.

Table 1.

Comparison of amino acid cost measures

Env. (units)	Our cost		CW	AG	Sel
	Day (ATP)	Night (ATP)	ATP	ATP	g/mol
Cys	19.33	19.33	24.5	24.7	121.16
Asp	25.33	31.30	1	12.7	133.10
Asn	26.66	32.63	4	14.7	132.12
Glu	31.33	49.33	8.5	15.3	147.13
Gln	32.66	50.66	9.5	16.3	146.15
Ser	19.33	19.33	15	11.7	105.09
Gly	13.33	13.33	14.5	11.7	75.07
Thr	25.33	31.33	6	18.7	119.12
His	39.99	45.99	33	38.3	155.16
Ala	19.33	19.33	12.5	11.7	89.09
Tyr	55.33	61.33	56.5	50	181.19
Arg	41.32	53.32	18.5	27.3	174.20
Val	31.33	37.33	25	23.3	117.15
Trp	68.66	74.66	78.5	74.3	204.23
Met	31.33	43.33	18.5	34.3	149.21
Phe	55.33	61.33	63	52	165.19
Ile	37.33	49.33	20	32.3	131.17
Leu	37.33	55.33	33	27.3	131.17
Lys	38.66	50.65	18.5	30.3	146.19
Pro	31.33	49.33	12.5	20.3	115.13

FBA-based cost measure of amino acid synthesis in terms of ATP for the day (first column) and the night (second column) environment. Columns labeled CW, AG and Sel contain the costs according to Craig and Weber (1998), Akashi and Gojobori (2002) and Seligmann (2003), respectively.

With respect to the energetic relations between the day and night environments, without distinguishing the function and conversion ability of the amino acids, the two costs are significantly correlated, τ = 0.864, P < 0.01. Significant correlations (P < 0.01) can also be demonstrated for the environment-specific costs within the groups of minor (i.e. His, Arg, Tyr, Trp, Met, Val, Phe, Ile, Leu and Lys) and major amino acids, with τ = 0.744 and τ = 0.988. However, there is no statistical significance for observing concordant and discordant pairs of costs within the ketogenic amino acids, including: Leu, Lys, Ile, Phe, Thr, Tyr, Trp. In contrast to the glycogenic amino acids which can be converted into glucose, ketogenic amino acids can be converted into ketone bodies by both breakdown of lipids and the formation of energy source.

Akashi and Gojobori (2002) pointed out that A- and T-rich codons tend to encode more costly amino acids, supported by significant Kendall rank correlation coefficient (P < 0.05). We conducted a similar analysis for the costs from the two considered scenarios and did not find any significant association with the mean codon GC content, despite the significant correlation between our and the cost measure of Akashi and Gojobori (2002). This indicates that the usage of our cost measure to explain levels of the considered system constituents (i.e. amino acids and proteins) may not be confounded by GC-content effects.

These three findings demonstrate that, indeed, both energetic and physicochemical characteristics of the amino acids shape their costs, and that by considering only one of the aspects on its own, we cannot distinguish between the investigated environments.

Next, we calculate the cost C_P of a protein P with n amino acids a_i, 1 ≤ i ≤ n according to C_P = 4 · 16n + ∑_i=1ⁿC_ai + 2. The term 4 · 16n + 2 indicates the number of ATP molecules consumed in the three main stages of protein synthesis: initiation, elongation and release (Zerihun et al., 1998). Proteins of A.thaliana from different functional and process categories may differ in terms of their levels and energetic costs between the two different environments. To control for these effects, we examined the associations between costs and protein concentrations within both, function and process, categories for the two investigated conditions.

From the 1153 and 2109 identified proteins, 616 and 978 were reliably quantified for the day and night conditions, respectively. From these, there were 202 proteins with assigned function category and 196 proteins with resolved process category in both conditions. We then considered how these proteins, occurring in both environments, are distributed across the GO slim function and process terms obtained from TAIR (Berardini et al., 2004).

The Kendall rank correlation coefficients between costs and protein levels for both, function and process categories were negative for the two conditions, as indicated in Table 2. This finding implies that it is more likely for expensive proteins to be present at low levels as compared with cheap proteins. Interestingly, we observed that the determined associations are smaller in the day as compared with the night. This suggests that our cost measure captures the economizing mode in which the cell may enter during the night, forcing it to increase the level of cheaper proteins.

Table 2.

Association of protein costs and GO slim categories

	nP	τ day	τ night
Function
Hydrolase activity	20	−0.097*	0.037*
Kinase activity	7	0*	−0.666*
Transferase activity	17	−0.240*	−0.322*
Other enzyme activity	66	−0.341	−0.289
DNA or RNA binding	11	0*	−0.050*
Nucleotide binding	41	−0.316	−0.314
Protein binding	14	0.142*	−0.314*
Other binding	62	−0.302	−0.254
Structural molecule activity	46	−0.210	−0.080*
Other molecular functions	10	0.6*	0*
Process
Transport	11	−0.71	−0.428*
Other cellular processes	100	−0.346	−0.388
Protein metabolism	64	−0.474	−0.406
Other metabolic processes	103	−0.360	−0.339
Other biological processes	76	−0.099*	−0.160*

Only GO slim categories for which n_P, the number of proteins, is greater than zero are shown. The Kendall rank correlation coefficients which are not significant at level 0.05 are marked with * following the value for τ.

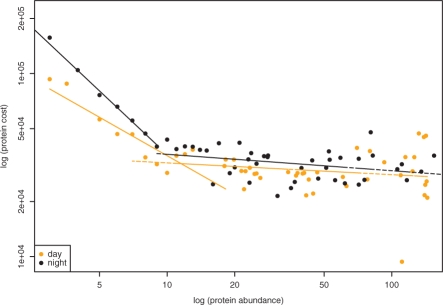
Moreover, by investigating the relationship between the abundance of proteins and their respective costs, we were able to determine two scale-free laws. The first scale-free law holds for proteins which are present at small relative levels (below 8); its exponent for the day is −0.697 (Fig. 1), while for the night environment it is −1.154. The second scale-free law holds for proteins with relative abundance above 8 units, again with a larger exponent of −0.064 for the day condition as compared to −0.089 for the night condition. The larger exponents for the night demonstrate that the pressure for cheaper proteins is more prominent in the night.

Fig. 1.

Scale-free relationship between relative abundances and costs of proteins for day and night environment. Proteins which occur at same levels with different price are binned. The x-axis shows the average protein abundance per bin, while the y-axis depicts the average cost of proteins per bin. Both day and night environments exhibit two scale-free laws: one at average protein abundances below 8 and the other above a value of 8.

We point out that these findings in terms of proteomics data do not necessarily imply that there is squandering of resources in the day environment. To demonstrate that this, indeed, is the case, we revisit the levels of amino acids which are essential for protein synthesis.

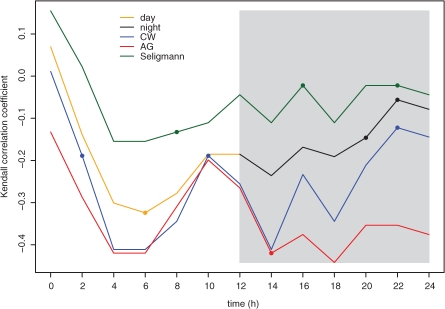
In terms of the Kendall correlation coefficient, the association between the five costs for 14 amino acids (i.e. Glu, Gln, Asp, Ala, Pro, Thr, Ile, Leu, Val, Met, Phe, Tyr, Trp and Arg) and their experimentally determined levels in A.thaliana Col0 wild-type for 12 h of light followed by 12 h of darkness is shown in Figure 2. It can be seen that all costs behave similarly for the day environment, while our cost for the night environment shows difference in trend.

Fig. 2.

Association between amino acid levels and their costs. The Kendall rank correlation coefficients between the amino acids and the day costs (orange), night cost (black), CW cost from Craig and Weber (1998) (blue), AG cost from Akashi and Gojobori (2002) and the cost from Seligmann (2003) are calculated for a period of 24 h. The night environment is depicted in gray. Correlations which are not significant (P ≥ 0.05) are shown with filled points.

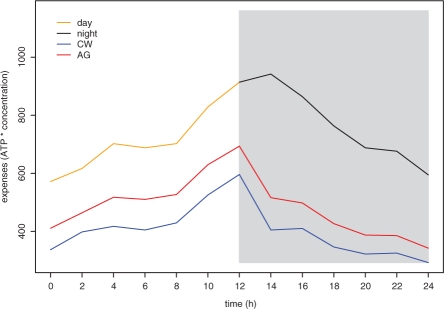
This becomes pronounced when we compare the cost measures via the expense for production of amino acids, determined by expense = ∑_a l_a · C_a, where C_a is the cost of an amino acid and l_a is its level. The behavior of the expense for the three measures yielding ATP-equivalent cost is shown in Figure 3. It is striking that both measures, from Craig and Weber (1998) and Akashi and Gojobori (2002), show smaller expense at the end of the night (Hours 24) compared with the beginning of the day (Hour 0) as well as a sharp decline in the expenses at the switching point between light and dark. On the other hand, our measures for the day and night environments resolve this discrepancy and also provide quantification for the adjustment to the switch in conditions; namely, the increasing trend in the expenses from the light condition continues for two more hours in the dark, followed by decline ‘symmetric’ to the expenses incurred under the light condition.

Fig. 3.

Expenses for amino acid synthesis calculated in ATP times relative concentration. The expenses for our day cost (orange) and night cost (black) as well as the costs from Craig and Weber (1998) (blue) and Seligmann (2003) (red) are calculated for a period of 24 h. The night environment is depicted in gray. The expense for Seligmann's cost is not shown due to difference in units.

Assuming that the cell has a maximum allowable energy budget (Hand and Hardewig, 1996), these findings imply that the energy status may be an important mechanism for the control of amino acid synthesis and its related processes, allowing spending which would not jeopardize the vitality of the cell.

Finally, we point out that the approach can be applied to any environmental condition which can be appropriately reflected in a given genome-scale metabolic network (e.g. via exclusion and inclusion of reactions, as performed here, or by choosing suitable uptake and production rates which match experimental observations). The biological interpretation of the results directly depends on: (i) the quality of the metabolic network and (ii) the choice of the optimization criterion.

It has to be mentioned that the network of A.thaliana employed in this study contains inconsistencies in H⁺ and O, which has been resolved by setting H⁺ and H₂O to external. This may lead to an oxidative potential and, thus, to production of energy out of nothing. Moreover, the considered model is not compartmentalized, but is consistent with a standard view of metabolic compartmentation between plastid and cytosol (Poolman et al., 2009). Moreover, according to Poolman et al. (2009), the lack of a separate plastidic compartment can be seen to be justifiable for heterotrophic plant cells, which may not be the case for autotrophic plants. Finally, although we do not explicitly consider the protein turnover cost, our measure qualitatively reflects the turnover cost due to protein synthesis.

It may be debatable whether or not the chosen objective in the FBA analysis should be linear in plants species, as it is often the practice with FBA-based studies of micro-organisms. However, we believe that minimization of the nutrient uptake is suitable for scarce resources and could be used to investigate the effects of such scenario on the cost of amino acid and protein synthesis. We note that the consideration of a nonlinear optimization function would require an extension of the approach since in this case Proposition 1 does not hold. In this case, the cost calculation can be slightly altered to incorporate measured data for the biomass transporter reaction flux rates. The objective function of the nonlinear program then yields the uptake fluxes v_p for the situation of full production of measured biomass components. The calculation is repeated with setting the transporter reaction flux rate v_a of the amino acid of interest to zero, yielding the precursor metabolite uptake fluxes v_p^a→0 for the altered constraint. Then the cost is given by the difference of precursor metabolite uptake fluxes for the two situations divided by the measured efflux rate of the compound of interest, i.e. C_a = (v_p − v_p^a→0)/v_a. This approach will be investigated for other published plant organ-specific compartmentalized networks (e.g. Grafahrend-Belau et al., 2009) and their coupling with ‘omics’ data.

5 CONCLUSIONS

We developed the first environment-specific cost measure for amino acid synthesis based on FBA of genome-scale metabolic networks. This measure allows for calculating the costs of protein synthesis under different environmental scenarios. In addition, we devised an approach for integrating the ATP-equivalent amino acid and protein costs with function- and process-resolved metabolomics and proteomics data. By applying the approach on a genome-scale network of A.thaliana under light and dark conditions, with the help of the available omics data, we demonstrated that the control of the cellular energy balance may play an important role as a global regulatory mechanism of not only amino acid but also protein synthesis.