Integrated study of copy number states and genotype calls using high-density SNP arrays

Abstract

We propose a statistical framework, named genoCN, to simultaneously dissect copy number states and genotypes using high-density SNP (single nucleotide polymorphism) arrays. There are at least two types of genomic DNA copy number differences: copy number variations (CNVs) and copy number aberrations (CNAs). While CNVs are naturally occurring and inheritable, CNAs are acquired somatic alterations most often observed in tumor tissues only. CNVs tend to be short and more sparsely located in the genome compared with CNAs. GenoCN consists of two components, genoCNV and genoCNA, designed for CNV and CNA studies, respectively. In contrast to most existing methods, genoCN is more flexible in that the model parameters are estimated from the data instead of being decided a priori. GenoCNA also incorporates two important strategies for CNA studies. First, the effects of tissue contamination are explicitly modeled. Second, if SNP arrays are performed for both tumor and normal tissues of one individual, the genotype calls from normal tissue are used to study CNAs in tumor tissue. We evaluated genoCN by applications to 162 HapMap individuals and a brain tumor (glioblastoma) dataset and showed that our method can successfully identify both types of copy number differences and produce high-quality genotype calls.

INTRODUCTION

Several recent studies have documented the extensive presence of inheritable copy number variations (CNVs) in the human genome (1–8). Copy number aberrations (CNAs), which are acquired somatic alterations, are often observed in tumor tissues (9,10). In contrast to CNVs, CNAs tend to be longer and occupy a significant proportion of the genome. In addition to the traditional array CGH approach (11), CNVs or CNAs can also be detected by SNP arrays, which typically have higher resolution and are able to capture allele-specific information (12). In this article, we propose a statistical framework to simultaneously dissect copy number states and genotypes within CNV/CNA regions. Currently, the two most frequently used SNP array platforms are from Affymetrix (8) and Illumina (13). In this article, we focus on Illumina SNP arrays, however, our method, accompanied with an appropriate normalization and transformation of the raw data, can also be applied to Affymetrix SNP arrays. Adjustments for CNV and CNA are also needed to ensure precise genotype calls when using SNP arrays for genotyping.

Various methods have been proposed to study copy number alterations. These methods can be classified based on their input and output data. We first briefly introduce different types of input data. Denote the two alleles of one SNP as A and B, respectively, and let X/Y be the normalized intensities of allele A/B, i.e. allele-specific copy number measurements. X and Y can be transformed to a measure of overall copy number and a measure of allelic contrast. For example, the outputs of Illumina SNP arrays are Log R ratio (LRR) and B allele frequency (BAF), which are overall copy number measure and allelic contrast measure, respectively (13). The calculation of LRR and BAF is elaborated at the beginning of the ‘Method’ section.

First, segmentation methods such as circular binary segmentation (14) and forward–backward fragment assembling (FASeg) (15) have been applied to dissect copy number states based on overall copy number measurements (e.g. LRR). These methods are simple and robust, but have the limitation that they cannot produce allele-specific copy number estimates. A more advanced segmentation method is proposed by Staaf et al. (16), which is able to detect allelic imbalance and loss of heterozygosity (LOH).

Second, model-based approaches such as CARAT (17) and PLASQ (18) have been developed to identify CNAs in tumor tissue based on the assumption that the relationship between copy number and probe intensity is approximately linear on a log–log scale. The inputs are genotypes in normal tissues and allele-specific copy number measurements (i.e. X and Y) in both normal and tumor tissues. The outputs are allele-specific copy number estimates in tumor tissue. Specifically, a linear model in log–log scale is build for each SNP based on the data from normal tissues, and then the resulting model is used to predict the copy number in tumor tissue. At the end, the results are further smoothed across SNPs. One weakness of these approaches is that the model parameters estimated from normal tissue may not be appropriate for tumor tissue, for example, due to normal tissue contamination. Normal tissue contamination is inevitable in cancer studies and it may be due to different reasons. For example, normal tissue adjacent to tumor tissue that is incompletely removed during the process, and/or the presence of nontumor stromal cells and immune cells, which are typically a part of every solid tumors examined.

The third type of approach focuses on identifying LOH together with qualitative copy number states (e.g. deletion, normal and amplification) in tumor tissue (19) or in generic situations (20). Their inputs include copy number measurements and some prior knowledge regarding the copy number and/or genotypes. Specifically, in Yamamoto et al. (19), a genomic region of copy number 2 in tumor tissue needs to be known and the heterozygosity of each SNP needs to be redefined based on empirical results. Scharpf et al. (20) proposed a hidden Markov model (HMM) integrating observed heterozygosity status and copy number measurements. Their method enjoys the ability to exploit the confidence scores of the genotype calls. One shared limitation of these two methods is that the prior knowledge of the copy number and/or genotype may not be available, or may be inaccurate in CNV/CNA regions.

A recent paper (21) proposed a framework for integrated study of genotype and copy number by analyzing common and rare CNVs separately. Specifically, Korn et al. (21) treated those common CNVs (>1% frequency in the population) as copy number polymorphisms (CNPs) with known locations as well as a few allele-specific copy number states. Therefore the identification of common CNVs reduced to ‘genotyping’ the CNPs. For the rare CNVs (≤1% frequency), they identified copy number states within each sample by an HMM using allele-specific copy number measurements. Then the genotypes of each SNP within CNV regions are identified by a two dimensional clustering across individuals.

All the above methods are mainly designed for Affymetrix SNP arrays. For Illumina SNP arrays, two HMM-based approaches, QuantiSNP (22) and PennCNV (23), have been developed to identify copy number states based on both LRR and BAF. Both QuantiSNP and PennCNV are based on a HMM with hidden states listed in Table 1. PennCNV assumes that the mean value and SD of LRR and BAF for each HMM state are known. QuantiSNP imposes some common priors for the LRR/BAF parameters so that only a few hyper-parameters need to be estimated. In addition, PennCNV has an additional advantage that family relationships can be utilized. However, both methods are not designed for CNA studies and do not provide output on allele-specific information, such as genotypes.

Table 1.

Six states of genoCNV

State	Copy number	Genotype
1	2	AA, AB, BB
2	2	AA, BB
3	0	Null
4	1	A, B
5	3	AAA, AAB, ABB, BBB
6	4	AAAA, AAAB, AABB, ABBB, BBBB

Despite the successes of the aforementioned methods in different applications, some important issues remain to be addressed, which motivated our study. First, as we mentioned previously, normal tissue contamination in tumors occurs and complicates the determination of true tumor-specific copy alterations of solid tumors, and as shown in the ‘Results’ section, it may lead to significant changes of the data. However, no method has been designed to dissect copy number and genotype calls within CNA regions in the presence of normal tissue contamination. Although both CARAT (17) and PLASQ (18) are able to dissect allele-specific copy number states, and hence genotypes, none of them has taken normal tissue contamination into account. In addition, these two methods heavily depend on the design of Affymetrix SNP arrays, thus it is not trivial to extend them to the data generated from Illumina SNP arrays. Secondly, existing methods such as QuantiSNP and PennCNV either assume that the model parameters are known or impose some common priors. These restrictions may be reasonable for CNV studies, but they reduce the flexibility of CNA studies. For example, varying proportions of normal tissue contamination across samples require sample-specific model parameters.

In this article, we propose a more sophisticated HMM-based framework: genoCN. GenoCN consists of two components: genoCNV and genoCNA, which are designed for CNV and CNA studies, respectively. The input data are LRR and BAF of each SNP. For CNA studies, the genotype calls of normal tissue (of the same patient) are an optional input. The outputs are the posterior probabilities of copy number and genotype of each SNP. A complete parameter estimation scheme is developed so that those HMM parameters are estimated from the data. The HMMs for genoCNV and genoCNA are designed differently to incorporate different genotype classes in CNV and CNA data as well as the effects of tissue contamination in CNA data. In addition, genoCNA is able to utilize genotype calls from normal tissue to improve its robustness and accuracy.

METHOD

Calculation of LRR and BAF

Recall that for each SNP, X and Y are the normalized intensity measurements of allele A and B, respectively. X and Y are first transformed to be R = X + Y and θ = arctan(Y/X)/(π/2) so that R measures the overall copy number and θ measures the allelic contrast. LRR is defined as log₂(R_observed/R_expected). If SNP arrays are performed for both tumor and normal samples of the same individual, we simply have R_observed = R_tumor and R_expected = R_normal. Otherwise, R_expected is computed by linear interpolation of the canonical genotype cluster centroids. The canonical genotype clusters are three clusters corresponding to genotype AA, AB and BB on the scatter plot of R versus θ [Figure 1 of Peiffer et al. (13)]. The canonical genotype clusters for each SNP can be generated from all the samples in the study or from a set of reference samples, such as HapMap samples. The BAF is normalized θ. Specifically,

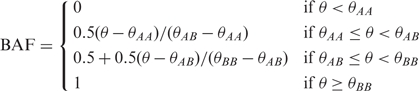where θ_AA, θ_AB and θ_BB are the θ values for the centroids of the three canonical genotype clusters corresponding AA, AB and BB, respectively. Based on the above formula, BAF should be around 0, 0.5 and 1 for genotype AA, AB and BB, respectively. If the BAF value of an SNP is deviated away from these three values, it may indicate copy number alterations. For example, a BAF value 0.33 may indicate a genotype of AAB.

Figure 1.

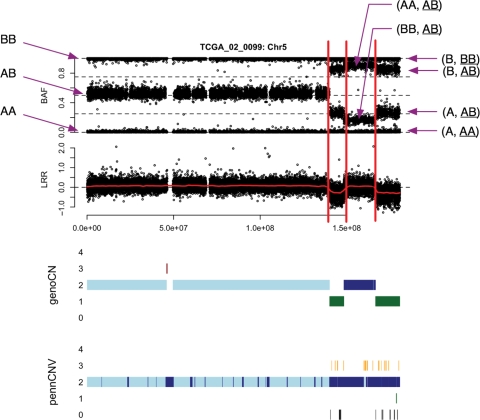
BAF and LRR of chromosome 5 of TCGA sample 02_0099, as well as the results of genoCNA and PennCNV. The y-axis of the results of genoCNA/PennCNV corresponds to copy number. For a certain copy number, there may be different states, which are distinguished by different colors. In this example, for copy number 2, ‘light blue’ and ‘dark blue’ indicate States 1 and 2 of genoCNA, respectively. When copy number is 3, ‘orange’ and ‘dark red’ indicate States 5 and 6 of genoCNA, respectively.

Two continuous time HMMs with discrete states

We employ HMM to infer both copy number states and genotypes from SNP array data. HMMs have been widely used in speech recognition (24), and more recently in DNA/protein sequence alignment (25). In those applications, the ‘time’ space of the Markov process is discrete. For example, in DNA sequence studies, one time point is just 1 nt. Therefore, discrete time HMMs are used in these studies. In the studies of SNP array data, ‘time’ is equivalent to the genomic location. Because the data (DNA allele intensities) are only observed at SNP probes and the distances between adjacent SNP probes vary, we employ continuous time HMM to model the transition between adjacent probes. Two HMMs with different states are designed for CNV and CNA studies, which we refer to as genoCNV and genoCNA, respectively.

Similar to the previous studies (22,23), genoCNV has six states (Table 1). The State 2 is often referred to be ‘copy number neutral LOH’. It is a genomic aberration, which may be due to uniparental disomy, mitotic recombination events or deletion of one allele and subsequent duplication of the remaining allele. LOH has been related with cancer since losing one allele of a tumor suppressor gene may lead to cancer genesis. Unlike the previous studies (22,23), we estimate the parameters from data instead of fixing them or imposing prior distributions. More importantly, genoCNV dissects both copy number and genotype calls, while the previous studies (22,23) only output copy number state estimates.

Unlike genoCNV, genoCNA has nine states (Table 2). For copy number 3 or 4, it is possible that one allele is deleted first before the other allele is amplified. States 6 and 8 correspond to this situation. State 7 is due to simultaneous amplification of both alleles, and State 9 is due to the amplification of one allele twice. In addition, tissue contamination leads to two extra genotype classes for the states having only homozygous genotypes (States 2, 4, 6 and 8). For example, in a locus of hemizygous deletions (loss of one allele) in tumor tissue, the remaining allele could be either A (corresponding to AA or AB in normal tissue) or B (corresponding to AB or BB in normal tissue). With tissue contamination, the observed LRR and BAF reflect the mixture distribution of (A, AA), (A, AB), (B, AB) and (B, BB). Here we use underscore to indicate that the genotype is from normal tissue contamination. The expected LRR of these four mixtures are the same, but closer to 0 compared with the LRR without normal tissue contamination. This is because without normal tissue contamination, the copy number is 1, and the corresponding LRR is negative, denoted by β (β < 0). In contrast, the copy number within normal tissue is 2, thus the corresponding LRR is ∼0. With normal tissue contamination, the copy number is between 1 and 2, and thus the LRR for the mixture is between β and 0. The expected BAFs of (A, AA) and (B, BB) are still 0 and 1, respectively. The BAFs of (A, AB) and (B, AB) are no longer 0 and 1. Their exact values depend on the proportion of tissue contamination and they form two extra bands in BAF plot, or equivalently, two genotype classes.

Table 2.

Nine states of genoCNA

State	Copy number	Genotype
1	2	AA, AB, BB
2	2	AA, (AA, AB), (BB, AB), BB
3	0	Null
4	1	(A, AA), (A, AB), (B, AB), (B, BB)
5	3	(AAA, AA), (AAB, AB), (ABB, AB), (BBB, BB)
6	3	(AAA, AA), (AAA, AB), (BBB,AB), (BBB, BB)
7	4	(AAAA, AA), (AABB, AB), (BBBB, BB)
8	4	(AAAA, AA), (AAAA, AB), (BBBB, AB), (BBBB, BB)
9	4	(AAAA, AA), (AAAB, AB), (ABBB, AB), (BBBB, BB)

Genotype classes in parenthesis, such as (A, AB) are due to normal tissue contamination of genotype A from tumor tissue and genotype AB from normal tissue. Here we use underscore to indicate that the genotype is from normal tissue contamination.

Following the notations of Wang et al. (23), we use r_i, b_i and z_i to indicate the LRR, BAF, and the hidden state at the i-th SNP probe, respectively. Assuming that the LRR and BAF are independent given the underlying states, the full likelihood is

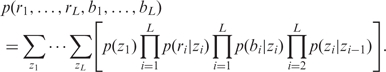1

If SNP arrays are performed in both tumor and normal tissues of the same individual, we incorporate the genotype calls in normal tissue into genoCNA. Let g_i be the genotype of the i-th SNP in normal tissue, we have the overall likelihood:

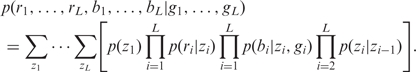2

The genotype in normal tissue is based on the assumption that the copy number is 2, thus it can only be AA, AB or BB; therefore it does not provide information of the actual copy number in tumor tissue. This is why the likelihood of r_i does not depend on g_i. However, the genotype in normal tissue restricts the genotype in tumor tissue. For example, if the genotype in normal tissue is AA, then either deletion or amplification can only produce genotypes of homozygous A. Specifically, Table 3 lists all the possible correspondences between genotypes in normal tissue and tumor tissue. We also allow a small probability that those correspondences are violated, which could be due to genotyping error in normal tissue.

Table 3.

Correspondence between genotypes in normal tissue and tumor tissue

Normal	HMM states and genotypes in tumor tissue
	1	2	3	4	5	6	7	8	9
AA	AA	AA	Null	A	AAA	AAA	AAAA	AAAA	AAAA
BB	BB	BB	Null	B	BBB	BBB	BBBB	BBBB	BBBB
AB	AB	AA, BB	Null	A, B	AAB, ABB	AAA, BBB	AABB	AAAA, BBBB	AAAB, ABBB

The full likelihoods in Equations (1) and (2) include transition probabilities (p(z_i|z_i−1)) and the emission probabilities of LRR (p(r_i|z_i)) and BAF (p(b_i|z_i) or p(b_i|z_i, g_i)). Some SNP arrays incorporate some copy-number-only probes, which only have one allele. For those probes, we discard the BAF information, and only keep the emission probability of LRR and transition probability in the full likelihood. Next we discuss how to formulate these probabilities.

Transition probability

For continuous time HMM, the transition probability is evaluated according to time. p_jk(t) ≡ p(s(w + t) = k|s(w) = j) is the transition probability from state j to k during time t, where s(w) and s(w + t) indicate states at time w and w + t, respectively. An intensity matrix Λ = (λ_jk) is used to model the instantaneous transition rate, where λ_jk = lim_Δt→0p_jk(Δt)/Δt, j ≠ k and λ_jj = −∑_k≠j λ_jk. The transition probability can be calculated by matrix exponential: p_jk(t) = exp(tΛ). However, matrix exponentials are often difficult to compute efficiently and reliably (26). We bypass this problem by assuming that there is at most one state transition between two adjacent SNP probes. Under this assumption, no matrix exponential is needed. This assumption is reasonable for high-density SNP arrays, as the adjacent SNP probes are generally close to each other. Occasionally, the distance between two adjacent SNP probes is big (or in the extreme case, if we consider two chromosomes), then we restart the Markov process.

Let λ_j = ∑_k≠j λ_jk. The waiting time that the Markov process stays at state j, denoted by T_j, follows an exponential distribution with parameter λ_j. Let d_i be the distance between the (i − 1)-th probe and the i-th probe.

3

For a Markov process at time i and state j, once it leaves state j, the transition probability to another state k is a_jk = λ_jk/λ_j. In addition, T_j is independent with the destination state k (27). Based on our assumption that ‘there is at most one state transition between two adjacent probes’, the transition probability from state j to k (k ≠ j) is

4

where ∑_k≠ja_jk = 1.

Emission probability of LRR

Similar to the previous studies (22,23), we model the emission probability of LRR (denoted as r) by the mixture of a uniform distribution and a normal distribution. Let φ(r; μ, σ) be the density function of normal distribution with mean μ and SD σ.

5

where the uniform distribution (with density 1/R_m) models the background noise, the normal distribution with mean μ_r,z and SD σ_r,z models the LRR signals of state z, and π_r,z is the mixture proportion of the uniform component. We treat R_m as a known constant, which is simply the length of LRR's range.

Emission probability of BAF

We model BAF (denoted as b) by the mixture of a uniform component for background noise and several (truncated) normal components:

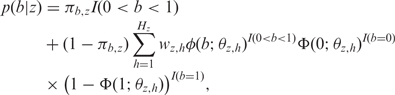6

where π_b,z is the mixture proportion of the uniform component for state z, I(.) is the indicator function, H_z indicates the total number of normal components of state z, and w_z,h is the weight of the h-th component. φ and Φ indicate normal density and cumulative normal distribution, and θ_z,h = {μ_b,z,h, σ_b,z,h} indicates the mean and SD of the h-th normal component for state z. The genotype classes of one state are ordered by the number of B alleles as shown in Tables 1 and 2.

Now we discuss the values of w_{z, h}. The weight for State 3 (the null state with both alleles deleted) is 1 for either genoCNV or genoCNA. Besides State 3, for genoCNV or genoCNA without genotype from normal tissue, w_z,h are binomial probabilities based on the population frequencies of the B alleles. For genoCNA with genotype from normal tissue, we can refine the weights w_z,h according to the correspondences in Table 3. First, if the genotype in normal tissue is homozygous, the genotype in tumor tissue is also homozygous for the same allele. Second, if the genotype in normal tissue is heterozygous, BAF in tumor tissue follows a mixture distribution with less components than in a general situation (except state 2). In either case, there is a small probability of exception, which can be attributed to factors such as genotyping error. See the Supplementary Data for the detailed formulation.

The parameters to be estimated

There are a large number of parameters to be estimated for either genoCNV or genoCNA. We reduce the number of parameters by some reasonable or obvious simplifications. First, in either genoCNV or genoCNA, some states share the same copy number and the same genotype, so that the corresponding parameters can be estimated jointly. For example, in genoCNA, States 7, 8 and 9 have the same copy number and they all share the genotype classes AAAA and BBBB. Second, mean values of some normal components of BAF can be assumed as constants. Specifically, for State 3, the null state with both allele deleted, we assume μ_b,3,1 = 0.5. For the other states, we assume μ_b,z,1 = 0 for genotypes of homozygous A allele and μ_b,z, _Hz = 1.0 for genotypes of homozygous B allele.

For transition probability, we set λ_j as constant based on prior knowledge/preference. Because the duration of state j follows an exponential distribution with parameter λ_j, the average duration, denoted as 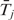, equals to 1/λ_j. Therefore, λ_j can be estimated by 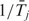. However, 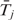is difficult to estimate because (i) state changes could occur at any position between two adjacent probes, which we cannot observe and (ii) even if we assume that state changes always happen at SNP probes, the Baum–Welch algorithm (24) for parameter estimation requires the posterior probability that any segment arises from state j, which is computationally infeasible because the number of segments increases exponentially as the total length of DNA sequence increases. Due to the above computational difficulties, and also because λ_j can be treated as a tuning parameter that determines the duration of state j, we choose to specify λ_j based on prior knowledge/preference.

Parameter and state posterior probability estimation

The final maximum likelihood estimations (MLEs) of the parameters can be obtained by an EM (Expectation–Maximization) algorithm known as the Baum–Welch or forward–backward algorithm (24), by numerical optimization methods (28), or by MCMC (Markov chain Monte Carlo) methods (29). Numerical optimization methods, such as the Nelder–Mead method, become less reliable if there are a large number of parameters, which is the case in our study. The MCMC methods are computationally demanding, especially for large-scale studies such as a genome-wide dissection of CNVs/CNAs. Therefore we employ the Baum–Welch algorithm to estimate the parameters. The estimation algorithm is briefly described as follows and the details are left in the Supplementary Data.

Let Θ be all the parameters to be estimated. First, given 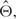, either initial values or estimates from the previous EM step, we can calculate the posterior probability that probe i is from state z, i.e. 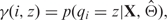, where q_i indicates the state of probe i, and X indicates the observed data. Furthermore, we can calculate the posterior probability that probe i is from state z and it belongs to a particular genotype class, i.e. 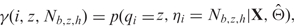, where η_i = N_b,z,h indicates that probe i belongs to the h-th genotype class of state z, and the subscript b indicates this is the normal component for BAF. With these posterior probability estimates, we can re-estimate Θ. We iterate this procedure until the estimates of Θ converges. By default, we use the convergence criterion that for at least 10 iterations, the maximum change of any parameter estimate is <0.002.

At the end, using the parameters at convergence, we can estimate the posterior probabilities for each SNP belonging to a particular copy number state or a genotype class. These posterior probability estimates are our final outputs. The posterior probability of certain copy number is either γ(i, z) or the summation of γ(i, z)'s of all the HMM states corresponding to the same copy number. For example, the copy numbers of States 1 and 2 are both 2, so

Similarly, the posterior probability of certain genotype class is the summation of all the corresponding γ(i, z, N_b,z,h)'s.

RESULTS

CNVs in HapMap individuals

To evaluate genoCNV, we applied it to study CNVs in chromosome 1–22 of 162 HapMap individuals (30): 12 CEU parents–child trios, 17 YRI trios and 75 CHB+JPT individuals. The data were generated using the Illumina Human 610-Quad array. There are 600 470 probes on chromosome 1–22, among which 17 931 (∼3%) are copy-number-only probes. Five individuals had been excluded due to unexpected chromosome-wide amplification or highly noisy array data. See the Supplementary Data for details.

PennCNV (23) is a state-of-the-art CNV identification method that is specifically designed for Illumina SNP arrays. We compared the results of genoCNV and PennCNV by two different approaches. First, we counted the number of CNVs identified by either genoCNV or PennCNV, and among them, the number/proportion of CNVs that match the common CNVs reported in a recent study by McCarroll et al. (8). Specifically, we say a CNV matches another if the center of the former lies within the latter and they have the same copy number calls. The set of CNVs identified by McCarroll et al. is a reasonable standard to evaluate our method because they identified CNVs using the same HapMap population and their results have a good degree of agreement with other existing data (8). As shown in Table 4, PennCNV (P) and genoCNV (X) have comparable performances.

Table 4.

Comparison of PennCNV (P) and genoCNV (X) by the number/proportion of CNVs that match the common CNVs reported by McCarroll et al. (8)

	36 CEU samples		51 YRI samples		75 CHB+JPT samples
	P	X	P	X	P	X
Total	1483	1444	2113	2289	2550	2440
Match (%)	479 (32)	478 (33)	889 (42)	886 (39)	997 (39)	961 (39)

Second, using the family information of the 12 CEU trios and the 17 YRI trios, we checked the number of CNVs identified in the offsprings that matched a CNV identified in at least one parent. Because CNVs are inheritable, the number and proportion of CNVs shared between parents and child are indirect, but reasonable measures of the methods' performances. For the 12 CEU trios, 480/474 CNVs are identified by genoCNV and PennCNV, respectively, among which 194/206 match at least one CNV in the parents. For the 17 YRI trios, 801/757 CNVs are identified by genoCNV and PennCNV, respectively, among which 326/339 match at least one CNV in the parents. See the Supplementary Data for the number of matches per family.

In summary, overall genoCNV and PennCNV have similar performances in terms of identifying CNVs in these HapMap individuals. However, genoCNV provides genotype calls in CNV regions while PennCNV does not. The genotype calls can have important applications such as studying the allele-specific effects for gene expression or other complex traits (see the ‘Discussion’ section for details).

CNAs in brain tumors

Next, we sought to evaluate the performance of genoCNA by applying it to a brain tumor dataset (Illumina Hap550 SNP arrays) from The Cancer Genome Atlas project (TCGA) (31). We compared the results of genoCNA and PennCNV to justify the strategies employed in genoCNA. By default, PennCNV adjusts the LRR values so that the median of LRR is 0, adjusts the BAF values so that the median of those BAF values between 0.25 and 0.75 is 0.5, and suppresses the state of copy number neutral LOH. In CNA studies, these adjustments are not appropriate for the following reasons. (i) If a significant proportion of the genome is deleted or amplified, the median of LRR is deviated from 0. (ii) Due to tissue contamination, BAF distribution may have a mode <0.25 or >0.75. For example, the mixture (A, AB) corresponds to one mode of the BAF distribution (recall the underscore in AB indicates it is from normal tissue). Suppose the proportion of normal tissue is 10%, then the proportion of B allele is 1/11, which should correspond to a model well <0.25, but >0. (iii) The state of copy number neutral LOH is often of interest. Therefore, we changed the default of PennCNV to skip median adjustments for LRR/BAF and to keep the copy number neutral LOH state.

CNV methods often fail in CNA studies

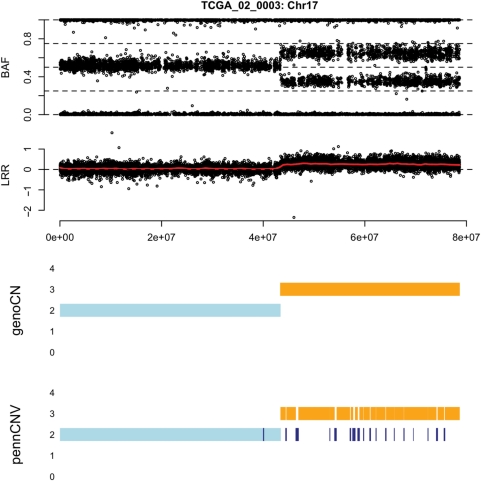
We first demonstrate that CNV methods often fail to identify CNA regions. As shown in Figure 1, at the end of chromosome 5 of TCGA sample 02_0099, there are three CNA regions: two hemizygous deletion regions separated by a region of copy number neutral LOH. PennCNV fails to identify the deletion regions. In contrast, genoCNA captures these CNAs by employing genotypes from normal tissue and explicitly modeling tissue contamination (Figure 1). Figure 2 shows an example of amplification. Due to tissue contamination, the LRR in the amplified regions is lower than expected, and hence the results of PennCNV fluctuate between copy numbers 2 and 3 (Figure 2). Note that these results should not be taken as a criticism of PennCNV. Instead, they demonstrate the difference between CNV and CNA studies, and the methods designed for the former should not be used for the latter without modification.

Figure 2.

BAF and LRR of chromosome 17 of TCGA sample 02_0003, as well as the results of genoCNA and PennCNV.

One observation from Figure 1 is that the extra bands of BAF resulting from tissue contamination have different mean values for mixtures (A, AB) and (B, AB) compared with mixtures (AA, AB) and (BB, AB). This is expected since CNA regions with larger copy number are less sensitive to tissue contamination. For example, if the proportion of contamination is 0.5, the B allele account for 1/3 and 1/4 of the intensity for (A, AB) and (AA, AB), respectively. Another observation from Figures 1 and 2 is that the BAF appears to be asymmetric around the expected central BAF = 0.5. This asymmetry is most likely due to dye bias, and Staaf et al. (32) proposed a quantile normalization method with an intensity transformation threshold correction to handle this problem. In our genoCN framework, all the parameters are estimated from data and are already adapted to the asymmetry, thus a pre-normalization is not necessary. The final observation is that besides inaccurate copy number calls, PennCNV also identifies many regions as copy number neutral LOH, which are most likely false positives due to the difficulty to distinguish normal state and copy number neutral LOH. We demonstrate in the next section how genoCNA overcomes this problem.

Tissue contamination and genotype from normal tissue

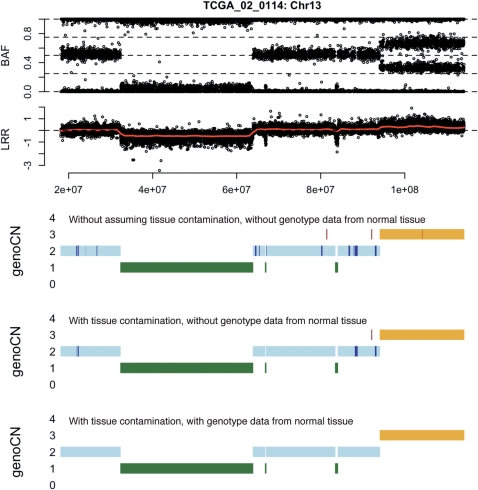
Unlike CNV methods (e.g. genoCNV or PennCNV), genoCNA has two features: it explicitly models the effect of tissue contamination and it can utilize genotype data from normal tissue of the same patient. Figure 3 illustrates the difference made by these two features in chromosome 13 of TCGA sample 02_0114. The CNA patterns become cleaner after any one or both features are employed. Specifically, short CNAs, especially those regions of copy number neutral LOH, disappear.

Figure 3.

BAF and LRR of chromosome 13 of TCGA sample 02_0114, as well as the results of genoCNA with three different setups in terms whether we assume tissue contamination and whether to use genotype from normal tissue. When copy number is 3, two colors ‘orange’ and ‘dark red’ indicate States 5 and 6 of genoCNA, respectively.

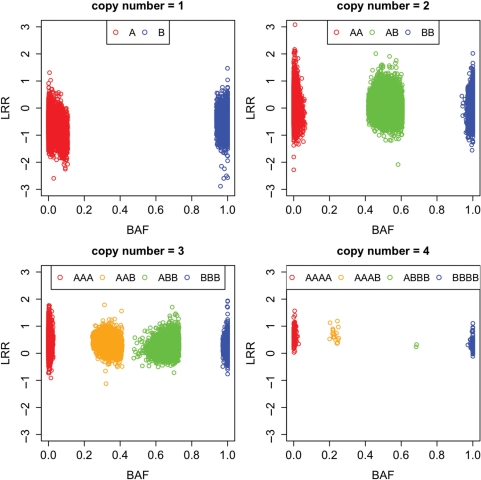
GenoCN (either genoCNA or genoCNV) not only outputs the most likely copy number state and genotype call for each SNP, but also the corresponding posterior probabilities. The proportion of SNPs with high posterior probabilities is a convenient measure of the success of the algorithm. Examining the whole genome (more than 500 000 SNPs) of TCGA sample 02_0114, we see that the tissue contamination assumption and the usage of genotype data from normal tissue lead to a small increase of the proportion of high-confidence copy number calls (notice that the posterior probability of a copy number state is the summation of the posterior probabilities of all the corresponding HMM states. Thus elimination of copy number neutral LOH as shown in Figure 3 does not have big effect on the posterior probability of copy number state), but a significant improvement of the proportion of high-confidence genotype calls (Table 5). We further illustrate the LRR and BAF of the SNPs with high-confidence genotype calls (posterior probability >0.95, Figure 4). The apparent clustering structure in Figure 4 demonstrates the high accuracy of the genotype calls.

Table 5.

Proportion of the SNPs of TCGA sample 02_0114 that have high posterior probabilities of copy number/genotype calls

Tissue contamination	Genotype from normal tissue	Posterior probability
		≥0.8	≥0.9	≥0.95	≥0.99
No	No	99.8/97.1	99.7/95.8	99.6/93.6	99.3/84.7
Yes	No	99.9/97.9	99.8/97.0	99.7/95.3	99.5/87.8
Yes	Yes	100.0/98.9	99.9/98.6	99.9/98.3	99.8/97.0

There are two numbers in each cell: a/b, where a is the proportion for copy number states and b is the proportion for genotype states.

Figure 4.

Scatter plot of LRR and BAF for 547 458 SNPs of TCGA sample 02_0114. These SNPs are from CNA regions (including copy number neutral LOH) and the posterior probabilities of the most likely genotype class are >0.95.

Empirical measurements of tumor purity

For each sample, after dissecting the CNA regions and estimating the parameters of LRR or BAF distributions, we can derive an empirical measurement of tumor purity, i.e. the proportion of tumor tissue in this sample. We denote this proportion as p_T, which can be estimated by expressing the observed mean value of LRR/BAF as a function of p_T and the expected LRR/BAF in pure tumor tissue. In this article, we choose to use BAF to estimate p_T because the expected LRR in pure tumor tissue is not well defined; in contrast, the expected BAF is 0 or 1 for homozygous genotypes, and 0.5 for heterozygous genotypes with equal number of A and B alleles, regardless of the copy number. Following Staaf et al. (16), assuming that BAF can be approximated by the ratio of the number of B alleles and the total number of alleles, we can estimate the tumor purity from BAF data (see Section C of the Supplementary Data for details).

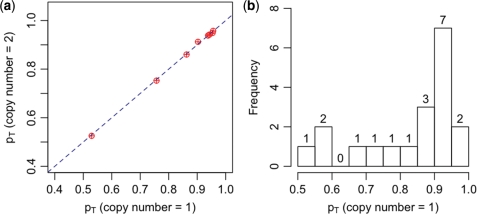
We use 19 glioblastoma samples from TCGA study to demonstrate the tumor purity estimation (Supplementary Table C1). These samples are selected from 42 TCGA samples produced by Stanford group, by examining the LRR/BAF patterns to ensure they have diploid genomic background, similar to the approach of Gardina et al. (33). We first estimate p_T based on the BAF values from CNA regions corresponding to States 2, 4 and 5 (Table 2), which correspond to copy numbers 1, 2 and 3, respectively. We denote these three sets of tumor purity estimates as p_T1, p_T2 and p_T3, respectively. Note for each individual, p_Tj (j = 1, 2, 3) is estimated only if there are at least 500 SNPs belonging to the corresponding CNA state with high confidence (specifically, posterior probability belonging to the CNA state >0.95). Consequently, p_T1 and p_T3 are estimated for all the 19 samples, but p_T2 are only estimated for eight samples. Figure 5a shows that p_T1 and p_T2 are highly consistent. Overall, p_T1 and p_T3 are also consistent, although it appear that the estimates of p_T3 are more noisy (see Supplementary Figure C1). We illustrate the distribution of p_T1 in Figure 5b. More than half of the samples have tumor purity <90%, and three of them have tumor purity <60%.

Figure 5.

(a) Comparison of the proportion of tumor sample (p_T) estimated using mean BAF values when copy number is 1 [genotype (A, AB)] and two [genotype (AA, AB)]. Each point corresponds to one sample. The diagonal line is y = x. (b) The distribution of p_T, estimated using mean BAF values when copy number is 1.

For each tumor sample, top and bottom frozen sections were stained with hematoxylin and eosin to determine the percentage of tumor nuclei (31). We refer to the average tumor percentage estimated from top and bottom sections as clinically estimated tumor purity. Next we compare our data-driven estimates of tumor purity with the clinically estimated tumor purity (Supplementary Table C1). The clinically estimated tumor purity is 100% for all the 19 samples except for TCGA_02_0054 (95%), TCGA_02_0099 (97.5%) and TCGA_02_0102 (97.5%). The data-driven estimates of tumor purity for these three samples are 53, 76, and 90%, respectively. The apparent extra bands in the BAF plot when copy number is 1 clearly indicate relatively low tumor purity (e.g. Figure 1 and Supplementary Figure C2), which contradict the clinically estimated high tumor purity. Therefore our results suggest a need for data-driven estimates of tumor purity.

Parental-specific deletion/amplification

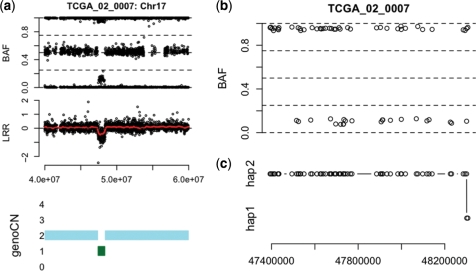
Given the copy number state and the genotype call of each SNP within a copy number altered region, an immediate follow-up question is the parental origin of the deleted/amplified DNA segment. For example, as shown in Figure 6a, there is a deletion in TCGA sample 01_0007 at chromosome 17. GenoCNA can identify this CNA region and estimate the genotype of each SNP within it. Then we would ask whether the deleted segment is composed of several smaller segments from either the paternal or maternal copy of the chromosome or the entire deleted region is from one copy of the chromosome. In order to answer this question, we need to know the haplotypes in normal tissue. While accurate haplotype information is not available, we employed fastPHASE (34) to infer the missing haplotypic phase. Because SNPs with homozygous genotype are not informative for the haplotype origin, we only examined the SNPs that are heterozygous in normal tissue. Comparing the imputed haplotypic phases in normal tissue with the estimated genotypes in tumor tissue, most SNPs in this CNA region is from the same haplotype, with a phase switch at the end of this region (Figure 6). Note that this phase switch may reflect a real genetic event or may be due to switch error of fastPHASE. We can be more confident about the haplotype if genetic data from other family members are available. Nevertheless, the results presented here clearly demonstrate that at least the majority of the deletion is from one parental allele. Given familiar inheritance data, such parental-specific studies would provide more insights about the genetic factors affecting cancer susceptibility and tumorigenesis.

Figure 6.

Parental-specific deletion at chromosome 17 of TCGA sample 02_0007. (a) The BAF, LRR and copy number calls by genoCN around a CNA (deletion) region. (b) In the BAF of the SNPs (of which the genotypes are heterozygous in normal tissue) in this CNA region. (c) This shows which haplotype the remaining allele belongs to at each SNP.

Allelic bias in copy number-altered regions

Since genoCN outputs the genotypes in CNV/CNA regions, it identifies the allelic bias of deletion/amplication for each individual. An interesting question is whether some allelic bias is conserved across individuals. Such allelic bias may be biologically more important than parental bias. The previous publication by The Cancer Genome Atlas Research Network (31) has shown that a large proportion of the glioblastoma samples have deletion on chromosome 10. To demonstrate the allelic bias study across individuals, we examine the SNPs on chromosome 10 in 19 of the brain tumor samples. We restrict our attention to the 301 SNPs with heterozygous genotype in normal tissue and hemizygous deletion in tumor tissue for at least 11 of the 19 samples. Since the SNPs are heterozygous in normal tissue, without allelic bias, either allele A or B should be deleted with probability 0.5. We quantify the allelic bias of the i-th SNP (across individuals) by a binomial P-value: pbinom(min(k_i, n_i − k_i), n_i, 0.5), where pbinom denotes the cumulative distribution function of binomial distribution, n_i is the number of samples with heterozygous genotype in normal tissue and hemizygous deletion in tumor tissue, and k_i is the number of cases (among n_i) where allele A is deleted. With a suggestive P-value cut-off 0.0005, we identify three SNPs with significant allelic bias: rs10887549 (Chr10:87764377), rs10788478 (Chr10:87797370) and rs10887554 (Chr10:87814218). They are all located within gene GRID1, which encodes a subunit of glutamate receptor channels. These channels mediate most of the fast excitatory synaptic transmission in the central nervous system and play key roles in synaptic plasticity. Previous association study has suggested that GRID1 is a candidate gene of schizophrenia (35). Here our allelic bias study suggests a potential relation between GRID1 and glioblastoma.

DISCUSSION

We propose a statistical framework to dissect both CNVs or CNAs and estimate genotypes of the SNPs within copy number-altered regions. In this article, we mainly discussed the application for Illumina SNP arrays. Accompanied with an appropriate normalization and transformation method, our method can also be applied to Affymetrix SNP arrays. The normalization procedure of Affymetrix SNP array data is itself an active research topic; see Rigaill et al. (36) for an example.

In our empirical studies, genoCNV and PennCNV have similar performances for identifying CNVs, but genoCNV has the advantage of reporting genotype information within CNV regions. In fact, genoCNV can be used to estimate genotypes in the whole genome, not necessarily in the CNV regions. The advantage compared with most existing genotyping techniques (37–39) is that the genotype can be estimated within a single sample. One exception is the genotyping method developed by Giannoulatou et al. (40), which can also be applied to a single sample, although it is not designed to determine the genotype in CNV regions.

For CNA studies, genoCNA has apparently better performance than PennCNV due to different model design, data-driven parameter estimation, normal tissue contamination consideration and incorporation of genotype data from normal tissue. One remaining issue is to take into account the possibility that the chromosomal background may not be diploid (33). For those samples presented in this article, we have examined the genome-wide LRR and BAF data to make sure that the chromosomal background was diploid. We are actively developing a method to dissect the ploidy status.

The availability of both copy number states and genotype calls from CNV or CNA regions, provided by genoCN, enables many important genetic studies. For example, gene expression quantitative trait loci studies have attracted many research interests recently (41). Previous studies have correlated gene expression with copy number and genotype separately (42). However, the joint study of copy number and genotype effects on gene expression has not been reported, at least partly due to the lack of reliable genotype calls in copy number-altered regions. The availability of genoCN, or similar solutions in the future would greatly facilitate such joint study, not only for gene expression traits, but also for complex traits such as cancer susceptibility or even causal relations that connect the genetic variation and complex traits (43).

genoCN has been implemented in an R package, with computational intensive parts written in C code. The R package can be downloaded at http://www.bios.unc.edu/∼wsun/software.htm

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NCI and The Cancer Genome Atlas Project Grant U24-CA126544, in part); Lillemor Grobstoks legacy for cancer research (in part to S.H.N.). Innovation Award from the UNC University Cancer Research Fund, NHLBI grant R01HL095396, and EPA STAR RD832720 (to F.A.W.). Funding for open access charge: An Innovation Award from the UNC University Cancer Research Fund.

Conflict of interest statement. None declared.