Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Aug 26.
Published in final edited form as: J Biomech. 2010 May 23;43(12):2418–2424. doi: 10.1016/j.jbiomech.2010.04.019

Correlations between Local Strains and Tissue Phenotypes in an Experimental Model of Skeletal Healing

Elise F Morgan 1,2, Kristy T Salisbury Palomares 1,2, Ryan E Gleason 1,2, Daniel L Bellin 1,2, Karen B Chien 1,2, Ginu U Unnikrishnan 1,2, Pui L Leong 1,2
PMCID: PMC2935472  NIHMSID: NIHMS210321  PMID: 20546756

Abstract

Defining how mechanical cues regulate tissue differentiation during skeletal healing can benefit treatment of orthopaedic injuries and may also provide insight into the influence of the mechanical environment on skeletal development. Different global (i.e., organ-level) mechanical loads applied to bone fractures or osteotomies are known to result in different healing outcomes. However, the local stimuli that promote formation of different skeletal tissues have yet to be established. Finite element analyses can estimate local stresses and strains but require many assumptions regarding tissue material properties and boundary conditions. This study used an experimental approach to investigate relationships between the strains experienced by tissues in a mechanically stimulated osteotomy gap and the patterns of tissue differentiation that occur during healing. Strains induced by the applied, global mechanical loads were quantified on the mid-sagittal plane of the callus using digital image correlation. Strain fields were then compared to the distribution of tissue phenotypes, as quantified by histomorphometry, using logistic regression. Significant and consistent associations were found between the strains experienced by a region of the callus and the tissue type present in that region. Specifically, the probability of encountering cartilage increased, and that of encountering woven bone decreased, with increasing octahedral shear strain and, to a lesser extent, maximum principal strain. Volumetric strain was the least consistent predictor of tissue type, although towards the end of the four-week stimulation timecourse, cartilage was associated with increasingly negative volumetric strains. These results indicate that shear strain may be an important regulator of tissue fate during skeletal healing.

Keywords: mechanobiology, fracture healing, shear strain, tensile strain, tissue differentiation, pseudarthrosis

Introduction

Tissue differentiation during healing of skeletal injuries is governed in part by stimuli present in the microenvironment of the injury site. Bone repair is sensitive to mechanical factors, though the mechanisms underlying this sensitivity are not well understood. Identifying the mechanical stimuli that regulate formation of different tissue phenotypes during skeletal healing has direct applications in treatment of skeletal injuries. Further, given the close relationship between processes active during skeletal repair and those central to skeletal development (Ferguson, et al., 1999; Gerstenfeld, et al., 2003), a better understanding of the role of the mechanical environment in skeletal healing may also shed light on how mechanical factors modulate skeletogenesis.

Prior studies on the effects of the mechanical environment on skeletal repair have typically described the type of loading in terms of the global, or organ-level, motion. For example, cyclic, axial, compressive displacements applied across an osteotomy gap can enhance healing via increased callus formation and accelerated endochondral ossification (Claes, et al., 1995; Goodship and Kenwright, 1985; Kenwright, et al., 1991). Application of static, tensile displacements across an osteotomy gap, as is done in distraction osteogenesis, also promotes bone healing, although primarily via intramembranous ossification (Jazrawi, et al., 1998; Tay, et al., 1998). In contrast, bending movements have been shown to promote cartilage formation while preventing ossification within the gap (Cullinane, et al., 2002; Cullinane, et al., 2003; Salisbury Palomares, et al., 2009).

Although these studies demonstrate the potent effect of the mechanical environment on skeletal healing, knowledge of only the global motion is insufficient for defining relationships between mechanical stimuli and tissue differentiation. Due to the irregular geometry of the callus and the spatially heterogeneous distribution of tissues, even simple, global displacements, forces, or moments can produce complex distributions of local, or tissue-level, stimuli. The role of these local stimuli in directing skeletal tissue differentiation has been the subject of theories that have postulated that shear strain and interstitial fluid flow (Lacroix and Prendergast, 2002; Prendergast, et al., 1997), tensile strain and hydrostatic pressure (Carter, et al., 1998), or normal strains (longitudinal and transverse) and hydrostatic pressure (Claes and Heigele, 1999) are the mechanical stimuli relevant to the fate of multipotent mesenchymal tissue. These theories have been applied to numerous clinical and experimental scenarios (e.g., (Gardner and Mishra, 2003; Giori, et al., 1993; Hayward and Morgan, 2009; Isaksson, et al., 2007; Isaksson, et al., 2006a; Kelly and Prendergast, 2005; Loboa, et al., 2001; Wren, et al., 2000). However, tests of these theories to date have relied heavily on finite element (FE) analysis to estimate distributions of local mechanical stimuli. These analyses require many assumptions regarding tissue mechanical properties, and in some cases, boundary conditions. To a great extent, the results have not been validated experimentally, and they can be very sensitive to the assumed material properties (Isaksson, et al., 2009).

Experimental methods for full-field measurement of strains in musculoskeletal tissues have been applied in a range of biomechanical investigations. For example, digital image correlation (Thompson, et al., 2007) and electronic speckle pattern interferometry (Bottlang, et al., 2008) were applied recently to measure strains in a thin section of a fracture callus. These studies indicate the potential of experimental techniques for probing correspondence between the mechanical strain environment and tissue fate during skeletal healing.

The overall goal of this study was to investigate relationships between the strains experienced by tissues in a mechanically stimulated bone defect and the patterns of tissue differentiation that occur during healing. A previously developed pseudoarthrosis model was used in which a bending motion applied to an osteotomy results in characteristic spatial patterns of cartilage, bone, and fibrocartilage (Salisbury Palomares, et al., 2009). The objectives of this study were: 1) to measure spatial distributions of strains in the callus; and 2) to identify associations between the strain distributions and the spatial patterns of tissue differentiation.

Methods

All protocols were approved by the Institutional Animal Care and Use Committee at Boston University. Thirty-two male, Sprague-Dawley rats underwent production of a 1.5-mm-thick transverse osteotomy in the right femoral mid-diaphysis followed by daily bending stimulation as described previously (Salisbury Palomares, et al., 2009). The osteotomy gap was stabilized with a hinged, external fixator that permits bending in the sagittal plane, about the gap center. Beginning on post-operative day (POD) 10, stimulation was carried out for five consecutive days followed by two days of rest each week. The stimulation consisted of a 60° (+35/-25°) bending motion applied at 1 Hz for 15 minutes. The hinge was locked at 0° during all other times. Animals returned to normal weight-bearing activity following surgery and were allowed unrestricted cage activity.

On POD 10, 24, and 38, femora were harvested with fixators still attached. Previous histological analyses indicated that undifferentiated mesenchymal tissue was present in the calluses at each of these timepoints, with the amount of this tissue decreasing over time (Salisbury Palomares, et al., 2009). For each callus, the mid-sagittal plane was exposed using a circular blade (Brasseler USA, Savannah, GA) attached to a dental hand motor (Model #GX-7, A.M.D. Dental Manufacturing Inc., Cranbury, NJ, Figure 1A). The tissue was speckled with black enamel using an airbrush (Model #155, Badger Airbrush Co, Franklin Park, IL) (Figure 1B), and the specimen was mounted to the linkage system that was used for the in vivo stimulation. A digital camera (Model #PL-A622, PixeLINK, Ottawa, ON) with a 0.55× lens and a stereo-zoom microscope (Model #SMZ800, Nikon Inc, Melville, NY) with a 0.50× lens were used to capture a series of images (0.0155 mm/pixel) at approximately 64 Hz as the 60° bending motion was applied at 1 Hz for 15 minutes. The specimen was kept moist with 0.9% phosphate buffered saline.

Figure 1.

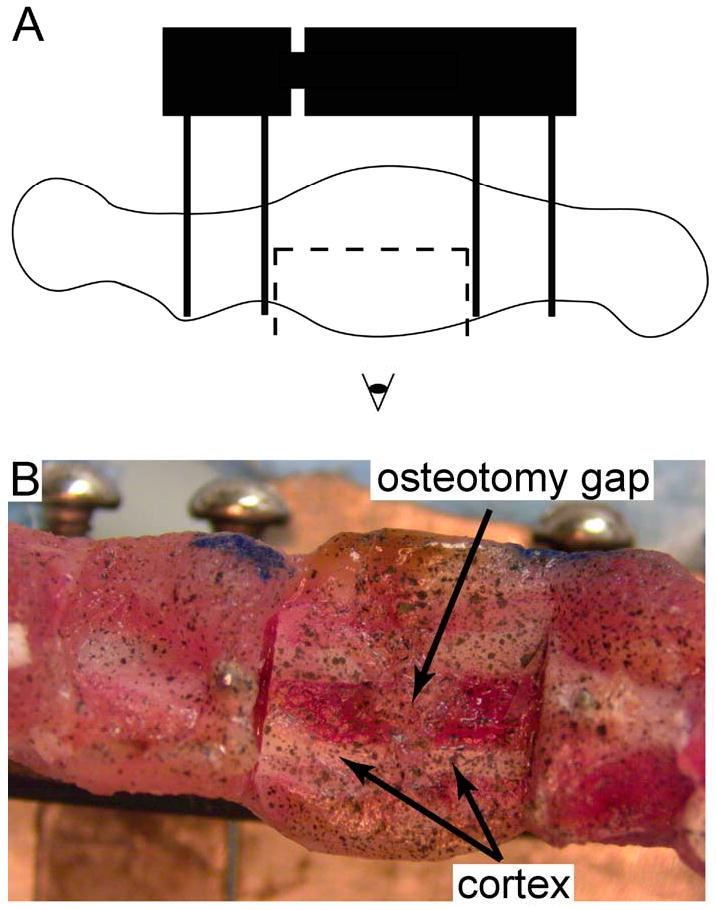
Figure 1

Open in a new tab

In preparation for the strain measurements, (A) the lateral half of the portion of the callus located between the two inner pins was removed using a circular blade attached to a dental hand motor, and (B) the newly exposed, mid-sagittal plane was specked with black enamel paint using an airbrush.

Each neighboring pair of images (i.e. image 1 and image 2, image 2 and image 3, etc.) was analyzed using a digital image correlation technique, sequential maximum likelihood estimation (SMLE), in order to estimate the displacement and strain fields induced in the mid-sagittal plane by the bending motion. The first image of each pair was discretized using linear quadrilateral finite elements approximately 50 pixels on a side (Figure 2).

Figure 2.

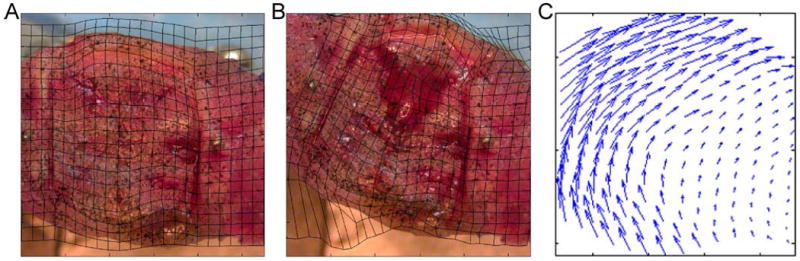
Figure 2

Open in a new tab

(A) The first image of each image pair that is analyzed using the SMLE digital image correlation method is discretized into finite elements in such a way that the mesh conforms to the regions of interest. The mesh geometry was generated from the digital images using Matlab (Mathworks, Natick, MA) and Truegrid (XYZ Scientific Applications, Inc., Livermore, CA). This process involved defining the boundaries of the region of interest (the portion of the exposed mid-sagittal plane that was located between the two inner pins) and then projecting a rectangular mesh onto these boundaries. (B) The corresponding deformed mesh at a bending angle of 35°; the displacement of each node from its original position in panel A was determined using the SMLE digital image correlation technique. (C) Nodal displacements, displayed as vectors, in the region of interest

The nodal displacements (u) were calculated by minimizing the functional

∏[u]=∫Ω(I1(x)−I2(x+u))2dx+∫Ωω(∇u•∇u)2du (1)

where Ω is the domain of a given element, x is the position, I1(x) and I2(x+u) are the first and second images of the pair, respectively, and ω is a regularization parameter that restricts large displacement gradients (Gokhale, et al., 2004; Oberai, et al., 2003). Nodal displacements were calculated one column of elements at a time, beginning at the right-most edge of the images where little tissue displacement occurred because the distal end of the specimen remains fixed during stimulation. An initial guess of zero was used for these displacements. Subsequently, the calculated displacements for this first column were used as the initial guess for the adjacent column, and this process was repeated throughout the entire image. The results for the entire mesh were then used as an initial guess for a refinement step that involved minimizing equation (1) over the entire mesh. Green-Lagrange strains were calculated from the nodal displacements and the derivatives of the FE shape functions. Displacement errors were estimated to be less than 0.33% (Supplemental Data). Strain errors were typically less than 0.0091 mm/mm.

An ancillary analysis was carried out to estimate the effect of removal of the lateral portion of the callus on the mid-sagittal strains (Supplemental Data). The estimated percentage errors ranged 0.4–0.7% for all three strains (maximum principal strain, volumetric strain, and octahedral shear strain) investigated.

Logistic regression was used to compare the experimentally measured strain fields to the distribution of tissues observed in mid-sagittal histological sections of a separate cohort of specimens (n=47; PODs 17, 24, 38) from a previous study (Salisbury Palomares, et al., 2009). Grid points were distributed over the region of interest (Figure 3A-C), and the type of tissue—cortical bone (diaphysis), trabeculated woven bone (newly formed bone), cartilage, or fibrocartilage—present at each point was identified. Strain fields were sampled at corresponding points (Figure 3D). At each grid point, the peak (maximum) value, and also average value, of a given type of strain that occurred over the entire first bending cycle were averaged across all specimens at a given timepoint. Prior to averaging, strains exceeding the range (-0.3, 0.3) mm/mm were excluded to reduce the effect of tissue tearing on the regressions. The camera images revealed that tearing sometimes occurred in regions tangent to the periosteal aspect of the osteotomy cut. The bounds (-0.3, 0.3) mm/mm were based on a literature review of failure strains for fibrous, cartilaginous, and fibrocartilaginous tissues tested either parallel to or perpendicular to the fiber direction (e.g., (Martin, et al., 1998; Sasazaki, et al., 2006; Tissakht and Ahmed, 1995; Villegas, et al., 2007; Williamson, et al., 2003)). The occurrence of tissue tearing also precluded use of strains from all but the first bending cycle—and hence also precluded investigation of the magnitude of viscoelastic effects—because the measured strains in the torn regions were non-physical.

Figure 3.

Figure 3

Open in a new tab

For each histological section, a grid of points was defined in the (A) anterior, (B) central, and (C) posterior regions of the portion of the callus located between the two inner pins. The anterior and posterior boundaries of each region were defined by the periosteal surface of the cortex and by the anterior and posterior boundaries of the callus. A fixed number of grid points (N1, N2, and N3 for the anterior, central and posterior regions, respectively) was used for each region. For POD 17 sections, N1=55×15, N2=55×30, and N3=55×15. For POD 24 and 38 sections, N1=55×30, N2=55×35, and N3=55×35. These were the minimum numbers of points that reproduced the trends in tissue areas measured previously via histomorphometry (Salisbury Palomares, et al., 2009). For each region in each histological section, each rectangular grid of points was made to conform to the shape of the region via projection of the grid onto the boundaries of the region (TrueGrid, XYZ Scientific, Livermore, CA). During the segmentation process that was carried out in the previous histomorphometric analyses, the digital images of the histological sections were converted to grayscale with each tissue type represented by a single grayvalue. No fibrocartilage was present in this section. The tissue type “Other” included any tissue other than cartilage, fibrocartilage, cortical bone, and woven bone as well as void space. (D) The strain fields computed from the SMLE technique were sampled at corresponding points. Correspondence was determined by using the digital camera images (Figure 1B) to identify the locations of the periosteal surface of the cortex; these locations allowed subdivision of the strain fields into anterior, central, and posterior regions (boundaries shown with black lines). The locations of the grid points were defined using the same boundary projection method that was used for the histological sections.

Logistic regression analyses, with tissue type as the dependent variable and strain as the independent variable, were carried out for each histological section and each type of strain at each timepoint. A significance level of 0.05 was used. These analyses were performed within timepoints, i.e. day-24 strain fields and day-38 strain fields compared to the histological sections at the respective timepoints, and also between adjacent timepoints, i.e. day-10 strains compared to day-17 histological sections and day-24 strains compared to day-38 histological sections. The within-timepoint and between-timepoint comparisons were used to account for short and long response times, respectively, of tissue differentiation to mechanical stimulation. The strain and histology measurements were viewed as representative of the deformation fields and tissue distributions that are present at and around a particular post-operative day. Thus, even for the within-timepoint comparisons, the results were used to provide insight into the strains that may result in the observed distribution of differentiated tissues, as opposed to simply the strains that the differentiated tissues experience.

Results

At each timepoint, strains varied considerably throughout the callus (Figure 4). The maximum principal strain was generally highest in the peripheral region of the osteotomy gap, and the octahedral shear strains were highest at the anterior and posterior edges of the mid-callus. No consistent pattern was observed among specimens for volumetric strain. Although strains tended to be low in regions corresponding to the cortex, due to the finite size of the elements (0.575 mm), strains in some of these regions reflected deformation not only of the cortex but also of the adjacent soft tissue. Hence, strains in these regions were sometimes in excess of the tensile fracture strain of cortical bone (2-5% (McCalden, et al., 1993)).

Figure 4.

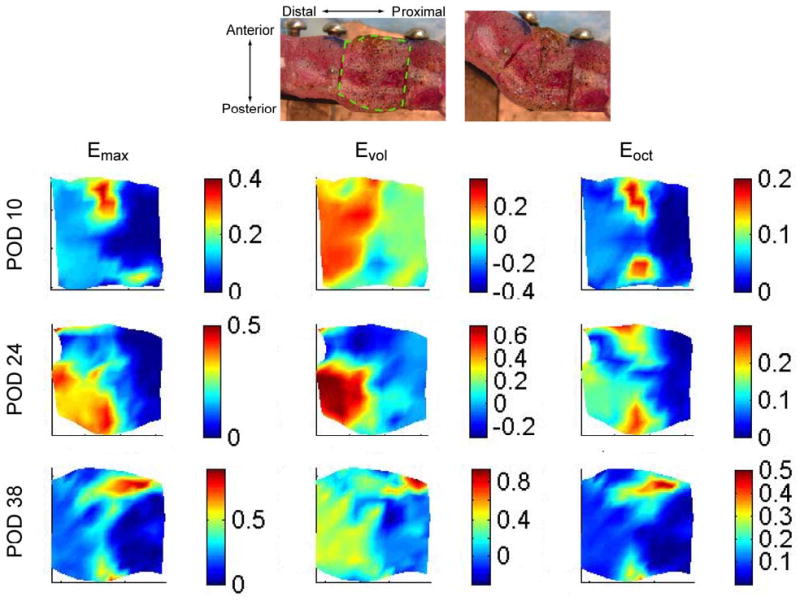
Figure 4

Open in a new tab

Representative strain fields for the regions of interest in specimens at POD 10, 24, and 38 at a bending angle of 35°. The strains are shown only on the region of interest, which is depicted for a representative specimen via the dashed line superimposed on the top left digital image. The strains are plotted using the original (0°) coordinates; however, in order to illustrate the direction of the applied bending motion, the corresponding digital image at 35° is shown at the top right. During the bending motion, the right (proximal) side of the region of interest stays approximately fixed, while the left (distal) side is displaced upwards and to the right. Emax is the maximum principal strain, Evol the volumetric strain, and Eoct the octahedral shear strain. Strains are displayed in units of mm/mm.

Significant associations were found between tissue type and peak strain, particularly for the later timepoints (Figures 5 and 6). For the majority of the histological sections, the probability of encountering cartilage in a given region increased with increasing shear and maximum principal strains. These associations were most predominant at day 24 (day-24 strains compared to day-24 histology). At this timepoint, the odds of encountering cartilage rather than another tissue type increased by a factor of 4.1 for every increase in shear strain of 0.1 mm/mm (Table 1). In contrast, the probability of encountering woven bone decreased with increasing shear and tensile strains for the majority of sections. No consistent correspondence was found between volumetric strain and either cartilage or woven bone, with the exception of the later timepoints (day-24 and day-38 strains compared to day-38 histology) for which negative correlations were observed between volumetric strain and both tissue types. As would be expected, negative correlations were found between cortical bone and all three strains for nearly all histological sections at most timepoints. At the later timepoints (day 24 – day 38 and day 38 – day 38 comparisons), the probability of encountering fibrocartilage either decreased with or did not depend on increasing values of each type of strain, but the results for fibrocartilage were mixed at the earlier timepoints. For all four tissue types, octahedral shear strain demonstrated the most consistent correlations with tissue type in that for each tissue type, a larger majority of histological sections exhibited a consistent type of correlation (positive or negative), and fewer sections exhibited non-significant correlations, with octahedral shear strain as compared to the other two strains.

Figure 5.

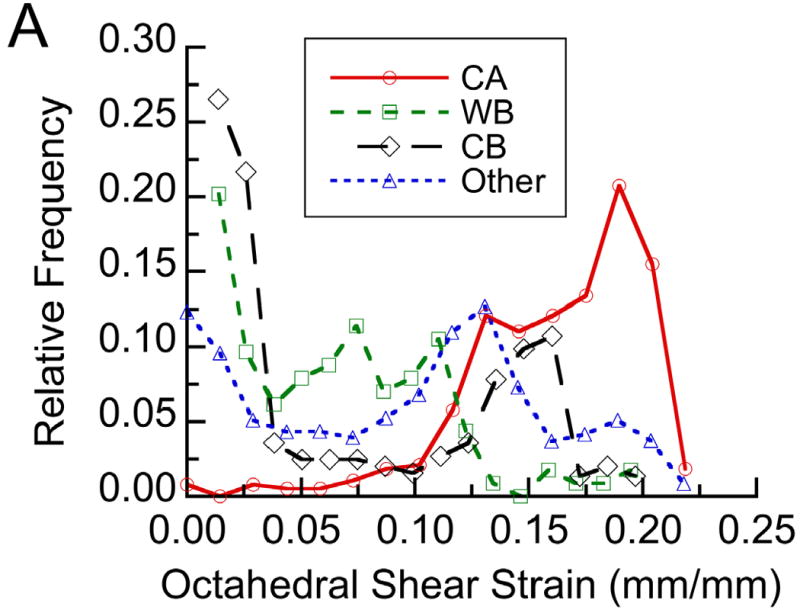
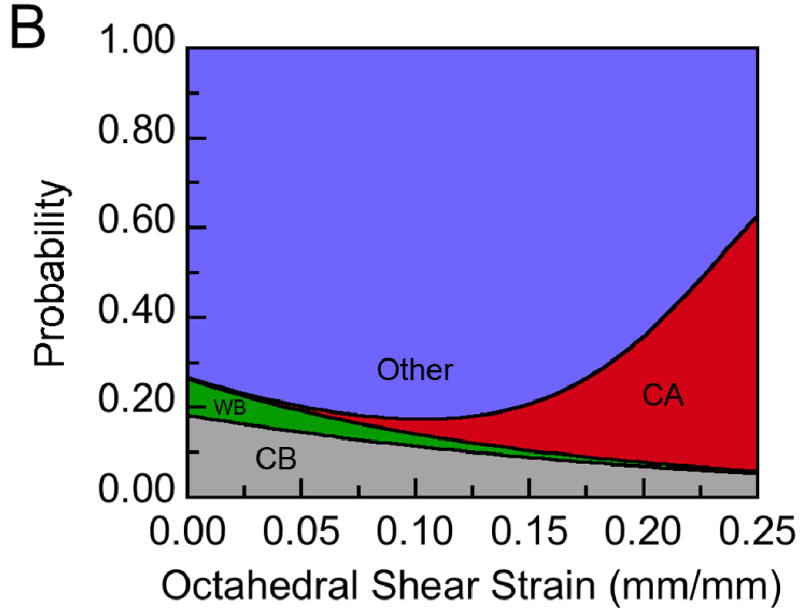
Figure 5

Figure 5

Open in a new tab

(A) The distribution of each tissue type within a representative histological section at post-operative day 24 with respect to the average distribution of octahedral shear strain measured at post-operative day 24: The distribution is expressed in terms of relative frequency, defined for each tissue type as the number of grid points experiencing a given value of shear strain and occupied by that tissue type normalized by the total number of grid points occupied by that tissue type. Tissue type is abbreviated as “CA” for cartilage, “WB” for newly formed woven bone, and “CB” for cortical bone (the cortex). No fibrocartilage was found in this section. (B) Results from the logistic regression analysis performed on this histological section: Each tissue type is represented by a color, and the height of the colored area at a given value of octahedral shear strain corresponds to the probability of encountering that tissue type at that value of shear strain. For this section, the probability of encountering cartilage increased, and the probabilities of encountering woven bone and cortical bone decreased, with increasing shear strain (p<0.05).

Figure 6.

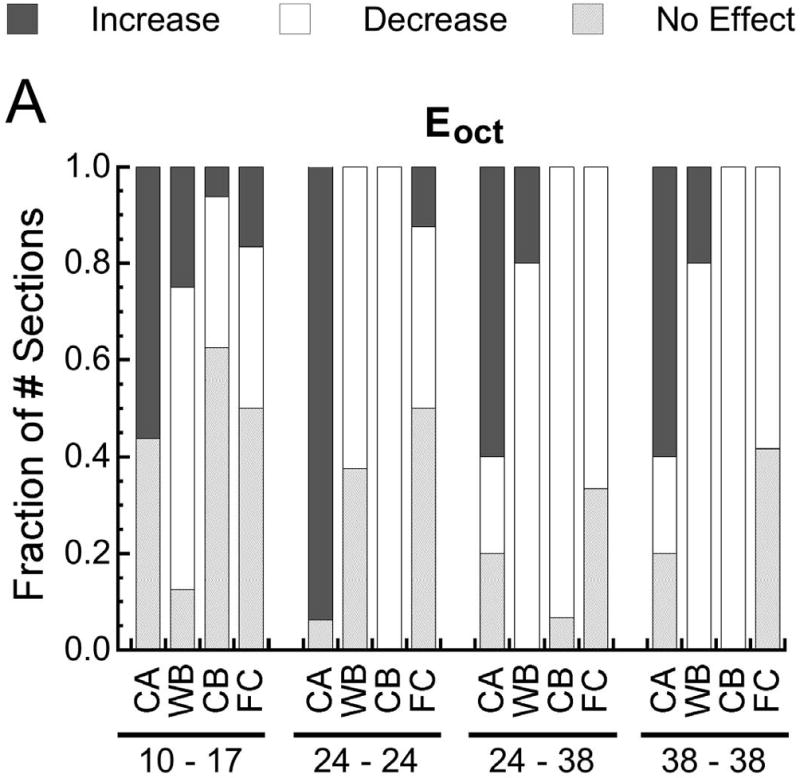
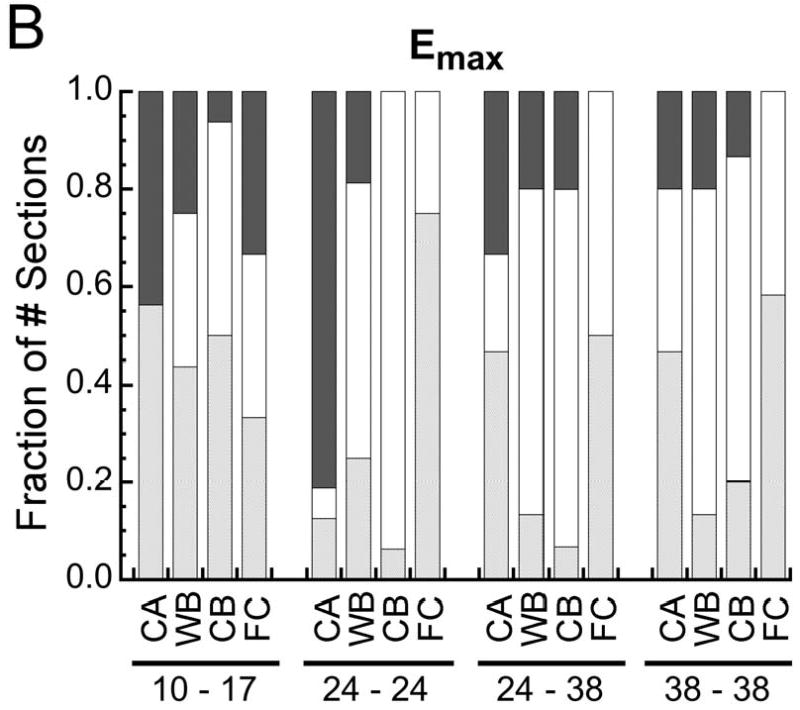
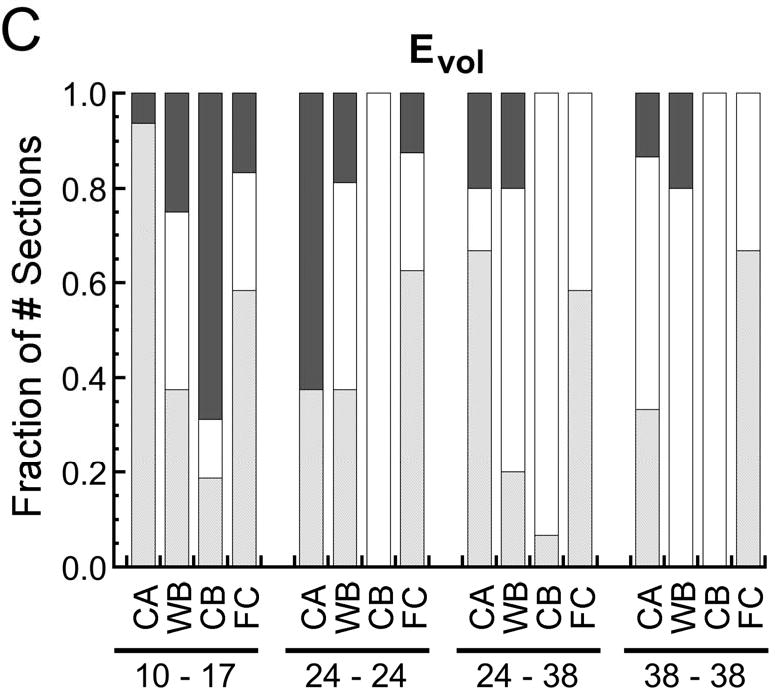
Figure 6

Figure 6

Figure 6

Open in a new tab

Fraction of the number of histological sections for which the probability of encountering a given type of tissue increased with (p<0.05), decreased with (p<0.05), or did not change (p>0.05) with increasing (A) octahedral shear strain (Eoct), (B) maximum principal strain (Emax), and (C) volumetric strain (Evol). In the pairs of numbers at the bottom of each plot, the first number is the post-operative day at which the strains were measured, and the second number is the post-operative day at which the histological analysis was conducted. Tissue type is abbreviated as “CA” for cartilage, “WB” for woven bone, “CB” for cortical bone (the cortex), and “FC” for fibrocartilage. In all cases the fraction of the number of sections is reported as the fraction of the number of sections in which the tissue type was found. Fibrocartilage was found in only 30-75% of the sections, depending on the timpoint, and the other tissue types were found in all sections.

Table 1.

Change in the odds of encountering a given tissue type for each increase of 0.1 mm/mm in octahedral shear strain (Eoct), maximum principal strain (Emax), and volumetric strain (Emax). “CA” = cartilage, “WB” = woven bone (newly formed bone), “CB” = cortical bone (cortex), “FC” = fibrocartilage. The odds are reported relative to tissue type “Other”, which refers to void space or any tissue not classified as one of the preceeding four types. Data are only presented in this table for cases in which the majority of histological sections at a given timepoint were in agreement with respect to either in increase or decrease in the odds ratio.

Strain – Histology Timepoints CA WB CB FC
Eoct 1.54 0.74 — —
10 – 17 Emax — — — —
Evol — — 1.18 —
Eoct 4.10 0.56 0.55 —
24 – 24 Emax 1.57 0.77 0.71 —
Evol 1.56 — 0.52 —
Eoct 1.54 0.30 0.61 0.20
24 – 38 Emax — 0.62 0.84 0.32
Evol — 0.37 0.53 —
Eoct 1.26 0.19 0.34 0.06
38 – 38 Emax — 0.48 0.75 —
Evol 0.85 0.50 0.49 —
Open in a new tab

Very similar results were found when the regression analyses used the cycle-average rather than peak strains. The only notable differences were that slightly more consistency among histological sections was found for the average strains and that for the later timepoints, an even greater number of sections displayed negative associations between cartilage and volumetric strain. In addition, the changes in odds of encountering a particular type of tissue for a given increase in strain were greater when using the average vs. peak strain.

Discussion

The results of this study revealed significant and consistent associations between the amount of shear strain experienced by a given region of the callus and the type of tissue that forms in that region. The likelihood of encountering cartilage increased, and that of encountering woven bone decreased, with increasing values of shear strain. Significant associations were also found for maximum principal strain, although this strain was a less consistent predictor of tissue phenotype. Of the three strains investigated, volumetric strain was the least consistent predictor. These results indicate that in the context of skeletal healing, shear strain may be an important regulator of tissue fate.

The principal contribution of this study is the experimental approach to quantify the local strains created by the applied, global mechanical motion. No assumptions were made regarding material properties and, by using the same stimulation device as was used in vivo, preserved many of the in vivo boundary conditions. We established that the accuracy and precision of the strain measurement technique were sufficient, given the strain magnitudes generated by the bending motion.

The experimental approach also had limitations. First, the study design was such that the results could reveal correlations, but not yet cause-effect relationships, between the mechanical environment and the patterns of tissue differentiation. Second, because this approach could only measure surface strains, some sectioning of the specimens was required in order to measure internal deformation. Although we estimated that the effect of the sectioning was minor, some very small regions of the callus were likely affected in a non-negligible manner (Supplemental Figure 2). Moreover, because these estimates were obtained via finite element analyses that used assumed material properties and representative, though realistic, geometry, we cannot guarantee that the sectioning effect was small for all specimens. Third, deformations occurring out of the mid-sagittal plane were not quantified. Fourth, the comparisons of strains to histology data were not on a per-specimen basis but rather between two different cohorts of specimens. Histology was not carried out on the specimens used for the strain analyses, because the medial half of the callus was removed in multiple pieces during specimen preparation, thus rendering the specimens unable to provide intact, mid-sagittal histological sections. Histological sections from the lateral half were also unusable, because the occurrence of tissue tearing in some regions of the callus and also general wear and tear sustained during the ex vivo experiments resulted in large voids and severe, non-uniform distortion in these sections once the histological processing (fixation, decalcification, embedding) was finished. Due to biological heterogeneity, the use of two different cohorts of specimens necessarily reduced the statistical power to detect correlations between strains and tissue phenotypes. Additional correlations may have been found had the regressions been carried out on a per-specimen basis. One final limitation is that the regression analyses assumed linear associations between strain and the probability of encountering a given type of tissue. To investigate the possibility of nonlinear associations, ordinal logistic regressions were also carried out (Selvin, 1994); the results revealed no evidence of nonlinearity.

The results of this study can be compared to components of existing mechano-regulation theories of skeletal tissue differentiation. Our finding that the probability of encountering cartilage rather than woven bone increased with shear strain and maximum principal strain is consistent with the theory put forth by Prendergast and co-workers (Prendergast, et al., 1997) but is inconsistent with the theory developed by Carter and co-workers (Carter, et al., 1998). In the latter, cartilage and bone are equally probable at a given value of maximum principal strain. As originally stated in the theory of Claes and Heigele (Claes and Heigele, 1999), the strain stimulus is merely longitudinal and transverse strains, although subsequent studies that have tested this theory have used maximum principal strain instead (Geris, et al., 2003; Isaksson, et al., 2006b). We did perform regressions using the longitudinal and transverse strains and found very similar results to those for maximum principal strain, indicating that our findings are consistent with the postulate of Claes and Heigele that with increasing strain, formation of fibrocartilage and other connective tissues (including cartilage) is more likely than intramembranous ossification. Both the Prendergast and Carter theories predict that fibrocartilage would be more likely than cartilage or bone to form in regions experiencing the highest shear or tensile strains. Although our data show either no correlation or a negative correlation between fibrocartilage probability and both shear and tensile strains, we believe that the very small amounts of fibrocartilage present in the calluses (<2.3% of the callus volume (Salisbury Palomares, et al., 2009)), together with the fact that the comparisons of strains to histology were conducted across two different cohorts of specimens, resulted in too little statistical power to detect correlations in many of the sections. The small areas of fibrocartilage would also be susceptible to errors in image registration, leading to less reliable correlation results. Thus, it may be premature to use the fibrocartilage results to comment on the existing theories. Also, because we did not measure fluid velocity and hydrostatic pressure (the other stimuli in the existing theories), our results do not provide a complete validation or refutation of these theories.

Consideration of the results for multiple timepoints provides insight into the dynamic nature of the association between the mechanical environment and tissue response. The least consistency among histological sections was observed for the comparison of day-10 strains to day-17 histology, while the comparisons of day-24 strains to day-38 histology and those of day-38 strains to day-38 histology gave very similar results (Figure 6). One explanation is that the tissue response occurs more quickly during the earlier phases of healing and stimulation—making the eight-day interval between PODs 10 and 17 too long to allow detection of correlations between strain and tissue type—and then subsequently equilibrates. This scenario is consistent with a published simulation for this animal model, which predicts initially rapid changes in tissue distribution followed by equilibration (Hayward and Morgan, 2009).

The changes in regression results over time also indicate that the role of the strain stimuli may change over the healing timecourse. After day 24, the number of histological sections with a positive association between shear strain and cartilage decreased, while the number of sections with a negative association between volumetric strain and cartilage increased (Figure 6). Hence, after day 24, which is the point at which the volume of cartilage in the bending-stimulated callus is fully established (Salisbury Palomares, et al., 2009), the probability of encountering cartilage increases with decreasing dilatation. Given that negative dilatation is caused by positive pressure, these data agree with numerous studies that have shown the beneficial effect of hydrostatic pressure on chondrocyte metabolism and cartilage matrix synthesis (reviewed in (Elder and Athanasiou, 2009)). Moreover, since the amount of undifferentiated mesenchyme vs. differentiated tissues in the callus decreases from day 10 to day 38, these findings suggest that while shear strain may regulate chondrogenic differentiation, volumetric strain may become more influential for cartilage maintenance. Indeed, the response of chondrocytes to different mechanical stimuli can differ from that of mesenchymal stem cells (Mauck, et al., 2007). Taken together, these data suggest a complexity to the mechanobiology of skeletal tissues in that the effects of specific mechanical stimuli on tissue differentiation may differ from those on tissue homeostasis.

Supplementary Material

01
02
03
04
05
06

Acknowledgments

Funding was provided by S10-RR021072-01, NIH AR053353 (EFM) and the Whitaker Foundation (KTSP). The authors thank Dr. Paul Barbone for many helpful discussions about the SMLE technique and Mark Slater and Lauren Hayward for technical assistance.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bottlang M, Mohr M, Simon U, Claes L. Acquisition of full-field strain distributions on ovine fracture callus cross-sections with electronic speckle pattern interferometry. J Biomech. 2008;41:701–5. doi: 10.1016/j.jbiomech.2007.10.024. [DOI] [PubMed] [Google Scholar]
  2. Carter DR, Beaupre GS, Giori NJ, Helms JA. Mechanobiology of skeletal regeneration. Clin Orthop. 1998:S41–55. doi: 10.1097/00003086-199810001-00006. [DOI] [PubMed] [Google Scholar]
  3. Claes LE, Heigele CA. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J Biomech. 1999;32:255–66. doi: 10.1016/s0021-9290(98)00153-5. [DOI] [PubMed] [Google Scholar]
  4. Claes LE, Wilke HJ, Augat P, Rubenacker S, Margevicius KJ. Effect of dynamization on gap healing of diaphyseal fractures under external fixation. Clin Biomech (Bristol, Avon) 1995;10:227–34. doi: 10.1016/0268-0033(95)99799-8. [DOI] [PubMed] [Google Scholar]
  5. Cullinane DM, Fredrick A, Eisenberg SR, Pacicca D, Elman MV, Lee C, Salisbury K, Gerstenfeld LC, Einhorn TA. Induction of a neoarthrosis by precisely controlled motion in an experimental mid-femoral defect. J Orthop Res. 2002;20:579–86. doi: 10.1016/S0736-0266(01)00131-0. [DOI] [PubMed] [Google Scholar]
  6. Cullinane DM, Salisbury KT, Alkhiary Y, Eisenberg S, Gerstenfeld L, Einhorn TA. Effects of the local mechanical environment on vertebrate tissue differentiation during repair: does repair recapitulate development? J Exp Biol. 2003;206:2459–71. doi: 10.1242/jeb.00453. [DOI] [PubMed] [Google Scholar]
  7. Elder BD, Athanasiou KA. Hydrostatic pressure in articular cartilage tissue engineering: from chondrocytes to tissue regeneration. Tissue Eng Part B Rev. 2009;15:43–53. doi: 10.1089/ten.teb.2008.0435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ferguson C, Alpern E, Miclau T, Helms JA. Does adult fracture repair recapitulate embryonic skeletal formation? Mech Dev. 1999;87:57–66. doi: 10.1016/s0925-4773(99)00142-2. [DOI] [PubMed] [Google Scholar]
  9. Gardner TN, Mishra S. The biomechanical environment of a bone fracture and its influence upon the morphology of healing. Med Eng Phys. 2003;25:455–64. doi: 10.1016/s1350-4533(03)00036-5. [DOI] [PubMed] [Google Scholar]
  10. Geris L, Van Oosterwyck H, Vander Sloten J, Duyck J, Naert I. Assessment of mechanobiological models for the numerical simulation of tissue differentiation around immediately loaded implants. Comput Methods Biomech Biomed Engin. 2003;6:277–88. doi: 10.1080/10255840310001634412. [DOI] [PubMed] [Google Scholar]
  11. Gerstenfeld LC, Cullinane DM, Barnes GL, Graves DT, Einhorn TA. Fracture healing as a post-natal developmental process: molecular, spatial, and temporal aspects of its regulation. J Cell Biochem. 2003;88:873–84. doi: 10.1002/jcb.10435. [DOI] [PubMed] [Google Scholar]
  12. Giori NJ, Beaupre GS, Carter DR. Cellular shape and pressure may mediate mechanical control of tissue composition in tendons. J Orthop Res. 1993;11:581–91. doi: 10.1002/jor.1100110413. [DOI] [PubMed] [Google Scholar]
  13. Gokhale N, Richards M, Oberai A, Barbone P. Simultaneous image registration and elastic modulus reconstruction. IEEE Int Symp Biomed Imaging; Arlington, VA. 2004. [Google Scholar]
  14. Goodship AE, Kenwright J. The influence of induced micromovement upon the healing of experimental tibial fractures. J Bone Joint Surg Br. 1985;67:650–5. doi: 10.1302/0301-620X.67B4.4030869. [DOI] [PubMed] [Google Scholar]
  15. Hayward LN, Morgan EF. Assessment of a mechano-regulation theory of skeletal tissue differentiation in an in vivo model of mechanically induced cartilage formation. Biomech Model Mechanobiol. 2009 Jan 21; doi: 10.1007/s10237-009-0148-3. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Isaksson H, Comas O, van Donkelaar CC, Mediavilla J, Wilson W, Huiskes R, Ito K. Bone regeneration during distraction osteogenesis: mechano-regulation by shear strain and fluid velocity. J Biomech. 2007;40:2002–11. doi: 10.1016/j.jbiomech.2006.09.028. [DOI] [PubMed] [Google Scholar]
  17. Isaksson H, van Donkelaar CC, Huiskes R, Ito K. Corroboration of mechanoregulatory algorithms for tissue differentiation during fracture healing: Comparison with in vivo results. J Orthop Res. 2006a;24:898–907. doi: 10.1002/jor.20118. [DOI] [PubMed] [Google Scholar]
  18. Isaksson H, van Donkelaar CC, Ito K. Sensitivity of tissue differentiation and bone healing predictions to tissue properties. J Biomech. 2009;42:555–64. doi: 10.1016/j.jbiomech.2009.01.001. [DOI] [PubMed] [Google Scholar]
  19. Isaksson H, Wilson W, van Donkelaar CC, Huiskes R, Ito K. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J Biomech. 2006b;39:1507–16. doi: 10.1016/j.jbiomech.2005.01.037. [DOI] [PubMed] [Google Scholar]
  20. Jazrawi LM, Majeska RJ, Klein ML, Kagel E, Stromberg L, Einhorn TA. Bone and cartilage formation in an experimental model of distraction osteogenesis. J Orthop Trauma. 1998;12:111–6. doi: 10.1097/00005131-199802000-00008. [DOI] [PubMed] [Google Scholar]
  21. Kelly DJ, Prendergast PJ. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. J Biomech. 2005;38:1413–22. doi: 10.1016/j.jbiomech.2004.06.026. [DOI] [PubMed] [Google Scholar]
  22. Kenwright J, Richardson JB, Cunningham JL, White SH, Goodship AE, Adams MA, Magnussen PA, Newman JH. Axial movement and tibial fractures. A controlled randomised trial of treatment. J Bone Joint Surg Br. 1991;73:654–9. doi: 10.1302/0301-620X.73B4.2071654. [DOI] [PubMed] [Google Scholar]
  23. Lacroix D, Prendergast PJ. A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J Biomech. 2002;35:1163–71. doi: 10.1016/s0021-9290(02)00086-6. [DOI] [PubMed] [Google Scholar]
  24. Loboa EG, Beaupre GS, Carter DR. Mechanobiology of initial pseudarthrosis formation with oblique fractures. J Orthop Res. 2001;19:1067–72. doi: 10.1016/S0736-0266(01)00028-6. [DOI] [PubMed] [Google Scholar]
  25. Martin R, Burr D, Sharkey N. Skeletal Tissue Mechanics. Springer Verlag; New York: 1998. p. 392. [Google Scholar]
  26. Mauck RL, Byers BA, Yuan X, Tuan RS. Regulation of cartilaginous ECM gene transcription by chondrocytes and MSCs in 3D culture in response to dynamic loading. Biomech Model Mechanobiol. 2007;6:113–25. doi: 10.1007/s10237-006-0042-1. [DOI] [PubMed] [Google Scholar]
  27. McCalden RW, McGeough JA, Barker MB, Court-Brown CM. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. Journal of Bone and Joint Surgery. 1993;American Volume 75:1193–205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
  28. Oberai AA, Gokhale N, Feijoo GR. Solution of Inverse Problems in Elasticity Imaging Using the Adjoint Method. Inverse Problems. 2003;19:297–313. [Google Scholar]
  29. Prendergast PJ, Huiskes R, Soballe K. ESB Research Award 1996. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech. 1997;30:539–48. doi: 10.1016/s0021-9290(96)00140-6. [DOI] [PubMed] [Google Scholar]
  30. Salisbury Palomares KT, Gleason RE, Mason ZD, Cullinane DM, Einhorn TA, Gerstenfeld LC, Morgan EF. Mechanical stimulation alters tissue differentiation and molecular expression during bone healing. J Orthop Res. 2009;27:1123–32. doi: 10.1002/jor.20863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sasazaki Y, Shore R, Seedhom BB. Deformation and failure of cartilage in the tensile mode. J Anat. 2006;208:681–94. doi: 10.1111/j.1469-7580.2006.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Selvin S. Practical biostatistical methods. Duxbury Press; 1994. p. 528. [Google Scholar]
  33. Tay BK, Le AX, Gould SE, Helms JA. Histochemical and molecular analyses of distraction osteogenesis in a mouse model. J Orthop Res. 1998;16:636–42. doi: 10.1002/jor.1100160518. [DOI] [PubMed] [Google Scholar]
  34. Thompson MS, Schell H, Lienau J, Duda GN. Digital image correlation: a technique for determining local mechanical conditions within early bone callus. Medical Engineering and Physics. 2007;29:820–3. doi: 10.1016/j.medengphy.2006.08.012. [DOI] [PubMed] [Google Scholar]
  35. Tissakht M, Ahmed AM. Tensile stress-strain characteristics of the human meniscal material. J Biomech. 1995;28:411–22. doi: 10.1016/0021-9290(94)00081-e. [DOI] [PubMed] [Google Scholar]
  36. Villegas DF, Maes JA, Magee SD, Donahue TL. Failure properties and strain distribution analysis of meniscal attachments. J Biomech. 2007;40:2655–62. doi: 10.1016/j.jbiomech.2007.01.015. [DOI] [PubMed] [Google Scholar]
  37. Williamson AK, Chen AC, Masuda K, Thonar EJ, Sah RL. Tensile mechanical properties of bovine articular cartilage: variations with growth and relationships to collagen network components. J Orthop Res. 2003;21:872–80. doi: 10.1016/S0736-0266(03)00030-5. [DOI] [PubMed] [Google Scholar]
  38. Wren TA, Beaupre GS, Carter DR. Mechanobiology of tendon adaptation to compressive loading through fibrocartilaginous metaplasia. J Rehabil Res Dev. 2000;37:135–43. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS210321-supplement-01.doc (43.5KB, doc)
02
NIHMS210321-supplement-02.tif (243.6KB, tif)
03
NIHMS210321-supplement-03.tif (242.8KB, tif)
04
NIHMS210321-supplement-04.tif (245.5KB, tif)
05
NIHMS210321-supplement-05.tif (247.9KB, tif)
06
NIHMS210321-supplement-06.tif (15.9MB, tif)

RESOURCES