Why do insects have such a high density of flow-sensing hairs? Insights from the hydromechanics of biomimetic MEMS sensors

Abstract

Insects and arachnids are often quite hairy. The reasons for this high density of sensory hairs are unknown. Previous studies have predicted strong hydrodynamic coupling between densely packed airflow-sensitive hairs. Flow perturbation owing to single hairs and between tandem hairs, however, has never been experimentally measured. This paper aims to quantify the extent of flow perturbation by single and tandem hairs directly, using biomimetic microelectromechanical system (MEMS) hairs as physical models and particle image velocimetry (PIV) for flow visualization. Single and tandem MEMS hairs of varying interhair distances were subjected to oscillatory flows of varying frequency. Decreasing hair-to-hair distance markedly reduced flow velocity amplitude and increased the phase shift between the far-field flow and the flow between hairs. These effects were stronger for lower flow frequencies. We predict strong hydrodynamic coupling within whole natural hair canopies exposed to natural stimuli, depending on arthropod and hair sizes, and hair density. Thus, rather than asking why arthropods have so many hairs, it may be useful to address why hairs are packed together at such high densities, particularly given the exquisite sensitivity of a single hair.

1. Introduction

Most arthropods have many hairs, often packed together at an unusually high density. Functional explanations for this high density depend on the type of hair. Indeed, the high density of small setae in the foot of many insects results in increased adherence (Federle 2006), whereas a countless number of aquatic and terrestrial arthropods also use hairs for particle capture, flying or swimming (Cheer & Koehl 1987). In wood crickets, the density of airflow-sensing hairs can reach values higher than 400 hairs mm⁻² (Dangles et al. 2006). The reasons for such a high number and density of sensors are unclear, in particular since several studies have shown that the early instars of cockroaches and crickets, which suffer the highest mortality, have much fewer hairs, down to two in the first cockroach instars (Camhi 1984). Furthermore, the relationship between number and density changes over the course of ontogeny in a complex nonlinear manner, the highest hair density corresponding to the smallest number of hairs in wood crickets (Dangles et al. 2006). Using an analogy with neuronal population coding, one may assume that a high density of sensors, often each of extreme sensitivity (Shimozawa et al. 2003), increases the ability to characterize spatio-temporal patterns of stimuli at very small spatial scales. Such high densities imply, however, that there are hydrodynamic interactions between hairs, and thus that hairs do not act independently. The extent of the influence of a hair on its neighbours through flow perturbation has recently been addressed using experimental, theoretical and computational approaches. The aim of this work is to present experimental data on the flow field between two biomimetic microelectromechanical system (MEMS) hairs using a systematic set of stimulus velocities, frequencies and interhair spacings, and to provide a quantitative test of the theory and mathematical models derived in earlier studies.

Using spider legs exposed to oscillatory flows, Bathellier et al. (2005) determined the deflection angle of tandem airflow-sensing hairs using optical methods. They did not observe fluid-mediated interactions (called thereafter viscous coupling owing to the low Reynolds number) for two freely moving hairs of similar length. By contrast, they identified a strong viscous effect if one of the hairs was immobilized, or if the hairs were of different lengths. They developed a theoretical model of viscous coupling that fitted their data well. The model also explained why viscous coupling could not be observed for two freely movable hairs of similar length: damping and driving torques cancel each other and viscous losses dominate the other effects. These authors extended their theory to hairs of dissimilar lengths, predicting an effect of viscous coupling over a distance of 30 hair diameters or more.

Recently, Cummins et al. (2007) applied computational methods to the same problem. Their results largely confirmed those of Bathellier et al. (2005) with two exceptions. First, they observed significant coupling for hairs of similar length. Second, they extended their findings to larger distances, predicting viscous coupling over 50 hair diameters or more. This was also recently observed in another computational study by Heys et al. (2008). Furthermore, Cummins et al. (2007) computed interactions for a group of several hairs and predicted (i) large phase shifts between hairs and (ii) the presence of ‘dead zones’ within the hair canopy, caused by strong coupling between hairs. More recently, Lewin & Hallam (in press) showed, again using computational fluid dynamics models, that viscous coupling can be negative when hairs are arranged perpendicular to the flow, implying an increased sensitivity of a hair owing to the inhibitory effects of its neighbour (see also Cheer & Koehl (1987), for an earlier study on variable interactions depending on the flow direction relative to hair arrangement). The predictions by Bathellier et al. (2005), and in subsequent studies, are based on the various theories developed over the past 10 years for single hairs (reviewed in Humphrey & Barth 2008). None of these studies have measured the flow field around hairs. Rather, the flow field has been invariably inferred from observed and computed hair movement, using existing theories.

Several limitations have so far prevented the direct measurement of airflow around biological hairs. The measurement of boundary layers around real hairs using particle image velocimetry (PIV), combined with laser-based techniques, presents a number of difficulties. First, it is nearly impossible to find a hair arrangement and laser positioning that ensures that the laser light sheet is in the focal plane of both (i) the two hairs and (ii) their common plane of movement. This is important as hairs have preferential planes of movement (Landolfa & Jacobs 1995); misalignments, therefore, lead to biased estimates. Second, owing to the high density of the hairs, other nearby, but out-of-plane, hairs may disturb the flow. This would require cutting away all but two of the hairs, a tedious and delicate task. Third, the surface of the appendages bearing the hairs to be studied, such as that of the two antenna-like structures at the rear of crickets, called cerci, contains many spines and other ultrastructures, which could increase the boundary layer of the appendage itself (Steinmann et al. 2006; Dangles et al. 2008). Any of these features may have an unknown effect on the estimation of the boundary layer around the hairs. The alternative use of physical models overcomes many of these limitations. Here, we use biomimetic MEMS sensory hairs, designed partly based on cricket hairs (Krijnen et al. 2006). The conditions in which flow measurements are taken with MEMS can be fully controlled, allowing us to design experiments with tandem MEMS hairs of varying interhair distances to measure the perturbation to flow directly, using PIV. We used a so-called parallel flow system, the most widely used system for such studies, in which the flow is in the direction defined by the plane of the two hairs.

2. Material and methods

2.1. Design of MEMS hairs

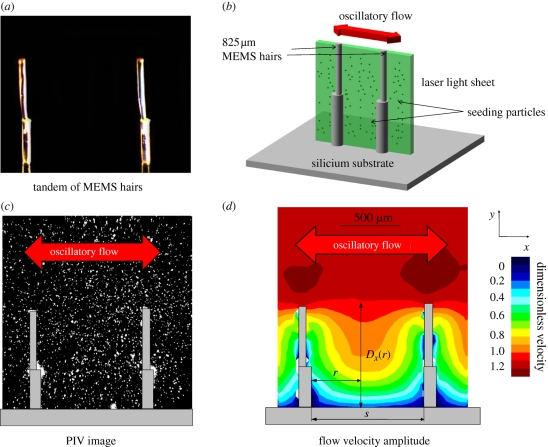
MEMS hairs were made of SU-8, an epoxy that can be structured by photolithography. To obtain sufficiently long hairs, two deposition/exposure cycles of about 450 µm each are used. Depending on (i) the exact SU-8 solution, (ii) the spinning conditions, as well as (iii) the temperature-dependent shrinking effects during curing, there exist wafer-scale variations in the final SU-8 layer thickness. Catering to the negative-tone resist properties of SU-8, i.e. what is illuminated will remain after exposure and development, and the limited aspect ratio of the overall photolithographic process of about 10–20, the first layer is exposed prior to the deposition of the second layer. This allows the diameters of the hairs in the first and second layer to be dissimilar. However, this is only by design: actual diameters deviate from designed values and are invariably smaller at the bottom than at the top owing to the optical intensity profile during exposure (light is absorbed and hence the intensity decreases from top to bottom). Design values for the hair diameters of the first and second layers were 50 and 25 µm, respectively. The smaller diameter of the second part of the hairs is caused by a substantial reduction in the moment of inertia (by around 65%) allowing for increased sensitivity for a given bandwidth (Krijnen et al. 2007) but is non-essential in this study. Owing to technical limitations in alignment (because of the large thickness of the layers) as well as curing-induced deformations, the second part of the hair is slightly eccentric over the first part (see figure 1a). The diameter of the second part of the hairs was tapered from top to bottom. The total length of the MEMS hairs was 825 µm. Only fixed hairs were used in this study, given that hair movement for fully functional MEMS hairs is limited and hardly measurable with PIV (displacements of the nanometre range) and that it is much simpler to construct fixed hairs. Details of the fabrication of fully functional hair sensors are described in Bruinink et al. (2009). The distance between hairs varied between 450 and 2800 µm, corresponding to 9–56 hair diameters.

Figure 1.

Set-up and definition of variables.

2.2. Experimental set-up

Single or tandem 825 µm MEMS hairs, fixed on plates of dimensions 10 × 10 mm², were placed in a glass container (dimensions: 10 × 10 × 10 cm³). One loudspeaker (40 W) was connected at one side to a sinusoidal signal generator. The air inside the sealed glass box was seeded with 0.2 µm oil particles (di-ethyl-hexyl-sebacate) using an aerosol generator. The PIV-pulsed laser (NewWave Research Solo PIV 2, 532 nm, 30 mJ, Nd:YAG, dual-pulsed; Dantec Dynamics A/S) illuminated the flow through the glass from the top. The laser sheet (width = 17 mm, thickness at focus point = 50 µm) was operated at low power (3 mJ at 532 nm wavelength) to minimize glare, and the pulse duration was 4 ± 1 ns.

A target area was imaged onto the charge-coupled device (CCD) array of a digital camera (696 × 512 pixels) using a stereomicroscope. The field of view was 2700 × 2000 µm. Particle velocities were extracted from the images by cross correlation. Owing to the information contained in the grey-level values as captured by CCD as well as the relatively large number of particles used in the cross-correlation calculations, a particle displacement precision of 0.1 pixels can be obtained. Given the entire set-up, this translates into a measurable displacement of 0.4 µm. We set the time between two pairs of images at 200 µs to provide a sufficient dynamic range of velocities, giving a velocity precision of 2 mm s⁻¹. We chose a precision level larger than 1 per cent (1% of the velocity amplitude), setting the far-field flow amplitude to between 150 and 200 mm s⁻¹. For a 50 µm diameter MEMS hair in air at 20°C, this corresponds to a Reynolds number of between 0.5 and 0.7, relatively close to the Reynolds number of 0.19 observed for a 10 µm diameter cricket hair. Thus, this experimental set-up provides a flow system comparable to that experienced in nature.

We used the stroboscopic principle to measure different phases of sinusoidal flow with a PIV system limited to 20 Hz. As explained in Steinmann et al. (2006), it consists of sampling a signal of high frequency at a frequency slightly lower than a sub-multiple of the signal frequency. This technique allows us to estimate the flow phase by inference. The flow velocity fields presented in this article are proportional to the amplitude of the flow velocity, i.e. the difference between the maximum velocity measured at ωt = (π/2) and the minimum velocity measured at ωt =−(π/2).

2.3. Theoretical approximations

Viscous coupling can be inferred by measuring the proportional change in the angle of movement of a single undisturbed hair relative to the angle of the movement of one of a pair of hairs that are coupled through flow. This change will be a function of the change in the forces acting on the hairs. These forces, in turn, are a function of the integral of the surface-normal gradient of the flow velocity over the total surface area of the hairs. Previous authors have calculated viscosity-mediated coupling as the change in the torque acting on one of a pair of hairs, relative to the torque acting on undisturbed (single) hairs.

In this study, we are interested in the flow perturbation, rather than the hair response. Let us first describe V_∞(y), the horizontal (x-axis) component of the non-perturbed velocity on a flat plate. The infinity symbol describes the fact that this velocity does not depend on x when there is no hair, or when the velocity is measured at an infinite distance from a hair. We used the model proposed by Shimozawa & Kanou (1984) for modelling the plate boundary layer,

2.1

where .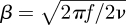

The change D_x (in the x-direction) in near-field velocities V_x(r,y) around a single hair, normalized to the far-field velocity at a height y, V_∞(y), is defined as

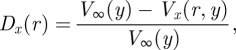2.2

with r being the distance from the hair. This perturbation thus has a value of 1 at the surface of the flow-disrupting hair. A theoretical approximation of flow perturbation D_x was initially proposed by Bathellier et al. (2005); see the subsequent corrections in Lewin & Hallam (in press) and by the authors (Bathellier et al. 2005), and we refer readers to these publications for its derivation. The proposed model assumes hairs of constant diameter and infinite hair length. As explained below, the perturbation is independent of y once the plate boundary layer has been factored out, so that we drop the dependence on y in the following. The flow perturbation is then given by the following equation:

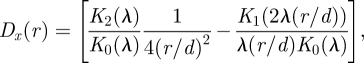2.3

where K₀, K₁ and K₂ are modified Bessel functions of the second kind, d is the hair diameter, the dimensionless parameter 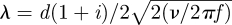, and ν and f are the kinematic viscosity and the fluid flow frequency, respectively.

The phase shift between the far-field flow and the flow within a hair canopy is also perturbed by the hairs. The phase shift between the far-field flow and the flow near a flat substrate without hairs, measured in the vertical y-axis, is described by the following (Shimozawa & Kanou 1984):

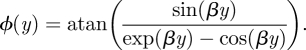2.4

We use equation (2.4) on a comparative basis when analysing the phase shift due to the presence of hairs.

2.4. Perturbation by two hairs

Following Bathellier et al. (2005), the flow velocity at any location between two non-moving hairs at a distance s apart can be expressed as the sum of: (i) the unperturbed flow V_∞(y), (ii) plus the velocity perturbation D_x(r) associated with hair 1, and (iii) plus the perturbation D_x(r−s) for hair 2,

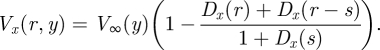2.5

The total perturbation is

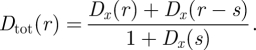2.6

2.5. Perturbation measurements

PIV measurements provide two-dimensional flow velocities in the cross-section of a hair (or a pair of hairs) in the flow direction, as shown in figure 1. We first conducted measurements on a flat surface without hairs (data not shown) to obtain experimental values of V_∞(y) at the four frequencies. They were used to validate equation (2.1). The perturbation at a distance r from the hair surface, D_x(r), is then determined as the average, over the entire hair height (in steps of 100 µm), of equation (2.2).

3. Results

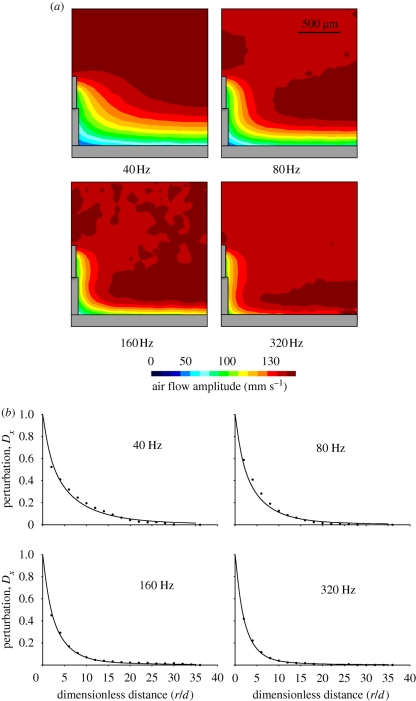
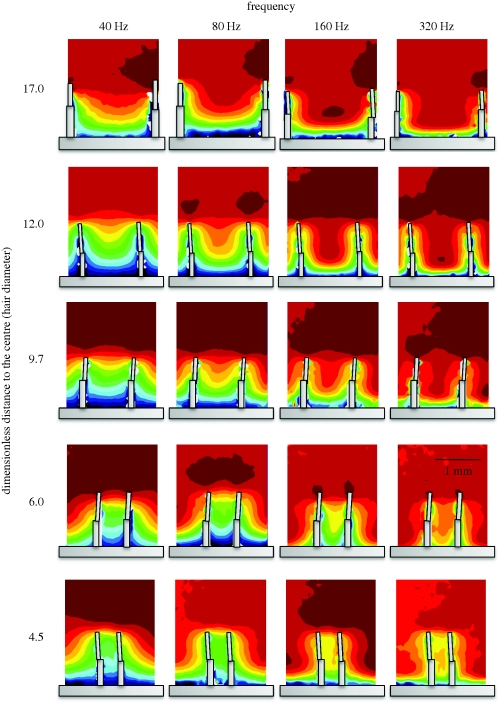
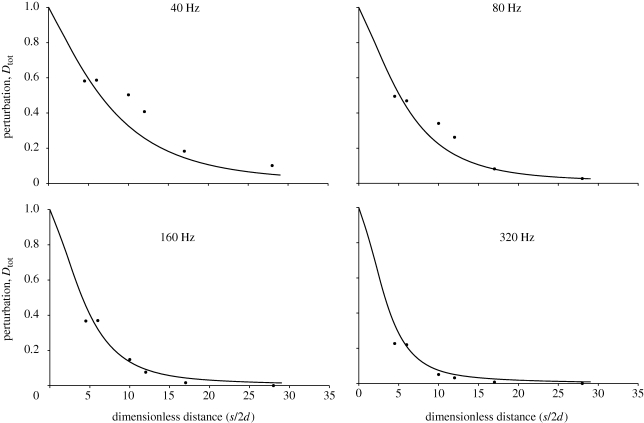
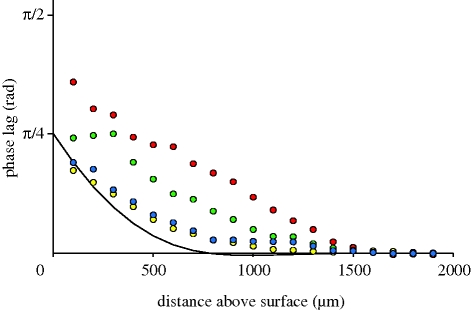
The theoretical model for the flow velocity shows a good fit for data obtained for single MEMS hairs, despite its numerous approximations (figure 2). In particular, the decrease in flow perturbation with increasing frequency, the decrease in the extent of the boundary layers and the merging of the substrate and hair boundary layers are very clear to see. A full factorial design of flow analysis using MEMS hairs arranged in tandem, with frequency and interhair distances as variables, is presented in figure 3. Data obtained for hairs spaced at an interhair distance of 2800 µm were not plotted owing to scaling difficulties. The model for tandem hairs showed a good fit for the shortest and longest distance from the hairs, with an improvement in the fit at high frequencies (figure 4). Again, the decrease of flow velocity perturbation with increasing frequency and increasing interhair distance is quite obvious. A phase shift between the flow in the far field and the flow near the substrate is expected even in the absence of hairs and their presence increases it. Reduced interhair distances lead to increased phase shifts between the far-field flow and the flow measured between two hairs (figure 5). At distances of 1.5 mm or greater, the effect of a hair on its neighbour, in terms of this phase shift, becomes negligible. The increased variability observed within the first hundred micrometres of the boundary around the substrate is due to low seeding density, a common limitation inherent to PIV.

Figure 2.

Perturbation of flow by a single MEMS hair at four different frequencies. (a) Half of the full-field image. (b) Dots represent observed data and lines show predictions of the analytical model (equation (2.3)). The distance from the hair is denoted by r and the hair diameter by d. (a) Scale bar, 500 µm.

Figure 3.

Full-field data for flow in the vicinity of MEMS hairs arranged in tandem, as a function of frequency and interhair distance. Data for the largest interhair distance are not shown owing to the need for different scaling.

Figure 4.

Flow perturbation between two MEMS hairs, as a function of interhair distance and flow frequency. Filled circles represent measurements while lines represent predicted data from the analytical model (equation (2.6)). The distance between the two hairs is denoted by s and the hair diameter by d.

Figure 5.

Observed phase lag between the far-field and local flow for two MEMS hairs as a function of interhair distance (red 600 µm, green 1000 µm, blue 1700 µm and yellow 2800 µm) at the flow frequency of 80 Hz. The solid line represents the expected phase lag on a flat plate, given in equation (2.4).

4. Discussion

Our data obtained from single and tandem MEMS hairs are consistent with the theoretical models. The form of the observed relationship at low frequencies is somewhat different from the one predicted by the theoretical models, so that several assumptions are, therefore, worth discussing here. First, the finite length of a hair implies that its boundary layer is reduced near the tip, leading to an underestimation of the flow perturbation, compared with the infinite length assumption. Thus, strictly speaking, the theory is not developed for hairs of finite length and will show discrepancies with measurements, but this aspect cannot account for the reduced fit. Second, the theory assumes constant hair diameter, whereas our MEMS hairs have varying diameters. This has a negligible influence on the boundary layer at the tested frequencies, so that we used the assumption of a hair of constant diameter of 50 µm in all our computations. We observed variations at the junctions of the two parts of the hairs at frequencies higher than those analysed. Third, the theoretical models assume that the fluid inertial terms of the Navier–Stokes equation can be neglected for low values of 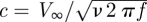, an assumption that might be valid at the highest frequency (c = 0.3 for 320 Hz), but less so at the lowest frequency (c = 0.8 at 40 Hz). There is thus a need for an improved theory of flow perturbation for such conditions. Given the overall good fits, our approach using MEMS, therefore, allows us to use the predictions obtained using computational fluid dynamics models and to predict the expected effects for natural hairs, taking into account the similarities and differences between these artificial hairs and natural hairs.

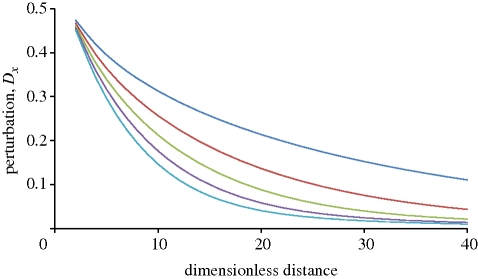
The range of distances between individual MEMS hairs used in these experiments overlaps with that observed for crickets (Dangles et al. 2008). Indeed, for large cricket hairs (L > 500 um) with diameters d between 7 and 12 µm, 90 per cent of their nearest neighbouring hairs are at a distance s of between 30 and 60 µm, giving a dimensionless spacing distance of 2.5 < s/d < 8.5. Smaller hairs, with diameters of 1–3 µm, are randomly distributed with distances between neighbouring hairs of 10–60 µm, giving a dimensionless spacing distance of 3 < s/d < 60. The MEMS set-up covered a range of 9 < s/d < 56. However, two major differences should be noted. First, in contrast to the negligible movements of MEMS hairs, natural hairs move. This movement, with hairs following the direction of flow, reduces the flow perturbation and hence the viscous coupling (Bathellier et al. 2005). Second, MEMS hairs have a much larger diameter than natural hairs. Hair diameter has a substantial effect on the extent of viscous coupling (figure 6), whereas the effect on flow caused by thin hairs is smaller in absolute terms, it is larger when flow perturbation is considered relative to hair diameter. Given the above caveats, our limited understanding of the effect of transverse flow on hydrodynamic interactions (Lewin & Hallam in press) and even poorer understanding for groups of hairs (Cummins et al. 2007), we are far from a thorough intuitive grasp of hydrodynamic interactions within hair canopies.

Figure 6.

Effect of hair diameter on flow perturbation. Smaller hairs have a greater effect on flow perturbation when data are normalized, but a smaller effect for absolute values of flow perturbation. Blue line, 10 µm; red line, 20 µm; green line, 30 µm; violet line, 40 µm; light blue, 50 µm.

4.1. Implications for natural hairs

Using optical techniques to measure natural hair movement and theoretical models, Bathellier et al. (2005) concluded that viscous coupling can exert a strong effect over a distance of up to 30 hair diameters. Later, Cummins et al. (2007) and Heys et al. (2008), using increasingly realistic computational models, proposed that viscous coupling extends even further, up to at least 50 or more hair diameters. Strong viscous coupling corresponds to a proportional loss of independence between hairs, reducing movement amplitude, and major alterations in the phase shifts between the far-field flow velocity and the local flow between individual hairs in the canopy. These factors together determine the likelihood and timing of action potentials being fired in the hair nerve cell. This has major effects on the function of the cercus, as shown recently by Mulder-Rosi et al. (in press). The relative timing of the firing of different hairs along the cercus allows the proper integration of signals, thus determining the overall signalling profile for incoming danger in the terminal abdominal ganglion. Indeed, bulk flow or flow generated in the backward direction may give weak signals or no signal at all (Mulder-Rosi et al. in press).

Determining the extent of viscous coupling provides further insight into the working of the cercal organ as a whole. The observed interhair distances and the short length of the cercus (0.8–4.5 mm; Dangles et al. 2006) suggest that strong viscous coupling is acting over the entire hair canopy, with a single hair exerting an effect on flow over nearly half of the cercus. This is reinforced by the fact that viscous coupling is particularly strong for low-frequency flows, predominantly present in the signals produced by spiders approaching their prey (Casas et al. 2008; Kant & Humphrey 2009). Observations by Lewin & Hallam (in press) suggesting that, depending on the spatial arrangement of its neighbours, a hair's response may be increased support the idea that the position of a hair may be as important as its individual characteristics in predicting its mechanical and physiological response (as first observed by Cummins et al. (2007)). Thus, further work is needed to elucidate the implications of group effects: the density of neighbouring hairs, their length and their preferred plane of movement.

In conclusion, the effect of a cricket hair on the canopy response cannot be determined by examining the contribution of a hair in isolation, despite previous attempts to do so (e.g. Magal et al. 2006). This conclusion contrasts with an entire body of work that has focused on the response of single hairs over many years (reviewed in Humphrey & Barth 2008; Casas & Dangles 2010). Thus, this represents a major shift of focus: with such a high density of hairs, the entire hair canopy is most likely to work as a hydrodynamically coupled set of resonators. Thus, rather than ask the question of why arthropods bear so many hairs, we need to address the issue of why hairs are packed together at such high density. How the extreme sensitivity of individual hairs is related to their loss of independence within the canopy also needs to be addressed. These phenomena may be explained by highly nonlinear ensemble reactions, the neurophysiological mechanisms of which have been only very recently tackled using appropriate geometric arrangements of hair and relevant stimuli (Mulder-Rosi et al. in press).