Abstract
In this communication, we analyse the passage of oxygen and carbon dioxide over the respiratory membrane. The lung surfactant membrane at the alveolar interface can have a very special arrangement, which affects the diffusional transport. We present a theoretical model for the diffusion of small molecules in membranes with a complex structure, and we specifically compare a membrane composed of a tubular bilayer network with a membrane consisting of a stack of bilayers. Oxygen and carbon dioxide differ in terms of their solubility in the aqueous and the lipid regions of the membrane, and we show that this difference clearly influences their transport properties in the different membrane structures. During normal respiration, the rate-limiting step for carbon dioxide transport is in the gas phase of the different compartments in the lung. For oxygen, on the other hand, the rate is limited by the transport between alveoli and the capillary blood vessels, including the lung surfactant membrane. In a membrane with a structure of a continuous tubular lipid network, oxygen transport is facilitated to a significant extent compared with the structure of aligned lipid bilayers. The model calculations in the present study show that transport of oxygen through the tubular structure is indeed ca 30 per cent faster than transport through a membrane composed of stacked bilayers. The tubular network will also facilitate the transport of apolar substances between the gas phase and the blood. Important examples are ethanol and other volatile liquids that can leave the blood through the lungs, and gaseous anaesthetics or volatile solvents that are inhaled. This exemplifies a new physiological role of a tubular lipid network in the lung surfactant membrane.
Keywords: respiratory membrane, pulmonary surfactant, tubular myelin, diffusion
1. Introduction
The functional role of respiration is to induce the exchange of volatile molecules between the blood and the ambient air. Most significant is the oxygen taken from the air to the body and its primary metabolic breakdown product, carbon dioxide, which is released to the air. Respiration also potentially involves transport of many other compounds like ethanol from the blood to the air, or anaesthetics from a gas phase to the blood. Transport over long distances has to occur as fluid flow in order to be effective, and in the case of respiration it is driven by the cardiac, respiratory and other muscles. However, the transport process also involves a step where the molecules change between a liquid and a gaseous state. This necessarily involves the passing of an interface and there the net molecular transport occurs through diffusion. Both the heart and breathing frequency cover a certain range between rest and maximum load. The diffusional processes, on the other hand, are determined by design parameters, and they cannot be regulated on a short time scale. Hence, one would expect that the diffusional processes are rate limiting only at maximum load conditions for healthy individuals. There are pathological states, such as acute respiratory distress syndrome or lung oedema, where the diffusional transport between the air and the blood is hindered so that the respiration does not function properly.
In this communication, we analyse the diffusional transport of small molecules across the interface between the lung alveoli and the capillary vessels of the lung. Studies of lung surfactant ultrastructure have revealed two types of bilayer organization: lamellar bodies and tubular myelin (cf. Williams 1977). Lamellar bodies are the form in which lung surfactant is secreted by the alveolar type II cells. The role of tubular myelin, however, has been more elusive. This tubular structure as revealed by electron microscopy is assumed to consist of two sets of lipid bilayers intersecting each other into a square cross-section pattern with a lateral periodicity of about 50 nm, and is a most abundant form of lung surfactant in the lung (Gil 1985). The generation and maintenance of tubular myelin is known to involve surfactant protein A, surfactant protein B and calcium (Suzuki et al. 1989; Larsson et al. 2003a). There is accumulating evidence of an interconnected membrane structure in the alveolar surfactant layer (Baoukina et al. 2007; Pocivavsek et al. 2008a), and a very special arrangement, called a CLP (crossed layers of parallels) tubular network continuum (Larsson et al. 1999, 2002; Larsson 2002), has been proposed by one of us. The gross structure of the CLP bilayer arrangement is the same as in the traditional model of tubular myelin, but the CLP bilayers cross each other without intersections and form a minimal surface. Whatever the functional role or internal membrane structure of tubular myelin might be, the fact remains that this structure is abundantly present at the alveolar lining, and it is directly associated with the air/condensed state interface, and, thus, an analysis of gas transport in such a structure is warranted. We show that the lipid–protein membrane structure affects, in a significant way, the diffusional transport of small molecules.
2. The lipid monolayer
In a properly functioning lung, the interface between the gas and the condensed phase is covered by a monolayer composed primarily of phospholipids (Kahn et al. 1995). This monolayer has a strong influence on the interfacial properties. It is often stated that there is a very low interfacial tension of the order of 1 mN m−1 at the alveolar interface. This can be misleading for the following reason: in a liquid phase, there can be no permanent stresses in the bulk, and the surface excess free energy gives rise to a surface tension that have numerically the same value. For solids and other condensed phases that can support internal stresses, the equivalence between surface tension and surface free energy no longer applies. In the lung, there is clearly a large-scale framework that responds to muscular activity. On a smaller scale, there is a network of capillary vessels that can support mechanical stresses, and there are also other structural units around the alveoli that provide mechanical support. The role of the lung surfactant phospholipid monolayer is, within this conceptual framework, to lower the surface free energy. For hydrocarbon-based systems, one typically reaches a surface free energy no smaller than 20 mJ m−2 (corresponding to 20 mN m−1 surface tension) of a hydrocarbon–air interface. There is no way to reduce the effect of the always present van der Waals forces below this value (unless one goes to anomalously low densities of the condensed phase). To come to a situation where the surface tension is as low as 1 mN m−1, it is therefore necessary that there are additional mechanical forces acting through the structures, as for example line tension in the underlying lipid–protein alveolar membrane (Kashchiev & Exerowa 2001) or mechanical stress caused by compression of the barriers in Langmuir monolayer model systems (Pocivavsek et al. 2008b). Unless one has a detailed model of the structure, it is not known how this contribution to the tension varies with the size of the alveoli.
One can identify four different functional roles of the lipid monolayer. At birth when the lung is first exposed to air, the work of expanding the alveoli is reduced by a factor of at most 72/20 = 3.6 relative to the pure water case (Guyton & Hall 2000a). Insufficient surfactant levels at preterm birth result in infant respiratory distress syndrome, and the standard therapy for this condition is substitution therapy with exogenous lung surfactant, usually of porcine origin (Pérez-Gil 2008; Nkadi et al. 2009). Though it is still a question of discussion (Namati et al. 2008), it has been suggested that the surface area of the alveoli changes during respiration. The energy contribution from changing the interfacial area is reduced with a lower surface free energy. Another important aspect of the alveolar interface is to avoid capillary condensation in the humid environment inside the lung. For this purpose, it is necessary that the contact angle, θ, for surface–water–air is larger than 90°, which only occurs for very hydrophobic surfaces (Evans & Wennerström 1999a). A surface free energy of 20 mJ m−2 corresponds to θ = 115°. A fourth aspect of the surface free energy is that it contributes to the Laplace pressure
| 2.1 |
where H is the mean curvature (Evans & Wennerström 1999b). In general, the local radius of curvature, i.e. the radius of an osculating circle, depends on the direction along the surface. However, the maximum and minimum radius of curvature, R1 and R2, can be used to define the mean curvature, H, uniquely up to a sign (Struik 1988)
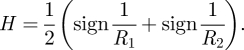 |
In equation (2.1), the Laplace pressure is written with the convention that the sign of the radius of curvature is positive if the surface is curved towards the gas, and negative if it curves away. For a given shape, the Laplace pressure is larger the smaller the size of the alveoli, and the larger the surface tension. Other conditions being equal, the Laplace pressure will tend to push gas from smaller compartments to larger ones. The film in the lung that separates the gas and condensed phases has a complex topology with a highly negative Euler characteristic (Weibel 1963). This implies through the Gauss–Bonnet theorem (Struik 1988) that, on average, the two radii of curvature R1 and R2 have different signs and the mean curvature has a lower magnitude than for a bubble of corresponding size. Thus, an elementary calculation, based solely on the alveolus size and neglecting the differing signs of the local radii of curvature, would tend to overestimate the magnitude of the Laplace pressure.
3. The lipid reservoir
The alveolar interface is a highly dynamic environment. Numerous electron microscopy ultrastructural works have shown that lung surfactant forms lipid bilayer association structures of two types: a bilayer structure in so-called lamellar bodies with spherically concentric bilayers alternating with water layers, and a tetragonal structure with a period along the c-axis of between 400 and 600 Å termed tubular myelin (Williams 1977; Pérez-Gil 2008). During breathing, the pressure in the alveoli changes, which might lead to variations in the area. Lipid monolayers in the condensed state have a low lateral compressibility, and area changes can occur readily only when lipids can easily transfer between the monolayer and a reservoir. The reservoir has been envisioned as a monolayer-associated interconnected bilayer reservoir that can fold and unfold upon compression and expansion (Baoukina et al. 2007; Pocivavsek et al. 2008a). Based on electron microscopic images of carefully prepared lung samples, Larsson et al. suggested a model where the monolayer is connected to a network of lipid bilayers organized in a tetragonal symmetrical phase of tubules extending parallel to the monolayer surface (Larsson 2002; Larsson et al. 2002). This complex structure was further proposed to follow the CLP minimal surface (Hyde et al. 1997; Larsson et al. 1999), and it is also consistent with morphological studies of the lipid bilayers in the tubular myelin (Larsson et al. 2003b). Figure 1b shows an illustration of the CLP minimal surface. The CLP structure is a functional continuum and as such it provides both a support and a reservoir of material for the monolayer by which the entire lipid core in tubular myelin/CLP is in some extent in lateral contact with the monolayer towards air. The alveolar lining is on average 0.2 µm thick and could accommodate approximately four stacked tubes in the direction perpendicular to the interface (Kashchiev & Exerowa 2001). Such an arrangement is relatively mechanically robust, and it allows for rapid transport of lipid as the interfacial area is changed. It also allows for rapid exchange/flow of lipid molecules between interface and bulk, compensating for chemical degradation.
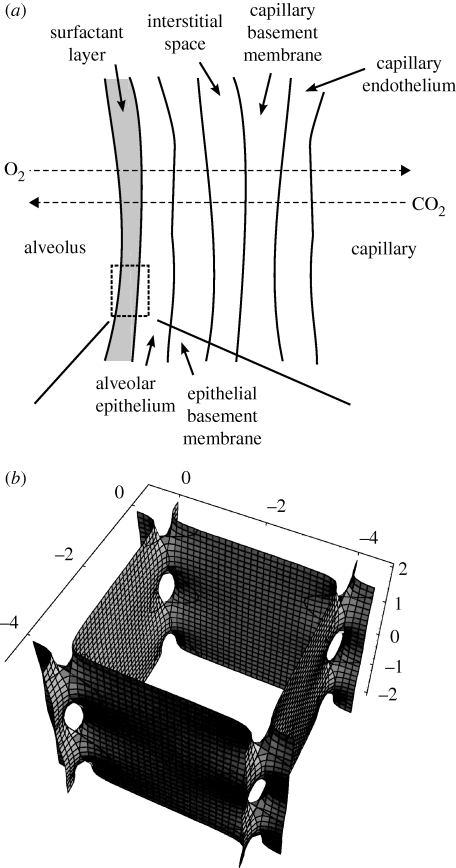
Figure 1.
(a) Schematic of the constitutive parts of the respiratory membrane separating the gas phase in the alveoli from the capillaries. Adapted from Guyton & Hall (2000b). The focus of the present investigation is on the surfactant layer. (b) Part of the CLP minimal surface proposed as the structure for tubular myelin (Larsson 2002; Larsson et al. 2002). The surface represents the centre of the bilayers. Catenoids tie the unit cells to each other. Calculation made with Mathematica (Wolfram Research Inc., USA).
4. Diffusion transport in lung alveoli
The respiratory unit is, from a molecular perspective, a very heterogeneous system. The gaseous phase in the alveoli borders a lipid–protein membrane structure, which is followed by the alveolar epithelial cells, a basement membrane, an interstitial space, another basement membrane, and finally the capillary blood vessel wall; see figure 1a for a schematic illustration. The total distance between the blood in the vessels and the air in the alveoli is on average 0.6 µm (Guyton & Hall 2000b). In the functioning system, there is a gradient in the chemical potential of oxygen from the air to the blood, and a corresponding gradient in the chemical potential of carbon dioxide in the opposite direction. Water is present in all tissues at a chemical potential corresponding to physiological saline, and dry ambient air that is inhaled is continuously moisturized during breathing. We assume that there is rapid equilibration between the body and the gas phase in the lung with respect to water. The diffusion flow, Ji, of compound i is, particularly for a heterogeneous system, most easily described through a generalized Fick's first law (Evans & Wennerström 1999c)
| 4.1 |
where Di(α) is the translational diffusion coefficient of i in environment α, ci is its local concentration and μi the chemical potential. In a heterogeneous system, the diffusion coefficient and the local concentration can vary strongly, while the chemical potential changes smoothly. For example, at the boundary between the gas phase and the lipid membrane, the diffusion coefficient changes by four to five orders of magnitude (Cussler 1997), but there can be a local distribution equilibrium so that
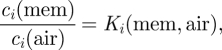 |
4.2 |
where Ki is the partition coefficient of species i between the two media and the concentrations ci refer to the conditions in the respective media in direct contact with the boundary. Within a medium, on the other hand, it is often a good approximation to assume ideal solution behaviour for the gas components so that
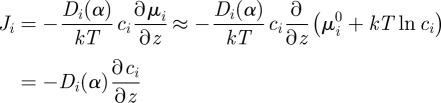 |
4.3 |
as in the more common version of Fick's first law.
In the lung, one can identify four different molecular environments, gas phase, lipid regions, the main respiratory membrane (alveolar epithelium, basement membrane, interstitial space, basement membrane and capillary endothelium) and the blood, where the solubility of oxygen and carbon dioxide is enhanced owing to the presence of haemoglobin and carbanhydrase, respectively, figure 1a. We will discuss diffusional transport over this membrane under steady-state conditions, so that the flux over the membrane is independent of time. This is justified since respiration normally exchanges only a part of the full lung gas volume, thus keeping variations in the concentrations of the metabolic gases small during normal respiration (Guyton & Hall 2000b). One often introduces the concept of permeability to characterize how readily a small molecule passes through a complex structure by diffusion. This concept is particularly useful at steady-state conditions. A major advantage of this concept is that the inverse of the total permeability of a composite membrane can be written as the sum of the permeabilities of the constitutive parts; in the case of the respiratory unit,
| 4.4 |
where Pgas, Plip and Pmain denote the permeability of the gas phase, the lipid regions and the main respiratory membrane, respectively. In the present case, diffusion takes place in very different media and there is a difficulty in applying the conventional definition of permeability
| 4.5 |
where c2,1 are the concentrations on the either side of the region with permeability P. However, provided that each sublayer of the structure is intrinsically homogeneous, we can use equation (4.3) to determine the permeability. To be useful in equation (4.5), the permeabilities should refer to a common reference system, and we choose a pure aqueous solution as the reference state. Then, for a layer of thickness lα, we find from equations (4.3) and (4.2) that the permeability of compound i is
| 4.6 |
There exist reference literature data so that one can determine the relevant distribution coefficients that enter into equation (4.2). The major difference in diffusional transport between oxygen and carbon dioxide comes from the difference in concentrations (different solubilities) in the membrane, while diffusion coefficients are very similar given the medium. Carbon dioxide is approximately a factor of 20 more soluble in water than oxygen relative to a gas phase. This has the important consequence that CO2 has a more efficient diffusional transport than O2 across aqueous regions between the capillary blood vessels and the gas phase of the alveoli. In the gas phase, on the other hand, O2 is more abundant, resulting in a more efficient transport. Table 1 shows typical data for the partial pressure of O2 and CO2 in venous blood, in alveolar air and in atmospheric air. The observation is that for CO2 there is only a minor difference in chemical potential between the venous blood and the gas of the alveoli, while there is a major difference relative to ambient air. For O2, on the other hand, there is a major difference in chemical potential between the venous blood and the alveolar air. Under steady-state conditions, the gradients in chemical potential have adjusted such that the flux is constant and there are no local build-ups in concentration. A large gradient in chemical potential is therefore a reaction to a low permeability in order to keep the flux high, and vice versa. Thus, the conclusion is that for CO2, it is the transport within the gas phase of the lungs that is rate limiting, while for O2, it is the diffusion from alveoli to capillary vessels that determines the rate.
Table 1.
Partial pressures of O2 and CO2 in venous blood, alveolar air and atmospheric air (Guyton & Hall 2000b).
| venous blood | alveolar air | atmospheric air | |
|---|---|---|---|
| pO2 (atm) | 0.05 | 0.14 | 0.21 |
| pCO2 (atm) | 0.06 | 0.05 | 0.00004 |
At present, we have no reliable estimate of the permeability of the main respiratory membrane, Pmain. It is therefore not feasible to connect this description to a more macroscopic description of respiration that includes also the exchange with the pulmonary capillary system, as in the work of Milhorn & Pulley (1968). In the following, our focus will therefore be on the effect of the lipid structure on diffusional transport.
5. Diffusion transport over the alveolar surfactant layer
One interesting aspect of a lipid reservoir organized according to the CLP model (illustrated in figure 1b) is its effect on the diffusional properties. Judging from the observed gradients in O2 and CO2, the latter readily passes the lipid–protein membrane and the intracellular layer between the blood capillaries and the alveoli, while for O2 the diffusion through these layers appears to be a rate-limiting step of the whole transport chain. This suggests that one functional role of the alveolar surfactant layer is to facilitate oxygen diffusional transport. For a stack of bilayers, the passing of the aqueous regions is more sluggish for oxygen.
The lung surfactant consists of about 90 per cent lipids and 10 per cent proteins. The main lipid components are phospholipids and cholesterol, and the dominating molecular organization of these lipids is probably a liquid-disordered phase with a low acyl chain order (Ipsen et al. 1987). However, the relatively high content of saturated phospholipids and cholesterol probably leads to an increased lipid acyl chain order and can lead to the formation of liquid-ordered domains (Discher et al. 1996; Nag et al. 1998; de la Serna et al. 2004). The lung surfactant also contains proteins, which also influence the molecular organization (Palaniyar et al. 1999; Sáenz et al. 2007; Pérez-Gil 2008).
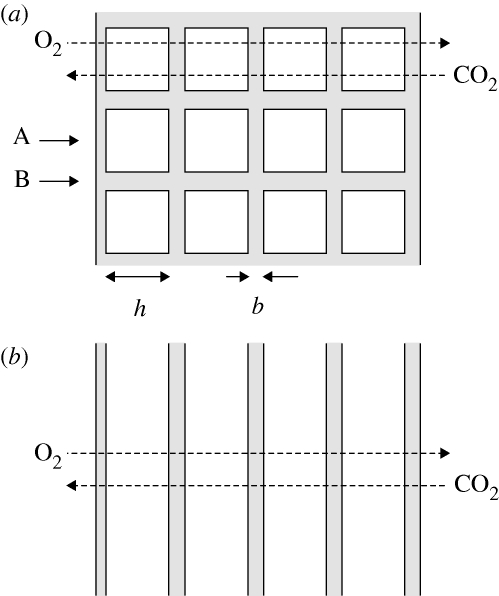
Under the assumption that the lipids are predominantly in a liquid-disordered state, we can estimate the partition coefficient between a bilayer and water, Ki(bilayer, aq), with the oil/water partition coefficient. Since the O2 oil/water partition coefficient is around 4.4 (Battino et al. 1968), the aqueous domains are the main resistance to diffusional transport (Marrink & Berendsen 1996). In the CLP model, there is a continuous network of lipids, which facilitates diffusion for compounds with Ki(bilayer, aq) > 1. We compare diffusion through the surfactant membrane in the CLP model with the one obtained for a membrane composed of a stack of bilayers with the same number of repeating bilayer units (figure 2b).
Figure 2.
(a) Simplified picture of the structure of tubular myelin. The repeat unit of this structure according to the CLP model is shown in figure 1b. h denotes the size of the aqueous regions, and b the bilayer thickness. (b) A stack of bilayers with the same dimensions. In both cases, the gas phase is to the left, so that the (overall) gradients of O2 and CO2 are in the directions indicated by dashed arrows.
To analyse the effects quantitatively, we estimate the permeability of the alveolar surfactant layer according to the CLP model, Plip, using the simplified view, depicted in figure 2a, of the bilayer arrangement. The tubular network is two dimensional, and, strictly speaking, the constitutive parts of a composite membrane whose permeability fulfils equation (4.4) have to be homogeneous in the directions perpendicular to the gradient. However, we make the simplifying assumption that the flux is completely aligned with the (overall) gradient (i.e. in reference to figure 2a, that the flux is strictly horizontal). In that case, we can introduce an effective permeability as the weighted average of the permeabilities at points A and B in figure 2a, so that
| 5.1 |
where h is the size of the aqueous domains, and b the bilayer thickness (defined in the figure). In the electronic supplementary material, we show that the assumption that the flux and the (overall) gradient are parallel is an excellent approximation for partition coefficients Ki(bilayer, aq)≲10.
The permeability for horizontal transport at point A is, in analogy with equation (4.4), given by
| 5.2 |
where Pbilayer and Paq are the permeabilities of a bilayer and an aqueous domain, respectively. We view diffusion through the monolayer in contact with the gas phase as diffusion through half a bilayer, so that the number of bilayers is Nbilayer = 4.5 in figure 2a. Similarly, the number of aqueous domains is Naq = 4. The permeabilities of the individual bilayers and aqueous domains are given by equation (4.6) as
| 5.3 |
and
| 5.4 |
since we consider the permeabilities defined with respect to pure water. In using equation (4.6) for the permeabilities Pbilayer and Paq, we have, for simplicity, assumed that the respective regions are homogeneous.
At point B, horizontal diffusion occurs through a pure lipid phase, and the permeability is given by
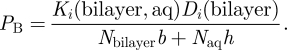 |
5.5 |
Equations (5.1)–(5.5) specify the total permeability for transport across the CLP model of the alveolar surfactant layer within the simple approximation of considering only horizontal transport. In the numerical evaluation, we have used h = 45 nm and b = 5 nm for the size of the aqueous domains and bilayer thickness, respectively (Gil & Weibel 1969; Kashchiev & Exerowa 2001). The diffusion coefficients were kept equal in the aqueous and lipid regions, Di(water) = Di(bilayer) = 1.5 × 10−9 m2 s−1 (Cussler 1997), since the local mobility within the liquid-disordered phase is not significantly different from that in bulk water (Marrink & Berendsen 1996).
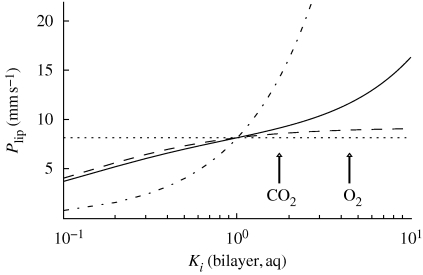
Figure 3 shows the permeability of the alveolar surfactant layer according to the CLP model as a function of the lipid bilayer/water partition coefficient, Ki(bilayer, aq). As expected, the tubular structure shows faster transport for compounds with larger bilayer/water partition coefficients, owing to a continuous route in lipid layers throughout the structure. The situation is clearly assymmetric, in the sense that for a lipophilic compound (Ki(bilayer, aq) > 1), there is a beneficial continuous route, whereas no such route is available for a hydrophilic compound (Ki(bilayer, aq) < 1). This is in sharp contrast to a bicontinuous structure, where also a hydrophilic compound would have access to a continuous route.
Figure 3.
The permeability, Plip, of the lipid layer as a function of the bilayer/water partition coefficient, Ki(bilayer, aq), for different structures. Solid line, the CLP model of the alveolar surfactant layer as depicted in figure 2a; dashed line, stack of bilayers separated by aqueous films of the same size as the CLP model as depicted in figure 2b; dotted and dash-dotted line, homogeneous aqueous and hydrocarbon phase, respectively. Partition coefficients for O2 and CO2 (estimated from octanol/water partition coefficient; Battino et al. 1968) are indicated by arrows.
As a comparison, figure 3 also shows the permeability of a stack of bilayers at the same positions as the vertical bilayers of the alveolar surfactant membrane according to the CLP model, as in figure 2b. The permeability of the bilayer stack is the same as the permeability at point A in figure 2a, i.e. PA. For partition coefficients Ki(bilayer, aq) close to unity or smaller, the permeability of the stack of bilayers is very similar to the tubular structure. This is due to the fact that for the more hydrophilic compounds with lower partition coefficients, transport through the vertical lipid layers contributes little. The CO2 partition coefficient is around Ki(bilayer, aq) = 1.7 (Battino et al. 1968), which is within the range where the alveolar surfactant membrane according to the CLP model shows no functionality for transport. However, for larger partition coefficients, say, Ki(bilayer, aq) > 2, there is a clear difference between the two structures. In particular, for O2 with an estimated partition coefficient of Ki(bilayer, aq) = 4.4 (Battino et al. 1968), transport through the alveolar surfactant membrane in the CLP model is ca 30 per cent faster than transport through the corresponding membrane composed of a bilayer stack. Qualitatively similar results would be expected also for a less-ordered network structure of interconnected bilayers if the bilayers form a continuous route through the surfactant membrane. We also expect similar results if the lipid protein composition varies between, e.g. regions with different curvatures, as long as the local environment is fluid and hydrophobic. The results are also compared with the extreme (but unrealistic) cases of homogeneous aqueous or hydrocarbon layers. These ‘reference states’ basically serve to show the minimum and maximum effect a lipid structure can have on transport.
In all calculations of the diffusional flux, we have made the restrictive assumptions that the diffusion coefficients and the partition coefficients are uniform in each aqueous and lipid layer and that the interfacial resistance is negligible. This implies that the bilayers are treated as homogeneous. In a more detailed description, the inhomogeneities within the bilayers should also be considered. Computer simulations on diffusion through phospholipid bilayers have shown that the diffusion rate is lower in the interfacial regions compared with the aqueous layers and the central parts of the bilayers (Marrink & Berendsen 1994, 1996). Thus, for a more complete description, the interfacial regions should also be incorporated as separate layers in the model. This would slightly change the quantitative results, although the general description and the trends would remain the same.
Equation (5.3) defines the permeability of a bilayer within the description of diffusion outlined in §4. In the numerical calculations, we have used representative data for diffusion coefficients and partition coefficients (Battino et al. 1968; Cussler 1997). For these parameter values, we find that the bilayer permeability for oxygen is of the order of 0.1 m s−1, which is one order of magnitude lower than the oxygen permeability reported previously (Marrink & Berendsen 1996). Formally, one could take this difference into account by increasing the partition coefficient, Ki(bilayer, aq) (a lower permeability could obviously be taken into account by the corresponding decrease). The net effect of a higher bilayer permeability would be a larger difference between the permeability of the alveolar surfactant layer in the CLP model and a stack of bilayers (figure 3) for oxygen, but we leave the present result as an underestimate of the effect.
6. Conclusions
In this communication, we have analysed the passage of oxygen and carbon dioxide over the respiratory membrane with particular attention to the influence of the structure of the lipid reservoir lining the alveolar surface. During normal respiration, the rate-limiting step for carbon dioxide transport is between different compartments in the gas phase of the lung. For oxygen, on the other hand, the rate is limited by the transport between alveoli and the capillary blood vessels. By having a continuous tubular lipid network, oxygen transport is facilitated to an extent that is likely to be large enough to provide an evolutionary advantage. However, even without a tubular network structure, oxygen diffusional transport is rapid enough to support a normal metabolism. Thus, for knockout mice lacking the tubular network (Ikegami et al. 1998), our calculations suggest that they be less apt to sustain physical stress, while, from the aspect of oxygen uptake, they should be able to live otherwise normal lives. The tubular network will also facilitate the transport of apolar substances between the gas phase and the blood. Important examples are ethanol and other volatile liquids that can leave the blood through the lungs and gaseous anaesthetics or volatile solvents that are inhaled. The conclusion that a continuous tubular lipid network results in a more efficient oxygen exchange over the respiratory membrane gives this type of structure a novel physiological role.
Acknowledgements
E.S. and H.W. gratefully acknowledge financial support from the Swedish Research Council (Vetenskapsrådet) both through regular grants and a Linnaeus programme. E.S. acknowledges The Swedish Foundation for Strategic Research (Stiftelsen för Strategisk Forskning) for financial support. M.L. is supported by an ALF grant, Medical Faculty, Lund University.
References
- Baoukina S., Monticelli L., Amrein M., Tieleman D. P. 2007. The molecular mechanism of monolayer-bilayer transformations of lung surfactant from molecular dynamics simulations. Biophys. J. 93, 3775–3782. ( 10.1529/biophysj.107.113399) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battino R., Evans F., Danforth W. 1968. The solubilities of seven gases in olive oil with reference to theories of transport through the cell membrane. J. Am. Oil. Chem. Soc. 45, 830–833. ( 10.1007/BF02540163) [DOI] [PubMed] [Google Scholar]
- Cussler E. L. 1997. Diffusion: mass transfer in fluid systems. Cambridge, UK: Cambridge University Press. [Google Scholar]
- de la Serna J. B., Perez-Gil J., Simonsen A. C., Bagatolli L. A. 2004. Cholesterol rules. Direct observation of the coexistence of two fluid phases in native pulmonary surfactant membranes at physiological temperatures. J. Biol. Chem. 279, 40 715–40 722. ( 10.1074/jbc.M404648200) [DOI] [PubMed] [Google Scholar]
- Discher B., Maloney K., Schief W., Grainger D., Vogel V., Hall S. 1996. Lateral phase separation in interfacial films of pulmonary surfactant. Biophys. J. 71, 2583–2590. ( 10.1016/S0006-3495(96)79450-X) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans D. F., Wennerström H. 1999a. The colloidal domain—where physics, chemistry, biology and technology meet, ch. 2, pp. 45–98, 2nd edn. New York, NY: Wiley-VCH. [Google Scholar]
- Evans D. F., Wennerström H. 1999b. The colloidal domain—where physics, chemistry, biology and technology meet, ch. 11, pp. 539–599, 2nd edn. New York, NY: Wiley-VCH. [Google Scholar]
- Evans D. F., Wennerström H. 1999c. The colloidal domain—where physics, chemistry, biology and technology meet, ch. 1, pp. 1–43, 2nd edn. New York, NY: Wiley-VCH. [Google Scholar]
- Gil J. 1985. Histological preservation and ultrastructure of alveolar surfactant. Annu. Rev. Physiol. 47, 753–763. ( 10.1146/annurev.ph.47.030185.003541) [DOI] [PubMed] [Google Scholar]
- Gil J., Weibel E. R. 1969. Improvements in demonstration of lining layer of lung alveoli by electron microscopy. Respir. Physiol. 8, 13–36. ( 10.1016/0034-5687(69)90042-5) [DOI] [PubMed] [Google Scholar]
- Guyton A. C., Hall J. E. 2000a. Textbook of medical physiology, ch. 37, pp. 432–443, 10th edn. Philadelphia, PA: W.B. Saunders Company, [Google Scholar]
- Guyton A. C., Hall J. E. 2000b. Textbook of medical physiology, ch. 39, pp. 452–462, 10th edn. Philadelphia, PA: W.B. Saunders Company [Google Scholar]
- Hyde S., Andersson S., Larsson K., Blum Z., Landh T., Lidin S., Ninham B. W. 1997. The language of shape. The role of curvature in condensed matter: physics, chemistry and biology. Amsterdam, The Netherlands: Elsevier Science B. V. [Google Scholar]
- Ikegami M., Korfhagen T. R., Whitsett J. A., Bruno M. D., Wert S. E., Wada K., Jobe A. H. 1998. Characteristics of surfactant from SP-A-deficient mice. Am. J. Physiol. Lung Cell. Mol. Physiol. 275, L247–L254. [DOI] [PubMed] [Google Scholar]
- Ipsen J. H., Karlström G., Mouritsen O. G., Wennerström H., Zuckermann M. J. 1987. Phase equilibria in the phosphatidylcholine-cholesterol system. Biochim. Biophys. Acta Biomembr. 905, 162–172. ( 10.1016/0005-2736(87)90020-4) [DOI] [PubMed] [Google Scholar]
- Kahn M. C., Anderson G. J., Anyan W. R., Hall S. B. 1995. Phosphatidylcholine molecular species of calf lung surfactant. Am. J. Physiol. Lung Cell. Mol. Physiol. 269, L567–L573. [DOI] [PubMed] [Google Scholar]
- Kashchiev D., Exerowa D. 2001. Structure and surface energy of the surfactant layer on the alveolar surface. Eur. Biophys. J. 30, 34–41. ( 10.1007/s002490000120) [DOI] [PubMed] [Google Scholar]
- Larsson M. 2002. Surface phase model of the alveolar surface lining: ultra-structural analysis and in vivo applications. PhD thesis, Lund University, Lund, Sweden. [Google Scholar]
- Larsson M., Larsson K., Andersson S., Kakhar J., Nylander T., Ninham B., Wollmer P. 1999. The alveolar surface structure: transformation from a liposome-like dispersion into a tetragonal CLP bilayer phase. J. Dispers. Sci. Technol. 20, 1–12. ( 10.1080/01932699908943775) [DOI] [Google Scholar]
- Larsson M., Larsson K., Wollmer P. 2002. The alveolar surface is lined by a coherent liquid-crystalline phase. Prog. Colloid Polym. Sci. 120, 28–34. ( 10.1007/3-540-45291-5_4) [DOI] [Google Scholar]
- Larsson M., Iwaarden J. F., Haitsma J. J., Lachmann B., Wollmer P. 2003a. Human SP-A and a pharmacy-grade porcine lung surfactant extract can be reconstituted into tubular myelin—a comparative structural study of alveolar surfactants using cryo-transmission electron microscopy. Clin. Physiol. Funct. Imaging 23, 199–203. ( 10.1046/j.1475-097X.2003.00495.x) [DOI] [PubMed] [Google Scholar]
- Larsson M., Terasaki O., Larsson K. 2003b. A solid state transition in the tetragonal lipid bilayer structure at the lung alveolar surface. Solid State Sci. 5, 109–114. ( 10.1016/S1293-2558(02)00084-5) [DOI] [Google Scholar]
- Marrink S.-J., Berendsen H. J. C. 1994. Simulation of water transport through a lipid membrane. J. Phys. Chem. 98, 4155–4168. ( 10.1021/j100066a040) [DOI] [Google Scholar]
- Marrink S. J., Berendsen H. J. C. 1996. Permeation process of small molecules across lipid membranes studied by molecular dynamics simulations. J. Phys. Chem. 100, 16 729–16 738. ( 10.1021/jp952956f) [DOI] [Google Scholar]
- Milhorn H. T., Jr, Pulley P. E. 1968. A theoretical study of pulmonary capillary gas exchange and venous admixture. Biophys. J. 8, 337–357. ( 10.1016/S0006-3495(68)86492-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nag K., Perez-Gil J., Ruano M. L., Worthman L. A. D., Stewart J., Casals C., Keough K. M. 1998. Phase transitions in films of lung surfactant at the air–water interface. Biophys. J. 71, 2983–2995. ( 10.1016/S0006-3495(98)78005-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Namati E., Thiesse J., de Ryk J., McLennan G. 2008. Alveolar dynamics during respiration. Are the pores of Kohn a pathway to recruitment? Am. J. Respir. Cell Mol. Biol. 38, 572–578. ( 10.1165/rcmb.2007-0120OC) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nkadi P. O., Merritt T. A., Pillers D.-A. M. 2009. An overview of pulmonary surfactant in the neonate: genetics, metabolism, and the role of surfactant in health and disease. Mol. Genet. Metab. 97, 95–101. ( 10.1016/j.ymgme.2009.01.015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palaniyar N., Ridsdale R. A., Hearn S. A., Possmayer F., Harauz G. 1999. Formation of membrane lattice structures and their specific interactions with surfactant protein A. Am. J. Physiol. Lung Cell. Mol. Physiol. 276, L642–L649. [DOI] [PubMed] [Google Scholar]
- Pérez-Gil J. 2008. Structure of pulmonary surfactant membranes and films: the role of proteins and lipid–protein interactions. Biochim. Biophys. Acta Biomembr. 1778, 1676–1695. ( 10.1016/j.bbamem.2008.05.003) [DOI] [PubMed] [Google Scholar]
- Pocivavsek L., Dellsy R., Kern A., Johnson S., Lin B., Lee K. Y. C., Cerda E. 2008a. Stress and fold localization in thin elastic membranes. Science, 320, 912–916. ( 10.1126/science.1154069) [DOI] [PubMed] [Google Scholar]
- Pocivavsek L., et al. 2008b. Lateral stress relaxation and collapse in lipid monolayers. Soft Matter 4, 2019–2029. ( 10.1039/b804611e) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sáenz A., Cañadas O., Bagatolli L. A., Sánchez-Barbero F., Johnson M. E., Casals C. 2007. Effect of surfactant protein A on the physical properties and surface activity of KL4-surfactant. Biophys. J. 92, 482–492. ( 10.1529/biophysj.106.090217) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Struik D. J. 1988. Lectures on classical differential geometry, 2nd edn. New York, NY: Dover Publications, Inc. [Google Scholar]
- Suzuki Y., Fujita Y., Kogishi K. 1989. Reconstitution of tubular myelin from synthetic lipids and proteins associated with pig pulmonary surfactant. Am. Rev. Resp. Dis. 140, 75–81. [DOI] [PubMed] [Google Scholar]
- Weibel E. R. 1963. Morphometry of the human lung. Zürich, Switzerland: Springer-Verlag. [Google Scholar]
- Williams M. C. 1977. Conversion of lamellar body membranes into tubular myelin in alveoli of fetal rat lungs. J. Cell Biol. 72, 260–277. [DOI] [PMC free article] [PubMed] [Google Scholar]