Abstract
Sensitivity to acoustic amplitude modulation in crickets differs between species and depends on carrier frequency (e.g., calling song vs. bat-ultrasound bands). Using computational tools, we explore how Ca2+-dependent mechanisms underlying selective attention can contribute to such differences in amplitude modulation sensitivity. For omega neuron 1 (ON1), selective attention is mediated by Ca2+-dependent feedback: [Ca2+]internal increases with excitation, activating a Ca2+-dependent after-hyperpolarizing current. We propose that Ca2+ removal rate and the size of the after-hyperpolarizing current can determine ON1’s temporal modulation transfer function (TMTF). This is tested using a conductance-based simulation calibrated to responses in vivo. The model shows that parameter values that simulate responses to single pulses are sufficient in simulating responses to modulated stimuli: no special modulation-sensitive mechanisms are necessary, as high and low-pass portions of the TMTF are due to Ca2+-dependent spike frequency adaptation and post-synaptic potential depression, respectively. Furthermore, variance in the two biophysical parameters is sufficient to produce TMTFs of varying bandwidth, shifting amplitude modulation sensitivity like that in different species and in response to different carrier frequencies. Thus, the hypothesis that the size of after-hyperpolarizing current and the rate of Ca2+ removal can affect amplitude modulation sensitivity is computationally validated.
Keywords: Adaptation, Temporal processing, Roex filter, Evolution, Temperature
Introduction
Shifts in auditory filtering may be accomplished by changing intrinsic biophysical properties of single units (Fortune and Rose 1997; Zakon 2003; Hildebrandt et al. 2009). For example, the frequency of electrical resonance in certain hair cells is determined by the kinetics of the BK conductance, with the expression of different BK splice variants in different hair cells shifting the resonant band across the papilla (Art et al. 1995). Beyond the cells of a single papilla, however, intrinsic biophysical filters can be employed in different dendritic compartments of single auditory cells (adjusting response to different inputs) or auditory cells in different organisms, producing changes in sensitivity for different species and hybrids (Zakon 2003). This paper examines (1) how an intrinsic mechanism can contribute to the different temporal filters exhibited in response to mating versus predator sounds in an identified auditory cell in crickets; and (2) if the mechanism would be capable of producing the shifts in sensitivity found between species.
In crickets (Gryllidae), amplitude-modulated calling songs are produced by repeated closure of the forewings (Bennet-Clark 1989). Song amplitude modulation structure is species specific, meaning temporal sensitivity plays an important role in mediating mate choice (Walker 1957; Pollack and Hoy 1979; Shaw 2000; Shaw and Herlihy 2000). At least one mechanism for auditory temporal filtering in this system is that underlying selective attention, where sensitivity and phonotaxis are directed to only one of several otherwise attractive songs (Pollack 1986; Pollack 1988). Neural correlates of selective attention have been shown in omega neuron 1 (ON1), a pair of intrasegmental auditory units in the prothoracic ganglion. ON1s are post-synaptic to auditory receptors and, in part, transfer input to contralateral ascending neurons to enhance binaural contrast (Selverston et al. 1985; Horseman and Huber 1994). When presented simultaneously with a pair of calling songs of different amplitude, the response of ON1 is biased toward the higher amplitude song, even though both songs elicit excitation when presented alone (Pollack 1988). Such selectivity is mediated by the cell’s mechanisms for adaptation (cf. Sah and Faber 2002; Bond et al. 2005): excitation increases intracellular [Ca2+], activating an outward, hyperpolarizing conductance and subsequently decreasing the response to a maintained stimulus (Sobel and Tank 1994; Baden and Hedwig 2007). This feedback mechanism shifts the cell’s I/O curve to higher amplitude stimuli, with the lower amplitude song now below threshold on the curve. The result is selective attention that is sensitive to both the amplitude and the timing of the elements of the two songs, with songs occurring during “after-hyperpolarization” (ahp) less likely to elicit a response. The mechanism is thus a form of temporal filtering (Harris and Dallos 1979; Frisina 2001): filtering pulses that are too close together in time (Sobel and Tank 1994; Farris et al. 2004; Marsat and Pollack 2004; Baden and Hedwig 2007).
Several lines of evidence suggest that the temporal properties of selective attention in ON1 are specialized for processing amplitude modulation. For example, ON1 responses differ for calling song and ultrasound inputs (Sabourin et al. 2008). In particular, ON1 band-pass filters the amplitude modulation of sounds with lower carrier frequencies (i.e., near calling songs) to slow amplitude modulation rates, but exhibits broadly tuned low-pass filtering of amplitude-modulated ultrasound (i.e., bat-like sonar; Marsat and Pollack 2004). Although this can partly be explained by receptor (presynaptic) sensitivity (Sabourin and Pollack 2010), mechanisms in ON1 (postsynaptic) are clearly implicated, as excitation-induced ahp is enhanced for song-like carrier frequencies compared to that generated by ultrasound input (Pollack 1988). Importantly, this difference in ahp may be due to dendritic tonotopy in internal Ca2+ ([Ca2+]i): ultrasound stimuli elicit less [Ca2+]i in certain dendritic compartments than calling songs do (Baden and Hedwig 2007). In addition, Tunstall and Pollack (2005) showed that sensitivity of ON1 to amplitude modulation in a slow-singing species is more narrowly tuned to slower modulation rates than that for a fast-singing species. Furthermore, the extent of adaptation was greater in the more narrowly tuned species. Taken together, these data suggest that processing of amplitude modulation in ON1 is influenced by the properties of Ca2+-dependent feedback, which may be specialized to increase the binaural processing of functionally relevant sounds (Marsat and Pollack 2004, 2005).
Thus, we use a computational model based on omega neurons in Gryllids (Sobel and Tank 1994; Farris et al. 2004; Baden and Hedwig 2007) to first show that simulating the Ca2+-dependent mechanisms of selective attention is sufficient to simulate the in vivo responses to amplitude-modulated stimuli. Second, we test the prediction that variance in these mechanisms is sufficient to produce differences in temporal filtering. In particular, a biophysical parameter analysis shows that sensitivity to amplitude modulation can be shifted (similar to the effect of different carrier frequencies) by varying the size of the Ca2+-sensitive ahp conductance and the rate of Ca2+ removal. In addition, the model allows for these Ca2+- dependent shifts to be compared to those produced by changing the speed of spike-generating mechanisms using temperature. Third, from a functional point of view, we extend the interpretation of the results beyond carrier-dependent filtering, as the model provides evidence that variance in these mechanisms could contribute to general shifts in temporal sensitivity, including those in ON1 that are found between species (Tunstall and Pollack 2005).
Methods
Although measurements of ON1 from several different laboratories are available, they are mostly collected in current clamp or through Ca2+ imaging. We are not aware of any voltage clamp approaches with ON1, making few data available for certain biophysical components. Whether the components are taken from ON1 or other cells is thus noted. However, parameter values were calibrated to fit experimental data (see below).
A modified Hodgkin and Huxley (1952; Huguenard and McCormack 1994) conductance-based model simulated the membrane potential of ON1 in response to afferent input. The model integrates voltage and Ca2+-sensitive conductances to produce the membrane response:
| (1) |
The current components are: spike-generating sodium (INa) and potassium (IK); voltage-sensitive calcium (ICa); two Ca2+-sensitive after-hyperpolarizing currents (Iahp); a leak and the stimulus current. C is membrane capacitance.
Spike-generating conductances (INa and IK) were treated as generic and based on characteristics of vertebrate interneurons (Traub et al. 1991; McCormick and Huguenard 1992). Parameter values were ultimately chosen, however, to model action potentials recorded from ON1 in vivo (Farris et al. 2004; see below). For all parameters, their units, initial value of variables and value of constants, see Table 1.
Table 1.
Values for constants and initial values (at time = 0) for particular variables
| Constants | Value |
|---|---|
| Sodium equilibrium potential (ENa) | 55 mV |
| Potassium equilibrium potential (EK) | −85 mV |
| Calcium equilibrium potential (ECa) | 100 mV |
| Faraday constant (F) | 96480 C |
| Action potential threshold (νthreshold) | −55 mV |
| Ideal gas constant (R) | 8.314 V−C(°C)−1 |
| Membrane capacitance (C) | 1 μF cm−2 |
| Sodium conductance (ḡNa) | 0.11 S cm−2 |
| Potassium conductance (ḡK) | 0.1 S cm−2 |
| Calcium permeability (P̄Ca) | 0.0005 cm sec−1 |
| Sodium permeability (P̄Na) | 0.000000207 cm sec−1 |
| Potassium permeability (P̄K) | 0.00000345 cm sec−1 |
| Variables | Initial value |
| Membrane potential (V) | −65 mV |
| Internal calcium concentration pool 1 ([Ca2+]i,1) | 0.00001 mM |
| Internal calcium concentration pool 2 ([Ca2+]i,2) | 0.00001 mM |
| External calcium concentration ([Ca2+]o) | 2 mM |
| Sodium activating (m) | 0 |
| Sodium inactivating (h) | 1 |
| Potassium activating (n) | 0 |
The simulated currents and gating variables are as follows. The rate of change of the activating and inactivating variables is described by a first-order differential equation:
| (2) |
where τx represents the time constant of the activating or inactivating variable, x,
| (3) |
and αx and βx are gating functions shown with each ion’s conductance.
Sodium current, INa
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
with ḡ being the conductance of the ion; m and h representing the activation and inactivation, respectively (Fig. 1); and ν2 the voltage relative to spike threshold (for both INa and IK):
| (13) |
Fig. 1.
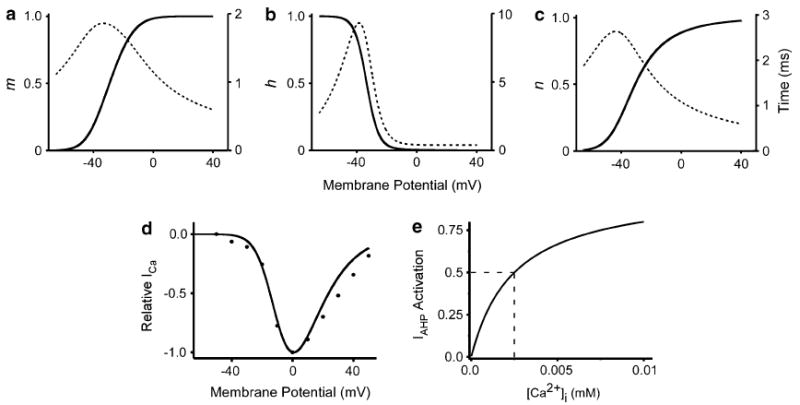
Activation, inactivation (solid lines) and time constants (dotted lines) for model conductances. a INa activation. b INa inactivation. c IK activation. Solid lines correspond to left axes, dotted lines correspond to right axes. d I/V relationship for ICa. Curve is the simulation. Points are data from cockroach (Wicher and Penzlin 1997) e Ca2+ sensitivity of Iahp; dashes note half activation point
Potassium current, IK
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
with n representing activation.
The temperature control was maintained over the sodium and potassium currents by the following equation:
| (19) |
where C is temperature (°C). Q10 was set at 1.5 in all the simulations (Machne and Orozco 1970; McCormick and Huguenard 1992). All simulations were run using 25°C unless noted otherwise.
Calcium current, ICa
The calcium current is modeled after those recorded in cockroach (Periplaneta americana) interneurons (Wicher and Penzlin 1997) and the L-type Ca2+ current in cricket (G. bimaculatus) myocytes (Mutoh and Yoshino 2004; Numata and Yoshino 2005) (Fig. 1). The current is assumed to be uniform across all areas of the cell and is represented by the Goldman–Hodgkin–Katz current equation (Hille 1992):
| (20) |
where P̄Ca is the permeability of the calcium channel and mCa is the voltage-activating variable ranging from 0 to 1,
| (21) |
Γ uses the typical Goldman–Hodgkin–Katz parameters to describe the driving force as a function of voltage and internal and external Ca2+ ([Ca2+]i and [Ca2+]o)(this notation previously used by Engel et al. 1999). The valence of Ca2+ equals 2.
With respect to the [Ca2+]i, the omega neuron has at least two distinguishable compartments with relatively fast and slow change in [Ca2+]i: whereas the [Ca2+]i in the dendritic areas decreases after excitation with a time constant (τremoval) near 237 ms, the [Ca2+]i in the spike generation zone exhibits slower changes, τremoval = 1265 ms (Baden and Hedwig 2007). When taken together with the fact that ON1 spike frequency adaptation exhibits a double exponential decay (Fig. 2), it suggests that these different Ca2+ dynamics contribute to different rates of Ca2+-activated adaptation. Thus, based on the differing rates of Ca2+ extrusion in different anatomical compartments and the double exponential spike frequency adaptation found in vivo, the model contains two pools of internal Ca2+: [Ca2+]i,pool1 and [Ca2+]i,pool2 (the notation ‘i’ is not an index and represents internal Ca2+). The modeled pools are functionally independent with respect to their associated Ca2+-activated after-hyperpolarizing conductance, or Iahp (i.e., a compartmentalization of [Ca2+] and associated Ca2+-activated currents). This separation allows for the separate contributions of two Ca2+-activated after-hyperpolarizing conductances (Wang 1998; but see Roper et al. 2003). It is important to note, however, that [Ca2+]i used to calculate ICa in the Goldman–Hodgkin–Katz current equation above is the sum of all [Ca2+]. That is, [Ca2+]i = [Ca2+]i,pool1 + [Ca2+]i,pool2. Thus, although there are two pools that affect an associated Iahp1 or 2, there is a simplification to only one pool that affects the driving force of ICa.
Fig. 2.
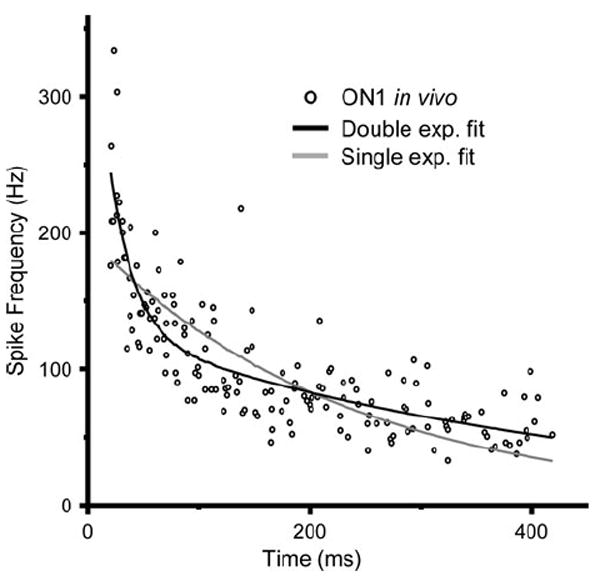
Points show instantaneous spike frequency during adaptation for a real ON1 in response to 400 ms duration pulse of 5 kHz (5 repetitions)(Farris et al. 2004). Black and gray curves are the double (a*e−t/τfast + b*e−t/τslow) and single (d*e−t/τ) exponential fits to the data, respectively. Double exponential parameters (n = 9): τslow = 1054.3 ± 470.2 ms; τfast = 23.2 ± 13.2 ms; a = 607 ± 581; b = 188 ± 44; single exponential parameters: τ = 520 ± 171 ms; d = 235 ± 53
Ca2+ change and removal
The rate of Ca2+ entry and exit in each pool is described by a first-order differential equation,
| (22) |
where j is an index that designates the pool, j = 1, 2; αCa is a constant chosen to scale [Ca2+]i so that it varies across the steep portion of the Iahp calcium activation curve (Fig. 1). The relative size of αCa,1 and αCa,2 reflects the surface area to volume ratio of the two pools: αCa,2 = αCa,1/3. Although the value of this relationship was previously chosen (Wang 1998) to help describe the different Ca2+ modes of the soma and dendrites of cortical pyramidal neurons, it is also used here because it satisfactorily modeled that for the proposed location of the two pools in ON1: the spike generation zone and dendrites of ON1 (Baden and Hedwig 2007). τremoval,j determines the rate at which [Ca2+]i,j changes in each pool. The removal represents the functional result of all mechanisms of Ca2+ removal: binding, sequestration and extrusion.
Ca2+-activated after-hyperpolarizing current, Iahp,j
The currents are modeled after voltage-independent SK conductances (Engel et al. 1999; Faber and Sah 2007) and control spike frequency adaptation and input resistance by generating hyperpolarizing current in response to [Ca2+]i,j in one of the two compartments (j):
| (23) |
where ḡahp,j is the maximum conductance and ms is the sensitivity of Iahp activation to [Ca2+]i:
| (24) |
The open–close action of the ahp (c.f. SK) channel is fast compared to the calcium concentration change, so the dynamics of the ahp channel is described by a function instead of a differential equation. Although Ca2+-activated K+ channels have been identified in insects (McCormack 2003) and other invertebrates (Wei et al. 1996; Burrell and Crisp 2008), most measures of their Ca2+ sensitivity are from vertebrate cells. For those, the reported half activation concentrations for SK currents vary (Leinders and Vijverberg 1992; Tucker and Fettiplace 1996; Xia et al. 1998; Hirschberg et al. 1999; Stocker et al. 2004). In our simulations Cahalf_activation = 2.5 μM (Engel et al. 1999), but its actual numeric value is irrelevant to the model, as [Ca2+]i has been scaled to vary across the non-saturating portions of the Iahp activation curve (ms) using αCa (Fig. 1). This is a requirement, as in vivo recordings of ON1 show that variance in [Ca2+]i elicits variance in adaptation (Sobel and Tank 1994; Baden and Hedwig 2007), which would not occur if [Ca2+]i saturated Iahp sensitivity (Roper et al. 2003).
Leak currents, ILeak
The leak current is the sum of each ion’s (Na+, K+, Ca2+) leak, which takes the form of the Goldman–Hodgkin–Katz current equation (Hille 1992; Huguenard and McCormack 1994):
| (25) |
| (26) |
The model was simulated using the Runge–Kutta method in XPP software (http://www.math.pitt.edu/~bard/xpp/xpp.html).
Calibration of model parameters
Model parameters were calibrated using ON1 responses to a single acoustic pulse in nine female Gryllus rubens (Farris et al. 2004). This species was chosen because the male calling song consists of a long-duration series of pulses (trill), making the amplitude modulation structure relatively simple in that there is only one interpulse interval (11 ms duration pulses at 45 pulses/s at 22°C; Walker 1962; Bentley and Hoy 1972). Adaptation of the ON1 spike trains were produced in response to five repetitions (2 s stimulus interval) of a 400 ms duration pulse of 5 kHz (90 dB SPL). In simulating these spike trains, very little change was required for the voltage-sensitive parameters (e.g., parameters of ICa, INa and IK) taken from vertebrate neurons, roach neurons and cricket muscles; these parameters were “tuned” by eye and remained the same for all nine simulations of each cell’s spike frequency adaptation. The five parameters that contribute to adaptation, however, were systematically adjusted using a least-squares fit procedure between the real and simulated spike frequencies. The amplitude of Istim, an idealized square pulse, was calibrated first to a value that generated the appropriate initial spike frequency (instantaneous frequency of the first five spikes). Subsequently, ḡahp,1 and τremoval,1 were adjusted to model the spike frequency change of the initial short time constant. Lastly, the same procedure was then used to calibrate parameter values for the mechanisms producing the slower time constant for change in spike frequency (ḡahp,2 and τremoval,2). Whereas starting parameter values in this least-squares method were arbitrarily chosen for ḡahp,j, starting values for τremoval,1 and τremoval,2 were the Ca2+ decay times measured in the dendritic (237 ms) and spike generation zone (1265 ms) of ON1 in G. bimaculatus, respectively (Baden and Hedwig 2007).
With respect to adaptation, it is important to note that studies in another cricket auditory interneuron (AN1) have shown that the reduced coding of fast amplitude modulation rates during sinusoidal input (but not randomly modulated input) may not be due to the adaptive shift in the input/output (I/O) curve, but instead to a subsequent compression of the I/O curve itself: the spike frequency dynamic range of the shifted curve becomes smaller, reducing the mean spike frequency and thus limiting the modulation rates that spikes can copy (Benda and Hennig 2008). In contrast, however, for ON1 in vivo, neither the adapted nor the maximum spike frequencies explain the shape of the TMTF at high-amplitude modulation rates (Marsat and Pollack 2004); and adapted I/O curves appear to shift to the right, but not compress (Sobel and Tank 1994). This is illustrated by the fact that although the mean adapted firing rate to amplitude-modulated ultrasound stimuli is lower (20-30 Hz less) than that for calling song stimuli, its TMTF extends to higher amplitude modulation rates (Marsat and Pollack 2004). Furthermore, ON1 spike rate often remains greater than the behaviorally relevant amplitude modulation rates (Nabatiyan et al. 2003; Baden and Hedwig 2007). Thus, our model makes a parsimonious assumption as to the effect of adaptation and does not incorporate any special terms to reduce the maximum adapted firing rate (Benda and Hennig 2008). The model uses only the known mechanisms of selective attention: excitation-induced ahp. This mechanism simply shifted the I/O curve to the right, rather than compressing it (Fig. 3). Such a shift without compression would not be unique to ON1, as it has been found in other auditory interneurons (Dean et al. 2005, 2008).
Fig. 3.
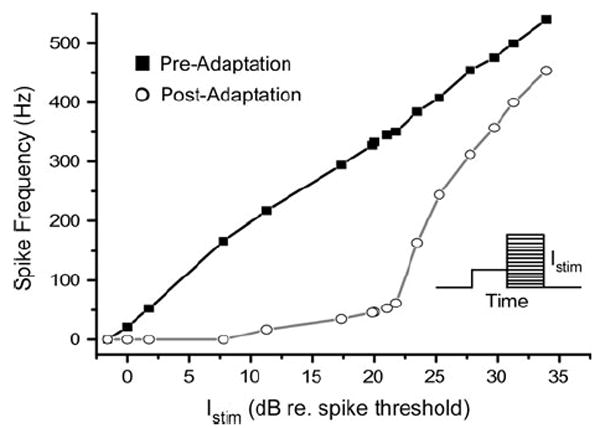
Adaptation of the model shifts the rate–intensity function to the right, but does not compress the curve by limiting maximum spike frequency. Squares are the instantaneous spike frequency (first two spikes) when stimulating at rest; circles are that following 1.5 s stimulation of Istim = 21 dB (relative to spike threshold). The linear-like response is similar to that found in vivo (Baden and Hedwig 2007). Inset shows schematic of stimulus for adapted I/O curve. A 1.5 s pulse at mean Istim is followed by a second 1.5 s pulse at variable amplitude
Stimulus and spike train analysis
The amplitude-modulated stimulus was a periodic square wave at nine rates (1–120 Hz), with amplitude alternating from 0 to Istim in each cycle (3 s total duration). Although synaptic and receptor filtering are implicated in ON1 responses (Marsat and Pollack 2004; Sabourin and Pollack 2010), this was chosen as an idealized input so that our analysis focused solely on filtering due to the post-synaptic mechanisms of the model and not the input itself (Faulkes and Pollack 2001). The stimulus had a 50% duty cycle, meaning response variance depends only on the rate of stimulation, not on overall energy. The amplitude of Istim was calibrated to the mean voltage that best simulated the responses of ON1 to 90 dB stimuli (n = 9 cells; see results).
Although several methods have been used to assess response to amplitude-modulated stimuli in crickets (Hennig 2003; Nabatiyan et al. 2003; Farris et al. 2004; Marsat and Pollack 2004), we employed two methods similar to those previously shown to be successful in analyzing ON1 temporal sensitivity in vivo. The first method tests whether the number of peaks in instantaneous spike frequency varied between stimuli with different amplitude modulation rates (Nabatiyan et al. 2003). Thus, the dependent variable for the filter is the number of spike frequency peaks (SFP) per stimulus pulse. The threshold for discriminating an SFP was 200 Hz, the same as that used for ON1 in vivo (Nabatiyan et al. 2003). The limitation of this method, however, is that it fails to record high-pass filtering well, as low-frequency amplitude-modulated stimuli still elicit SFPs even though adaptation causes a failure to code their long-duration pulses. Thus, this method yielded temporal modulation transfer functions that were low pass in shape. This low-pass filter was analyzed using a single-sided rounded exponential function (see below).
The second method of analysis takes a spectral approach (e.g., Tunstall and Pollack 2005). Voltage responses are first converted to instantaneous spike frequency, r (t). Sub-sequently, in lieu of bins, we used a linear interpolation (50 μs sampling period) variant of the discontinuous fft (Fan and Liu 2004) to transform r (t) into the spectral domain: r (t) is first converted to a continuous function, R (t), and then analyzed for spectral content using the fft transform. This generates the power in the spike frequency waveform at the stimulus modulation frequency. The transfer function is then plotted using the signal-to-noise ratio in the spectrum at each stimulus frequency: 10*log(SNR), where SNR = response power at the stimulus modulation frequency/spectral density in ±1 octave. This method has no limitation on calculating high and low-pass components and delivered band pass like TMTFs.
The flanks of this band-pass filter (i.e., on either side of the best amplitude modulation frequency) or the single flank of the low-pass filter produced by the peak counting method above were analyzed with the rounded exponential function, roex(p,r):
| (27) |
where g is the normalized deviation of frequency from the center frequency, cf, g = |(f–cf)|/cf; p is a dimensionless parameter determining the slope of the flanks of the TMTF, and r is a constant that sets the range limitation of the roex filter. The TMTFs were assumed to be asymmetrical around the center amplitude modulation frequency, and separate slopes (p) were calculated for the upper and lower frequency flanks; r was limited to be the minimum measure on either side of the cf. When there was no high-pass component, only the low-pass component was calculated. The model was fit using a least-squares method to solve for the slope parameter (p) of each side of the peak frequency. From these parameters, the equivalent rectangular band-width (ERB) of the filter can be calculated (Hartmann 1998), facilitating comparisons of filtering properties across taxa (Patterson et al. 1982; Moore et al. 1988; Farris and Hoy 2002; Witte et al. 2005; Farris et al. 2006).
Note that we did not use methods measuring synchrony (Farris et al. 2004; Marsat and Pollack 2004) for the following reason. When Istim elicited a spike, it was often in the same stimulus phase. Thus, even when many stimulus pulses were not coded, those that were coded produced high measures of phase locking, resulting in very little variance in the synchronization coefficient.
All filter parameters were solved using the Minerr function in MathCad (PTC, Needham, MA, USA). All means are reported as ±standard deviation.
Results
Adaptation to a single pulse
For a single acoustic stimulus (400 ms duration; 5 kHz), spike frequency adaptation of ON1 (in vivo) in G. rubens exhibited a double exponential decay (Fig. 2): compared to the single exponential fit, the double exponential fit explained more of the change in spike frequency (R2 single 0.527 ± 0.078; R2 double 0.655 ± 0.085; n = 9 cells). There was a consistently large difference between the slow (τslow = 1054.3 ± 470.2 ms) and fast (τfast = 23.2 ± 13.2 ms) time constants for the double exponential fit, as the within cell ratio was 41.3 (±0.01). Thus, we assume that multiple processes with different rates contribute to adaptation and therefore the model required a fast and a slow mechanism for its simulation. This was accomplished by having two separate Ca2+ removal times (τremoval,1 and τremoval,2) and two associated after-hyperpolarizing Ca2+-activated conductances (ḡahp,1 and ḡahp,2) (Fig. 4).
Fig. 4.
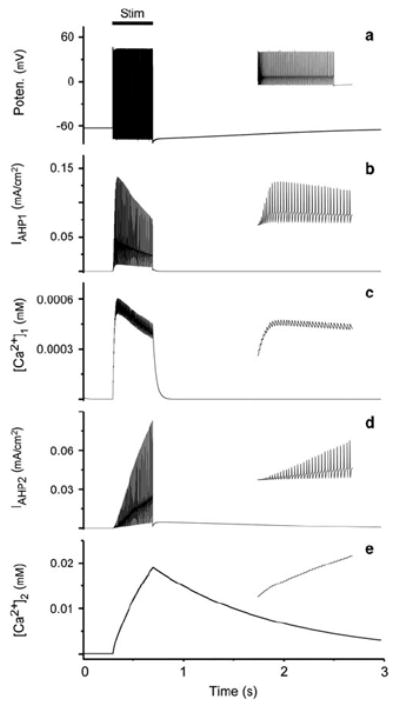
a Voltage response using mean adaptation parameters generated from simulation of the nine cells. b–e Iahp and corresponding [Ca2+]i for the simulation in a (see y axis label for parameter). Insets show expansion of response over 500 ms in a and over 200 ms in b–e. Stimulus duration is 400 ms
During single pulse acoustic stimulation in vivo (Fig. 5), the maximum (i.e., initial) spike frequency was different for each cell (356 ± 68 Hz). Thus, simulations required different model stimulus amplitudes (Istim = 0.074 ± 0.034 mA/cm2; used in all multipulse experiments below). This variance in peak spike frequency notwithstanding, the extent of adaptation was relatively constant for all cells (83 ± 8%), meaning no cells used to calibrate the model exhibited evidence for saturation of the adaptation mechanisms. In simulating the single pulse response (Fig. 5), we found that Ca2+ removal times (τremoval) for the two Ca2+ pools were similar to the two exponential time constants measured above, generating mean removal times of τremoval,1 = 34.4 ± 11 ms and τremoval,2 = 1,265 ms. There was no variance for τremoval,2 because the least-squares fit showed little or no improvement for changes to the initial seed value. Thus, this value was the same for all nine cells.
Fig. 5.
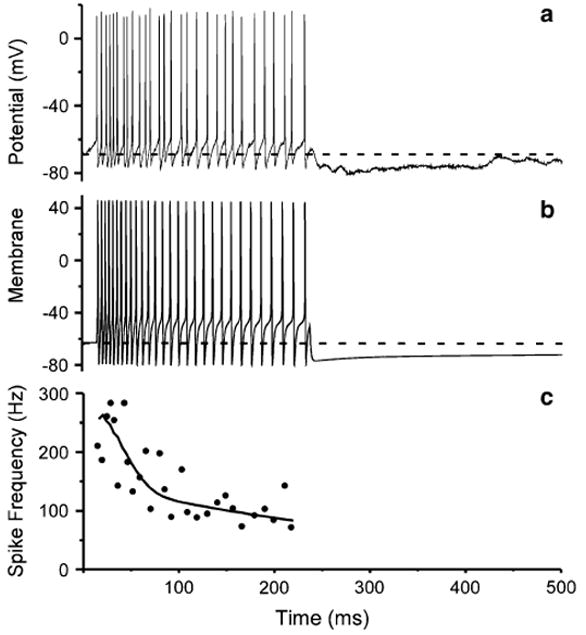
Simulation of ON1 response. a Response of ON1 in G. rubens female to a 200 ms duration pulse of 5 kHz (1 ms ramps). b Simulation of response in a following adaptive least-squares fit of adaptation parameters. Gray dashed line is resting potential. c Comparison of instantaneous spike frequency in a (filled circles) and b (black curve)
The size of the ḡahp conductances (and thus Iahp) differed by an order of magnitude for the two Ca2+ pools, with ḡahp,1 = 0.047 ± 0.02 S/cm2 and ḡahp,2 = 0.0053 ± 0.003 S/cm2. This difference reflects the need to generate greater adaptation at the onset of the stimulus (Figs. 2, 4, 5). The mean parameter values generated from simulating the nine cells (τremoval,1; τremoval,2; ḡahp,1 and ḡahp,2) were then used to test whether parameters based on adaptation to a single acoustic pulse were sufficient to simulate the response to paired and multipulse stimuli.
Paired pulse selective attention
Similar to the response found in vivo to paired pulse acoustic stimuli (Sobel and Tank 1994), a preceding pulse affects the response to a subsequent one in simulations (Fig. 6). Shown to be a mechanism of selective attention (Pollack 1988), responses to the second of a pair of current pulses are reduced when the second pulse is delivered during the after-hyperpolarization elicited by the preceding pulse (Fig. 6). The model captures well the shift of the linear I/O curves of spike number per pulse (Sobel and Tank 1994) and reveals that the mechanisms of adaptation generate a temporal filter, as stimuli occurring close together in time (i.e., faster amplitude modulation) are less likely to elicit full responses.
Fig. 6.
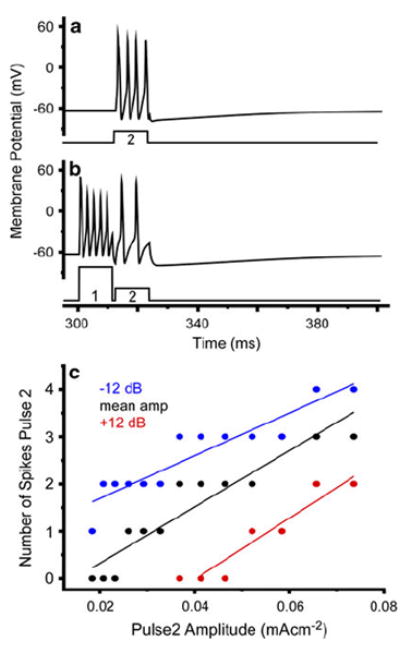
Simulation exhibits selective attention in the form of greater sensitivity to the preceding pulse. a Voltage response to current pulse 2 alone (Istim = 0.0657 mA/cm2). b Addition of current pulse 1 (0.185 mA/cm2; 9 dB relative to pulse 2) reduces response to pulse 2. c Number of spikes (for pulse 2) as a function of pulse 2 amplitude for three different pulse 1 amplitudes (mA/cm2): 0.0184 (blue); 0.074 (black); 0.293 (red). Plots are linear regression fits for the three pulse 1 amplitudes (blue slope = 45.3; intercept = 0.78; black: slope = 59.7, intercept = −0.88; red: slope = 64.7, intercept = −2.61). Increases in pulse 1 amplitude shifts the I/O response to the right
Multipulse stimuli: temporal modulation transfer function
[Ca2+]i,pool1 exhibits the fastest dynamics and is considered here to functionally represent the faster Ca2+ dynamics of the dendrites (Baden and Hedwig 2007). Thus, the hypothesis that the broader TMTF for ultrasound is caused by less dendritic calcium-induced ahp can be tested by comparing coding of amplitude modulation when ḡahp,1 is reduced relative to the mean parameter value. Whether coding is analyzed using SFP or the spectrum of the spike frequency waveform, the model confirms the hypothesis, as adjusting ḡahp,1 affects amplitude modulation coding. The TMTFs generated from the spike frequency waveforms (e.g., Fig. 7) for three different values of ḡahp,1 are shown in Fig. 8. In vivo, dendrites coding ultrasound show ~47% of the [Ca2+]i compared to those responding to 5 kHz (Baden and Hedwig 2007). The TMTF of the model dendrite coding ultrasound (47% of the mean ḡahp,1) is a broader filter, as both the high-pass and low-pass portions are affected (low-pass cutoff frequency increased to 46.5 Hz; Fig. 8; red curve). In contrast, when the mean value (or greater) for ḡahp,1 is used, the TMTF is band limited and more narrow with a lower amplitude modulation cutoff frequency of 26.1 Hz (Fig. 8; black and blue curves). As shown in other cells (Benda and Herz 2003; Benda and Hennig 2008), the source of the high-pass filter is spike frequency adaptation (Fig. 3). However, we do not have compression of the I/O curve in ON1. Thus, exploration of the source of the low-pass filter shows that it results from PSP depression (Fortune and Rose 1997, 2001; Rose and Fortune 1999). When Iahp is on there is a change in input resistance, shunting Istim (Fig. 8). This means the membrane’s RC response is changed:
Fig. 7.
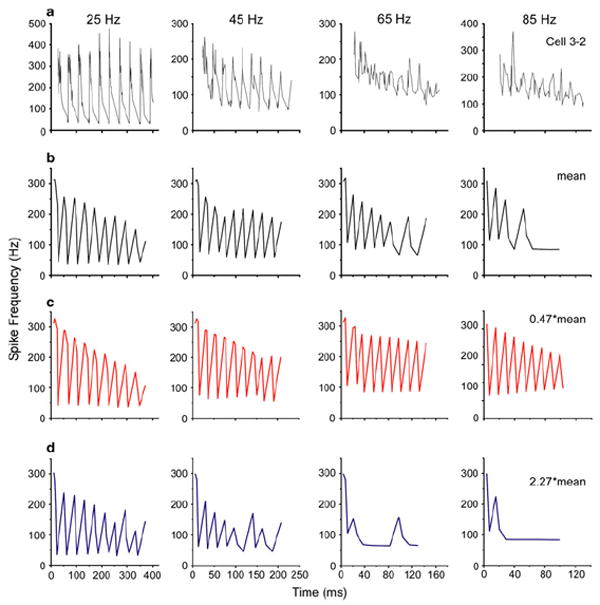
Examples of spike frequency waveform in response to ten cycles of modulated stimuli. a Response of a real ON1 to an amplitude-modulated tone (5 kHz) at four different rates near that for the calling song. The parameters used to simulate this cell’s response to a single acoustic pulse were near the mean. b Response of the model using the mean parameters. This response is altered when ḡahp,1 is decreased (c) or increased (d). Modulation rates are noted above each column
Fig. 8.
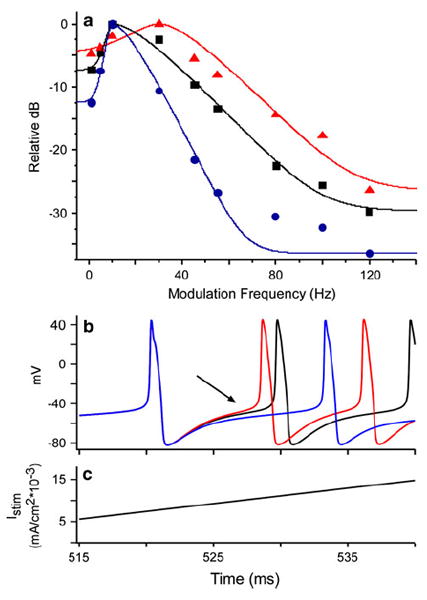
a Temporal modulation transfer functions (TMTF) for three values of ḡahp,1. Each point is the relative power in the spike frequency waveform at the stimulus modulation frequency. Curves are the roex model fit for each TMTF. Whereas the black data are for the mean parameter value (ḡahp,1 = 0.047 S/cm2), blue are for an increase (ḡahp,1 = 0.107 S/cm2) and red a decrease (ḡahp,1 = 0.022 S/cm2). These changes had the opposite effect on TMTF bandwidth (cutoff frequency: red 46.5 Hz; black 26.1 Hz; blue 18.7 Hz). The value for the parameter decrease (red curve) was chosen to match the calcium signal observed in ON1 dendrites in response to ultrasound relative to that for 5 kHz (47%; Baden and Hedwig 2007). b Membrane response to a ramped stimulus (c) is used to show difference in input resistance (Chen and Toney 2009). Colors represent the same ḡahp,1 values as in a. Arrow shows that after the depolarization of the first spike when Iahp is activated, the same Istim does not elicit the same depolarization. Higher values of ḡahp,1 require longer stimulation to elicit the next spike. Note that ramp stimulus starts at 500 ms
R is the membrane resistance, RC is the time constant and ω is the radian input frequency. When simulations use greater ḡahp,1, there is more Iahp, reducing input resistance and reducing the coupling between Istim and PSP. Thus, R functionally increases (i.e., the sub-threshold passive response to inward current is diminished), increasing the time constant and thus lowering the bandwidth of response (Getting 1974; Horowitz and Hill 1989; Hartmann 1998). With respect to amplitude modulation, longer duration pulses are now required to overcome the slower integration. Furthermore, faster amplitude modulation increases the number of pulses occurring when Iahp is on. Consequently, increases in Iahp (ḡahp,1) or the duration it is activated imposes greater low-pass filtering of amplitude modulation (Fig. 9). Although the other Ca2+-dependent parameters were also capable of shifting sensitivity in both amplitude modulation cutoff frequency and bandwidth, the parameters affecting the fast component (ḡahp,1 and τremoval,1) were slightly more effective, having the largest effect on filter bandwidth (ERB; Fig. 9; Table 2).
Fig. 9.
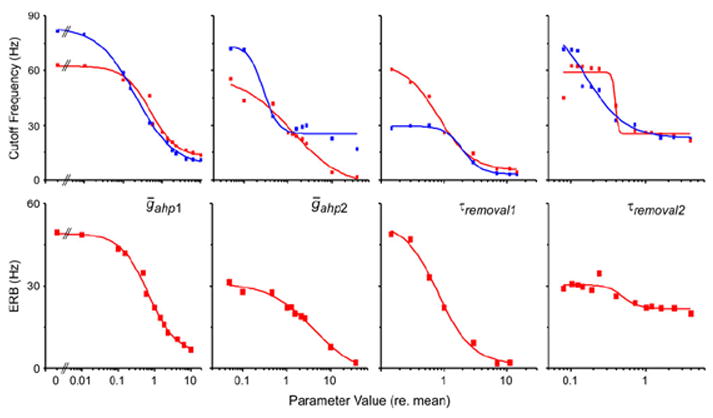
Change in temporal modulation transfer function associated with variance in the four adaptation parameters (noted in each column). The top row is the low-pass cutoff frequency as a function of parameter value (relative to mean parameter value from the simulation of nine G. rubens ON1s using response to a single pulse). Red symbols are for spectral analysis of the spike frequency waveform. Blue symbols are from analysis using spike frequency peaks/stimulus pulse, in which peak discrimination threshold is 200 Hz. The bottom row is the equivalent rectangular bandwidth of the spectral filter versus parameter value. Steepness of the ERB curves demonstrates the extent to which the change in cutoff frequency in the top row is due to a change in filter bandwidth as opposed to shifting center frequency. Only one parameter is varied at a time, with other parameter values equaling the mean. All curves are single Boltzman fits to the data (Table 2)
Table 2.
Parameters for fitted curves shown in Fig. 9, which show the change in the cutoff frequency of the temporal modulation transfer functions (for two methods of analysis) and equivalent rectangular bandwidth (ERB; Hartmann 1998) as a function of biophysical parameter value
| Spike train analysis method | Biophysical parameter | Inflection point (relative to mean value) | Function range (Hz) | Slope | R2 fit |
|---|---|---|---|---|---|
| Spike frequency peaks | ḡahp,1 | 0.216 | 75.93 | 0.88 | 0.996 |
| ḡahp,2 | 0.276 | 48.40 | 2.58 | 0.966 | |
| τremoval,1 | 2.011 | 26.48 | 2.97 | 0.998 | |
| τremoval,2 | 0.160 | 67.14 | 1.65 | 0.965 | |
| Spike frequency spectrum | ḡahp,1 | 0.515 | 49.57 | 1.29 | 0.978 |
| ḡahp,2 | 1.247 | 60.61 | 0.75 | 0.965 | |
| τremoval,1 | 0.8177 | 58.99 | 1.62 | 0.989 | |
| τremoval,2 | 0.392 | 33.96 | 22.47 | 0.931 | |
| ERB of spike frequency spectrum | ḡahp,1 | 0.683 | 44.05 | 1.13 | 0.994 |
| ḡahp,2 | 4.169 | 33.67 | 0.84 | 0.987 | |
| τremoval,1 | 0.808 | 52.34 | 1.57 | 0.995 | |
| τremoval,2 | 0.497 | 8.87 | 4.10 | 0.875 |
Columns are the inflection point of the Boltzman curve normalized to the mean biophysical parameter value; the minimum to maximum range of the function; the slope and the R2 value of the curve fit. The biophysical parameters are the ahp conductances (ḡahp) and the Ca2+ removal times (τremoval) for pools 1 and 2
Overall, these results show that calibrating the model to the single pulse response in vivo was sufficient to simulate selective attention (i.e., paired pulse) and the TMTF of this species. Furthermore, the results show that the amplitude modulation sensitivity difference between ultrasound and calling song input can be simulated by adjusting the fast (i.e., dendritic) adaptation parameters; and such adjustments are sufficient to produce continuous changes to the TMTF of the cell.
Temperature and the TMTF
Temperature is only coupled to the model through the ICa, IK and INa activation and inactivation parameters (and not Iahp). Thus, change in temperature affects the TMTF response through effects on spike structure (Fig. 10). Using the mean values for the four adaptation parameters, the model shows that increases in simulation temperature caused a decrease in spike duration in the first spike, as well as those after the first adaptation time constant (i.e., spikes later than τremoval,1). There was no measurement after τremoval,2, as adaptation had eliminated spiking at this time under the mean parameter conditions. The TMTF shows a linear increase in the filter cutoff frequency with increasing temperature (slope = 1.11; intercept = 0.88). However, this change was much less than that found for singing males (Fig. 10).
Fig. 10.
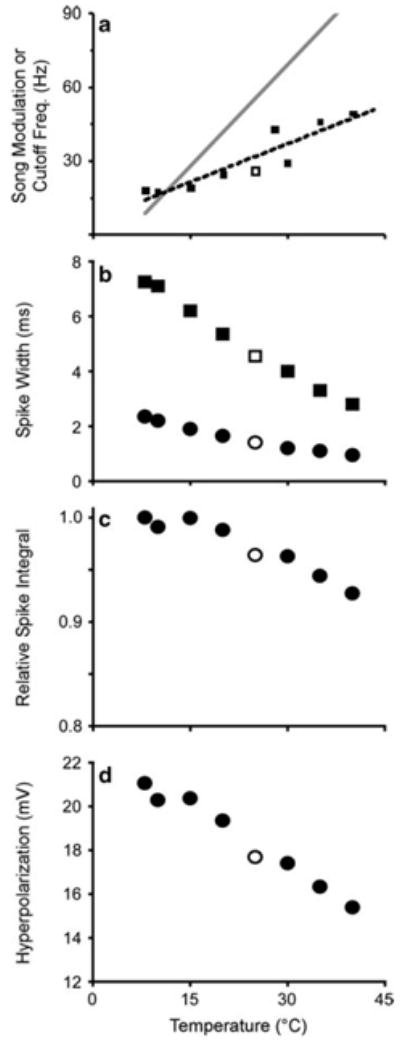
Effect of temperature on spike generation and adaptation. a TMTF of amplitude modulation coding. Dotted line is linear fit to data (slope = 1.04; intercept = 5.9). This slope is shallow relative to the change in song modulation frequency with temperature exhibited by males (solid gray line slope = 2.756; intercept = −13.12; Walker 1962). b Speed of spike generation increases with temperature. Plot shows the spike width (duration) during depolarization above −55 mV. Squares and circles are the widths of the first spike and the first spike after τremoval,1 (34.4 ms), respectively. c Reduced spike width caused by increasing temperature reduces the integral of depolarization by ~ 10%. This reduction leads to reduced activation of ICa and Iahp, reducing hyperpolarization as shown in d. Open symbols are simulations run at the standard 25°C
Discussion
Cells may code aspects of stimulus amplitude, temporal structure and duration using intracellular Ca2+ accumulation. This mechanism often leads to spike frequency adaptation and PSP depression, as Ca2+-activated K+ conductances (e.g., SK) respond to the ‘accumulation measure’ by providing a form of feedback inhibition, reducing the input resistance of the cell and producing hyperpolarization (Wang 1998; Engel et al. 1999). A primary function of these effects is to reduce responses to background noise or low amplitude stimuli (Fig. 6; see also Pollack 1988; Sobel and Tank 1994; Benda et al. 2005). But, coding of repetitive or amplitude-modulated stimuli is also affected, causing responses to change at both ends of the modulation scale. We have shown in this computational study that variance in Ca2+ feedback mechanisms (ahp) can contribute to differences in temporal responses of ON1 (e.g., like those for different carrier frequencies; Pollack 1988; Marsat and Pollack 2004; Sabourin et al. 2008). Furthermore, we also found that these mechanisms can produce sufficient variance in TMTFs to function in the context of the evolution of interspecific differences in sensitivity.
Significance of multiple Ca2+ pools
Spike frequency adaptation in ON1 is well described by a double exponential decay (Fig. 2; see also Tunstall and Pollack 2005), necessitating the use of two ahp conductances and associated Ca2+ pools for adequate simulation. Integration of multiple adaptation rates within cells are not uncommon and often reflect the contribution of different ahp conductances expressing different activation characteristics or kinetics (Storm 1990). These separate pools, and thus adaptation characteristics, could be the result of different Ca2+ dynamics in different cellular zones. Baden and Hedwig (2007) showed that the rate of Ca2+ decay in ON1 dendrites and the spike generation zone differ by an order of magnitude. Our model suggests that with respect to adaptation, these two Ca2+ zones are functional, as integration of two similar Ca2+ removal times simulates adaptation well. If Ca2+ dynamics were separated in such a way as to limit or bias integration of one Ca2+ pool relative to the other (e.g., for different frequency inputs), the characteristics of adaptation would be changed, being carrier frequency specific. This seems to be the case in ON1 as Ca2+ imaging shows that the amount of internal Ca2+ in certain portions of the dendritic tree depends on stimulus carrier frequency (Baden and Hedwig 2007). When taken together with our model, we propose that such a separation could contribute to the different temporal response of ON1 for different carrier frequency inputs (Marsat and Pollack 2004). Supporting this hypothesis are data showing: (1) anatomical segregation of afferent central projections from different frequency receptors (Esch et al. 1980) and the contralateral ON1; (2) ultrasound input does not generate large after-hyperpolarizations (Pollack 1988); (3) the input resistances of the two frequency inputs appear different, as integration time and recovery from adaptation suggest higher input resistance (less Iahp) for high frequencies (Sabourin et al. 2008); (4) the synaptic input from receptors to ON1 differs between ultrasound versus low carrier frequency-sensitive receptors (Pollack 1994; Faulkes and Pollack 2001). In contradiction though, direct synaptic contact from low-frequency and high-frequency receptors to ON1 does not appear to be located in very different ON1 dendritic regions (Imaizumi and Pollack 2005). The hypothesis, however, does not require great differences in synaptic locations and could be mediated in microdomains between the post-synaptic zone and the spike generation zone. Indeed, stimulus-dependent separation of Ca2+ accumulation has been shown in the visual neuropil of flies (Egelhaaf and Borst 1995). It is important to note that this endogenous filtering hypothesis does not eliminate synaptic or pre-synaptic mechanisms (French 1986; Gollisch and Herz 2004; Marsat and Pollack 2004; Sabourin and Pollack 2010). But, taken together with the empirically derived Ca2+-sensitive adaptation mechanisms (Sobel and Tank 1994; Baden and Hedwig 2007), the model does argue that variance in these Ca2+-dependent parameters alone is sufficient to explain the differences in temporal code, as the model does not need intervening circuits or synaptic filters.
Implications for selective pressure and song coding
In orthopterans, auditory decisions, including species recognition, are based in part on the structure of amplitude modulation in calling songs, such that phonotaxis is elicited by a particular species-specific range of modulation rates (Walker 1957; Thorson et al. 1982; Schildberger 1984; Doherty 1985b; Hennig and Weber 1997; Schul 1998; Shaw and Herlihy 2000). Comparisons across taxa show that song modulation rate can evolve across a wide range, as interspecific variance is broadly distributed (Walker 1962) and exhibits evidence for quantitative underlying genetics (Shaw et al. 2007). Indeed, hybrids of species with different amplitude modulation rates produce intermediate songs: hybrid modulation rate is halfway between those of parental species. Interestingly, song preference in females matches this variation, with female hybrids preferring the intermediate songs (Hoy and Paul 1973; Hoy 1974; Hoy et al. 1977; Shaw 2000). This suggests that, like the motor mechanisms of song production, the mechanisms underlying temporal auditory filtering are under quantitative control and thus capable of being altered to produce shifts in sensitivity along a continuous amplitude modulation scale.
Although other neurons in crickets are more directly implicated in delivering song modulation information to the brain (Hennig 1988; Schildberger et al. 1989), there are several lines of evidence that support ON1’s role in amplitude modulation coding as well. First, amplitude modulation tuning to calling song carrier frequencies matches that of phonotaxis behavior and is positively correlated to species-specific amplitude modulation song rates (Nabatiyan et al. 2003; Marsat and Pollack 2004; Tunstall and Pollack 2005). Second, sensitivity to amplitude modulation is carrier frequency dependent (Marsat and Pollack 2004; Sabourin et al. 2008), and there is little evidence for Ca2+-induced ahp for ultrasound stimulation (Pollack 1988). Third, as an intrasegmental neuron, ON1 functions, in part, to increase binaural contrast through inhibition of the contralateral ON1 and ascending units (Selverston et al. 1985; Horseman and Huber 1994). But, the mechanisms of coding amplitude modulation appear to operate independently of the directional mechanisms (Marsat and Pollack 2005), meaning sensitivity to amplitude modulation is not an artifact or emergent property of binaural mechanisms. Fourth, during the Ca2+-mediated selective attention (Sobel and Tank 1994), filtering must be timed correctly to prevent the filtering of subsequent pulses from the attended male (i.e., filter too slow) or coding song pulses from other males falling in the attended male’s interpulse interval (i.e., filter too fast). Fifth, specialized amplitude modulation coding in ON1 increases the binaural contrast in ascending neurons for behaviorally relevant sounds (Marsat and Pollack 2004). Thus, the temporal properties of ON1 appear important to processing song amplitude modulation and phonotaxis.
The model shows that Ca2+-sensitive adaptation and depression in ON1 are sufficient to mediate these temporal properties and capable of shifting sensitivity to different song modulation rates. Thus, this model generates a hypothesis for the underlying mechanism for interspecific (and hybrid) differences in temporal sensitivity: differences in the size and kinetics of the biophysical mechanisms of Ca2+-mediated adaptation and PSP depression (e.g., Hirschberg et al. 1999; Pedarzani et al. 2001; Pedarzani et al. 2005; Nolting et al. 2007). As with other systems, our results suggest that small changes would be required to shift sensitivity (Katz and Harris-Warrick 1999).
Temperature coupling between sender and receiver
Temporal sensitivity in orthopterans varies not only between species, hybrids and for different carrier frequencies, but also with the temperature (Pires and Hoy 1992a, b). There is a linear relationship between song modulation rate and temperature (Walker 1962), which female sensitivity tracks (Doherty 1985a). With respect to omega neurons, in vivo recordings by Janiszewski and Otto (1989) showed that temporal coding varied with thoracic temperature. Lower temperatures were correlated to: reduced instantaneous spike frequency; reduced coding of faster song modulation rates; and increased spike duration. The latter result suggests, at the very least, that the kinetics of spike production is under temperature control. Thus, in proposing and testing a mechanism for changing temporal sensitivity in these neurons, the model included temperature in calculating INa activation and inactivation, and IK activation (note that although temperature is used in the Goldman–Hodgkin–Katz equation to calculate ICa, the change in temperature over the range tested did not affect the activation curve of ICa; data not shown). As in those results in vivo (Janiszewski and Otto 1989), the model showed that temporal coding was positively correlated to temperature: higher temperatures increase the TMTF cutoff frequency. There are two possible mechanisms for this effect. First, reductions in spike duration at high temperatures (Fig. 10) increase the simulation’s ability to respond to faster changes in stimulus envelope by increasing the spike rate. Second, the reduction in spike duration at high temperatures decreases the time spent depolarized, as shown by changes in the integral of the spike train as a function of temperature (Fig. 10). Because this integral (i.e., the depolarization time) determines the activation of the voltage-sensitive Ca2+ conductance, it also determines the extent of hyperpolarization or adaptation. Thus, reduced spike duration reduces Ca2+ feedback, which broadens the TMTF.
The changes in temperature did not produce the quantitative shift in TMTF like that found in singing males (Walker 1962; Fig. 10), which is predicted for the temperature coupled cricket system (Doherty 1985a). Thus, based on our model, temperature-sensitive mechanisms other than those voltage-sensitive mechanisms that generate spikes must also contribute to the temporal response of omega neurons. Hypothetically, one such mechanism could be to couple temperature to the rate of Ca2+ removal, in which buffering, sequestering or extrusion would slow down at lower temperatures (Kang et al. 2008), producing longer activation of Ca2+-activated ahp currents, increasing PSP depression (Lee et al. 2005).
In conclusion, this study adds to the other predictive models for amplitude modulation filtering in insects (Benda et al. 2001; Hennig 2003; Bush and Schul 2006). It is distinguished, however, in that it offers computational evidence that particular biophysical mechanisms, the Ca2+-mediated mechanisms of selective attention, are sufficient to explain the temporal sensitivity of omega neurons. Furthermore, the model shows that small changes (<1 SD) in the parameters of these biophysical mechanisms can shift temporal sensitivity, an important character in the contexts of speciation and predator detection. From a neuroethological point of view, empirical validation of this prediction would require, at the very least, an extension of the comparative analysis by Marsat and Pollack (2004) to include measurements of ahp rates across taxa (or hybrids) with different calling song modulation structure.
Acknowledgments
Two anonymous reviewers as well as C. Canavier, S. Selvakumar, S. Achuthan and W. Gordon provided useful comments on the project and/or manuscript. N. Bazan generously provided equipment and software. No animals were used for this computational project. The study was funded in part by the NIH Grant # P20RR016816 to N. Bazan.
Abbreviations
- Ahp
After-hyperpolarizing
- ERB
Equivalent rectangular bandwidth
- I/O
Input/output
- ON1
Omega neuron 1
- PSP
Postsynaptic potential
- SFP
Spike frequency peak
- SNR
Signal-to-noise ratio
- τfast
Fast adaptation time constant
- TMTF
Temporal modulation transfer function
- τremoval
Time constant for Ca2+ removal
- τslow
Slow adaptation time constant
References
- Art JJ, Wu YC, Fettiplace R. The calcium-activated potassium channels of turtle hair-cells. J Gen Physiol. 1995;105:49–72. doi: 10.1085/jgp.105.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baden T, Hedwig B. Neurite-specific Ca2+ dynamics underlying sound processing in an auditory interneurone. Dev Neurobiol. 2007;67:68–80. doi: 10.1002/dneu.20323. [DOI] [PubMed] [Google Scholar]
- Benda J, Hennig RM. Spike-frequency adaptation generates intensity invariance in a primary auditory interneuron. J Comput Neurosci. 2008;24:113–136. doi: 10.1007/s10827-007-0044-8. [DOI] [PubMed] [Google Scholar]
- Benda J, Herz AVM. A universal model for spike-frequency adaptation. Neural Comput. 2003;15:2523–2564. doi: 10.1162/089976603322385063. [DOI] [PubMed] [Google Scholar]
- Benda J, Bethge M, Hennig M, Pawelzik K, Herz AVM. Spike-frequency adaptation: phenomenological model and experimental tests. Neurocomputing. 2001;38:105–110. [Google Scholar]
- Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25:2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennet-Clark HC. Songs and the physics of sound production. In: Huber F, Moore TE, Loher W, editors. Cricket behavior and neurobiology. Cornell University Press; Ithaca: 1989. pp. 227–261. [Google Scholar]
- Bentley DR, Hoy RR. Genetic-control of neuronal network generating cricket (Teleogryllus–Gryllus) song patterns. Anim Behav. 1972;20:478–492. doi: 10.1016/s0003-3472(72)80012-5. [DOI] [PubMed] [Google Scholar]
- Bond CT, Maylie J, Adelman JP. SK channels in excitability, pacemaking and synaptic integration. Curr Opin Neurobiol. 2005;15:305–311. doi: 10.1016/j.conb.2005.05.001. [DOI] [PubMed] [Google Scholar]
- Burrell BD, Crisp KM. Serotonergic modulation of afterhyperpolarization in a neuron that contributes to learning in the leech. J Neurophysiol. 2008;99:605–616. doi: 10.1152/jn.00989.2007. [DOI] [PubMed] [Google Scholar]
- Bush SL, Schul J. Pulse-rate recognition in an insect: evidence of a role for oscillatory neurons. J Comp Physiol A. 2006;192:113–121. doi: 10.1007/s00359-005-0053-x. [DOI] [PubMed] [Google Scholar]
- Chen QH, Toney GM. Excitability of paraventricular nucleus neurones that project to the rostral ventrolateral medulla is regulated by small-conductance Ca2+-activated K+ channels. J Physiol. 2009;587:4235–4247. doi: 10.1113/jphysiol.2009.175364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
- Dean I, Robinson BL, Harper NS, McAlpine D. Rapid neural adaptation to sound level statistics. J Neurosci. 2008;28:6430–6438. doi: 10.1523/JNEUROSCI.0470-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doherty JA. Temperature coupling and trade-off phenomena in the acoustic communication-system of the cricket, Gryllus bimaculatus de Geer (Gryllidae) J Exp Biol. 1985a;114:17–35. [Google Scholar]
- Doherty JA. Trade-off phenomena in calling song recognition and phonotaxis in the cricket, Gryllus bimaculatus (Orthoptera, Gryllidae) J Comp Physiol A. 1985b;156:787–801. [Google Scholar]
- Egelhaaf M, Borst A. Calcium accumulation in visual interneurons of the fly—stimulus dependence and relationship to membrane-potential. J Neurophysiol. 1995;73:2540–2552. doi: 10.1152/jn.1995.73.6.2540. [DOI] [PubMed] [Google Scholar]
- Engel J, Schultens HA, Schild D. Small conductance potassium channels cause an activity-dependent spike frequency adaptation and make the transfer function of neurons logarithmic. Biophys J. 1999;76:1310–1319. doi: 10.1016/S0006-3495(99)77293-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esch H, Huber F, Wohlers DW. Primary auditory neurons in crickets—physiology and central projections. J Comp Physiol. 1980;137:27–38. [Google Scholar]
- Faber ES, Sah P. Functions of SK channels in central neurons. Clin Exp Pharmacol Physiol. 2007;34:1077–1083. doi: 10.1111/j.1440-1681.2007.04725.x. [DOI] [PubMed] [Google Scholar]
- Fan G-X, Liu QH. Fast Fourier transform for discontinuous functions. IEEE Trans Antennas Propag. 2004;52:461–465. [Google Scholar]
- Farris HE, Hoy RR. Two-tone suppression in the cricket, Eunemobius carolinus (Gryllidae, Nemobiinae) J Acoust Soc Am. 2002;111:1475–1485. doi: 10.1121/1.1451069. [DOI] [PubMed] [Google Scholar]
- Farris HE, Mason AC, Hoy RR. Identified auditory neurons in the cricket Gryllus rubens: temporal processing in calling song sensitive units. Hear Res. 2004;193:121–133. doi: 10.1016/j.heares.2004.02.008. [DOI] [PubMed] [Google Scholar]
- Farris HE, Wells GB, Ricci AJ. Steady-state adaptation of mechanotransduction modulates the resting potential of auditory hair cells, providing an assay for endolymph [Ca2+] J Neurosci. 2006;26:12526–12536. doi: 10.1523/JNEUROSCI.3569-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faulkes Z, Pollack GS. Mechanisms of frequency-specific responses of omega neuron 1 in crickets (Teleogryllus oceanicus): a polysynaptic pathway for song? J Exp Biol. 2001;204:1295–1305. doi: 10.1242/jeb.204.7.1295. [DOI] [PubMed] [Google Scholar]
- Fortune ES, Rose GJ. Passive and active membrane properties contribute to the temporal filtering properties of midbrain neurons in vivo. J Neurosci. 1997;17:3815–3825. doi: 10.1523/JNEUROSCI.17-10-03815.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune ES, Rose GJ. Short-term synaptic plasticity as a temporal filter. Trends Neurosci. 2001;24:381–385. doi: 10.1016/s0166-2236(00)01835-x. [DOI] [PubMed] [Google Scholar]
- French AS. The role of calcium in the rapid adaptation of an insect mechanoreceptor. J Neurosci. 1986;6:2322–2326. doi: 10.1523/JNEUROSCI.06-08-02322.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisina RD. Subcortical neural coding mechanisms for auditory temporal processing. Hear Res. 2001;158:1–27. doi: 10.1016/s0378-5955(01)00296-9. [DOI] [PubMed] [Google Scholar]
- Getting PA. Modification of neuron properties by electrotonic synapses. I Input resistance, time constant, and integration. J Neurophysiol. 1974;37:846–857. doi: 10.1152/jn.1974.37.5.846. [DOI] [PubMed] [Google Scholar]
- Gollisch T, Herz AVM. Input-driven components of spike-frequency adaptation can be unmasked in vivo. J Neurosci. 2004;24:7435–7444. doi: 10.1523/JNEUROSCI.0398-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris DM, Dallos P. Forward masking of auditory nerve fiber responses. J Neurophysiol. 1979;42:1083–1107. doi: 10.1152/jn.1979.42.4.1083. [DOI] [PubMed] [Google Scholar]
- Hartmann WH. Signals, sound, and sensation. AIP Press; New York: 1998. [Google Scholar]
- Hennig RM. Ascending auditory interneurons in the cricket Teleogryllus commodus (Walker)—comparative physiology and direct connections with afferents. J Comp Physiol A. 1988;163:135–143. doi: 10.1007/BF00612003. [DOI] [PubMed] [Google Scholar]
- Hennig RM. Acoustic feature extraction by cross-correlation in crickets? J Comp Physiol A. 2003;189:589–598. doi: 10.1007/s00359-003-0438-7. [DOI] [PubMed] [Google Scholar]
- Hennig RM, Weber T. Filtering of temporal parameters of the calling song by cricket females of two closely related species: a behavioral analysis. J Comp Physiol A. 1997;180:621–630. [Google Scholar]
- Hildebrandt KJ, Benda J, Hennig RM. The origin of adaptation in the auditory pathway of locusts is specific to cell type and function. J Neurosci. 2009;29:2626–2636. doi: 10.1523/JNEUROSCI.4800-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ionic conductances of excitable membranes. Sinaurer Associates Inc; Sunderland: 1992. [Google Scholar]
- Hirschberg B, Maylie J, Adelman JP, Marrion NV. Gating properties of single SK channels in hippocampal CA1 pyramidal neurons. Biophys J. 1999;77:1905–1913. doi: 10.1016/S0006-3495(99)77032-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horowitz P, Hill W. The art of electronics. Cambridge University Press; Cambridge: 1989. [Google Scholar]
- Horseman G, Huber F. Sound localization in crickets.1. contralateral inhibition of an ascending auditory interneuron (An1) in the cricket Gryllus bimaculatus. J Comp Physiol A. 1994;175:389–398. [Google Scholar]
- Hoy RR. Genetic-control of acoustic behavior in crickets. Am Zool. 1974;14:1067–1080. [Google Scholar]
- Hoy RR, Paul RC. Genetic-control of song specificity in crickets. Science. 1973;180:82–83. doi: 10.1126/science.180.4081.82. [DOI] [PubMed] [Google Scholar]
- Hoy RR, Hahn J, Paul RC. Hybrid cricket auditory-behavior—evidence for genetic coupling in animal communication. Science. 1977;195:82–84. doi: 10.1126/science.831260. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, McCormack TJ. Electrophysiology of the neuron. Oxford University Press; New York: 1994. [Google Scholar]
- Imaizumi K, Pollack GS. Central projections of auditory receptor neurons of crickets. J Comp Neurol. 2005;493:439–447. doi: 10.1002/cne.20756. [DOI] [PubMed] [Google Scholar]
- Janiszewski J, Otto D. Responses and song pattern copying of omega-type I-neurons in the cricket, Gryllus bimaculatus, at different prothoracic temperatures. J Comp Physiol A. 1989;164:443–450. [Google Scholar]
- Kang SH, Carl A, McHugh JM, Goff HR, Kenyon JL. Roles of mitochondria and temperature in the control of intracellular calcium in adult rat sensory neurons. Cell Calcium. 2008;43:388–404. doi: 10.1016/j.ceca.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz PS, Harris-Warrick RM. The evolution of neuronal circuits underlying species-specific behavior. Curr Opin Neurobiol. 1999;9:628–633. doi: 10.1016/S0959-4388(99)00012-4. [DOI] [PubMed] [Google Scholar]
- Lee JCF, Callaway JC, Foehring RC. Effects of temperature on calcium transients and Ca2+-dependent afterhyperpolarizations in neocortical pyramidal neurons. J Neurophysiol. 2005;93:2012–2020. doi: 10.1152/jn.01017.2004. [DOI] [PubMed] [Google Scholar]
- Leinders T, Vijverberg HP. Ca2+ dependence of small Ca(2+)-activated K+ channels in cultured N1E–115 mouse neuroblastoma cells. Pflugers Arch. 1992;422:223–232. doi: 10.1007/BF00376206. [DOI] [PubMed] [Google Scholar]
- Machne X, Orozco R. Electrical properties of axons of Callinectes sapidus. Am J Physiol. 1970;219:1147–1153. doi: 10.1152/ajplegacy.1970.219.4.1147. [DOI] [PubMed] [Google Scholar]
- Marsat G, Pollack GS. Differential temporal coding of rhythmically diverse acoustic signals by a single interneuron. J Neurophysiol. 2004;92:939–948. doi: 10.1152/jn.00111.2004. [DOI] [PubMed] [Google Scholar]
- Marsat G, Pollack GS. Effect of the temporal pattern of contralateral inhibition on sound localization cues. J Neurosci. 2005;25:6137–6144. doi: 10.1523/JNEUROSCI.0646-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack TJ. Comparison of K+-channel genes within the genomes of Anopheles gambiae and Drosophila melanogaster. Genome Biol. 2003;4:R58. doi: 10.1186/gb-2003-4-9-r58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Huguenard JR. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- Moore BC, Glasberg BR, Plack CJ, Biswas AK. The shape of the ear’s temporal window. J Acoust Soc Am. 1988;83:1102–1116. doi: 10.1121/1.396055. [DOI] [PubMed] [Google Scholar]
- Mutoh H, Yoshino M. L-type Ca2+ channel and Ca2+-permeable nonselective cation channel as a Ca2+ conducting pathway in myocytes isolated from the cricket lateral oviduct. J Comp Physiol B. 2004;174:21–28. doi: 10.1007/s00360-003-0385-1. [DOI] [PubMed] [Google Scholar]
- Nabatiyan A, Poulet JF, de Polavieja GG, Hedwig B. Temporal pattern recognition based on instantaneous spike rate coding in a simple auditory system. J Neurophysiol. 2003;90:2484–2493. doi: 10.1152/jn.00259.2003. [DOI] [PubMed] [Google Scholar]
- Nolting A, Ferraro T, D’hoedt D, Stocker M. An amino acid outside the pore region influences apamin sensitivity in small conductance Ca2+-activated K+ channels. J Biol Chem. 2007;282:3478–3486. doi: 10.1074/jbc.M607213200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numata T, Yoshino M. Characterization of single L-type Ca2+ channels in myocytes isolated from the cricket lateral oviduct. J Comp Physiol B. 2005;175:257–263. doi: 10.1007/s00360-005-0480-6. [DOI] [PubMed] [Google Scholar]
- Patterson RD, Nimmo-Smith I, Weber DL, Milroy R. The deterioration of hearing with age: frequency selectivity, the critical ratio, the audiogram, and speech threshold. J Acoust Soc Am. 1982;72:1788–1803. doi: 10.1121/1.388652. [DOI] [PubMed] [Google Scholar]
- Pedarzani P, Mosbacher J, Rivard A, Cingolani LA, Oliver D, Stocker M, Adelman JP, Fakler B. Control of electrical activity in central neurons by modulating the gating of small conductance Ca2+-activated K+ channels. J Biol Chem. 2001;276:9762–9769. doi: 10.1074/jbc.M010001200. [DOI] [PubMed] [Google Scholar]
- Pedarzani P, McCutcheon JE, Rogge G, Jensen BS, Christophersen P, Hougaard C, Strobaek D, Stocker M. Specific enhancement of SK channel activity selectively potentiates the afterhyperpolarizing current I(AHP) and modulates the firing properties of hippocampal pyramidal neurons. J Biol Chem. 2005;280:41404–41411. doi: 10.1074/jbc.M509610200. [DOI] [PubMed] [Google Scholar]
- Pires A, Hoy RR. Temperature coupling in cricket acoustic communication I Field and laboratory studies of temperature effects on calling song production and recognition in Gryllus firmus. J Comp Physiol A. 1992a;171:69–78. doi: 10.1007/BF00195962. [DOI] [PubMed] [Google Scholar]
- Pires A, Hoy RR. Temperature coupling in cricket acoustic communication II Localization of temperature effects on song production and recognition networks in Gryllus firmus. J Comp Physiol A. 1992b;171:79–92. doi: 10.1007/BF00195963. [DOI] [PubMed] [Google Scholar]
- Pollack GS. Discrimination of calling song models by the cricket, Teleogryllus oceanicus—the influence of sound direction on neural encoding of the stimulus temporal pattern and on phonotactic behavior. J Comp Physiol A. 1986;158:549–561. [Google Scholar]
- Pollack GS. Selective attention in an insect auditory neuron. J Neurosci. 1988;8:2635–2639. doi: 10.1523/JNEUROSCI.08-07-02635.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollack GS. Synaptic inputs to the omega neuron of the cricket Teleogryllus oceanicus: differences in epsp wave-forms evoke by low and high sound frequencies. J Comp Physiol A. 1994;174:83–89. [Google Scholar]
- Pollack GS, Hoy RR. Temporal pattern as a cue for species-specific calling song recognition in crickets. Science. 1979;204:429–432. doi: 10.1126/science.204.4391.429. [DOI] [PubMed] [Google Scholar]
- Roper P, Callaway J, Shevchenko T, Teruyama R, Armstrong W. AHP’s, HAP’s and DAP’s: how potassium currents regulate the excitability of rat supraoptic neurones. J Comput Neurosci. 2003;15:367–389. doi: 10.1023/a:1027424128972. [DOI] [PubMed] [Google Scholar]
- Rose GJ, Fortune ES. Frequency-dependent PSP depression contributes to low-pass temporal filtering in Eigenmannia. J Neurosci. 1999;19:7629–7639. doi: 10.1523/JNEUROSCI.19-17-07629.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabourin P, Pollack GS. Temporal coding by populations of auditory receptor neurons. J Neurophysiol. 2010;103:1614–1621. doi: 10.1152/jn.00621.2009. [DOI] [PubMed] [Google Scholar]
- Sabourin P, Gottlieb H, Pollack GS. Carrier-dependent temporal processing in an auditory interneuron. J Acoust Soc Am. 2008;123:2910–2917. doi: 10.1121/1.2897025. [DOI] [PubMed] [Google Scholar]
- Sah P, Faber ESL. Channels underlying neuronal calcium-activated potassium currents. Prog Neurobiol. 2002;66:345–353. doi: 10.1016/s0301-0082(02)00004-7. [DOI] [PubMed] [Google Scholar]
- Schildberger K. Temporal selectivity of identified auditory neurons in the cricket brain. J Comp Physiol. 1984;155:171–185. [Google Scholar]
- Schildberger K, Huber F, Wohlers DW. Central auditory pathway: neuronal correlates of phonotactic behavior. In: Huber F, Moore TE, Loher W, editors. Cricket behavior and neurobiology. Cornell University Press; Ithaca: 1989. pp. 423–458. [Google Scholar]
- Schul J. Song recognition by temporal cues in a group of closely related bushcricket species (genus Tettigonia) J Comp Physiol A. 1998;183:401–410. [Google Scholar]
- Selverston AI, Kleindienst HU, Huber F. Synaptic connectivity between cricket auditory interneurons as studied by selective photoinactivation. J Neurosci. 1985;5:1283–1292. doi: 10.1523/JNEUROSCI.05-05-01283.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw KL. Interspecific genetics of mate recognition: Inheritance of female acoustic preference in Hawaiian crickets. Evolution. 2000;54:1303–1312. doi: 10.1111/j.0014-3820.2000.tb00563.x. [DOI] [PubMed] [Google Scholar]
- Shaw KL, Herlihy DP. Acoustic preference functions and song variability in the Hawaiian cricket Laupala cerasina. Proc R Soc Biol Sci. 2000;267:577–584. doi: 10.1098/rspb.2000.1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw KL, Parsons YM, Lesnick SC. QTL analysis of a rapidly evolving speciation phenotype in the Hawaiian cricket Laupala. Mol Ecol. 2007;16:2879–2892. doi: 10.1111/j.1365-294X.2007.03321.x. [DOI] [PubMed] [Google Scholar]
- Sobel EC, Tank DW. In vivo Ca2+ dynamics in a cricket auditory neuron—an example of chemical computation. Science. 1994;263:823–826. doi: 10.1126/science.263.5148.823. [DOI] [PubMed] [Google Scholar]
- Stocker M, Hirzel K, D’hoedt D, Pedarzani P. Matching molecules to function: neuronal Ca2+-activated K+ channels and afterhyperpolarizations. Toxicon. 2004;43:933–949. doi: 10.1016/j.toxicon.2003.12.009. [DOI] [PubMed] [Google Scholar]
- Storm JF. Potassium currents in hippocampal pyramidal cells. Prog Brain Res. 1990;83:161–187. doi: 10.1016/s0079-6123(08)61248-0. [DOI] [PubMed] [Google Scholar]
- Thorson J, Weber T, Huber F. Auditory-behavior of the cricket. II Simplicity of calling-song recognition in Gryllus, and anomalous phonotaxis at abnormal carrier frequencies. J Comp Physiol. 1982;146:361–378. [Google Scholar]
- Traub RD, Wong RK, Miles R, Michelson H. A model of a CA3 hippocampal pyramidal neuron incorporating voltage-clamp data on intrinsic conductances. J Neurophysiol. 1991;66:635–650. doi: 10.1152/jn.1991.66.2.635. [DOI] [PubMed] [Google Scholar]
- Tucker TR, Fettiplace R. Monitoring calcium in turtle hair cells with a calcium-activated potassium channel. J Physiol. 1996;494(Pt 3):613–626. doi: 10.1113/jphysiol.1996.sp021519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tunstall DN, Pollack GS. Temporal and directional processing by an identified interneuron, ON1, compared in cricket species that sing with different tempos. J Comp Physiol A. 2005;191:363–372. doi: 10.1007/s00359-004-0591-7. [DOI] [PubMed] [Google Scholar]
- Walker TJ. Specificity in the response of female tree crickets (Orthoptera: Gryllidae: Oecanthinae) to calling songs of the males. Ann Entomol Soc Am. 1957;50:626–636. [Google Scholar]
- Walker TJ. Factors responsible for intraspecific variation in calling songs of crickets. Evolution. 1962;16:407–428. [Google Scholar]
- Wang XJ. Calcium coding and adaptive temporal computation in cortical pyramidal neurons. J Neurophysiol. 1998;79:1549–1566. doi: 10.1152/jn.1998.79.3.1549. [DOI] [PubMed] [Google Scholar]
- Wei A, Jegla T, Salkoff L. Eight potassium channel families revealed by the C. elegans genome project. Neuropharmacology. 1996;35:805–829. doi: 10.1016/0028-3908(96)00126-8. [DOI] [PubMed] [Google Scholar]
- Wicher D, Penzlin H. Ca2+ currents in central insect neurons: electrophysiological and pharmacological properties. J Neurophysiol. 1997;77:186–199. doi: 10.1152/jn.1997.77.1.186. [DOI] [PubMed] [Google Scholar]
- Witte K, Farris HE, Ryan MJ, Wilczynski W. How cricket frog females deal with a noisy world: habitat-related differences in auditory tuning. Behav Ecol. 2005;16:571–579. [Google Scholar]
- Xia XM, Fakler B, Rivard A, Wayman G, Johnson-Pais T, Keen JE, Ishii T, Hirschberg B, Bond CT, Lutsenko S, Maylie J, Adelman JP. Mechanism of calcium gating in small-conductance calcium-activated potassium channels. Nature. 1998;395:503–507. doi: 10.1038/26758. [DOI] [PubMed] [Google Scholar]
- Zakon HH. Insight into the mechanisms of neuronal processing from electric fish. Curr Opin Neurobiol. 2003;13:744–750. doi: 10.1016/j.conb.2003.07.001. [DOI] [PubMed] [Google Scholar]


