Discriminating early stage Aβ42 monomer structures using chirality-induced 2DIR spectroscopy in a simulation study

Abstract

Elucidating the structural features of the Aβ monomer, the peptide constituent of amyloid fibrils found in Alzheimer’s disease, can enable a direct characterization of aggregation pathways. Recent studies support the view that the ensemble of Aβ42 monomers is a mixture of diverse ordered and disordered conformational species, which can be classified according to the formation of a characteristic β-hairpin conformation in a certain region. Despite the disparity in the structural features of these species, commonly used spectroscopic techniques such as NMR may not directly trace the conformational dynamics in the ensemble due to the limited time resolution and the lack of well-resolved spectral features for different comformers. Here we use molecular dynamics simulations combined with simulations of two-dimensional IR (2DIR) spectra to investigate the structure of these species, their interchange kinetics, and their spectral features. We show that while the discrimination efficiency of the ordinary, nonchiral 2DIR signal is limited due to its intrinsic dependence on common order parameters that are dominated by the generally unstructured part of the sequence, signals with carefully designed chirality-sensitive pulse configurations have the high resolution required for differentiating the various monomer structures. Our combined simulation studies indicate the power of the chirality-induced (CI) 2DIR technique in investigating early events in Aβ42 aggregation and open the possibility for their use as a novel experimental tool.

The aggregation of amyloidogenic peptides into insoluble amyloid fibrils has been identified as the pathological hallmark of more than 20 diseases including Alzheimer’s disease (AD), which is characterized by the progressive deterioration in cognitive function and behavioral symptoms related to alterations in neural and glial function in certain regions of the brain. Amyloid peptides are products of the proteolytic cleavage of a multidomain integral membrane protein, Amyloid-β Precursor Protein (APP) (1, 2). The cleavage can happen at different transmembrane sites of APP that result in different lengths of the Aβ product, which varies from 38 to 43 residues. The 42-residue derivative, Aβ42, has a much stronger tendency to form fibrils in vitro. It is widely believed that in aqueous solution the Aβ peptide is generally unstructured. Its fibrils, however, have dominating β sheet structure, as shown in two recently reported models of both Aβ40 and 42 (3, 4). Moreover, Aβ peptides may also form key oligomeric species with neurotoxic properties. Little is known about the structure of the oligomeric species and the mechanism of transitions among monomers, oligomers, and fibrils. Understanding this process is essential for designing therapeutics that target amyloid formation at an early stage of the disease (5). Characterization of the structural features of the monomers is thus of particular interest because they may provide a starting point for modeling the aggregation pathways. Different monomer conformations can provide the seed for pathologic oligomeric species as well as intermediates en route to fibril formation.

Several spectroscopic and computational studies have focused on structural features of the Alzheimer’s peptides Aβ(1–40) and Aβ(1–42) and various fragments. (6–19). Recent evidence supports the view that, at the monomeric level, the ensemble of Aβ is a mixture of multiple, nearly isoenergenic conformational species, in agreement with the energy landscape view of protein dynamics proposed by Frauenfelder and coworkers (22). In a recent combined molecular dynamics (MD) simulation and NMR study, Sgourakis and coworkers generated, through the MD simulation, the monomeric forms of Aβ40 and 42 in aqueous solution (20), which nicely reproduced the NMR J-coupling data. They then investigated the structural diversity of the structural ensemble of Aβ42. This study showed that in a significant population of the sampled structures of Aβ42 (28%), the C terminus had a fairly well defined β-hairpin structure involving short strands at residues 31–34 and 38–41. It was further proposed that this structural feature may rigidify the peptide C terminus. This is consistent with two independent NMR NOE and relaxation studies, which both reported a more rigid C terminus for Aβ42 relative to the less fibrilogenic isoform Aβ40 (10, 19). Based on this experimental evidence, Yan and Wang have proposed that this formation of hairpin structure might reduce the C-terminal flexibility of the Aβ42 and be responsible for the higher propensity of this peptide to form amyloids (19). Furthermore, a previously published 3D profile study has indicated that this region has the lowest energy in the fibril state (21). Taken together, both experiments and computations support the presence of a more structured C terminus for Aβ42, thus providing a plausible structural basis for the high amyloidogenic potential of this toxic Aβ isoform.

Whether and how the completely disordered conformations of the monomer turn into the relatively ordered is of considerable interest because they represent the earliest step along the aggregation pathway (18). In order to explore the possible nucleation pathways, suitable experimental tools will be needed that can probe the structures with adequate temporal, spectral, and spatial resolution. The conformational changes in peptides of this size are expected to start to occur on the submillisecond to millisecond time scale. While the agreement between the experimental (NMR) and the theoretical (MD) J-coupling data justifies the correctness of the MD-generated structural ensemble, thus strongly supporting the existence of multiple monomeric forms, an experimental tool with direct spectral features distinguishing these forms will still be needed for monitoring the variation of different components. Also, an ideal technique should possess a higher temporal resolution to help generate a more complete picture of the early aggregation events.

Two-dimensional IR (2DIR) spectroscopy with 20–100 fs laser pulses is a potentially useful tool to investigate ultrafast kinetics in real time (30–32). In 2D optical experiments, three ultrashort laser pulses interact with the molecular system to generate a coherent nonlinear signal, which depends parametrically on three consecutive time delays t₁, t₂, and t₃. Two-dimensional correlation plots are obtained by a double Fourier transform of the signal with respect to t₁ and t₃, holding t₂ fixed (33). By spreading the congested transitions of linear absorption in two dimensions, these techniques significantly enhance the spectral resolution. The cross peaks (off diagonal peaks in 2D frequency correlation plots) carry signatures of intermode couplings, and their spectral line shapes probe solvent and conformational fluctuations. Optical 2D techniques have been successfully used toward the study of fast peptide folding kinetics (32, 34), hydrogen bonding dynamics (35), ultrafast chemical exchange (30, 31), and energy transport in photosynthetic antennae (36). Very recently, there has been considerable interest in the 2DIR field in studying the structure and formation kinetics of various kinds of amyloid aggregates (12–15).

In this paper, we have used enhanced-sampling MD simulation protocols described in ref. 20 and MD simulations to investigate the interchange time scale between the ordered and disordered structures. Due to the similar highly unstructured nature of the two conformers, common order parameters such as backbone dihedral angles can not discriminate between them, thus rendering traditional 2DIR techniques insensitive to their structural differences. We thus propose to improve 2DIR’s differentiation between the two conformers by making use of chirality. We demonstrate that the two conformer ensembles have very different structural chirality characteristics, and the chirality-induced (CI) 2DIR signals (37, 38) provide direct and clean spectral features to distinguish between them and thus have the capacity to monitor the structural variation during the early aggregation.

MD Simulations of Interchange Kinetics Between the Two Conformers

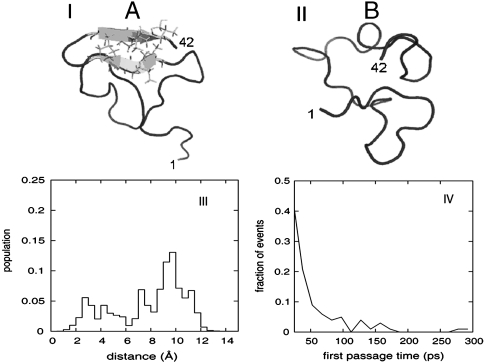
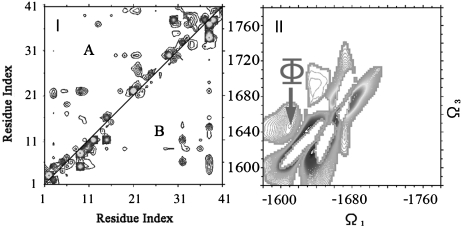
Using clustering analysis, we have previously identified distinct types of conformational species in an ensemble of Aβ42 that was generated by means of replica-exchange MD (REMD) and further validated by three bond J-coupling data from NMR (20). The ensemble of conformations can be adequately classified into two populations based on patterns of secondary structural elements: The first population (A) contains conformations that display a characteristic β5-hairpin motif toward the C terminus of the sequence, while the second (B) is devoid of any elements of regular secondary structure other than transient turns. Representative structures of these two groups are shown in Fig. 1 I and II. In the present study, we have sampled fluctuations starting from representative conformations of the two conformational species using 10 ns trajectories of NPT molecular dynamics at room temperature (300 K). This resulted in the generation of two structural ensembles of 10,000 conformations each, which were used as a starting point for the calculation of the IR spectra.

Fig. 1.

I and II) Representative conformations of the two ensemble populations of Aβ (1–42) used to model the locally structured “A” and disordered “B” states, as extracted from the replica exchange molecular dynamics (REMD) trajectories. Atoms of residues that participate in the C-terminal β-hairpin are explicitly shown. The first and last residues of each conformation are numbered for clarity. Graphics were generated by mean of the visualization suite pymol (www.pymol.org). (III) Distribution of atomistic (Cα) rmsd from the representative conformation of the B (locally ordered) state, as calculated for all REMD conformations sampled at low temperature. All conformations were sampled over a range of temperatures from 276 K to 305 K. A bimodal distribution with a gap at 6 Å indicates the existence of two populations with distinct structural characteristics. (IV) Distribution of transition times (first passage time) between the A (locally ordered) and B (disordered) states, as observed in the low-temperature segments of the REMD trajectories. All events happen over a range of temperatures from 276 K to 305 K. The majority (> 80%) of events take place in the sub-100 ps time scale, which makes our dataset suitable for analysis with the 2DIR simulation method.

We are guided by the original REMD trajectories to obtain an estimate for the interconversion time scale between the two ensemble populations. The distribution of atomistic root mean square deviations from the representative conformation with the β-hairpin motif of Fig. 1I, which was used to assign the room-temperature REMD ensemble into the two populations, is shown in Fig. 1III. We obtain a bimodal distribution between the ordered and the disordered species. According to this analysis, a rmsd threshold of 6 Å is sufficient in discriminating between the two populations and was further used to identify exchange events. The population ratio of the two species is (A∶B) 28∶72. Analysis of interconversions between the two populations along room-temperature segments of the REMD simulation trajectories shows that the exchange between the two conformers occurs at the subnanosecond time scale. This is shown in Fig. 1IV. We find that approximately 60% of the transitions occur within 20 ps and more than 80% in less than 100 ps. In the next section, we compare the ordinary (nonchiral) 2DIR signals of the two conformers.

Similarity of the Nonchiral 2DIR Features for the Two Conformers and Its Structural Basis

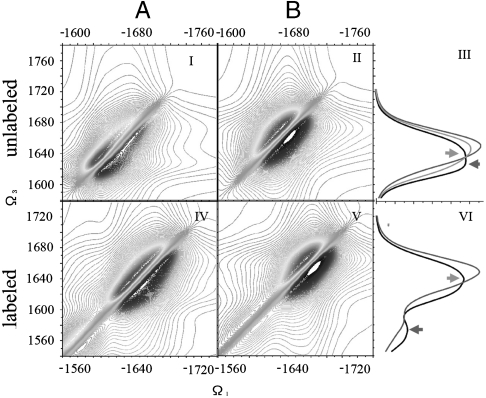
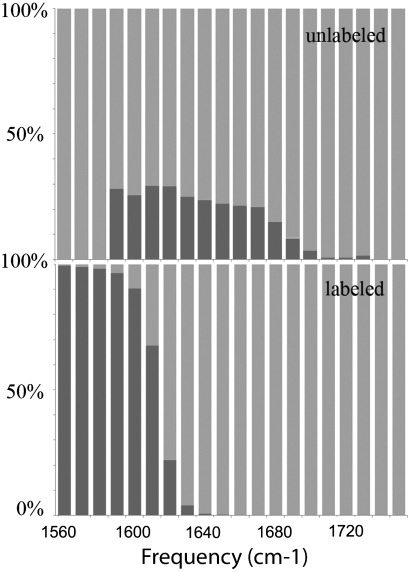
The amide-I band of xxxx photon echo signal (imaginary part) of both conformers in the Amide I range are shown in Fig. 2 together with their absorption spectra. Here all optical pulses are polarized along X direction. This is a nonchiral technique. The 2D signals do not reveal additional information compared with the absorption because the cross peaks are covered by the broad diagonal peaks. For the unlabeled samples, both conformers have a single peak. The maximum of A’s peak (black in the absorption signal) is about 20 cm^-1 red-shifted compared with B’s (red in the absorption signal) and slightly (10 cm^-1) broader. It also has a slightly asymmetric feature with a maximum at approximately 1,630 cm^-1, consistent with the typical feature of β-hairpin in the literature. B has an almost perfect gaussian shape. The A and B signals are very similar, as demonstrated by the ensemble-averaged absorption signal of 28%A + 72%B. For samples with residues 31–34 and 38–41, the hairpin region in conformer A, labeled with ¹³C¹⁸O, we observed an isotope band at approximately 1,575 cm^-1 for A and approximately 1,595 cm^-1 for B. These two peaks thus have the same splitting as in the unlabeled samples. At the same time, the main “random coil” band of A becomes symmetric and gaussian-like as B, and its shift from the main band of B is approximately 5 cm^-1. This suggests that A and B have very similar nonchiral vibrational signal features, especially in the random coil segments. Fig. 3 Upper shows the decomposition of the various normal modes in the unlabeled sample of A (NMD) into the two structural motifs β-hairpin (red) and coil (green). Modes 1,630 cm^-1 have the most significant β strand content, which causes the characteristic β strand feature peak in the absorption signal, labeled with a red arrow in Fig. 2III, while the shoulder labeled with a green arrow mainly contains the coil feature. Fig. 3 Lower shows the same analysis for the labeled sample, in which the β-strand components are shifted to below 1,630 cm^-1, which gave the peak at approximately 1,575 cm^-1 in Fig. 3VI, labeled with a red arrow. Now in the major band, the peak labeled with a green arrow becomes dominant. This explains why an apparent significant red shift (15 cm^-1) in the absorption signal is caused by a labeling a relatively small portion of the structure ( only 20% of the structure is hairpin).

Fig. 2.

(Column A) 2D photon echo signal of conformer A (imaginary part) with XXXX polarizations configuration. The upper panel shows the signal for the unlabled samples, while the lower panel is for samples with residues 31–34 and 38–41 isotopically labeled by ¹³C¹⁸O. (Column B) Same signals for conformer B. (Right Column) The upper panel gives the absorption signal of the unlabeled samples. A (black), B (Red), and A + B (green). The signal of A is red-shifted compared with B. The lower panel gives the absorption signal of samples with both 31–34 and 38–41 labeled by ¹³C¹⁸O. There is a ∼20 cm^-1 shift between the isotope peak of A and B.

Fig. 3.

The NMD diagram for conformer A. The upper panel shows the NMD for the unlabeled samples, while the lower panel is for samples with residues 31–34 and 38–41 isotopically labeled by ¹³C¹⁸O. The β-strand is shown in red and coil in green, respectively.

Introducing Chirality into the 2D Picture

Structural chirality allows for novel spectroscopic probes. Typical molecules’ response to the optical field is adequately described by the dipole approximation because they are smaller than the optical wavelength. Here the field is uniform across the molecule. Taking the spatial variation of the field into account yields new contributions to the response stemming from the variation of the phase of the optical field at different points within the molecule. These contributions are typically 100 to 1,000 times weaker than the leading dipole contributions. (This is due to the ratio of protein size and the optical wavelength). However, by choosing certain polarization configurations of the laser fields, the higher multipole corrections generate distinct background-free signals. These signals are finite only in chiral systems and vanish in racemates and nonchiral molecules.

Circular dichroism (CD) is an important example of such signals in linear spectroscopy (39–41), broadly applied for probing the folding states of proteins and their conformational stability. We recently theoretically proposed a chirality-induced 2DIR (CI-2DIR) technique (37), in which the structural sensitivity can be greatly enhanced by a judicious choice of polarization configurations aimed at chiral structures. These CI techniques thus constitute a natural extension of CD to nonlinear spectroscopy. We next apply this technique to calculate the CI-2DIR spectra of the A and B conformational species of Aβ42.

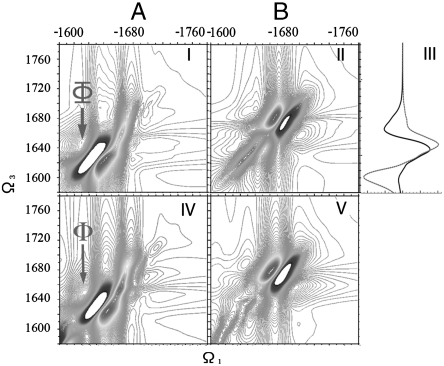
In Fig. 4, the simulated 2D CI (XXXY) signals (I, II) as well as the (linear) circular dichroism signal (III) of both conformers are presented. The signals of the two conformers show significant differences: Along the diagonal line, A’s CI-2DIR signal has a strong pair of (positive plus negative) lobes around 1,630 cm^-1 and a weak peak around 1,670 cm^-1 regime, while B has a strong pair of lobes around 1,670 cm^-1 and a weak pair around 1,630 cm^-1. Similar to the CD signals (III), these different features originate from the system structural chirality and can thus differentiate between the two conformer ensembles. However, these partially overlapping diagonal features do not offer a clean spectral window for our observation of fast exchange kinetics.

Fig. 4.

(I and II) 2D photon echo signal of A and B with XXXY polarization. (III) Circular dichroism of A (black) and B (red). (IV and V) Similar 2D signals as I and II, with both 31–34 and 38–41 labeled by ¹³C¹⁸O.

2D techniques significantly enhance the spectral resolution by spreading the congested transitions of linear absorption in two dimensions. The cross peaks carry signatures of intermode couplings, and their spectral line shapes probe solvent and conformational fluctuations. One feature of particular interest is peak Φ at (-1,610 cm^-1, 1,640 cm^-1) (marked by a red arrow), which is absent in the B conformer. Fig. 4 V–VI depicts the simulated CI-2DIR signals of both conformers with the residues 31–34 and 38-–41 (hairpin region in A) labeled (with ¹³C¹⁸O). The Φ peak remains at the same location.

These results demonstrate the resolving power of CI-2DIR on the Aβ monomer system. To analyze these signals, we define the following function η(ω₁,ω₃) of the two conformer ensembles A and B:

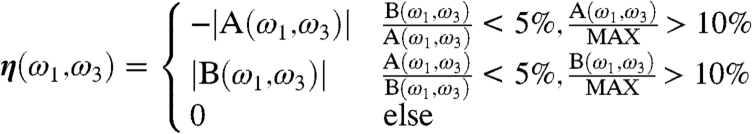[1]

Here A(ω₁,ω₃) and B(ω₁,ω₃) are the 2D signals of A and B at the (ω₁,ω₃) point, and MAX is the maximum of the absolute value of signals. Negative (positive) values of η(ω₁,ω₃) thus represent a significant signal with dominating contribution from A (B) ensembles. Blue regions Fig. 5II have dominant contribution from A. The diagonal features, similar to the CD signals, give clearly different signals for the two conformers. However, the features are highly congested in the 1,600 cm^-1 ∼ 1,700 cm^-1 frequency range. All of the diagonal features partially overlap. This makes it difficult to find an adequate window to monitor the interchanging kinetics between the conformers and the follow-up oligomerization. In contrast, the cross peak Φ, as denoted by the red arrow, is the well-resolved and separated peak that has a dominant A contribution. This gives a good window for monitoring the interchanging kinetics of the Aβ monomers.

Fig. 5.

(I) The plot of chirality factor of A and B, as defined in Eq. 2. (II) 2D plot of η(ω₁,ω₃), as defined in Eq. 1. Negative values are colored blue, positive are colored red.

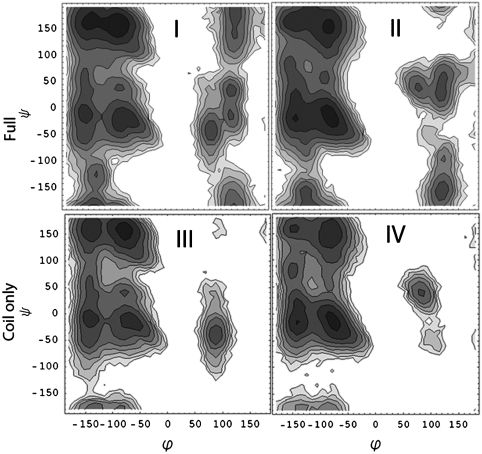
Furthermore, the similar gaussian shape of A and B conventional 2DIR spectra originates from the similar randomly coiled structure in both conformers. As suggested by the combined MD/NMR study (20), the two main conformers are generally unstructured and may not be distinguished by commonly used order parameters. This is contrasted with the case of a stable, folded protein in which the RMSD to the native state can be used quite efficiently to describe the unfolding/folding equilibrium. Fig. 6 I and II depicts the Ramachandran plots of the two conformers. The similarity of two plots indicates that the differences in the structural features of the two monomers cannot be attributed to local features of the backbone, implying that features other than secondary structure alone may be crucial in shaping the energy landscape of this dynamic peptide system. We further demonstrate this trend in the Ramachandran plots of the random coil part of the sequence (residues 1–30 in Fig. 6 III and IV) that corresponds to a region with no observed elements of cooperative secondary structure for both of the conformational subensembles, A and B. We observe two very similar patterns, which indicates that even in the presence of a systematic conformational difference between the random coil part of the two conformers, routine order parameters such as backbone dihedral angles will not be able to differentiate it, as illustrated in the Fig. 6.

Fig. 6.

(I and II) The Ramachandran plots of two conformers. The basins that correspond to extended, polyproline type 2 and helical conformations can be observed. Contours are based on a log scale of counts from the simulation trajectories. Glycine residues at positions 9, 25, and 29 have been omitted from this analysis. (III and IV) Same Ramachandran plots of the unlabeled (“random coil” ) part of the sequence (residues 1–30).

For a system such as Aβ that consists of a multitude of diverse conformational species, the absence of a typical order parameter limits the characterization of the transitions between unstructured conformations and conformations with some elements of secondary structure that could serve as the nucleation sites for the assembly of larger oligomers, en route to amyloid formation. On the other hand, the CI-2DIR signals are different for the entire structure of the two Aβ conformers due to their differences in structural chirality. In the signals with the hairpin region (in A) labeled, we see that the Φ peak remains at the same location. Φ is therefore related to the chirality of the entire random coil segment and reflects the intrinsic, global structural difference between A and B. To quantify this difference in chirality, we define a chirality factor (CF):

[2]

Here, m, n are the indices of local amide I modes,Ψ_em is the eigen state e wavefunction given as a superposition of localized amide I states.R_mn is the displacement vector between the locations of two transition dipoles μ_m and μ_n. Sum over all the eigenstates at one frequency for 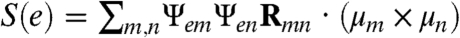will give the circular dichroism signal (neglecting the magnetic dipole contribution). Thus the chirality factor reveals the contribution of a specific pair of chromphores m and n to the chirality-induced CD signal. Fig. 5I shows the CF(m,n) for A (upper triangle) and B (lower triangle). The spectral regime between m = (31,41) and n = (31,41) shows significant differences between A and B. This is attributed to the difference of structural chirality between the hairpin-like (in A) and randomly coiled (in B) structures. Interestingly, the CF of the unstructured part of the sequence (residues 1–30) also shows clear differences. This implies that structural features that do not manifest themselves as elements of regular secondary structure, such as clusters of locally interacting atoms, could play an important role in shaping the energy landscape of the system. Also, the random coil parts of the two conformers, which are indistinguishable with ordinary order parameters, show very different chirality-related structural properties. The chirality factor carries information about the distribution of the localized amide I transition dipoles and shows a different pattern for the two conformers. Thus it can be considered as a chirality-related spectroscopic order parameter that monitors the structural transition between the two conformers.

Discussion

Molecular dynamics simulations validated by NMR experimental data suggested that the Aβ42 monomer system can be described as a diverse ensemble of conformations with various degrees of ordered structure (20). The present analysis based on the simulation suggests a sub-100 ps interchange time scale between the ordered and disordered conformations of the Aβ42 peptide. We propose a previously undescribed optical spectroscopic method, chirality-induced 2DIR spectroscopy (CI-2DIR), to characterize the ensemble of Aβ42 and investigate its thermodynamic and kinetic properties. In addition to the spectral resolution required to discriminate between the two major conformational species, CI-2DIR offers ps time scale temporal resolution and can thus monitor the transition from disordered to ordered conformations.

Vibrational spectroscopies offers unique advatages in the structural characterization of peptides and proteins. Vibrational transitions are sensitive to the peptide local structure and are ideal for distinguishing between various secondary structural motifs and monitoring the effects of changing environments through hydrogen bonding and dielectric effects. The 1,600–1,700 cm^-1 amid I band that originates from the stretching motion of the C = O peptide bond (coupled to in-phase N-H bending and C-H stretching) is particularly suitable for this purpose because it has a strong transition dipole moment and is spectrally well-separated from other vibrational modes. The up to 20 cm^-1 variation of the amid I frequency with secondary structure and conformation is widely used as a marker in polypeptide and protein structure determination.

Compared with the linear IR signals, 2DIR significantly enhances the spectral resolution by spreading the congested transitions of linear absorption in two dimensions. The cross peaks carry signatures of intermode couplings, and their spectral line shapes probe solvent and conformational fluctuations. However, for larger peptides and proteins 2DIR still suffers from an insufficient spectral resolution. The cross peaks are congested and overlap with the strong diagonal features. The number of independent structural unknowns is much larger than the number of independent measured quantities.

There are efforts to extend chiral-sensitive techniques into nonlinear regimes (45). Chirality-related techniques such as CI-2DIR show much richer features than their chirality-insensitive counterparts and greatly improve the spectral resolution. For extended systems such as Aβ, we estimate the chirality-related to the global (e.g., helical) arrangement of the residues to be the dominating effect and neglect the local chiral characteristics of the individual residues in the following argument: The nonchiral nonlinear response to three pulses depends on the orientationally averaged product of four dipoles 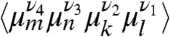whereas its CI component depends on products of the form 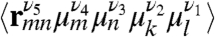. Here 〈⋯〉 denotes orientational averaging of molecules with respect to the lab frame. μ_m is the mth cartesian component (ν = x, y, z) of transition dipole of the mth chromophore, and 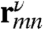is the distance between the mth and nth chromophores. Nonchiral techniques depend on the structure only implicitly through its effect on the frequencies and transition dipoles that affect peak positions and intensities. The explicit coordinate (r_mn) dependence of the chiral response amplifies the cross peaks, thus resulting in a higher sensitivity to fine details of the structure.

The indistinguishable distribution patterns of the ordinary (chirality-insensitive) order parameters imply that the normal nonchiral signals of the two conformer ensembles might be intrinsically indistinguishable regardless of the spectral resolution. On the other hand, there exist significant chirality-related differences between the conformer structures, demonstrated by the chirality factor discussed above. CI-2DIR spectroscopy shows a high discrimination power for the Aβ monomer system. We identified a well-resolved cross peak Φ associated with the dominating conformer A contribution. This feature can thus be used as a window for investigating the monomer conformational kinetics. This could reveal useful information about the seeding, oligomerization, and fibrilization processes. CI-2DIR has strong potential in investigating early Aβ misfolding events. A systematic characterization of the Aβ conformer moieties based on a statistical analysis of all interactions in the low-temperature ensemble will be an interesting topic for future research.

Methods

Replica-exchange MD simulations were performed using a variety of force fields and validated by NMR data as described in ref. 20. This study has shown that, at the limit of extensive sampling, the ensemble derived using the OPLS/AA force field (23) is consistent with the three-bond J_HNHα data. We have used the previously described MD trajectories to extract representative conformations of the “ordered” and “disordered” populations, identified using the clustering algorithms described in ref. 20 as well as to investigate the exchange time scale between the two species Fig. 1III. To perform this task, we have first ranked the transitions according to the time difference between their observation in the REMD trajectory segments. Events occurring during temperature exchanges larger than 30 K have been omitted from this analysis because they correspond to much lower probability transitions at physiological temperature. (The average temperature spacing between the eight replicas sampling at low T was 3.6 K.) In addition to the existing simulation dataset, we performed constant-temperature (NPT) simulations in explicit solvent to adequately sample fluctuations within the free energy basin of each representative conformation. The OPLS/AA force field (23) and TIP3P water model (24) were used in these calculations. To build these systems, we started from the protein coordinates extracted from the REMD simulations, which we solvated by adding 3,670 water molecules. The total number of solvent molecules was equal for both peptide conformations. The solvated systems were equilibrated at constant temperature (300 K) and pressure (1 atm) for 100 ps, using an integration time step of 1 fs. Finally, molecular dynamics simulations were performed starting from the equilibrated systems for 10 ns each. At this stage, the implementation of the LINCS (25) and SETTLE (26) algorithms to restrain high-frequency bond vibrations allowed the use of a larer integration timestep (2 fs). All simulations were performed using the GROMACS simulation package (28). The Nose–Hoover (27) method was used to couple the system to a heat bath, while the method by Berendsen was used to control pressure (29).

The simulation protocol of the 2DIR spectra is described in (42), the fluctuating exciton hamiltonian for these snapshots uses an electrostatic map (33, 42), which had been proved to be able to reproduce 2DIR signals for peptide amide I band quantitatively comparable to the experimental data (37, 42–44). The truncated NEE technique with the truncation coefficient η = 0.3 (42) was used to simulate the signal. All transitions have a Lorentzian line-shape with 4.5 cm^-1 (43) full-width at half maximum. ¹³C¹⁸O isotope labeling was simulated by 65 cm^-1 red-shift of the local model frequency (43).

The NMD was calculated by summing the squares of its expansion coefficients for all of the local modes belonging to a given structural motif. The components were then binned for all eigenmodes in the frequency window (± 5 cm^-1) to obtain the NMD figures.